1. Introduction

Analogous to the principle of tuning forks, optical microcavity could confine light to a certain volume to create resonant recirculation. The principle of optical microcavity is based on the light-matter interaction. Because of the total reflection, light is restricted in the optical microcavity that has a symmetrical configuration. The light in the microcavity couples with the light in the fiber. Under certain conditions, the intensity of light will be strengthened. Optical microcavity has its own resonant mode because of its special configuration. When molecules adhere to the surface of a microcavity, the change in system configuration leads to the change of the resonant mode. Generally speaking, these changes in the form of frequencies are easy to observe. The ideal condition is that the resonator can be indefinite or lossless, so the resonant frequencies are precise. The quality of optical microcavity is measured by Q factor [1–3]. Q factor and the microcavity volume are the main parameters of optical microcavity [4–6]. According to the confinement style, optical microcavities could be divided into three categories: Fabry–Perot microcavity [7–10], photonic crystal microcavity [11], and whispering gallery mode (WGM) microcavity [12–14]. Fabry–Perot microcavities [7, 8] have two mirrors to feedback light. The emitter of micropost (quantum dot for example) triggers single photon emission via the Purcell effect. The high Q and small volume could reach Q = 2000 and V = 5 (λ/n)³, where n is the refraction index. Instead of the center of mass motion, the ultracold atom in a strong couple system interacted with the vacuum cavity mode has a ultrahigh Q: F = 4.8 × 10⁵ (F is opposed to Q) with V = 1.69 × 10³μm³ [9, 10]. Photonic crystal microcavities [11] have a hole drilled in the middle of the structure, and a neutral atom located in the hole forms the donor mode geometries with Q = 1.3 × 10⁴. High Q WGM microcavities include microdiscs [15–18] with Q = 12000 and add/drop filters (semiconductor or polymer) [19, 20] with Q = 7000 or Q = 1.3 × 10⁵ respectively. Silica or quartz microsphere [21] and microdisk type [5, 22] WGMs are ultrahigh Q microcavities with Q = 8 × 10⁹ and Q = 10⁸. Lights are reflected continuously in spherical and toroidal structures. Because of the high sensitivities and practicabilities of nanoparticle detection, we focus on microsphere WGMs.

WGM optical microcavity is a highly potential technology in forensic science. It has many advantages. First, the price is much cheaper than other traditional instruments such as a gas chromatograph spectrometer. Second, some detection technologies search certain ligand rather than the whole molecule [23, 24]. This will cause the high error detection rate. Optical microcavity detects the molecule, so this technology has more accuracy [25, 26]. Third, traditional instruments detect either liquid phase or gas phase (only one phase), and the samplings are all liquid phases (gas phase needs to heat the liquid sampling). This is a limitation. The sample injection of optical microcavity can be liquid phase or gas phase which means there is no need to prepare the gas sample into solution. The gas sample can be detected by injecting the gas directly into microcavity [27]. Fourth, as long as there is a molecule attached to the microcavity, the response to the change in frequencies is obvious [28, 29]. Optical microcavity has ultrahigh sensitivity which could reach nanoscale [30, 31]. Fifth, it is easy to operate and really takes a short time to get the result. When the sample is injected into or onto optical microcavity (depends on the configuration of microcavity), the results will be immediate and obvious. This is a dynamic real-time processing. All of these advantages show the necessity and potential of this technology application in forensic science. In this paper, we show the viability of this detection technology in forensic science, so we use the WGM silica microsphere cavity to detect RDX as an example.

This paper is organized as follows: In Section II, we introduce the method and apparatus used in our experiment. In section III, we give the results of detection of solutions of different concentrations and compare them with the results of solution with no determinant. Finally, in section IV, the main results are concluded and further work is discussed.

2. Method and Apparatus

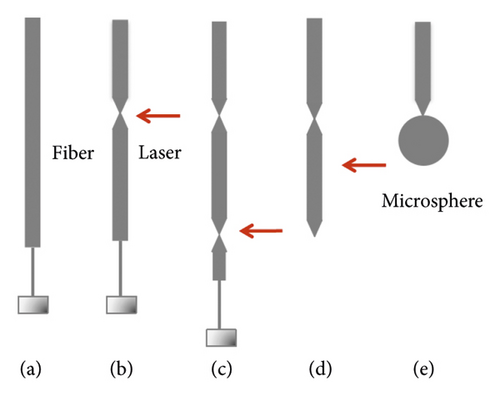
In the first step, we fabricate the microsphere cavities with diameter 64 μm using CO₂ laser device of SYNRAD 48-2KAM-AP (see Figure 1). First of all, we get rid of the protective layer of the optical fiber (taper fiber), clean it with alcohol, and weight an object at the end of the fiber vertically. Lately, the fiber has been heated by a low-power CO₂ laser. The heat melts the fiber but it doesn’t break it. Next, we cut off the weight at the appropriate position of the fiber using a high-power CO₂ laser. After that, the rest of the fiber is heated to reflux. Finally, we get a microsphere cavity.

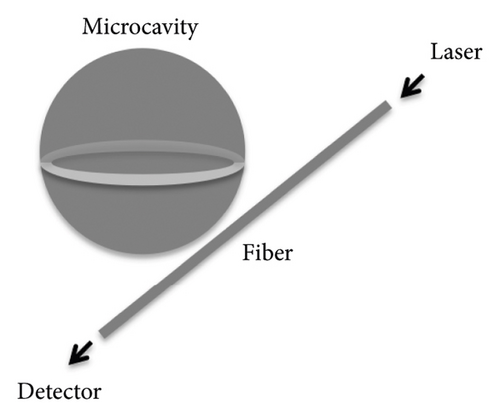
In the second step, we dip the microsphere cavities into a diluted solution or drip the solution drop onto the microsphere cavities. The laser propagates along the optical fiber and interacts with the molecules suspended in the solution (see Figure 2). The molecules suspended in the solution change the vibration mode of the microsphere cavity. These changes affect the responses on the oscilloscopes. The laser device is the New Focus Tunable Laser Controller TLB-6700. The wave range from 1540 nm to 1550 nm. The power of the laser we used is 2 mW. The signal generator used in the experiment is Tektronix AFG3022C and the oscilloscope is Tektronix MDO3104. We use a triangular wave with frequency 50 Hz and amplitude 2V(−1V ~ 1V). The standard solution is made of the explosive of Cyclotrimethylenetrinitramine (RDX) in acetone of concentration of 1000 ppm, and it is diluted by alcoholic.

3. The Results and Analysis of Diluted Standard Solution of Different Concentration

The microsphere cavities of whispering gallery mode (WGM) could be used to detect very few molecules and small microparticles. On the contrary, too many molecules and small microparticles would reduce the Q factor and thus make the results unreasonable. According to this, we dilute the standard solution into three concentrations. The ratios of the standard solution and the alcoholic solution are 1 : 1, 1 : 2, and 1 : 3. And we compare the 1 : 2 result with acetone solution which is diluted by equivalent alcohol. All experiments with different concentrations are repeated three times, and the results are similar. According to the standard deviations, we chose the figures of the best results here to demonstrate.

3.1. The Result of Ratio 1 : 1 (Standard Solution: Alcoholic Solution)

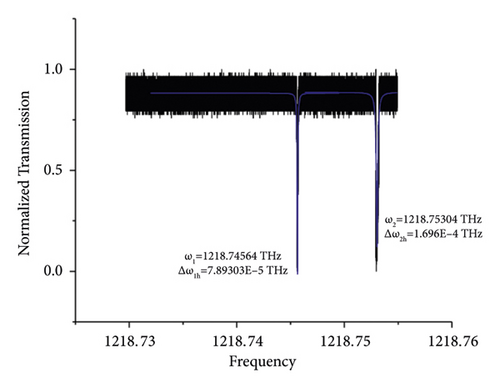
We dip the microsphere cavities in the diluted solution of ratio 1 : 1. The vibration mode of the microsphere cavity is changed because of the existence of the molecules suspended in the solution (see Figures 3 and 4). Figure 3 shows the original mode of the microsphere cavity. In this case, the central frequencies of two modes are ω₁ = 1218.74564 THz and ω₂ = 1218.75304 THz. The widths of them are Δω_1h = 7.89303 × 10⁻⁵ THz and Δω_2h = 1.69600 × 10⁻⁴ THz. The vertical coordinate is the normalized transmission spectrum. In Figure 4, after we dip the microsphere cavities into diluted solution, both of the two original modes move towards left and split into two parts. The first frequency ω₁ turns to ω₁₁ = 1218.73921 THz and ω₁₂ = 1218.73952 THz. The widths are Δω_11h = 1.77393 × 10⁻⁴ THz and Δω_12h = 1.50420 × 10⁻⁴ THz, respectively. The second frequency ω₂ becomes ω₂₁ = 1218.74438 THz and ω₂₂ = 1218.74473 THz. The widths of them are Δω_21h = 6.41991 × 10⁻⁵ THz and Δω_22h = 6.20527 × 10⁻⁵ THz. The split frequency of the first mode is ω₁₂ − ω₁₁ = 0.31 GHz, and that of the second mode is ω₂₂ − ω₂₁ = 0.35 GHz. The RDX molecules suspended in the solution adhere to the microsphere cavity cause the split. The losses in the experiment are divided into intrinsic losses and coupling losses. We summarize the result in the Table 1.

Table 1. The result of ratio 1 : 1 (standard solution: alcoholic solution).

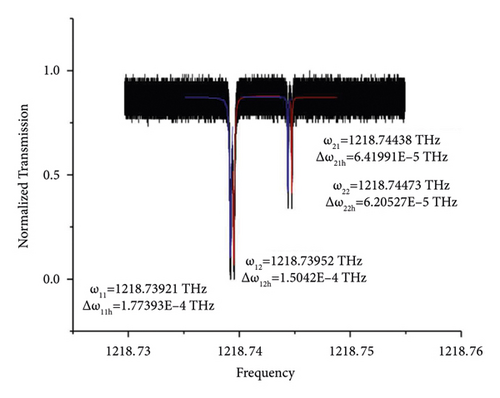
Original mode	ω1 = 1218.74564 THz
Original mode	ω2 = 1218.75304 THz
Widths	Δω1h = 7.89303 × 10−5 THz
Widths	Δω2h = 1.69600 × 10−4 THz
RDX mode	ω11 = 1218.73921 THz, ω12 = 1218.73952 THz
RDX mode	ω21 = 1218.74438 THz, ω22 = 1218.74473 THz
Widths	Δω11h = 1.77393 × 10−4 THz, Δω12h = 1.50420 × 10−4 THz
Widths	Δω21h = 6.41991 × 10−5 THz, Δω22h = 6.20527 × 10−5 THz
Split frequency	ω12 − ω11 = 0.31 GHz
Split frequency	ω22 − ω21 = 0.35 GHz

3.2. The Result of Ratio 1 : 2 (Standard Solution: Alcoholic Solution)

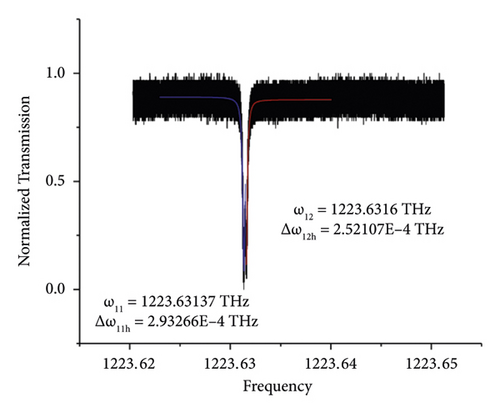
As per the procedure we mentioned above, we dilute the standard solution with alcohol of the ratio 1 : 2 this time. The frequency of the original mode is ω₁ = 1223.64186 THz. Its width is Δω_1h = 5.79740 × 10⁻⁵ THz. The target molecules in the diluted solution result in the left move and the split of the original mode. Two frequencies of new modes are ω₁₁ = 1223.63137 THz and ω₁₂ = 1223.63160 THz. Their widths are Δω_11h = 2.93266 × 10⁻⁴ THz and Δω_12h = 2.52107 × 10⁻⁴ THz. The split frequency becomes ω₁₂ − ω₁₁ = 0.23GHz (see Figures 5 and 6). The result is summarized in Table 2.

Table 2. The result of ratio 1 : 2 (standard solution: alcoholic solution).

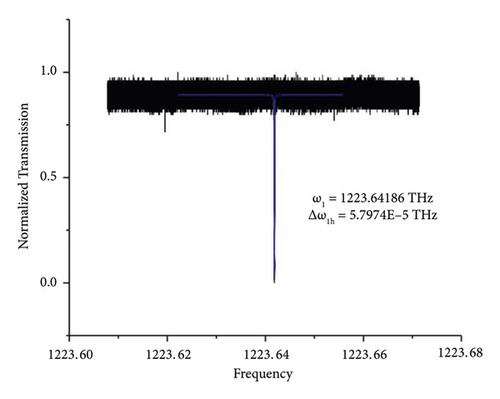
Original mode	ω1 = 1223.64186 THz
Widths	Δω1h = 5.79740 × 10−5 THz
RDX mode	ω11 = 1223.63137 THz, ω12 = 1223.63160 THz
Widths	Δω11h = 2.93266 × 10−4 THz, Δω12h = 2.52107 × 10−4 THz
Split frequency	ω12 − ω11 = 0.23 GHz

3.3. The Result of Ratio 1 : 3 (Standard Solution: Alcoholic Solution)

We continue diluting the standard solution with alcohol in the ratio 1 : 3. In the beginning, the frequency of the vibration mode of the cavity is ω₁ = 1223.13682 THz with width Δω_1h = 5.71579 × 10⁻⁵ THz. The target molecules are adsorbed to the external surface of the cavity which gives us two smaller frequencies of new modes ω₁₁ = 1223.13536 THz and ω₁₂ = 1223.13556 THz. Their widths are Δω_11h = 2.79271 × 10⁻⁴ THz and Δω_12h = 3.09351 × 10⁻⁴ THz. The split frequency turns to be ω₁₂ − ω₁₁ = 0.20 GHz (see Figures 7 and 8). From the results above, we can conclude, the lower the concentration is the smaller the split frequency becomes (see Table 3).

Table 3. The result of ratio 1 : 3 (standard solution: alcoholic solution).

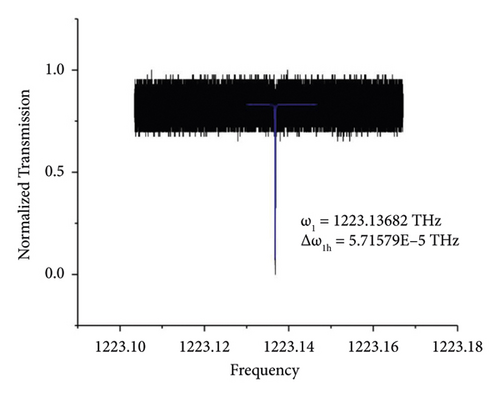
Original mode	ω1 = 1223.13682 THz
Widths	Δω1h = 5.71579 × 10−5 THz
RDX mode	ω11 = 1223.13536 THz, ω12 = 1223.13556 THz
Widths	Δω11h = 2.79271 × 10−4 THz, Δω12h = 3.09351 × 10−4 THz
Split frequency	ω12 − ω11 = 0.20 GHz

3.4. The Result of the Solution with No Determinant (Acetone Solution: Alcoholic Solution = 1 : 2)

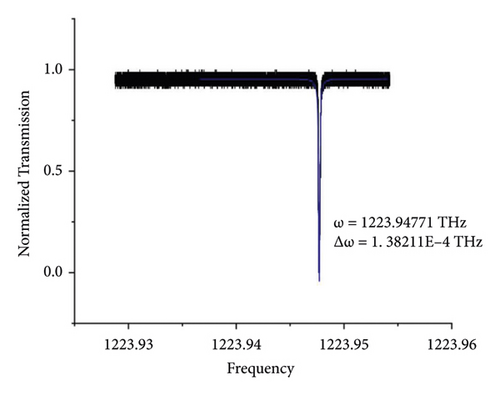
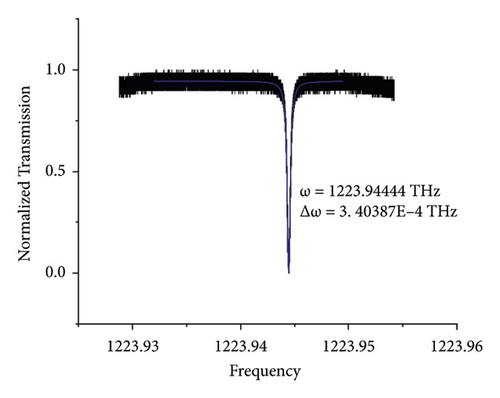
In the end, we discuss the solution of pure acetone with no RDX molecules and compare it with the result above. Because of the absence of target molecules, the mode of microcavity does not split. The peak of the mode frequency only moves from ω = 1223.94771 THz to another position 1223.94444 THz with the broadening of the width from Δω = 1.38211 × 10⁻⁴ THz to 3.40387 × 10⁻⁴ THz. The change of the frequency reads 3.27 GHz (see Figures 9 and 10). Whether there exist RDX molecules in the solution or not, the peaks of the diluted solution change to smaller values. Because the solution with no RDX molecules changes the mode volume (the mode distribution) of the microcavity. When the RDX molecules adhere to the microcavity, besides the shift of the frequency peaks, the peaks split and broaden simultaneously.

4. Conclusion and Discussion

The optical microcavity, which is widely used in medical science [32], biology [33], and environmental science [34], is a new kind of sensor with ultrahigh sensitivity [35–37]. For example the applications include diagnosis of diseases, detection of protein of blood, the pollution of environment and so on [38–40]. We want to research the usage of optical microcavity sensor in public security field because the appearance of more and more terrorist attacks. Optical microcavity has its advantage of ultrahigh sensitivity which could reach nanoscale [30, 31]. Not only the explosive itself but also things and people that used to touch the explosive can be found using optical microcavity sensor. For example, we wipe someone’s hands or clothes or something using filter papers, and then prepare the liquid or gas sample detecting in the optical microcavity sensor. The result will tell us whether someone or something touched explosive before. Because even only one nanoparticle of explosive adhere to the microcavity, it could cause the split and movement of the mode frequency peak.

In this paper, we use silica or quartz microsphere type whispering gallery mode (WGM) microcavity to show the effect of the detection of typical explosive RDX. After dipping the microsphere cavities into diluted solution, RDX molecules suspended in the solution adsorb onto the microsphere cavities and change the original vibration mode. We give three kinds of concentration as examples. The ratio of the standard solution and the alcoholic solution are 1 : 1, 1 : 2, 1 : 3. As shown in figures above, RDX molecules low, split and broaden the frequency peak obviously. When there is no RDX molecule in the standard solution which means pure acetone, the frequency peak only moves to a lower value and no split appears. The effective refraction index of the microcavity increases due to the solution, the frequency of original vibration mode shift to a lower value. According to the symmetry of the microcavity, waves in the microcavity are divided into clockwise mode and counterclockwise mode. When the molecules enter the microcavity, due to scattering, the modes of the two waves become coupled, and the frequency peak is broadened. The degeneracy due to the coupling causes the split of the frequency. The scale of the frequency split is GHz. The available concentration of diluted solution can be extremely low. The research of the detect limitations of different molecules is still processing. The noise is unavoidable in experiment. The main noises in microcavity experiment are laser wavelength drift noise, vibration of the fiber taper, quantum shot noise and the thermo refractive noise. There are several solutions to reduce the experimental noises, one can lock the vibration mode and tighten the fiber to conquer the first two noises. To reduce the quantum shot noise and thermo refractive noise, reduction of light intensity and derivation of the microcavity heat using optimization of material or configuration that has good thermal property are suggested [41]. Besides, these noises can be suppressed using the method called back-scattered light [42]. Contamination and impurity is the pretreatment of detection. The purification and extraction of chemicals is another topic. We focus on the detection process. Here, we studied RDX only one explosive to show the viability of microcavity technique and the procedure detail. We focus on the viability of technique itself in forensic science (explosive RDX as an example). It is worth noting that in this work, we only analyze the feasibility of this method, so the number of experiments is relatively small. For the later study of particle properties, a large number of experiments are needed, and the experimental data should be statistically significant. We can use this method to identify explosives. On the basis of the viability, the comparisons of different explosives and different configurations of microcavities are further works in the future.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Authors’ Contributions

Yao Shen is responsible for conceptualization, methodology, writing of the original draft, and validation. Kai Wang was responsible for experimental operation. Bai-En Guo was responsible for writing, illustration, and editing. Min Wang was responsible for validation and supervision. All authors have read and agreed to the published version of the manuscript.