International Journal of Antennas and Propagation

Volume 2024, Issue 1 9928507

Research Article

Open Access

An Improved Adaptive Frequency Sweep Strategies Based on Asymptotic Waveform Evaluation Technique for Broadband Antenna Simulation

Zhijun Cai,

Zhijun Cai

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Lingzhi Ren,

Lingzhi Ren

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Shuangbing Liu,

Shuangbing Liu

orcid.org/0000-0002-7419-005X

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Gen Wang,

Gen Wang

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Peng Gao,

Peng Gao

China Longyuan Power Group , Anhui Longyuan New Energy Co. Ltd , Hefei , 238000 , China

Search for more papers by this author

Tianyuan Zhang,

Tianyuan Zhang

China Longyuan Power Group , Anhui Longyuan New Energy Co. Ltd , Hefei , 238000 , China

Search for more papers by this author

Yuanjie Fang,

Yuanjie Fang

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Haili Zhang,

Corresponding Author

Haili Zhang

[email protected]

orcid.org/0000-0003-2693-2052

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Zhijun Cai,

Zhijun Cai

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Lingzhi Ren,

Lingzhi Ren

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Shuangbing Liu,

Shuangbing Liu

orcid.org/0000-0002-7419-005X

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Gen Wang,

Gen Wang

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Peng Gao,

Peng Gao

China Longyuan Power Group , Anhui Longyuan New Energy Co. Ltd , Hefei , 238000 , China

Search for more papers by this author

Tianyuan Zhang,

Tianyuan Zhang

China Longyuan Power Group , Anhui Longyuan New Energy Co. Ltd , Hefei , 238000 , China

Search for more papers by this author

Yuanjie Fang,

Yuanjie Fang

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

Haili Zhang,

Corresponding Author

Haili Zhang

[email protected]

orcid.org/0000-0003-2693-2052

School of Electronic Engineering , Chaohu University , Hefei , 238024 , China , chu.edu.cn

Search for more papers by this author

First published: 08 November 2024

https://doi.org/10.1155/2024/9928507

Academic Editor: Venkata Kishore Kothapudi

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, we propose an improved adaptive frequency sweep strategy based on the asymptotic waveform evaluation (AWE) technique for simulating broadband antennas across a wide frequency range. Our approach maintains high accuracy compared to traditional frequency sweep methods, as demonstrated through simulation results of several commonly used broadband antennas. A novel error function is introduced specifically designed for broadband antenna simulation, which effectively improves the adaptive frequency sweep process. By analyzing the relationship between target error and computational time, we determine the optimal balance zone between efficiency and accuracy. Our findings provide valuable insights for efficient and accurate simulation of broadband antennas.

1. Introduction

Broadband antennas play a critical role in the field of communications, as they enable support for multiple frequency bands, high data transfer rates, and enhanced reliability for wireless communication systems [1]. Broadband antenna simulation is crucial for optimizing antenna performance, providing accurate predictions and guidance for effective signal transmission and reception, and making it an essential tool for achieving optimal performance and reliable communication systems [2].

The finite element method (FEM) is a widely adopted and accurate technique for antenna simulation [3]. However, accurately conducting frequency sweeps over a wide range poses a challenge in simulating broadband devices [4]. Traditionally, this challenge involves solving the frequency-dependent FEM system at each sampling point, resulting in computational expenses and practical limitations due to the high dimension of FEM matrices [5].

Model order reduction (MOR) [6] is a widely adopted technique for efficiently solving parameter-dependent linear systems of equations to reduce computational and memory costs [7]. These parameters typically involve frequency [8], material properties [9], and observation angles [10]. The MOR can be used to fast solve the optimization of array located on the PEC carrier inside the dielectric radome with parameters’ variation [11]. The article presents a new, efficient model-order reduction technique for microwave simulations, using a projection basis from FEM poles and zeros, with enhanced parallelism and accuracy compared to the reduced-basis method [12]. A streamlined self-adjoint sensitivity analysis for microwave components is presented using MOR, enhancing speed and accuracy in a wide frequency range [13]. One commonly employed MOR method for electromagnetic (EM) scattering [14], radiation [15], and waveguide [16] is the asymptotic waveform evaluation (AWE) method.

In the AWE method, the unknown vector is expanded into Taylor or Padé series, and the system is then approximated with a lower order approximation by moment matching [17]. A series of rational function interpolation/extrapolation algorithms have been developed for scattering parameter curves. Effective frequency sweep algorithms can be established by introducing Padé approximation [18] and Cauchy method [19–21]. In order to avoid derivative calculations at interpolation nodes, vector fitting methods [22], and Neville-type Stoer–Bulirsch methods [23] have been proposed for broadband microwave-circuit frequency sweep computations. Building upon Newmann’s impedance matrix fitting function [24], Yeo and Mittra [25] have developed a broadband frequency sweep algorithm for microstrip patch antennas to improve computational accuracy through segmented interpolation.

The range of validity of FEM-AWE decreases when the size of the problem increases, and this problem cannot be overcome simply by increasing the order of the Taylor or Padé approximation [26]. Multipoint (MP) must be used for FEM-AWE and ensure the accuracy of the antenna simulation over a width band [27]. The experimental results indicate that the accuracy and efficiency of MP algorithms are influenced by error indicators and adaptive strategies [28]. Furthermore, bisection is shown to be equally efficient as the greedy method, and both approaches demonstrate exponential convergence. An adaptive interpolation scheme divides sampling points into groups to mitigate Runge’s phenomenon and error fluctuations, applying varied strategies for accurate wideband response calculation in EM simulations [29]. In this paper, we propose a novel approach to improve the efficiency of the AWE and MP methods by investigating the target error and error-calculation function. A more effective solution is provided for addressing the challenges posed by complex systems. This strategy holds significant promise for enhancing the efficiency and accuracy of broadband antenna simulation methods crucial in modern telecommunications and radar systems. By addressing the limitations of existing methods, our approach not only aims to improve simulation outcomes but also opens doors to broader applications in antenna design optimization and EM compatibility testing.

In this paper, the formulation of the AWE based on Taylor and Padé expansion is elaborated in Section 2.1 and Section 2.2. The comprehensive flow of the adaptive frequency sweeping method is detailed in Section 2.3. We conduct extensive experimentation using several commonly employed broadband antennas to validate the accuracy of the AWE-FEM. The details are elaborated upon in Section 3.1, Section 3.2, and Section 3.4. In addition, in Section 3.4, we propose and validate several techniques aimed at enhancing the effectiveness of the adaptive frequency sweeping method. Finally, in Section 4, we provide a concise summary and conclusion of our research.

2. Methods

The FEM involves transforming the EM problem into a mathematical equation in order to obtain the desired solution. In the case of broadband antenna simulation, the system of linear equation can be represented as follows:

(1)

where k represents the wave number corresponding to the sweeping frequency, A(k) is a square sparse finite element matrix, x(k) is an unknown quantity, and y(k) is a known quantity. It is obvious that A(k), x(k), and y(k) are functions of k.

2.1. Formulation of AWE-Taylor Method

To approximate the unknown quantity around a specific parameter value, a truncated Taylor expansion of x(k) around some parameter value k₀ can be written as

(2)

where N denotes the order of the Taylor expansion. The unknown coefficient m_i can be calculated using the following expressions:

(3)

(4)

where A⁽ⁱ⁾(k₀) represents the i-order derivative of A(k₀) and y⁽ⁿ⁾(k) is the n-order derivative of y(k).

2.2. Formulation of AWE-Padé Method

To extend the approximation beyond the limited radius of convergence offered by the Taylor series, researchers often employ the Padé approximation method [30] for broadband simulation, which represents the function as a rational function:

(5)

where L and M are the order of Padé approximation, and L ≥ M. In the numerical examples presented in this paper, we set L = M. This choice is consistent across all simulations and is aimed at providing a fair comparison between different situations. Coefficients a_i and b_j of Padé approximation can be computed using the following equations [31]:

(6)

(7)

By substituting coefficients a_i and b_j into equation (5), the unknown vector x(k) can be solved across a frequency band, and then calculate the S-parameter response of the broadband antenna.

Expand approximate functions using the Taylor series. Taylor series is an approximation at a certain point, which contains information about the derivative of a function at that point. The AWE-Taylor method usually performs well in areas where the function changes smoothly. Padé approximation is a rational function approximation that combines the polynomial part of Taylor series and its reciprocal polynomial to improve behavior approaching singularities. The AWE-Padé method is usually more stable when dealing with high-frequency oscillation problems [32].

2.3. Adaptive Frequency Sweep Methodology

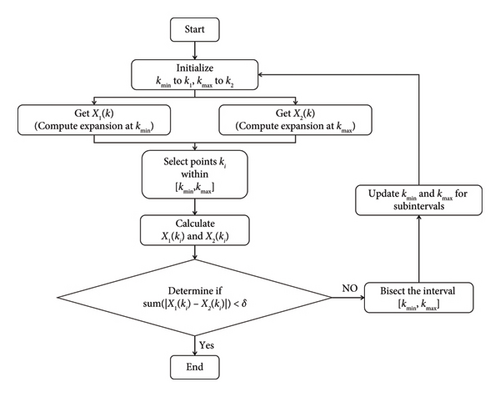
Through the AWE, a solution can be obtained, but this solution only maintains good accuracy in the vicinity of the expansion frequency point. If the frequency is far from this expansion point, the accuracy of the solution cannot be guaranteed in general. In practical broadband antenna simulations, a MP expansion strategy [15] is generally necessary.

To achieve reasonable accuracy for the entire frequency interval [k₁, k₂] with a target accuracy of δ, the following iterative approach can be employed:

(1)
Initialization:
Let k_min = k₁ and k_max = k₂ represent the minimum and maximum frequencies, respectively.
(2)
Expansions:
Perform expansions around k_min and k_max to obtain approximations of X(k). Denote the approximation obtained from the expansion around k_min as X₁(k), and the one from the expansion around k_max as X₂(k).
(3)
Point Selection and Computation:
Choose one or several points, k_i, within the frequency interval. Compute the corresponding values of X₁(k_i) and X₂(k_i) using the respective expansions.
(4)
Accuracy Check:
Calculate the sum of the absolute differences between X₁(k_i) and X₂(k_i).
If the sum is less than δ, the iterations are considered complete, and the desired accuracy is achieved.
Otherwise, proceed to the next step.
(5)
Interval Bisection:
Bisect the original frequency interval [k₁, k₂] into two subintervals, namely, [k₁, (k₁ + k₂)/2] and [(k₁ + k₂)/2, k₂].
Repeat the entire process from step 2 independently for both subintervals.
(6)
Iterative Refinement:

Continue iterating by selecting new points and recalculating X₁(k_i) and X₂(k_i) until the sum of the absolute differences between X₁(k_i) and X₂(k_i) falls below δ for all chosen points in each subinterval.

This iterative approach ensures that the entire frequency interval [k₁, k₂] achieves a reasonable accuracy level within the target accuracy δ. It allows for refining the approximations through successive iterations, bisecting the interval when necessary, and evaluating the accuracy at selected points. The process continues until the desired accuracy is obtained. The flowchart of adaptive frequency sweep methodology–based AWE algorithm is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flowchart of the adaptive frequency sweep methodology.

3. Numerical Results

To validate the accuracy and precision of the algorithms, this paper provides three commonly used broadband antenna structures. All simulations were performed on a PC platform, utilizing an Intel(R) Core(TM) i7-8700 CPU operating at a clock speed of 3.2 GHz. The mesh size used in the simulation cases in this study was set to 0.1 times the wavelength of the highest frequency. During the frequency sweep process, the size of the mesh remains unchanged.

3.1. Vivaldi Antenna

The first numerical example is the Vivaldi antenna [33, 34]. The structure, current distribution, and radiation of the Vivaldi antenna at 5 GHz are shown in Figure 2. It is implemented on a thin dielectric substrate by printing a gradient slot pattern on the top of the substrate. A simple exponential function e^0.044x is used to form the gradient slot curve, with one end of the slot open and the other end featuring a circular slot. A 50 Ω microstrip feed line is set at the bottom of the substrate. The dielectric substrate of the antenna has the following parameters: width 110 mm, depth 80 mm, thickness 1.524 mm, and relative permittivity ε_r = 3.38. The width of the gradient slot is 0.5 mm, the width of the feed line is 3.2 mm, the length of the feed line is 40.25 mm, and the height of the feed line is 1.524 mm. This design aims to achieve broadband performance on a thin dielectric substrate by effectively radiating and receiving EM waves through the gradient slot pattern and circular slot structure.

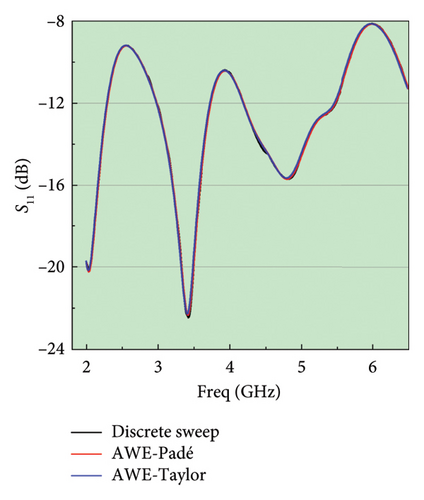
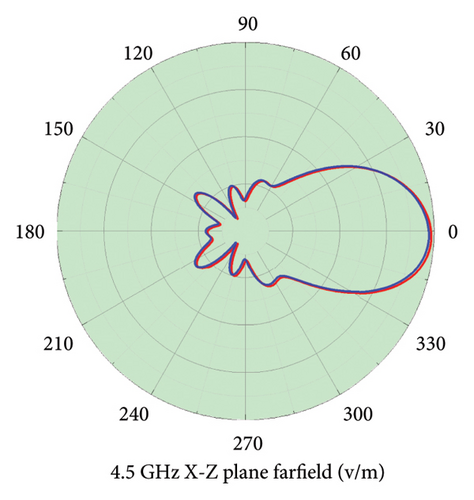
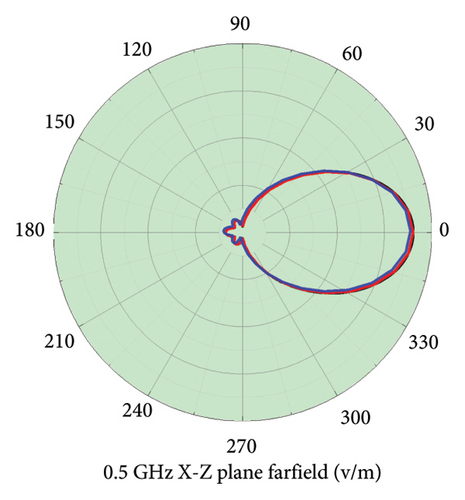
The simulation results of the S11 of the Vivaldi antenna and the radiation pattern in Figure 3 demonstrate the complete consistency between the discrete sweep frequency method, AWE-Padé algorithm, and AWE-Taylor algorithm. The consistency of the different algorithms has been robustly ensured across various directions and broad frequency ranges.

3.2. Spiral Slot Antenna

The spiral slot antenna exhibits circular polarization, frequency independence, and consistent impedance and radiation patterns across a wide frequency range [35, 36]. The spiral slot antenna consists of a dual-arm Archimedean spiral slot printed on a single-sided thin metal substrate using a parameterized curve. The excitation port is located at the center of the spiral slot for exciting the antenna. The selected dielectric substrate has the following parameters: radius 40 mm, height thickness 1.524 mm, and relative permittivity ε_r = 3.38. This design aims to implement a spiral slot antenna on a substrate by carefully constructing the Archimedean spiral slot. The parameters of the substrate and the configuration of the port are carefully chosen to maximize the performance of the antenna. We use a PEC to simulate the metal surface, which helps simplify the model and better understand the behavior of the antenna. Figure 4 illustrates the geometry, current distribution, and radiation characteristics of the spiral slot antenna operating at a frequency of 3.0 GHz.

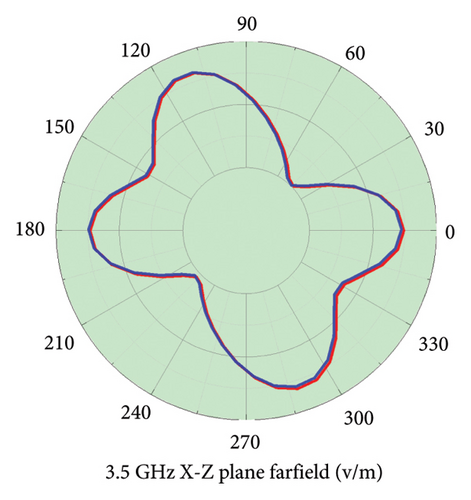
Figure 5 shows that the S11 and radiation pattern of the spiral slot antenna exhibit almost perfect agreement between the discrete sweep frequency method and the AWE method based on either Padé or Taylor expansion. The results further demonstrate that the AWE algorithm is applicable to broadband circularly polarized antennas as well.

3.3. Log-Periodic Antenna

The log-periodic [37, 38] antenna is implemented by mounting a coplanar dipole array on a pair of metallic frames. The excitation port is located at one end of the gap between the two frames and also on a pair of shortest rods. It is noteworthy that the lengths of the dipole rods decrease along the direction towards the excitation port at a constant ratio. A repeating pattern of the radiation structure can be constructed using parameterized geometric parts.

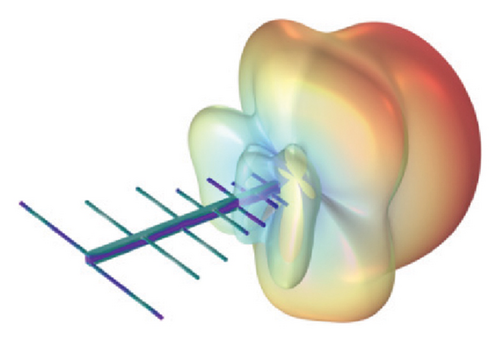
The specific parameters are as follows: the width of the metallic rods is 0.02 mm and the depth is 0.01 mm. The length of the longest rod in the dipole array is 0.2998 mm, the rod radius is 0.005 mm, the rod scaling factor ratio is 1.27, and the spacing between the first two elements is 0.15 mm. The gap size between the frames is 1 cm. Figure 6 depicts the geometric structure, current distribution, and radiation properties of the spiral slot antenna operating at a frequency of 0.75 GHz.

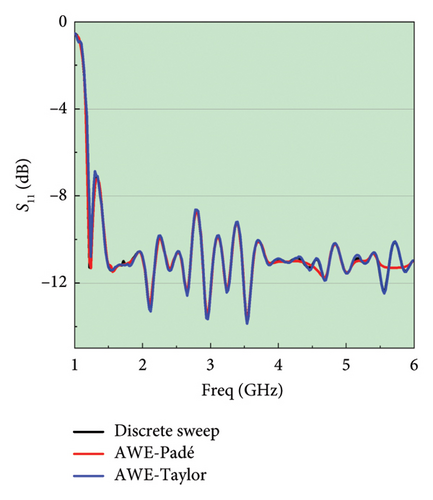
The simulation results depicted in Figure 7 provide evidence of the full equivalence between the discrete sweep frequency method and the fast sweeps method, as demonstrated by the matching S11 and radiation pattern of the log-periodic antenna. At approximately 0.7 GHz, some deviations were observed in the results obtained by the AWE-Padé and discrete sweep frequency algorithms. However, the AWE-Taylor algorithm consistently maintained a high level of accuracy. This observation suggests that, when subjected to the same relative tolerance, the Taylor expansion method achieves superior precision.

3.4. Comparison and Analysis

As depicted in Figure 8, we compared three different cases based on AWE-Padé to study the relationship between relative error and simulation time. When the relative tolerance is greater than 0.02, increasing the relative tolerance does not significantly reduce the simulation time. However, when the relative tolerance is set to less than 0.01, there is an exponential increase in simulation time, leading to a significant decrease in simulation efficiency. Based on the above analysis, setting the relative tolerance between 0.01 and 0.02 strikes a balance between simulation efficiency and accuracy.

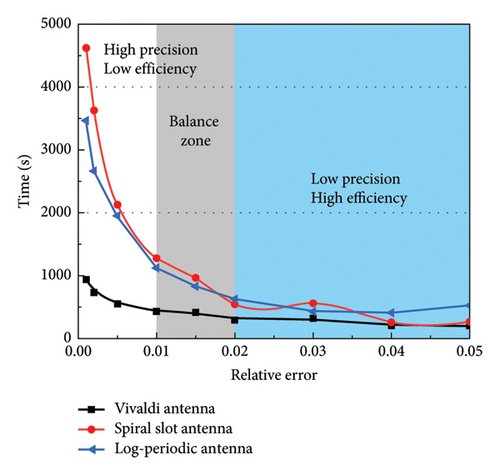
In the AWE-Padé method, the relationship between relative error and simulation time is determined by the precision requirements of the numerical solution process. When the relative tolerance is set relatively high (greater than 0.02), the simulation can be completed quickly with lower precision, as fewer iterations and less computational effort are required. However, when the relative tolerance is reduced to below 0.01, achieving higher precision necessitates more iterations and finer computations, which results in an exponential increase in computation time, thereby reducing simulation efficiency. Therefore, setting the relative tolerance between 0.01 and 0.02 allows for an optimal balance between simulation accuracy and computational cost, avoiding unnecessary computational overhead while ensuring result accuracy [39].

The AWE frequency sweeping algorithm, although effective in accurately depicting field behavior near resonant points and addressing high-Q value issues, has certain limitations [39]. For instance, it typically performs adaptive mesh refinement based on the center frequency of the frequency band, which may result in reduced accuracy at the band edges compared to the center. In addition, when the relative tolerance is set too low, computation time increases exponentially, impacting efficiency. Moreover, the AWE algorithm does not refine the mesh during the solution process which may restrict its application complex or highly variable EM field problems.

The S₁₁ is related to the reflection of energy by an antenna, while the quantity is related to the radiation capability of the antenna. From a physical perspective, both functions can reflect the performance of the antenna. When comparing their numerical result, it can be concluded that the error function outperforms |S₁₁| in Figure 9 and Table 1.

Table 1. Efficiency comparison of different conditions.

		FEM	AWE-Taylor	AWE-Padé	AWE-Taylor	AWE-Padé
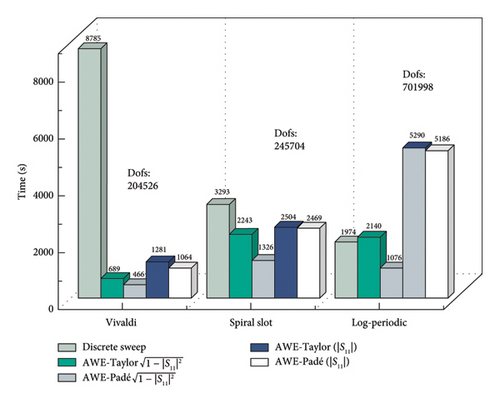
	Dofs	The time required for the simulations
					\|S₁₁\|
Vivaldi antenna	204526	8785	689	466	1281	1064
Spiral slot antenna	245704	3293	2243	1326	2504	2469
Log-periodic antenna	701998	1974	2140	1076	5290	5186

4. Conclusions

Based on the actual simulation results presented in this paper, several measures can be taken to improve the AWE algorithm–based broadband antenna simulation. Firstly, a relative tolerance setting between 0.01 and 0.02 is an efficient and balanced range for broad antenna simulations. Secondly, Padé expansion can be faster than Taylor expansion in broadband antenna simulations. However, for some null points, Taylor expansion may provide higher accuracy than Padé expansion. Finally, the error function is better than |S₁₁|, especially in terms of efficiency. In conclusion, our study demonstrates the effectiveness of the proposed adaptive frequency sweep strategy in enhancing the accuracy and efficiency of the broadband antenna simulation. This advancement is poised to benefit various real-world applications such as satellite communications, 5G technology development, and radar systems. Furthermore, by improving simulation fidelity and reducing computational overhead, our approach lays a foundation for future advancements in broad band antenna design optimization and EM compatibility testing. As we look ahead, further research could explore integrating this strategy into commercial simulation software packages, thereby facilitating its widespread adoption and impact across industries.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) under Grant 62303076, Chaohu University Key Scientific Research Projects under Grant XLZ-202206, the Anhui Provincial Colleges Science Foundation for Distinguished Young Scholars Grant 2022AH020093, Science Research Project of the Education Department of Anhui Province under Grant KJ2021A1024, Initial Scientific Research Fund of Young Teachers in Chaohu University Grant KYQD-2023066, and National Training Program of Innovation and Entrepreneurship for Undergraduates under Grant S202310380042 and 202410380021.

Acknowledgments

The authors thank Wiley’s English language service and MDPI’s English editing service for preparing this manuscript. The authors thank ChatGPT for assisting with the spelling and grammar checks throughout the drafting process of this paper.

Open Research

Data Availability Statement

The numerical and experimental data used to support the findings of this study are included within the article.

References

1 Goel T. and Patnaik A., Novel Broadband Antennas for Future Mobile Communications, IEEE Transactions on Antennas and Propagation. (2018) 66, no. 5, 2299–2308, https://doi.org/10.1109/tap.2018.2816660, 2-s2.0-85044021506.
10.1109/TAP.2018.2816660
Web of Science® Google Scholar
2 Chen Y. H., Coates R. T., and Chew W. C., FDTD Modeling and Analysis of a Broadband Antenna Suitable for Oil-Field Imaging While Drilling, IEEE Transactions on Geoscience and Remote Sensing. (2002) 40, no. 2, 434–442, https://doi.org/10.1109/36.992807, 2-s2.0-0036476994.
10.1109/36.992807
Google Scholar
3 Jin J. M., Lou Z., Li Y. J., Riley N. W., and Riley D. J., Finite Element Analysis of Complex Antennas and Arrays, IEEE Transactions on Antennas and Propagation. (2008) 56, no. 8, 2222–2240, https://doi.org/10.1109/tap.2008.926776, 2-s2.0-49749127071.
10.1109/TAP.2008.926776
Web of Science® Google Scholar
4 Zheng L. and Ming Jin J., Modeling and Simulation of Broad-Band Antennas Using the Time-Domain Finite Element Method, IEEE Transactions on Antennas and Propagation. (2005) 53, no. 12, 4099–4110, https://doi.org/10.1109/tap.2005.859905, 2-s2.0-29444439034.
10.1109/TAP.2005.859905
Google Scholar
5 Jin J. M., The Finite Element Method in Electromagnetics, 2015, John Wiley & Sons, New York.
Google Scholar
6 Sommer A., Farle O., and Dyczij-Edlinger R., A New Method for Accurate and Efficient Residual Computation in Adaptive Model-Order Reduction, IEEE Transactions on Magnetics. (2015) 51, no. 3, 1–4, https://doi.org/10.1109/tmag.2014.2352812, 2-s2.0-84928820084.
10.1109/TMAG.2014.2352812
Google Scholar
7 Xie X. and Liu Y. J., An Adaptive Model Order Reduction Method for Boundary Element-Based Multi-Frequency Acoustic Wave Problems, Computer Methods in Applied Mechanics and Engineering. (2021) 373, https://doi.org/10.1016/j.cma.2020.113532.
10.1016/j.cma.2020.113532
Google Scholar
8 Slone R. D., Lee R., and Lee J.-F., Broadband Model Order Reduction of Polynomial Matrix Equations Using Single-Point Well-Conditioned Asymptotic Waveform Evaluation: Derivations and Theory, International Journal for Numerical Methods in Engineering. (2003) 58, no. 15, 2325–2342, https://doi.org/10.1002/nme.855, 2-s2.0-0347565952.
10.1002/nme.855
Web of Science® Google Scholar
9 Chen Y., Hesthaven J. S., Maday Y., and Rodríguez J., Certified Reduced Basis Methods and Output Bounds for the Harmonic Maxwell’s Equations, SIAM Journal on Scientific Computing. (2010) 32, no. 2, 970–996, https://doi.org/10.1137/09075250x, 2-s2.0-77950893798.
10.1137/09075250X
Web of Science® Google Scholar
10 Hesthaven J. S., Stamm B., and Zhang S., Certified Reduced Basis Method for the Electric Field Integral Equation, SIAM Journal on Scientific Computing. (2012) 34, no. 3, A1777–A1799, https://doi.org/10.1137/110848268.
10.1137/110848268
Google Scholar
11 Cheng X. and Shao H., Fast Simulation of Antenna Array with Parameters Variation, 2024 IEEE International Conference on Computational Electromagnetics (ICCEM). (2024) 1–2, https://doi.org/10.1109/iccem60619.2024.10558966.
10.1109/iccem60619.2024.10558966
Google Scholar
12 Fotyga G., Szypulski D., Lamecki A. et al., An MOR Algorithm Based on the Immittance Zero and Pole Eigenvectors for Fast FEM Simulations of Two-Port Microwave Structures, IEEE Transactions on Microwave Theory and Techniques. (2022) 70, no. 6, 2979–2988, https://doi.org/10.1109/tmtt.2022.3166657.
10.1109/TMTT.2022.3166657
Google Scholar
13 Feng F., Xue J., Zhang J., Li M., Liu W., and Zhang Q.-J., Concise and Compatible MOR-Based Self-Adjoint EM Sensitivity Analysis for Fast Frequency Sweep, IEEE Transactions on Microwave Theory and Techniques. (2023) 71, no. 9, 3829–3840, https://doi.org/10.1109/tmtt.2023.3248167.
10.1109/TMTT.2023.3248167
Google Scholar
14 Peng Z. and Sheng X. Q., A Bandwidth Estimation Approach for the Asymptotic Waveform Evaluation Technique, IEEE Transactions on Antennas and Propagation. (2008) 56, no. 3, 913–917, https://doi.org/10.1109/tap.2008.917017, 2-s2.0-41649104131.
10.1109/TAP.2008.917017
Google Scholar
15 Slone R. D., Lee R., and Lee J. F., Multipoint Galerkin Asymptotic Waveform Evaluation for Model Order Reduction of Frequency Domain FEM Electromagnetic Radiation Problems, IEEE Transactions on Antennas and Propagation. (2001) 49, no. 10, 1504–1513, https://doi.org/10.1109/8.954940, 2-s2.0-0035471322.
10.1109/8.954940
Web of Science® Google Scholar
16 Baltes R., Schultschik A., Farle O., and Dyczij-Edlinger R., A Finite-Element-Based Fast Frequency Sweep Framework Including Excitation by Frequency-Dependent Waveguide Mode Patterns, IEEE Transactions on Microwave Theory and Techniques. (2017) 65, no. 7, 2249–2260, https://doi.org/10.1109/tmtt.2017.2679181, 2-s2.0-85016402577.
10.1109/TMTT.2017.2679181
Google Scholar
17 Reddy C. J., Deshpande M. D., Cockrell C. R., and Beck F. B., Fast RCS Computation over a Frequency Band Using Method of Moments in Conjunction With Asymptotic Waveform Evaluation Technique, IEEE Transactions on Antennas and Propagation. (1998) 46, no. 8, 1229–1233, https://doi.org/10.1109/8.718579, 2-s2.0-0032140028.
10.1109/8.718579
Web of Science® Google Scholar
18 Brezinski C., Padé-type Approximation and General Orthogonal Polynomials, Birkhèauser. (1980) 50, 126–177.
Google Scholar
19 Adve R. S., Sarkar T. K., Rao S. M., Miller E. K., and Pflug D. R., Application of the Cauchy Method for Extrapolating/Interpolating Narrowband System Responses, IEEE Transactions on Microwave Theory and Techniques. (1997) 45, no. 5, 837–845, https://doi.org/10.1109/22.575608, 2-s2.0-0031140446.
10.1109/22.575608
Google Scholar
20 Peik S. F., Mansour R. R., and Chow Y. L., Multidimensional Cauchy Method and Adaptive Sampling for an Accurate Microwave Circuit Modeling, IEEE Transactions on Microwave Theory and Techniques. (1998) 46, no. 12, 2364–2371, https://doi.org/10.1109/22.739224, 2-s2.0-0032304024.
10.1109/22.739224
Web of Science® Google Scholar
21 Timmins I. and Wu K. L., An Efficient Systematic Approach to Model Extraction for Passive Microwave Circuits, IEEE Transactions on Microwave Theory and Techniques. (2000) 48, no. 9, 1565–1573, https://doi.org/10.1109/22.869009, 2-s2.0-0034271133.
10.1109/22.869009
Web of Science® Google Scholar
22 Gustavsen B. and Semlyen A., Rational Approximation of Frequency Domain Responses by Vector Fitting, IEEE Transactions on Power Delivery. (1999) 14, no. 3, 1052–1061, https://doi.org/10.1109/61.772353, 2-s2.0-0032666467.
10.1109/61.772353
Web of Science® Google Scholar
23 Ding Y., Wu K. L., and Fang D. G., A Broad-Band Adaptive-Frequency- Sampling Approach for Microwave-Circuit EM Simulation Exploiting Stoer-Bulirsch Algorithm, IEEE Transactions on Microwave Theory and Techniques. (2003) 51, no. 3, 928–934, https://doi.org/10.1109/tmtt.2003.808694, 2-s2.0-0037360087.
10.1109/TMTT.2003.808694
Web of Science® Google Scholar
24 Newman E. H., Generation of Wide-Band Data From the Method of Moments by Interpolating the Impedance Matrix (EM Problems), IEEE Transactions on Antennas and Propagation. (1988) 36, no. 12, 1820–1824, https://doi.org/10.1109/8.14404, 2-s2.0-0024171880.
10.1109/8.14404
Web of Science® Google Scholar
25 Yeo J. and Mittra R., An Algorithm for Interpolating the Frequency Variations of Method-of-Moments Matrices Arising in the Analysis of Planar Microstrip Structures, IEEE Transactions on Microwave Theory and Techniques. (2003) 51, no. 3, 1018–1025, https://doi.org/10.1109/tmtt.2003.808703, 2-s2.0-0037361023.
10.1109/TMTT.2003.808703
Web of Science® Google Scholar
26 Zhang J. P. and Jin J. M., Preliminary Study of AWE Method for FEM Analysis of Scattering Problems, Microwave and Optical Technology Letters. (1998) 17, no. 1, 7–12, https://doi.org/10.1002/(sici)1098-2760(199801)17:1%3A7::aid-mop2%3E3.0.co;2-o.
10.1002/(SICI)1098-2760(199801)17:1<7::AID-MOP2>3.0.CO;2-O
Web of Science® Google Scholar
27 Sun D. K., Cendes Z., and Lee J. F., ALPS—A New Fast Frequencysweep Procedure for Microwave Devices, IEEE Transactions on Microwave Theory and Techniques. (2001) 49, no. 2, 398–402, https://doi.org/10.1109/22.903107, 2-s2.0-0035249887.
10.1109/22.903107
Web of Science® Google Scholar
28 Konkel Y., Farle O., Köhler A., Schultschik A., and Dyczij-Edlinger R., Adaptive Strategies for Fast Frequency Sweeps, COMPEL: The International Journal for Computation & Mathematics in Electrical & Electronic Engineering. (2011) 30, no. 6, 1855–1869, https://doi.org/10.1108/03321641111168156, 2-s2.0-83755185640.
10.1108/03321641111168156
Google Scholar
29 Zhu K., Wang J., and Yang S., An Adaptive Interpolation Scheme for Wideband Frequency Sweep in Electromagnetic Simulations, IEEE Antennas and Wireless Propagation Letters. (2022) 21, no. 3, 471–475, https://doi.org/10.1109/lawp.2021.3135958.
10.1109/LAWP.2021.3135958
Google Scholar
30 Honshuku Y. and Isakari H., BEM-Based Fast Frequency Sweep for Acoustic Scattering by Periodic Slab, Journal of Computational Physics. (2024) 509, https://doi.org/10.1016/j.jcp.2024.113046.
10.1016/j.jcp.2024.113046
Google Scholar
31 Feldmann P. and Freund R. W., Efficient Linear Circuit Analysis by Padé Approximation via the Lanczos Process, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. (1995) 14, no. 5, 639–649, https://doi.org/10.1109/43.384428, 2-s2.0-0029308198.
10.1109/43.384428
Web of Science® Google Scholar
32 Prajapati A. K. and Prasad R., Model Reduction Using the Balanced Truncation Method and the Padé Approximation Method, IETE Technical Review. (2022) 39, no. 2, 257–269, https://doi.org/10.1080/02564602.2020.1842257.
10.1080/02564602.2020.1842257
Google Scholar
33 Cicchetti R., Cicchetti V., Faraone A., Foged L., and Testa O., A Compact High-Gain Wideband Lens Vivaldi Antenna for Wireless Communications and Through-the-Wall Imaging, IEEE Transactions on Antennas and Propagation. (2021) 69, no. 6, 3177–3192, https://doi.org/10.1109/tap.2020.3037777.
10.1109/TAP.2020.3037777
Web of Science® Google Scholar
34 Shi X., Cao Y., Hu Y., Luo X., Yang H., and Ye L. H., A High-Gain Antipodal Vivaldi Antenna with Director and Metamaterial at 1–28 GHz, IEEE Antennas and Wireless Propagation Letters. (2021) 20, no. 12, 2432–2436, https://doi.org/10.1109/lawp.2021.3114061.
10.1109/LAWP.2021.3114061
Web of Science® Google Scholar
35 Li X., Wang J., Li Z. et al., Archimedean Spiral Slotted Leaky-Wave Antenna, IEEE Transactions on Antennas and Propagation. (2022) 70, no. 5, 3208–3222, https://doi.org/10.1109/tap.2021.3139945.
10.1109/TAP.2021.3139945
Google Scholar
36 De A., Roy B., Bhattacharya A., and Bhattacharjee A. K., Investigations on a Circular UWB Antenna With Archimedean Spiral Slot for WLAN/Wi-MAX and Satellite X-Band Filtering Feature, International Journal Of Microwave And Wireless Technologies. (2022) 14, no. 6, 781–789, https://doi.org/10.1017/s1759078721000891.
10.1017/S1759078721000891
Web of Science® Google Scholar
37 Chen Y., Wang S., Shi S. et al., Landstorfer Printed Log-Periodic Dipole Array Antenna With Enhanced Stable High Gain for 5G Communication, IEEE Transactions on Antennas and Propagation. (2021) 69, no. 12, 8407–8414, https://doi.org/10.1109/tap.2021.3090079.
10.1109/TAP.2021.3090079
Web of Science® Google Scholar
38 Mistry K. K., Lazaridis P. I., Zaharis Z. D., and Loh T. H., Design and Optimization of Compact Printed Log-Periodic Dipole Array Antennas With Extended Low-Frequency Response, Electronics. (2021) 10, no. 17, https://doi.org/10.3390/electronics10172044.
10.3390/electronics10172044
Google Scholar
39 Jiao D., Zhu X. Y., and Jin J., Fast and Accurate Frequency-Sweep Calculations Using Asymptotic Waveform Evaluation and the Combined-Field Integral Equation, Radio Science. (1999) 34, no. 5, 1055–1063, https://doi.org/10.1029/1999rs900068, 2-s2.0-0033310174.
10.1029/1999RS900068
Web of Science® Google Scholar

All articles

An Improved Adaptive Frequency Sweep Strategies Based on Asymptotic Waveform Evaluation Technique for Broadband Antenna Simulation

Abstract

1. Introduction