Parameter Identification of Photovoltaic Models by an Enhanced RIME Algorithm
Abstract
Accurate identification of photovoltaic (PV) model parameters is crucial for the study of factors affecting PV power generation efficiency. This study addresses this challenge by introducing the enhanced RIME algorithm (ERIME). ERIME achieves a fine balance between exploration and exploitation by combining a modified soft-rime search strategy and a shared information mutation mechanism, thus ensuring population diversity. To assess the efficacy of ERIME, the recognized CEC2022 test function suite is adopted to evaluate its search performance. Furthermore, to validate the versatility of ERIME in parameter identification of PV model, we tested the proposed method on several PV models, including single diode model (SDM), double diode model (DDM), triple diode model (TDM), and multiple PV module models (PVM). An in-depth statistical analysis of the results and a comparative study with the popular existing research methods highlight the superiority of ERIME. Specifically, ERIME improves the best value metrics of SDM, DDM, and TDM by 6.63E−06, 2.28E−05, and 1.36E−04, respectively, compared to RIME and reduces the standard deviation by 2.02E−03,1.75E−03, and 1.54E−03, respectively, compared to MVO. Comprehensive results show that the proposed method has better robustness and convergence accuracy than the state-of-the-art algorithm.
1. Introduction
With the increasing concern of global mankind for environmental protection and sustainable development, the development and utilization of renewable energy have gradually become the mainstream direction of global energy transition [1]. As an important renewable energy technology, solar power has been widely recognized and promoted in recent years because of its high environmental cleanliness [2]. Photovoltaic (PV) cells [3, 4, 5] convert solar energy into electricity with the help of light and get a constant supply of energy through the power generation controller [6], which makes PV power generation a long-term usable energy source for power supply.
To ensure the optimal functioning of PV cells, precise mathematical models are imperative for elucidating the intricate behaviors exhibited by these cells in distinct scenarios and for assessing the unknown parameters inherent in their models [7, 8]. Through the meticulous evaluation of acquired PV cell parameters, it becomes feasible to discern the power generation characteristics of the PV cell, along with the identification of potential faults and manifestations of aging [9].
Evaluation of parameters in PV cells is a nonlinear optimization problem [10]. A lot of work has been done by research scholars to be able to extract the parameters of PV cells efficiently. There are two main categories [11]: mathematical optimization methods and intelligent algorithms inspired by nature. Mathematical optimization methods usually require specific problems and scenarios to be effective. They may not be applicable to some PV parameter estimation problems or may not yield optimal solutions in some cases. For example, gradient-based mathematical optimization methods require the objective to be a convex function in order to obtain a globally optimal solution [12]. Nonconvex optimization problems usually need to be transformed into convex optimization form, which will undoubtedly result in a significant loss of solution accuracy [13]. Intelligent algorithms [14] do not require cumbersome problem-specific computation and reasoning, simplify the modeling process, and are well adapted to nonlinear problems. An improved elephant herding optimization algorithm (IEHOA) [15] was proposed to extract PV cell model, which employs a fast-moving operator and an elite strategy to effectively improve the convergence speed of the algorithm and shorten the optimization time of the algorithm. An improved lion swarm optimization (ILSO) [16] was employed to solve parameter identification of PV cells; the experimental results verify the superiority and effectiveness of the method. A diversification-enhanced Harris hawks optimization (DEHHO) [17] with chaotic drifts and an opposition-based exploratory strategy to be employed for identify unknown parameters of PV model modules; the experimental results show that the proposed method is capable of providing high-quality solutions. A multiple learning backtracking search algorithm (MLBSA) [18] is adopted, which effectively solves the parameter identification problem of different PV models by introducing different learning approaches and elite chaotic local search strategies. A new adaptive teaching–learning-based optimization with experience learning referred as adaptive TLBO algorithm (ELATLBO) [19] was developed to extract single diode models (SDM), dual diode models, and single diode PV modules. An efficient sine-cosine differential gradient-based optimization method (BSDGB) [20] is proposed for the identification of unknown parameters of PV models. A chaotic improved artificial bee colony (CIABC) [21] is proposed with tent chaotic map to identify solar cell models. Additionally, there are several other popular techniques proven to be accurate for PV parameter estimation, including improved tunicate swarm optimization (ITSA) [22], modified salp swarm optimization (MSSA) [23], improved Lozi map based chaotic optimization algorithm (ILCOA) [24, 25], whippy Harris hawks optimization (WHHO) [26], springy whale optimization algorithm (SWOA) [27], termed Modified RIME (TMRIME) [28], and variant of butterfly optimization algorithm (EABOA) [29]. The contributions of the above series of algorithms are listed in Table 1. As can be seen from Table 1, all the related researches have been conducted to extract the unknown parameters of the PV model by improving the original algorithm so as to enhance the efficiency of the light energy conversion [30, 31, 32, 33, 34, 35]. The above family of algorithms provides a tractable approach to the improvement of parameter identification performance of PV models. However, there still exists a varying degree of imbalance in the exploration and exploitation phases during the search process of these algorithms, as well as the possibility of falling into local minima. In addition, unreasonable parameter settings can affect convergence speed and robustness as the algorithmic search process proceeds [36].
| Reference | Proposed algorithm | Models | Contribution |
|---|---|---|---|
| [15] | IEHOA | SDM, DDM, and PV Module | Employ a fast-moving operator and an elite strategy |
| [16] | ILSO | SDM and DDM | Combine the tent chaotic map and chaotic search strategy |
| [17] | DEHHO | SDM, DDM, and PV Module |
|
| [18] | MLBSA | SDM, DDM, and PV Module |
|
| [19] | ELATLBO | SDM, DDM, and PV Module | Propose experience learning strategy |
| [20] | BSDGB | SDM, DDM, and TDM | Propose a strategy adaptive combination of three algorithms |
| [21] | CIABC | SDM and DDM | Improved artificial bee colony by chaotic maps |
| [22] | ITSA | SDM, DDM, and PV Module | Propose a two-stage improved search strategy |
| [23] | MSSA | SDM, DDM, and PV Module | Propose a new position update formula |
| [24, 25] | ILCOA | SDM, DDM, and PV Module | Updated the algorithm with Improved Lozi map strategy |
| [26] | WHHO | SDM, DDM, TDM, and PV Module | Introduce elimination period to HHO |
| [27] | SWOA | SDM, DDM, TDM, and PV Module | A novel WOA approach is proposed |
| [28] | TMRIME | SDM and DDM |
|
| [29] | EABOA | SDM, DDM, and PV Module |
|
The RIME algorithm is a newly proposed and more popular intelligent algorithm based on the physical laws of nature in recent years [37]. The RIME algorithm performs well in most optimization tasks by dynamically balancing exploration and small-scale exploitation, ensuring the breadth and depth of the search process. Its mechanism improves the accuracy and efficiency of the solution, effectively preventing performance degradation and maintaining high-quality solutions. Although the RIME algorithm has achieved promising results in some engineering fields [38, 39, 40], it has been found that RIME has fewer applications in the field of PV parameter identification and suffers from unbalanced exploration and exploitation and tendency to fall into local optimal points. In this study, an enhanced RIME algorithm (ERIME) is proposed to solve the PV parameter identification problem by combining the modified soft-rime search strategy and shared information mutation strategy, and the modified soft-rime search strategy can help to ensure the balance between exploration and exploitation and improve the solution accuracy; the shared information mutation strategy can help to increase the information exchange between population agents and guide the population to evolve in a favorable direction. To verify the effectiveness of the methods, four types of PV models are used for simulation experiments, while five methods are introduced as competitors for comparison. Through effective statistical analysis of the experimental results, the results verify that the proposed method can enhance more accurate results than the existing popular methods.
- (1)
An ERIME is proposed by combining the modified soft-rime search strategy and shared information mutation mechanism. The search performance and solution accuracy of the proposed method is verified by the state-of-the-art test function suite, and the statistical test results show the significance of the proposed method.
- (2)
A careful comparison of the proposed method with five existing state-of-the-art methods in SDM, DDM, TDM, and three PVM modeling products (Photowatt-PWP201, STM6-40/36, and STP6-120/36) is carried out to validate the effectiveness of the proposed method.
- (3)
The experimental results show that the proposed method is able to obtain the best results on all PV models with several statistical indicators, such as the optimal value, the mean value, and the worst value, which are obtained through several statistical experiments. In addition, a comparison of the simulated data obtained by the proposed method with the measured data shows that the proposed method is able to identify the parameters of the PV models with a high degree of accuracy.
The rest of the paper is organized. Section 2 establish the PV problem formulation; Section 3 gives the brief description of RIME algorithm; Section 4 presents the ERIME algorithm; Section 5 gives the numeral experimental results; Section 6 presents experimental results and discussions on PV problems, and conclusions are given in Section 7.
2. PV Problem Formulation
Accurate PV cell models are essential for studying the operation of PV systems. There are four main types of PV parameter identification models: SDM, double diode models (DDM), triple diode models (TDM), and PV module models (PVM). The model and its objective function are described below.
2.1. SDM
The SDM [41] consists mainly of a current source, a diode in parallel with the current source, a series resistor, and a shunt resistor, as shown in Figure 1. The current source depends on its material properties and external environmental factors; the series resistor helps to equalize the current and improve the thermal stability of the PV cell; and the shunt resistor characterizes the shunt leakage current in the semiconductor.
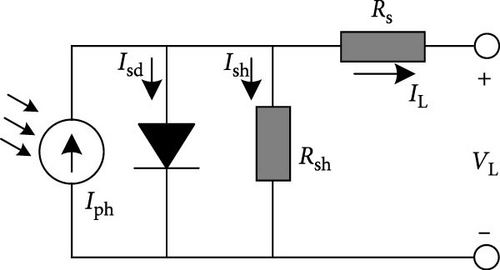
Equation (4) shows that there are {Iph, Isd, Rs, Rsh, and n} five unknown parameters that need to be extracted in the SDM.
2.2. DDM
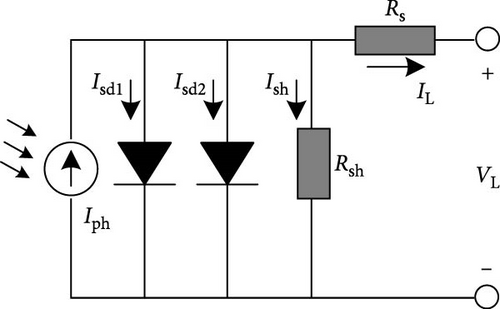
2.3. TDM
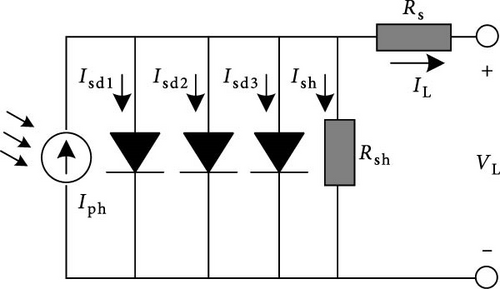
2.4. PVM
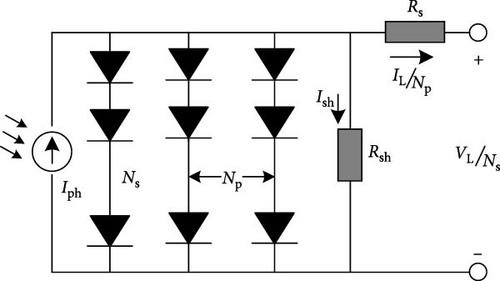
2.5. Objective Functions Formulation
3. RIME Algorithm (RIME)
The RIME algorithm mainly completes the search process through the rime initialization phase, soft-rime search phase, hard-rime puncture search phase, and positive greedy selection phase [37]; the soft-rime search phase and hard-rime puncture search phase are shown in Figure 5; and the main principle of RIME is expressed as follows:
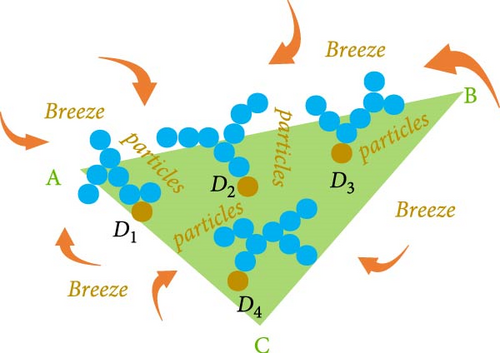
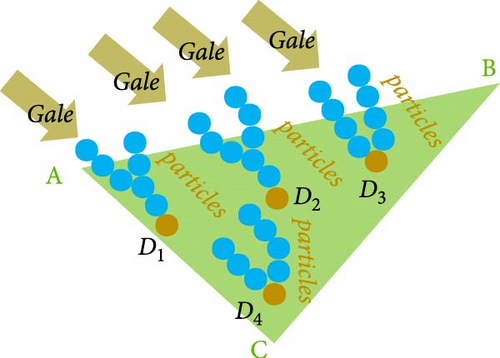
3.1. Rime Initialization Phase
3.2. Soft-Rime Search Phase
3.3. Hard-Rime Puncture Search Phase
3.4. Positive Greedy Selection Phase
3.5. Flowchart of RIME
The Pseudo-code of the RIME algorithm is given in Algorithm 1.
-
Algorithm 1: Pseudo-code of RIME.
-
1. Random initialization of swarm the search space by Equation (14)
-
2. Evaluate the fitness value of each agent and get the best rime agent in the swarm
-
3. Whilet < T
-
4. Calculate the attachment coefficient E by Equation (16)
-
// Soft-rime search phase
-
5. Ifr2 < E
-
6. Update the agent position of by Equation (15) and Equations (17)–(18)
-
7. End If
-
// Hard-rime search phase
-
8. Calculate the normalized fitness value Fnormr () by Equation (20)
-
9. Ifr3 < Fnormr ()
-
10. Update the agent position of via Equation (19)
-
11. End If
-
// Positive greedy selection phase
-
12. Comparing the fitness of agents and by Equation (21)
-
13. t = t + 1
-
14. End while
-
15. Output optimal rime agent in the swarm.
4. The ERIME Algorithm
4.1. Motivations
PV model parameter identification is a typical nonlinear optimization problem in the field of optimization, which poses unpredictable challenges to existing methods due to the presence of multiple local minima. In order to solve the PV parameter identification problem, it is usually necessary to propose targeted algorithms or integrate problem-appropriate heuristic strategies into existing methods to satisfy the search requirements at different stages. Therefore, various integration techniques have been developed to effectively solve this problem [10, 46, 47, 47]. However, according to the no free lunch (NFL) theory [48], any one method cannot obtain the optimal solution scheme in all problems; meanwhile, it is found that the RIME method exhibits significant drawbacks in the context of PV parameter identification, particularly manifesting as local stagnation and an imbalance between the exploration and exploitation processes. These deficiencies hinder its ability to efficiently and accurately identify optimal solutions. Local stagnation prevents the algorithm from progressing beyond suboptimal points, while the imbalance between exploration and exploitation limits its capacity to thoroughly search the solution space and effectively refine potential solutions. Consequently, the performance of the RIME method in identifying PV parameters is compromised, necessitating improvements to overcome these limitations. To this end, this paper proposes an ERIME algorithm that combines a modified soft-rime search strategy and a shared information mutation mechanism, which is able to ensure the algorithm’s reasonable balance between exploration and exploitation while avoiding falling into the group local optimum stagnation. The proposed algorithm compensates for the insufficient exploitation of the RIME population by adopting a modified soft-rime search strategy, which effectively improves the solution accuracy. In addition, the shared information mutation mechanism divides the population into two subpopulations for mutation operations; however, unlike the traditional two-population mutation mechanism, there is a common information exchange region in ERIME, which ensures that the algorithm fully utilizes the favorable information in the populations.
4.2. The Modified Soft-Rime Search Strategy
4.3. The Shared Information Mutation Mechanism
4.4. Framework of Proposed Algorithm
Combining the two proposed effective improvement strategies, this paper proposes an ERIME algorithm, which distinguishes itself from existing optimization algorithms used in power systems by emphasizing balanced exploration and exploitation, achieved through a modified soft-rime search strategy. This approach integrates a normal distribution function to enhance exploration around each agent while preserving the ability to exploit promising areas. Additionally, RIME incorporates a shared information mutation mechanism to facilitate information exchange among agents of different subpopulations, ensuring robust global search capabilities and mitigating the risk of local optima. These features collectively improve the accuracy and efficiency of PV parameter identification. The detailed execution process refers to Algorithm 1, and the flowchart is shown in Figure 7, as follows:
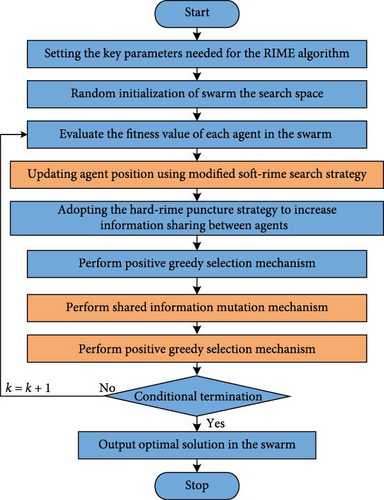
5. Numeral Experimental
5.1. Experiment Settings and Function Details
In order to demonstrate the search performance of the proposed algorithm in numerical optimization problems, in this section, simulation experiments of the method are carried out using the currently popular CEC2022 test suite, as given in Table 2. At the same time, five better-performing control methods are used for comparison to highlight the optimality of the algorithms, including particle swarm algorithm (PSO) [49], multi-verse optimizer (MVO) [50], improved JAYA (IJAYA) [51], whale optimization algorithm (WOA) [52], and RIME [37]. In order to be fair in the comparison of the different algorithms, the search stopping criterion of reaching the maximum number of evaluations of 30,000 is used, with the dimensionality set to 20; the population size is uniformly set to 30; and the algorithms are run independently for 20 runs to statistically analyze the experimental results. Each algorithm was run independently for 20 times to statistically analyze the results. The detailed hyperparameter settings of each algorithm are shown in Table 3.
| Type | No. | Fmin | Range | |
|---|---|---|---|---|
| Unimodal | F1 | Shifted and full rotated Zakharov function | 300 | [−100, 100]D |
| Basic functions | F2 | Shifted and full rotated Rosenbrock’s function | 400 | [−100, 100]D |
| F3 | Shifted and full rotated expanded Schaffer’s f6 function | 600 | [−100, 100]D | |
| F4 | Shifted and full rotated noncontinuous Rastrigin’s function | 800 | [−100, 100]D | |
| F5 | Shifted and full rotated Levy function | 900 | [−100, 100]D | |
| Hybrid functions | F6 | Hybrid Function 1 (N = 3) | 1,800 | [−100, 100]D |
| F7 | Hybrid Function 2 (N = 6) | 2,000 | [−100, 100]D | |
| F8 | Hybrid Function 3 (N = 5) | 2,200 | [−100, 100]D | |
| Composition functions | F9 | Composition Function 1 (N = 5) | 2,300 | [−100, 100]D |
| F10 | Composition Function 2 (N = 4) | 2,400 | [−100, 100]D | |
| F11 | Composition Function 3 (N = 5) | 2,600 | [−100, 100]D | |
| F12 | Composition Function 4 (N = 6) | 2,700 | [−100, 100]D | |
| Algorithm | Parameters |
|---|---|
| PSO | N = 30; personal constant C1 = 2.0; social constants C2 = 2.0 |
| MVO | N = 30; probability p = 6.0 |
| WOA | N = 30; constant factor a = 2.0 |
| IJAYA | N = 30 |
| RIME | N = 30; control factor w = 5.0 |
| ERIME | N = 30; control factor w = 5.0, mean μ = 0; standard deviation σ = 1 |
5.2. Performance Comparison and Analysis of ERIME
Table 4 shows the statistical results of ERIME with the other five methods, mainly consisting of mean and standard deviation. The optimal results of several methods in terms of statistical indicators have been marked in bold. It can be seen that the proposed method excels in overall aspects. In terms of mean values, the proposed method is close to the other popular methods in terms of the F1, F3, and F7 functions, although the results are not optimal. In the other nine test functions, the proposed method achieves the best results in the mean value. This shows that the proposed method is able to maintain a high level of search capability in complex problems. In addition, ERIME is able to achieve the best results in most of the problems, which is a good indication of the stability of the algorithm.
| Function | Indictor | ERIME | IJAYA | MVO | PSO | RIME | WOA |
|---|---|---|---|---|---|---|---|
| F1 | Mean | 300.0003 | 36,129.1195 | 8,812.176 | 27,135.84283 | 7,262.611 | 15,532.24 |
| STD | 0.000153 | 8,082.21996 | 4,773.212 | 12,579.44259 | 4,467.763 | 4,172.2666 | |
| F2 | Mean | 441.649 | 474.9469 | 469.7775 | 568.3457791 | 457.8179 | 533.20058 |
| STD | 18.53256 | 12.549739 | 28.31282 | 92.46921573 | 32.57485 | 49.185793 | |
| F3 | Mean | 618.2604 | 619.355602 | 649.6165 | 616.3373193 | 624.5321 | 669.11972 |
| STD | 6.600541 | 2.29268154 | 11.572 | 6.622678286 | 5.360862 | 13.988938 | |
| F4 | Mean | 858.6475 | 880.79192 | 915.0768 | 921.6744587 | 872.6324 | 922.8266 |
| STD | 12.57622 | 20.9927106 | 35.44931 | 17.30577899 | 18.8416 | 38.572963 | |
| F5 | Mean | 1,608.96 | 3,156.01002 | 3,994.949 | 2,094.321823 | 2,166.804 | 4,213.4535 |
| STD | 769.397 | 659.159082 | 1,262.518 | 738.7364581 | 502.4909 | 1,759.4927 | |
| F6 | Mean | 1,973.927 | 250,803.076 | 7,169.645 | 2,396,482.595 | 8,350.829 | 8,4857.413 |
| STD | 82.66188 | 261,138.554 | 3,502.739 | 9,614,460.962 | 6,599.932 | 98,492.471 | |
| F7 | Mean | 2,090.009 | 2,109.1512 | 2,227.569 | 2,082.766193 | 2,087.344 | 2,210.3037 |
| STD | 42.25706 | 16.8285378 | 115.8984 | 29.10666718 | 43.23436 | 68.54229 | |
| F8 | Mean | 2,226.06 | 2,239.96354 | 2,408.188 | 2,313.006445 | 2,301.956 | 2,273.7696 |
| STD | 5.043835 | 6.74776693 | 134.7116 | 73.55556677 | 73.51321 | 61.473868 | |
| F9 | Mean | 2,480.781 | 2,483.80188 | 2,496.115 | 2,581.323589 | 2,483.254 | 2,533.657 |
| STD | 0.000108 | 1.00645029 | 26.41138 | 90.66332607 | 3.194421 | 34.362823 | |
| F10 | Mean | 3,095.272 | 3,906.58809 | 4,471.547 | 3,867.797449 | 3,297.933 | 4,726.6701 |
| STD | 343.5699 | 1,321.47608 | 681.421 | 776.2521077 | 528.7197 | 1,302.3993 | |
| F11 | Mean | 2,900.047 | 3,324.50269 | 3,016.182 | 4,719.745011 | 3,237.2 | 3,164.8922 |
| STD | 79.46173 | 132.700665 | 209.2697 | 771.6220033 | 1,244.424 | 190.11188 | |
| F12 | Mean | 2,964.387 | 2,948.41323 | 3,236.341 | 3,030.06564 | 3,035.993 | 3,082.7276 |
| STD | 21.12499 | 4.23928791 | 100.9231 | 60.85677211 | 39.94388 | 96.028653 | |
| Friedman rank | 1.33 | 3.67 | 4.25 | 4.08 | 2.83 | 4.83 | |
| Rank | 1 | 3 | 5 | 4 | 2 | 6 | |
- The bold values indicate the best result.
The last two rows of Table 4 give the Friedman test [53] to check whether the proposed method is statistically significant. It can be seen that the proposed method has the best average ranking, with RIME and IJAYA ranking second and third, respectively. Table 5 further gives the results of the Wilcoxon signed-rank test [54] at α = 5%, and the experimental results show that the proposed method is able to continue to outperform its rivals.
| Indicator | ERIME vs. IJAYA | ERIME vs. MVO | ERIME vs. PSO | ERIME vs. RIME | ERIME vs. WOA |
|---|---|---|---|---|---|
| Win | 11 | 12 | 10 | 11 | 12 |
| Tie | 0 | 0 | 0 | 0 | 0 |
| Lose | 1 | 0 | 2 | 1 | 0 |
| R+ | 74 | 78 | 75 | 76 | 78 |
| R- | 4 | 0 | 3 | 2 | 0 |
| P-value | 6.04 × 10−03 | 2.22 × 10−03 | 4.74 × 10−03 | 3.70 × 10−03 | 2.22 × 10−03 |
| Hypothesis | 1 | 1 | 1 | 1 | 1 |
Figure 8 shows the convergence curves of RIME with other methods on the test suite. In F1, the RIME method converges at a similar speed and accuracy to the control method up to 3,000 times, after which it searches for results with higher accuracy at a faster rate, while the other methods have fallen into local optima. In the convergence graphs of functions F2–F6, the proposed method is able to find a more satisfactory solution at the beginning of the search and develop it further. In addition, although the problems of functions F7–F9 are more complicated, the proposed method can still maintain high accuracy and search efficiency. In conclusion, it can be shown that the proposed method is an efficient optimization problem-solving tool.
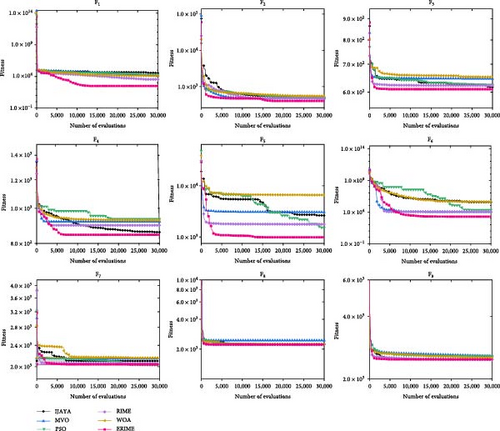
6. Experimental Results and Discussions on PV Problem
To verify the performance of the proposed method on SDM, DDM, TDM, and PVM models. Firstly, the current and voltage datasets of 26 pairs of commercial RTC France PV cell measured under the irradiance of 1,000 W/m2 and the temperature of 33°C are selected as the measurement data of SDM, DDM, and TDM to evaluate the unknown parameters of the model [55]. Further, under the irradiance of 1,000 W/m2, the current and voltage data collected by Photowatt-PWP 201, single crystal STM6-40/36, and polycrystalline STP6-120/36 module cells at 45, 51, and 55°C were adopted as measurement data to be evaluated with unknown parameters of PVM [56]. In order to be more convincing, the four most popular methods so far, such as PSO, MVO, IJAYA, RIME, and WOA; repairable grey wolf optimization (RGWO) [57]; flexible particle swarm optimization algorithm (FPSO) [36]; and adaptive rat swarm optimization (ARSO) [58], are introduced as control methods for comparison. In order to ensure fair comparison between algorithms, the hyperparameters of each algorithm are consistent with the original literature settings. The maximum number of function evaluations for all methods was set to 40,000, and 20 independent running experiments were performed. The key parameters of different algorithms are set as in the above experiment, and the problem boundary settings of different models are given in Table 6. The performance evaluation index is given by the equation.
| Parameter | SDM/DDM/TDM | Photowatt-PWP201 | STM6-40/36 | STP6-120/36 | ||||
|---|---|---|---|---|---|---|---|---|
| Lb | Ub | Lb | Ub | Lb | Ub | Lb | Ub | |
| Iph (A) | 0 | 1 | 0 | 2 | 0 | 2 | 0 | 8 |
| RS (Ω) | 0 | 0.5 | 0 | 2 | 0 | 0.36 | 0 | 0.36 |
| Rsh (Ω) | 0 | 100 | 0 | 2,000 | 0 | 1,000 | 0 | 1,500 |
| Isd, Isd1, Isd2, and Isd3 (μA) | 0 | 1 | 0 | 50 | 0 | 50 | 0 | 50 |
| n, n1, n2, and n3 | 1 | 2 | 1 | 50 | 1 | 60 | 1 | 50 |
6.1. Results on SDM, DDM, and TDM
6.1.1. Results on SDM
Table 7 shows the optimal parameter results extracted by ERIME with the control methods (PSO, MVO, IJAYA, WOA, and RIME), where the optimal results have been shown in bold. Table 8 further gives the statistical results of the error values of the simulation data and measured data obtained by the proposed method through the optimal parameter results. From the above two tables, it can be seen that the results obtained by the proposed method are the best as compared to the control method, and the proposed method is able to obtain very small absolute error values with respect to most of the measured values.
| Algorithm | RMSE | Iph (A) | Isd (μA) | RS (Ω) | Rsh (Ω) | n |
|---|---|---|---|---|---|---|
| PSO | 0.001068181 | 0.760666874 | 0.398676401 | 0.03553906 | 61.52614977 | 1.502649717 |
| MVO | 0.001132318 | 0.761139577 | 0.339954315 | 0.035972223 | 48.3226622 | 1.486415638 |
| IJAYA | 0.000986586 | 0.760769337 | 0.320332355 | 0.036410397 | 53.32473299 | 1.480344347 |
| WOA | 0.001453948 | 0.759885813 | 0.424449194 | 0.035188799 | 86.33212159 | 1.508908902 |
| RIME | 0.000992647 | 0.760573283 | 0.322478172 | 0.036407889 | 55.70615572 | 1.48098448 |
| ERIME | 0.000986022 | 0.76077553 | 0.323020799 | 0.036377093 | 53.71852311 | 1.481183587 |
- The bold values indicate the best result.
| Item | Measured data | Simulated current data | Simulated power data | ||||
|---|---|---|---|---|---|---|---|
| V (V) | I (A) | I (A) | IAE (A) | IRE (%) | P (W) | PAE (W) | |
| 1 | −0.2057 | 0.7640 | 7.64087704E−01 | 8.77039372E−05 | 1.14795729E−02 | −1.57172841E−01 | −1.80406999E−05 |
| 2 | −0.1291 | 0.7620 | 7.62663086E−01 | 6.63086234E−04 | 8.70191908E−02 | −9.84598044E−02 | −8.56044328E−05 |
| 3 | −0.0588 | 0.7605 | 7.61355307E−01 | 8.55307161E−04 | 1.12466425E−01 | −4.47676921E−02 | −5.02920611E−05 |
| 4 | 0.0057 | 0.7605 | 7.60153991E−01 | −3.46009034E−04 | −4.54975719E−02 | 4.33287775E−03 | −1.97225150E−06 |
| 5 | 0.0646 | 0.7600 | 7.59055209E−01 | −9.44791209E−04 | −1.24314633E−01 | 4.90349665E−02 | −6.10335121E−05 |
| 6 | 0.1185 | 0.7590 | 7.58042345E−01 | −9.57654900E−04 | −1.26173241E−01 | 8.98280179E−02 | −1.13482106E−04 |
| 7 | 0.1678 | 0.7570 | 7.57091654E−01 | 9.16538033E−05 | 1.21075037E−02 | 1.27039980E−01 | 1.53795082E−05 |
| 8 | 0.2132 | 0.7570 | 7.56141365E−01 | −8.58635376E−04 | −1.13426073E−01 | 1.61209339E−01 | −1.83061062E−04 |
| 9 | 0.2545 | 0.7555 | 7.55086873E−01 | −4.13127445E−04 | −5.46826533E−02 | 1.92169609E−01 | −1.05140935E−04 |
| 10 | 0.2924 | 0.7540 | 7.53663878E−01 | −3.36121923E−04 | −4.45785044E−02 | 2.20371318E−01 | −9.82820503E−05 |
| 11 | 0.3269 | 0.7505 | 7.51390966E−01 | 8.90966402E−04 | 1.18716376E−01 | 2.45629707E−01 | 2.91256917E−04 |
| 12 | 0.3585 | 0.7465 | 7.47353851E−01 | 8.53851350E−04 | 1.14380623E−01 | 2.67926356E−01 | 3.06105709E−04 |
| 13 | 0.3873 | 0.7385 | 7.40117222E−01 | 1.61722196E−03 | 2.18987402E−01 | 2.86647400E−01 | 6.26350066E−04 |
| 14 | 0.4137 | 0.7280 | 7.27382225E−01 | −6.17774906E−04 | −8.48591905E−02 | 3.00918027E−01 | −2.55573479E−04 |
| 15 | 0.4373 | 0.7065 | 7.06972652E−01 | 4.72651504E−04 | 6.69004252E−02 | 3.09159141E−01 | 2.06690503E−04 |
| 16 | 0.4590 | 0.6755 | 6.75280152E−01 | −2.19848396E−04 | −3.25460246E−02 | 3.09953590E−01 | −1.00910414E−04 |
| 17 | 0.4784 | 0.6320 | 6.30758272E−01 | −1.24172750E−03 | −1.96475871E−01 | 3.01754758E−01 | −5.94042438E−04 |
| 18 | 0.4960 | 0.5730 | 5.71928358E−01 | −1.07164167E−03 | −1.87022980E−01 | 2.83676466E−01 | −5.31534270E−04 |
| 19 | 0.5119 | 0.4990 | 4.99607019E−01 | 6.07018567E−04 | 1.21647007E−01 | 2.55748833E−01 | 3.10732805E−04 |
| 20 | 0.5265 | 0.4130 | 4.13648792E−01 | 6.48791945E−04 | 1.57092481E−01 | 2.17786089E−01 | 3.41588959E−04 |
| 21 | 0.5398 | 0.3165 | 3.17510109E−01 | 1.01010921E−03 | 3.19149828E−01 | 1.71391957E−01 | 5.45256950E−04 |
| 22 | 0.5521 | 0.2120 | 2.12154939E−01 | 1.54938670E−04 | 7.30842783E−02 | 1.17130742E−01 | 8.55416397E−05 |
| 23 | 0.5633 | 0.1035 | 1.02251311E−01 | −1.24868865E−03 | −1.20646247E + 00 | 5.75981637E−02 | −7.03386318E−04 |
| 24 | 0.5736 | −0.0100 | −8.71754195E−03 | 1.28245805E−03 | −1.28245805E + 01 | −5.00038206E−03 | 7.35617936E−04 |
| 25 | 0.5833 | −0.1230 | −1.25507413E−01 | −2.50741273E−03 | 2.03854693E + 00 | −7.32084738E−02 | −1.46257384E−03 |
| 26 | 0.5900 | −0.2100 | −2.08472326E−01 | 1.52767392E−03 | −7.27463771E−01 | −1.22998672E−01 | 9.01327613E−04 |
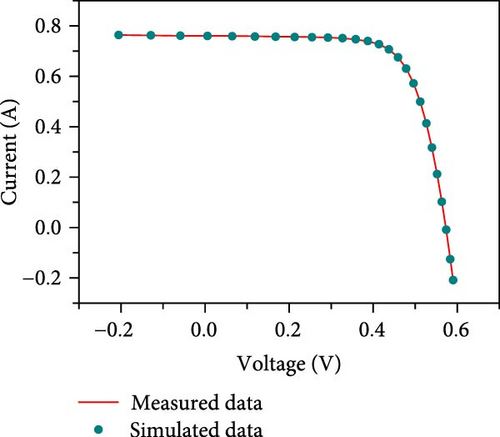
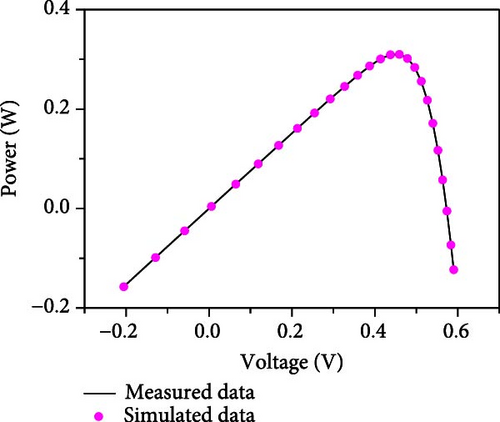
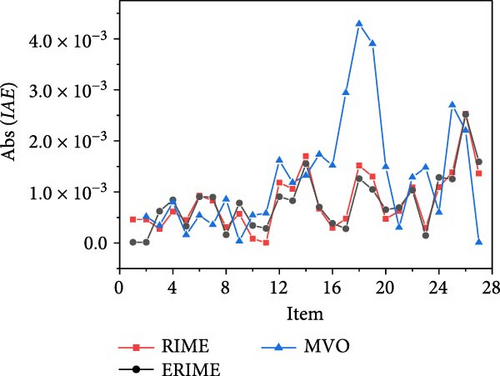
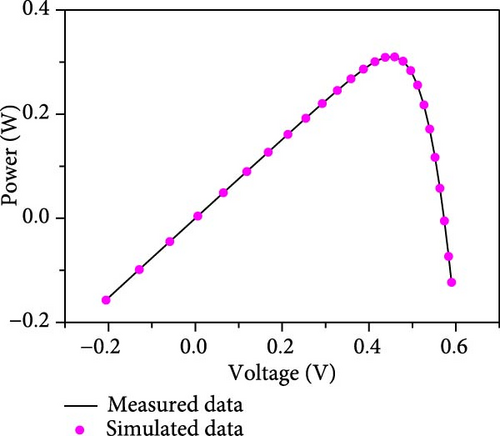
The results of the current–voltage (I–V), power–voltage (P–V) and current error value (IAE) fits are further given in Figures 9(a), 9(b), and 9(c) in conjunction with the measured data. From the figure, it can be seen that the proposed method is able to obtain reliable parameter identification results in the SDM problem.
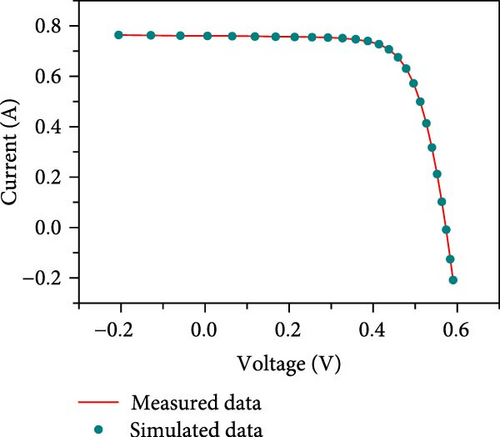
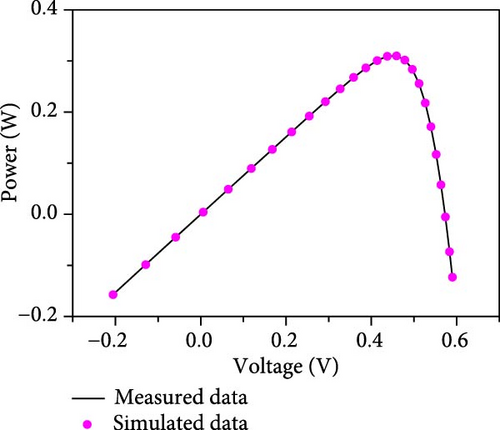
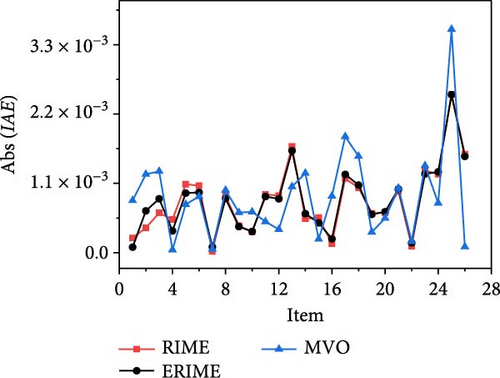
6.1.2. Results on DDM
The parameter results of the DDM model extracted by ERIME are shown in Table 9. Also, the optimal parameter results of the control methods (PSO, MVO, IJAYA, WOA, and RIME) are listed in the table. It can be seen that the proposed method gives the best RMSE values even if the number of parameters to be determined increases. The simulated current and power data obtained through ERIME results are given in Table 10. By comparing with the real current and power results, it can be seen that the proposed method has very low error values.
| Algorithm | RMSE | Iph (A) | Isd1 (μA) | RS (Ω) | Rsh (Ω) | n1 | Isd2 (μA) | n2 |
|---|---|---|---|---|---|---|---|---|
| PSO | 0.000990127 | 0.76075025 | 0.32843973 | 0.036200774 | 55.11305065 | 1.483698232 | 0.025510287 | 1.749030543 |
| MVO | 0.001697627 | 0.760805833 | 0.528696471 | 0.033735429 | 67.24729401 | 1.537531561 | 0.207947585 | 1.811797321 |
| IJAYA | 0.000986874 | 0.760820578 | 0.241969453 | 0.036581817 | 55.14230812 | 1.458574158 | 0.31125081 | 1.826206022 |
| WOA | 0.00118447 | 0.759965069 | 0.071462985 | 0.035675563 | 75.72135471 | 1.687534217 | 0.359550315 | 1.495665929 |
| RIME | 0.001005833 | 0.760601256 | 0.254812457 | 0.03634022 | 60.58674374 | 1.462588269 | 0.735193716 | 2 |
| ERIME | 0.000983051 | 0.760780431 | 0.484418375 | 0.036585433 | 54.95105908 | 1.998129861 | 0.25901387 | 1.462542472 |
- The bold values indicate the best result.
| Item | Measured data | Simulated current data | Simulated power data | ||||
|---|---|---|---|---|---|---|---|
| V (V) | I (A) | I (A) | IAE (A) | IRE (%) | P (W) | PAE (W) | |
| 1 | −0.2057 | 0.7640 | 7.64015829E−01 | 1.58288634E−05 | 2.07184077E−03 | −1.57158056E−01 | −3.25599721E−06 |
| 2 | −0.1291 | 0.7620 | 7.62623122E−01 | 6.23122168E−04 | 8.17745627E−02 | −9.84546451E−02 | −8.04450718E−05 |
| 3 | −0.0588 | 0.7605 | 7.61344505E−01 | 8.44505221E−04 | 1.11046051E−01 | −4.47670569E−02 | −4.96569070E−05 |
| 4 | 0.0057 | 0.7605 | 7.60169586E−01 | −3.30413777E−04 | −4.34469134E−02 | 4.33296664E−03 | −1.88335853E−06 |
| 5 | 0.0646 | 0.7600 | 7.59093952E−01 | −9.06047586E−04 | −1.19216788E−01 | 4.90374693E−02 | −5.85306740E−05 |
| 6 | 0.1185 | 0.7590 | 7.58100142E−01 | −8.99858068E−04 | −1.18558375E−01 | 8.98348668E−02 | −1.06633181E−04 |
| 7 | 0.1678 | 0.7570 | 7.57162700E−01 | 1.62699520E−04 | 2.14926710E−02 | 1.27051901E−01 | 2.73009794E−05 |
| 8 | 0.2132 | 0.7570 | 7.56217331E−01 | −7.82668948E−04 | −1.03390878E−01 | 1.61225535E−01 | −1.66865020E−04 |
| 9 | 0.2545 | 0.7555 | 7.55156402E−01 | −3.43597525E−04 | −4.54794871E−02 | 1.92187304E−01 | −8.74455701E−05 |
| 10 | 0.2924 | 0.7540 | 7.53713432E−01 | −2.86568356E−04 | −3.80064133E−02 | 2.20385807E−01 | −8.37925873E−05 |
| 11 | 0.3269 | 0.7505 | 7.51407747E−01 | 9.07747317E−04 | 1.20952341E−01 | 2.45635193E−01 | 2.96742598E−04 |
| 12 | 0.3585 | 0.7465 | 7.47329729E−01 | 8.29729236E−04 | 1.11149261E−01 | 2.67917708E−01 | 2.97457931E−04 |
| 13 | 0.3873 | 0.7385 | 7.40054290E−01 | 1.55428987E−03 | 2.10465791E−01 | 2.86623026E−01 | 6.01976466E−04 |
| 14 | 0.4137 | 0.7280 | 7.27294626E−01 | −7.05373508E−04 | −9.68919654E−02 | 3.00881787E−01 | −2.91813020E−04 |
| 15 | 0.4373 | 0.7065 | 7.06885724E−01 | 3.85723646E−04 | 5.45964114E−02 | 3.09121127E−01 | 1.68676950E−04 |
| 16 | 0.4590 | 0.6755 | 6.75219544E−01 | −2.80456041E−04 | −4.15182889E−02 | 3.09925771E−01 | −1.28729323E−04 |
| 17 | 0.4784 | 0.6320 | 6.30738979E−01 | −1.26102101E−03 | −1.99528640E−01 | 3.01745528E−01 | −6.03272449E−04 |
| 18 | 0.4960 | 0.5730 | 5.71949456E−01 | −1.05054397E−03 | −1.83341007E−01 | 2.83686930E−01 | −5.21069810E−04 |
| 19 | 0.5119 | 0.4990 | 4.99653382E−01 | 6.53381754E−04 | 1.30938227E−01 | 2.55772566E−01 | 3.34466120E−04 |
| 20 | 0.5265 | 0.4130 | 4.13694842E−01 | 6.94842395E−04 | 1.68242711E−01 | 2.17810335E−01 | 3.65834521E−04 |
| 21 | 0.5398 | 0.3165 | 3.17535671E−01 | 1.03567104E−03 | 3.27226236E−01 | 1.71405755E−01 | 5.59055226E−04 |
| 22 | 0.5521 | 0.2120 | 2.12147337E−01 | 1.47336526E−04 | 6.94983612E−02 | 1.17126544E−01 | 8.13444958E−05 |
| 23 | 0.5633 | 0.1035 | 1.02214664E−01 | −1.28533597E−03 | −1.24187050E + 00 | 5.75775202E−02 | −7.24029753E−04 |
| 24 | 0.5736 | −0.0100 | −8.74637807E−03 | 1.25362193E−03 | −1.25362193E + 01 | −5.01692246E−03 | 7.19077542E−04 |
| 25 | 0.5833 | −0.1230 | −1.25517899E−01 | −2.51789851E−03 | 2.04707196E + 00 | −7.32145902E−02 | −1.46869020E−03 |
| 26 | 0.5900 | −0.2100 | −2.08409158E−01 | 1.59084188E−03 | −7.57543750E−01 | −1.22961403E−01 | 9.38596707E−04 |
The characteristic curves of I–V,P–V and current error value (IAE) further obtained through ERIME parameter extraction results are given in Figures 10(a), 10(b), and 10(c). It can be noticed that the proposed method is effective in assessing the quality of the cell for the DDM model structure.
6.1.3. Results on TDM
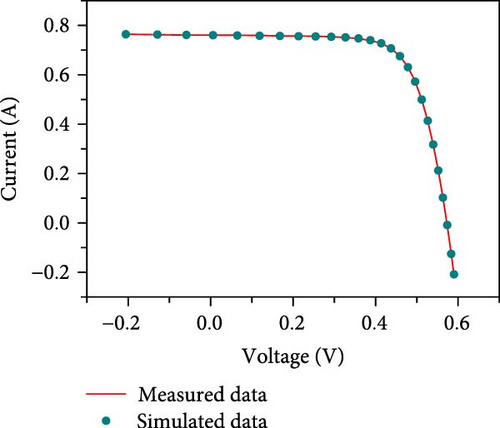
Similarly, the proposed method with the control method is used to extract the TDM model with nine unknown parameters. Table 11 gives the optimal parameter extraction results of different methods for the TDM problem. The error values between the simulated data and the real data obtained by the proposed method are given in Table 12. It is clear to see that the IAE as well as PAE obtained by the proposed method is very low even when more unknown parameters are to be extracted, which proves the robustness of the method.
| Algorithm | RMSE | Iph (A) | Isd1 (μA) | RS (Ω) | Rsh (Ω) | n1 | Isd2 (μA) | n2 | Isd3 (μA) | n3 |
|---|---|---|---|---|---|---|---|---|---|---|
| PSO | 0.000994332 | 0.760760023 | 0 | 0.036097921 | 55.28322567 | 1 | 0.344935424 | 1.487827882 | 0 | 2 |
| MVO | 0.001887555 | 0.763125962 | 0.855898465 | 0.036765656 | 35.03862067 | 1.97118878 | 0.248176626 | 1.953639942 | 0.159859083 | 1.422754282 |
| IJAYA | 0.000992341 | 0.760784876 | 0.426237886 | 0.037061683 | 58.3033387 | 1.964276044 | 0.550783207 | 1.799127303 | 0.126555353 | 1.408181542 |
| WOA | 0.001347989 | 0.75950189 | 0 | 0.036869057 | 74.30746136 | 1.155647828 | 0 | 1.083939433 | 0.319084001 | 1.479686995 |
| RIME | 0.001118644 | 0.760074662 | 0.226941018 | 0.036756397 | 72.20923886 | 1.727060862 | 0.361026843 | 1.571126538 | 0.030996839 | 1.343175481 |
| ERIME | 0.000982601 | 0.760781489 | 0.624216927 | 0.036684854 | 55.2087035 | 1.99948144 | 0.009226936 | 1.928946253 | 0.239033778 | 1.4557175 |
- The bold values indicate the best result.
| Item | Measured data | Simulated current data | Simulated power data | ||||
|---|---|---|---|---|---|---|---|
| V (V) | I (A) | I (A) | IAE (A) | IRE (%) | P (W) | PAE (W) | |
| 1 | −0.2057 | 0.7640 | 7.64000540E−01 | 5.39715444E−07 | 7.06433827E−05 | −1.57154911E−01 | −1.11019467E−07 |
| 2 | −0.1291 | 0.7620 | 7.62614320E−01 | 6.14320221E−04 | 8.06194515E−02 | −9.84535087E−02 | −7.93087405E−05 |
| 3 | −0.0588 | 0.7605 | 7.61341618E−01 | 8.41617746E−04 | 1.10666370E−01 | −4.47668871E−02 | −4.94871235E−05 |
| 4 | 0.0057 | 0.7605 | 7.60172012E−01 | −3.27988283E−04 | −4.31279793E−02 | 4.33298047E−03 | −1.86953321E−06 |
| 5 | 0.0646 | 0.7600 | 7.59100938E−01 | −8.99061968E−04 | −1.18297627E−01 | 4.90379206E−02 | −5.80794032E−05 |
| 6 | 0.1185 | 0.7590 | 7.58110657E−01 | −8.89342882E−04 | −1.17172975E−01 | 8.98361129E−02 | −1.05387131E−04 |
| 7 | 0.1678 | 0.7570 | 7.57175201E−01 | 1.75201495E−04 | 2.31441869E−02 | 1.27053999E−01 | 2.93988109E−05 |
| 8 | 0.2132 | 0.7570 | 7.56229547E−01 | −7.70453014E−04 | −1.01777149E−01 | 1.61228139E−01 | −1.64260583E−04 |
| 9 | 0.2545 | 0.7555 | 7.55165329E−01 | −3.34671056E−04 | −4.42979558E−02 | 1.92189576E−01 | −8.51737838E−05 |
| 10 | 0.2924 | 0.7540 | 7.53715721E−01 | −2.84278646E−04 | −3.77027382E−02 | 2.20386477E−01 | −8.31230760E−05 |
| 11 | 0.3269 | 0.7505 | 7.51400840E−01 | 9.00840186E−04 | 1.20032004E−01 | 2.45632935E−01 | 2.94484657E−04 |
| 12 | 0.3585 | 0.7465 | 7.47313207E−01 | 8.13206707E−04 | 1.08935929E−01 | 2.67911785E−01 | 2.91534604E−04 |
| 13 | 0.3873 | 0.7385 | 7.40031485E−01 | 1.53148470E−03 | 2.07377752E−01 | 2.86614194E−01 | 5.93144024E−04 |
| 14 | 0.4137 | 0.7280 | 7.27272658E−01 | −7.27341748E−04 | −9.99095808E−02 | 3.00872699E−01 | −3.00901281E−04 |
| 15 | 0.4373 | 0.7065 | 7.06873890E−01 | 3.73889820E−04 | 5.29214183E−02 | 3.09115952E−01 | 1.63502018E−04 |
| 16 | 0.4590 | 0.6755 | 6.75225050E−01 | −2.74950401E−04 | −4.07032422E−02 | 3.09928298E−01 | −1.26202234E−04 |
| 17 | 0.4784 | 0.6320 | 6.30762346E−01 | −1.23765448E−03 | −1.95831405E−01 | 3.01756706E−01 | −5.92093902E−04 |
| 18 | 0.4960 | 0.5730 | 5.71984046E−01 | −1.01595443E−03 | −1.77304437E−01 | 2.83704087E−01 | −5.03913395E−04 |
| 19 | 0.5119 | 0.4990 | 4.99687815E−01 | 6.87814959E−04 | 1.37838669E−01 | 2.55790192E−01 | 3.52092478E−04 |
| 20 | 0.5265 | 0.4130 | 4.13715243E−01 | 7.15242761E−04 | 1.73182267E−01 | 2.17821075E−01 | 3.76575314E−04 |
| 21 | 0.5398 | 0.3165 | 3.17533746E−01 | 1.03374613E−03 | 3.26618049E−01 | 1.71404716E−01 | 5.58016158E−04 |
| 22 | 0.5521 | 0.2120 | 2.12120499E−01 | 1.20498587E−04 | 5.68389561E−02 | 1.17111727E−01 | 6.65272699E−05 |
| 23 | 0.5633 | 0.1035 | 1.02170071E−01 | −1.32992900E−03 | −1.28495556E + 00 | 5.75524010E−02 | −7.49149007E−04 |
| 24 | 0.5736 | −0.0100 | −8.78531060E−03 | 1.21468940E−03 | −1.21468940E + 01 | −5.03925416E−03 | 6.96745838E−04 |
| 25 | 0.5833 | −0.1230 | −1.25539930E−01 | −2.53993048E−03 | 2.06498413E + 00 | −7.32274414E−02 | −1.48154145E−03 |
| 26 | 0.5900 | −0.2100 | −2.08386436E−01 | 1.61356449E−03 | −7.68364042E−01 | −1.22947997E−01 | 9.52003048E−04 |
The characteristic curves of current, power versus voltage and current error value (IAE) plotted in conjunction with Table 12 are given in Figures 11(a), 11(b), and 11(c). The high accuracy of the proposed method for parameter extraction for the TDM model is further illustrated.
6.2. Experiments on Different PVM
To demonstrate the practicality of the proposed method, this study evaluates the proposed method in three different PVM model products.
6.2.1. Results on Photowatt-PWP201
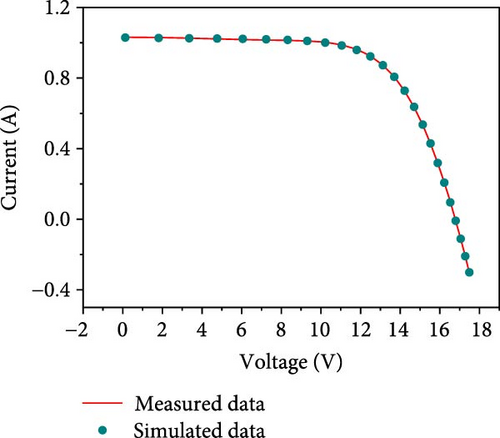
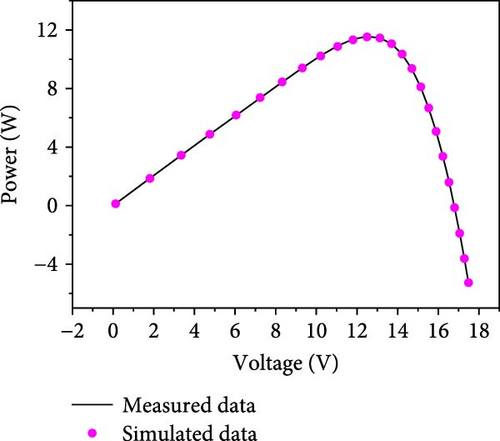
Table 13 presents the optimal parameter statistics for multiple methods in the Photowatt-PWP201 model. Building on the results from Table 13, Table 14 further provides a comparison of the proposed method with other methods using measured data. It is evident that the proposed method outperforms all other methods. Additionally, the statistics of error values show that the current error varies between −4.83282782E−03 and 4.43068116E−03, while the voltage error varies between −7.98581302E−02 and 3.87772777E−02. These small errors indicate that the proposed method achieves the highest accuracy in unknown parameter extraction within PVM models. The robustness of the proposed method is further illustrated by the characteristic curves of I–V and P–V, and IAE, which are plotted in Figures 12(a), 12(b), and 12(c).
| Algorithm | RMSE | Iph (A) | Isd (μA) | RS (Ω) | Rsh (Ω) | n |
|---|---|---|---|---|---|---|
| PSO | 0.002445336 | 1.029847098 | 3.898829489 | 1.189410271 | 1122.847617 | 49.07897292 |
| MVO | 0.002431777 | 1.030834508 | 3.395411267 | 1.204679263 | 959.6998811 | 48.5457469 |
| IJAYA | 0.002426502 | 1.030440845 | 3.493455099 | 1.200710015 | 982.4075136 | 48.65518758 |
| WOA | 0.002708903 | 1.028738172 | 2.985086984 | 1.229504732 | 1189.286689 | 48.04671727 |
| RIME | 0.002440897 | 1.030520594 | 3.216021917 | 1.210457426 | 954.0354524 | 48.33772907 |
| ERIME | 0.002425075 | 1.030514298 | 3.482263117 | 1.201271005 | 981.9823871 | 48.64283508 |
- The bold values indicate the best result.
| Item | Measured data | Simulated current data | Simulated power data | |||
|---|---|---|---|---|---|---|
| V (V) | I (A) | I (A) | IAE (A) | P (W) | PAE (W) | |
| 1 | 0.1248 | 1.0315 | 1.02911916E + 00 | −2.38083926E−03 | 1.28434071E−01 | −2.97128740E−04 |
| 2 | 1.8093 | 1.03 | 1.02738107E + 00 | −2.61892720E−03 | 1.85884058E + 00 | −4.73842499E−03 |
| 3 | 3.3511 | 1.026 | 1.02574180E + 00 | −2.58203239E−04 | 3.43736334E + 00 | −8.65264875E−04 |
| 4 | 4.7622 | 1.022 | 1.02410715E + 00 | 2.10715480E−03 | 4.87700309E + 00 | 1.00346926E−02 |
| 5 | 6.0538 | 1.018 | 1.02229180E + 00 | 4.29180473E−03 | 6.18875013E + 00 | 2.59817275E−02 |
| 6 | 7.2364 | 1.0155 | 1.01993068E + 00 | 4.43068116E−03 | 7.38062638E + 00 | 3.20621812E−02 |
| 7 | 8.3189 | 1.014 | 1.01636311E + 00 | 2.36310604E−03 | 8.45502304E + 00 | 1.96584428E−02 |
| 8 | 9.3097 | 1.01 | 1.01049615E + 00 | 4.96151707E−04 | 9.40741602E + 00 | 4.61902355E−03 |
| 9 | 10.2163 | 1.0035 | 1.00062897E + 00 | −2.87102993E−03 | 1.02227257E + 01 | −2.93313030E−02 |
| 10 | 11.0449 | 0.988 | 9.84548379E−01 | −3.45162126E−03 | 1.08742384E + 01 | −3.81228116E−02 |
| 11 | 11.8018 | 0.963 | 9.59521676E−01 | −3.47832379E−03 | 1.13240829E + 01 | −4.10504817E−02 |
| 12 | 12.4929 | 0.9255 | 9.22838818E−01 | −2.66118202E−03 | 1.15289331E + 01 | −3.32458809E−02 |
| 13 | 13.1231 | 0.8725 | 8.72599663E−01 | 9.96626005E−05 | 1.14512126E + 01 | 1.30788227E−03 |
| 14 | 13.6983 | 0.8075 | 8.07274263E−01 | −2.25736625E−04 | 1.10582850E + 01 | −3.09220801E−03 |
| 15 | 14.2221 | 0.7265 | 7.28336478E−01 | 1.83647769E−03 | 1.03584742E + 01 | 2.61185693E−02 |
| 16 | 14.6995 | 0.6345 | 6.37138000E−01 | 2.63799978E−03 | 9.36561003E + 00 | 3.87772777E−02 |
| 17 | 15.1346 | 0.5345 | 5.36213063E−01 | 1.71306303E−03 | 8.11537022E + 00 | 2.59265238E−02 |
| 18 | 15.5311 | 0.4275 | 4.29511325E−01 | 2.01132493E−03 | 6.67078334E + 00 | 3.12380886E−02 |
| 19 | 15.8929 | 0.3185 | 3.18774483E−01 | 2.74482949E−04 | 5.06625098E + 00 | 4.36233005E−03 |
| 20 | 16.2229 | 0.2085 | 2.07389507E−01 | −1.11049303E−03 | 3.36445923E + 00 | −1.80154174E−02 |
| 21 | 16.5241 | 0.101 | 9.61671722E−02 | −4.83282782E−03 | 1.58907597E + 00 | −7.98581302E−02 |
| 22 | 16.7987 | −0.008 | −8.32538570E−03 | −3.25385697E−04 | −1.39855657E−01 | −5.46605672E−03 |
| 23 | 17.0499 | −0.111 | −1.10936482E−01 | 6.35177170E−05 | −1.89145593E + 00 | 1.08297072E−03 |
| 24 | 17.2793 | −0.209 | −2.09247265E−01 | −2.47265493E−04 | −3.61564627E + 00 | −4.27257463E−03 |
| 25 | 17.4885 | −0.303 | −3.00863587E−01 | 2.13641342E−03 | −5.26165283E + 00 | 3.73626660E−02 |
6.2.2. Result on STM6-40/36
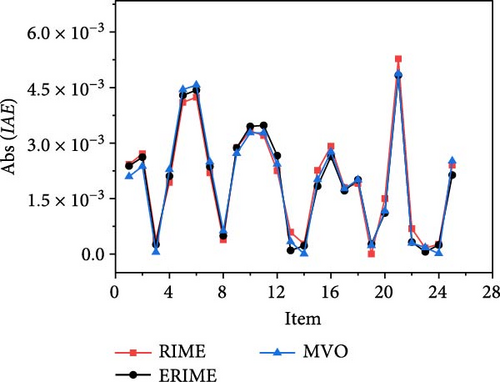
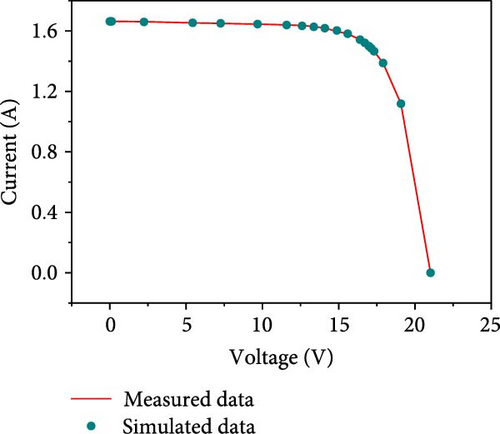
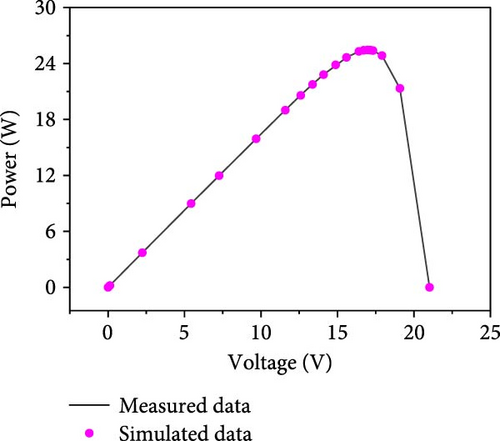
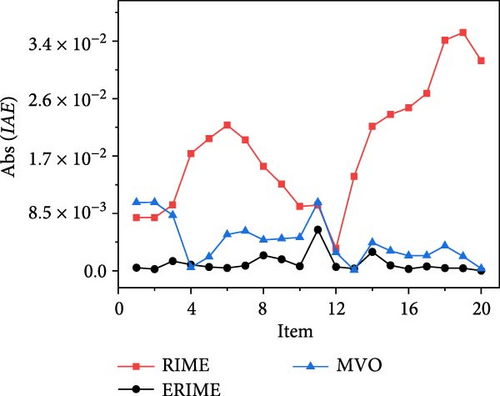
For STM6-40/36 case, the comparison results of the proposed method with the control method are given in Table 15. It can be seen that the proposed method reduces the RMSE values by 0.00160064, 0.003627511, 0.000028539, 0.006867368, and 0.018499327 as compared to PSO, MVO, IJAYA, WOA, and RIME, respectively, which is a good indication of the fact that the proposed method is more efficient than the control method in terms of RMSE values, and it is a good indication of the fact that the proposed method is less expensive than the control method in terms of RMSE value. Table 16 further gives the ratio of the error values of the proposed method for the current and voltage to the measured data, and it can be seen that they are very close to each other for both current and voltage data. Figures 13(a), 13(b), and 13(c) further illustrates the fitting results of the measured and simulated data for the I–V and P–V characteristics (Figures 13(a) and 13(b)), along with the corresponding error statistics shown in Figure 13(c). It is noteworthy that the simulated current and voltage data from the proposed method closely align with the measured data, exhibiting smaller error results. This sufficiently demonstrates that the proposed method effectively enhances the search performance of the algorithm by integrating improved strategies.
| Algorithm | RMSE | Iph (A) | Isd (μA) | RS (Ω) | Rsh (Ω) | n |
|---|---|---|---|---|---|---|
| PSO | 0.003330454 | 1.661447864 | 5.53805806 | 0 | 23.87605311 | 1.659298281 |
| MVO | 0.005357325 | 1.652871807 | 7.080456896 | 0.000329425 | 710.3947536 | 1.691191338 |
| IJAYA | 0.001758353 | 1.664420087 | 1.547190751 | 0.004666306 | 15.34698132 | 1.507564962 |
| WOA | 0.008597182 | 1.646746518 | 4.757037726 | 0 | 886.5880522 | 1.638288982 |
| RIME | 0.020229141 | 1.67089394 | 24.405172 | 0 | 990.0226787 | 1.880632472 |
| ERIME | 0.001729814 | 1.663904777 | 1.738656855 | 0.004273771 | 15.92829406 | 1.520302919 |
- The bold values indicate the best result.
| Item | Measured data | Simulated current data | Simulated power data | |||
|---|---|---|---|---|---|---|
| V (V) | I (A) | I (A) | IAE (A) | P (W) | PAE (W) | |
| 1 | 0 | 1.663 | 1.66345826E + 00 | 4.58255416E−04 | 0.00000000E + 00 | 0.00000000E + 00 |
| 2 | 0.118 | 1.663 | 1.66325231E + 00 | 2.52307134E−04 | 1.96263772E−01 | 2.97722418E−05 |
| 3 | 2.237 | 1.661 | 1.65955081E + 00 | −1.44919403E−03 | 3.71241515E + 00 | −3.24184705E−03 |
| 4 | 5.434 | 1.653 | 1.65391470E + 00 | 9.14696546E−04 | 8.98737246E + 00 | 4.97046103E−03 |
| 5 | 7.26 | 1.65 | 1.65056591E + 00 | 5.65911344E−04 | 1.19831085E + 01 | 4.10851636E−03 |
| 6 | 9.68 | 1.645 | 1.64543060E + 00 | 4.30602302E−04 | 1.59277682E + 01 | 4.16823028E−03 |
| 7 | 11.59 | 1.64 | 1.63923353E + 00 | −7.66465624E−04 | 1.89987167E + 01 | −8.88333658E−03 |
| 8 | 12.6 | 1.636 | 1.63371269E + 00 | −2.28730663E−03 | 2.05847799E + 01 | −2.88200635E−02 |
| 9 | 13.37 | 1.629 | 1.62728581E + 00 | −1.71419453E−03 | 2.17568112E + 01 | −2.29187809E−02 |
| 10 | 14.09 | 1.619 | 1.61831357E + 00 | −6.86426933E−04 | 2.28020382E + 01 | −9.67175548E−03 |
| 11 | 14.88 | 1.597 | 1.60309004E + 00 | 6.09004222E−03 | 2.38539798E + 01 | 9.06198282E−02 |
| 12 | 15.59 | 1.581 | 1.58158837E + 00 | 5.88373650E−04 | 2.46569627E + 01 | 9.17274520E−03 |
| 13 | 16.4 | 1.542 | 1.54233059E + 00 | 3.30588167E−04 | 2.52942216E + 01 | 5.42164594E−03 |
| 14 | 16.71 | 1.524 | 1.52119263E + 00 | −2.80736900E−03 | 2.54191289E + 01 | −4.69111359E−02 |
| 15 | 16.98 | 1.5 | 1.49919474E + 00 | −8.05258487E−04 | 2.54563267E + 01 | −1.36732891E−02 |
| 16 | 17.13 | 1.485 | 1.48527527E + 00 | 2.75267308E−04 | 2.54427653E + 01 | 4.71532899E−03 |
| 17 | 17.32 | 1.465 | 1.46565424E + 00 | 6.54239621E−04 | 2.53851314E + 01 | 1.13314302E−02 |
| 18 | 17.91 | 1.388 | 1.38758937E + 00 | −4.10633745E−04 | 2.48517255E + 01 | −7.35445037E−03 |
| 19 | 19.08 | 1.118 | 1.11839137E + 00 | 3.91374448E−04 | 2.13389074E + 01 | 7.46742447E−03 |
| 20 | 21.02 | 0 | −2.48104389E−05 | −2.48104389E−05 | −5.21515426E−04 | −5.21515426E−04 |
6.2.3. Result on STP6-120/36
The results of the parameter identification of the proposed method with other control methods in the STP6-120/36 model are shown in Table 17, which mainly consists of five parameters along with the RMSE values. It can be seen from the table that ERIME obtains better RMSE results than other methods. Table 18 further gives the comparison between the simulated test data and the actual measured data obtained by the proposed method, and the results show that the IAE values of the proposed method are between −2.80736900E−03 and 6.09004222E−03, and the PAE values are between −4.69111359E−02 and 9.06198282E−02, and based on the above reported results, it can be concluded that the proposed method is able to identify the PVM model effectively.
| Algorithm | RSME | Iph (A) | Isd (μA) | RS (Ω) | Rsh (Ω) | n |
|---|---|---|---|---|---|---|
| PSO | 0.035402678 | 7.502848591 | 15.63249687 | 0.00351853 | 1,500 | 1.442259603 |
| MVO | 0.019032429 | 7.473604316 | 4.128533887 | 0.004334613 | 1,129.556374 | 1.309507916 |
| IJAYA | 0.016873239 | 7.459941061 | 2.734017349 | 0.004530463 | 1,500 | 1.273353099 |
| WOA | 0.043841975 | 7.495409095 | 18.73263706 | 0.003216758 | 1,440.355312 | 1.46158395 |
| RIME | 0.041089462 | 7.514991671 | 22.16233966 | 0.00329236 | 1,500 | 1.481555705 |
| ERIME | 0.016600603 | 7.472529901 | 2.334995084 | 0.004594635 | 22.21993012 | 1.260103479 |
- The bold values indicate the best result.
| Item | Measured data | Simulated current data | Simulated power data | |||
|---|---|---|---|---|---|---|
| V (V) | I (A) | I (A) | IAE (A) | P (W) | PAE (W) | |
| 1 | 19.21 | 0 | 2.28263097E−03 | 2.28263097E−03 | 4.38493409E−02 | 4.38493409E−02 |
| 2 | 17.65 | 3.83 | 3.83334720E + 00 | 3.34719744E−03 | 6.76585780E + 01 | 5.90780349E−02 |
| 3 | 17.41 | 4.29 | 4.26733758E + 00 | −2.26624167E−02 | 7.42943473E + 01 | −3.94552676E−01 |
| 4 | 17.25 | 4.56 | 4.54114855E + 00 | −1.88514535E−02 | 7.83348124E + 01 | −3.25187572E−01 |
| 5 | 17.1 | 4.79 | 4.78440021E + 00 | −5.59978786E−03 | 8.18132436E + 01 | −9.57563724E−02 |
| 6 | 16.9 | 5.07 | 5.08557807E + 00 | 1.55780683E−02 | 8.59462694E + 01 | 2.63269355E−01 |
| 7 | 16.76 | 5.27 | 5.27482246E + 00 | 4.82246041E−03 | 8.84060244E + 01 | 8.08244364E−02 |
| 8 | 16.34 | 5.75 | 5.78259748E + 00 | 3.25974776E−02 | 9.44876428E + 01 | 5.32642784E−01 |
| 9 | 16.08 | 6 | 6.04431798E + 00 | 4.43179788E−02 | 9.71926331E + 01 | 7.12633099E−01 |
| 10 | 15.71 | 6.36 | 6.34712091E + 00 | −1.28790944E−02 | 9.97132694E + 01 | −2.02330573E−01 |
| 11 | 15.39 | 6.58 | 6.56654991E + 00 | −1.34500908E−02 | 1.01059203E + 02 | −2.06996897E−01 |
| 12 | 14.93 | 6.83 | 6.81361105E + 00 | −1.63889512E−02 | 1.01727213E + 02 | −2.44687042E−01 |
| 13 | 14.58 | 6.97 | 6.95770972E + 00 | −1.22902826E−02 | 1.01443408E + 02 | −1.79192321E−01 |
| 14 | 14.17 | 7.1 | 7.08757580E + 00 | −1.24242037E−02 | 1.00430949E + 02 | −1.76050967E−01 |
| 15 | 13.59 | 7.23 | 7.21738487E + 00 | −1.26151333E−02 | 9.80842603E + 01 | −1.71439662E−01 |
| 16 | 13.16 | 7.29 | 7.28399958E + 00 | −6.00042274E−03 | 9.58574344E + 01 | −7.89655633E−02 |
| 17 | 12.74 | 7.34 | 7.33134549E + 00 | −8.65451049E−03 | 9.34013415E + 01 | −1.10258464E−01 |
| 18 | 12.36 | 7.37 | 7.36318321E + 00 | −6.81678782E−03 | 9.10089445E + 01 | −8.42554974E−02 |
| 19 | 11.81 | 7.38 | 7.39599986E + 00 | 1.59998557E−02 | 8.73467583E + 01 | 1.88958296E−01 |
| 20 | 11.17 | 7.41 | 7.42031576E + 00 | 1.03157604E−02 | 8.28849270E + 01 | 1.15227044E−01 |
| 21 | 10.32 | 7.44 | 7.43908982E + 00 | −9.10179676E−04 | 7.67714069E + 01 | −9.39305426E−03 |
| 22 | 9.74 | 7.42 | 7.44676210E + 00 | 2.67621030E−02 | 7.25314629E + 01 | 2.60662884E−01 |
| 23 | 9.06 | 7.45 | 7.45254041E + 00 | 2.54040638E−03 | 6.75200161E + 01 | 2.30160818E−02 |
| 24 | 0 | 7.48 | 7.47097940E + 00 | −9.02060320E−03 | 0.00000000E + 00 | 0.00000000E + 00 |
Figures 14(a), 14(b), and 14(c) presents a detailed comparison of the estimated values of ERIME with the actual measurements. From the simulation results, it can be seen that the simulated current–voltage and simulated power–voltage obtained by the proposed method are in good agreement with the actual characteristic curves, which demonstrates the ability of the proposed RIME method to accurately capture the power generation characteristics of PV cells.
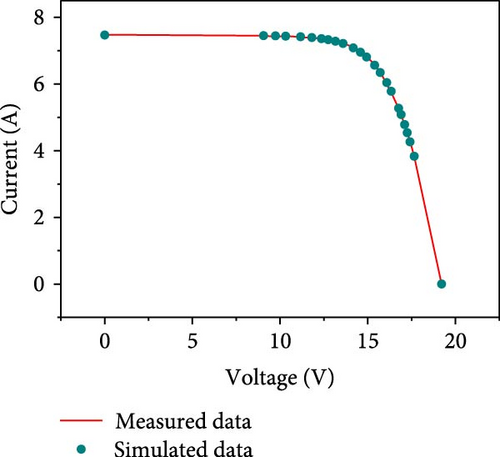
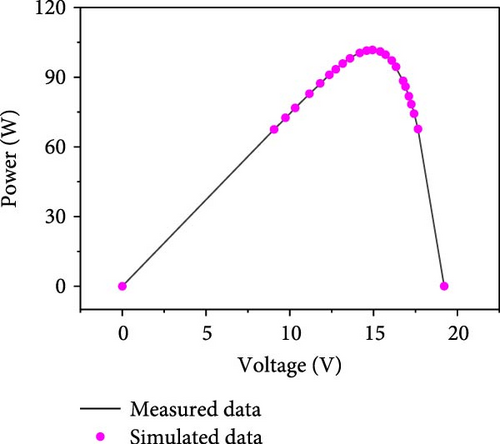
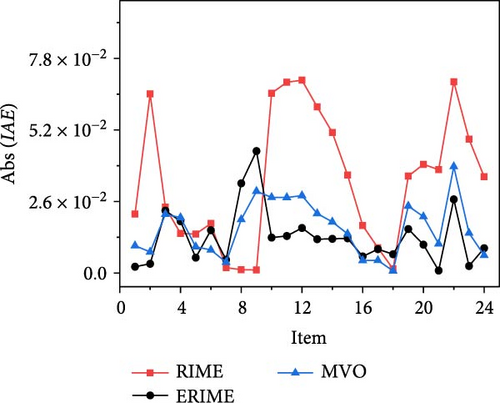
6.3. Statistical Results Analysis
The performance evaluation of the proposed ERIME algorithm needs to be evaluated by multiple computational metrics. Table 19 gives details of the computational metrics, including the optimal value, median, mean, worst value, standard deviation, and (time) average execution time of the algorithms, for each of the algorithms under different PV models for 20 independent runs. Among them, the smaller optimal value indicates the higher accuracy of the algorithm, and the smaller mean and STD (standard deviation) characterize the higher level of the algorithm to avoid premature convergence. From the table, we can see that the proposed method is better than the other eight control methods in terms of optimal value, median, mean, worst value, and standard deviation; specifically, in terms of standard deviation in SDM, the proposed method reduces 1.12E−02, 2.02E−03, 8.84E−05, 1.89E−02, 1.27E−02,1.53E−02,1.17E-02, and 6.72E−04, respectively, compared to PSO, MVO, IJAYA, WOA, RIME, ARSO, FPSO, and RGWO. In terms of average execution time, the proposed method though is similar to the other methods.
| Function | Method | Best | Median | Mean | Worst | STD | Time |
|---|---|---|---|---|---|---|---|
| SDM | PSO | 0.001068181 | 0.001998167 | 0.005531128 | 0.038151316 | 0.011166373 | 0.087 |
| MVO | 0.001132318 | 0.002057314 | 0.003068542 | 0.007217234 | 0.002019791 | 0.102 | |
| IJAYA | 0.000986586 | 0.000998598 | 0.001028925 | 0.001366016 | 8.84437E−05 | 0.096 | |
| WOA | 0.001453948 | 0.006687895 | 0.018043656 | 0.046856357 | 0.018912314 | 0.091 | |
| ARSO | 0.01444009 | 0.023741551 | 0.028398838 | 0.054457317 | 0.012717496 | 0.039 | |
| FPSO | 0.001012725 | 0.002126272 | 0.008158853 | 0.046013568 | 0.015263371 | 0.038 | |
| RGWO | 0.002939514 | 0.009149124 | 0.013172087 | 0.040511369 | 0.011740014 | 0.053 | |
| RIME | 0.000992647 | 0.002079889 | 0.002101248 | 0.003551153 | 0.000671535 | 0.097 | |
| ERIME | 9.86021878E−04 | 9.86021878E−04 | 9.86021878E−04 | 9.86021878E−04 | 4.00791594E−17 | 0.104 | |
| DDM | PSO | 0.000990127 | 0.002427166 | 0.009023655 | 0.03948799 | 0.014312674 | 0.103 |
| MVO | 0.001697627 | 0.003236121 | 0.003738357 | 0.008885977 | 0.001752205 | 0.109 | |
| IJAYA | 0.000986874 | 0.0010161 | 0.001062595 | 0.001338666 | 0.000101312 | 0.109 | |
| WOA | 0.00118447 | 0.002122955 | 0.006957991 | 0.042112577 | 0.010158958 | 0.110 | |
| ARSO | 0.004046547 | 0.021715086 | 0.021982001 | 0.042107176 | 0.011785614 | 0.051 | |
| FPSO | 0.001215071 | 0.002448049 | 0.007338198 | 0.043495207 | 0.012835419 | 0.051 | |
| RGWO | 0.003966691 | 0.007197173 | 0.008835605 | 0.042122235 | 0.008189208 | 0.072 | |
| RIME | 0.001005833 | 0.001823055 | 0.002010876 | 0.004040904 | 0.000985289 | 0.115 | |
| ERIME | 9.83051497E−04 | 9.84993563E−04 | 9.85003917E−04 | 9.87672700E−04 | 1.25947672E−06 | 0.117 | |
| TDM | PSO | 0.000994332 | 0.002276351 | 0.017536177 | 0.191125756 | 0.042828628 | 0.137 |
| MVO | 0.001887555 | 0.002797808 | 0.003333507 | 0.00692121 | 0.001553588 | 0.137 | |
| IJAYA | 0.000992341 | 0.001013985 | 0.001096751 | 0.001398399 | 0.00013416 | 0.129 | |
| WOA | 0.001347989 | 0.004153205 | 0.009189198 | 0.044536284 | 0.012012349 | 0.124 | |
| ARSO | 0.007805789 | 0.024399956 | 0.025072666 | 0.034305855 | 0.005634489 | 0.058 | |
| FPSO | 0.001368654 | 0.002167688 | 0.008327167 | 0.036297802 | 0.012719265 | 0.061 | |
| RGWO | 0.005409982 | 0.010472056 | 0.018219709 | 0.041970137 | 0.013738068 | 0.088 | |
| RIME | 0.001118644 | 0.002441621 | 0.002494416 | 0.004491961 | 0.00094356 | 0.133 | |
| ERIME | 9.82600674E−04 | 9.85546404E−04 | 9.88652857E−04 | 1.03889189E−03 | 1.20837572E−05 | 0.142 | |
| PV_PWP201 | PSO | 0.002445336 | 0.002608134 | 0.036804184 | 0.274250778 | 0.084007926 | 0.074 |
| MVO | 0.002431777 | 0.002665561 | 0.016490241 | 0.274250823 | 0.060673253 | 0.142 | |
| IJAYA | 0.002426502 | 0.002432762 | 0.00243897 | 0.002527151 | 2.16361E-05 | 0.080 | |
| WOA | 0.002708903 | 0.012038495 | 0.116728217 | 0.274352338 | 0.13314498 | 0.077 | |
| ARSO | 0.013150219 | 0.027232241 | 0.02623238 | 0.040542673 | 0.008894267 | 0.038 | |
| FPSO | 0.00247552 | 0.002608134 | 0.029143791 | 0.274250778 | 0.065882268 | 0.034 | |
| RGWO | 0.004488224 | 0.007757141 | 0.035192878 | 0.274292152 | 0.081860987 | 0.053 | |
| RIME | 0.002440897 | 0.002606807 | 0.002953233 | 0.005063505 | 0.000665031 | 0.089 | |
| ERIME | 2.42507487E−03 | 2.42507487E−03 | 2.42507487E−03 | 2.42507487E−03 | 2.34379915E−17 | 0.082 | |
| PV_STM6_40 | PSO | 0.003330454 | 0.005360369 | 0.086701769 | 0.310757409 | 0.133212246 | 0.073 |
| MVO | 0.005357325 | 0.023471373 | 0.105507261 | 0.310757448 | 0.138048163 | 0.080 | |
| IJAYA | 0.001758353 | 0.002103419 | 0.002225532 | 0.003329793 | 0.00044539 | 0.086 | |
| WOA | 0.008597182 | 0.025267461 | 0.057896963 | 0.310965197 | 0.089020092 | 0.087 | |
| ARSO | 0.007265003 | 0.02259609 | 0.022655042 | 0.063728938 | 0.012868287 | 0.035 | |
| FPSO | 0.003330321 | 0.004966507 | 0.111368941 | 0.310757409 | 0.150113441 | 0.032 | |
| RGWO | 0.006220049 | 0.012464276 | 0.014176619 | 0.051723576 | 0.009717092 | 0.051 | |
| RIME | 0.020229141 | 0.032755934 | 0.031601786 | 0.033339326 | 0.003329882 | 0.077 | |
| ERIME | 1.72981371E−03 | 1.72981371E−03 | 1.72981371E−03 | 1.72981371E−03 | 3.49060259E−13 | 0.089 | |
| PV_STP6_120 | PSO | 0.035402678 | 0.249523985 | 0.726613588 | 1.413122041 | 0.640914017 | 0.066 |
| MVO | 0.019032429 | 0.054405107 | 0.252639044 | 1.413121505 | 0.500248446 | 0.092 | |
| IJAYA | 0.016873239 | 0.017572389 | 0.01818413 | 0.024365155 | 0.002115459 | 0.076 | |
| WOA | 0.043841975 | 0.430899334 | 0.621754493 | 1.715656706 | 0.530687957 | 0.077 | |
| ARSO | 0.093082339 | 0.323020844 | 0.313795587 | 0.574137574 | 0.129178508 | 0.038 | |
| FPSO | 0.017315179 | 0.247968398 | 0.668896023 | 1.413122041 | 0.627840292 | 0.033 | |
| RGWO | 0.058030304 | 0.094848335 | 0.306418152 | 1.413122662 | 0.480692984 | 0.053 | |
| RIME | 0.041089462 | 0.055037931 | 0.053591986 | 0.055433217 | 0.003331194 | 0.080 | |
| ERIME | 1.66006031E−02 | 1.66006031E−02 | 1.66006037E−02 | 1.66006100E−02 | 1.75412134E−09 | 0.086 | |
- The bold values indicate the best result.
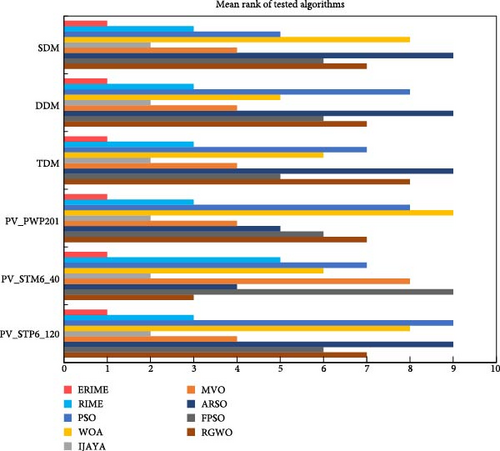
Figure 15 further gives the ranking of the mean values of the different methods on the different tested models; it can be seen that the proposed method has the best ranking among all the six models, followed by the IJAYA method; and the worst overall ranking is the WOA method, which shows the ease with which WOA can fall into a local optimum in solving the PV problem. Therefore, we can conclude that the parameter estimates obtained by the proposed method have a higher accuracy and perform better on average compared to the PV evaluation parameter results obtained by the other eight methods used.
7. Conclusions
- (1)
Firstly, modified soft-rime search strategy is proposed to enhance the exploitation of the original RIME algorithm, which effectively improves the accuracy of the algorithm; furthermore, a shared information mutation mechanism is proposed to increase the degree of information exchange between different agents of the population throughout the search process, which is conducive to the preservation of the diversity of the population as well as to increase the ability of jumping out of the local optimal point.
- (2)
To verify the method search performance, the proposed method is compared with its opponents on the latest test suites. Statistical results show that the proposed method is superior to its peers in terms of convergence speed and solution accuracy and can better balance the exploration and development process. The comparison between the Friedman test and the Wilcoxon signed-rank test also illustrates the advantages of the proposed method.
- (3)
The proposed method is employed along with the control method to extract the unknown parameters of different PV cell panels. Simulation results in 20 repetitions of the experiment with RMSE as the optimization objective show that the proposed method is able to produce more accurate results than other methods in SDM, DDM, TDM, and PVM PV cell models. In the statistical analysis of the multiple methods, we can clearly see that the optimal values, mean, and standard deviation obtained by the proposed method are lower than the optimization results obtained by the control method.
Therefore, we finally conclude that the proposed method can effectively improve the level of PV parameter identification and has been proved to be a good method for PV parameter estimation. In future work, we will further consider the modeling of the proposed method under different extreme environmental conditions, such as temperature, light irradiance, and wind speed, and try to improve the adaptability of the proposed method.
Conflicts of Interest
The authors declare no conflict of interest.
Open Research
Data Availability
Data are available on request.




