International Journal of Differential Equations

Volume 2024, Issue 1 9141971

Research Article

Open Access

Implementing Bernstein Operational Matrices to Solve a Fractional-Order Smoking Epidemic Model

Jalal Al Hallak,

Corresponding Author

Jalal Al Hallak

[email protected]

orcid.org/0000-0001-8350-5511

Department of Mathematical Sciences , Universiti Kebangsaan Malaysia , Bangi , 43600 , Selangor, Malaysia , ukm.my

College of Interdisciplinary Studies , Zayed University , Abu Dhabi , UAE , zu.ac.ae

Search for more papers by this author

Mohammed Alshbool,

Corresponding Author

Mohammed Alshbool

[email protected]

orcid.org/0000-0002-4832-8772

Department of Mathematics and Statistics , Zayed University , Abu Dhabi , UAE , zu.ac.ae

Search for more papers by this author

Ishak Hashim,

Ishak Hashim

orcid.org/0000-0003-4237-7140

Department of Mathematical Sciences , Universiti Kebangsaan Malaysia , Bangi , 43600 , Selangor, Malaysia , ukm.my

Nonlinear Dynamics Research Center (NDRC) , Ajman University , P.O. Box 346, Ajman , UAE , ajman.ac.ae

Search for more papers by this author

Jalal Al Hallak,

Corresponding Author

Jalal Al Hallak

[email protected]

orcid.org/0000-0001-8350-5511

Department of Mathematical Sciences , Universiti Kebangsaan Malaysia , Bangi , 43600 , Selangor, Malaysia , ukm.my

College of Interdisciplinary Studies , Zayed University , Abu Dhabi , UAE , zu.ac.ae

Search for more papers by this author

Mohammed Alshbool,

Corresponding Author

Mohammed Alshbool

[email protected]

orcid.org/0000-0002-4832-8772

Department of Mathematics and Statistics , Zayed University , Abu Dhabi , UAE , zu.ac.ae

Search for more papers by this author

Ishak Hashim,

Ishak Hashim

orcid.org/0000-0003-4237-7140

Department of Mathematical Sciences , Universiti Kebangsaan Malaysia , Bangi , 43600 , Selangor, Malaysia , ukm.my

Nonlinear Dynamics Research Center (NDRC) , Ajman University , P.O. Box 346, Ajman , UAE , ajman.ac.ae

Search for more papers by this author

First published: 18 November 2024

https://doi.org/10.1155/2024/9141971

Academic Editor: Amar Nath Chatterjee

Share a link

Email
Wechat
Bluesky

Abstract

This paper leverages the Bernstein operational matrices method for the first time in order to resolve the nonlinear fractional smoking epidemic model presented in terms of Caputo’s fractional derivative. An approximate solution is derived using Bernstein’s operational matrices and strategically chosen collocation points. This is followed by the validation of the proposed method’s accuracy and reliability against the established Runge–Kutta fourth-order method. Furthermore, a comprehensive comparative analysis is conducted against two prominent techniques: the fractional differential transform method (FDTM) and the q-homotopy analysis transform method (q-HATM). The results show a superior and significant performance regarding accuracy as well as approximation. A residual corrected error technique is employed to enhance the precision of the presented method, thus effectively minimising absolute errors.

1. Introduction

The global response to infectious diseases highlights the importance of utilising mathematical epidemic models to comprehend and manage disease spread. As these models become more complex, the demand for advanced computing systems capable of handling this complexity with high accuracy and efficiency grows. Recently, numerous research papers have been published showcasing the latest advancements in computational techniques aimed at enhancing the reliability and performance of epidemic and biological modelling. These developments offer a crucial perspective on addressing current and future outbreaks [1–4].

Smoking denotes an example of an extremely hazardous behaviour that spreads through the population, like infectious diseases. It can cause cancer, chronic lung disease, cardiovascular disease and diabetes. According to the World Health Organization (WHO), tobacco use causes the deaths of over eight million people each year. In addition, 1.3 million nonsmokers are estimated to be exposed to secondhand smoke every year [5]. Approximately 80% of the world’s 1.3 billion tobacco users live in low- and middle-income countries. Data from 2020 show that 22.3% of the global population used tobacco, with usage being significantly higher among males (36.7%) compared with females (7.8%). As a result, numerical analysis modelling is often employed to study smoking behaviour.

In the year 1997, Garsow et al. [6] introduced a basic and simple model for smoking cessation so as to better understand the manner in which smoking spreads in a community. They divided the population into three distinct groups: potential smokers, represented by P; active smokers, signified by S; and quit smokers, denoted by Q, with the possibility of size changes over a period of time. Building upon this initial work, Zaman [7] expanded the smoking epidemic model through the inclusion of another group, occasional or light smokers. Zaman [8] further placed emphasis on controlling the smoking epidemic by considering optimal campaigns and proposing two control measures: treating smokers with medication and educating potential smokers about the hazards of smoking. The researcher formulated a control problem and exemplified the existence of an optimal control strategy, emphasising the prevalence of smoking can be reduced significantly by ensuring the proper implementation of both measures. Further investigations integrated supplementary parameters and smoking-related characteristics into the modelling approach.

A novel model for giving up smoking was proposed by Zeb et al. [9], who explored the local as well as global stability of the epidemic model, along with its general solutions. Subsequently, Erturk et al. [10] introduced fractional-order derivatives into the ordinary differential equation model by Zeb et al. [9] and employed generalised Euler as well as the generalised multistep differential transform. On the other hand, Khalid et al. [11] employed a perturbation–iteration algorithm in order to examine a smoking model consisting of five variables, incorporating the Caputo fractional derivative. Meanwhile, Haq et al. [12] implemented the Laplace transformation to determine numerical approximations for the smoking model with a Caputo fractional derivative. Furthermore, Singh et al. [13] established theorems with respect to the existence and uniqueness of a smoking cessation model equipped with the Caputo–Fabrizio derivative, employing the fixed-point postulate. Then, Uçar et al. [14] aimed to analyse the outcome of the Atangana–Baleanu derivative by addressing the smoking model introduced to delve into the existence and uniqueness of the fractionalised model. Recently, the q-homotopy analysis transform method (q-HATM) was utilised to approximate the fractional smoking model by Veeresha et al. [15] and then Günerhan et al. [16] used the fractional differential transform method (FDTM) to resolve the model, also comparing their results with q-HATM. Thereafter, Haidong et al. [17] investigated a new time noninteger-order smoking system of equations with a Caputo fractional-type derivative operator and examined its qualitative aspects. The model exhibited stability and convergence, with improved stability being showcased by smaller fractional orders displaying. Numerous other researchers have performed extensive investigations on the mathematical epidemic smoking model [18–26].

The model explored in this study is the fractional smoking epidemic model, designed to study and forecast how smoking affects individuals’ health and the population as a whole. The model divides the population into five distinct groups: potential smokers, occasional smokers, smokers, permanent quitters and temporary quitters. The investigation’s parameters include the recruiting rate, effective contact rate, natural death rate, smoking cessation rate and transition rates among smoking classes. Integrating fractional calculus into the model allows for the simulation of individual behaviour over time, incorporating memory effects and nonlocality. These variables are crucial for accurately representing physical activities such as smoking habits. The model provides a framework for studying and understanding how smoking habits evolve within a community, helping scholars address specific issues related to smoking trends. The results indicate that both the fractional order and the parameter system significantly influence the development of smoking. The solutions discovered for various categories of smokers are potential, occasional and permanent quitters, which offer meaningful insights into smoking habits over time and the impact of different factors on the model’s stability.

Numerous scientists have put forth various methodologies for evaluating smoking trends and the role of mathematical models in addressing this significant public health issue. The endeavour of this research is to provide an approximate solution for a fractional-order smoking pandemic model using the Bernstein operational matrices approach. This method assesses the impact of smoking on various population groups and compares the effectiveness of the Bernstein operational matrices technique to other well-established methods. This work lays the groundwork for future investigations into smoking behaviour and the development of strategies to reduce smoking-related illnesses and fatalities. Consequently, there will be comprehensive model improvements, an examination of additional factors influencing smoking behaviour and an expansion of the research to include diverse populations and geographical regions.

Fractional calculus has been an interest of many researchers and is extensively used in engineering and science, with numerous applications in electromagnetics, fluid mechanics and epidemiology [27–31]. Alshbool et al. [32] solved some mathematical systems comprising second-order BVPs, a Brusselator system, as well as a nonlinear stiff system using the Bernstein polynomials approach. This research extends the application of Bernstein polynomials to solve a fractional smoking epidemic system, offering several benefits. It reduces the time required to calculate approximate solutions, thereby accelerating numerical analysis and computation. At the same time, it decreases the computational workload compared to traditional methods whilst maintaining the accuracy and efficiency of the approximate solutions. This method is particularly powerful for analysing nonlinear fractional differential equations in complex problems across epidemiology, science and engineering.

This study provides unique insights into smoking cessation dynamics and presents a significant approximate solution. However, practical applications of these findings should consider other factors, such as the complexity of human behaviour and the social and environmental influences on smoking. The need for interdisciplinary collaboration is essential to translate the mathematical model into effective smoking-cessation programs. Therefore, while the study offers an intriguing framework for explaining smoking habit dynamics, its real-life application may require further research and collaboration with specialists in public health, psychiatry and behavioural sciences.

The structure of the paper is as follows. In Section 2, important definitions and preliminaries necessary for the study are presented. Section 3 presents the fractional order smoking epidemic mathematical model, the existence of the smoking-free equilibrium (SFE), the basic reproduction number R₀, and the stability of the endemic equilibrium of the smoking system. Section 4 illustrates the Bernstein operational matrices method. In Section 5, numerical approximation results of the fractional smoking epidemic model are presented, with comparisons made to FDTM and q-HATM from the literature, along with error estimates. Section 6 elaborates on the residual correction technique. Section 7 discusses the numerical findings of the smoking model. Finally, Section 8 provides a summary of the study’s findings.

2. Preliminaries

In this section, essential definitions and properties of fractional derivatives in Caputo’s sense that are needed throughout this paper to numerically solve the given smoking system of fractional order are introduced [33–36].

Definition 1. The Caputo fractional derivative of a function g(t) having an order of α > 0 is given by

()

such that s − 1 < α < s, s ∈ N, t > 0, and

, where

is the space of functions with minimal smoothness, ensuring the Caputo derivative is well defined for 0 ≤ α ≤ s.

For the Caputo fractional derivative, we have two essential properties defined as

a.
For , s ∈ N, we have D^αg is well defined when 0 ≤ α ≤ s and D^αg ∈ C₋₁.
b.
For s − 1 ≤ α ≤ s, s ∈ N, for q ≥ −1, where is a smoother function space ensuring continuity and differentiability for s − 1 ≤ α ≤ s, we have

()

In the case of the Caputo derivative, we have

a.
D^αk = 0, (k constant),
b.

Definition 2. The Bernstein polynomial of order n on the interval [0, 1] is

()

Employing the Binomial theorem in equation (3), we obtain

()

Definition 3. The Bernstein polynomial of order n on the interval [0, R] is

()

Definition 4. The Bernstein polynomial of order n on the interval [a, b] is

()

Substituting t⟶t^α in equation (3), we obtain the fractional Bernstein polynomial on [0, 1] as follows:

()

3. Analysis of the Fractional-Order Smoking Epidemic Model

In this section, we present the fractional-order smoking epidemic mathematical model, the existence of the SFE, the process of finding the basic reproduction number R₀ using the next-generation matrix method, and we assess the stability of the endemic equilibrium for the given fractional-order smoking model.

3.1. Fractional-Order Smoking Epidemic Model

This research investigates an existing fractional-order epidemic system of equations from literature [15, 16] used for simulating the dynamics of smoking. The Caputo fractional form incorporates the fractional derivative; the system is expressed as follows:

()

with initial conditions

()

In the system of equation (8), D^α denotes the operator for the fractional-order derivative of order α such that (0 < α ≤ 1). At time t, the whole population size is represented as T(t) and splits into five distinct subgroups: potential smokers represented as P(t), occasional smokers as O(t), smokers as S(t), people who have quit smoking permanently as L(t) and those who have quit smoking temporarily as Q(t).

The following parameters are accorded special significance in the given system of equation (8), where the recruitment rate is represented by ω, the linkage index between light and potential smokers is signified by σ, the natural mortality rate is denoted by κ, the smoking cessation rate is represented by η, the smokers who never smoke again are signified by μ, the rate between light and heavy smokers are denoted by β and λ showcases the linkage index between temporary quitters who might get back to smoking.

3.2. Existence of the SFE

The existence of the SFE is crucial, as it represents a state where the smoking prevalence reaches zero, indicating no further progression. It can be found by setting the time derivatives of the system (8) to zero at equilibrium.

()

The SFE point for system (8) may be calculated directly as follows:

()

where the population at this point consists entirely of potential smokers, with no active smokers, occasional smokers, temporary quitters or permanent quitters [37].

3.3. Basic Reproduction Number R₀

In this section, the process of finding the basic reproduction number R₀ for the fractional-order smoking model using the next-generation matrix method is illustrated. The focus is on the infected compartments of the system, particularly the smokers S(t) and occasional smokers O(t), and linearise the system around the SFE to calculate R₀ [38–41]. The governing equations for S(t) and O(t) are

()

At the SFE, S₀ = 0, O₀ = 0, and P₀ = ω/k. We linearise the system around this point to form the Jacobian matrix J. It is constructed by taking the partial derivatives of the system with respect to S(t) and O(t) as follows:

()

To find the basic reproduction number R₀, we use the next-generation matrix method. The matrix F represents new infections, and V represents the transitions and removals. They are given by

()

The inverse of V is calculated as

()

Multiply F and V⁻¹ to get the next-generation matrix G as follows:

()

This results in

()

The basic reproduction number R₀ is the spectral radius of the next-generation matrix G which is found as follows:

()

If R₀ < 1, then E₀ is locally stable, indicating a decrease in smoking behaviour within the population. If R₀ > 1, then E₀ is unstable, indicating that smoking behaviour will spread among the population. Figure 1 illustrates a graphical phase diagram of R₀ in relation to σ and ω for system (8), where κ, η, and β are constant parameters from Table 1, highlighting the stable and unstable regions.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Phase plan of R₀ with respect to σ and ω for system (8) demonstrating the stable and unstable regions. (a) Stable region. (b) Unstable region.

Table 1. Specified parameter values for equation (8).

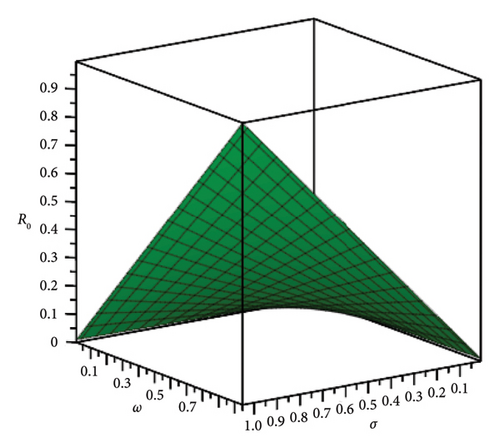
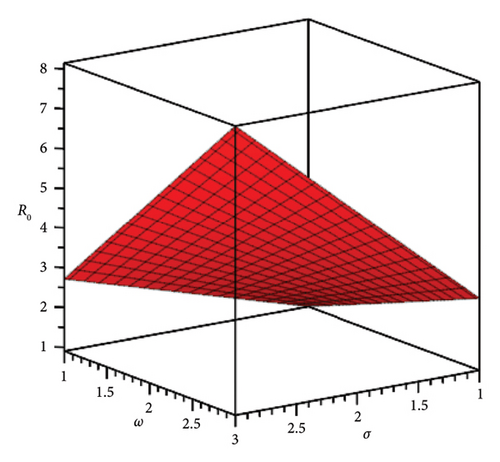
Parameter	Description	Value (unit: 1/time) Source [15]
ω	Recruitment rate in P(t)	1
σ	Linkage index between S(t) and P(t)	0.14
κ	Natural mortality rate	0.05
β	Rate at which O(t) become S(t)	0.002
λ	Linkage index between Q(t) who might get back to smoking	0.0025
η	Smoking cessation rate	0.8
μ	Remaining fraction of smokers who permanently quit smoking	0.1

3.4. Endemic Equilibrium

In this section, we assess the stability of the endemic equilibrium for the fractional smoking model. Using the system of equations provided in the model, we first compute the endemic equilibrium points and then analyse the stability using the Jacobian matrix and eigenvalues.

The endemic equilibrium points for the smoking fractional model in steady state can be summarised as follows:

()

where

()

Using the parameter values from Table 1 and assuming S^∗ = 1 for simplicity, we compute the approximate endemic equilibrium values as follows.

To assess the stability of the endemic equilibrium, we compute the Jacobian matrix J(E^∗) by taking the partial derivatives of the system’s equations with respect to P, O, S, Q, and L. The Jacobian at endemic equilibrium is given by

()

Using the parameter values from Table 1 and assuming S^∗ = 1, the Jacobian at the endemic equilibrium is given by

()

The eigenvalues of the Jacobian matrix are

()

For fractional-order systems, the stability criterion differs slightly from the classical integer-order case. The equilibrium is locally asymptotically stable if the real parts of all eigenvalues λ_i satisfy

()

Given that all the real parts of the eigenvalues are negative, the endemic equilibrium E^∗ is locally asymptotically stable for any fractional order 0 < α ≤ 1 [42].

4. Numerical Method

In this section, the Bernstein operational matrices approximation method [43] is presented using the Caputo fractional derivative properties and the collocation points to solve numerically the nonlinear system of fractional order of the epidemic smoking model presented in equation (8).

We start by considering the system of fractional differential equations as follows:

()

subject to the following initial conditions:

()

where θ_j are constants and j = 1, 2, …, k. Our initial approach is to rewrite equation (26) in the following form:

()

subject to the initial conditions (27).

The Bernstein polynomials of the n th degree are defined by

()

To change equation (29) to fractional Bernstein polynomial, we substitute t⟶t^α into B_i,n(t) to obtain the following:

()

For mathematical convenience, we set the following

, if i < 0 or i > n. In the present method, we approximate any function g_j(t) with the first (n + 1) Bernstein polynomials as follows:

()

where

()

We express the vector ϕ(t) as follows:

()

where

()

such that

()

For j = 1, we have

()

where

()

etc. For j = k, we have

()

where

()

The vector ϕ(t) can be expressed as a fractional derivative as follows:

()

where D^α is (n + 1) × (n + 1) operational matrix of derivative defined as

()

given that

()

By applying equations (31) and (40) in system (28), we obtain the residual

which measures the error in approximating the fractional differential equation as follows:

()

with initial conditions

()

To avoid integration difficulty, the collocation points t₀, t₁, …, t_k in system (43) can be determined by implementing the Chebyshev roots as follows:

()

Consequently, solving the system of equation (43) can be done by finding the collocation points using the equation (45) and using the given initial conditions of (44) to calculate all the c_j,i. Applying all this process will enable us to find approximate solutions g₁(t), g₂(t), …, g_k(t) of the system of fractional order (26).

5. Numerical Results and Error Estimates

In this section, the application of the illustrated method in Section 4 on the given system of equations of fractional order for the smoking epidemic model presented in equation (8) with different parameters is demonstrated. Moreover, a comparison is made between the method in Section 4 with two recent methods applied to the same equation (8), i.e., q-HATM [15] and FDTM [16].

For k = 5 and n = 7, we start implementing our presented method by letting

()

We substitute all the variables in (46) in the system of smoking model (8), then we find residual

as follows:

()

subject to the following initial conditions:

()

Specified values for the parameters in the system of equation (8) are given in Table 1 to verify the effectiveness and precision of the method used in this research.

By finding the collocation points using equation (45) and using the given initial conditions in (48), we calculate all the c_j,i with the help of Maple Software. Then, we find approximate solutions of P(t), O(t), S(t), Q(t) and L(t). The efficiency and accuracy of the presented method are verified when comparing it with the well-known Runge–Kutta fourth-order method (RK4).

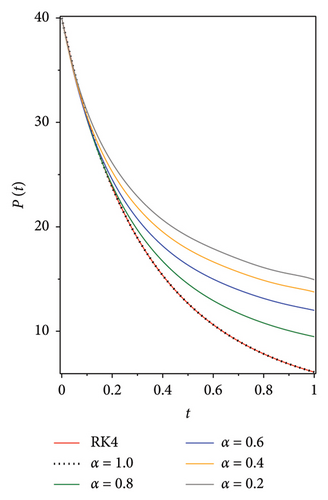
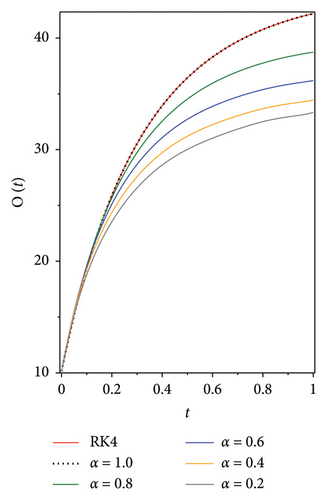
The following graphs show the approximate solutions of P(t), O(t), S(t), Q(t) and L(t) with different values of α, as shown in Figure 2. The accuracy and efficiency of the presented method are clearly seen in all the graphs. Moreover, Tables 2, 3, 4, 5 and 6 show the comparisons of the approximated solutions of the Bernstein operational matrices method with RK4, FDTM, and q-HATM for the given smoking epidemic model 8 at α = 1 and α = 0.9. The results show strong evidence for the validity of the presented method.

Table 2. Approximate solutions of P(t) at n = 7 when α = 1 and α = 0.9 for Bernstein operational matrices, FDTM and q-HATM.

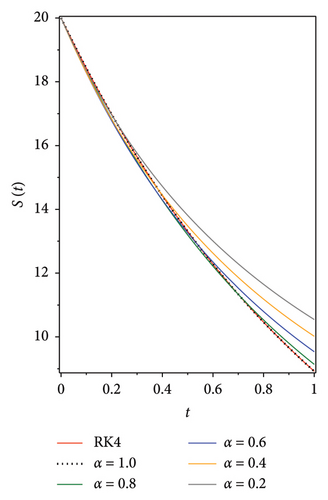
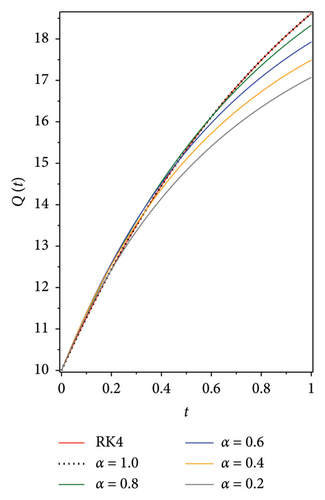
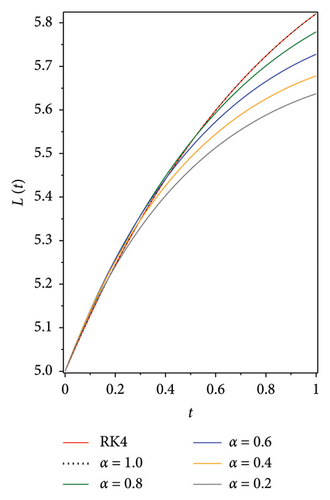
P(t)
t	RK4	α = 1			α = 0.9
t	RK4	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	40	40	40	40	40	40	40
0.1	30.5072	30.5063	30.9766	30.7667	30.3581	26.2807	29.1162
0.2	23.7850	23.7853	24.174	25.6668	23.8256	17.8878	26.0052
0.3	18.9262	18.9271	19.2495	24.7002	19.2628	12.8287	28.4733
0.4	15.3484	15.3480	15.6184	27.867	15.9889	9.6387	35.8752
0.5	12.6687	12.6675	12.8957	35.1672	13.5890	7.5495	47.8402
0.6	10.6306	10.6304	10.8229	46.6008	11.7965	6.1373	64.1152
0.7	9.0588	9.0596	9.223	62.1678	10.4314	5.158	84.5111
0.8	7.8313	7.8315	7.9727	81.8682	9.3728	4.4654	108.878
0.9	6.8620	6.8614	6.9847	105.702	8.5440	3.9687	137.095
1	6.0889	6.0890	6.1962	133.669	7.8904	3.6099	169.057

Table 3. Approximate solutions of O(t) at n = 7 when α = 1 and α = 0.9 for Bernstein operational matrices, FDTM and q-HATM.

O(t)
t	RK4	α = 1			α = 0.9
t	RK4	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	10	10	10	10	10	10	10
0.05	15.0909	15.0913	14.5834	15.0559	15.2268	17.3313	16.6946
0.1	19.3402	19.3411	18.8789	19.0756	19.4832	23.474	20.6741
0.15	22.9048	22.9053	22.4858	22.059	22.9735	28.0928	22.8892
0.2	25.9090	25.9087	25.5286	24.0063	25.8561	31.6072	23.5858
0.25	28.4522	28.4513	28.1067	24.9173	28.2532	34.3096	22.8977
0.3	30.6140	30.6131	30.2999	24.7922	30.2590	36.4067	20.9135
0.35	32.4585	32.4582	32.1728	23.6308	31.9467	38.047	17.6978
0.4	34.0380	34.0385	33.7777	21.4332	33.3732	39.3381	13.3004
0.45	35.3950	35.3959	35.1575	18.1994	34.5835	40.3594	7.76208
0.5	36.5641	36.5653	36.3473	13.9294	35.6138	41.1701	1.11636

Table 4. Approximate solutions of S(t) at n = 7 when α = 1 and α = 0.9 for Bernstein operational matrices, FDTM and q-HATM.

S(t)
t	RK4	α = 1			α = 0.9
t	RK4	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	20	20	20	20	20	20	20
0.1	18.4221	18.4221	18.5009	18.4244	18.3696	17.5281	17.9798
0.2	16.9756	16.9756	17.0509	16.9938	16.8930	15.2715	16.4515
0.3	15.6484	15.6484	15.7202	15.708	15.5537	13.3178	15.1913
0.4	14.4298	14.4298	14.4982	14.5671	14.3372	11.6235	14.1491
0.5	13.3102	13.3102	13.3753	13.5711	13.2309	10.1521	13.2994
0.6	12.2810	12.2810	12.3429	12.7201	12.2235	8.8727	12.626
0.7	11.3344	11.3344	11.3932	12.0138	11.3053	7.7594	12.1178
0.8	10.4633	10.4633	10.5192	11.4525	10.4675	6.7897	11.7662
0.9	9.6615	9.6615	9.7144	11.036	9.7023	5.9444	11.5645
1	8.9231	8.9231	8.9733	10.7645	9.0028	5.2073	11.5073

Table 5. Approximate solutions of Q(t) at n = 7 when α = 1 and α = 0.9 for Bernstein operational matrices, FDTM and q-HATM.

Q(t)
t	RK4	α = 1			α = 0.9
t	RK4	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	10	10	10	10	10	10	10
0.1	11.2780	11.2780	11.2142	11.276	11.3198	11.9966	11.6331
0.2	12.4398	12.4398	12.3791	12.4241	12.5034	13.7923	12.852
0.3	13.4959	13.4959	13.4382	13.4443	13.5654	15.3195	13.8408
0.4	14.4556	14.4556	14.401	14.3365	14.5184	16.6167	14.6413
0.5	15.3276	15.3276	15.2759	15.1008	15.3737	17.7164	15.2749
0.6	16.1194	16.1194	16.0705	15.7372	15.3737	18.6462	15.755
0.7	16.8381	16.8381	16.7919	16.2456	16.8297	19.4293	16.0913
0.8	17.4898	17.4898	17.4462	16.626	17.4471	20.0859	16.2908
0.9	18.0802	18.0802	18.0392	16.8786	18.0003	20.6329	16.3594
1	18.6145	18.6145	18.5759	17.0032	18.4954	21.0851	16.3015

Table 6. Approximate solutions of L(t) at n = 7 when α = 1 and α = 0.9 for Bernstein operational matrices, FDTM and q-HATM.

L(t)
t	RK4	α = 1			α = 0.9
t	RK4	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	5	5	5	5	5	5	5
0.1	5.1283	5.1283	5.1218	5.128	5.1324	5.1998	5.1636
0.2	5.2438	5.2438	5.2377	5.2422	5.2499	5.3765	5.2841
0.3	5.3478	5.3478	5.342	5.3426	5.3540	5.5235	5.3803
0.4	5.4410	5.4410	5.4356	5.4291	5.4460	5.6446	5.4564
0.5	5.5245	5.5245	5.5194	5.5017	5.5271	5.7434	5.5148
0.6	5.5990	5.5990	5.5942	5.5605	5.5983	5.8229	5.5567
0.7	5.6653	5.6653	5.6608	5.6054	5.6606	5.8856	5.5832
0.8	5.7239	5.7239	5.7197	5.6365	5.7149	5.9338	5.595
0.9	5.7756	5.7756	5.7717	5.6537	5.7618	5.9693	5.5928
1	5.8209	5.8209	5.8173	5.657	5.8021	5.9939	5.577

Tables 7, 8, and 9 compare the absolute error of P(t), O(t), S(t), Q(t) and L(t) when α = 1 and n = 7 for Bernstein operational method, FDTM, q-HATM and RK4. The calculations show that the absolute error for all the functions in our presented method is less than the other two methods (FDTM and q-HATM).

Table 7. Absolute error of P(t) and S(t) at n = 7 when α = 1 for Bernstein operational, FDTM, q-HATM and RK4.

t	Absolute error of P(t)			Absolute error of S(t)
t	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	0	0	0	0	0	0
0.1	9.0 × 10⁻⁴	4.7 × 10⁻¹	2.6 × 10⁻¹	3.3 × 10⁻⁷	7.9 × 10⁻²	2.3 × 10⁻³
0.2	2.5 × 10⁻⁴	3.9 × 10⁻¹	1.9 × 10⁰	2.4 × 10⁻⁷	7.5 × 10⁻²	1.8 × 10⁻²
0.3	8.9 × 10⁻⁴	3.2 × 10⁻¹	5.8 × 10⁰	4.0 × 10⁻⁷	7.2 × 10⁻²	6.0 × 10⁻²
0.4	4.1 × 10⁻⁴	2.7 × 10⁻¹	1.2 × 10¹	2.4 × 10⁻⁷	6.8 × 10⁻²	1.4 × 10⁻¹
0.5	1.1 × 10⁻³	2.3 × 10⁻¹	2.3 × 10¹	4.4 × 10⁻⁷	6.5 × 10⁻²	2.6 × 10⁻¹
0.6	1.4 × 10⁻⁴	1.9 × 10⁻¹	3.6 × 10¹	2.0 × 10⁻⁷	6.2 × 10⁻²	4.4 × 10⁻¹
0.7	8.4 × 10⁻⁴	1.6 × 10⁻¹	5.3 × 10¹	7.1 × 10⁻⁷	5.9 × 10⁻²	6.8 × 10⁻²
0.8	1.6 × 10⁻⁴	1.4 × 10⁻¹	7.4 × 10⁻¹	3.2 × 10⁻⁷	5.6 × 10⁻²	9.9 × 10⁻¹
0.9	5.8 × 10⁻⁴	1.2 × 10⁻¹	9.9 × 10¹	1.2 × 10⁻⁷	5.3 × 10⁻²	1.4 × 10⁰
1	9.8 × 10⁻⁵	1.1 × 10⁻¹	1.3 × 10²	8.4 × 10⁻⁷	5.0 × 10⁻²	1.8 × 10⁰

Table 8. Absolute error of Q(t) and L(t) at n = 7 when α = 1 for Bernstein operational, FDTM, q-HATM and RK4.

t	Absolute error of Q(t)			Absolute error of L(t)
t	Present method	FDTM	q-HATM	Present method	FDTM	q-HATM
0	0	0	0	0	0	0
0.1	1.1 × 10⁻⁷	6.4 × 10⁻²	2.0 × 10⁻³	6.9 × 10⁻⁹	6.5 × 10⁻³	3 × 10⁻⁴
0.2	4.4 × 10⁻⁸	6.0 × 10⁻²	1.6 × 10⁻²	3.8 × 10⁻⁹	6.1 × 10⁻³	1.6 × 10⁻³
0.3	7.8 × 10⁻⁷	5.8 × 10⁻²	5.2 × 10⁻²	5.0 × 10⁻⁹	5.8 × 10⁻³	5.2 × 10⁻³
0.4	8.6 × 10⁻⁸	5.5 × 10⁻²	1.2 × 10⁻¹	1.1 × 10⁻⁸	5.4 × 10⁻³	1.2 × 10⁻²
0.5	1.8 × 10⁻⁷	5.2 × 10⁻²	2.3 × 10⁻¹	2.5 × 10⁻⁸	5.1 × 10⁻³	2.3 × 10⁻²
0.6	4.5 × 10⁻⁸	4.9 × 10⁻²	3.8 × 10⁻²	2.9 × 10⁻⁹	4.8 × 10⁻³	3.9 × 10⁻²
0.7	1.2 × 10⁻⁷	4.6 × 10⁻²	5.9 × 10⁻¹	6.9 × 10⁻⁸	4.5 × 10⁻³	6.0 × 10⁻²
0.8	1.3 × 10⁻⁷	4.4 × 10⁻²	8.6 × 10⁻¹	8.0 × 10⁻⁸	4.2 × 10⁻³	8.7 × 10⁻²
0.9	2.7 × 10⁻⁷	4.1 × 10⁻²	1.2 × 10⁰	1.3 × 10⁻⁷	3.9 × 10⁻³	1.2 × 10⁻¹
1	8.5 × 10⁻⁷	3.9 × 10⁻²	1.6 × 10⁰	1.6 × 10⁻⁷	3.6 × 10⁻³	1.6 × 10⁻¹

Table 9. Absolute error of O(t) at n = 7 when α = 1 for Bernstein operational, FDTM, q-HATM and RK4.

Absolute error of O(t)
t	Present method	FDTM	q-HATM
0	0	0	0
0.05	4.0 × 10⁻⁴	5.1 × 10⁻¹	3.5 × 10⁻²
0.1	9.2 × 10⁻⁴	4.6 × 10⁻¹	2.6 × 10⁻¹
0.15	5.4 × 10⁻⁴	4.2 × 10⁻¹	8.5 × 10⁻¹
0.2	8.9 × 10⁻⁴	3.8 × 10⁻¹	1.9 × 10⁰
0.25	8.9 × 10⁻⁴	3.5 × 10⁻¹	3.5 × 10⁰
0.3	4.0 × 10⁻⁴	3.1 × 10⁻¹	5.8 × 10⁰
0.35	3.5 × 10⁻⁴	2.9 × 10⁻¹	8.8 × 10⁰
0.4	4.1 × 10⁻⁴	2.6 × 10⁻¹	1.3 × 10¹
0.45	9.9 × 10⁻⁴	2.4 × 10⁻¹	1.7 × 10¹
0.5	1.1 × 10⁻³	2.2 × 10⁻¹	2.3 × 10¹

6. Residual Correction Technique

In this section, we introduce a residual correction technique to approximate the solutions for the system of differential equations by minimising the absolute error to the greatest extent possible.

Let g_j(t) and be the exact and the approximate solutions, respectively, of equation (26). In the following technique, a residual correction can be applied to improve the estimations of the absolute error.

We start the residual correction technique by writing equation (26) as follows:

()

Let R_j be defined as follows:

()

Adding and subtracting R_j from equation (26) produces the following equation for the absolute error.

()

We solve equation (51) using the presented method in Section 4 with degree m such that m > n, where having the following initial condition .

Corollary 1. Let and be the approximate solutions of equations (26) and (51), respectively. Then, is considered the corrected approximate solution of equation (26) having the following error function . Taking into consideration that if , then is the estimation of the absolute error. Furthermore, if , we can conclude that is more precise solution compared with in any given norm. The optimal n in the presented method that finds the minimal absolute error might be found by at any given norm.

Corollary 2. To find the approximate solutions for different values on n, we start first by using the triangle inequality that implies the following.

()

If the prior errors are sufficiently spread out, we may estimate a rough upper bound for the resultant error. To test the upper bound, we perform the following steps: if the error sequence is increasing (or decreasing), then

()

where |g(t) − g_n+1(t)| = K|g(t) − g_n(t)|0 ⩽ t < 1.

If K > 1, then both absolute errors can be considered very good approximations.

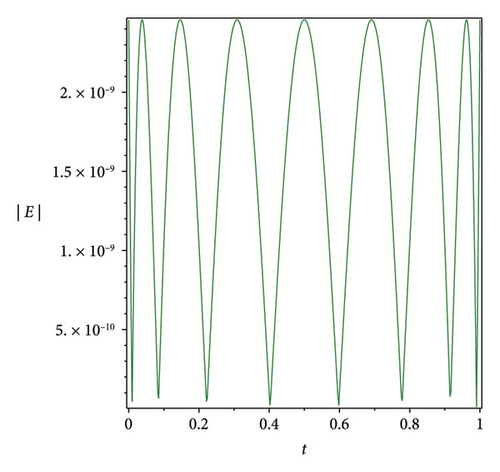
The efficiency residual correction technique is shown in Figure 3 where the absolute error function at n = 3 is much higher compared with the corrected absolute error function at n = 3 and m = 8 of the Bernstein operational matrices method at α = 1 for S(t), Q(t) and L(t), which shows the applicability, efficiency and accuracy of the corrected absolute error technique.

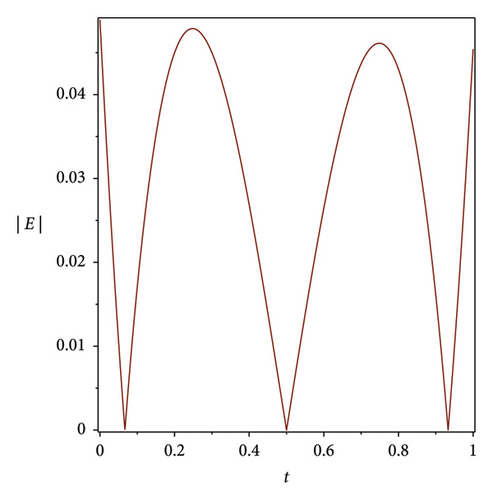
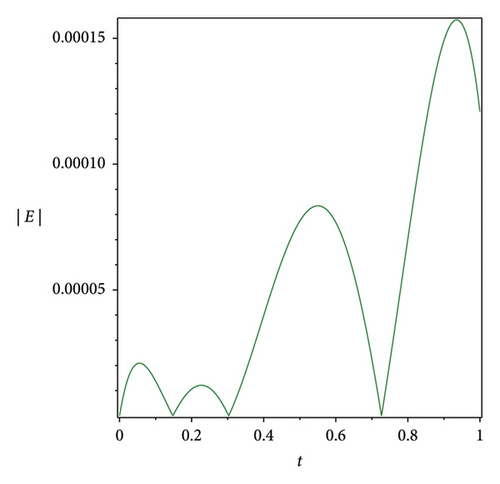
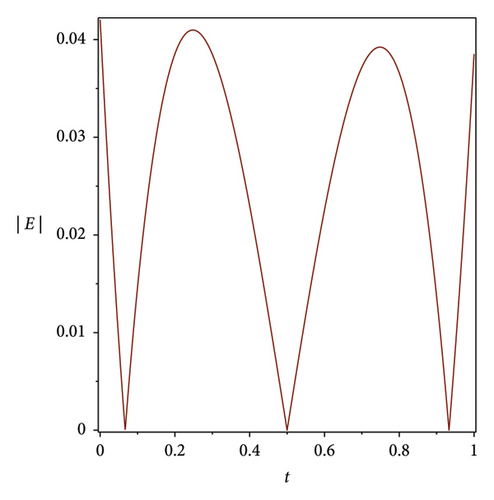
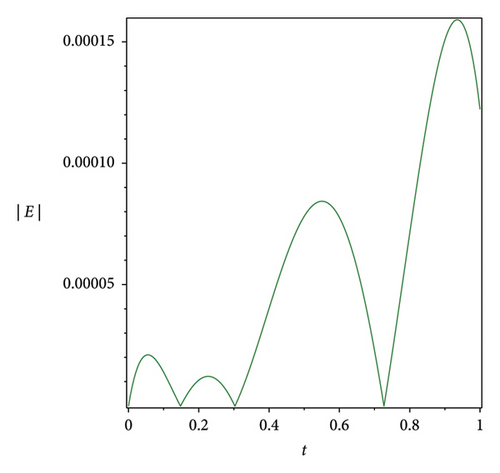
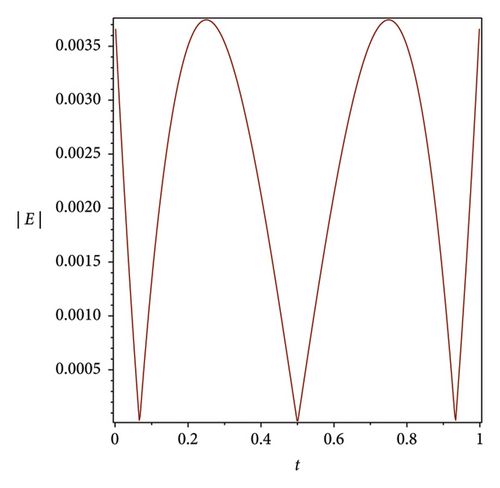
7. Discussion

The numerical results reveal distinct behaviours among the subgroups P(t), O(t), S(t), Q(t) and L(t) as the fractional order α varies, providing meaningful insights into smoking behaviour modelling. For α = 1, where memory effects are minimal, the decline in potential smokers P(t) and smokers S(t) is rapid, while permanent quitters L(t) increase quickly, indicating that interventions yield faster results. In this case, occasional smokers O(t) and temporary quitters Q(t) stabilise quickly, reflecting faster relapse and cessation dynamics. As α decreases (i.e., α < 1), the model incorporates stronger memory effects, leading to slower declines in P(t) and S(t) with more gradual transitions between states. This suggests that smoking behaviour becomes more persistent and deeply rooted, making cessation efforts more challenging. Prolonged fluctuations in O(t) and Q(t) further highlight the potential for relapse over time, underscoring the importance of sustained public health interventions. The reproduction number R₀ plays a crucial role in determining the system’s stability, with R₀ < 1 predicting a decline in smoking prevalence and R₀ > 1 indicating sustained or growing smoking behaviour. This implies that policies must aim to maintain R₀ < 1 by promoting smoking cessation and reducing initiation rates. In addition, the comparison between the Bernstein operational matrices method and other approaches—such as Runge–Kutta, FDTM and q-HATM—demonstrates the Bernstein method’s superior accuracy, efficiency and reduced computational error. These results validate the utility of Bernstein polynomials in solving complex nonlinear fractional models, reinforcing their value for studying public health dynamics.

8. Conclusions

This paper utilised the Bernstein operational matrices method to numerically solve a nonlinear system of fractional differential equations. By applying this method to the smoking epidemic model, we demonstrated its effectiveness and significance in this context. Our results underscored the method’s efficiency when compared with traditional approaches such as Runge–Kutta, emphasising the importance of integrating advanced techniques such as the Bernstein operational matrices method in modelling real-world problems. Furthermore, our findings revealed superior approximation outcomes compared with FDTM and q-HATM. In addition, the residual corrected error technique introduced in this research efficaciously minimised absolute error functions by refining previous approximation solutions for the given smoking model. The reliability of the model’s long-term predictions, derived from almost a decade of numerical analysis, is generally strong, particularly in capturing key trends in smoking behaviour over time. However, several factors could significantly alter these predictions, such as changes in public health policies, technological advances in cessation methods, the introduction of new tobacco products like e-cigarettes or shifts in societal attitudes towards smoking. These potential influences highlight the importance of continuously updating the model to maintain its accuracy and relevance. The presented method effectively captures the memory effect in smoking dynamics; however, future research could address constraints such as external influences affecting smoking behaviour and use sensitivity analysis to understand how parameter changes impact results. The application of machine learning for parameter estimation could further enhance model accuracy by adapting to real-time data. In addition, studying the social and economic aspects that influence smoking would improve the mathematical model and its use in public health planning. Finally, the successful implementation of the presented method in addressing epidemic models generates new research opportunities for precise simulation and analysis of complex systems across many disciplines of study.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The research was supported entirely by personal funds.

Open Research

Data Availability Statement

The datasets generated and analysed during the current study are available from the corresponding authors upon reasonable request.

References

1 Alhejili W., Khader M. M., Lotfy K., El-Bary A. A., and Adel M., Studying of the Covid-19 Model by Using the Finite Element Method: Theoretical and Numerical Simulation, Soft Computing. (2024) 28, no. 6, 5263–5273, https://doi.org/10.1007/s00500-023-09310-6.
10.1007/s00500-023-09310-6
Google Scholar
2 Adel M., Khader M. M., Assiri T. A., and Kallel W., Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique, Symmetry. (2023) 15, no. 4, https://doi.org/10.3390/sym15040931.
10.3390/sym15040931
PubMed Google Scholar
3 Ibrahim Y. F., Abd El-Bar S. E., Khader M. M., and Adel M., Studying and Simulating the Fractional Covid-19 Model Using an Efficient Spectral Collocation Approach, Fractal and Fractional. (2023) 7, no. 4, https://doi.org/10.3390/fractalfract7040307.
10.3390/fractalfract7040307
Google Scholar
4 Aboubakr A. F. S., Ismail G. M., Khader M. M., Abdelrahman M. A. E., AbdEl-Bar A. M. T., and Adel M., Derivation of an Approximate Formula of the Rabotnov Fractional-Exponential Kernel Fractional Derivative and Applied for Numerically Solving the Blood Ethanol Concentration System, AIMS Mathematics. (2023) 8, no. 12, 30704–30716, https://doi.org/10.3934/math.20231569.
10.3934/math.20231569
Google Scholar
5 World Health Organization, World Health Organization: Tobacco, 2023, WHO.
Google Scholar
6 Garsow C. C., Salivia G. J., and Herrera A. R., Mathematical Models for the Dynamics of Tobacco Use, Recovery and Relapse, Technical Report Series BU-1505-M. (1997) Cornell University, Ithaca, NY.
Google Scholar
7 Zaman G., Qualitative Behavior of Giving up Smoking Models, Bulletin of the Malaysian Mathematical Sciences Society. (2011) 34, no. 2, 403–415.
Web of Science® Google Scholar
8 Zaman G., Optimal Campaign in the Smoking Dynamics, Computational and Mathematical Methods in Medicine. (2011) 2011, 163834–163839, https://doi.org/10.1155/2011/163834, 2-s2.0-79953290764.
10.1155/2011/163834
PubMed Web of Science® Google Scholar
9 Zeb A., Zaman G., and Momani S., Square-root Dynamics of a Giving up Smoking Model, Applied Mathematical Modelling. (2013) 37, no. 7, 5326–5334, https://doi.org/10.1016/j.apm.2012.10.005, 2-s2.0-84872598848.
10.1016/j.apm.2012.10.005
Web of Science® Google Scholar
10 Erturk V. S., Zaman G., Alzalg B., Zeb A., and Momani S., Comparing Two Numerical Methods for Approximating a New Giving up Smoking Model Involving Fractional Order Derivatives, Iranian Journal of Science and Technology, Transactions A: Science. (2017) 41, no. 3, 569–575, https://doi.org/10.1007/s40995-017-0278-x, 2-s2.0-85032262808.
10.1007/s40995-017-0278-x
Google Scholar
11 Khalid M., Sami F., and Iqbal A., Perturbation-Iteration Algorithm to Solve Fractional Giving Up Smoking Mathematical Model, International Journal of Computer Applications. (2016) 142, no. 9, 1–6, https://doi.org/10.5120/ijca2016909891.
10.5120/ijca2016909891
Google Scholar
12 Haq F., Shah K., ur Rahman G., Shahzad M., and Shahzad M., Numerical Solution of Fractional Order Smoking Model via Laplace Adomian Decomposition Method, Alexandria Engineering Journal. (2018) 57, no. 2, 1061–1069, https://doi.org/10.1016/j.aej.2017.02.015, 2-s2.0-85014849830.
10.1016/j.aej.2017.02.015
Web of Science® Google Scholar
13 Singh J., Kumar D., Qurashi M. A., and Baleanu D., A New Fractional Model for Giving Up Smoking Dynamics, Advances in Difference Equations. (2017) 2017, no. 1, 88–16, https://doi.org/10.1186/s13662-017-1139-9, 2-s2.0-85016157209.
10.1186/s13662-017-1139-9
Web of Science® Google Scholar
14 Uçar S., Uçar E., Özdemir N., and Hammouch Z., Mathematical Analysis and Numerical Simulation for a Smoking Model With Atangana-Baleanu Derivative, Chaos, Solitons & Fractals. (2019) 118, 300–306, https://doi.org/10.1016/j.chaos.2018.12.003, 2-s2.0-85058047670.
10.1016/j.chaos.2018.12.003
Web of Science® Google Scholar
15 Veeresha P., Prakasha D. G., and Baskonus H. M., Solving Smoking Epidemic Model of Fractional Order Using a Modified Homotopy Analysis Transform Method, Mathematical Sciences. (2019) 13, no. 2, 115–128, https://doi.org/10.1007/s40096-019-0284-6.
10.1007/s40096-019-0284-6
Web of Science® Google Scholar
16 Günerhan H., Rezazadeh H., Adel W. et al., Analytical Approximate Solution of Fractional Order Smoking Epidemic Model, Advances in Mechanical Engineering. (2022) 14, no. 9, 1–11, https://doi.org/10.1177/16878132221123888.
10.1177/16878132221123888
Web of Science® Google Scholar
17 Haidong Q., Rahman M. U., and Arfan M., Fractional Model of Smoking with Relapse and Harmonic Mean Type Incidence Rate Under Caputo Operator, Journal of Applied Mathematics and Computing. (2023) 69, no. 1, 403–420, https://doi.org/10.1007/s12190-022-01747-6.
10.1007/s12190-022-01747-6
Google Scholar
18 Ilmayasinta N. and Purnawan H., Optimal Control in a Mathematical Model of Smoking, Journal of Mathematical and Fundamental Sciences. (2021) 53, no. 3, 380–394, https://doi.org/10.5614/j.math.fund.sci.2021.53.3.4.
10.5614/j.math.fund.sci.2021.53.3.4
CAS Google Scholar
19 Khyar O., Danane J., and Allali K., Mathematical Analysis and Optimal Control of Giving up the Smoking Model, International Journal of Differential Equations. (2021) 2021, 1–13, https://doi.org/10.1155/2021/8673020.
10.1155/2021/8673020
Google Scholar
20 Khan H., Alzabut J., Shah A., Etemad S., Rezapour S., and Park C., A Study on the Fractal-Fractional Tobacco Smoking Model, AIMS Mathematics. (2022) 7, no. 8, 13887–13909, https://doi.org/10.3934/math.2022767.
10.3934/math.2022767
Web of Science® Google Scholar
21 Liu P., Munir T., Cui T., Din A., and Wu P., Mathematical Assessment of the Dynamics of the Tobacco Smoking Model: An Application of Fractional Theory, AIMS Mathematics. (2022) 7, no. 4, 7143–7165, https://doi.org/10.3934/math.2022398.
10.3934/math.2022398
Web of Science® Google Scholar
22 Günerhan H., Kaabar M. K. A., and Çelik E., Novel Analytical and Approximate-Analytical Methods for Solving the Nonlinear Fractional Smoking Mathematical Model, Sigma: Linguistique Anglaise, Linguistique Generale. (2023) 41, no. 2, 331–343.
Google Scholar
23 Sofia I. R., Bandekar S. R., and Ghosh M., Mathematical Modeling of Smoking Dynamics in Society with Impact of Media Information and Awareness, Results in Control and Optimization. (2023) 11, https://doi.org/10.1016/j.rico.2023.100233.
10.1016/j.rico.2023.100233
Google Scholar
24 Nisar K. S., Tabassum R., Raja M. A. Z., and Shoaib M., Advanced Bio-Inspired Computing Paradigm for Nonlinear Smoking Model, Alexandria Engineering Journal. (2023) 76, 411–427, https://doi.org/10.1016/j.aej.2023.06.032.
10.1016/j.aej.2023.06.032
Google Scholar
25 Ullah A., Sakidin H., Gul S. et al., Sensitivity Analysis-Based Control Strategies of a Mathematical Model for Reducing Marijuana Smoking, AIMS Bioengineering. (2023) 10, no. 4, 491–510, https://doi.org/10.3934/bioeng.2023028.
10.3934/bioeng.2023028
Google Scholar
26 Chatterjee A. N. and Roy P. K., Smoking Habit: a Bio Mathematical Study, Commun. Math. Biol. Neurosci.(2020) 2020.
Google Scholar
27 Ray S. S., Atangana A., Noutchie S. C. O., Kurulay M., Bildik N., and Kilicman A., Fractional Calculus and its Applications in Applied Mathematics and Other Sciences, Mathematical Problems in Engineering. (2014) 2014, 1–2, https://doi.org/10.1155/2014/849395, 2-s2.0-84920417639.
10.1155/2014/849395
Web of Science® Google Scholar
28 Arqub O. A. and El-Ajou A., Solution of the Fractional Epidemic Model by Homotopy Analysis Method, Journal of King Saud University Science. (2013) 25, no. 1, 73–81, https://doi.org/10.1016/j.jksus.2012.01.003, 2-s2.0-84871119609.
10.1016/j.jksus.2012.01.003
Google Scholar
29 Farman M., Saleem M. U., Ahmad A., and Ahmad M. O., Analysis and Numerical Solution of SEIR Epidemic Model of Measles With Non-Integer Time Fractional Derivatives by Using Laplace Adomian Decomposition Method, Ain Shams Engineering Journal. (2018) 9, no. 4, 3391–3397, https://doi.org/10.1016/j.asej.2017.11.010, 2-s2.0-85056731231.
10.1016/j.asej.2017.11.010
Web of Science® Google Scholar
30 Adel M., Fractional Order System of Integro-Differential Equations: Theoretical and Numerical Simulations Using Appell-Type Changhee Polynomials, The Journal of Mathematics and Computer Science. (2024) 34, no. 01, 74–84, https://doi.org/10.22436/jmcs.034.01.07.
10.22436/jmcs.034.01.07
Google Scholar
31 Alshbool M. H. T., Bernstein Polynomials Method for Solving Multi-Order Fractional Neutral Pantograph Equations with Error and Stability Analysis, Results in Applied Mathematics. (2024) 22, https://doi.org/10.1016/j.rinam.2024.100451.
10.1016/j.rinam.2024.100451
Google Scholar
32 Alshbool M. H. T., Shatanawi W., Hashim I., and Sarr M., Residual Correction Procedure with Bernstein Polynomials for Solving Important Systems of Ordinary Differential Equations, Computers, Materials & Continua. (2020) 64, no. 1, 63–80, https://doi.org/10.32604/cmc.2020.09431.
10.32604/cmc.2020.09431
Google Scholar
33 Alshbool M. H., Isik O., and Hashim I., Fractional Bernstein Series Solution of Fractional Diffusion Equations With Error Estimate, Axioms. (2021) 10, no. 1, https://doi.org/10.3390/axioms10010006.
10.3390/axioms10010006
Google Scholar
34 Alshbool M. H. T., Mohammad M., Isik O., and Hashim I., Fractional Bernstein Operational Matrices for Solving Integro-Differential Equations Involved by Caputo Fractional Derivative, Results in Applied Mathematics. (2022) 14, no. 6, https://doi.org/10.1016/j.rinam.2022.100258.
10.1016/j.rinam.2022.100258
Google Scholar
35 Li W., Bai L., Chen Y., Santos S. D., and Li B., Solution of Linear Fractional Partial Differential Equations Based on the Operator Matrix of Fractional Bernstein Polynomials and Error Correction, International Journal of Innovative Computing and Applications. (2018) 14, 211–226.
Google Scholar
36 Alshbool M. H. T., Bataineh A. S., Hashim I., and Isik O. R., Solution of Fractional-Order Differential Equations Based on the Operational Matrices of New Fractional Bernstein Functions, Journal of King Saud University Science. (2017) 29, no. 1, 1–18, https://doi.org/10.1016/j.jksus.2015.11.004, 2-s2.0-84951135013.
10.1016/j.jksus.2015.11.004
Web of Science® Google Scholar
37 Hussain T., Awan A. U., Abro K. A. et al., A Passive Verses Active Exposure of Mathematical Smoking Model: a Role for Optimal and Dynamical Control, Nonlinear Engineering. (2022) 11, no. 1, 507–521, https://doi.org/10.1515/nleng-2022-0214.
10.1515/nleng-2022-0214
Google Scholar
38 Ullah R., Khan M., Zaman G. et al., Dynamical Features of a Mathematical Model on Smoking, Journal of Applied Environmental and Biological Sciences. (2016) 6, no. 1, 92–96.
Google Scholar
39 Sharma S. K., Chatterjee A. N., and Basir F. A., Hopf Bifurcation and Optimal Control of HCV/HIV Co-infection Dynamics within Human: A Theoretical Study, Results in Control and Optimization. (2023) 11, https://doi.org/10.1016/j.rico.2023.100234.
10.1016/j.rico.2023.100234
Google Scholar
40 Chatterjee A. N., Sharma S. K., and Al Basir F., A Compartmental Approach to Modeling the Measles Disease: A Fractional Order Optimal Control Model, Fractal and Fractional. (2024) 8, no. 8, https://doi.org/10.3390/fractalfract8080446.
10.3390/fractalfract8080446
Google Scholar
41 van den Driessche P. and Watmough J., Reproduction Numbers and Sub-threshold Endemic Equilibria for Compartmental Models of Disease Transmission, Mathematical Biosciences. (2002) 180, no. 1-2, 29–48, https://doi.org/10.1016/s0025-5564(02)00108-6, 2-s2.0-0036845274.
10.1016/S0025-5564(02)00108-6
CAS PubMed Web of Science® Google Scholar
42 Matignon D., Stability Results for Fractional Differential Equations with Applications to Control Processing, Computational Engineering in Systems Applications. (1996) 2, 963–968.
Google Scholar
43 Alshbool M. H. T. and Hashim I., Multistage Bernstein Polynomials for the Solutions of the Fractional Order Stiff Systems, Journal of King Saud University Science. (2016) 28, no. 4, 280–285, https://doi.org/10.1016/j.jksus.2015.06.001, 2-s2.0-84934301646.
10.1016/j.jksus.2015.06.001
Google Scholar

All articles

Implementing Bernstein Operational Matrices to Solve a Fractional-Order Smoking Epidemic Model

Abstract

1. Introduction

2. Preliminaries

3. Analysis of the Fractional-Order Smoking Epidemic Model