1. Introduction

High hypersonic aircraft technology is one of the commanding heights in the development of aerospace. With its unprecedented flight speeds, exceptional maneuverability, and potent destructive capabilities, hypersonic vehicle has far-reaching impacts on the development of military and technology [1].

The research on trajectory planning for hypersonic vehicles has consistently been a pivotal and prominent issue [2–4]. The trajectory of vehicle needs to satisfy multiple constraints, including dynamic pressure, heat flux density, terminal state requirements, and maneuverability. Constraints can be predefined before launch, such as waypoints and no-fly zones due to geographical obstacles, or they can be dynamically identified during flight, such as sudden threat areas detected by surveillance radars [5–7]. As the economy and society continue to develop, the increasing complexity in the number and distribution of no-fly zones poses a significant challenge to trajectory planning [8].

Scholars both domestically and internationally have shown significant interest in the trajectory planning of hypersonic vehicles under complex no-fly zone constraints. Current research on trajectory planning predominantly employs methods like pseudospectral methods [9], convex optimization [10], and heuristic algorithms [11], which incorporate constraints into the trajectory planning problem. The first two methods are known for their strong optimality and convergence properties. The outcomes derived from pseudospectral methods are notably sensitive to the selection of initial values [12], while convex optimization approaches may exhibit restricted efficacy when dealing with nonconvex constraints such as no-fly zones, necessitating the convexification of the problem [13]. Heuristic algorithms are well-suited for addressing global search problems but may exhibit reduced solution efficiency [14]. Researchers have refined these methodologies and obtained positive outcomes. Zhang et al. [15, 16] proposed a path-trajectory dual-level planning method for hypersonic vehicles under complex no-fly zone constraints to avoid getting trapped in local solutions and reduce the error caused by simplifying the motion model. Chen et al. [17] introduced an iterative algorithm to estimate the switching position and re-entry flight time, aiming to guide the hypersonic vehicle to enter the midterminal guidance switch window successfully while adhering to no-fly zone constraints in scenarios where the target is undergoing rapid maneuvers. Tian et al. [18] employed pseudospectral methods to discretize control and state variables, thereby converting the re-entry trajectory planning problem into a nonlinear programming problem, and the optimization objective was to minimize heat flux and trajectory oscillations during the re-entry phase.

The artificial potential field method (APFM) is a renowned path planning method extensively employed in domains such as unmanned vehicles [19], drones [20, 21], and robotic arms [22] owing to its succinct mathematical formulation and rapid computational efficiency. However, it is prone to be susceptible to get stuck in local optima and may fail to reach the target point if the distance to obstacles is too close, or alternatively, it may lead to potential collisions when the distance is excessive. Hence, it is common practice to implement enhancements to this method. Ren et al. [23] proposed a potential function that effectively captures the geometric characteristics of objects with arbitrary shapes. Li et al. [24] formulated an adaptive stride corridor through the integration of guidance and no-fly zone avoidance strategies utilizing the repulsive force of the artificial potential field, followed by a comprehensive analysis of its convergence properties. Hu et al. [25] conducted a quantitative assessment of the threat posed by no-fly zones and developed an enhanced adaptive heading corridor guidance strategy by leveraging improved APFM. Hu et al. [26] proposed a dynamic heading corridor design algorithm based on improved APFM, which employs sliding mode control to follow a prescribed trajectory while simultaneously guaranteeing no-fly zone avoidance without diverting from the desired target point. Wang et al. [27] took multiple constraints into account and used a piecewise analytical polynomial height-velocity profile to deduce the analytical expression for commands of bank angle, and this methodology effectively utilizes the width of the entry corridor and effectively meets extensive range requirements in flight missions.

The aforementioned methods encounter certain challenges when confronted with intricate no-fly zones. The no-fly zone avoidance strategies employed by APFM tend to be conservative, which results in ineffective avoidance maneuvers during flight. Moreover, the formulation of an avoidance strategy is contingent upon initial conditions, leading to limited adaptability to cope with dynamic constraints such as changing no-fly zones during flight. Consequently, it is necessary to find an appropriate strategy that lets vehicle avoid the no-fly zones without excessive maneuvering and can meet the needs of multiple types of no-fly zones.

Motivated by the preceding discussion and with the objective of addressing solving trajectory planning problem with complex distributed no-fly zone constraints, this paper proposes a trajectory planning algorithm for complex distributed no-fly zone avoidance problems. For the lateral motion of vehicle, the lift is changed by adjusting the angle of attack, and the angle of attack profile is designed in a coordinated manner. To satisfy terminal constraints, the bank angle is modified to correct the range and altitude. In order to regulate the vehicle’s lateral motion, an improved APFM is employed, which introduces improved attractive, repulsive, and velocity potential fields. Traditional APFM during flight always causes excessive maneuvering of vehicle during flight. To solve such problem, the avoidance strategy for lateral motion combined with repulsive force reconstruction is proposed to calculate the bank angle amplitude command, which can reduce the superposition of repulsive forces and decrease excessive maneuvering in flight. In order to avoid mismatched magnitudes of attractive and repulsive forces generated by APFM, a no-fly zone avoidance strategy based on minimum turning radius is proposed, which updates bank angle amplitude command when avoiding no-fly zones. The bank angle corridor is formulated to fulfill path constraints during flight. Simulation demonstrates the effectiveness of the proposed method, and the examples of sudden threat reflect the strong applicability of the method in addressing complex distributed no-fly zone avoidance challenges.

2. Dynamics Model and Constraints of Hypersonic Vehicle

In the formula, σ_max is the maximum bank angle, and $$ is the maximum rate of change of the bank angle.

3. Obstacle Avoidance Strategy

To avoid the no-fly zones, this paper proposes a trajectory planning algorithm based on improved APFM. When traditional APFM is used for trajectory planning, the trackability of the trajectory is usually not considered, and only geometrically feasible trajectories are obtained. However, the vehicle is limited by its own maneuvering capability and cannot track arbitrarily shaped geometric trajectories. Therefore, in the trajectory planning stage, this paper combines the vehicle’s dynamic model and constraints to design an avoidance strategy.

3.2. Avoidance Strategy for Lateral Motion

To control the lateral movement of vehicle, a strategy needs to be used to compute the appropriate magnitude of the bank angle for effectively tracking the reference profile, and such strategy is adopted to specify the sign of bank angle for eliminating heading errors. In this paper, besides the above discussion, the ability to avoid no-fly zones is also taken into consideration when designing the strategy. In this section, the lateral motion of vehicle is determined by APFM, and to avoid mismatched magnitudes of attractive and repulsive forces, a complementary avoidance strategy based on minimum turn radius is introduced when the vehicle is close to the obstacle.

3.2.1. Avoidance Strategy Based on Improved APFM

As shown in Figure 1, the position of the vehicle is denoted as A, and the line connecting the vehicle and the center of ith no-fly zone O_i is $$. If the vehicle is not close to the no-fly zone ($$, K_vo is distance factor), the improved APFM is employed to determine lateral motion. The force generated by improved APFM can be divided into attractive force and repulsive force. The magnitude of attractive force is related to the relative position of the aircraft and the no-fly zones. The magnitude of repulsive force is dictated by the relative position and relative speed of the aircraft and the no-fly zones. The resultant force of attractive and repulsive forces determines the command bank angle of the vehicle.

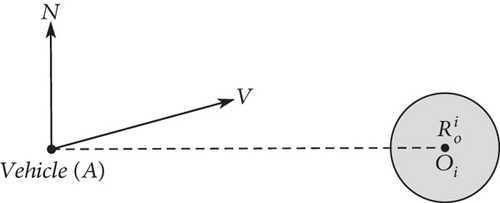
3.2.1.1. Design of Attractive Potential Field

The attractive potential function of the target is designed as

$$ (17)

In the formula, K_a is the attractive coefficient, p = (λ, φ) means the current longitude and latitude of vehicle, p_goal = (λ_goal, φ_goal) denotes the longitude and latitude of target, d(p, p_goal) is the geodesic distance between the current position of the vehicle and the target, and d_thres means the threshold distance between the vehicle and the target.

The force of attraction is the negative gradient of the attractive potential field and can be expressed as

$$ (18)

In this attractive field, when d(p, p_goal) ⩽ d_thres, the force of attraction experienced by the vehicle is positively correlated with distance between the vehicle and the target, and when d(p, p_goal) > d_thres, the force of attraction experienced by the vehicle is negatively correlated with distance between the vehicle and the target. It can prevent the issue of the vehicle failing to avoid no-fly zones due to excessive attractive force resulting from large distances.

3.2.1.2. Design of Repulsive Potential Field

The repulsive potential function is designed as

$$ (19)

where K_r is the repulsive coefficient, n₀ denotes the correction coefficient, $$ means the longitude and latitude of the center of ith no-fly zone, $$ is the radius, $$ denotes the geodesic distance from the current location of the vehicle and the center of ith no-fly zone, and K_o is the effective repulsive factor which describes the effective range of repulsion for no-fly zones.

The force of repulsion, which is the negative gradient of the repulsive potential field, is denoted as

$$ (20)

$$ (21)

$$ (22)

The repulsive function has been improved by introducing a correction coefficient $$, which avoids situations where the vehicle deviates from the target due to excessive repulsion when the vehicle is close to a no-fly zone. The repulsive function also combines the effective range of repulsion with the radius of the no-fly zone, enhancing its adaptability to different no-fly zones.

When the jth no-fly zone is moving, the velocity repulsive potential function $$ can be designed to enable the vehicle to have the ability to avoid the moving no-fly zone.

$$ (23)

In the formula, K_rv is the velocity repulsive coefficient, V_rel means the velocity of the vehicle relative to the jth no-fly zone, and η_rel represents the angle between the position vector of the vehicle relative to the center of the jth no-fly zone and V_rel.

The force of velocity, which is the negative gradient of the velocity repulsive potential field, is expressed as

$$ (24)

The repulsive function of jth no-fly zone is updated as follows:

$$ (25)

where $$ means the repulsive force calculation without considering the movement of the no-fly zone.

The resultant repulsive force is the sum of repulsive force from each no-fly zone acting on the vehicle.

$$ (26)

In the formula, N means the number of no-fly zones.

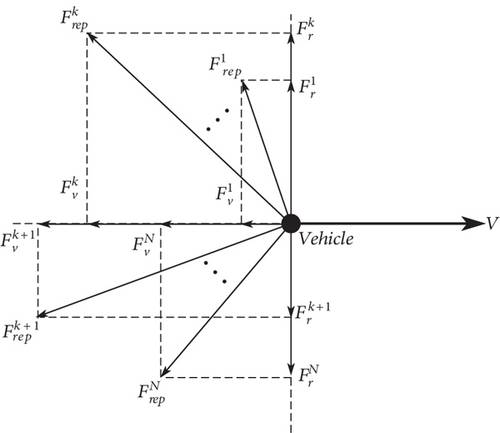
3.2.2. Repulsive Force Reconstruction

The resultant force acting on the vehicle under attractive and repulsive potential fields is denoted as F_all.

$$ (27)

The APFM may produce invalid maneuvers for no-fly zones that are not on the flight path of the vehicle. Many scholars have proposed collision prediction methods to avoid invalid maneuvers, but most of them are similar to the method in reference [33], which only uses the flight direction and relative position of the vehicle to the no-fly zone as prediction conditions, ignoring the resultant force acting on the vehicle.

This paper incorporates the resultant force into collision prediction. As shown in Figure 2, assuming that the repulsive force from ith no-fly zone is not considered, the resultant force acting on the vehicle is

$$ (28)

The angle between $$ and the north direction is denoted as ψ_all, the tangents to the boundaries of the ith no-fly zone from the vehicle are represented by l₁ and l₂, the angles between tangent and the north direction are η₁ and η₂, respectively (η₁ ⩽ η₂), and ψ_t means the angle between the direction of V and the north direction at time t. Under the influence of $$, ψ_all satisfies the following relationship:

$$ (29)

If the vehicle fails to avoid the no-fly zone, the direction of the velocity will point towards the no-fly zone at some point.

$$ (30)

If there is no intersection between the range of ψ_t in Equation (29) and Equation (30), it indicates that the vehicle will not enter the no-fly zone under the influence of the resultant force; thus, there is no need to consider the repulsive force generated by a no-fly zone, and $$ is assigned a value of 0. Based on the above discussion, the sufficient condition for the vehicle to disregard the repulsive force of the no-fly zone is expressed as

$$ (31)

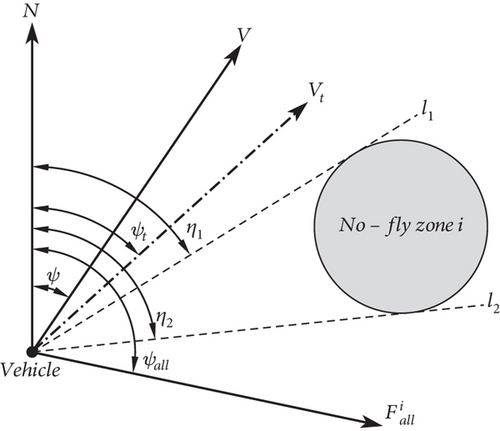
If Equation (31) is not satisfied, it indicates that the vehicle may enter the no-fly zone, so the repulsive force generated by the no-fly zone should be considered.

The traditional APFM often sums up all the repulsive forces to calculate the resultant force, leading to a cumulative effect of repulsion that causes excessive maneuvering of the vehicle. To mitigate this impact, this paper decomposes the repulsive force to reduce its cumulative effect. As shown in Figure 3, this study assumes that the repulsive force $$ is on one side of the velocity V, and the repulsive force $$ is on the other side. The repulsive force generated by ith no-fly zone is projected along the tangent and normal directions of velocity, denoted as $$ and $$, respectively. For $$, it is decomposed into sets $$ and $$.

$$ (32)

The repulsive force with the maximum scalar value from sets $$ and $$ is denoted as $$ and $$, respectively. It is evident that the resultant force of $$ satisfies the avoidance requirements of all the no-fly zones corresponding to the repulsive forces in $$. Similarly, $$ and $$ can be calculated. Therefore, the resultant repulsive force of repulsive force reconstruction is expressed as

$$ (33)

According to Equations (18) and (33), the resultant force F_all is recalculated. The reference heading angle ψ^∗ of the vehicle is the angle between the direction of F_all and the north direction. In this paper, the command bank angle σ_cmd is generated by resultant force F_all.

$$ (34)

where $$ is the projection of F_all along the longitude direction and K_σ represents the adjustment factor of command.

3.2.3. Avoidance Strategy Based on Minimum Turning Radius

The effectiveness of the APFM is highly dependent on the design parameters. When the vehicle is close to the obstacle, there is a risk of avoidance failure due to mismatched magnitudes of attractive and repulsive forces if parameters are designed unreasonably. To ensure successful avoidance, this paper proposes a strategy based on the minimum turning radius.

As shown in Figure 4, the angle between the $$ and the north direction is denoted as η₀. If the vehicle is close to the no-fly zone $$ at time t, the turn must be executed to avoid the no-fly zone. R_v means the turning radius, and O_v represents the center of turning. The angle between $$ and $$ is denoted as δ_θ.

For ease of calculation, assuming that the turning radius remains constant during the flight. After a period of time Δt, the vehicle moves to A^′ where the velocity direction is perpendicular to $$. If $$ does not intersect with the no-fly zone, the vehicle has the ability to avoid the no-fly zone at time t, and the following relationship holds

$$ (35)

Based on geometric relationships, $$ is expressed as

$$ (36)

Then, combine Equation (35) and Equation (36), which lead to

$$ (37)

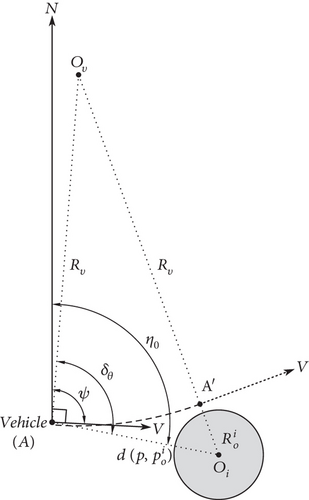
If $$, Equation (37) holds true, and the velocity direction of vehicle does not point towards the no-fly zone, so there is no need to make a maneuver, σ_cmd = 0.

If $$, Equation (37) can be transformed as

$$ (38)

For BTT vehicle, the turning process is achieved by generating a lateral component of lift through the use of banked wings. This provides the required centripetal force for turning. Assuming that the vehicle is in QEGC with no side slip during the turning process, then the flight path angle is approximately zero.

During the turning process, the required centripetal force is provided by the lateral component of lift Lsinσ; thus, the turning radius R_v satisfies the following equation:

$$ (39)

Then, combine the $$ in Equation (1) and Equation (39), which lead to

$$ (40)

By neglecting the centrifugal force within the horizontal turning plane, an approximate solution for the turning radius can be obtained as follows

$$ (41)

Replacing R_v in Equation (38) and Equation (41), the range of bank angle can be expressed as

$$ (42)

In this study, when $$, the command bank angle σ_cmd is valued as

$$ (43)

When using the avoidance strategy based on the minimum turning radius, the vehicle’s reference heading angle ψ^∗ remains consistent with its actual heading angle ψ, which means ψ^∗ = ψ.

3.4. Terminal Guidance Algorithm Design

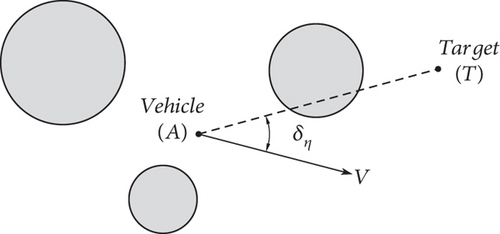
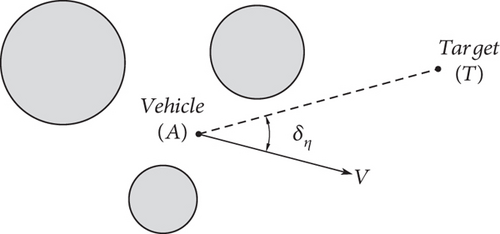
As shown in Figures 5 and 6, the position of vehicle is denoted as A, the position of target is denoted as T, and the angle between the vehicle’s velocity vector and the line $$ is denoted as δ_η.

If $$ intersect with no-fly zones (Figure 5), the vehicle has not avoided all obstacles. If there is no intersection (Figure 6), the vehicle is considered to have avoided all obstacles, and adjusting the command bank angle magnitude to align the vehicle’s flight direction with the target point.

$$ (50)

where K_ad is the adjusting factor and σ_cmdO denotes the original command bank angle before adjustment.

If the deviation between the vehicle’s motion direction and $$ is small, the vehicle is considered to be aligned with the target, then set σ_cmd to 0 until the vehicle reaches the target.

$$ (51)

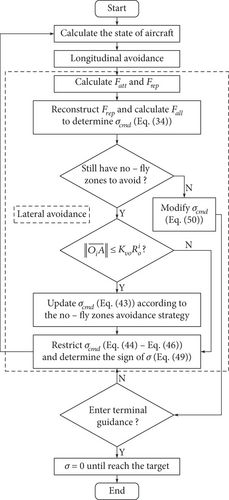
3.6. The Process of Avoidance Strategy

For strategy of longitudinal motion, this paper suppresses errors in altitude and range by designing the angle of attack profile and online correction of range. For strategy of lateral motion, this paper addresses the avoidance problem through improved APFM. To overcome the shortcomings of APFM, repulsive force reconstruction is introduced to mitigate excessive maneuvering, and avoidance strategies based on minimum turning radius are employed to deal with mismatched magnitudes of forces. The flowchart of the proposed avoidance strategy is shown in Figure 7.

4. Simulation and Analysis

In this section, the proposed avoidance strategy is applied to solve numerical examples of complex distributed no-fly zone avoidance problem, which illustrates the effectiveness of the method.

4.2. Trajectory Planning

To better illustrate the application effectiveness of the proposed method, a comparison is conducted by using multiple methods. Method 1 represents the method proposed in this paper. Method 2 refers to the dual-level path-trajectory generation method in reference [35]. Method 3 involves the Gaussian pseudospectral method, solved using the GPOPS toolbox in MATLAB.

The comparative simulation results of the three methods are shown in Figures 8–11, and Figures 12–15 show the simulation results of Method 1.

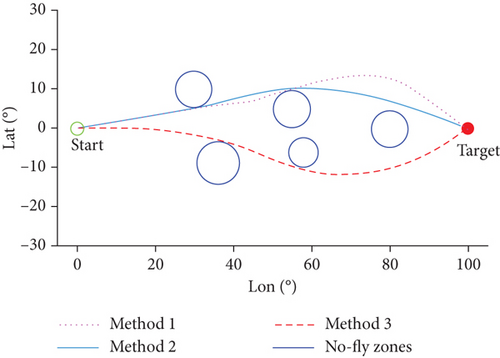
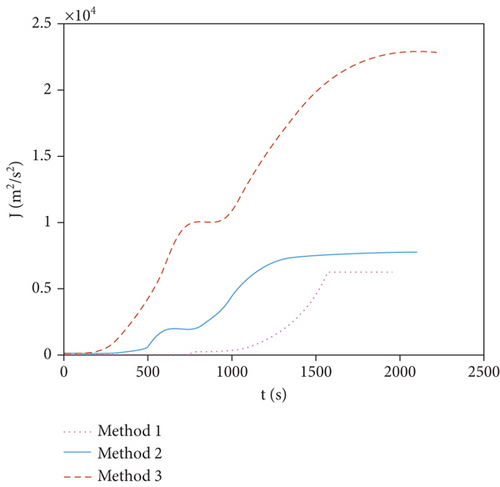
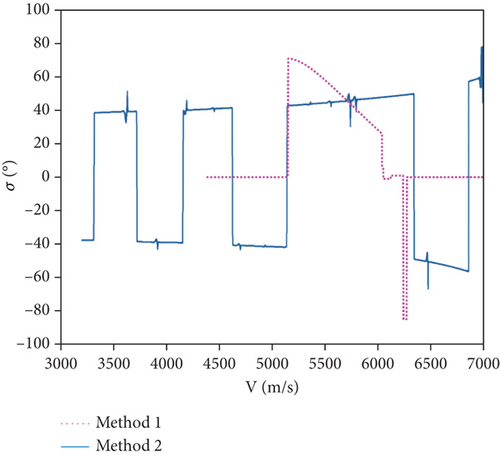
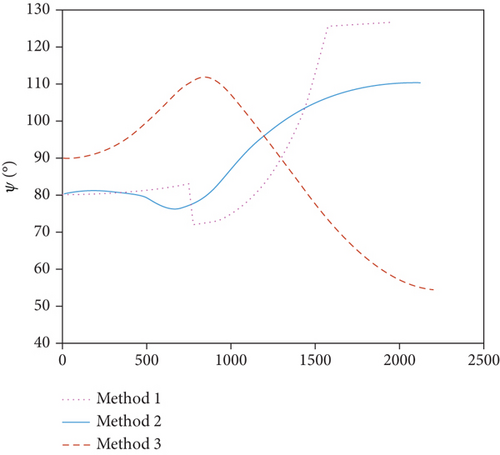
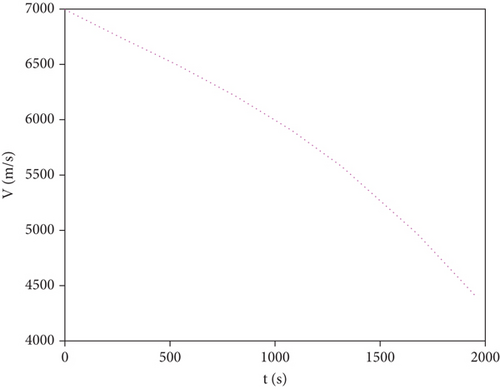
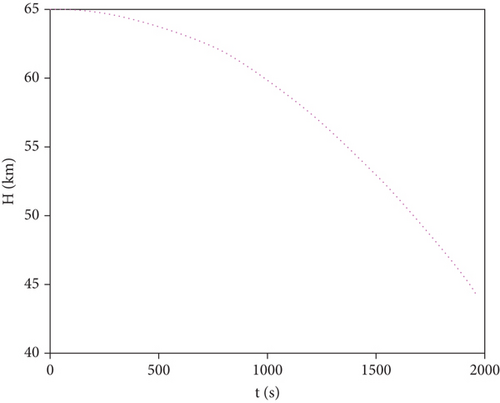
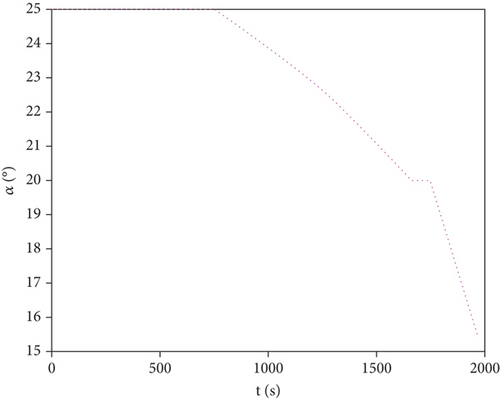
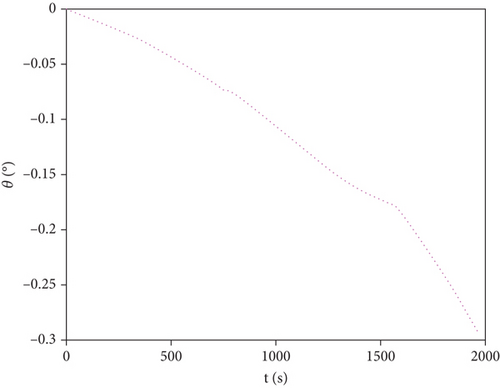
Figure 8 shows the comparison of trajectory ground track of the three methods, and it indicates that all three methods successfully avoid the no-fly zone. Method 3 has a different path direction compared to other methods, which is due to such method getting trapped in local optimum caused by the no-fly zones.

Figure 9 depicts the energy consumption index of the three methods. The index for Method 1 is 6183.42 m²/s², Method 2 is 7764.61 m²/s², and Method 3 is 23082.26 m²/s². Therefore, the method proposed in this paper is better than other methods due to less energy consumption for lateral control.

Figure 10 depicts the bank angle command values of Method 1 and Method 2. From the bank angle-velocity curve, it is evident that Method 2 maintains a relatively large bank angle for most of the flight. Method 1 avoids excessive maneuvering during flight, which results in generally smaller bank angles. Thus, by using Method 1, the energy consumption is lower, and the terminal velocity is larger than in Method 2.

Figure 11 depicts the comparison of heading angle. The changing trend of heading angle for Method 1 and Method 2 remains consistent, while Method 3 exhibits larger overall variations in heading angle. When using Method 1, there are sudden changes during the execution of the avoidance strategy based on minimum turning radius and during terminal guidance entry, while the heading angle remains stable during the rest of time.

From Figures 12 and 13, it can be seen that the velocity and height satisfy the terminal constraints, which means the vehicle has ability to execute subsequent missions after leaving no-fly zones.

Figures 14 and 15 indicate that the attack angle profile of the aircraft is reasonable, and the variation of speed and pitch angle during the flight is smooth.

4.3. Trajectory Planning With Sudden Threats

4.3.1. Static New No-Fly Zone

Assume that a new no-fly zone is discovered online with the center coordinates (90°, 5°) and a radius of 350 km at t = 1400 s. Simulation is carried out using the method proposed in this paper under the constraints of the new no-fly zone. The results are depicted in Figures 16 and 17.

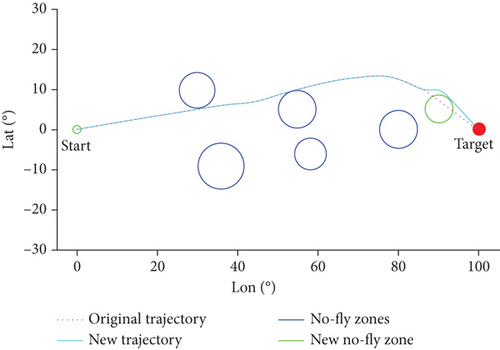
According to the result of simulation, the aircraft’s terminal height is 44.4 km, and its terminal velocity is 4350.83 m/s, satisfying the terminal constraints. Figure 15 shows the comparison of ground track between original constraints and constraints with static new no-fly zone. From Figure 15, it can be indicated that the aircraft successfully avoids the newly discovered no-fly zone and reaches the target.

Figure 16 displays the bank angle profile, and compared with the result without sudden threat, the vehicle makes larger maneuvering to avoid the new no-fly zone. It can be seen that the strategy proposed in this paper can be used for trajectory planning with sudden static threat, and the proposed method is highly applicable to cope with avoidance of changing no-fly zones.

4.3.2. Dynamic New No-Fly Zone

Assume that a new no-fly zone is discovered online with the center coordinates (90°, 5°) and a radius of 350 km at t = 1400 s. The new no-fly zone moves along the longitude direction with a speed of 5 m/s. Simulation calculations are conducted using the method proposed in this paper under the new constraints of the no-fly zones. The results of simulation are shown in Figures 18 and 19.

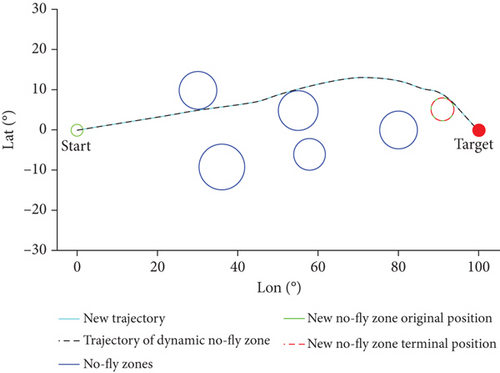
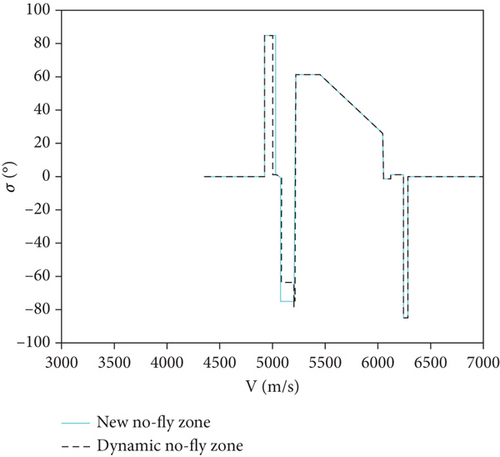
According to the result of simulation, the aircraft’s terminal height is 44.3 km, and its terminal velocity is 4364.37 m/s, which satisfies the terminal constraints. Figure 18 depicts the comparison of ground track between constraints with static new no-fly zone and constraints with dynamic new no-fly zone. Trajectories in Figure 18 show the success of avoidance of dynamic no-fly zone, and the vehicle moves to target.

Figure 19 displays the bank angle profile of two conditions. When meeting dynamic threat, the vehicle makes different maneuvering to avoid comparing with static no-fly zone, and it can be seen that the method is sensitive to the moving of no-fly zones. The results of simulation indicate that the proposed strategy in this paper can be suitable for trajectory planning with sudden dynamic threat.

5. Conclusion

Simulation results demonstrate the effectiveness of the proposed method. By using strategy in the paper, the vehicle is capable of avoiding complex no-fly zones with sudden threats. The simulation results show that the proposed strategy is an effective and feasible method to deal with complex distributed no-fly zone avoidance problems.

The strategy presented in this article provides an effective approach to solving the trajectory planning problem for high-speed aircraft in complex no-fly zones.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work is supported in part by the National Natural Science Foundation of China (U21B2028) and the Hunan Province Graduate Innovation Funding Project (CX20230062).