International Journal of Differential Equations
Volume 2024, Issue 1 8893138
Research Article
Open Access

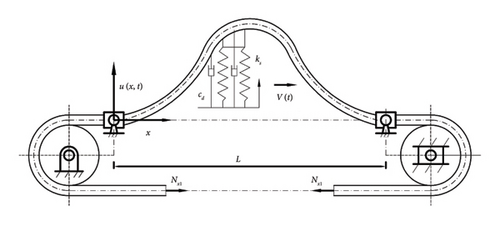
On Stability Analysis of Linear Axially Moving Damped Beam with Elastic Foundation

Ghulam Yameen Mallah, 

Corresponding Author

Ghulam Yameen Mallah

Department of Mathematics and Statistics, Quaid-e-Awam University of Engineering, Science and Technology, Nawabshah 67480, Sindh, Pakistan quest.edu.pk

Search for more papers by this author
Rajab Ali Malookani, 

Rajab Ali Malookani

Department of Mathematics and Statistics, Quaid-e-Awam University of Engineering, Science and Technology, Nawabshah 67480, Sindh, Pakistan quest.edu.pk

Search for more papers by this author
Sajad Hussain Sandilo, 

Sajad Hussain Sandilo

Department of Mathematics and Statistics, Quaid-e-Awam University of Engineering, Science and Technology, Nawabshah 67480, Sindh, Pakistan quest.edu.pk

Search for more papers by this author
Sanaullah Dehraj, 

Sanaullah Dehraj

Department of Mathematics and Statistics, Quaid-e-Awam University of Engineering, Science and Technology, Nawabshah 67480, Sindh, Pakistan quest.edu.pk

Search for more papers by this author
First published: 11 June 2024
https://doi.org/10.1155/2024/8893138
Academic Editor: Ram N. Quintanilla

Abstract

This study investigates the dynamical behavior of an axially moving beam with elastic foundation under viscous damping. The beam is taken to be simply supported at the ends. Axial speed of beam is assumed to be time-dependent function about a relatively low mean constant speed. The motion of axially moving beam in the term of transverse vibrations is expressed in the fourth-order linear and homogeneous partial differential equations with variable coefficients. The governing equations of motion are solved by using the two timescales perturbation method together with the Fourier expansion method. The sum and difference-type resonances are taken to examine the stability of the system. The influence of the parameters such as damping and stiffness of foundation on the transverse amplitude response of the system is seen. It is found out that the system is stable with the increase in damping.

1. Introduction

Axially moving systems form part of several mechanics in various disciplines of engineering such as mechanical, aerospace, and civil engineering [1, 2]. There are various mechanical and civil structures that represent engineering devices such as elevator cables, conveyor belt systems, crane cables, electric power lines, suspension bridges, saw-tooth blades, steel rod, medical nanorobots, and magnetic tapes [3–6]. Despite their vast usefulness and advantages, the vibrations, specifically transverse vibrations, have limited their performance and productivity. Various sources can trigger the vibrations in these devices such as wind and other loads which damage or destroy the structures. For instance, vibrations in elevator cable [4], leakages in pipelines [5], and destruction of the Tacoma Narrows suspension bridge USA in 1940 completely [6] are few examples of damaged structures. In order to optimize the design of such systems, numerous theoretical and experimental studies are carried out over the decades. Depending on the flexibility and geometric properties of the system, two models can be developed as string and beam models. The components are modeled as string-like models if there is relatively small effect of the bending and can be ignored. For example, threads in textile factories, cables in elevators, hoist roping [7–10]. In contrast, the model is classified as beam model if the bending stiffness is assumed to be essential [11–14]. For example, steel rod, robotic arm, saw of metal-coating, band-saw machines are few examples of beam-like models. Transverse vibrations of string-like and beam-like models may be controlled either by providing supports at end points [4], or by providing intermediate support in the moving span [11, 15, 16]. For the last one decade, a vast research is witnessed regarding the dynamics of moving string and beam systems with an intermediate foundation. From the physical perspective, the beam models are more accurate to analyze the dynamics of the system as compared to the string models. The transversal vibrations of axially moving beam are mathematically modeled as nonlinear fourth-order partial differential equation. Various numerical and analytical techniques are used to examine the stability of the systems. Laplace transform method [17] and Lie group theory [18] are used to examine the dynamical behavior of the linear models. In contrast, the nonlinear models are investigated by approximate methods such as the perturbation methods [19–23], Galerkin method [24, 25], differential quadrature method [26], finite difference method [27], and averaging method [28].

The Galerkin method is used in [29] to examine the free vibrations of moving beam with elastic foundation. The cosine-cosine function is used in [30] to examine the chaotic behavior of beam-like models resting on stiffness foundation. The axially loaded beam on variable elastic foundation is analyzed by the homotopy perturbation method in [31]. The dynamic response is examined of axially moving beam subject to an intermediate support by means of complex model analysis in [32].

This paper studies the stability analysis of transverse vibration of axially moving beams with low constant mean speed and time-dependent velocity varying harmonically subject to fixed boundary conditions under the effect of internal damping and elastic foundation. The Fourier expansion method is employed to discretize the governing equation of motion; subsequently, the infinite-dimensional system of coupled ordinary differential equations is tackled through the two timescales perturbation method.

The paper is structured as follows. The mathematical formulation of the governing equations of motion for the transverse vibrations of moving beam resting on elastic foundation is given in Section 2. Construction of formal asymptotic approximations with the method of two timescales for examining the stability of the system is presented in Section 3. Stability of the system in resonance regions is discussed in Section 4. Finally, conclusions of the paper are presented in Section 5.

2. Mathematical Formulation

An axially transporting beam moving with the velocity V(t) with the length L between two pulleys resting on elastic foundation is shown in Figure 1. The equations of motion that governs the transversal vibrations of an axially transporting moving beam is derived from Newton’s second law of motion [20] and can be represented as follows:
(1)
with the simply supported boundary conditions:
(2)
and the initial conditions:
(3)
where u(x, t) is the transverse displacement with spatial axis x and time t, ρ is the density, A is cross-sectional area, I is moment of inertia, E is Young’s modulus, ks is stiffness of foundation, cd is viscous damping, is the axial varying tension with P0 is the initial axial varying tension, and a is the axial support stiffness.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The schematic model of a moving beam [20].
The following dimensionless parameters are used to form equations (1)–(3) dimensionless:
(4)
where ϵ with 0 < ϵ ≪ 1 is a bookkeeping parameter which indicates the smallness of transverse motion, elastic foundation, and viscous damping. Substitution of equation (4) without asterisks into equations (1)–(3) yields the following nondimensional form:
(5)
(6)
(7)
The axial speed is assumed about a low mean speed α0 of order ϵ and harmonically varying velocity ϵα with a frequency Ω as
(8)
where α0, α, and Ω are constants with α0 > 0, Ω > 0 and with a condition α0 > |α|, that is belt move forward axially.

3. Construction of Formal Asymptotic Approximations

In this section a two timescales perturbation in conjunction with Fourier series method is used to construct the formal asymptotic approximations for the solution of initial-boundary value problem for equations (5)–(7). To satisfy the Dirichlet BC’s, we need to make all the terms in equation (5) odd. The terms such as uxt and xuxx are even and need to be made odd by multiplying them with the Fourier series of the functions H(x) and xH(x) [7] and given as under:
(9)
(10)
By substituting equations (8)–(10) into equation (5), we have
(11)
To discretize the PDE in equation (11), the Fourier expansion method is used. The solution of equation (11) is assumed in the form as under:
(12)
By putting equation (12) in equation (11), then multiplying the resulting equation with sin(kπx), k ∈ Ν and then integrating w.r.t “x” from 0 to 1 and observing the following orthogonality properties:
(13)
(14)
We obtain an infinite dimensional system of coupled ODEs
(15)
In order to solve equation (15), two timescales perturbation method will be used. Let us introduce the two timescales, the fast timescales (to = t) and slow timescales (t1 = ϵt). The parameter ϵ is taken small to ensure that the asymptotic expansion converges on long timescales. On the other hand, a larger ϵ will lead to a loss of accuracy in the approximate solution, as the perturbation method is no longer valid. With these timescales, the solution of equation (15) is assumed in the form:
(16)
The following time-derivatives are introduced:
(17)
(18)
with equations (15), (16)–(18) becomes:
(19)
Now assume.
(20)
By putting equation (20) into equation (19) and equating the coefficients of ϵ0 and ϵ1 to zero, we have O(1) problem and O(ϵ) problem, respectively:
(21)
(22)
The solution of equation (21) is
(23)
where is a natural frequency of the beam system.
Substituting equation (23) in the right side of equation (22), we obtain
(24)

4. Stability Analysis

The right side of equation (24) depicts that if the velocity variation frequency Ω is within the neighborhood of sum and difference of two natural frequencies  ωk, the system’s amplitude grows without bound. This phenomenon is known as resonance. From equation (24), it is observed that there are infinitely many resonances in the system if .

In this paper, we considered the following resonant Case 1. Ω = ω2 − ω1, 2. Ω = ω3 − ω2, 3. Ω = ω2 + ω1 and 4. Ω = ω3 + ω2 with detuning parameter ϕ and is of O(1).

Case 1. When Ω = ω2 − ω1 + ϵϕ

It is shown in appendix A that by substituting Ω = ω2 − ω1 + ϵϕ in equation (24) and making the terms equal to zero that cause resonances, we have the following coupled ordinary equations:

(25)

To transform the system into the polar coordinates, let Ak0(t1) = rk(t1)sin(ϕk(t1)) and Bk0(t1) = rk(t1)cos(ϕk(t1)), so from (25), we have:

(26)

From first two equations in equation (27); we have , where c1 is constant of integration. Now, let Φ(t1) = ϕ2(t1) − ϕ1(t1) + ϕt1, so from the last equation (26), we have

(27)

By introducing the following rescaling:

(28)
which results in:
(29)
with
(30)

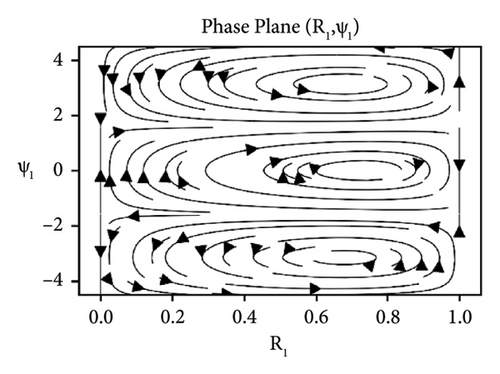
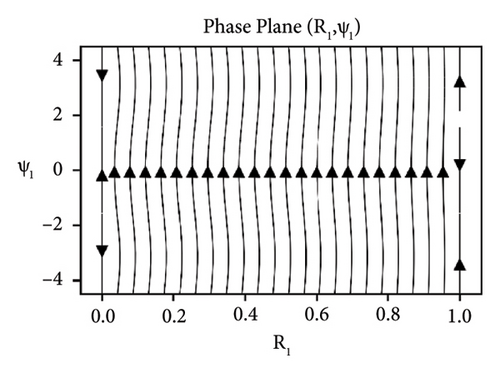
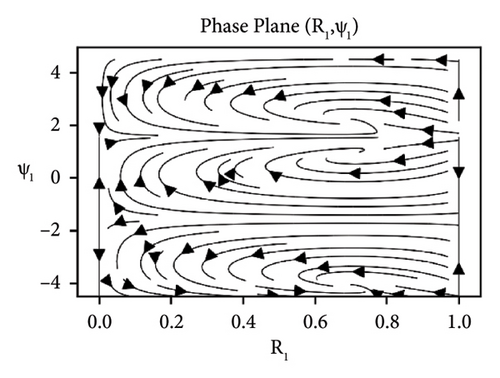
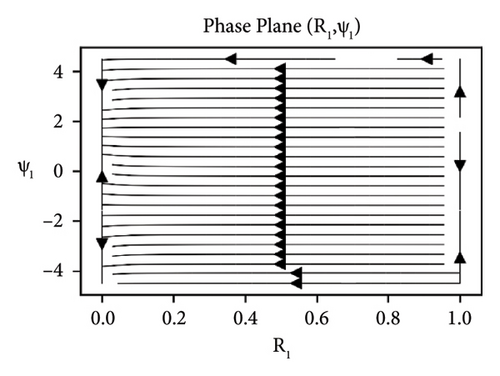
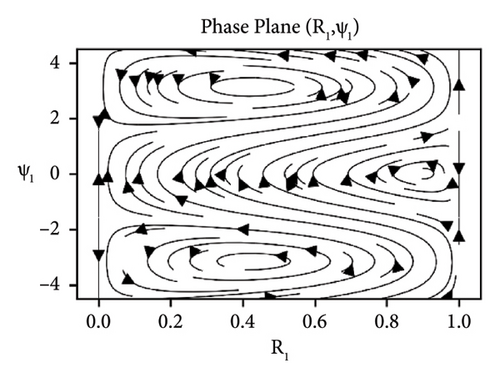
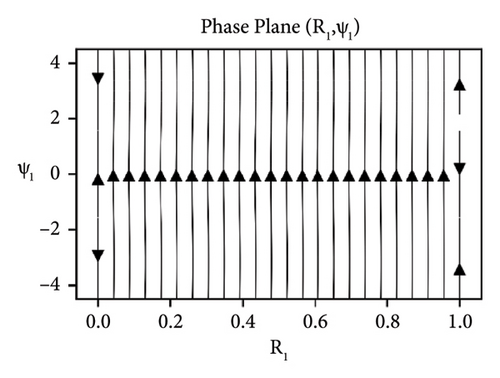
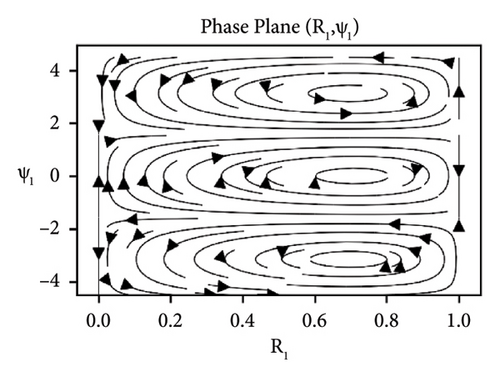
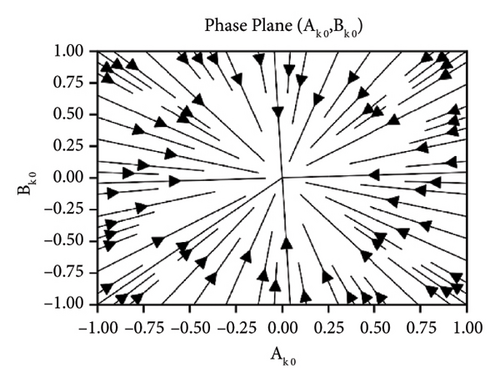
Equation (29) is a coupled system of nonlinear ODEs in R1 and ψ1. The effects of the parameters elastic foundation ks, internal damping cd and detuning parameter ϕ while keeping axial velocity α and flexural rigidity kf fixed to 0.01 and stability analysis of the beam in difference-type resonant of two modes are observed and shown in the form of phase portraits. Figure 2 depicts the behavior of beam under the effect of elastic foundation (ks). When the elastic foundation is relatively small, then all bounded solutions exist can be seen in Figure 2(a). However, the equilibrium points turn up at R1 = 0 and R1 = 1 (both stable and unstable), when there is relatively large elastic foundation can be seen in Figure 2(b). The effects of the damping cd are exhibited in Figure 3. It can clearly be seen in Figure 3(a) that there are only bounded solutions at the straight line R1 = 0 and R1 = 1 but not completely stable. When the damping parameter increases, all solutions converge to stable from unstable and vice versa, see Figure 3(b). The influence of detuning parameter ϕ is shown in Figure 4. It can be observed in Figure 4(a) that the unstable solutions emerge near resonances. However, stable solutions are found out at the straight line R1 = 0 and R1 = 1 when the system is kept away from the resonance regions can be seen in Figure 4(b).

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.

Case 2. When Ω = ω3 − ω2 + ϵϕ

The following coupled system is obtained in a similar way as discussed in Case 1:

(31)
with and .

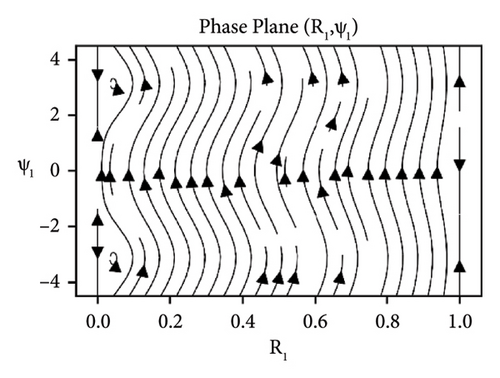
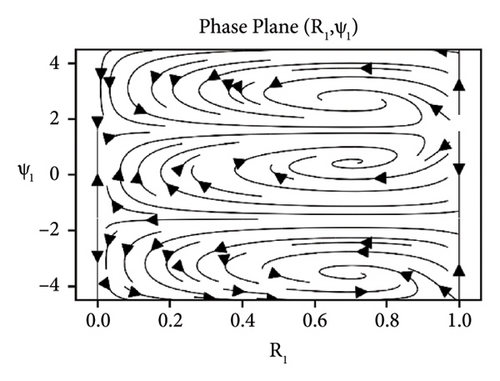
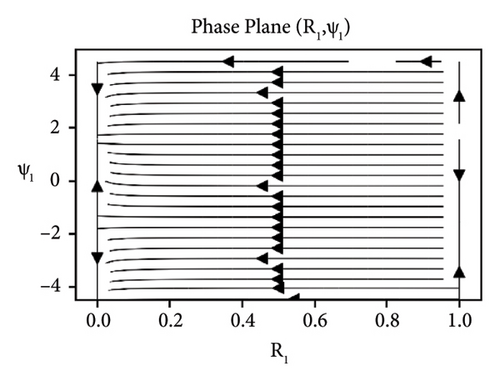
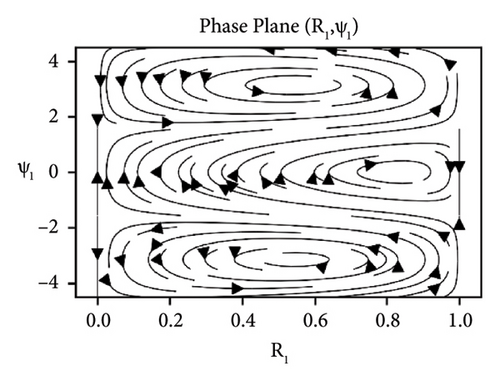
In Figures 5-7, the influence of the parameters ks, cd and ϕ under the difference-type resonance of second and third mode is shown. The similar dynamic behavior of the beam under damping and detuning parameter is observed. However, the additional equilibrium points or instability regions are occurred under the interaction of second and third mode, but stability regions can be increased by increasing the value of elastic foundation  ks.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = cd = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = cd = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.

Case 3. When Ω = ω2 + ω1 + ϵϕ

Substituting Ω = ω2 + ω1 + ϵϕ in (24) and making the terms equal to zero that cause resonances, we have the following coupled ordinary equations:

(32)

To transform the system into the polar coordinates, let Ak0(t1) = rk(t1)sin(ϕk(t1)) and Bk0(t1) = rk(t1)cos(ϕk(t1)), so from (32), we have

(33)

From first two equations in (28); we have , where c2 is constant of integration.

Now, let Φ(t1) = ϕ2(t1) + ϕ1(t1) + ϕt1, so from the last (33), we have

(34)

By introducing the following rescaling:

(35)

Which results in:

(36)
with and .

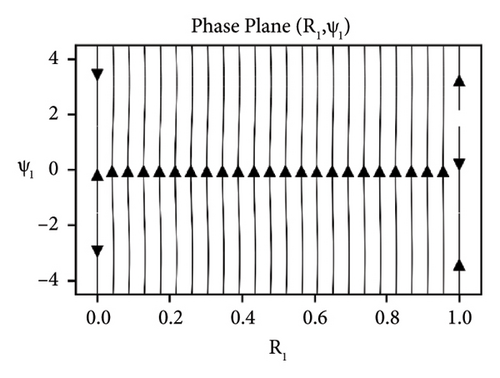
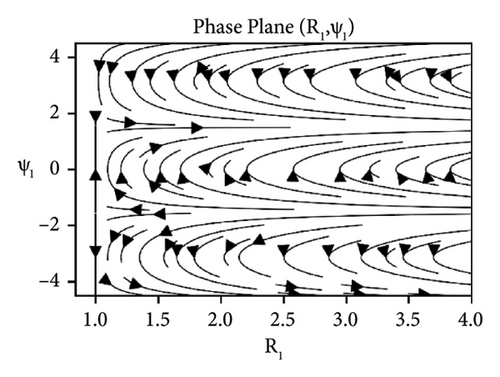
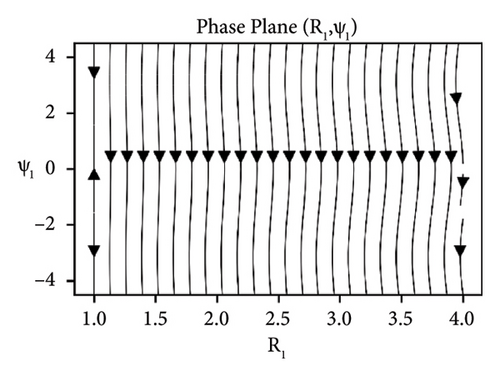
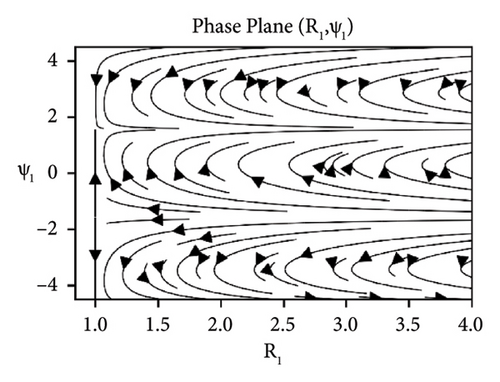
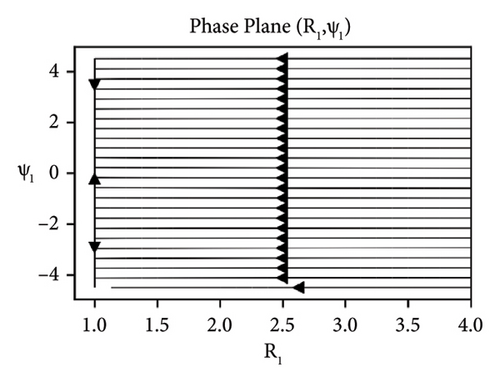
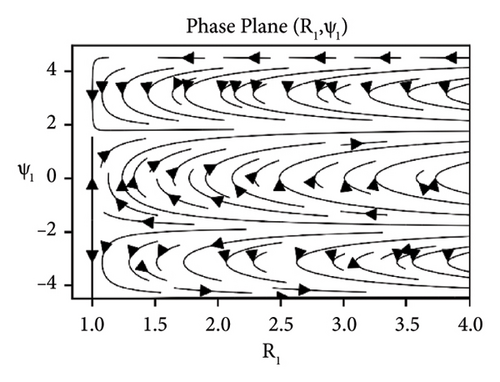
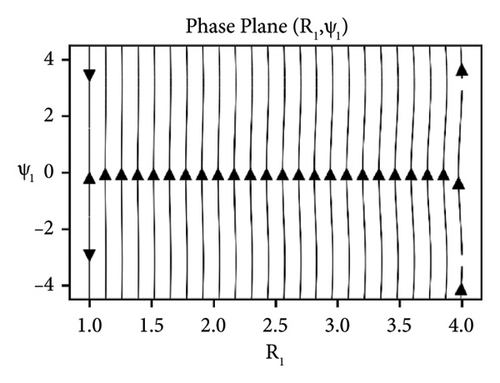
The stability analysis of the beam under the influence of the parameters such as elastic foundation ks, internal damping cd and detuning parameter ϕ while keeping axial velocity α and flexural rigidity kf fixed to 0.01 for the sum-type resonance of first two modes is discussed in the form of phase portraits, see Figures 8-10. The influence of the elastic foundation on the beam is depicted in Figure 8. It can be observed that the fixed points (both stable and unstable) occur only at the straight line R1 = 1, when there is relatively small value of elastic foundation parameter ks. If the value of ks increases, then the fixed points (both stable and unstable) occur at the straight line R1 = 1. In Figure 9, the effects of damping parameter are presented. It can clearly be seen in Figure 9(a), that for smaller values of damping parameter, the only stable and unstable solutions are found out at the straight line R1 = 1. While in Figure 9(b), for larger values of damping, all solutions converge to the straight line R1 = 1. Stability of the system near resonance and away from the resonance region is exhibited in Figure 10. The stable and unstable solutions emerge only at the straight line R1 = 1, when the system is at near resonance, see Figure 10(a). However, the stability regions increase when the system moves away from the resonance can be seen in Figure 10(b).

Details are in the caption following the image
Figure 8 (a)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 8 (b)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 9 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 9 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 10 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = cd = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.
Details are in the caption following the image
Figure 10 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = cd = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.

Case 4. When Ω = ω3 + ω2 + ϵϕ

The following coupled system is obtained in a similar way as discussed in Case 3:

(37)
with and .

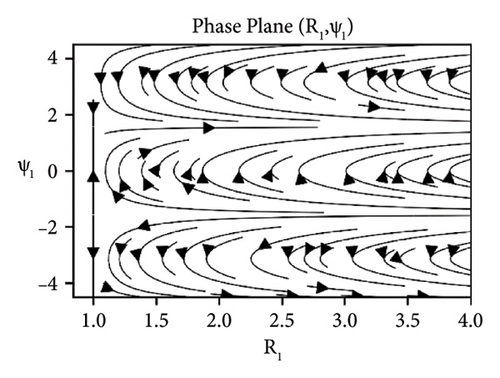
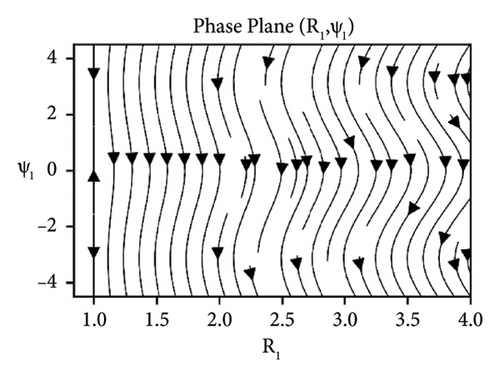
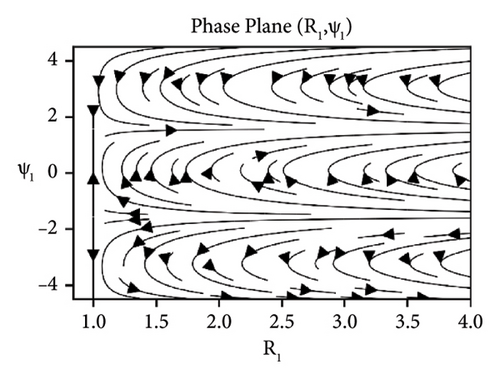
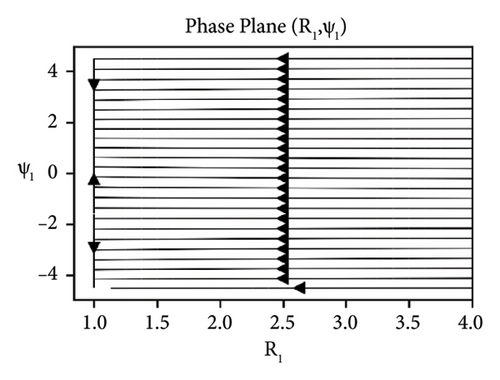
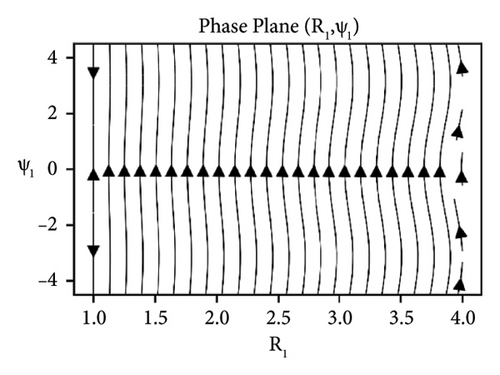
In Figures 11-13, the stability analysis of the system (37) is carried out via phase portraits under the sum-type resonance of second and third mode. The similar behavior of the system is observed as was obtained for first and second mode under the influence of damping and detuning. Whereas, as we increase the elastic foundation, the stability can be observed at the straight line R1 = 1.

Details are in the caption following the image
Figure 11 (a)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 11 (b)
Open in figure viewerPowerPoint
Phase portraits for cd = ϕ = 0.0001, when (a) ks = 0.01 and (b) ks = 10.
Details are in the caption following the image
Figure 12 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 12 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = ϕ = 0.0001, when (a) cd = 0.01 and (b) cd = 5.
Details are in the caption following the image
Figure 13 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = cd = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.
Details are in the caption following the image
Figure 13 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = cd = 0.0001, when (a) ϕ = 0.01 and (b) ϕ = 5.

Case 5. When (nonresonant case)

In this case, the velocity variation frequency Ω is not within the neighborhood of any natural frequency of the system. By eliminating the secular terms in O(1)-problem, that is, vk1(t0, t1), the following conditions are satisfied for the functions Ak0(t1) and Bk0(t1):

(38)

The solution of system in (38) is

(39)
where k1 and k2 are arbitrary constants.

By putting (39) into equation (23), we have the solution

(40)

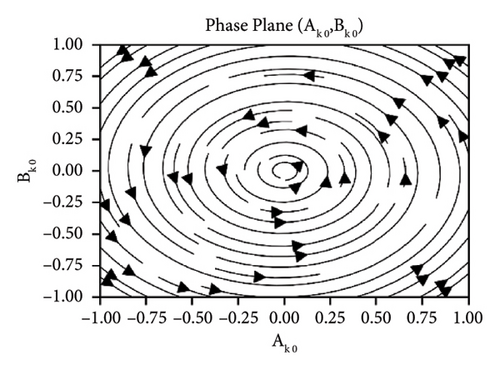
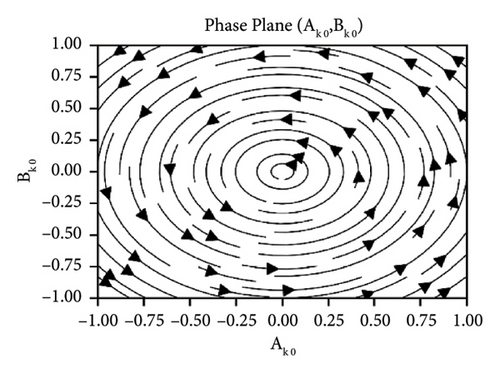
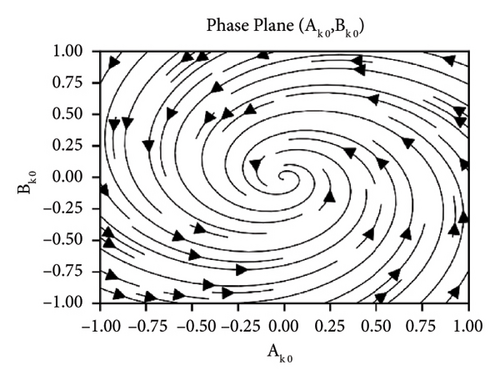
In this case, the influence of the parameter ks and cd is observed. Figure 14 depicts the periodic behavior near origin irrespective of increase or decrease in ks. Figure 15 exhibits the effect of the damping parameter cd. It is observed that all solutions spiral in toward origin for smaller values of damping in Figure 15(a), whereas it can clearly be seen in Figure 15(b) that for relatively larger values of damping, all solutions converge to origin asymptotically.

Details are in the caption following the image
Figure 14 (a)
Open in figure viewerPowerPoint
Phase portraits for cd = 0.001, when (a) ks = 0.1 and (b) ks = 10.
Details are in the caption following the image
Figure 14 (b)
Open in figure viewerPowerPoint
Phase portraits for cd = 0.001, when (a) ks = 0.1 and (b) ks = 10.
Details are in the caption following the image
Figure 15 (a)
Open in figure viewerPowerPoint
Phase portraits for ks = 0.001, when (a) cd = 0.0001 and (b) cd = 1.
Details are in the caption following the image
Figure 15 (b)
Open in figure viewerPowerPoint
Phase portraits for ks = 0.001, when (a) cd = 0.0001 and (b) cd = 1.

5. Conclusion

The stability of an axially moving damped beam under elastic foundation is examined. Mathematically, the transverse vibrations of the system are formulated as fourth order linear homogeneous partial differential equations (PDE) with variable coefficients. The PDE is discretized by means of the Fourier Expansion method and the resulting infinite dimensional systems of coupled ordinary differential equations are tackled via the application of two timescales perturbation method. It turned out that there are infinitely many resonances occur in the system, that is, Ω = ±ωn ± ωk. In this work, the stability of the system is examined at the sum and difference-type resonances of up to three modes. More specifically, the following resonance cases are taken into account:
  • (i)

    Difference-type resonance:

    (41)

  • (ii)

    Sum-type resonances:

    (42)

  • (iii)

    Nonresonant case:

    (43)

In difference and sum-type resonances, the effect of first-second mode and second-third mode is discussed under the influence of elastic foundation, damping, and detuning parameters. The phase portraits are drawn to examine the behavior of the beam model.

In difference-type resonances, it is observed that for smaller values of elastic foundation, the system exhibits stability and instability for some fixed points. While, for larger values of elastic foundation, it is found out that unstable fixed turns out to be stable. For smaller values of damping, there are only bounded solutions while for relatively large damping all solutions converge to stable from unstable and vice versa. For smaller values of detuning that is near resonance regions unstable solutions emerge and for larger values that is the system is kept away from the resonance regions the stable solutions are found.

In sum-type resonances, it is found that for smaller values of elastic foundation, the system exhibits stable and unstable fixed points with deviated trajectories. While, for larger values of elastic foundation, it is found that some stable and unstable fixed points occur, but all trajectories become constant. For smaller values of damping, there are stable and unstable solutions while for relatively large damping all solutions converge to stable and unstable solutions. Unstable solutions occur when the detuning parameter is smaller. However, the stability region increases as the detuning parameter becomes larger, that is, as the system moves away from the resonance region.

In difference and sum-type resonances, higher modes interaction have the same impact as the first two modes interaction have on the system for damping and detuning parameters except the elastic foundation that is stability regions decreases which can be increased by enhancing the value of elastic foundation.

In nonresonant case, the influence of elastic foundation and damping is discussed. It is found out that the periodic solutions around the origin occur irrespective of the variation in elastic foundation. However, the influence of damping in nonresonant is clearly observed for smaller as well as larger values of damping. For smaller values of damping, the solutions spiral in around the origin, whereas for larger values of damping, the solutions asymptotically converge toward the origin and are damped completely.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

Ghulam Yameen Mallah contributed to the methodology and wrote the original draft. Rajab Ali Malookani contributed to the formal analysis and supervised over all activities. Sajad Hussain Sandilo contributed to interpret the data. Sanaullah Dehraj contributed to the validation of code for graphs.

Acknowledgments

The authors have funded this research and publication personally.

    Appendix

    In this appendix, the derivation of coupled system of ODEs equation (26) is discussed in detail.

    The equation with only has solutions for k = 1 and n = 2 if , and k = 2 and n = 1 if , where k = n − 2j − 1, k = 2j + 1 + n and k = 2j + 1 + n with k, and (see [14] for solutions of k and n).

    It is shown that how the secular terms are eliminated in equation (25) for detuned case that is
    (A.1)
    When Ω = ω2 − ω1 + ϵϕ for k = 1 and n = 2, substituting in equation (A.1), we have
    (A.2)
    Simplifying and making the terms equal to zero in the right-hand side which generate resonances, we have
    (A.3)
    Simplifying and equating the coefficients of cos(ω1t0) and sin(ω1t0), respectively, we have
    (A.4)
    When Ω = ω2 − ω1 + ϵϕ for k = 2 and n = 1, substituting in equation (A.1), we have
    (A.5)
    Simplifying and making the terms equal to zero in the right-hand side which generate resonances, we have
    (A.6)
    Simplifying and equating the coefficients of cos(ω2t0) and sin(ω2t0), respectively, we have
    (A.7)
    Hence, we have the coupled system of ordinary differential equations:
    (A.8)

    Data Availability

    All the data used to support the finding of the results are included in the article.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.