International Journal of Energy Research

Volume 2024, Issue 1 8892634

Research Article

Open Access

Improved Deep Extreme Learning Machine for State of Health Estimation of Lithium-Ion Battery

Yan Chen

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Chongqing Innovation Center of Industrial Big-Data Co. Ltd, Chongqing 400707, China

Search for more papers by this author

Junli Meng,

Corresponding Author

Junli Meng

[email protected]

orcid.org/0009-0001-8466-7579

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Shunyang Ming,

Shunyang Ming

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Gengxin Tong,

Gengxin Tong

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Ziyi Qi,

Ziyi Qi

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Yan Chen,

Yan Chen

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Chongqing Innovation Center of Industrial Big-Data Co. Ltd, Chongqing 400707, China

Search for more papers by this author

Junli Meng,

Corresponding Author

Junli Meng

[email protected]

orcid.org/0009-0001-8466-7579

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Shunyang Ming,

Shunyang Ming

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Gengxin Tong,

Gengxin Tong

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

Ziyi Qi,

Ziyi Qi

School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author

First published: 18 May 2024

https://doi.org/10.1155/2024/8892634

Citations: 2

Academic Editor: Ahmad Azmin Mohamad

Share a link

Email
Wechat
Bluesky

Abstract

Prediction of state of health (SOH), a crucial aspect of battery management systems, necessitates accurate and reliable estimations for lithium-ion batteries. However, achieving high-precision SOH estimation using the deep extreme learning machine (DELM) in complex environments is challenging due to the instability caused by its random key parameters. To address this, we propose a novel approach that combines the improved bald eagle search (IBES) algorithm with DELM. By utilizing the IBES algorithm, we can extract highly relevant health indicators from the battery’s parameter curve during charging and discharging, as well as the incremental capacity curve. These indicators serve as inputs to the constructed estimation model, which predicts SOH under different working conditions. The proposed method has been validated using publicly available experimental data, with an overall error in SOH estimation of less than 1%. In comparison to the existing model, the proposed method achieves RMSE, MAE, and MAPE values lower than 0.35%, 0.26%, and 0.21%, respectively. These findings demonstrate that the proposed method excels in terms of both the speed and accuracy of SOH estimation, showcasing its enhanced robustness and reliability.

1. Introduction

Lithium-ion batteries (LiBs) are extensively used in various applications, including new energy vehicles and battery energy storage systems, due to their excellent energy efficiency, high power density, and prolonged self-discharge life [1]. The state of health (SOH) of LiBs is influenced by complex electrochemical reactions, resulting in internal irreversible changes [2]. Additionally, external factors such as ambient temperature, storage conditions, charge-discharge rate, and discharge depth can also impact the SOH [3, 4]. Since direct measurement of SOH using sensors is impractical, it is commonly characterized based on measurable parameters including voltage, current, temperature [5–7], and internal resistance [8]. Accurately and consistently estimating SOH is crucial as it enhances battery lifespan, reduces safety risks associated with battery aging and failure, improves battery energy storage system performance, and aids in the operation and maintenance of electrical equipment and ensuring driving safety.

There are two primary categories of existing methods for estimating the SOH: physical model-based methods and data-driven methods. The physical model-based methods establish effective physical models describing the degradation performance of LiBs through state-space equations or internal mechanisms. Examples of such models include equivalent circuit models [9] and electrochemical models [10]. Shi et al. [11] developed a second-order resistance-capacitance (RC) equivalent circuit model and employed an improved unscented particle filter (UPF) to estimate SOH. Sadabadi et al. [12] formulated a parameter-enhanced single-event model for predicting the remaining useful life, which can leverage electric vehicle charging data. Xiong et al. [13] simplified the P2D model using finite analysis and genetic algorithm optimization. Although physical models comprehensively consider lithium battery aging conditions and degradation mechanisms, offering high accuracy in SOH estimation, they are susceptible to battery load conditions, internal structure, and material quality [14]. The complexity of their principles and discretization of space make calculations computationally intensive, making them less suitable for practical applications.

The data-driven model eliminates the need to consider the complex mechanisms inside the battery. Instead, it establishes a nonlinear mapping relationship between the health factor and SOH in high-dimensional space using indicators that affect battery performance degradation as parameters [15]. By employing data processing and machine learning techniques [16], this model achieves SOH prediction for lithium-ion batteries. It offers strong flexibility and online scalability [17]. In recent years, data-driven methods such as support vector machines [18], Gaussian regression processes [19], logistic regression [20], random forest regression [21], artificial neural networks [22], and particle filters [23] have been widely applied in the estimation of the state of lithium-ion batteries. Li et al. [24] focused on short-term battery SOH estimation and long-term battery RUL prediction. They proposed a novel method called partial incremental capacity and double Gaussian process regression (GPR) fusion. Although GPR is an effective method for SOH estimation, its performance heavily relies on the selection of kernel function and hyperparameters. It is also sensitive to data noise and not suitable for high-dimensional data. Kumar et al. [25] estimated the SOH of a lithium-ion battery pack by analyzing capacity increment and combining it with the support vector regression (SVR) method. They verified the applicability and rationality of the framework through simulation. However, SVR involves numerous hyperparameters that profoundly impact the model’s prediction ability, generalization ability, and execution efficiency. Severson et al. [20] utilized logistic regression for predicting and classifying the cycle life of batteries. However, this method assumes linear relationships and is sensitive to outliers. Wang et al. [26] proposed a method that combines random forest (RF), empirical mode decomposition (EMD), and gated recurrent unit (GRU) to effectively estimate the SOH of lithium-ion batteries. Nonetheless, this approach is sensitive to the selection of hyperparameters. Based on the analysis of traditional particle filter algorithm (PF), Niu et al. [27] combined genetic algorithm to improve PF and established a mapping model of health index and SOH. To enhance the prediction performance of the PF, Ye et al. [28] proposed a prediction method based on chaotic particle swarm optimization particle filter (CPSO-PF).

In contrast to the aforementioned methods, the neural network model, due to its high fault tolerance and excellent stability, is more suitable for nonlinear and time-varying SOH estimation. Zhang et al. [29] proposed an online SOH estimation method for Li-ion batteries by incorporating attention mechanisms into long short-term memory (LSTM) neural networks. Catelani et al. [30] combined state-space estimation technique with recurrent neural network (RNN) to predict the remaining useful life of lithium-ion batteries. To overcome the limitation of RNN’s short memory, Li et al. [31] developed a model that combines recurrent neural networks with long short-term memory (LSTM-RNN) for accurate SOH estimation in Li-ion batteries. Based on the transfer learning method, Ma et al. [32] used convolutional neural network (CNN) to automatically extract features from raw charging voltage trajectories and then combined the improved domain adaptation method to construct the SOH estimation model. While the above-mentioned neural network models accurately predict SOH, they overlook the computational cost associated with the reverse fine-tuning process and the complexity of the network structure. It becomes challenging to strike a balance between network structure complexity and high-precision prediction. In comparison to traditional neural networks, extreme learning machines (ELM) achieve optimal model training without backpropagation [33]. ELM boasts advantages such as low computational cost, strong learning ability, minimal parameter adjustment requirements, and a simple structure. As a result, it finds numerous applications in Li-ion battery SOH estimation. For example, Ma et al. [34] designed an extensive learning extreme learning machine for battery SOH estimation. Nevertheless, ELM is still limited by its inherent model structure and may not fully capture feature information, particularly when dealing with higher dimensions and more complex data.

Deep learning methods have gained significant attention in the field of SOH estimation due to their powerful representation learning capabilities and advantages for handling large-scale data. Han et al. [35] introduced a novel deep learning framework that incorporates domain adaptation. They used a small number of target battery cycle data to establish a general capacity estimation model for differential batteries through deep LSTM. Xia and Qahouq [36] developed an index to quantify the aging behavior of batteries and used deep neural network (DNN) to extract and model the nonlinear complex correlation between the defined SOH index and SOH value of LiBs. Fei et al. [37] considered partial charging segments during incomplete charging based on two mainstream charging modes; then, an online SOH estimation method based on deep learning is proposed. To uncover the intricate connections between input and output, the deep extreme learning machine (DELM) combines the deep learning strategy with the ELM [38]. This integration facilitates the exploration of deeper relationships within the data. Compared to traditional deep learning models, DELM simplifies the complexity of the model, resulting in faster training speed and stronger generalization ability when processing large-scale and high-dimensional data. In the pursuit of high-precision SOH estimation, Li et al. [39] investigated the utilization of an improved sparrow search algorithm to optimize DELM. Similarly, Zhou et al. [40] incorporated the improved grey wolf optimization algorithm with DELM to predict remaining life and diagnose SOH in Li-ion batteries. While these methods have shown promising results, the identification of optimal initial weights and thresholds for the DELM network is still required. This enhances its ability to extract distinctive features and improve learning efficiency when handling vast amounts of data, ultimately enabling accurate and high-precision SOH estimation.

To overcome the challenges discussed earlier, this study proposes the utilization of the improved bald eagle search (IBES) algorithm to optimize key parameters within DELM for SOH estimation. The IBES algorithm addresses issues such as convergence towards suboptimal solutions and the balance between local and global search capabilities through corresponding enhancements. The proposed method extracts highly sensitive health indicators (HIs) from charge and discharge curves, as well as the incremental capacity curve, and employs them as input for the SOH estimation model based on IBES-DELM. Training and testing are performed using datasets encompassing various types of batteries under different operating conditions. The results showcase the superiority of the proposed method in terms of prediction accuracy, speed, and robustness. Consequently, it offers an effective approach to enhancing the reliability of battery systems.

2. Experimental and Methodology

2.1. Experimental Data Preparation

The charge and discharge characteristics vary among different types of batteries, which can lead to differences in the extraction of HIs and the prediction of SOH. To implement and validate the proposed method, this study selects two publicly available battery aging experimental datasets: the National Aeronautics and Space Administration (NASA) dataset [41] and the Center for Advanced Life Cycle Engineering (CALCE) dataset from the University of Maryland [42]. The specific details of the single cell tests are presented in Table 1.

Table 1. Lithium battery test information.

Battery number	Capacity (Ah)	Cycle	Charging current (A)	Charging cut-off voltage (V)	Charging cut-off current (mA)	Discharge current (A)	Discharge cut-off voltage (V)
B005	2	168	1.5	4.2	20	2	2.7
B007	2	168	1.5	4.2	20	2	2.2
B018	2	132	1.5	4.2	20	2	2.5
CS2-35	1.1	717	1	4.2	50	2	2.7
CS2-36	1.1	694	1	4.2	50	2	2.7
CS2-37	1.1	758	1	4.2	50	2	2.7
CS2-38	1.1	757	1	4.2	50	2	2.7

A set of 34 18650 lithium-ion batteries (LiBs), each with a nominal capacity of 2 Ah, was selected by the NASA research center for conducting experiments. Three batteries from this set were chosen to undergo charge and discharge experiments at an ambient temperature of 24°C, and the corresponding details of the testing procedure are provided in Table 1. During the experiments, the batteries were initially charged at a constant current of 1.5 A until reaching a voltage of 4.2 V. Subsequently, the charging process switched to constant-voltage mode until the current decreased to 20 mA, indicating the completion of the charging phase. Following this, the batteries were discharged at a current of 2 A until the voltages of the three battery groups reached 2.7 V, 2.2 V, and 2.5 V, respectively. Once these voltage thresholds were reached, the discharge process was terminated.

In addition, four batteries from the CALCE dataset, each initially with a capacity of approximately 1.1 Ah, are selected for further analysis. These batteries undergo a charging process with a constant current of 1 A until reaching a voltage level of 4.2 V. Subsequently, the batteries are kept at a voltage of 4.2 V while the charging current decreases to 0.05 A, indicating the completion of the charging phase. Once fully charged, the batteries are discharged at a constant current of 1 C until the voltage drops below the cut-off value of 2.7 V.

2.2. Health Indicator Extraction

The state of health of LiBs is commonly used as an indicator to assess the current level of degradation. In most cases, SOH is quantified in terms of capacity, which is calculated as the ratio of the current capacity to the nominal capacity [43].

()

where Q_i is the capacity of the i^th cycle of the battery and Q₀ is the nominal capacity of the battery.

Accurately estimating the SOH of LiBs is of utmost importance to ensure their safety and reliability. A crucial step in this process involves extracting HIs that reflect the level of battery degradation. The accuracy of this extraction directly impacts the precision of SOH prediction. To illustrate this, we use a NASA battery as an example. Figure 1(a) shows the capacity decay curve, while Figure 1(b) depicts the complete voltage and current curve of the B005 battery throughout a cycle, including the constant-current charge (CC Charge), constant-voltage charge (CV Charge), and constant-current discharge (CC Discharge) stages. In this study, HIs are extracted from parameter curves obtained during the battery’s charging and discharging processes. It is worth noting that the HI extraction process may produce some abnormal values, which are subsequently replaced with the average of the adjacent values.

Details are in the caption following the image — **Figure 1 (a) Capacity attenuation curve**
Open in figure viewer PowerPoint

Parameter curve of NASA battery.

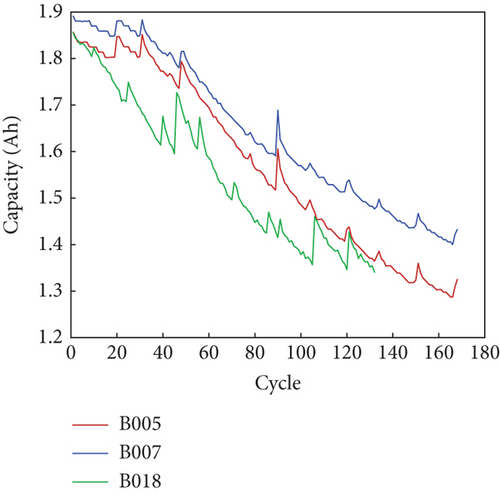
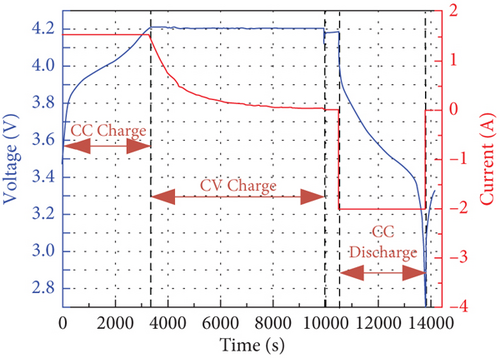
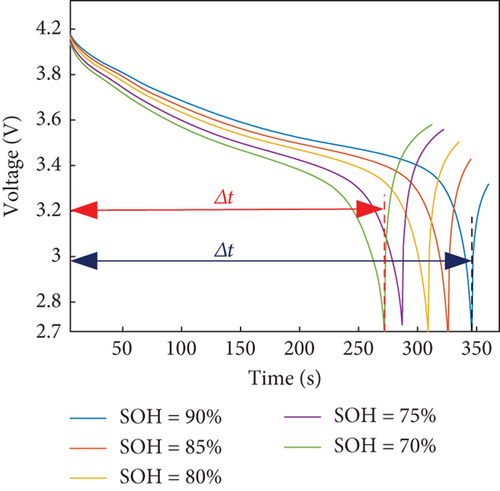
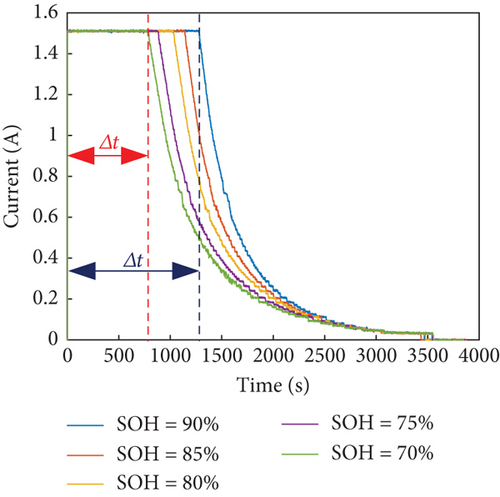
Figure 1(c) displays the voltage variation curve during the constant-current discharge (CC Discharge) stage, extracted from the B005 battery. Additionally, Figure 1(d) presents the extracted current change curve during the charging process from the B005 battery. It is evident from these figures that both the voltage and current curves undergo noticeable changes during the charge-discharge cycle. Moreover, the point at which the battery reaches the cut-off condition gradually shifts to an earlier time. This change exhibits a certain correlation with the SOH and follows a specific pattern that corresponds to the degradation of SOH.

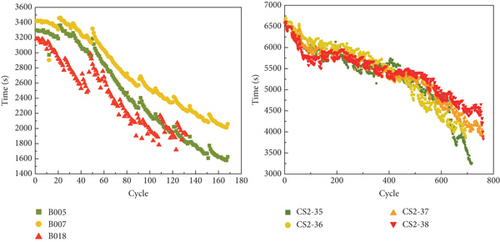
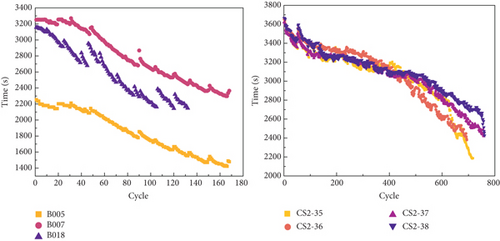
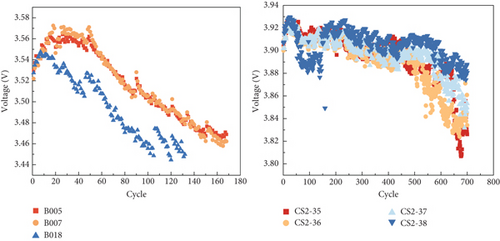
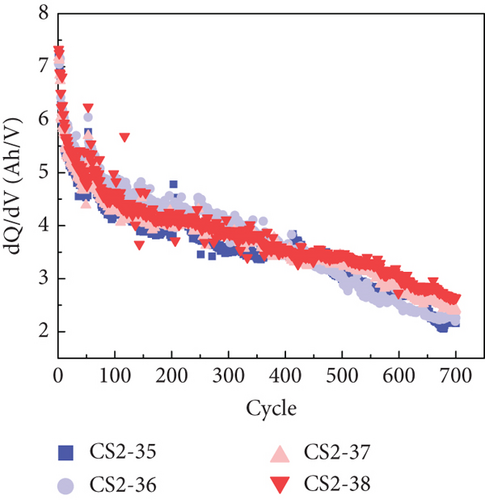
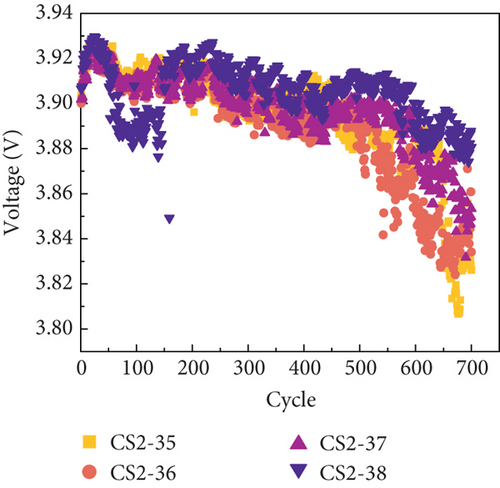
As the SOH diminishes, changes occur in the internal electrochemical reaction of the battery. This leads to a gradual reduction in the duration of constant-current charging during the charging process. Concurrently, as the batteries discharge, their capacity decreases while internal resistance increases. Consequently, the time taken for the voltage to drop from 4.2 V to 2.7 V becomes progressively shorter. To capture this phenomenon, the duration of constant-current charging during the charging process is denoted as HI1, while the duration of the same voltage drop in the discharge process is recorded as HI2. The change curves of these HIs for the two types of batteries are depicted in Figure 2. Moreover, Figure 2(c) illustrates that the average discharge voltage decreases with each cycle, exhibiting a trend similar to the decline in capacity. This observation suggests that the average discharge voltage, denoted as HI3, can be utilized as an additional HI to characterize the SOH.

Currently, the main methods employed for extracting HIs include incremental capacity analysis (ICA), differential voltage analysis (DVA), and isobaric energy analysis (IEA). The DVA method transforms the voltage curve platform into a valley on the DV curve, establishing a relationship between the internal and external changes of battery. However, it often introduces cumulative errors when utilizing the capacity obtained through current and time integration as the abscissa [44]. On the other hand, ICA converts the voltage platform into an IC peak, establishing a relationship between external characteristics and internal electrochemical characteristics [45]. By measuring the changes in current and voltage during battery charging and discharging, the residual capacity and performance state of the battery can be analyzed. Additionally, the IEA method is employed for HI extraction. IEA focuses on observing the energy change caused by the charging equivalent voltage during the constant-current charging process, effectively characterizing battery aging [46]. It estimates the SOH by measuring the voltage and current of the battery and analyzing the energy loss within it.

In this study, the ICA method is chosen to extract the HIs. ICA emphasizes the behavior of the battery system under small changes and unbalanced conditions. It offers the advantages of simplicity, rapidity, and accuracy, which make it suitable for real-time monitoring and evaluation of batteries during actual operation. This method is particularly well suited for estimating the SOH of batteries in dynamic environments. The IC curve is a valuable tool for evaluating the sensitivity of battery capacity changes. Analyzing the IC curve enables the timely implementation of measures to optimize battery utilization and management, leading to improved performance and reliability of LiBs. The dQ/dV curve, which represents the derivative of capacity with respect to voltage, is obtained by performing finite difference calculations on a set of n sampling points. The specific formula utilized for this calculation is as follows:

()

In the given formula, Q(k) denotes the charging capacity of the battery for the k^th sample, while V(k) represents the corresponding charging voltage. For this calculation, we assume a value of n = 10, ensuring sufficient sampling points are considered.

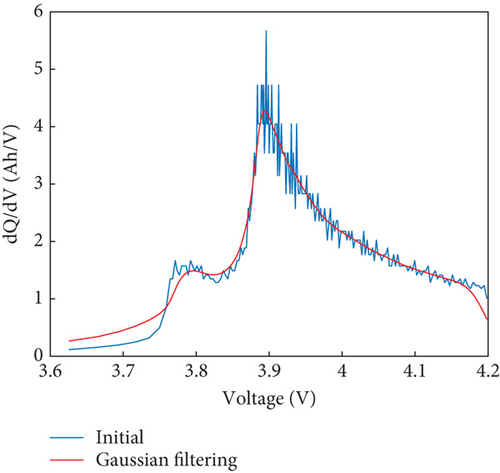
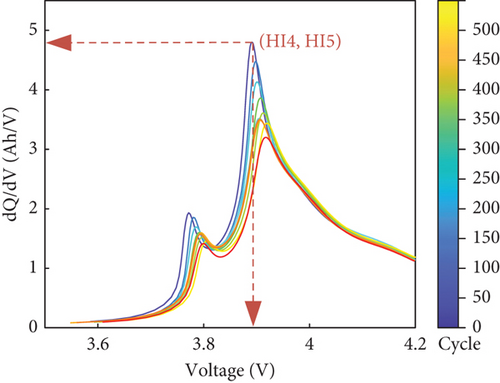
To minimize the impact of noise and enhance the clarity of the IC curve, the Gaussian filtering method is employed. This filtering technique effectively reduces noise and produces a smoothed curve, as demonstrated in Figure 3. The filtered curve clearly displays the peak positions, facilitating the extraction of health indicators. In the case of the CALCE dataset, Figure 3(b) represents the voltage variations observed at different charge levels in LiBs. The changes in the peak value of the IC curve directly correlate with the degradation of the active material inside the battery. This phenomenon effectively reflects the electrochemical reactions occurring during the charge and discharge stages. Hence, the health indicators extracted from the IC curve are the maximum peak value (HI4) and the corresponding maximum peak voltage (HI5). As depicted in Figures 4(a) and 4(b), both the maximum peak value and the maximum peak voltage exhibit a reduction as the number of cycles increases.

In conclusion, there exists a correlation between the attenuation trend of the HIs and the degradation process of SOH. Therefore, the health indicators HI1 to HI5 are utilized to characterize the degradation characteristics of SOH. These indicators are used as input for training the IBES-DELM model. The SOH can be mathematically expressed as follows:

()

2.3. Correlation Analysis of Health Indicators

The appropriate health indicators are one of the important factors that quantify the accuracy of battery degradation prediction results. Each HI exhibits a distinct correlation with the state of health. Furthermore, different combinations of these HIs as input variables in models can yield varying results in terms of SOH prediction. To accurately determine the relationship between these HIs and SOH, a quantitative analysis is required. The Pearson correlation coefficient is used to quantitatively measure the linear correlation between the HIs and SOH. The calculation of the Pearson correlation coefficient is determined as follows:

()

In the formula, r is the Pearson correlation coefficient, is the average value of the overall health indicator, and is the average value of the overall health states.

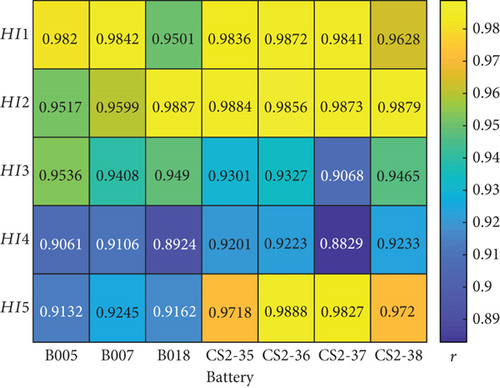
The correlation between the health indicators (HI1 to HI5) and the SOH can be assessed by examining the coefficient r. A stronger correlation is indicated by a higher absolute value of r closer to 1 or -1, while a value closer to 0 implies a weaker correlation. Figure 5 presents a heat map depicting the correlation coefficients between the selected health indicators and the SOH value. It is evident from the heat map that these health indicators exhibit a high correlation with the SOH, indicating their effectiveness in accurately reflecting the state of health in LiBs. This strong linear correlation provides robust support for the efficacy of the proposed IBES-DELM model.

2.4. DELM Battery Degradation Model

The degradation of LiBs is characterized by nonlinear and time-varying processes, coupled with intricate internal electrochemical reactions. Quantifying and modeling the degradation mechanism using specific spatial equations present significant challenges. Gated recurrent unit (GRU), broad learning system (BLS), and long short-term memory (LSTM) are commonly employed for constructing degradation models of lithium-ion batteries in the field of deep learning. LSTM, as a deep learning neural network, exploits the memory units in place of conventional hidden nodes and will not facing the issue of gradient disappearance [47]. Although it boasts high prediction accuracy, its convergence speed is relatively slow, and it incurs a high computational cost. GRU, as a variant of LSTM, simplifies the structure by employing only reset gate and update gate mechanisms. As a result, GRU significantly reduces complexity through a decreased number of parameters and can take into account both efficiency and accuracy [48]. However, it is vulnerable to the problem of gradient disappearance or gradient explosion. BLS, on the other hand, represents a single-layer neural network learning system, comprising random vectorization. Unlike certain neural networks, BLS eliminates the need for iterative parameter updates by effectively extracting crucial features from measurement data through random and enhanced feature mappings. This learning system demonstrates rapid learning speed and excellent generalization performance and avoids local optima issues [44]. However, due to its single-layer architecture, BLS depends significantly on the initial network parameters, and its capacity to express complex nonlinear relationships is relatively limited. Furthermore, while LSTM and GRU are well suited for handling sequential data and long-term dependencies, training and parameter tuning processes can be rather intricate.

DELM introduces a multilayer feedforward neural network, based on deep learning techniques. By extending the traditional ELM structure and incorporating multiple hidden layers, DELM enhances the model’s representation and learning abilities. This method benefits from rapid training speed, excellent generalization performance, and the lack of a need for extensive manual adjustment of hyperparameters. Compared to other deep learning neural networks, DELM exhibits lower structural complexity and offers strong applicability in SOH estimation. Consequently, the DELM method enables the establishment of a nonlinear mapping relationship between the input and output of LiB degradation features. This allows for effective SOH regression fitting through model training.

Figure 6(a) showcases the network structure of ELM, which serves as the foundation for DELM. By adhering to the principle of extreme learning machine, DELM preserves the rapid learning and strong generalization capabilities of ELM. Specifically, DELM consists of an extreme learning machine as autoencoder (ELM-AE) acting as the metastack. The weights within the network are initialized randomly and analytically solved, eliminating the requirement for layer-by-layer backpropagation. Despite its simpler structure, DELM achieves comparable performance to conventional deep neural networks while exhibiting faster convergence speed.

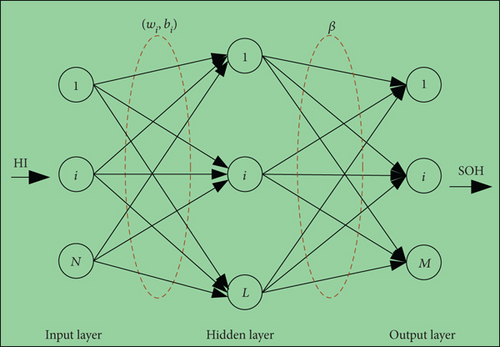
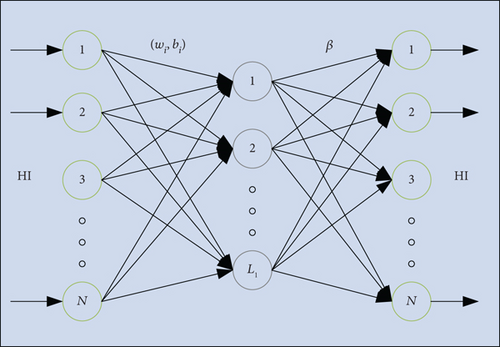
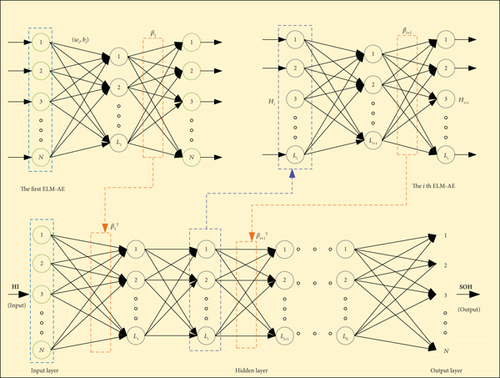
ELM-AE is a special neural network that can use autoencoder to extract and reduce the dimension of data features; its structure is shown in Figure 6(b). The training set consists of samples with features, denoted as S = {(HI_i, SOH_i), i = 1, 2, ⋯N}, where represents the feature vector of the i^th training sample, HI_i ∈ Rⁿ. SOH denotes the regression value associated with the i^th sample, SOH_i ∈ R^m.

Meanwhile, the output of hidden layer neurons, with L nodes in the hidden layer and employing an activation function g(x), is determined as follows:

()

Within the equation, h_i(HI) denotes the output of the i^th neuron located in the hidden layer. In this regard, the input weights w_i and the threshold b_i are randomly generated for each neuron within the hidden layer. Subsequently, these weights and thresholds are orthogonalized. The network output closely approximates the input, while the HI is fitted through regression via the output layer following the hidden layer. The regression function of the ELM-AE can be mathematically expressed as

()

Here, β_i represents the output weight of the i^th hidden layer, β = [β₁, β₂, ⋯, β_i]. H denote the output matrix of the hidden layer, H = [h₁(HI), h₂(HI), ⋯, h_i(HI)]. I is the unit matrix.

To enhance the generalization capability and mitigate overfitting in ELM-AE, the introduction of a regularization coefficient C is imperative. The network loss function serves as the objective function, which is minimized to obtain the optimal weight β.

()

The weight matrix β is obtained through the orthogonal mapping method, as shown in Equation (9). When N < L, ELM-AE achieves sparse representation, mapping the original high-dimensional features. When N = L, ELM-AE achieves feature representation in the same dimension. When N > L, ELM-AE achieves dimension compression, mapping the feature input from a high-dimensional space to a low-dimensional space.

()

DELM adopts a layer-wise training approach to develop deep logical relationships embedded in the input data through independent multiple layers. Figure 6(c) portrays the training structure of DELM. In this process, the initial ELM-AE solves for β₁ using the original sample data. During the training phase, the input weights w_i for each layer are represented by the transpose matrices of β_i. Subsequently, the hidden layer of each ELM-AE takes the output matrix H_i−1 from the previous hidden layer as its current input. This iterative process continues until the last ELM-AE is reached. Mathematically, this process can be expressed as follows:

()

The parameter k represents the number of stacks within the ELM-AE framework.

Building upon the preceding analysis, it can be concluded that DELM harnesses the power of matrix multiplication and exhibits orthogonal properties. This attribute enables DELM to expedite the training process of neural networks, minimize data loss during propagation, effectively capture intricate relationships within the data, and enhance the representation and nonlinear fitting capabilities of deep learning models. As a result, DELM emerges as a highly suitable method for SOH estimation.

Furthermore, in the original DELM approach, the initial weight w_i and threshold b_i hold significant importance as they significantly impact the accuracy of estimation and regression fitting during model training. In the conventional method, these parameters are randomly initialized. However, due to their dynamic nature during network training, this paper adopts the IBES method to determine an optimal initial parameter set (w_i, b_i). The objective of this approach is to enhance the ability and efficiency of network in learning feature inputs.

2.5. BES Optimization Algorithm

The bald eagle search (BES) optimization algorithm is a recently developed metaheuristic approach [49]. This algorithm possesses its own exploration and exploitation capabilities, allowing it to effectively search for globally optimal solutions to nonlinear optimization problems while exhibiting fast convergence speed and strong learning capabilities [50]. At the core of the BES algorithm lies the idea of mimicking the hunting behavior of bald eagles. By leveraging variations in their positions, this algorithm seeks to locate individual optimal solutions, thereby contributing to the search for a global optimum.

Given a D-dimensional search space, randomly initialize a population of n bald eagles:

()

The position of the i^th bald eagle within a D-dimensional space is denoted as follows:

()

The fitness of the population is employed to guide the search capability, wherein it is determined by the fitness function that is defined based on the mean square error loss function.

()

Here, m indicates the number of local variables, denotes the predicted value, and y_i represents the actual value.

To initialize the search space, random initialization is conducted. Just as bald eagles rely on predation density assessment to determine the optimum search space for optimization, the update process of the position vectors P_i,new at this stage can be described as follows:

()

Here, P_best denotes the current optimal position in the search, α is a parameter that controls the changes in position, α ∈ (1.5, 2], and P_mean represents the current average distributed position in the ongoing search.

Once the search space is determined, the bald eagles simulate the flight behavior of vultures as they search for optimal positions to dive and capture prey. The flight distance is determined by their current position, the position of the population center, and the location of the subsequent iteration. The flight behavior of a bald eagle is characterized by a spiral motion, which can be mathematically described using polar coordinate equations. Consequently, the position vectors P_i,new in the prey phase update process of the search space can be represented as

()

In the given context, the shape change parameters are denoted as a and R, a ∈ (5, 10], R ∈ (0.5, 2). Further, θ₁(i) represents the polar angle, while r₁(i) represents the polar radius during the spiral flight of the bald eagle. The function rand generates a random value within the range of (0,1). Meanwhile, x(i) and y(i) represent the position of the bald eagle in polar coordinates, with values falling within the range of (-1,1). P_i+1 corresponds to the next updated position.

Once the optimal position within the search space is identified, the bald eagles undergo a rapid descent towards their prey. During this stage, the population converges towards the best position and commences a targeted attack. The dynamic behavior of the bald eagles in this stage is still described by the polar coordinate equation. The updating process for the position vectors P_i,new during the diving and hunting stage can be expressed as follows:

()

where c₁ and c₂ are motion intensities, with a range of values between [1,2].

2.6. IBES Optimization Algorithm

The traditional BES algorithm demonstrates excellent optimization capabilities within the search space, requiring minimal adjustable parameters and offering ease of implementation. However, during the training process, the algorithm still encounters the following challenges: (1) As the number of iterations increases, the BES algorithm tends to become trapped in local optima, resulting in lower convergence accuracy. (2) In high-dimensional search spaces, the exploration and exploitation abilities of the BES algorithm can diminish. This imbalance negatively impacts both the local and global optimization capabilities, resulting in slow convergence speed and a need for enhanced search efficiency. These issues highlight areas that require improvement in order to enhance the effectiveness and efficiency of the BES algorithm during the training process.

2.6.1. Levey Flight Strategy

In the initial stage of the BES algorithm, the random initialization of the bald eagles’ positions can result in an uneven distribution of individuals, leading to reduced population diversity and slower optimization speed. To address this issue, the BES algorithm incorporates the Levy flight strategy, which combines accuracy and diversity in information exchange among the individuals. This strategy is aimed at enabling the algorithm to timely escape local optima, enhancing the exploration capability in the solution space, and improving the overall convergence effect. The Levy distribution formula, which underlies the Levy flight strategy, is as follows:

()

The random step size is solved by normal distribution:

()

where β = 1.5, δ_u and δ_v are parameter variances, u and v are both normally distributed with

and

, respectively. Г denotes the standard gamma function integral operation.

Equation (14) becomes the following equation after the introduction of the Levy flight strategy.

()

2.6.2. Dynamic Adaptive Inertia Weight

In the second stage, to mitigate the impact of individual neighborhood search ranges on the flight path of the bald eagles, the BES algorithm incorporates a dynamic adaptive inertia weight ω balancing algorithm. This algorithm adaptively adjusts the search positions during different iterations by introducing the fitness function into the inertia weight. By dynamically reflecting the current performance, the concentration of bald eagles at different positions is automatically adjusted. This balance enables the BES algorithm to strike a good compromise between local and global searches, thereby improving search accuracy. The proposed dynamic adaptive inertia weight ω can be described as follows:

()

where fitness(i) represents the fitness of the i^th particle during the iteration process.

According to Equation (16), the bald eagle position update becomes the following equation:

()

2.6.3. Golden Ratio Coefficients

The diving stage of the bald eagle, where it captures prey, plays a crucial role in determining the convergence speed of the BES algorithm. In this stage, the BES algorithm incorporates the golden ratio coefficients from the golden sine algorithm [51] as a local operator in the position updating formula. Furthermore, a warning threshold A is set to scan regions that are likely to yield favorable outcomes, effectively narrowing the search range.

By incorporating these measures, the BES algorithm experiences a notable acceleration in optimization speed, leading to improved search efficiency and convergence accuracy. This approach facilitates more efficient exploration of the search space and enables the algorithm to swiftly converge towards optimal solutions. The golden ratio coefficients a₁ and a₂, as well as the formula for calculating the golden ratio τ, can be described as follows:

()

According to Equation (18), the updating formula for the position becomes as

()

Here, r₁ denotes a randomly generated number within the range of [0, 2π], while r₂ represents a random number in [0, π]. In addition, the threshold value A is set to 0.6, and Equation (25) needs to satisfy the condition A > r.

IBES assists DELM in automatically learning and extracting crucial features from data through parameter optimization, thereby enhancing the model’s expressiveness and accuracy. Through continuous iterations, the IBES algorithm systematically searches for the optimal individual and determines the optimal position, denoted as P_best, within the solution space. This optimal position represents the best feature subset. This process not only reduces dimensionality but also improves the generalization ability of the model. The key parameters of DELM, such as the connection weights w_i and thresholds b_i between the initial input layer and the hidden layer of the initial ELM-AE, are then set to their optimal values corresponding to the optimal feature subset obtained through IBES. These adjusted parameters contribute to improving the training speed and learning capability of the DELM network.

To recapitulate, the SOH within LiBs undergoes a gradual and slow-varying change. In real-world scenarios, the choice of an appropriate model is crucial for accurately estimating SOH. The IBES-DELM model has displayed exceptional performance, making it an ideal selection for such purposes. The complete framework for SOH estimation is visually illustrated in Figure 7.

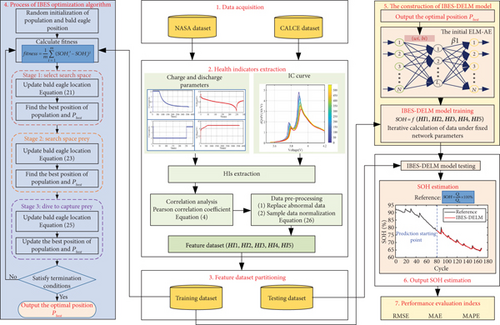
3. Results and Analysis

3.1. Parameter Settings and the Estimation Results of SOH Model

This experiment is conducted using MATLAB software, and the NASA dataset and CALCE dataset are selected as the experimental objects. The feature sample data obtained from these datasets is first normalized during the preprocessing stage. To create the training set, the initial 80 sample data points from the NASA dataset and the first 400 sample data points from the CALCE dataset are chosen. The remaining sample data points are then used as the test set. The formula for data normalization is represented as follows:

()

Here, the sample eigenvalues before and after data training are represented by y and y∗, respectively.

To evaluate the performance of the proposed method for SOH estimation, HI1~HI5 are utilized as input features for the estimation model, while the lithium-ion battery SOH values are considered as the output. The neural network architecture is configured with 5 neurons in the input layer, 6 neurons in the hidden layer, and 1 neuron in the output layer. In the IBES-DELM model, the population size of the bald eagles is set to 20, and the dimension of the fitness function D is 16. The maximum iteration times T is set to 100, while the position control parameter α is set to 2. The shape change parameters a and R are assigned values of 10 and 1.5, respectively. The motion intensities c₁ and c₂ are both set to 2. The upper and lower bounds for the inertia weight are set to 0.9 and 0.4, respectively. The search boundaries for the bald eagle are set to 1 and -1.

Figure 8 provides a visual representation of the SOH estimation results and error analysis for different models on the NASA battery dataset. On the other hand, Figure 9 depicts the performance of various models in estimating the SOH curve on the CALCE battery dataset. The analysis of the estimation results and errors highlights the superior performance of the IBES-DELM model in effectively capturing the SOH curve and delivering high fitting accuracy. The IBES-DELM model exhibits the capability to track the entire degradation process of LiBs accurately and capture local fluctuations well, showcasing enhanced accuracy and robustness. This signifies the optimization effect of IBES on DELM, achieving a balance between local and global searches, improving search efficiency, and enabling more accurate SOH estimation. In terms of error results, there may be a few individual data points with relatively large errors among the 7 battery samples. These errors could be attributed to complex internal electrochemical reactions within the batteries, environmental differences, and other factors. However, the errors for most data points are small and close to zero. The overall estimation error does not exceed 1%, further demonstrating the capability of the IBES-DELM model to accurately estimate the SOH.

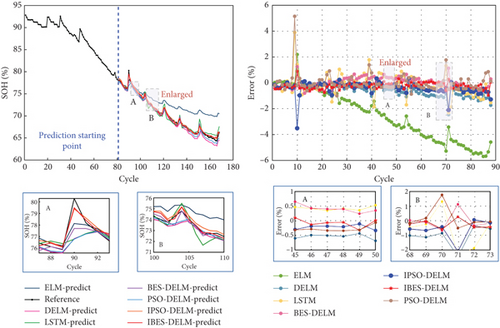
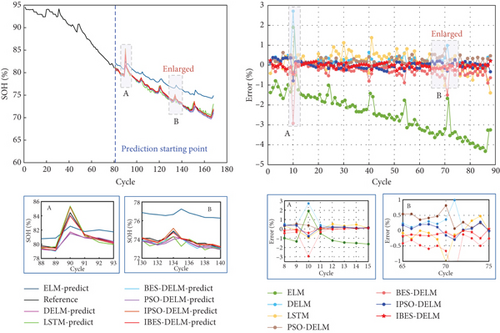
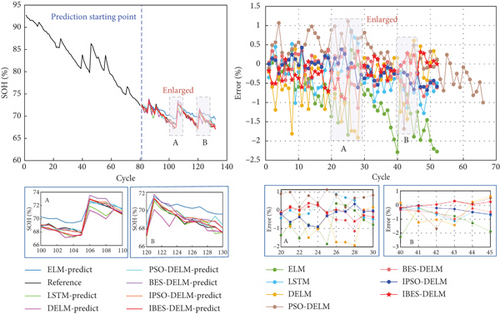
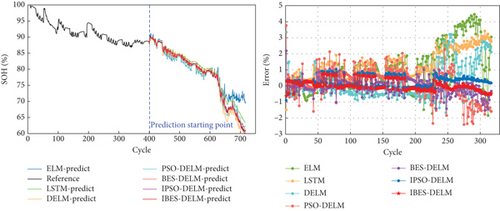
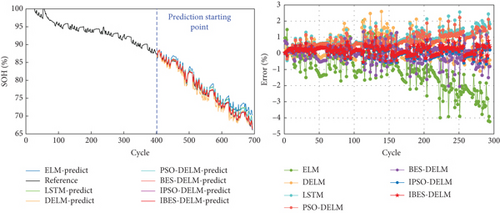
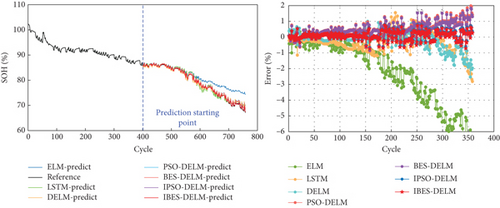
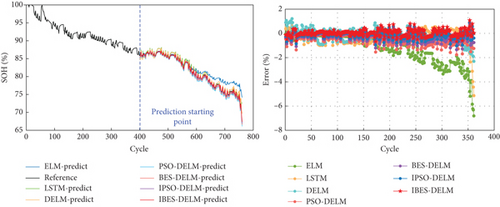
The ELM model is capable of effectively tracking the overall degradation trend of SOH in LiBs. However, it faces difficulties in promptly capturing localized capacity regeneration phenomena. This is mainly due to the randomly assigned weights w_i and thresholds b_i in the ELM model, which introduce instability in its later-stage predictions. Consequently, the ELM model gradually deviates from the actual values, resulting in the highest overall estimation error. In contrast, the DELM model exhibits comparable learning capabilities to LSTM and demonstrates superior generalization by effectively capturing complex relationships within large learning datasets. However, it is still susceptible to fluctuations caused by the randomly determined parameters. As a result, the prediction curve of the DELM model displays significant fluctuations, with a maximum error ranging from 3% to 4%.

The PSO-DELM and BES-DELM models slightly improve the accuracy of SOH estimation compared to the ELM and DELM models. However, they demonstrate excessive sensitivity to the positioning of the data and are less effective in capturing data fluctuations. In the later stages, these models may encounter overfitting or underfitting issues due to data fluctuations, resulting in an overall error ranging from 2% to 3%.On the other hand, the IPSO-DELM model performs well in terms of estimation accuracy, exhibiting relatively small errors. However, when compared to the IBES-DELM model, it shows relatively inadequate convergence and exhibits less stability in representing and fitting battery degradation data. Overall, the IBES-DELM model stands out by effectively capturing the complex degradation patterns of LiBs, displaying superior estimation accuracy, stability, and robustness.

3.2. Model Performance Analysis

To further assess the fitting capabilities of the models in the graph and quantitatively compare their estimation performance for lithium-ion battery SOH, the IBES-DELM model is compared with other models. The estimation performance is analyzed using commonly employed quantitative evaluation metrics, which can be categorized into absolute and relative error metrics. To evaluate the performance of the SOH estimation models, this study employs root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) as performance metrics. The equations representing these metrics are provided below:

()

Here, n represents the total number of samples, while SOH_i and denote the true value and predicted value for the i^th sample, respectively.

Table 2 presents the comparative results of evaluation indicators using different cycling data for LiBs. The findings clearly demonstrate that the IBES-DELM model outperforms other models in terms of fitting performance. Particularly, the IBES-DELM model excels in accuracy and stability for each battery sample, highlighting its superior advantages. Specifically, when compared to the BES-DELM estimation model, the IBES-optimized model reduces the RMSE indicators for the seven different battery samples by 0.12%, 0.23%, 0.30%, 0.36%, 0.36%, 0.34%, and 0.14%, respectively. The MAPE values are reduced by 0.05%, 0.12%, 0.05%, 0.11%, 0.19%, 0.18%, and 0.17%, respectively. The MAE values are reduced by 0.31%, 0.17%, 0.18%, 0.01%, 0.10%, 0.01%, and 0.01%, respectively. These results indicate that, under identical conditions, the IBES-DELM model achieves varying degrees of reduction in RMSE, MAE, and MAPE indicators, highlighting its superior fitting performance compared to other models. This advantage significantly facilitates accurate estimation and prediction of the health status of lithium-ion batteries, playing a vital role in battery management and maintenance. It provides robust support for extending battery life and enhancing system reliability.

Table 2. Indicators of estimation error under different models.

Battery	ELM	LSTM	DELM	PSO-DELM	BES-DELM	IPSO-DELM	IBES-DELM
RMSE
B005	2.110	0.859	0.726	0.504	0.437	0.333	0.319
B007	2.641	0.478	0.392	0.274	0.243	0.188	0.154
B018	1.137	0.603	0.539	0.456	0.400	0.308	0.105
CS2-35	2.804	1.453	1.087	0.944	0.469	0.177	0.107
CS2-36	1.544	0.862	0.753	0.699	0.530	0.240	0.169
CS2-37	2.386	0.727	0.594	0.477	0.410	0.081	0.071
CS2-38	1.721	0.665	0.553	0.451	0.204	0.098	0.063
MAE
B005	1.163	0.618	0.674	0.403	0.305	0.269	0.251
B007	2.469	0.242	0.371	0.339	0.217	0.145	0.097
B018	0.938	0.658	0.567	0.561	0.315	0.239	0.265
CS2-35	2.053	1.300	0.788	0.777	0.360	0.323	0.254
CS2-36	1.222	0.733	0.645	0.564	0.396	0.308	0.205
CS2-37	2.224	0.571	0.568	0.526	0.390	0.225	0.209
CS2-38	1.213	0.571	0.449	0.427	0.364	0.236	0.192
MAPE
B005	2.410	0.516	0.380	0.332	0.318	0.110	0.010
B007	2.931	0.433	0.278	0.255	0.167	0.010	0.002
B018	0.703	0.539	0.456	0.235	0.179	0.019	0.004
CS2-35	1.977	1.561	1.474	1.260	0.017	0.010	0.003
CS2-36	1.865	1.037	0.980	0.642	0.098	0.082	0.004
CS2-37	2.107	1.607	1.053	0.009	0.008	0.007	0.003
CS2-38	2.049	1.832	1.436	0.009	0.007	0.005	0.002

Figure 10 depicts the estimation performance of different models on SOH through a visual representation using the numerical values derived from Table 2. This bar chart provides a concise and clear comparison of the models’ performance based on the indicators. The IBES-DELM model showcases exceptional accuracy in estimating SOH, with RMSE values below 0.4% and MAE values below 0.3% across all seven battery samples. Moreover, the MAPE values remain consistently low, not exceeding 0.1%. Remarkably, the IBES-DELM model exhibits outstanding performance in MAPE values for the CS2-36, CS2-37, and CS2-38 battery samples, approaching an error margin of 0. This noteworthy achievement indicates the highly accurate estimation of model and prediction of SOH for these samples. Such results hold great practical significance in real battery management systems, especially in applications where precise estimation of battery states is critical.

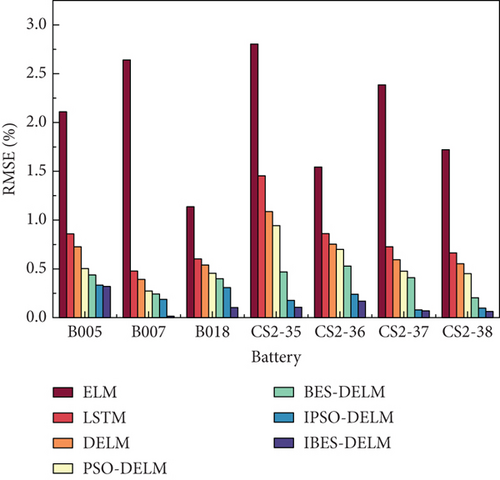
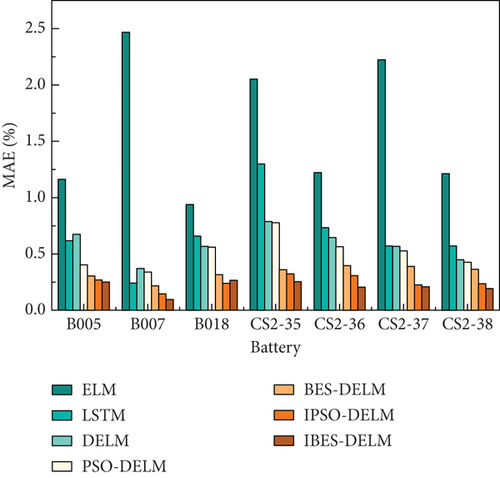
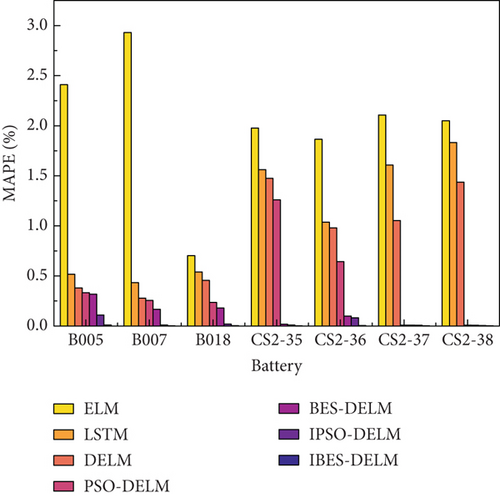
Table 3 presents a comparison of different methods using the NASA dataset. In Reference [52], the improved quantum particle swarm optimization (IQPSO) algorithm was employed to optimize the hyperparameters of the LSTM model, resulting in the IQPSO-LSTM model for SOH estimation. Reference [53] proposed an improved particle swarm optimization (IPSO) algorithm to optimize the SOH estimation model of GPR, providing only RMSE and MAE values. Upon careful examination, it is evident that the IBES-DELM model exhibits superior estimation results when applied to the NASA dataset. Its MAPE value is significantly lower compared to the value reported in Reference [52], while its RMSE and MAE values are lower than those of the other two methods. It is noteworthy that the method utilized in this paper yields smaller errors, effectively enhancing the accuracy of SOH estimation.

Table 3. Comparison of results of different methods under NASA dataset.

Battery	IBES-DELM	Ref. [52]	Ref. [53]	IBES-DELM	Ref. [52]	Ref. [53]	IBES-DELM	Ref. [52]	Ref. [53]
	RMSE (%)			MAE (%)			MAPE (%)
B005	0.319	0.6454	0.3505	0.251	0.4931	0.2663	0.010	0.6485	—
B007	0.154	0.5219	0.4668	0.097	0.419	0.375	0.002	0.5296	—
B018	0.105	0.6085	0.8055	0.265	0.4658	0.6196	0.004	0.608	—

Table 4 illustrates the comparison results of various methods using the CALCE dataset. In Reference [54], a layer-wise relevance propagation-driven (LRP-driven) CNN model was proposed for SOH estimation. Reference [55] utilized an improved bidirectional gated recurrent unit method with an attention mechanism (BiGRU-AM) for SOH prediction. The comparative analysis reveals that the estimation method employed by the IBES-DELM model outperforms others when applied to the CALCE dataset, with lower RMSE, MAE, and MAPE values in comparison to Reference [54, 55]. For instance, the IBES-DELM model reduces the RMSE, MAE, and MAPE values of the CS2-37 battery by 1.74%, 1.24%, and 2.0%, respectively, in comparison to Reference [55]. Furthermore, compared to Reference [55], the IBES-DELM model decreases the RMSE, MAE, and MAPE values of the CS2-37 battery by 0.52%, 0.25%, and 0.57%, respectively. These findings further emphasize the minimal estimation error of the IBES-DELM model on these samples, effectively enabling accurate prediction of SOH.

Table 4. Comparison of results of different methods in CALCE dataset.

Battery	IBES-DELM	Ref. [54]	Ref. [55]	IBES-DELM	Ref. [54]	Ref. [55]	IBES-DELM	Ref. [54]	Ref. [55]
	RMSE (%)			MAE (%)			MAPE (%)
CS2-35	0.107	1.233	0.34	0.254	1.076	0.55	0.003	1.336	0.45
CS2-36	0.169	2.301	0.63	0.205	1.838	0.52	0.004	2.383	0.68
CS2-37	0.071	1.816	0.59	0.209	1.446	0.46	0.003	2.020	0.58
CS2-38	0.063	9.303	0.41	0.192	9.216	0.33	0.002	11.072	0.40

4. Conclusion

To tackle the nonlinear and time-varying challenges of LiBs in practical operations, we propose an innovative approach that integrates the DELM and IBES algorithms. This integration is aimed at achieving reliable and accurate prediction of state of health (SOH) for LiBs. By addressing the limitations encountered in traditional DELM models, such as unstable network behavior and low convergence accuracy due to randomly generated key parameters, we incorporate the IBES algorithm. This integration optimizes the key parameters of the DELM model, resulting in the development of the IBES-DELM model. Consequently, improved network stability and enhanced convergence accuracy are achieved. Additionally, we extract five physically meaningful HIs that are suitable for real-world conditions and daily LiB operations. The Pearson correlation coefficient analysis demonstrates a strong correlation between the extracted HIs and SOH. Finally, the proposed method is validated using NASA and CALCE battery datasets. Experimental results demonstrate that compared to other models, the IBES-DELM estimation model has advantages in exploration ability, high convergence accuracy, and effectively improving the precision and stability of model predictions, achieving accurate SOH estimation and reliable forecasting. These results highlight the superior performance of the IBES-DELM model, aiding in timely detection of battery performance degradation trends, implementing corresponding maintenance and optimization measures to extend battery life, and enhancing system reliability.

In future work, it would be valuable to gather and utilize a wider range of lithium-ion battery datasets to evaluate the performance of model across different types of batteries and operating conditions, enhancing the diversity of the dataset. This would involve conducting performance tests under varying temperature changes, discharge rates, cycles, and usage environments. By expanding the dataset and improving the generalization ability of model, its applicability to real-world scenarios can be ensured. Furthermore, this study only extracts five HIs to train the prediction model. In future endeavors, we can explore the extraction of more concise, physically meaningful, and highly effective indirect characteristic variables. By thoroughly understanding the working principle, electrochemical processes, and degradation mechanisms of lithium-ion batteries, we can identify multiple physical parameters closely associated with changes in SOH. These parameters can then undergo multivariate correlation analysis to evaluate their physical interpretability and operational suitability in relation to SOH changes. This approach will enhance current research methods and improve the performance of SOH estimation.

Conflicts of Interest

The authors declare no conflict of interest.

Authors’ Contributions

Yan Chen was responsible for the funding acquisition and project administration and wrote, reviewed, and edited the manuscript. Junli Meng wrote the original draft, reviewed and edited the manuscript, and was responsible for the methodology. Shunyang Ming was responsible for the validation. Gengxin Tong was responsible for the resources and visualization. Ziyi Qi was responsible for the resources and visualization.

Acknowledgments

This research has received support from the Science and Technology Project of Chongqing Municipal Education Commission (KJZD-M202301104).

Open Research

Data Availability

The data supporting the findings of this study are openly accessible and can be obtained from the NASA PCOE Research Center (https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/#battery) and CALCE Battery Data (https://web.calce.umd.edu/batteries/data.htm).

References

1 Tran M., Panchal S., Khang T. D., Panchal K., Fraser R., and Fowler M., Concept review of a cloud-based smart battery management system for lithium-ion batteries feasibility, logistics, and functionality, Batteries. (2022) 8, no. 2, https://doi.org/10.3390/batteries8020019, 35910082.
10.3390/batteries8020019
PubMed Google Scholar
2 Liu W. and Xu Y., A comprehensive review of health indicators of Li-ion battery for online state of health estimation, 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), November 2019, Changsha, China, 1203–1208, https://doi.org/10.1109/EI247390.2019.9062037.
10.1109/EI247390.2019.9062037
Google Scholar
3 Kai W., Xiao F., Jinbo P., Jun R., Chongxiong D., and Liwei L., State of charge (SOC) estimation of lithium-ion battery based on adaptive square root unscented Kalman filter, International Journal of Electrochemical Science. (2020) 15, no. 9, 9499–9516, https://doi.org/10.20964/2020.09.84.
10.20964/2020.09.84
Web of Science® Google Scholar
4 Yang S., Zhang C., Jiang J., Zhang W., Zhang L., and Wang Y., Review on state-of-health of lithium-ion batteries: characterizations, estimations and applications, Journal of Cleaner Production. (2021) 314, article 128015, https://doi.org/10.1016/j.jclepro.2021.128015.
10.1016/j.jclepro.2021.128015
Web of Science® Google Scholar
5 Reddy D. Y., Routh B., Patra A., and Mukhopadhyay S., Gaussian process regression based state of health estimation of lithium-ion batteries using indirect battery health indicators, 2021 IEEE International Conference on Prognostics and Health Management (ICPHM), June 2021, Detroit (Romulus), MI, USA, 1–7, https://doi.org/10.1109/ICPHM51084.2021.9486519.
10.1109/ICPHM51084.2021.9486519
Google Scholar
6 Xiao B., Xiao B., and Liu L., State of health estimation for lithium-ion batteries based on the constant current–constant voltage charging curve, Electronics. (2020) 9, no. 8, https://doi.org/10.3390/electronics9081279.
10.3390/electronics9081279
PubMed Web of Science® Google Scholar
7 Yang Y., Wen J., Shi Y., and Zeng J., State of health prediction of lithium-ion batteries based on the discharge voltage and temperature, Electronics. (2021) 10, no. 12, https://doi.org/10.3390/electronics10121497.
10.3390/electronics10121497
PubMed Web of Science® Google Scholar
8 Shrivastava P., Soon T. K., Idris M. Y. I. B., and Mekhilef S., Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries, Renewable and Sustainable Energy Reviews. (2019) 113, article 109233, https://doi.org/10.1016/j.rser.2019.06.040, 2-s2.0-85067867691.
10.1016/j.rser.2019.06.040
Web of Science® Google Scholar
9 Bruch M., Millet L., Kowal J., and Vetter M., Novel method for the parameterization of a reliable equivalent circuit model for the precise simulation of a battery cell’s electric behavior, Journal of Power Sources. (2021) 490, article 229513, https://doi.org/10.1016/j.jpowsour.2021.229513.
10.1016/j.jpowsour.2021.229513
Web of Science® Google Scholar
10 Gao Y., Liu K., Zhu C., Zhang X., and Zhang D., Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electrochemical model, IEEE Transactions on Industrial Electronics. (2022) 69, no. 3, 2684–2696, https://doi.org/10.1109/TIE.2021.3066946.
10.1109/TIE.2021.3066946
Web of Science® Google Scholar
11 Shi E., Xia F., Peng D., Li L., Wang X., and Yu B., State-of-health estimation for lithium battery in electric vehicles based on improved unscented particle filter, Journal of Renewable and Sustainable Energy. (2019) 11, no. 2, article 024101, https://doi.org/10.1063/1.5065477, 2-s2.0-85062866664.
10.1063/1.5065477
Web of Science® Google Scholar
12 Sadabadi K. K., Jin X., and Rizzoni G., Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health, Journal of Power Sources. (2021) 481, article 228861, https://doi.org/10.1016/j.jpowsour.2020.228861.
10.1016/j.jpowsour.2020.228861
Web of Science® Google Scholar
13 Xiong R., Li L., Li Z., Yu Q., and Mu H., An electrochemical model based degradation state identification method of lithium-ion battery for all-climate electric vehicles application, Applied Energy. (2018) 219, 264–275, https://doi.org/10.1016/j.apenergy.2018.03.053, 2-s2.0-85044474887.
10.1016/j.apenergy.2018.03.053
CAS Web of Science® Google Scholar
14 Goh H. H., Lan Z., Zhang D., Dai W., Kurniawan T. A., and Goh K. C., Estimation of the state of health (SOH) of batteries using discrete curvature feature extraction, Journal of Energy Storage. (2022) 50, article 104646, https://doi.org/10.1016/j.est.2022.104646.
10.1016/j.est.2022.104646
Web of Science® Google Scholar
15 Yao X. Y., Chen G., Hu L., and Pecht M., A multi-model feature fusion model for lithium-ion battery state of health prediction, Journal of Energy Storage. (2022) 56, article 106051, https://doi.org/10.1016/j.est.2022.106051.
10.1016/j.est.2022.106051
Web of Science® Google Scholar
16 Meng J., Cai L., Stroe D.-I., Huang X., Peng J., Liu T., and Teodorescu R., An automatic weak learner formulation for lithium-ion battery state of health estimation, IEEE Transactions on Industrial Electronics. (2022) 69, no. 3, 2659–2668, https://doi.org/10.1109/TIE.2021.3065594.
10.1109/TIE.2021.3065594
Web of Science® Google Scholar
17 Li Y., Sheng H., Cheng Y., Stroe D.-I., and Teodorescu R., State-of-health estimation of lithium-ion batteries based on semi-supervised transfer component analysis, Applied Energy. (2022) 277, article 115504, https://doi.org/10.1016/j.apenergy.2020.115504.
10.1016/j.apenergy.2020.115504
Web of Science® Google Scholar
18 Feng X., Weng C., He X., Han X., Lu L., Ren D., and Ouyang M., Online state-of-health estimation for Li-ion battery using partial charging segment based on support vector machine, IEEE Transactions on Vehicular Technology. (2019) 68, no. 9, 8583–8592, https://doi.org/10.1109/TVT.2019.2927120.
10.1109/TVT.2019.2927120
Web of Science® Google Scholar
19 Liu K., Li Y., Hu X., Lucu M., and Widanage W. D., Gaussian process regression with automatic relevance determination kernel for calendar aging prediction of lithium-ion batteries, IEEE Transactions on Industrial Informatics. (2020) 16, no. 6, 3767–3777, https://doi.org/10.1109/TII.2019.2941747.
10.1109/TII.2019.2941747
Web of Science® Google Scholar
20 Severson K. A., Attia P. M., Jin N., Perkins N., Jiang B., Yang Z., Chen M. H., Aykol M., Herring P. K., Fraggedakis D., Bazant M. Z., Harris S. J., Chueh W. C., and Braatz R. D., Data-driven prediction of battery cycle life before capacity degradation, Nature Energy. (2019) 4, no. 5, 383–391, https://doi.org/10.1038/s41560-019-0356-8, 2-s2.0-85063567665.
10.1038/s41560-019-0356-8
Web of Science® Google Scholar
21 Liu K., Hu X., Zhou H., Tong L., Widanage W. D., and Marco J., Feature analyses and modeling of lithium-ion battery manufacturing based on random forest classification, IEEE/ASME Transactions on Mechatronics. (2021) 26, no. 6, 2944–2955, https://doi.org/10.1109/TMECH.2020.3049046.
10.1109/TMECH.2020.3049046
Web of Science® Google Scholar
22 Lin H. T., Liang T. J., and Chen S. M., Estimation of battery state of health using probabilistic neural network, IEEE Transactions on Industrial Informatics. (2013) 9, no. 2, 679–685, https://doi.org/10.1109/TII.2012.2222650, 2-s2.0-84883004568.
10.1109/TII.2012.2222650
Web of Science® Google Scholar
23 How D. N. T., Hannan M. A., Lipu M. S. H., Sahari K. S. M., Ker P. J., and Muttaqi K. M., State-of-charge estimation of Li-ion battery in electric vehicles: a deep neural network approach, IEEE Transactions on Industry Applications. (2020) 56, no. 5, 5565–5574, https://doi.org/10.1109/TIA.2020.3004294.
10.1109/TIA.2020.3004294
CAS Web of Science® Google Scholar
24 Li X., Wang Z., and Yan J., Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression, Journal of Power Sources. (2019) 421, 56–67, https://doi.org/10.1016/j.jpowsour.2019.03.008, 2-s2.0-85062567256.
10.1016/j.jpowsour.2019.03.008
CAS Web of Science® Google Scholar
25 Reddy K. R. K., Gunasekaran A., Kalpana P., Sreedharan V. R., and Kumar S. A., Developing a blockchain framework for the automotive supply chain: a systematic review, Computers & Industrial Engineering. (2021) 157, article 107334, https://doi.org/10.1016/j.cie.2021.107334.
10.1016/j.cie.2021.107334
Web of Science® Google Scholar
26 Wang X., Hu B., Su X., Xu L., and Zhu D., State of health estimation for lithium-ion batteries using random forest and gated recurrent unit, Journal of Energy Storage. (2024) 76, article 109796, https://doi.org/10.1016/j.est.2023.109796.
10.1016/j.est.2023.109796
Web of Science® Google Scholar
27 Niu B., Li L., Xu C., and Yu F., Study of SOH estimation of EMU battery based on improved particle filter, 2021 40th Chinese Control Conference (CCC), July 2021, Shanghai, China, 5816–5821, https://doi.org/10.23919/ccc52363.2021.9549726.
10.23919/ccc52363.2021.9549726
Google Scholar
28 Ye L.-H., Chen S. J., Shi Y. F., Peng D. H., and Shi A. P., Remaining useful life prediction of lithium-ion battery based on chaotic particle swarm optimization and particle filter, International Journal of Electrochemical Science. (2023) 18, no. 5, article 100122, https://doi.org/10.1016/j.ijoes.2023.100122.
10.1016/j.ijoes.2023.100122
Web of Science® Google Scholar
29 Zhang J., Hou J., and Zhang Z., Online state-of-health estimation for the lithium-ion battery based on an LSTM neural network with attention mechanism, 2020 Chinese Control and Decision Conference (CCDC), August 2020, Hefei, China, 1334–1339, https://doi.org/10.1109/ccdc49329.2020.9164547.
10.1109/ccdc49329.2020.9164547
Google Scholar
30 Catelani M., Ciani L., Fantacci R., Patrizi G., and Picano B., Remaining useful life estimation for prognostics of lithium-ion batteries based on recurrent neural network, IEEE Transactions on Instrumentation and Measurement. (2021) 70, no. 3524611, 1–11, https://doi.org/10.1109/TIM.2021.3111009.
10.1109/TIM.2021.3111009
PubMed Web of Science® Google Scholar
31 Li W., Sengupta N., Dechent P., Howey D., Annaswamy A., and Sauer D. U., Online capacity estimation of lithium-ion batteries with deep long short-term memory networks, Journal of Power Sources. (2021) 482, article 228863, https://doi.org/10.1016/j.jpowsour.2020.228863.
10.1016/j.jpowsour.2020.228863
Web of Science® Google Scholar
32 Ma G., Xu S., Yang T., Du Z., Zhu L., Ding H., and Yuan Y., A transfer learning-based method for personalized state of health estimation of lithium-ion batteries, IEEE Transactions on Neural Networks and Learning Systems. (2024) 35, no. 1, 759–769, https://doi.org/10.1109/TNNLS.2022.3176925.
10.1109/TNNLS.2022.3176925
Web of Science® Google Scholar
33 Chen K., Li J., Liu K., Bai C., Zhu J., Gao G., Wu G., and Laghrouche S., State of health estimation for lithium-ion battery based on particle swarm optimization algorithm and extreme learning machine, Green Energy and Intelligent Transportation. (2024) 3, no. 1, article 100151, https://doi.org/10.1016/j.geits.2024.100151.
10.1016/j.geits.2024.100151
Web of Science® Google Scholar
34 Ma Y., Wu L., Guan Y., and Peng Z., The capacity estimation and cycle life prediction of lithium-ion batteries using a new broad extreme learning machine approach, Journal of Power Sources. (2020) 476, article 228581, https://doi.org/10.1016/j.jpowsour.2020.228581.
10.1016/j.jpowsour.2020.228581
Web of Science® Google Scholar
35 Han T., Wang Z., and Meng H., End-to-end capacity estimation of Lithium-ion batteries with an enhanced long short-term memory network considering domain adaptation, Journal of Power Sources. (2022) 520, article 230823, https://doi.org/10.1016/j.jpowsour.2021.230823.
10.1016/j.jpowsour.2021.230823
Web of Science® Google Scholar
36 Xia Z. and Qahouq J. A. A., Lithium-ion battery ageing behavior pattern characterization and state-of-health estimation using data-driven method, IEEE Access. (2021) 9, 98287–98304, https://doi.org/10.1109/ACCESS.2021.3092743.
10.1109/ACCESS.2021.3092743
Web of Science® Google Scholar
37 Fei Z., Zhang Z., and Tsui K.-L., Deep learning powered online battery health estimation considering multitimescale aging dynamics and partial charging information, IEEE Transactions on Transportation Electrification. (2024) 10, no. 1, 42–54, https://doi.org/10.1109/TTE.2023.3264438.
10.1109/TTE.2023.3264438
Web of Science® Google Scholar
38 Li K., Xiong M., Li F., Su L., and Wu J., A novel fault diagnosis algorithm for rotating machinery based on a sparsity and neighborhood preserving deep extreme learning machine, Neurocomputing. (2019) 350, 261–270, https://doi.org/10.1016/j.neucom.2019.03.084, 2-s2.0-85064957367.
10.1016/j.neucom.2019.03.084
Web of Science® Google Scholar
39 Li Y., Wang S., Chen L., Qi C., and Fernandez C., Multiple layer kernel extreme learning machine modeling and eugenics genetic sparrow search algorithm for the state of health estimation of lithium-ion batteries, Energy. (2023) 282, article 128776, https://doi.org/10.1016/j.energy.2023.128776.
10.1016/j.energy.2023.128776
Web of Science® Google Scholar
40 Zhou Y., Wang S., Xie Y., Shen X., and Fernandez C., Remaining useful life prediction and state of health diagnosis for lithium-ion batteries based on improved grey wolf optimization algorithm-deep extreme learning machine algorithm, Energy. (2023) 285, article 128761, https://doi.org/10.1016/j.energy.2023.128761.
10.1016/j.energy.2023.128761
Web of Science® Google Scholar
41 Bhaskar S. and Kai G., Battery data set, 2007, NASA Ames Prognostics Data Repository, NASA Ames Research Center, Moffett Field, CA, January 2023, http://ti.arc.nasa.gov/project/prognostic-data-repository.
Google Scholar
42 CALCE Battery data, January 2023, https://web.calce.umd.edu/batteries/data.htm.
Google Scholar
43 Hu X., Feng F., Liu K., Lei Z., Xie J., and Liu B., State estimation for advanced battery management: key challenges and future trends, Renewable and Sustainable Energy Reviews. (2019) 114, article 109334, https://doi.org/10.1016/j.rser.2019.109334, 2-s2.0-85070541160.
10.1016/j.rser.2019.109334
Web of Science® Google Scholar
44 Zhang C., Zhao S., Yang Z., and Chen Y., A reliable data-driven state-of-health estimation model for lithium-ion batteries in electric vehicles, Frontiers in Energy Research. (2022) 10, article 1013800, https://doi.org/10.3389/fenrg.2022.1013800.
10.3389/fenrg.2022.1013800
Web of Science® Google Scholar
45 He J., Wei Z., Bian X., and Yan F., State-of-health estimation of lithium-ion batteries using incremental capacity analysis based on voltage–capacity model, IEEE Transactions on Transportation Electrification. (2020) 6, no. 2, 417–426, https://doi.org/10.1109/TTE.2020.2994543.
10.1109/TTE.2020.2994543
Web of Science® Google Scholar
46 Zhao S., Luo L., Jiang S., and Zhang C., Lithium-ion battery state-of-health estimation method using isobaric energy analysis and PSO-LSTM, Journal of Electrical and Computer Engineering. (2023) 2023, 11, 5566965, https://doi.org/10.1155/2023/5566965.
10.1155/2023/5566965
Web of Science® Google Scholar
47 Tian Y., Lai R., Li X., Xiang L., and Tian J., A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter, Applied Energy. (2020) 265, article 114789, https://doi.org/10.1016/j.apenergy.2020.114789.
10.1016/j.apenergy.2020.114789
Web of Science® Google Scholar
48 Sun H., Yang D., Du J., Li P., and Wang K., Prediction of Li-ion battery state of health based on data-driven algorithm, Energy Reports. (2022) 8, 442–449, https://doi.org/10.1016/j.egyr.2022.11.134.
10.1016/j.egyr.2022.11.134
Web of Science® Google Scholar
49 Alsattar H. A., Zaidan A. A., and Zaidan B. B., Novel metaheuristic bald eagle search optimisation algorithm, Artificial Intelligence Review. (2020) 53, no. 3, 2237–2264, https://doi.org/10.1007/s10462-019-09732-5, 2-s2.0-85068797452.
10.1007/s10462-019-09732-5
Web of Science® Google Scholar
50 Ramadan A., Kamel S., Hassan M. H., Khurshaid T., and Rahmann C., An improved bald eagle search algorithm for parameter estimation of different photovoltaic models, Processes. (2021) 9, no. 7, https://doi.org/10.3390/pr9071127.
10.3390/pr9071127
Web of Science® Google Scholar
51 Li Z., A local opposition-learning golden-sine grey wolf optimization algorithm for feature selection in data classification, Applied Soft Computing. (2023) 142, article 110319, https://doi.org/10.1016/j.asoc.2023.110319.
10.1016/j.asoc.2023.110319
Web of Science® Google Scholar
52 Peng S., Sun Y., Liu D., Yu Q., Kan J., and Pecht M., State of health estimation of lithium-ion batteries based on multi-health features extraction and improved long short-term memory neural network, Energy. (2023) 282, article 128956, https://doi.org/10.1016/j.energy.2023.128956.
10.1016/j.energy.2023.128956
Web of Science® Google Scholar
53 He Y., Bai W., Wang L., Wu H., and Ding M., SOH estimation for lithium-ion batteries: an improved GPR optimization method based on the developed feature extraction, Journal of Energy Storage. (2024) 83, article 110678, https://doi.org/10.1016/j.est.2024.110678.
10.1016/j.est.2024.110678
Web of Science® Google Scholar
54 Wang F., Zhao Z., Zhai Z., Shang Z., Yan R., and Chen X., Explainability-driven model improvement for SOH estimation of lithium-ion battery, Reliability Engineering and System Safety. (2023) 232, article 109046, https://doi.org/10.1016/j.ress.2022.109046.
10.1016/j.ress.2022.109046
Web of Science® Google Scholar
55 Xia F., Wang K., and Chen J., State of health and remaining useful life prediction of lithium-ion batteries based on a disturbance-free incremental capacity and differential voltage analysis method, Journal of Energy Storage. (2023) 64, article 107161, https://doi.org/10.1016/j.est.2023.107161.
10.1016/j.est.2023.107161
Web of Science® Google Scholar

Citing Literature

All articles

Improved Deep Extreme Learning Machine for State of Health Estimation of Lithium-Ion Battery

Abstract

1. Introduction