Advances in Mathematical Physics
Volume 2024, Issue 1 8889808
Research Article
Open Access

Higher Dimensional Kadomtsev–Petviashvili Equation: New Collision Phenomena

Hajar F. Ismael, 

Hajar F. Ismael

Department of Mathematics , College of Science , University of Zakho , Zakho , Iraq , uoz-krg.org

Department of Computer Science , College of Science , Knowledge University , Erbil , Iraq , knu.edu.iq

Search for more papers by this author
Usman Younas, 

Usman Younas

Department of Mathematics , Shanghai University , No. 99 Shangda Road, Shanghai , 200444 , China , shu.edu.cn

Search for more papers by this author
Tukur Abdulkadir Sulaiman, 

Tukur Abdulkadir Sulaiman

Department of Computer Science and Mathematics , Lebanese American University , Beirut , Lebanon , lau.edu.lb

Department of Mathematics , Federal University Dutse , Dutse , Jigawa , Nigeria , fud.edu.ng

Search for more papers by this author
Muhammad Amin S. Murad, 

Muhammad Amin S. Murad

Department of Mathematics , College of Science , University of Duhok , Duhok , Iraq , uod.ac

Search for more papers by this author
Nehad Ali Shah, 

Nehad Ali Shah

Department of Mathematics and Statistics , College of Science , Imam Mohammad Ibn Saud Islamic University (IMSIU) , Riyadh , 11623 , Saudi Arabia , imamu.edu.sa

Search for more papers by this author
Shams Forruque Ahmed, 

Corresponding Author

Shams Forruque Ahmed

Department of Mathematics & Physics , North South University , Dhaka , 1229 , Bangladesh , northsouth.edu

Search for more papers by this author
First published: 08 August 2024
https://doi.org/10.1155/2024/8889808
Citations: 2
Academic Editor: Leopoldo Greco

Abstract

This article analyzes the dynamics of waves to a new higher dimensional Kadomtsev−Petviashvili equation. The higher dimensional Kadomtsev−Petviashvili equation and its expansions have attracted a great deal of scientific interest during the past few decades. Several nonlinear phenomena in a range of domains, like the dynamics of long waves with modest amplitudes in oceans and plasma physics, are studied using this family. In this study, we successfully apply the Hirota bilinear method with the adoption of several test strategies. A set of results like breather, two-wave, and lump periodic solutions are secured. To visually depict the output, a variety of graphs featuring distinct shapes are produced in response to appropriate parameter values. The computational complexities and results emphasize the transparency, effectiveness, and ease of the technique, indicating the method’s applicability to many kinds of both static and dynamic nonlinear equations regarding evolutionary phenomena in computational physics, as well as other practical domains and research fields.

1. Introduction

The intriguing aspect of nature’s nonlinearity has captivated numerous scientists, who perceive it as the pivotal element for unraveling the mysteries inherent in the universe [1, 2, 3]. Complex systems with time-varying characteristics require an in-depth study of nonlinear partial differential equations (NLPDEs). From the beginning of the eighteenth century, scientists have been attempting to clarify complicated phenomena by reducing them to NLPDEs [4, 5, 6]. Nonlinear dispersive waves have become prevalent through various scientific and technical domains, such as fluid mechanics, mathematical biology, mathematical physics, weather forecasting, dynamical meteorology, geophysical fluid dynamics, electromagnetism, and theoretical oceanography. The solutions of NLPDEs can be used to describe the waves in any of these applications. To have a comprehensive understanding of the dynamics of a wave equation, it is noteworthy to consider the exceptional significance of its exact solutions. Scientists are motivated to discover the exact solutions of these equations in various expressions such as traveling waves, solitary waves, shock waves, plane waves, standing waves, transverse waves, and longitudinal waves. This quest aims to enhance their comprehension of the dynamics of wave equations within a given medium [7].

Investigating the solutions and properties of nonlinear PDEs helps one gain a more complete understanding of the structure they explain. There are a plethora of solutions including the solitary wave solutions [8, 9]. The phenomenon of solitary waves has interconnections with a diverse range of disciplines and fields [10, 11]. Therefore, it is of paramount importance to find solutions to the associated PDEs [12, 13]. Several effective methods like improved Bernoulli subequation function method [14], auxiliary equation method [15, 16], modified Kudryashov method [17], the tanh-function method [18], the exp-function method [19], the Adomian decomposition method [20], -expansion method [21, 22], extended direct algebraic method [23], Sardar subequation method [24, 25], Lie symmetry technique [26], and Bäcklund transformations [27] for revealing the exact soliton solutions have been discovered. The perturbation iteration method has been used in addressing boundary layer problems, ordinary differential equations, and singular perturbation problems, for the computation of the Hermite–Gaussian-like solitons with arbitrary peak numbers in nonlocal nonlinear media [28, 29, 30]. Each approach possesses a distinct set of prerequisites that must be fulfilled to be employed in the governing framework. Recently, there has been a growing interest among researchers and analysts in obtaining exact soliton solutions for nonlinear dynamical systems. This effort is facilitated by the availability of computer tools that ease the laborious and time-consuming mathematical calculations involved in this process.

NLPDEs are capable of generating an extensive variety of outcomes. In general, lump solutions are analytical rational function solutions localized in all directions in space. Lump solutions, which are regarded as highly advanced nonlinear wave phenomena, have been observed and studied across a wide range of disciplines. The aforementioned structures are commonly regarded as a constrained variant of solitons, exhibiting greater propagating energy in comparison to general solitons [31, 32]. As a result, these phenomena have the potential to cause significant destruction and even lead to catastrophic outcomes within specific systems. The ability to identify and predict lump solutions in practical applications holds vital significance. In recent years, there has been a notable increase in the number of studies conducted on lump solutions, which has consequently resulted in a greater focus on more specialized investigations. Hence, the theoretical examination of solutions plays a crucial role in advancing our comprehension and forecasting potential extremes in nonlinear systems [33, 34].

However, in this article, we are interested in extracting the different forms of solutions to the studied model by the application of HBM. Section 2 includes the studied model, and solutions via the proposed are discussed in Section 3. The conclusion is presented in Section 4.

2. The Studied Model

The Kadomtsev−Petviashvili equation (KPE) and its extensions have attracted a great deal of attention from academics over the past few decades. There have been many in-depth investigations of these nonlinear equations in areas as diverse as fluid mechanics, plasma physics, and nonlinear optics. Numerous nonlinear phenomena, such as the waves of small amplitudes through water and plasma, are studied by examining this family. The Kadomtsev−Petviashvili (KP) model is still a hot topic in the scientific community. The KPE is a mathematical extension of the KdV equation for the two-dimensional propagation of perturbed waves; this family of equations has been extensively used to study numerous nonlinear waves in various plasma models. Different scholars have developed the following KPE for analyzing the different complicated systems [35, 36]:
()
In Equation (1), the u = u(x, y, t) is a differentiable function. Thus, the KP hierarchy has been the subject of intensive study; with so much focus on the KPE, many important additions have been made to the original [37, 38, 39, 40].
In the recent study, a modified KPE has been discussed:
()
which was thoroughly examined in [37, 38].
The new extended multidimensional KPE reads [41]
()
where u = u(x, y, z, t) is a spatial and temporal differentiable function and coefficients λ, α, β, γ are nonzero parameters related to the model under consideration. The many variations of this equation have been successful in modeling a wide variety of physical phenomena, particularly in the fields of fluid mechanics, plasma physics, and relativistic fluid dynamics. So, our aim is to analyze Equation (3). Moreover, a nonlinear dynamical system’s exact solution can be found with the use of the HBM, which is one of the quickest and easiest methods available. Initially implemented by Hirota in 1971, it has since been utilized to generate various soliton solutions for integrable NLPDEs. In recent years, there has been a rise in interest in the practice of building solutions to integrable equations. Using bilinear forms and symbolic computation, one can make a solution solutions.
To solve the system (3), we adopt
()
Equations (4) and (3) provide the bilinear form
()
Equation (5) may be written as
()
Here, Dx, Dy, Dz and Dt are the Hirota’s operators.

3. Interaction Aspects

3.1. Lump Periodic-Type Solutions

Let
()
By tackling Equations (7) and (5), yield the following.

3.1.1. Set 1

()
Equations (8) and (7) provide
()
On tackling Equations (9) and (4), they give the following solution:
()

3.1.2. Set 2

()
Equations (11) and (7) yield
()
Hence,
()
where

.

3.1.3. Set 3

()
Equations (14) and (7) yield
()
Hence,
()
where

.

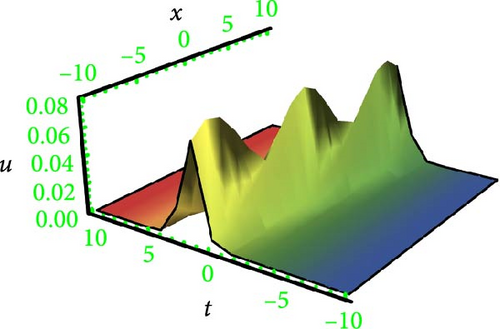
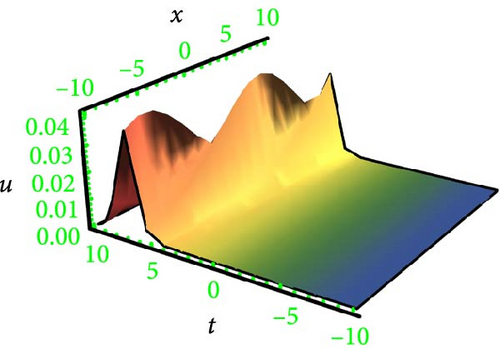
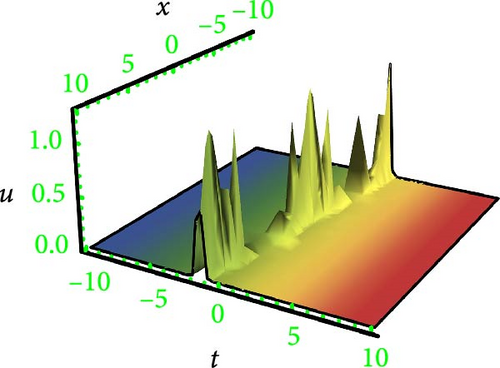
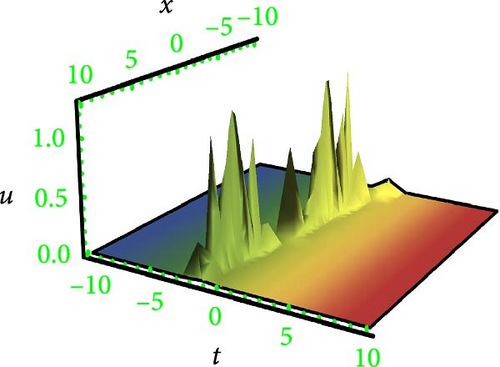
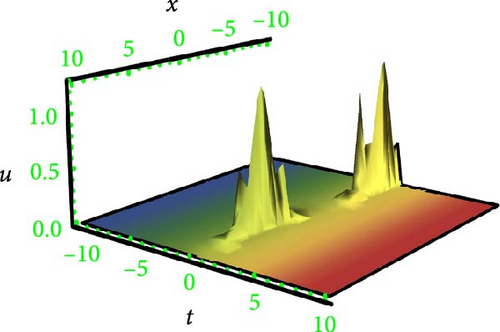
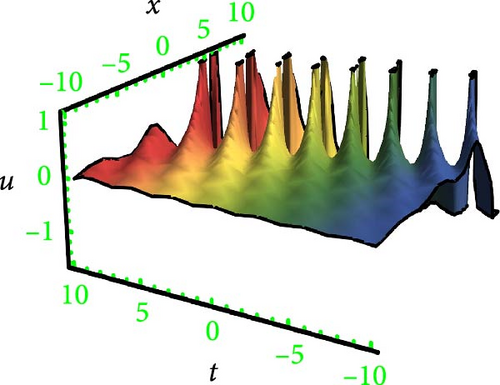
Lump waves (LWs), as superior nonlinear wave phenomena, have been visualized in various fields. These waves are theoretically viewed as a limited type of soliton and move with higher propagating energy compared to general solitons. Consequently, LWs can be destructive and even catastrophic in certain systems, such as in the ocean and finance. It is important to be able to find and anticipate LWs in practical applications. In recent years, studies on lump solutions have increased, leading to more specialized investigations. Therefore, theoretical investigations of LWs are instrumental in enhancing our understanding and predicting possible extremes in nonlinear systems.

3.2. Breather Solutions

Let us start with the following assumption:
()
where
()
Equations (17) and (5) give the following results.

3.2.1. Set 1

()
By solving Equations (19) and (17), they offer
()
We secure for set 1:
()
where

and

3.2.2. Set 2

()
The following results are obtained for set 2:
()
Hence, we secure
()
where

Ω7 = −2α − 2β − 2γ − d0 + 2λ − m0 and Ω8 = 2α + 2β + 2γ + d0 − 2λ + m0.

3.2.3. Set 3

()
and
()
Hence, we secure
()
where

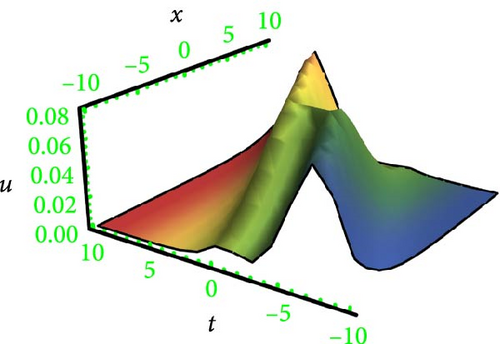
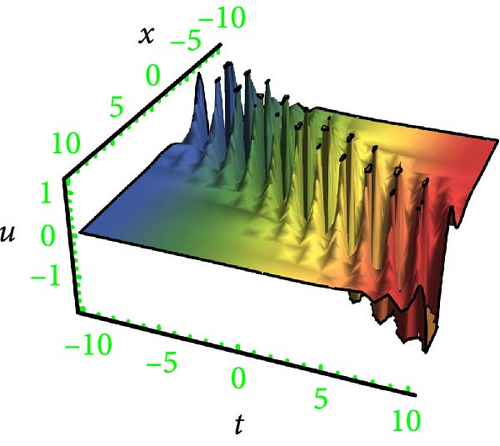
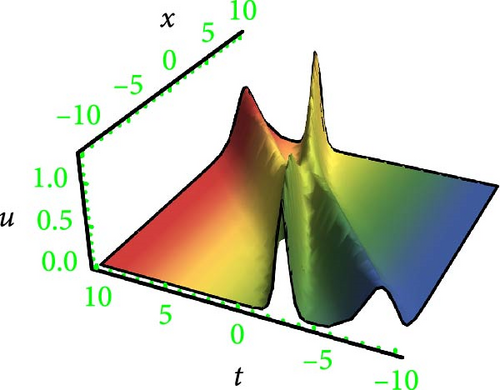
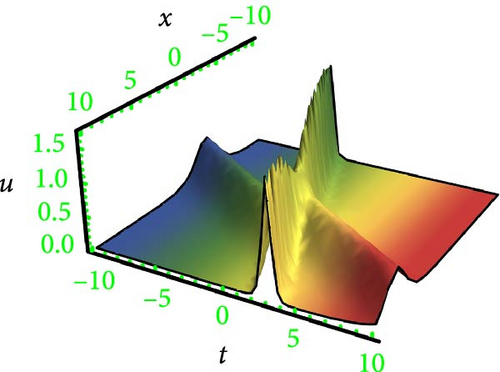
The breather is a kind of nonlinear wave solution whose energy is concentrated in local oscillation, and it is local in one direction and periodic in the other. Breathers comprise a vital class of solutions for NPDEs, so the study of interactions between them can potentially open a new area of research, which may solve the mystery of rogue waves in the ocean and help to generate useful rogue waves in different fields.

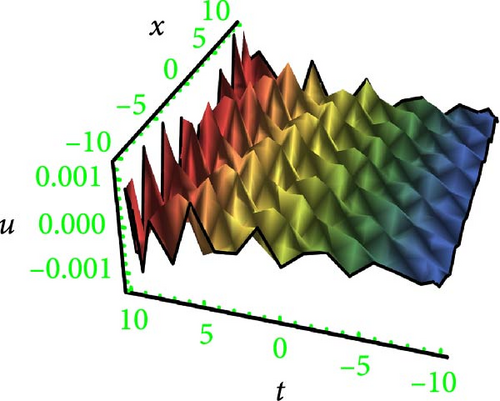
3.3. Two-Wave Solutions

Suppose
()
On solving Equations (28) and (5), we secure the following.

3.3.1. Set 1

()
Equations (29) and (28) give
()
The following solution is obtained:
()
where

Ω11 = α + β + γ − λ.

3.3.2. Set 2

()
Equations (32) and (28) provide
()
So, we extract
()

3.3.3. Set 3

()
Equations (35) and (28) provide
()
We have
()

4. Concluding Remarks

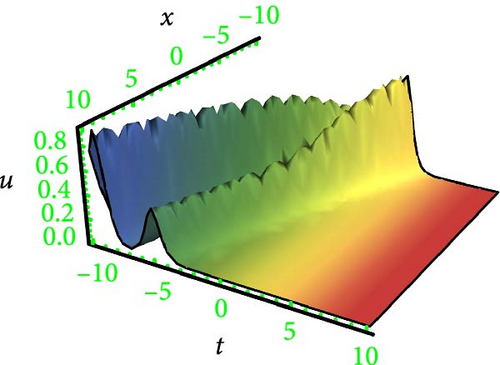
This research discusses the higher dimensional KP equation to discuss more dispersion effects in nonlinear fields. The higher dimensional KPE and its expansions have attracted a great deal of scientific interest during the past few decades. Different shapes of solutions like breather, lump periodic, and two-wave were secured with the assistance of HBM. The Hirota method is a well-known and dependable mathematical technique for locating solitons to NLPDEs. However, it needs systems to be in a bilinear form. Findings have the potential to provide insights into many different kinds of intricate physical phenomena. In order to better illustrate the solutions, 3D graphs were presented in Figures 1, 2, 3, and 4 for the selection of suitable parameters. The visualization of solutions in three-dimensional space and time facilitates the elucidation of waveform shape evolution during propagation. Notably, the emergence of secondary peaks, attributed to higher-order dispersion effects, becomes apparent. These plots effectively showcase the intricate interplay between nonlinearity, dispersion, and dissipation, offering a comprehensive perspective on the waveform shaping processes. Moreover, breathers are nonlinear waves in which energy is concentrated in a localized and oscillatory manner. The word “breather” derives from the fact that the majority of breathers are spatially localized and oscillate (breathe) in time. Breathers are very spatially localized, time periodic, stable, or extremely long-lived excitations that occur in geographically extended, discrete, periodic, or quasi-periodic systems. These solutions increase their amplitude either exponentially or according to power law in time. Breathers achieve their maximum amplitude and finally decay symmetrically to disappear forever. A real analytic solution, a lump solution, is a rational or semirational solution that decays uniformly in every direction in all time. Scientific fields such as optics, water waves, and plasma all deal with lumpy solutions. Lump soliton has been used extensively to investigate integrable equations. There has been an increasing interest in lump solutions and their interactions as a unique type of solution that rationally localizes in all directions in space, and they also play a significant role when discussing integrable equations. Such wave solutions are used to describe significant nonlinear wave phenomena in both oceanography and nonlinear optics, which received a great deal of recent attention in the mathematical physics community. To explore more soliton phenomena, it would be very interesting to consider multicomponent and higher-order extensions of lump solutions, more importantly in higher dimensional cases and fully discrete cases. The employed methodology is universally applicable to a broad category of NLPDEs; however, it has never been implemented on the model in this study before; thus, the outcomes presented here are completely novel. The results of our study indicate that the methodology employed in the study offers a prompt and efficient approach for addressing nonlinear dynamical systems.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Sketches of solution (13) with α = 0.1, b1 = 0.2, b3 = 0.72, b10 = 0.08, b11 = 0.92, β = 0.2, γ = 0.93, λ = 0.2, q1 = 0.3, q3 = 1.02, (a) y = 0.2, z = 0, (b) y = 0.003, z = 3, and (c) y = z = 3.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Sketches of solution (13) with α = 0.1, b1 = 0.2, b3 = 0.72, b10 = 0.08, b11 = 0.92, β = 0.2, γ = 0.93, λ = 0.2, q1 = 0.3, q3 = 1.02, (a) y = 0.2, z = 0, (b) y = 0.003, z = 3, and (c) y = z = 3.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
Sketches of solution (13) with α = 0.1, b1 = 0.2, b3 = 0.72, b10 = 0.08, b11 = 0.92, β = 0.2, γ = 0.93, λ = 0.2, q1 = 0.3, q3 = 1.02, (a) y = 0.2, z = 0, (b) y = 0.003, z = 3, and (c) y = z = 3.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Sketches of solution (16) with α = 2.1, b2 = 2, b4 = 0.002, b9 = 0.8, b11 = 2, β = 1.2, γ = 0.3, λ = 2, q1 = 1.3, q3 = 0.02, (a) y = 0.3, z = 0.003, (b) y = 2.3, z = 1.03, and (c) y = 0.376, z = 2.0773.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Sketches of solution (16) with α = 2.1, b2 = 2, b4 = 0.002, b9 = 0.8, b11 = 2, β = 1.2, γ = 0.3, λ = 2, q1 = 1.3, q3 = 0.02, (a) y = 0.3, z = 0.003, (b) y = 2.3, z = 1.03, and (c) y = 0.376, z = 2.0773.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
Sketches of solution (16) with α = 2.1, b2 = 2, b4 = 0.002, b9 = 0.8, b11 = 2, β = 1.2, γ = 0.3, λ = 2, q1 = 1.3, q3 = 0.02, (a) y = 0.3, z = 0.003, (b) y = 2.3, z = 1.03, and (c) y = 0.376, z = 2.0773.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Sketches of solution (21) with λ = 0.2, a1 = 2.8, α = 2.1, β = 2, γ = 3, p0 = 1.2, p1 = 2, (a) y = 0.02, z = 0.2, (b) y = z = 2, and (c) y = 1.7, z = 0.2.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Sketches of solution (21) with λ = 0.2, a1 = 2.8, α = 2.1, β = 2, γ = 3, p0 = 1.2, p1 = 2, (a) y = 0.02, z = 0.2, (b) y = z = 2, and (c) y = 1.7, z = 0.2.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Sketches of solution (21) with λ = 0.2, a1 = 2.8, α = 2.1, β = 2, γ = 3, p0 = 1.2, p1 = 2, (a) y = 0.02, z = 0.2, (b) y = z = 2, and (c) y = 1.7, z = 0.2.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Sketches of solution (27) with λ = 0.1, a1 = 0.3, α = 0.9, β = 1, γ = 1.4, m0 = 1, p1 = 0.2, (a) y = 2, z = 2.1), (b) y = 0.001, z = 0.6, and (c) y = 1, z = 6.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Sketches of solution (27) with λ = 0.1, a1 = 0.3, α = 0.9, β = 1, γ = 1.4, m0 = 1, p1 = 0.2, (a) y = 2, z = 2.1), (b) y = 0.001, z = 0.6, and (c) y = 1, z = 6.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
Sketches of solution (27) with λ = 0.1, a1 = 0.3, α = 0.9, β = 1, γ = 1.4, m0 = 1, p1 = 0.2, (a) y = 2, z = 2.1), (b) y = 0.001, z = 0.6, and (c) y = 1, z = 6.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

Hajar F. Ismael contributed to methodology; writing, original draft; formal analysis; validation; and software. Usman Younas contributed to resources, validation, and acquisition. Tukur Abdulkadir Sulaiman contributed to resources, acquisition, conceptualization, and review. Muhammad Amin S. Murad contributed to formal analysis, investigation, software, and validation. Nehad Ali Shah contributed to visualization, investigation, and writing, review and editing. Shams Forruque Ahmed contributed to visualization, investigation, and writing, review and editing.

Data Availability

All data generated or analyzed during this study are included in this published article.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.