Wireless rechargeable sensor network (WRSN) has become the most effective solution to the energy problem in wireless sensor networks (WSNs) by introducing mobile chargers (MCs) to replenish energy for energy-starved sensor nodes. In the studies of WRSN, there has been growing interest in using lightweight unmanned aerial vehicles (UAVs) as MCs to overcome geographical constraints. Recently, automatic landing pads (PADs) have been introduced in the UAV-based WRSN, enabling the UAV to automatically replenish energy during the charging flight. Consequently, the UAV’s service range is enlarged, and the UAV can now perform large-scale charging services. In this paper, we investigate the periodic charging scheduling problem in this novel form of WRSN with the goal of minimizing the charging delay. We present the problem’s definition and model and prove it is NP-hard. To address this problem, we propose two periodic charging schemes: SNBC (sensor-node-based charging scheme) and PBC (PAD-based charging scheme). We extensively simulated our proposed schemes in a UAV-based WRSN with PADs, evaluating them based on two key metrics: charging delay and UAV replenishment frequency. The results indicate the efficiency of our approaches. SNBC averaged a 7.2 × 10⁴ s charging delay, while PBC outperformed it with a 14.01% reduction in charging delay and a 13.66% decrease in replenishment frequency.

1. Introduction

With the rapid development of the Internet of Things (IoT), wireless sensor networks (WSNs) have become increasingly popular [1] and are widely employed in various fields, including environmental monitoring [2–5], agricultural production [6], and medical services [7]. Wireless rechargeable sensor network (WRSN) can address the energy problem in WSNs by introducing one or multiple ground mobile chargers (MCs) to recharge energy-hungry sensor nodes [8, 9]. Recently, emerging studies of WRSN employ lightweight unmanned aerial vehicles (UAVs) as MCs to support larger scale or challenging network scenarios by using UAVs’ longer flying range and geographical independence [10, 11]. Yoon and Noh [12] proposed a scheme for WSNs that integrates UAV-assisted charging with sensor solar energy harvesting to enhance energy efficiency and network connectivity.

However, UAVs consume huge amounts of energy during flight, which limits the flight distance of UAVs and cannot be applied to ultra–large-scale scenarios. To address this problem, Choi et al. [13] and Costea and Plesca [14] developed automatic landing pads (PADs) to automatically charge UAVs through a wireless power transfer (WPT) system. By placing many PADs inside the network region, the UAV can recharge energy during a flight from a closer PAD rather than returning to the base station (BS) every time it is about to run out of energy. As a result, the flying distance of UAVs may be effectively reduced, and the energy efficiency of UAVs can be increased, hence expanding the service range of UAVs [15, 16].

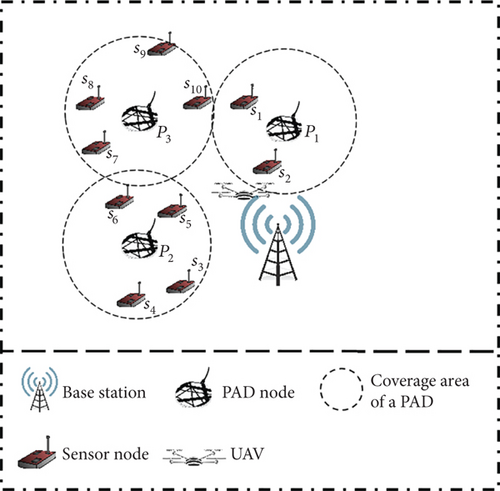
Chen, Yu, and Ouyang [17] first introduced PADs in a UAV-based WRSN and proposed four heuristic algorithms for deploying PADs. However, these deploying algorithms can only work with nodes uniformly distributed as well as in networks with BSs deployed centrally. Inspired by Chen, Yu, and Ouyang [17], our previous work [18] proposed a new PAD deployment method clustering-with-double-constraints and disks-shift-combining (CDC&DSC), which can operate in network scenarios with arbitrary node distribution and arbitrary BS location. Both Chen, Yu, and Ouyang [17] and Chen et al. [18] demonstrated that the PAD deployment in a UAV-based WRSN has to satisfy two constraints: the coverage constraint and the connectivity constraint. The coverage constraint means that for each node, there is at least one charging station (BS/PAD) whose distance does not exceed the charging range of the UAV so that each node can be charged. The connectivity constraint means that the maximum distance between each PAD and its closest PAD cannot exceed the maximum flight distance of the UAV, which makes each PAD reachable for the UAV. Figure 1 shows a paradigm of WRSN with deployed PADs. The introduction of PADs changed the design assumptions of charging scheduling algorithms, and none of the existing scheduling schemes for PAD-free scenarios can work in a WRSN with PADs. Chen, Yu, and Ouyang [17] proposed an on-demand charging scheduling scheme to find the shortest path to the node that sends the charging request and schedule the UAV to charge the node along this path. However, due to the inherent nature of on-demand charging, the algorithm [17] cannot guarantee that all sensor nodes in the network will receive timely energy replenishment.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

WRSN with deployed PADs.

There are two alternative charging scheduling schemes in WRSN. With the on-demand charging scheme, the MC only recharges the nodes after receiving charging requests [19–22], whereas the periodic charging scheme instructs the MC to periodically recharge the sensor nodes along a specified path. The on-demand charging scheme is indeed more flexible and can reduce waiting times. However, it may not always be the most efficient solution. Periodic charging is a centralized charging strategy where the charging trajectory is calculated at the BS, and the MC moves along this predetermined path to execute the charging task. Since each node gets charged cyclically under the periodic charging scheme, the leftover energy of each node likewise varies regularly, ensuring that no node runs out of energy. Hence, periodic charging schemes typically function better than on-demand schemes, especially in situations where data loss cannot be tolerated. Moreover, the on-demand charging method does not ensure that every node will be charged since it is contingent on sensors providing explicit charging requests. This process of issuing requests inevitably leads to further energy expenditure.

Based on the above considerations, we investigate how to schedule the UAV to periodically charge the sensor nodes in a WRSN with PADs. In periodic charging, a charging cycle is the process of the MC leaving the BS to charge all nodes and then returning to the BS. The time required by a charging cycle is known as charging delay, and it is a crucial parameter for evaluating the performance of the periodic charging scheme. Therefore, we choose to minimize the charging delay as the optimization objective. We name our problem as the problem of periodic charging with minimum charging delay in a WRSN with PADs (PCMCDP). In this work, we first define and formalize the PCMCDP problem and prove that it is NP-hard. Then, we propose two periodic charging schemes to schedule the UAV to charge the sensor nodes. Simulations show that the proposed schemes achieve significant performance. To the best of our knowledge, our work is the first work on the periodical charging scheduling in WRSN with PADs.

The rest of the paper is organized as follows. Section 2 reviews the related work. Section 3 introduces the network model and formulates our problem. Section 4 presents the two proposed schemes. Section 5 conducts simulations for performance evaluation. Section 6 concludes our work.

2. Related Work

This section reviews existing studies relevant to our work. We first investigate previous studies on periodic charging scheduling in WRSNs. Then, we go through previous research on UAV-based WRSN. Finally, the PAD Technology section discusses the studies on PADs.

2.1. Periodic Charging Scheduling

In the existing periodic charging scheduling studies, the MC continuously charges each sensor node during periodic operation, subject to the network scenario. The factors that determine the network scenario include the geographical distribution of nodes, the energy consumption model of the network, and the movement speed of the MC. The majority of present research focuses on determining a node access sequence with varied optimization goals. As a result, these studies attempt to turn their objective problem into a traveling salesman problem (TSP) and schedule the MC via the shortest Hamilton cycle. For instance, Rao et al. [23] proposed a periodic charging scheme by scheduling the MC to move along the shortest Hamilton cycle to recharge each sensor node in order to minimize the total travel time of the MC. Xie et al. [24] investigated an optimization problem that jointly optimizes the traveling path, stopping points, charging schedule, and flow routing. The authors in [24] converted the problem into a solvable TSP and then constructed a Hamiltonian cycle as a feasible charging path for MC. Han et al. [8] proposed a cooperative charging algorithm for WRSNs based on network density clustering. The algorithm utilizes a mother wireless charging vehicle carrying multiple subwireless charging vehicles to periodically charge nodes in each cluster via a gradient descent optimization algorithm. Das, Dash, and Yadav [25] proposed GPCS, a GA-based periodic partial charging scheme for WRSNs, optimizing sensor charging with a battery-constrained MC. The scheme minimizes sensor dead periods and energy consumption, outperforming existing methods in charging efficiency and latency.

However, most of these efforts use wireless charging vehicles as MCs, which may not be suitable for difficult terrain.

2.2. Charging Scheduling With UAV

With the development of wireless charging technology for UAVs, many researchers have proposed using lightweight UAVs as an alternative approach for efficient and flexible charging in large scale or challenging scenarios in WRSNs.

The related work on UAV charging investigates optimizing the path planning and charging strategies for UAVs to maximize charging efficiency. Zhao et al. [26] investigated bridge monitoring task in 3D-WRSN by simulating the bridge and obstacles and proposed an optimized ant colony algorithm to solve the 3D UAV path planning problem with obstacles and then designed a two-phase algorithm to optimize the wireless charging at each time slot. In [27], an on-demand charging algorithm was proposed for the UAV charging in WRSN. This approach involved sensor clustering with K-means algorithm and cluster sorting using fuzzy logic. To address UAV path planning, a gradient-based optimizer (GBO) was employed. Lin et al. [28] proposed a spatial discretization scheme to obtain the set of UAV charging points and maximize the total charging energy. Wu et al. [10] studied the trajectory of the UAV optimization problem to maximize the energy utilization efficiency of the UAV. Liu et al. [11] proposed an improved particle swarm optimization (IPSO) algorithm that utilizes a flexible dimensional mechanism and the K-means operator to determine the hovering position of UAVs. Additionally, a penalty and compensation mechanism is used to resolve a scheduling optimization problem involving charging UAVs.

Due to the limitation of the UAV battery capacity, the coverage range of the UAV in the network scenario is limited. This means that providing charging services in ultra-large-scale WRSNs is difficult and introducing external charging devices for UAVs is a feasible solution.

2.3. PAD Technology

With the growing prevalence of UAVs, there is an increasing need for efficient and flexible charging solutions. In response, researchers have introduced the use of the PAD, which can wirelessly transmit energy to a hovering UAV using a pair of lightweight induction coils [13].

The introduction of PAD technology into WRSNs has received sufficient technical support, and several studies have focused on the deployment of PADs. Chen, Yu, and Ouyang [17] introduced PADs in a UAV-enabled WRSN so that UAVs with low residual energy could fly to nearby PADs for recharging. Four heuristic PAD deployment algorithms were proposed to reduce the number of PADs. However, Chen, Yu, and Ouyang [17] only considered the uniform distribution of central BS and nodes, making it unsuitable for large scale or challenging scenarios. Inspired by [17], Chen et al. [18] investigated the problem of deploying a minimum number of PADs in UAV-based WRSNs and proposed an adaptive PAD deployment scheme that can be applied to arbitrary locations of BSs, the arbitrary geographical distribution of sensor nodes, and arbitrary network areas.

Currently, there is a lack of extensive research on scheduling UAV charging in WRSNs. In this paper, building on the scheme and network deployment scenario proposed by [18], we further explore the UAV periodic charging scheduling problem.

3. Preliminaries

In this section, we first introduce the network model and the energy model. Then, we define and formalize the PCMCDP problem. Table 1 lists all the notations used in the paper. Additionally, Table A1 in the Appendix A presents all abbreviations used in this paper.

Table 1. List of notations.

Notation	Description
E_UAV	Battery capacity of UAV
E_S	Battery capacity of the sensor
V_U	Flight speed of UAV
S	The set of sensor nodes
P^′	The set of charging stations
η	Energy transfer efficiency between UAV and sensors
E_mov	Energy consumption during the movement of UAV
E_hov	Energy consumption of UAV hovering
E_travel	The sum of E_mov and E_hov
E_charge	Energy consumption in the charging process of UAV
E_rec	The energy obtained by the sensor
P_hov	The hovering power of UAV
P_mov	The motion power of UAV
P_PAD	The power for charging stations
t_m	The flight time of the current charging cycle
t_h	The hovering time of the current charging cycle
Δ	The approximate time for UAV to charge each sensor
d_max	The maximum flight distance of the UAV
d_cover	The charging coverage of UAV

3.1. Network Model and Energy Model

We consider a large area with one BS, N static sensor nodes, a UAV, and M deployed PADs. Let S denotes the set of sensor nodes and P denotes the set of PADs. Since the BS, as well as the PADs, is capable of charging the UAV, they are sometimes collectively referred to as the charging stations in our work for the convenience of description. Let p₀ denotes the BS and P^′ = {p₀, p₁, p₂, ⋯p_m} denotes the set of charging stations. We also use p_i ∈ P^′ to denote the location of the PAD/BS. To simplify the problem, the energy supply of each charging station (the BS or a PAD) is unlimited.

Each sensor node s_i ∈ S is powered by a rechargeable battery with energy capacity E_S and deployed statically on a given location (x_i, y_i) known by the BS and the UAV. The BS is also deployed arbitrarily according to the network requirement, and it is responsible for data gathering, charging schedule, and serving the UAV. The deployment of PADs satisfies the coverage constraint and the connectivity constraint simultaneously.

The UAV is also powered by a rechargeable battery with high capacity E_UAV. The UAV flies at a constant speed V_U between the sensor nodes, the PAD nodes, and the BS, and it must fly to one charging station for energy replenishment before the power runs out. Only the charging station (the BS or PADs) can charge the UAV, and the battery is fully charged when the UAV departs from the charging station. The procedure by which the UAV departs from the BS, charges all nodes once, and then returns to the BS is known as a charging cycle, and the time T taken for one charging cycle is referred to as charging delay.

Without losing generality, we use the static average energy consumption rate ρ_i to depict the energy consumption of node s_i. Each sensor node may perform a different task in the network. Thus, they have different ρ_i. Let r_i denotes the residual energy of s_i. Then, when s_i is charged, r_i can be expressed as

(1)

The UAV employs a point-to-point and full-charge mode of operation for recharging sensor nodes, necessitating it to hover over the target node until the charging process is complete. While the partial charging strategy [29] can mitigate energy waste due to overcharging to a certain extent, for the sake of model simplicity and computational efficiency, we opt for a full-charging approach for sensors. The energy consumption of the UAV consists of two parts, namely, the energy consumed for traveling E_travel and the energy consumed for charging the sensor nodes E_charge. The energy consumption for traveling can be divided into two parts: One is the energy consumed in flight among different target devices (sensor nodes, PAD nodes, and BS) E_mov, and the other part is the energy consumed in hovering over the sensor nodes to perform charging operations E_hov. We can obtain the residual energy e_rem of the UAV as follows:

(2)

Let the energy transfer efficiency between the UAV and the node to be charged be η; then,

(3)

where E_rec is the total amount of energy to be replenished by the nodes to be charged.

Based on the propulsive power equation derived by Plun, Rozenberg, and Salomaa [30], the motion power P_mov and hovering power P_hov of the rotary-wing UAV are calculated. The motion energy E_mov and hovering energy of a charging flight E_hov are derived as follows:

(4)

(5)

where t_m and t_h are the flight time and hovering time of the current charging cycle, respectively. Since E_S ≪ E_UAV, the time for a sensor node to be fully charged is approximated as a constant Δ; we therefore have

(6)

where n is the number of charging nodes for the current charging cycle. Based on the predefined V_U and E_UAV, we calculate the maximum flight distance of the UAV d_max

(7)

After the derivation [30], the charging coverage of UAV can be obtained as

(8)

3.2. Problem Definition

In a WRSN with PADs, the deployment of PADs satisfies the coverage constraint and the connectivity constraint simultaneously. The coverage constraint means that the Euclidean distance from each sensor node to its nearest charging station is less than d_cover, which ensures that the UAV has enough power to fly to the nearest charging station for energy replenishment after charging a sensor node. The coverage constraint can be formalized as follows:

(9)

where dis(s_i, p_j) is the Euclidean distance between s_i and p_j. If the distance between s_i and p_j is less than d_cover, we call s_i covered by p_j and denote this relationship as follows:

(10)

where P(s_i) is the function that maps s_i to the charging station that covers it and C(p_j) is the set of all the nodes covered by p_j. According to Equation (9), we have

(11)

In the meanwhile, the connectivity constraint means that the Euclidean distance from each charging station (a PAD or the BS) to its nearest another charging station is less than d_max, which ensures that the UAV can reach all the charging stations. As a result, the UAV can return to the BS after a charging cycle from the BS. The connectivity constraint can be formalized as follows:

(12)

where dis(p_i, p_j) is the distance between p_i and p_j. If p_i and p_j satisfy Equation (12), we call p_j adjacent to p_i and denote this relationship as p_j ∈ Neighbor(p_i), where Neighbor(p_i) is the set of all charging stations which are adjacent to p_i. The connectivity constraint ensures that there is a weighted connected graph G = (P^′, E) for the UAV, where the vertexes are the charging stations, the edge (p_i, p_j) ∈ E, if p_j ∈ Neighbor(p_i), and the weight of the edge (p_i, p_j) is dis(p_i, p_j).

It is also to be noted that the coverage constraint and the connectivity constraint are the prerequisite assumptions of this paper. The two constraints need to be satisfied by the previous work [18], that is, the location of the PAD deployment of the network environment of this paper. The work in [18] is reviewed here and is not stated in the subsequent problem definition.

In the periodic charging scheme, the UAV departs from the BS to charge each sensor node and subsequently returns to the BS for each charging cycle. Following its return, the UAV completes a charging cycle and proceeds to conduct inspections and other operations at the BS. In our case, the sensor nodes are deployed across an expansive network area. These nodes exclusively rely on energy replenishment facilitated by UAV, as opposed to charging stations. This reliance stems from the physical structure of the charging station and the loss of energy transmission over long distances in complex scenarios. Therefore, we can divide the charging path of the UAV throughout the charging cycle into several subpaths that start and end at charging stations. It is worth noting that the starting and ending charging stations of a subpath may be the same if there are numerous nodes nearby that need to be charged. It is also important to notice that there are multiple routes between the two charging stations, depending on the sequence of the sensor nodes that the UAV passes through. Let SEQ_i,j denotes the set of all the possible sequences of sensor nodes that the UAV can pass through from p_i to p_j, where p_j ∈ Neighbor(p_i) ∪ {p_i}. Then, the x^th node sequence

can uniquely present one subpath from p_i to p_j, where

presents the m^th sensor node the UAV passes by in the subpath seq_i,j,x. Let S_i,j,x denotes the set of sensor nodes in seq_i,j,x. If seq_i,j,x = null, S_i,j,x = ∅, which means that the UAV flies from p_i to p_j directly without passing by any sensor nodes. Let l_i,j,x denotes the length of the subpath seq_i,j,x. According to the energy model before, we can present the energy consumption of the UAV as it flies along the subpath seq_i,j,x as follows:

(13)

Since it is difficult to obtain the r_k in real time, to simplify, in practice, we can consider the required supplementary energy of each node as the battery capacity of the node E_S. Thus, C_i,j,x can be expressed by the following equation.

(14)

And the time cost of the UAV as it flies along the subpath seq_i,j,x can be represented as follows:

(15)

Let us define a decision variable d_i,j,x as follows:

(16)

For simplicity, assume that the UAV has zero energy every time it lands on the PAD during the charging cycle. As a result, the time required for the UAV to charge at a single charging station is approximated as a constant. The charging delay can be represented as

(17)

To easily represent the set of nodes charged by the UAV, we define the following operation:

(18)

Based on the above analysis, the problem can be defined as follows:

Definition 1 (the PCMCDP). Given a monitoring area Ω, a BS p₀, a UAV, a set of sensor nodes S = {s₁, s₂, ⋯, S_N}, and a set of PADs P = {p₁, p₂, ⋯, p_m}, the objective of our problem is to find the charging loop with the minimum charging delay that charges all the sensor nodes. This problem can be formulated as follows:

(19)

(20)

(21)

(22)

(23)

(24)

Equation (20) ensures that all possible subpaths cannot exceed the energy limit of the UAV, while Equations (21) and (22) ensure that all N sensor nodes are accessed by the UAV and only once. Equation (23) demonstrates the travel of the UAV starts and ends at the BS. Equation (24) guarantees that each sensor cannot die because the battery runs out.

Theorem 1. The PCMCDP is NP-hard.

Proof 1. According to the above mathematical model of the PCMCDP problem, if ignoring the energy limit of the UAV (Equation (20)), the UAV will not need to access any PAD for energy replenishment during the charging process. In this case, the PCMCDP problem becomes a problem to find a loop that minimizes T of traversing each sensor node from BS as the start and end point. According to Equation (17), if no PAD is accessed, T is directly proportional to the loop length. Therefore, if the energy limit of the UAV is ignored, the PCMCDP problem equals a standard TSP. Thus, the PCMCDP problem is the TSP with UAV energy limitation constraint. Since the TSP is NP-complete, we prove that the PCMCDP problem is NP-hard.

4. The Proposed Schemes

We have analyzed and formalized the PCMCDP problem so far. In this section, we present two algorithms to solve the PCMCDP problem, namely, sensor-node-based charging (SNBC) and PAD-based charging (PBC), respectively.

4.1. SNBC Scheme

The SNBC scheme finds the charging path from the perspective of sensor nodes.

According to the above analysis, the PCMCDP problem is essentially a TSP with the UAV energy limit constraint. Therefore, the basic idea of SNBC is pretty straight. The SNBC algorithm first creates a Hamiltonian loop for all the sensor nodes to be charged, then checks whether the loop satisfies the energy constraint of the UAV, inserts the charging stations into the loop, and finally obtains the charging path of the UAV.

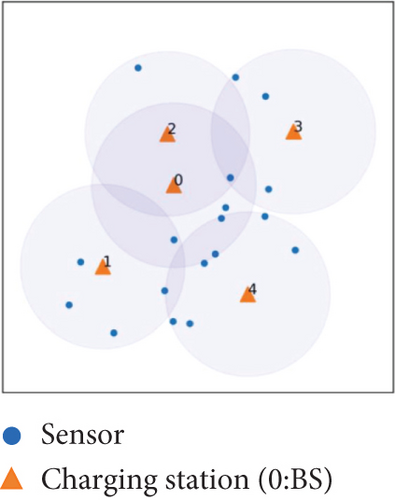
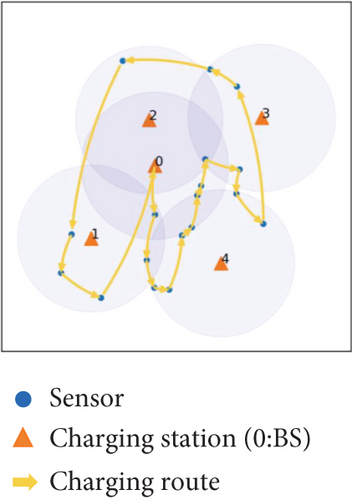
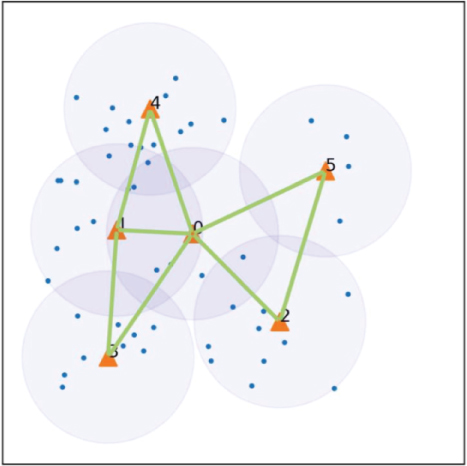
Figure 2(a) presents a diagram of the initial network environment for SNBC scheme, illustrating the deployment locations of the charging stations and sensors, as well as the coverage area of the charging stations. We first ignore the UAV energy limit constraint and get the shortest distance Hamiltonian cycle including all the sensors and the BS by the LKH algorithm [31]. This Hamiltonian cycle can be represented as a sequence , where s′_i ∈ S represents the i^th sensor node in this cycle. To easily illuminate our algorithm, with an element m in the sequence Seq, let PRE(m) and SUCC(m) denote the predecessor and the successor of m, respectively. This process is depicted in Figure 2(b).

After constructing the above sequence, we check, for the node

in the sequence, whether the remaining energy of the UAV after charging

satisfies the following equation:

(25)

In Equation (25), we still use the node battery capacity instead of the energy that the node needs to replenish for simplicity.

If e_rem cannot meet Equation (25), we insert the charging station

into the cycle after the node

, corresponding to Lines 5 and 6 in Algorithm 1. The remaining energy of the UAV after charging

can be calculated by the following equation:

(26)

where

is a charging station and there is no charging station between

and

in the sequence.

We notice that it is possible that the UAV does not have enough energy to fly from the charging station p_j in the sequence to SUCC(p_j) since building the sequence initially without considering the energy limit (considering SUCC(p_j) is a sensor node and covered by another charging station). Therefore, we have to check the energy limitation between each charging station p_j and SUCC(p_j) by the following equation:

(27)

Without losing generality, we use the node battery capacity instead of the energy that the node needs to replenish for simplicity in Equation (27).

If Equation (27) cannot be met, we find the shortest path from p_j to P(SUCC(p_j)) from the connected graph G which only includes charging stations, get all the charging stations in this path except p_j, and insert them between p_j and SUCC(p_j), corresponding to Lines 7 and 8 in Algorithm 1. We perform this energy limitation check not only for the charging stations that are postinserted in the sequence but also for p₀, to avoid the BS being in a very remote location, and the UAV could not charge from p₀, corresponding to Lines 2 and 3 in Algorithm 1.

On the other hand, we also check the energy limitation between

and p₀ in case the UAV has not enough energy to return to p₀ from

, corresponding to Lines 9 and 10 in Algorithm 1. The limitation check equation is presented as follows:

(28)

If the UAV’s residual energy can meet Equation (28), we find the shortest path from

to p₀ based on G and insert all the charging stations in the shortest path except p₀ between

and p₀.

After checking the energy limitation of all the elements in Seq, we get the charging cycle of the UAV. The process is presented in Figure 2(c), and the details of the SNBC algorithm are depicted in Algorithm 1.

Algorithm 1: SNBC scheme.

Input: charging stations set P^′, sensor nodes set S, UAV
Output: the cruise path of UAV Seq
1 Seq ⟵ LKH({p₀, S}) //obtain the shortest path of
sensors
2 if UAV cannot cruise from p₀ to by checking Eq 27
then
3 insert shortest path only including charging
stations (p₀,) between p₀ and in Seq
4 for i ⟵1 to N − 1do
5 if UAV cannot satisfy energy constraint Eq 25 then
6 insert into Seq after the node
7 if not satisfy the constraint Eq 27
then
8 insert shortest path only including
charging stations () between
and in Seq
9 if UAV cannot cruise from to p₀ by checking Eq 28
then
10 insert shortest path only including charging
stations () between and p₀ in Seq
11 return Seq

4.2. PBC Scheme

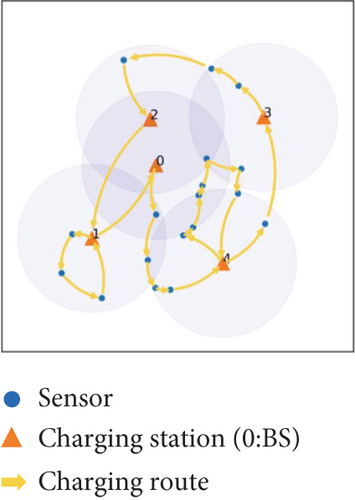
Recalling the coverage and connectivity constraints for the deployment of PADs described in the Problem Definition section, all the sensor nodes are covered by charging stations, and the charging stations are connected. The UAV can charge any sensor node s_i from the charging station P(s_i). Based on the above consideration, we propose a PBC scheme, which builds the charging path based on PADs. PBC first creates a loop that visits all PADs from the BS and returns to the BS. Consequently, the UAV moves according to this loop. When the UAV arrives at a charging station, it can charge the sensor nodes covered by that charging station. It is noted that if the two charging stations are relatively close, the UAV may have enough energy to charge certain sensor nodes while flying from one charging station to the other. In PBC, we call that these nodes can be piggyback-charged. As a result, the PBC scheme is divided into three steps: first, building a loop based on charging stations, then determining the piggyback-charged nodes, and finally for each charging station, determining the charging path for the uncharged nodes it covers. The process of PBC scheme is diagrammed in Figure 3.

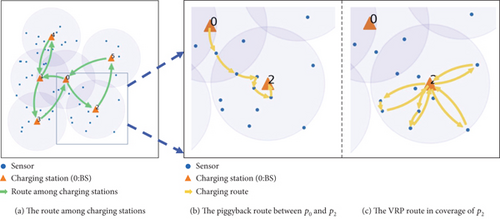
Designing a circuit that encompasses all charging stations resembles a TSP. However, although we already have the connected graph of charging stations G, there is no guarantee that G is a Hamiltonian graph. As a result, we can not use any TSP algorithm to build the loop based on charging stations directly. But we can get our loop based on the result of the TSP algorithm.

We construct an auxiliary weighted complete graph G^′ = (P^′, E^′) based on G = (P^′, E) as Figure 4. To construct the complete graph, we first add E into E^′. Then, we check, for a charging station p_i, whether the edge (p_i, p_j) ∈ E, i ≠ j. If not, we add (p_i, p_j) into E^′ and find the shortest path shortestpath(p_i, p_j) from p_i to p_j in G and the weight of (p_i, p_j) ∈ E^′ is set as the length of shortestpath(p_i, p_j). After completing this operation for all the charging stations, we get the weighted complete graph G^′, corresponding to Line 1 to Line 9 in Algorithm 2.

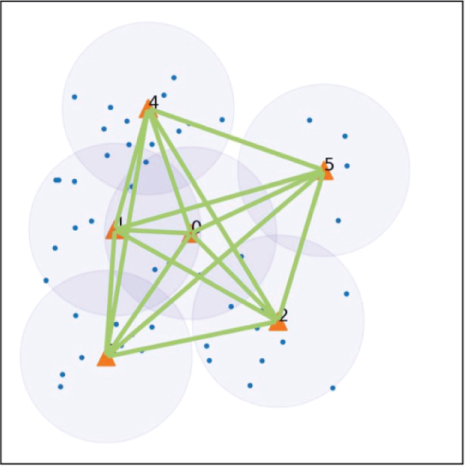
Then, we can run the LKH algorithm on G^′ to get a minimum weighted Hamiltonian cycle that starts and ends at p₀. We check each edge (p_j, SUCC(p_j)), j = 0, ⋯, M. If (p_j, SUCC(p_j)) ∉ E, we replace this edge with shortestpath(p_j, SUCC(p_j)). In this way, we can get the minimum cycle including all the charging stations, corresponding to Line 10 to Line 13 in Algorithm 2.

After obtaining the charging loop including all charging stations, we get the order of accessing all charging stations for the UAV. We now need to determine which sensor nodes can be piggyback-charged as the UAV flies from one charging station to its successor charging station.

For any partial (p_i, p_j) in the charging station loop, we use the following steps to select the nodes where the UAV can piggyback charge during the flight from p_i to p_j. We first construct an ellipse with p_i and p_j as the two focal points of this ellipse. The long axis of this ellipse is determined by the following equation:

(29)

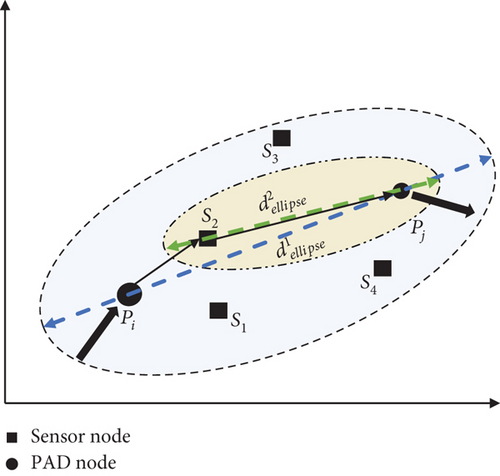
Since the UAV leaves p_i with full energy, e_rem = E_UAV in this case. Obviously, according to the property of the ellipse, the UAV has enough energy to charge any sensor node located in this ellipse from p_i before flying to p_j. If there are multiple sensor nodes in this ellipse, we select the node s_t with the closest distance to p_i as the piggyback-charged node. Then, we try to build another ellipse to find the next piggyback-charged node, where s_t and p_j as the focal points and the long axis is determined by Equation (29) in which e_rem is the remaining energy of UAV after charging s_t. And we check whether the ellipse can be formed, by observing whether the long axis d_ellipse is more than the focal length. If so, we can repeat the above steps until there are no sensor nodes in the newly constructed ellipse, corresponding to Line 14 to Line 23 in Algorithm 2. Then, we add the selected piggyback-charged nodes into a sequence seq_i,j. Figure 5 illuminates the steps to select the piggyback-charged nodes in (p_i, p_j).

We can get all the piggyback-charged nodes by applying the above operation to all segments in the charging loop.

When reaching a charging station p_j, the UAV can charge the remaining nodes except the piggyback-charged nodes . According to [32], the problem to schedule the UAV to charge the nodes in C(p_j) from p_j is essentially a vehicle routing problem (VRP). We solve this problem by introducing a genetic algorithm similar to [33] and obtaining the charging path of the UAV, corresponding to Line 24 to Line 27 in Algorithm 2. Figure 3(c) shows the route for in p₂’s coverage.

The details of the PBC scheme are depicted in Algorithm 2.

Algorithm 2: PAD-based charging scheme.

Input: charging stations set P^′, sensor nodes set S, UAV
Output: the charging path of UAV Path
1 construct the connected graph G = (P^′, E)
2 //construct the complete graph G^′ = (P^′, E^′) based on G = (P^′, E)
3 add E into E^′
4 for PAD p_i in P^′do
5 for PAD p_j in P^′\{p_i}do
6 if edge (p_i, p_j) not in E then
7 add (p_i, p_j) into E^′
8 find shortestpath(p_i, p_j) in G
9 the weight of (p_i, p_j)⟵the length of shortestpath(p_i, p_j)
10 Path⟵LKH(G^′)
11 for p_j in Pathdo
12 if (p_j, SUCC(p_j)) not in Ethen
13 replace (p_j, SUCC(p_j)) with shortestpath(p_j, SUCC(p_j))
14 for p_i in Pathdo
15 startNode⟵p_i
16 calculate d_ellipse according to Eq 29
17 construct Ellipse(startNode,SUCC(p_i),d_ellipse)
18 while the ellipse cover new nodes do
19 s_t ⟵the nearest node of startNode
20 if UAV cannot fly to SUCC(p_i) after charging s_tthen
21 break
22 insert s_t to Path
23 startNode⟵s_t
24 for p_i in P^′do
25 C(p_i) -
26 ⟵ GA()
27 insert into Path
28 return Path

5. Experimental Simulation and Analysis

In this section, we evaluate the performance of the two proposed schemes. To illustrate the effectiveness of our proposed scheme, we conduct three groups of simulations by varying the number of sensor nodes, the size of the network region, and the UAV battery capacity. We only compare the performance of the two proposed schemes because this is the first work on periodic charge scheduling schemes in UAV-based WRSN with PADs and there is no baseline to compare with. We use two performance metrics: the charging delay and the times of replenishment at charging stations. The charging delay is our optimization goal and the most essential metric in periodic charging scheduling, which indicates the highest energy consumption rate of nodes that the periodic charging scheduling algorithm can handle. The times of replenishment at charging stations is the total number of times the UAV gets charged at charging stations during the whole charging cycle. Obviously, the fewer times the UAV is charged at a single charging station during a charging cycle represents a smaller total energy consumption of the charging cycle, which means a higher charging efficiency.

In each simulation, static rechargeable sensor nodes are deployed randomly over a square area. The BS is located at the center of the region. We run the PAD deployment algorithm in [18] first to generate the locations of PADs. The parameters of PADs are set according to the PAD model presented in the literature [34]. In addition, we use the energy consumption model and the energy charging model introduced in [30]. We use the average results of 10 sets of data to smooth the data for each simulation. The default parameters used in the simulations are listed in Table 2.

Table 2. Default parameters.

Parameter	Value
Region size	16,000 m × 16,000 m
Number of nodes	200
E_UAV(10⁴J)	7.8
BS location	[8000,8000] (central)
E_S	30 J
V_U	20 m/s
η	90% [35]
Δ	2 s
P_PAD	87.42 W [34]

5.1. Impact of the Number of Sensor Nodes

Figure 6 depicts the simulation results of changing the number of nodes from 50 to 500. According to [18], changing the number of nodes has approximately no effect on the number of deployed PADs because the number of PADs is determined mostly by the UAV’s coverage radius and network size, with node density having a minor impact.

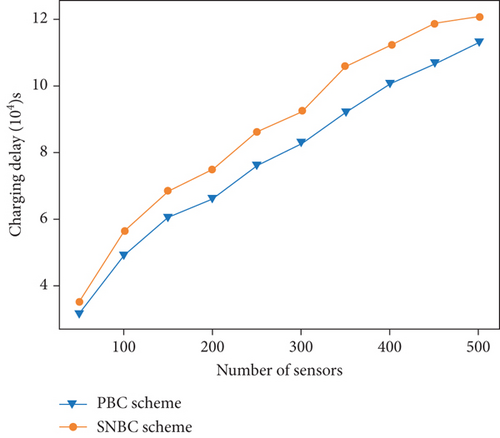
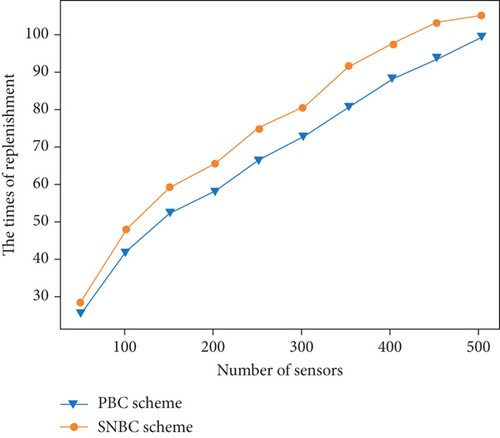
As expected, for the two schemes, the charging delay and the times of replenishment at charging stations increase as the number of sensor nodes increases. It is natural that more nodes need to be charged in one charging cycle as the number of nodes increases. As a result, the flight distance of the UAV in one charging cycle must also increase, which triggers the charging delay and the times of replenishment at charging stations grow. We notice that the PBC scheme outperforms the SNBC scheme on both performance metrics. This is because in the SNBC scheme, the UAV is scheduled to charge the sensor nodes along a TSP path of sensor nodes and then fly to charging stations for energy replenishment if the energy constraint is not met. Meanwhile, the PBC scheme creates a charging loop of charging stations so that the UAV can piggyback charge a portion of the sensor nodes as it flies from one charging station to the next and charge the remainder of the nodes from charging stations that cover them with a VRP algorithm. In other words, the SNBC scheme only optimizes the travel between sensor nodes, while the PBC scheme optimizes the travel between charging stations, between charging stations and nodes, and between nodes.

5.2. Impact of Regional Scale

Figure 7 shows the simulation results of varying the size of the network area from 12,000 m × 12,000 m to 21,000 m × 21,000 m. Different from varying the number of nodes, varying the size of the network causes varying PAD deployment. The larger the network area, the more PADs need to be deployed to ensure connectivity constraint and coverage constraint.

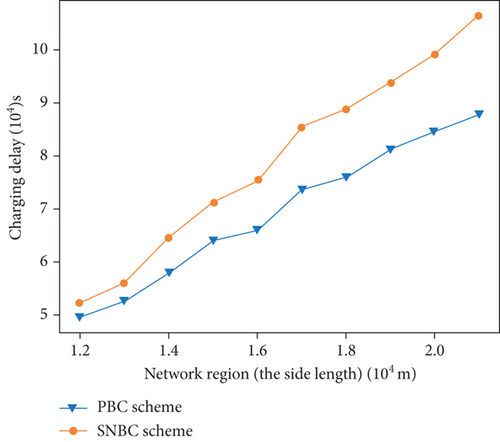
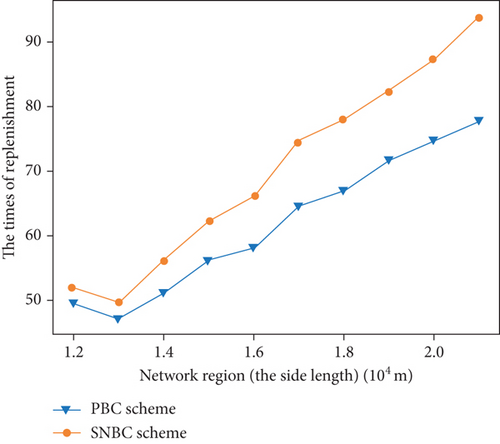
According to Figure 7, as the network area grows, so do the charging delay and the times of replenishment at charging stations. This is due to the fact that the density of nodes decreases as the network area grows. As a result, the UAV must fly greater distances to charge a specific node in a network with a larger area. Still, we can find that the PBC scheme achieves a better performance than the SNBC scheme. We can conclude a similar conclusion with Figure 6. The SNBC scheme only optimizes the travel between sensor nodes, while the PBC scheme optimizes the whole charging path. This conclusion is supported by Figure 7, which shows that as the network area grows, the performance advantage of PBC over SNBC grows.

5.3. Impact of UAV Energy

We varied the battery capacity of the UAV in this simulation, and Figure 8 shows the simulation results of changing the UAV battery capacity from 64,000 to 82,000 J. As the capacity of the UAV battery increases, the two evaluation metrics perform differently for the two schemes.

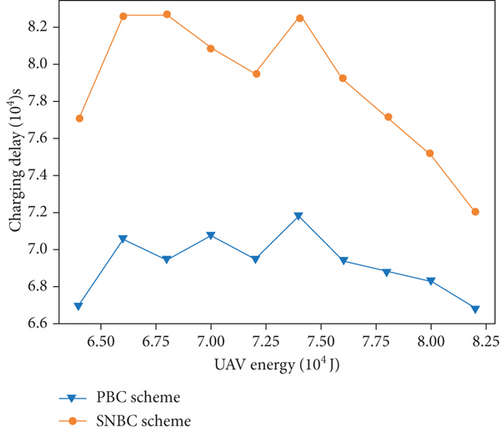
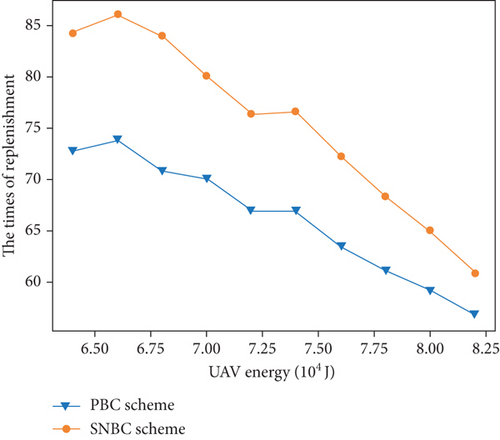
From Figure 8(a), the charging delay of the two schemes oscillates, although a downward trend is visible in some intervals. This is because the UAV battery capacity determines the maximum flight distance d_max and the coverage range d_cover of the UAV. The larger the UAV battery capacity, the larger d_max and d_cover become. According to Equations (9) and (12), due to the connectivity constraint and the coverage constraint, the coverage range of charging stations increases as d_cover grows, and the maximum distance between two adjacent charging stations increases as d_max grows. Consequently, the number of deployed PADs reduces as the UAV battery capacity increases, which explains the down trends of the charging delay in some intervals. On the other hand, as the UAV battery capacity increases, the time required to recharge the UAV at charging stations also increases, leading to an increase in the charging delay, which can result in oscillations. Figure 8(b) depicts how the times of replenishment at charging stations for the two approaches reduce as the UAV battery capacity increases. This is to state that the more energy the UAV can carry, the more nodes it can charge in a single flight. As a result, the frequency with which the UAV visits charging stations for battery replenishment lowers. Still, we notice that the PBC scheme outperforms the SNBC scheme.

5.4. Result Discussion

In the above simulations, we can make a comparison table of the results of the PBC algorithm and SNBC algorithm as Tables 3 and 4. The average charging delay and the average number of returns to the charging station for charging are shown for PBC and SNBC in different network scenarios.

Table 3. Comparison of average charging delay (10⁴ s).

	Varying nodes	Varying regions	Varying E_UAV
PBC	7.778	6.933	6.918
SNBC	8.725	7.935	7.890

Table 4. Comparison of average return times.

	Varying nodes	Varying regions	Varying E_UAV
PBC	67.79	61.74	66.20
SNBC	75.45	70.18	75.40

In the scenario of varying number of sensor nodes, the PBC algorithm reduces charging delay by 12.57% on average and the times of replenishment by 11.87% on average compared to the SNBC algorithm. In the scenario of varying regional scale, the PBC algorithm reduces charging delay by 13.64% on average and the times of replenishment by 12.90% on average compared to the SNBC algorithm. In the scenario of varying UAV energy, the PBC algorithm reduces charging delay by 14.01% on average and the times of replenishment by 13.66% on average compared to the SNBC algorithm.

These results demonstrate that in multiple scenarios, the PBC algorithm outperforms the SNBC algorithm, significantly improving network efficiency, extending network lifespan, and reducing energy wastage. However, it is crucial to note that in cases with ample UAV battery capacity, small network regions, and limited number of sensor nodes, the SNBC algorithm still performs acceptably and is particularly suitable for these specific conditions.

We delve into the performance of our algorithm and evaluate it based on two key metrics: the charging delay and the times of replenishment. The charging delay represents the shortest time interval between two consecutive charges of a node and indicates the node’s maximum energy consumption rate that our charging scheduling algorithms allow. In the meanwhile, the times of replenishment at charging stations can be roughly extrapolated to the total energy used by the UAV during a charging cycle, which in turn can be used to calculate the charging efficiency during a charging cycle.

We roughly consider the amount of energy charged to each node as the node’s battery capacity E_S and the amount of energy charged to the UAV at charging stations as the UAV’s battery capacity E_UAV. Therefore, the tolerable maximum energy consumption rate of the sensor nodes ρ_max and the charging efficiency of the network eff can be calculated according to Equations (30) and (31).

(30)

(31)

where times is the times of replenishment.

According to Equations (30) and (31), the values of the max tolerable energy consumption rate of the sensors ρ_max and the charging efficiency of the network eff can be calculated for different scenarios. Figure 9 illustrates the results of ρ_max and eff in scenarios with various numbers of sensors. As the number of sensors expands, both the tolerable energy consumption of the sensor and network efficiency decrease. The decline in ρ_max is primarily attributed to the increasing charging delay, which grows with the greater number of sensors. According to Equation (31), we can observe that eff is influenced by two parameters: the number of sensor nodes and the return times for UAV replenishment. By observing Figure 6(b), it is evident that the rate of increase in the return times is smaller than the rate of increase in the number of sensor nodes. Hence, eff increases with the growth in the number of sensor nodes. On average, the PBC algorithm exhibits a 15.60% increase in ρ_max and a 15.02% improvement in eff when compared to the SNBC algorithm.

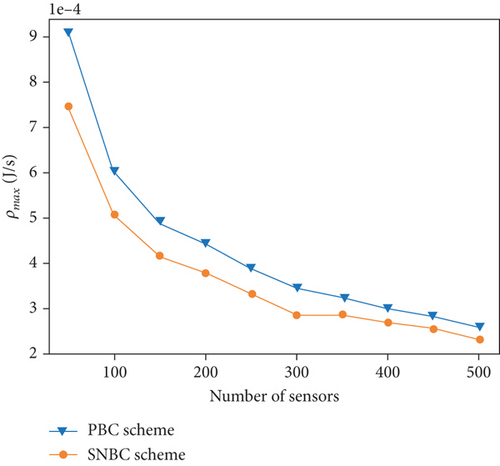
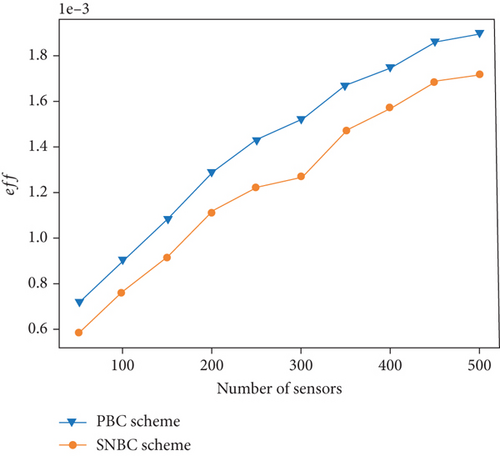
Figure 10 illustrates the results of ρ_max and eff in various region sizes. As the network region expands, both the tolerable energy consumption of the sensor and network efficiency decrease. The decline in ρ_max is primarily attributed to the increasing charging delay, which grows with the larger network region. Similarly, the reduction in eff is predominantly due to the increasing number of return times for the UAV, which also escalates with the larger network region. On average, the PBC algorithm exhibits a 15.91% increase in ρ_max and a 15.62% improvement in eff when compared to the SNBC algorithm.

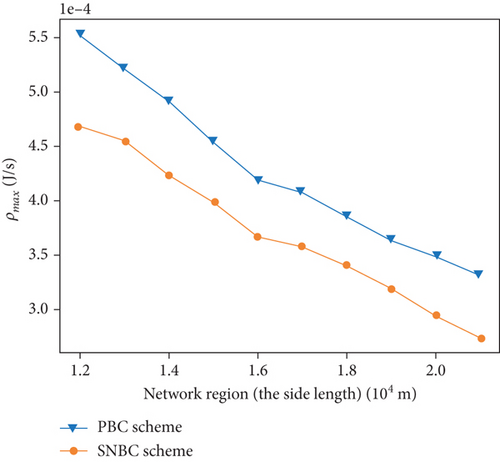
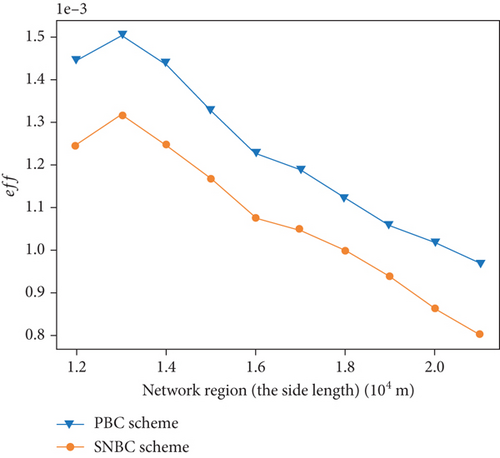
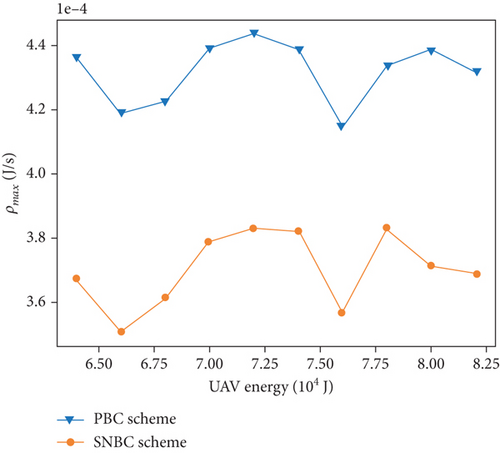
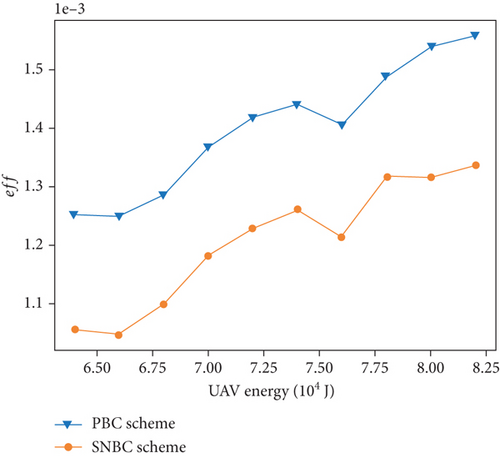
Figure 11 illustrates the results of ρ_max and eff in scenarios with various UAV energy capabilities E_UAV. As the energy of UAV E_UAV increases, the tolerable energy consumption of the sensor oscillates and network efficiency increase. The oscillation in ρ_max is primarily attributed to the charging delay shown in Figure 8(a). The reason of oscillation of charging delay has been discussed before. According to Equation (31), eff is influenced by the UAV’s energy and the return times for UAV replenishment, with the fixed number of sensor nodes. By examining Figure 8(b), it becomes evident that the rate of decrease in the return times for UAV replenishment is greater than the rate of increase in the UAV’s energy. This overall trend results in an upward trajectory for eff. On average, the PBC algorithm exhibits a 16.60% increase in ρ_max and a 16.32% improvement in eff when compared to the SNBC algorithm.

It is evident that PBC excels in terms of network efficiency and demonstrates a high tolerance for sensor energy consumption. However, it is worth noting that the results achieved by SNBC remain within an acceptable range.

6. Conclusion

The application of UAV in WRSN holds great promise. Building on our previous work [18] on PAD deployment schemes, this paper further studies the problem of periodic charging with minimal charging delay in a WRSN with PADs and proposes two schemes from two different perspectives: the SNBC scheme and the PBC scheme.

In the SNBC scheme, we schedule the UAV to charge the sensors along a TSP path of sensor nodes and fly to charging stations for energy replenishment once the energy constraint is not satisfied. In the PBC scheme, we construct the PAD-based route of the UAV for charging the sensors. Initially, the UAV moves along the loop of PADs. Additionally, we introduce a piggyback scheme to charge part of sensor nodes along the movement between two adjacent PADs. Then, we employ a genetic algorithm to charge the remaining sensors covered by each PAD except the piggyback-charged nodes. Simulation results demonstrate that our two proposed schemes are feasible and the PBC scheme performs better than the SNBC scheme in terms of charging delay and total travel distance, particularly in a large scale of WRSN. To the best of our knowledge, this is the first study to address the periodic charging scheduling problem in a UAV-based WRSN with PADs, offering new insights into this area.

It is noted that all periodic charging algorithms, including our work, have an inherent disadvantage. Once the node charging sequence is established by a periodic charging algorithm, the MC (UAV) recharges nodes in the same order during each cycle, failing to adapt to fluctuations in node energy consumption rates and limiting the maximum energy consumption rate of the network’s nodes. In contrast, on-demand charging algorithms dynamically select energy-depleted nodes for recharging based on their energy status, offering better adaptability to variations in energy consumption. Additionally, our proposed periodic charging algorithms only consider the deployment of a single UAV. The simultaneous charging by multiple UAVs could reduce charging delays, enhance efficiency, and expand the network’s monitoring area. However, coordinating multiple UAVs in a WRSN introduces a new challenge. We are dedicated to exploring the integration of periodic partial charging to improve energy efficiency and sustainability in WRSNs. We will also investigate the synergistic effects of combining energy harvesting technologies, such as solar power, with wireless energy transfer to establish a more resilient and eco-friendly charging ecosystem.

Moving forward, our future research will address on-demand charging, multi-UAV collaboration, and partial charging, integrating hybrid energy harvesting techniques to dynamically optimize energy distribution for efficient and sustainable network operation.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work is supported by Sichuan Science and Technology Program (grant no. 2022YFQ0035).

Appendix A

Table A1. List of abbreviations.

Abbreviation	Definition
Wireless rechargeable sensor network	WRSN
Internet of Things	IoT
Wireless sensor network	WSN
Unmanned aerial vehicle	UAV
Automatic landing pad	PAD
Sensor-node-based charging	SNBC
PAD-based charging	PBC
Wireless power transfer	WPT
Clustering-with-double-constraints and disks-shift-combining	CDC&DSC
Base station	BS
Mobile charger	MC
The Problem of Periodic Charging with Minimum Charging Delay in a WRSN with PADs	PCMCDP
Traveling Salesman Problem	TSP
Vehicle routing problem	VRP

Open Research

Data Availability Statement

The data that support the findings of this study are not publicly available due to privacy concerns. Data are however available from the authors upon reasonable request.

References

1 Fascista A., Toward integrated large-scale environmental monitoring using wsn/uav/crowdsensing: a review of applications, signal processing, and future perspectives, Sensors. (2022) 22, no. 5, https://doi.org/10.3390/s22051824, 35270970.
10.3390/s22051824
PubMed Web of Science® Google Scholar
2 Sathish K., Hamdi M., Chinthaginjala R., Pau G., Ksibi A., Anbazhagan R., Abbas M., and Usman M., Reliable data transmission in underwater wireless sensor networks using a cluster-based routing protocol endorsed by member nodes, Electronics. (2023) 12, no. 6, https://doi.org/10.3390/electronics12061287.
10.3390/electronics12061287
Web of Science® Google Scholar
3 Sathish K. and Ravikumar C., Energy balanced reliable and effective clustering for underwater wireless sensor networks, Alexandria Engineering Journal. (2023) 77, 41–62, https://doi.org/10.1016/j.aej.2023.06.083.
10.1016/j.aej.2023.06.083
Google Scholar
4 Sathish K., Ravikumar C. V., Rajesh A., and Pau G., Underwater wireless sensor network performance analysis using diverse routing protocols, Journal of Sensor and Actuator Networks. (2022) 11, no. 4, https://doi.org/10.3390/jsan11040064.
10.3390/jsan11040064
Web of Science® Google Scholar
5 Sathish K., Venkata R. C., Anbazhagan R., and Pau G., Review of localization and clustering in USV and AUV for underwater wireless sensor networks, Telecom. (2023) 4, no. 1, 43–64, https://doi.org/10.3390/telecom4010004.
10.3390/telecom4010004
Google Scholar
6 Hamami L. and Nassereddine B., Application of wireless sensor networks in the field of irrigation: a review, Computers and Electronics in Agriculture. (2020) 179, article 105782, https://doi.org/10.1016/j.compag.2020.105782.
10.1016/j.compag.2020.105782
Google Scholar
7 Gaurav A., Psannis K., and Perakovic D., Security of cloud-based medical internet of things (MIoTs), International Journal of Software Science and Computational Intelligence (IJSSCI). (2022) 14, no. 1, 1–16, https://doi.org/10.4018/IJSSCI.285593.
10.4018/IJSSCI.285593
Google Scholar
8 Han G. J., Wu J. W., Wang H., Guizani M., Ansere J. A., and Zhang W. B., A multicharger cooperative energy provision algorithm based on density clustering in the industrial Internet of Things, IEEE Internet of Things Journal. (2019) 6, no. 5, 9165–9174, https://doi.org/10.1109/JIOT.2019.2928557, 2-s2.0-85073477601.
10.1109/JIOT.2019.2928557
Web of Science® Google Scholar
9 Lyu Z., Wei Z., Wang X., Fan Y., Xia C., and Shi L., A periodic multinode charging and data collection scheme with optimal traveling path in WRSNs, IEEE Systems Journal. (2020) 14, no. 3, 3518–3529, https://doi.org/10.1109/JSYST.2020.2977984.
10.1109/JSYST.2020.2977984
Web of Science® Google Scholar
10 Wu P., Xiao F., Sha C., Huang H., and Sun L., Trajectory optimization for UAVs’ efficient charging in wireless rechargeable sensor networks, IEEE Transactions on Vehicular Technology. (2020) 69, no. 4, 4207–4220, https://doi.org/10.1109/TVT.2020.2969220.
10.1109/TVT.2020.2969220
Web of Science® Google Scholar
11 Liu Y., Pan H., Sun G., and Wang A., Scheduling Optimization of Charging UAV in Wireless Rechargeable Sensor Networks, 2021 IEEE Symposium on Computers and Communications (ISCC), 2021, Athens, Greece, 1–7, https://doi.org/10.1109/ISCC53001.2021.9631448.
10.1109/ISCC53001.2021.9631448
Google Scholar
12 Yoon I. and Noh D. K., Adaptive data collection using UAV with wireless power transfer for wireless rechargeable sensor networks, IEEE Access. (2022) 10, 9729–9743, https://doi.org/10.1109/ACCESS.2022.3144846.
10.1109/ACCESS.2022.3144846
Google Scholar
13 Choi C. H., Jang H. J., Lim S. G., Lim H. C., Cho S. H., and Gaponov I., Automatic wireless drone charging station creating essential environment for continuous drone operation, 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), 2016, Ansan, Korea (South), 132–136, https://doi.org/10.1109/ICCAIS.2016.7822448, 2-s2.0-85013861084.
10.1109/ICCAIS.2016.7822448
Google Scholar
14 Costea I. M. and Pleşca V., Automatic battery charging system for electric powered drones, 2018 IEEE 24th International Symposium for Design and Technology in Electronic Packaging (SIITME), 2018, Iasi, Romania, 377–381, https://doi.org/10.1109/SIITME.2018.8599208, 2-s2.0-85061787821.
10.1109/SIITME.2018.8599208
Google Scholar
15 Cai C., Wang J., Nie H., Zhang P., Lin Z., and Zhou Y. -G., Effective-Configuration WPT Systems for Drones Charging Area Extension Featuring Quasi-Uniform Magnetic Coupling, IEEE Transactions on Transportation Electrification. (2020) 6, no. 3, 920–934, https://doi.org/10.1109/TTE.2020.2995733.
10.1109/TTE.2020.2995733
Web of Science® Google Scholar
16 Campi T., Cruciani S., Feliziani M., and Maradei F., High efficiency and lightweight wireless charging system for drone batteries, 2017 AEIT International Annual Conference, 2017, Cagliari, Italy, 1–6, https://doi.org/10.23919/AEIT.2017.8240539, 2-s2.0-85044335312.
10.23919/AEIT.2017.8240539
Google Scholar
17 Chen J., Yu C. W., and Ouyang W., Efficient Wireless Charging Pad Deployment in Wireless Rechargeable Sensor Networks, IEEE Access. (2020) 8, 39056–39077, https://doi.org/10.1109/ACCESS.2020.2975635.
10.1109/ACCESS.2020.2975635
Google Scholar
18 Chen Y., Gu Y., Li P., and Lin F., Minimizing the number of wireless charging pad for unmanned aerial vehicle-based wireless rechargeable sensor networks, International Journal of Distributed Sensor Networks. (2021) 17, no. 12, 155014772110559, https://doi.org/10.1177/15501477211055958.
10.1177/15501477211055958
Google Scholar
19 Das R. and Dash D., Joint on-demand data gathering and recharging by multiple mobile vehicles in delay sensitive WRSN using variable length GA, Computer Communications. (2023) 204, 130–146, https://doi.org/10.1016/j.comcom.2023.03.022.
10.1016/j.comcom.2023.03.022
Google Scholar
20 Tomar A., Anwit R., and Jana P. K., An efficient scheme for on-demand energy replenishment in wireless rechargeable sensor networks, 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), 2017, Udupi, India, 125–130, https://doi.org/10.1109/ICACCI.2017.8125828, 2-s2.0-85042643829.
10.1109/ICACCI.2017.8125828
Google Scholar
21 Tomar A. and Jana P. K., G. Fahrnberger, S. Gopinathan, and L. Parida, Mobile Charging of Wireless Sensor Networks for Internet of Things: A Multi-Attribute Decision Making Approach, Distributed Computing and Internet Technology. ICDCIT 2019, 2019, 11319, Springer, Cham, Lecture Notes in Computer Science(), https://doi.org/10.1007/978-3-030-05366-6_26, 2-s2.0-85059951227.
10.1007/978-3-030-05366-6_26
Google Scholar
22 Feng Y., Guo L., Fu X., and Liu N., Efficient mobile energy replenishment scheme based on hybrid mode for wireless rechargeable sensor networks, IEEE Sensors Journal. (2019) 19, no. 21, 10131–10143, https://doi.org/10.1109/JSEN.2019.2928169, 2-s2.0-85073218291.
10.1109/JSEN.2019.2928169
Web of Science® Google Scholar
23 Rao X., Yang P., Yan Y., Zhou H., and Wu X., Optimal recharging with practical considerations in wireless rechargeable sensor network, Access. (2017) 5, 4401–4409, https://doi.org/10.1109/ACCESS.2017.2665471, 2-s2.0-85018335326.
10.1109/ACCESS.2017.2665471
Web of Science® Google Scholar
24 Xie L., Shi Y., Hou Y., Lou W., and Sherali H., On traveling path and related problems for a mobile station in a rechargeable sensor network, Proceedings of the Fourteenth ACM International Symposium on Mobile Ad Hoc Networking and Computing, 2013, Bangalore, India, https://doi.org/10.1145/2491288.2491291, 2-s2.0-84883019354.
10.1145/2491288.2491291
Google Scholar
25 Das R., Dash D., and Yadav C. B. K., An efficient charging scheme using battery constrained mobile charger in wireless rechargeable sensor networks, Telecommunication Systems. (2022) 81, no. 3, 389–415, https://doi.org/10.1007/s11235-022-00951-w.
10.1007/s11235-022-00951-w
Web of Science® Google Scholar
26 Zhao C., Wang Y., Zhang X., Chen S., Wu C., and Teo K. L., UAV Dispatch Planning for a Wireless Rechargeable Sensor Network for Bridge Monitoring, IEEE Transactions on Sustainable Computing. (2023) 8, no. 2, 293–309, https://doi.org/10.1109/TSUSC.2022.3224442.
10.1109/TSUSC.2022.3224442
Google Scholar
27 Habibi P., Hassanifard G., Ghaderzadeh A., and Nosratpour A., Offering a demand-based charging method using the GBO algorithm and fuzzy logic in the wrsn for wireless power transfer by UAV, Journal of Sensors. (2023) 2023, 19, https://doi.org/10.1155/2023/6326423, 6326423.
10.1155/2023/6326423
Google Scholar
28 Lin C., Guo C., Dai H., Wang L., and Wu G., Near Optimal Charging Scheduling for 3-D Wireless Rechargeable Sensor Networks with Energy Constraints, 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), 2019, Dallas, TX, USA, 624–633, https://doi.org/10.1109/ICDCS.2019.00068.
10.1109/ICDCS.2019.00068
Google Scholar
29 Wang K., Wang L., Obaidat M. S., Lin C., and Alam M., Extending network lifetime for wireless rechargeable sensor network systems through partial charge, IEEE Systems Journal. (2021) 15, no. 1, 1307–1317, https://doi.org/10.1109/JSYST.2020.2968628.
10.1109/JSYST.2020.2968628
Web of Science® Google Scholar
30 Plun G., Rozenberg G., and Salomaa A., Current Trends in Theoretical Computer Science, 2004, World Scientific, https://doi.org/10.1142/5491.
10.1142/5491
Google Scholar
31 Helsgaun K., An extension of the Lin-Kernighan-Helsgaun TSP solver for constrained traveling salesman and vehicle routing problems, 2017, Roskilde: Roskilde University.
Google Scholar
32 Dai R., Fotedar S., Radmanesh M., and Kumar M., Quality-aware UAV coverage and path planning in geometrically complex environments, Ad Hoc Networks. (2018) 73, 95–105, https://doi.org/10.1016/j.adhoc.2018.02.008, 2-s2.0-85044664403.
10.1016/j.adhoc.2018.02.008
Web of Science® Google Scholar
33 Wu Q., Sun P., and Boukerche A., An Energy-efficient UAV-based Data Aggregation Protocol in Wireless Sensor Networks, Proceedings of the 8th ACM Symposium on Design and Analysis of Intelligent Vehicular Networks and Applications 2018, DIVANet’18, 2018, Montreal, QC, Canada, 34–40, https://doi.org/10.1145/3272036.3272047, 2-s2.0-85058246575.
10.1145/3272036.3272047
Google Scholar
34 Wu S., Cai C., Jiang L., Li J., and Yang S., Unmanned Aerial Vehicle Wireless Charging System With Orthogonal Magnetic Structure and Position Correction Aid Device, IEEE Transactions on Power Electronics. (2021) 36, no. 7, 7564–7575, https://doi.org/10.1109/TPEL.2020.3047384.
10.1109/TPEL.2020.3047384
Web of Science® Google Scholar
35 Car battery efficiencies, 2010, http://large.stanford.edu/courses/2010/ph240/sun1/.
Google Scholar

Citing Literature

All articles

Charging Between PADs: Periodic Charging Scheduling in the UAV-Based WRSN With PADs

Abstract

1. Introduction

2. Related Work

2.1. Periodic Charging Scheduling

2.2. Charging Scheduling With UAV

2.3. PAD Technology

3. Preliminaries

3.1. Network Model and Energy Model

3.2. Problem Definition

4. The Proposed Schemes

4.1. SNBC Scheme

4.2. PBC Scheme

5. Experimental Simulation and Analysis

5.1. Impact of the Number of Sensor Nodes

5.2. Impact of Regional Scale

5.3. Impact of UAV Energy

5.4. Result Discussion

6. Conclusion

Conflicts of Interest

Funding

Appendix A

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley