Normal and aberrant cognitive functions are the result of the dynamic interplay between large-scale neural circuits. Describing the nature of these interactions has been a challenging task yet important for neurodegenerative disease evolution. Fusing modern dynamic graph network theory techniques and control theory applied on complex brain networks creates a new framework for neurodegenerative disease research by determining disease evolution at the subject level, facilitating a predictive treatment response and revealing key mechanisms responsible for disease alterations. It has been shown that two types of controllability—the average and the modal controllability—are relevant for the mechanistic explanation of how the brain navigates between cognitive states. The average controllability favors highly connected areas which move the brain to easily reachable states, while the modal controllability favors weakly connected areas representative for difficult-to-reach states. We propose two different techniques to achieve these two types of controllability: a centrality measure based on a sensitivity analysis of the Laplacian matrix is employed to determine the average controllability, while graph distances form the basis of the modal controllability. The concepts of “choosing the best driver set” and “graph distances” are applied to measure the average controllability and the modal controllability, respectively. Based on these new techniques, we obtain important disease descriptors that visualize alterations in the disease trajectory by revealing densely connected hubs or sparser areas. Our results suggest that these two techniques can accurately describe the different node roles in controlling trajectories of brain networks.

1. Introduction

Novel concepts in dynamic graph networks theory derived from modern network controllability have proven to be useful in understanding and describing the dynamics of large-scale neural circuits or networks and deriving theory-driven imaging biomarkers for disease prediction at the patient level. It differs significantly from static graph theory, heavily now used in brain studies, since it considers the structural or functional connectivity matrix and models the dynamics of state changes of that structure.

While the study of communication principles applied to neural systems has developed in parallel with our understanding of the brain, the application of control theory to support the dynamical analysis of brain systems is in its incipient phase. Furthermore, modern control theory including dynamic graph networks is an unchartered territory in brain research offering a huge potential for providing simplified computer models for predicting disease evolution and identifying disease epicenters and thus supporting longitudinal study with a-priori information for many neurogenerative diseases such as dementia, Alzheimer’s disease, and Parkinson’s disease. Neuroimaging techniques such as Positron Emission Tomography (PET), single-photon emission computed tomography (SPECT), and magnetic resonance imaging (MRI) represent the standard methods to diagnose functional and structural information.

It has been shown that cognitive control [1–7] plays an important role in connecting multiple sources of information required to solve complex problems and retrieving information from memory. The classical cognitive theory of control is based on the concept of competitive dynamics in frontal cortices; however, recent studies in functional neuroimaging suggest that control functions are facilitated by transitory changes of cooperation and competition patterns between distributed neural systems found in default mode, attention, and frontoparietal networks [8]. Furthermore, disease evolution and the different state changes found in dynamic functional MRI representative for many neurodegenerative diseases prompted a new view of cognitive control mechanisms that can be described by the control theory in engineering.

An analogy between networked systems in the brain and modern dynamic graph networks can be made: neural ensembles or regions in the brain correspond to nodes in graph theory and their structural or functional connections correspond to links. Both concepts of controllability and observability are of crucial importance for understanding operational and dynamical brain networks impacting neural function, disease, development, and rehabilitation. Controllability refers to the capability of driving the network system along a desired trajectory, while observability refers to infer the internal states from knowing the external outputs.

Human brain networks exhibit a multitude of temporal characteristics as seen for example in mental disorders. Temporal connectivity has been used to detect the regions of interest (ROIs) in the epileptic brain network [9]. Dynamical graph properties of temporal brain networks were successfully applied to the identification of subjects with chronic schizophrenia [10]. Applying the control theory of complex networks to human brain networks could provide powerful methods to unveil the longitudinal behavior of mechanistic models for other diseases. Temporal networks are more biologically motivated than their static counterparts since they use orders of magnitude less control energy, have more compact control trajectories, and reach controllability faster [11, 12].

In [3, 13, 14], it was shown that certain brain regions or nodes in the connectivity graph (structural or functional) can act as drivers and move the system (brain) into specific states of action. These influence the cognitive functions. Looking into brain networks’ graph architectures, we discover highly connected and weakly connected areas. In [3], it was shown that two different types of controllability concepts apply to this aspect. The so-called “average controllability” quantifies the position of a node in directing a network to easily reachable states. Those nodes represent highly connected hubs. On the other hand, “modal controllability” refers to nodes in weakly connected areas moving the brain to difficult-to-reach states. The mathematical conditions necessary to fulfill the requirements for these two controllability types were derived.

Most of the current research on controllability of dynamical systems applied to brain networks is centred on the structural properties of the network and assumes that the dynamics of each node is of order of one. In this paper, we propose more general conditions for the two controllability definitions and illustrate in examples the theoretical analysis. Compared to previous studies, we analysed two new aspects of controllability. The average controllability which determines the densely connected hubs and quantifies the energy required for controlling the network. For the average controllability, we employ the method proposed in [15] determining a ranking of the best driver sets and thus of the network’s hubs. On the other hand, the modal controllability determines difficult-to reach states, favours sparsely connected nodes, and requires no knowledge of the edges’ values in the network but is based only on the graph architecture. For the modal controllability, we employ the method proposed by [16] which operates based on the graph distances to determine the controllability. In this study, we employ two different aspects of controllability that determine both the highly connected hubs and the best driver nodes and thus enhance the descriptive biomarkers. The outcomes of this investigation have potential applications beyond fMRI which are briefly reviewed in the “Discussion” section.

2. Preliminary Controllability Concepts and Definitions

In [3], it was shown that a simple noise-free linear discrete-time and time-invariant model can be employed to describe the neural dynamics measured by fMRI:

()

where x ∈ Rⁿ is the magnitude of the neurophysiological activity (state) of the brain regions over time, A ∈ R^n×n is the adjacency matrix, B_K ∈ R^n×m is the input matrix, and u_K ∈ R^m is the input vector. The input matrix identifies the control nodes K in the brain. Linear time-invariant systems as described in equation (1) have been widely applied to neuroscience where the system matrix A represents very often the structural connectivity matrix [3]. The state vector x represents the activity levels such as the mean firing rate or local potential of the defined brain subregions. The input vector u models either external like neurostimulation [17] or internal sources like a cognitive signal originating in the frontal cortex.

In [3], it was given as the condition for controllability of the network, described in equation (1), that the controllability Gramian W_K is invertible with

()

Two definitions of controllability are used: the average and the modal controllability. The average controllability is given as the average input energy from a set of control nodes and over all possible target states. In [18], a measure of average controllability is given as trace(W_k). Regions of high average controllability are known to be most leading in the control of the network dynamics. The modal controllability is employed to identify states that are difficult to control and identifies weakly connected areas. In [19], it was stated that the modal controllability is computed from the eigenvector matrix of the network adjacency matrix A.

A dynamical system such as the brain is said to be controllable if it can be controlled from any initial state to any final state in a given amount of time. Structural controllability has been proposed to eliminate the influence of disturbances on system parameters and to reduce numerical instabilities. The minimum number of driver nodes to structural control the brain network is topology-characteristic.

3. Average Controllability Based on Determining the Best Driver Set

Suppose system (1) includes N interconnected identical dynamical nodes with the following equations of motion:

()

including the state vector x_i ∈ R and a unified coupling strength constant σ. The connection network between nodes is supposed to be undirected and unweighted. β_i = 1 for drivers, i.e., those nodes to which external control signals are applied, and β_i = 0 for others. The interaction network is presented by its Laplacian matrix L = [l_ij], where l_ij = −1; i ≠ j if there is a link between nodes i and j, and 0 otherwise [20]. The i^th diagonal element is l_ii = −∑_jl_ij which forms the Laplacian as a zero-row-sum matrix. H determines coupled elements of nodes. Modern imaging techniques capture the information not only at the single neural unit [21] but across a plenitude of such units [22]. This can be theoretically described by interconnected units in form of an interaction network or l_ij in equation (3).

Pinning control is a control approach in complex dynamical networks in which a set of driver nodes are controlled to synchronize the whole network to a reference state, i.e., x₁(t) = x₂(t) = ⋯ = x_N(t) = s(t) [23]:

()

Linear state feedback controllers can be applied to drivers in order to facilitate the synchrony:

()

where k_i is the feedback gain for the i^th node. The master stability function approach, introduced in [24], relates the local stability of such a system to structural properties of the connection network under some conditions. Inspired by this approach, the stability of the system can be evaluated in terms of the following N decoupled blocks [25]:

()

where e_i = x_i − s and a_i = σλ_ci where λ_ci is the i^th eigenvalue of the following augmented Laplacian matrix:

()

The concept of controllability metrics and minimum energy has been recently applied in imaging connectomics [3, 26] and raised important questions related to the neurobiological interpretation of controllability metrics and possible intervention strategies. Here, we are looking for a computationally simple yet accurate metric to choose the best driver nodes to facilitate synchrony.

The matrix C inherits some features from the Laplacian matrix, such as 0 < λ₁ ⩽ λ₂ ⩽ ⋯⩽λ_N. From the synchronizability perspective, it has been shown that larger values of the eigen ratio η = λ₁/λ_N indicate synchronizability over a wider coupling range [25]. In other words, local synchronizability of the system can be interestingly related to spectral properties of the interaction network as well as the set of the drivers [27]. On the other hand, the structure of this matrix in equation (7) shows that control gains of driver nodes act as perturbations on diagonal elements. Clearly, if none of the nodes are controlled, i.e., β_i = 0; ∀i, the matrix C backs to the ordinary Laplacian matrix. To facilitate our study using the eigenvalue perturbation theory, all control gains k_i are assumed to be identical and very small. If λ_m,

, and u_m are eigenvalues of the matrix L(p) and its associated left and right eigenvectors, respectively, the eigenvalue perturbation theory relates changes in λ_m to perturbation on p as

()

In our problem, if node i is selected as the driver, only the element l_ii of the matrix C is affected which impacts η as

()

where the superscript i indicates the i^th element of the vector, all elements of the eigenvector u₁, corresponding to the eigenvalue λ₁ = 0, are equal to 1 and v_n = u_n since the graph is undirected. This equation proposes node i with a maximum value of

as a driver node since it results in smaller dη/dl_ii which means that η is nearer to the maximum value.

This metric can be extended to achieve the best set of driver nodes as more than one driver node is practically required for proper control performance of the whole network. Using the same methodology as the single node perturbation study, one can find the effect of a subset Sμ of μ nodes on the eigenratio η as follows:

()

where Δ represents the gradient. Therefore, the metric

()

It ranks all subsets of nodes based on their influence on η [15]. It only depends on the topology of the interaction network and performs ranking by using only a single eigen-decomposition of the Laplacian matrix.

Example 1. We apply the controllability concepts on functional (FDG-PET) and structural (MRI) connectivity graphs [28] for control (CN), mild cognitive impairment (MCI), and Alzheimer’s disease (AD) subjects. In total, 249 subjects have been considered, consisting of 68 normal/control, 111 MCI, and 70 AD. According to [28], MRI and PET images from the ADNI database have been spatially normalized according to the PET and VBM-T1 templates, respectively, ensuring that each image voxel corresponds to the same anatomical position. MRI images are segmented into White Matter (WM) and Gray Matter (GM) tissues. PET images are also normalized in intensity to compute comparable levels among the images. Intensity normalization is performed by means of the mean image, which is used as a normalization template. The structural and functional graphs [28] consider only 42 dementia-relevant regions out of the 116 from the AAL in the frontal, parietal, occipital, and temporal lobes (Table 1). These dementia-relevant regions represent the nodes in the graph, while the connections describe the interregional covariation of gray matter volumes in different areas for the structural data, while in the case of functional data, they capture the glucose uptake between different regions.

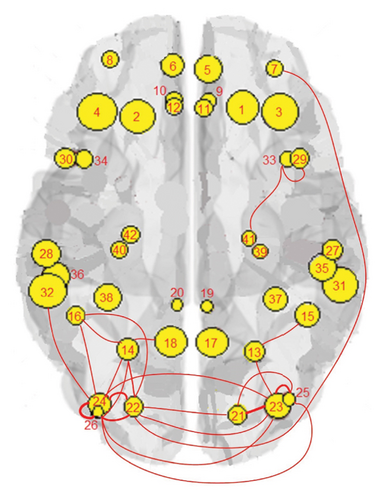
Figure 1 shows the clusters found on the functional data for (a) controls, (b) MCI, and (c) AD, while Figure 2 shows the clusters found on the structural data [28]. Thicker lines in these graphs correspond to stronger connections. The nodes correspond to the regions located in the frontal, parietal, occipital, and temporal lobes because they are considered to be related to AD.

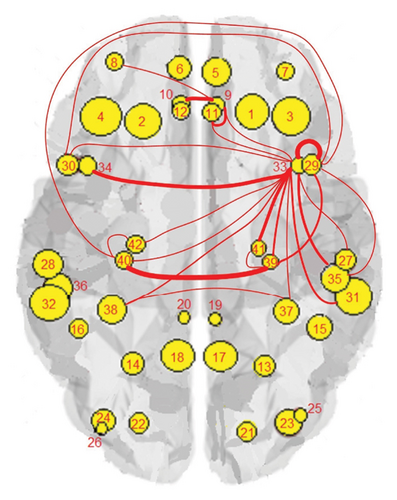
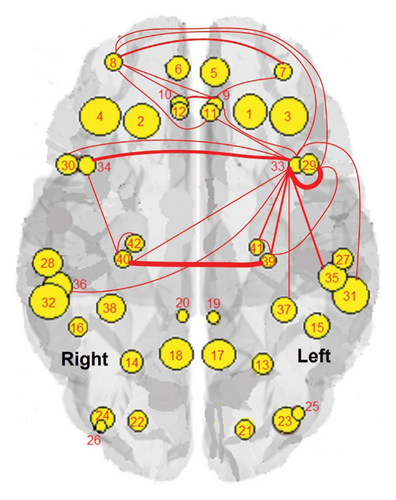
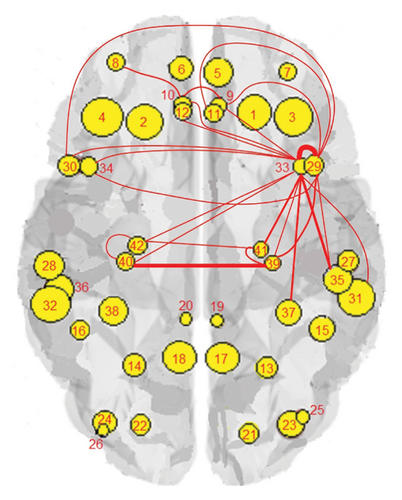
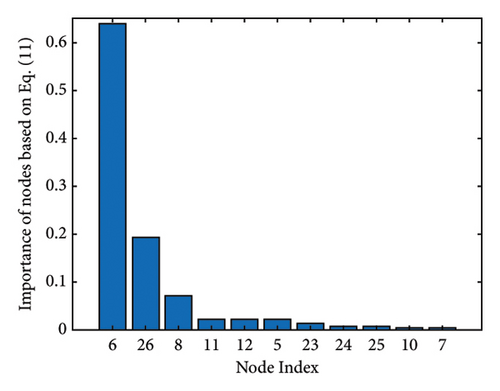
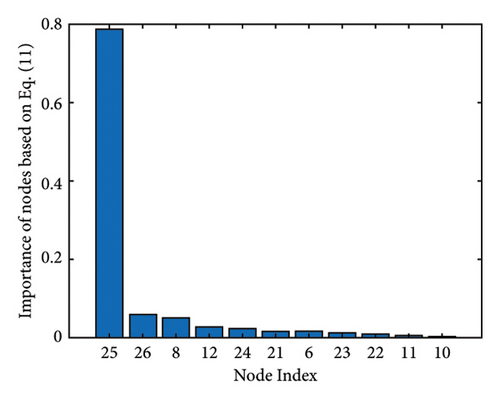
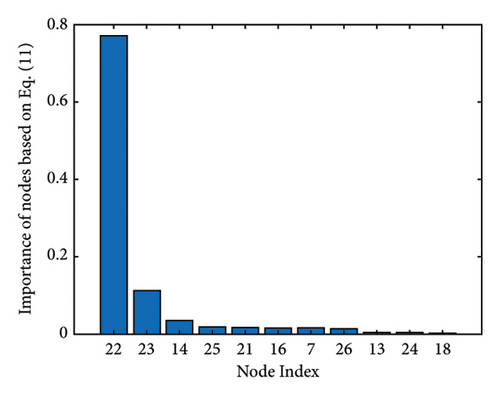
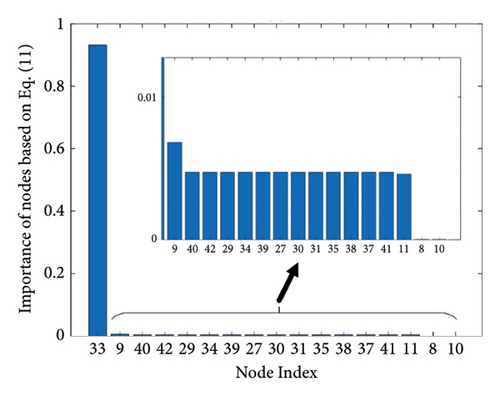
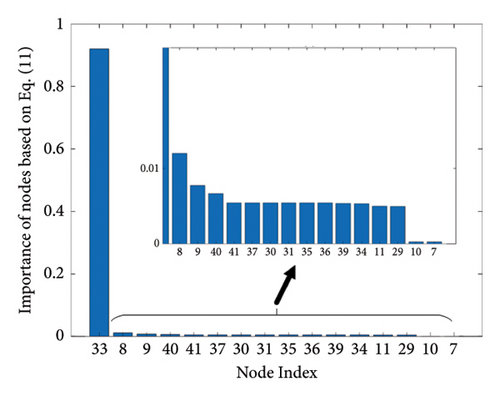
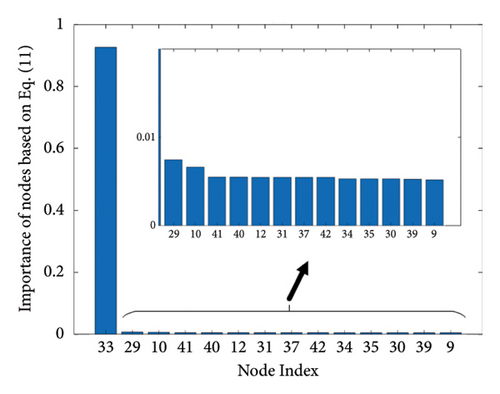
The results of the in-depth dynamical analysis for controllability based on choosing the best driver set for functional and structural networks are shown in Figures 3 and 4. The results show that the proposed method detects in a ranking the most significant “hubs”. Figure 3 shows the node six, i.e., the Frontal_Sup_Medial_R, being the highest ranked node as a hub in the frontal lobe for controls, the node twenty-five in the occipital lobe for MCI, and the node twenty-two also in the occipital lobe for AD for functional networks. The obtained ranking of hubs based on the proposed method shows that it is a valid method for determining the average controllability. Figure 4 shows the node thirty-three in the temporal lobe being the highest ranked node as a hub for controls, MCI, and AD for structural networks. In fact, for functional brain networks, the average controllability correctly determined the highest ranking hubs in the frontal lobe for controls and in the occipital lobe for MC and AD. For structural brain networks, all three groups have the highest ranking hub in the temporal lobe.

Table 1. Names and indices of 42 dementia-relevant regions [28].

Frontal lobe		Parietal lobe		Occipital lobe		Temporal lobe
1	Frontal_Sup_L	13	Parietal_Sup_L	21	Occipital_Sup_L	27	Temporal_Sup_L
2	Frontal_Sup_R	14	Parietal_Sup_R	22	Occipital_Sup_R	28	Temporal_Sup_R
3	Frontal_Mid_L	15	Parietal_Inf_L	23	Occipital_Mid_L	29	Temporal_Pole_Sup_L
4	Frontal_Mid_R	16	Parietal_Inf_R	24	Occipital_Mid_R	30	Temporal_Pole_Sup_R
5	Frontal_Sup_Medial_L	17	Precuneus_L	25	Occipital_Inf_L	31	Temporal_Mid_L
6	Frontal_Sup_Medial_R	18	Precuneus_R	26	Occipital_Inf_R	32	Temporal_Mid_R
7	Frontal_Mid_Orb_L	19	Cingulum_Post_L			33	Temporal_Pole_Mid_L
8	Frontal_Mid_Orb_R	20	Cingulum_Post_R			34	Temporal_Pole_Mid_R
9	Rectus_L					35	Temporal_Inf_L 8301
10	Rectus_R					36	Temporal_Inf_R 8302
11	Cingulum_Ant_L					37	Fusiform_L
12	Cingulum_Ant_R					38	Fusiform_R
						39	Hippocampus_L
						40	Hippocampus_R
						41	ParaHippocampal_L
						42	ParaHippocampal_R

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Areas of the connectivity graph for functional data for (a) controls, (b) MCI, and (c) AD. Reprinted with permission from frontiers in computational neuroscience.

4. Modal Controllability Based on Graph Distances

In the context of target control of complex networks, the distance between drivers and target nodes, known as the control distance, plays an important role in the required control energy [23]. In this section, we employ these distances to define a tight lower bound on the rank of the controllability matrix. For a network with m leaders denoted by l_j, j ∈ {1, 2, …, m}, Distance-to-Leaders (DL) vector D_i ∈ R^m for each node i can be defined as

()

where D_i,j shows the j^th entry of D_i. A sequence of vectors D = [D_i] is called Pseudo-Monotonically Increasing (PMI) sequence if for every D_i, there exists some α(i) ∈ {1, 2, …, m} such that

()

For example, a PMI sequence of five DL vectors can be built for the network in Figure 5 as

()

Encircled items are clearly smaller than those in subsequent vectors. For any connected graph G = (V, E) and any set of leaders L⊆V, let D_L denote the set of all PMI sequences. If δ_L is the length of the longest sequence, then the controllability matrix Γ satisfies [16]

()

for any link weighting function ω : E⟶R⁺. In other words, the lower bound δ_L on the rank of the controllability matrix is independent from the edge weights.

The leader selection problem can be stated as determining a minimum number of leaders that ensures the controllability of a given network. If edge weights of the graph G are known, one can execute exhaustive search to compute the rank of controllability matrix for any possible subset of leaders and select the minimal set. In addition to the computational cost, this method is not possible when edge weights are unknown. In this case, one can convert the leader selection problem into an optimization problem, ensuring that the dimension of the controllable subspace is not less than a specified value k ∈ {1, 2, …, n}. That is,

()

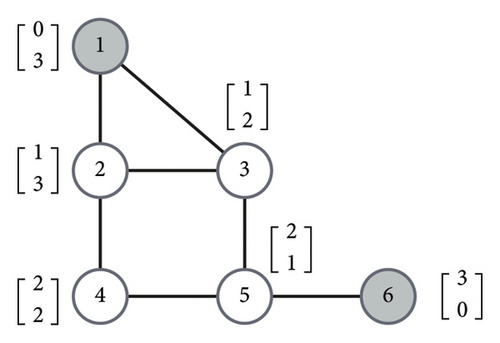
It is worth noting that this optimization problem is always feasible since at least L = V is a solution.

Example 2. We apply the graph theoretical results on the same functional (FDG-PET) and structural (MRI) connectivity graphs [28] for control (CN), mild cognitive impairment (MCI), and Alzheimer’s disease (AD) subjects.

Using the distance-based structural controllability results from [16], it can be shown that functional networks would be completely controllable under any weighted consensus-type dynamics if the leaders are selected as Table 2. Interestingly, the driver nodes for controls and MCI in this table are mainly from frontal and occipital lobes, respectively. This is the same result as what we achieved in the average controllability of functional networks in Example 1.

The structural networks would be completely controllable under any weighted consensus-type dynamics if the leaders are selected as Table 3. The found leaders based on this method avoid the central hub, i.e., the node with the highest degree, and that it is a valid method for determining the modal controllability. However, compared to the average controllability approach, nodes 33, 38, and 40 are common between the “Controls” column in Table 3 and the top-five nodes ranked in Figure 4(a). That means both approaches suggest the nodes in the temporal lobe as drivers for structural networks. The same comparison for the MCI suggests nodes 8 and 9 from the frontal lobe as drivers.

It is important to mention that these are not necessarily the smallest set of leaders that ensures the controllability of those networks, but they are the smallest sets that can be obtained by relying on the distance-based results from [16].

Table 2. Driver nodes for functional networks.

	Controls	MCI	AD
Indices	1, 2, 5, 7, 12, 25, 33, 40	7, 9, 22, 24, 26	7, 16, 18, 21, 29

Nodes	Frontal_Sup_L	Frontal_Mid_Orb_L	Frontal_Mid_Orb_L
	Frontal_Sup_R	Rectus_L	Parietal_Inf_R
	Frontal_Sup_Medial_L	Occipital_Sup_R	Precuneus_R
	Frontal_Mid_Orb_L	Occipital_Mid_R	Occipital_Sup_L
	Cingulum_Ant_R	Occipital_Inf_R	Temporal_Pole_Sup_L
	Occipital_Inf_L
	Temporal_Pole_Mid_L
	Hippocampus_R

Table 3. Driver nodes for structural networks.

	Controls	MCI	AD
Indices	13, 14, 81, 83, 84, 143, 144, 175, 187	11, 12, 13, 14, 81, 82, 83, 84, 136, 137, 144, 151, 154, 176, 182	42, 82, 83, 84, 144, 152, 154, 176, 182

Nodes	Frontal_Mid_Orb_R	Frontal_Mid_Orb_L	Rectus_L
	Rectus_R	Frontal_Mid_Orb_R	Cingulum_Ant_L
	Temporal_Sup_L	Rectus_L	Cingulum_Ant_R
	Temporal_Pole_Sup_L	Cingulum_Ant_L	Temporal_Pole_Sup_R
	Temporal_Pole_Sup_R	Temporal_Pole_Sup_R	Temporal_Mid_L
	Temporal_Pole_Mid_L	Temporal_Mid_L	Temporal_Pole_Mid_R
	Temporal_Pole_Mid_R	Temporal_Inf_R 8302	Hippocampus_L
	Fusiform_R	Fusiform_L	ParaHippocampal_L
	Hippocampus_R	Hippocampus_L
		ParaHippocampal_R

5. Discussion

In this paper, we applied novel dynamic graph theory methods to determining the average and modal controllability of functional and structural brain connectivity networks. These two concepts play an important role in dynamic imaging connectomics since they describe the dynamical behavior of areas in the brain with respect to their type of connectivity (dense or weak) and the movement of the brain to either easy reachable or difficult-to-reach states.

An important aspect in structural network topology is hubs. While hubs support the brain’s capability to be robust to lesions, or, for example, for better synchronizability, they may be avoided in control theory since they do not belong to the regions that steer the network dynamics to difficult-to-reach patterns of activity [29]. Hubs might efficiently transmit control signals across the connectome in order to achieve new patterns of activity. Another important role of the hubs is that they enable the integration of functionally specialized and anatomically disparate neural regions. We applied the new concept of choosing the best driver set for average controllability and that of graph distances for the modal controllability. Based on these new techniques, we obtain important disease descriptors that visualize alterations in the disease trajectory by revealing densely connected hubs or sparser areas. Examples show the importance of the theoretical results for both new concepts. For both structural and functional networks, the relevance of hubs and the number of driver nodes decreases from controls to AD. The observation of those changes can offer important indications about the status of disease evolution in a patient and can thus be applied in longitudinal and intervention studies.

While derived graph measures and their changes over time in static graph theory show the differences between disease and normal control, looking at the brain as a dynamical networked system undergoing changes in patterns of cooperation and competition opens a new research avenue. The key concept of controllability plays a central role determining the driver nodes in a brain network. These transitions of the brain between diverse cognitive states are believed to have far-reaching implications for the clinical areas. Thus, it allows an in-depth study of the differences between disease and control groups and provides a diversity of temporal characteristic features to better discriminate these groups. Finally, it improves personalized medicine by looking into individual differences in diagnostics based on network controllability.

Another important aspect is the connected network architecture at multiple spatiotemporal scales achieved based on multilayer networks with intra- and interlayer edges. Each layer’s nodes represent brain regions; however, there is a unique dynamics (time scale) associated with the layer. An interesting future direction would be how to control such a complex dynamics [30]. Finally, network control theory can open a new avenue to study cognitive control [2, 3, 5, 26] by describing the way how the brain influences its behavior to be able to perform certain tasks, the collective role of brain networks in fluid intelligence [7], its critical role in the pathophysiology of schizophrenia [31], the importance of the left inferior frontal gyrus in controlled language performance [6], the brain network organization between cognitive control and reward regions [4], and the crucial connection between the spontaneous metastability of large-scale networks in the cerebral cortex and cognition [1].

The application of graph theory to explore the intricacies of the brain’s functional and structural characteristics extends in the literature beyond human fMRI networks. For instance, a study in macaque monkeys [32] unveils the complexity of the functional single neuron network in three frontoparietal areas during active behavior, emphasizing the heterogeneous importance of individual neurons. Another study in monkeys [33], grounded in graph theory, delineates the hierarchical emergence of anticorrelation hubs within the local PMd network before motor execution, implying that these hubs serve as indicators of motor plan readiness and impending movement initiation. Other investigations [34, 35] underscore the significance of specialized interconnected groups, often termed “rich clubs,” in neural computations and the comprehensive understanding of structural and functional attributes within local cortical circuits. In addition, graph theoretical analyses have been instrumental in revealing a robust and nontrivial hierarchical modular structure in the mouse brain’s functional connectivity [36], as well as identifying hubs of anticorrelation in resting-state fMRI [37, 38]. Finally, a recent study [39, 40] demonstrates altered hierarchical modularity and the presence of multiple topologically equivalent backbones in schizophrenia, aligning with the disconnection hypothesis that characterizes the illness as a disruption in functional integration among brain regions. Indeed, the outcomes of this investigation offer the potential for a more extensive contextualization of the research, potentially facilitating the future application of the proposed methods beyond fMRI data, extending to other vital sources of electrophysiological signals such as firing rates, multi-unit activity (MUA), local field potentials (LFP), and more. Finally, novel and reliable biomarkers derived from PET, SPECT, and MRI will be employed in future to effectively differentiate and predict the dementia evolution.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

A. Moradi Amani and A. Meyer-Baese contributed equally to this paper.

Acknowledgments

We acknowledge funding through a Fulbright Franco-American Commission and Marie Sklodowska-Curie Actions. We are grateful to Dr. Yasin Yazicioglu for sharing his codes and expertise with us.

Open Research

Data Availability

No underlying data were collected or produced in this study.

References

1 Alderson T., Bokde A. L. W., Kelso J. A. S., Maguire L., and Coyle D., Metastable neural dynamics underlies cognitive performance across multiple behavioural paradigms, Human Brain Mapping. (2020) 41, 3212–3234.
10.1002/hbm.25009
PubMed Web of Science® Google Scholar
2 Griffith T. D. and Hubbard J. E., System identification methods for dynamic models of brain activity, Biomedical Signal Processing and Control. (2021) 102765.
Google Scholar
3 Gu S., Pasqualetti F., Cieslak M., Telesford Q., Yu A., Kahn A., Medaglia J., Vettel J., Miller M., Grafton S., and Bassett D., Controllability of structural brain networks, Nature Communications. (2015) 6, 8414–8510, https://doi.org/10.1038/ncomms9414, 2-s2.0-84943197033.
10.1038/ncomms9414
CAS PubMed Web of Science® Google Scholar
4 Huskey R., Wilcox S., and Weber R., Network neuroscience reveals distinct neuromarkers of flow during media use, Journal of Communication. (2018) 68, no. 5, 872–895, https://doi.org/10.1093/joc/jqy043, 2-s2.0-85061900371.
10.1093/joc/jqy043
Web of Science® Google Scholar
5 Kenett Y. N., Medaglia J. D., Beaty R. E., Chen Q., Betzel R. F., Thompson-Schill S. L., and Qiu J., Driving the brain towards creativity and intelligence: A network control theory analysis, Neuropsychologia. (2018) 118, 79–90, https://doi.org/10.1016/j.neuropsychologia.2018.01.001, 2-s2.0-85040576915.
10.1016/j.neuropsychologia.2018.01.001
PubMed Web of Science® Google Scholar
6 Medaglia J. D., Harvey D. Y., and Hamilton R. H., Language tasks and the network control role of the left inferior frontal gyrus, ENEURO. (2021) 4, 493–501.
Google Scholar
7 Wilcox R. R. and Barbey A. K., Connectome-based predictive modeling of fluid intelligence: Evidence for a global system of functionally integrated brain networks, Cerebral Cortex. (2023) 4.
Google Scholar
8 Cocchi L., Zalesky A., Fornito A., and Mattingley J. B., Dynamic cooperation and competition between brain systems during cognitive control, Trends in Cognitive Sciences. (2013) 17, no. 10, 493–501, https://doi.org/10.1016/j.tics.2013.08.006, 2-s2.0-84884419435.
10.1016/j.tics.2013.08.006
PubMed Web of Science® Google Scholar
9 Storti S. F., Galazzo J. B., Khan S., Manganotti P., and Menegaz G., Exploring the epileptic brain network using time-variant eective connectivity and graph theory, IEEE Journal of Biomedical and Health Informatics. (2017) 21, 1411–1.
10.1109/JBHI.2016.2607802
PubMed Web of Science® Google Scholar
10 Chen B. and Li X., Temporal functional connectomics in schizophrenia and healthy controls, 21, Proceedings of the IEEE International Conference on Systems, Man, Machine and Cybernetics, October 2017, Banff, Canada.
Google Scholar
11 Srighakollapu M. V., Kalaimani R. K., and Pasumarthy R., Optimizing driver nodes for structural controllability of temporal networks, IEEE Transactions on Control of Network Systems. (2021) 21, no. 1.
Google Scholar
12 Yao P. and Li X., Toward optimizing control signal paths in functional brain networks, Chaos. (2019) 29, no. 10, 103144–103151, https://doi.org/10.1063/1.5119974.
10.1063/1.5119974
PubMed Google Scholar
13 Meyer-Baese A., Roberts R., Illan I., Meyer-Baese U., Lobbes M., Stadlbauer A., and Pinker-Domenig K., Dynamical graph theory networks methods for the analysis of sparse functional connectivity networks and for determining pinning observability in brain networks, Frontiers in Computational Neuroscience. (2017) 11, https://doi.org/10.3389/fncom.2017.00087, 2-s2.0-85031998802.
10.3389/fncom.2017.00087
Google Scholar
14 Tahmassebi A., Meyer-Baese U., and Meyer-Baese A., Structural target controllability of brain networks in dementia, Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, November 2021, Mexico, 3978–3981, https://doi.org/10.1109/EMBC46164.2021.9630496.
10.1109/EMBC46164.2021.9630496
Google Scholar
15 Amani A. M., Jalili M., Yu X., and Stone L., Controllability of complex networks: Choosing the best driver set, Physical Review E. (2018) 98, no. 3, 030302–030308, https://doi.org/10.1103/physreve.98.030302, 2-s2.0-85053816264.
10.1103/PhysRevE.98.030302
CAS Web of Science® Google Scholar
16 Yazicioglu A. Y., Abbas W., and Egerstedt M., Graph distances and controllability of networks, IEEE Transactions on Automatic Control. (2016) 61, no. 12, 4125–4130, https://doi.org/10.1109/tac.2016.2546180, 2-s2.0-85003811154.
10.1109/TAC.2016.2546180
Google Scholar
17 Ehrens D., Sritharan D., and Sarma S. V., Closed-loop control of a fragile network: Application to seizure-like dynamics of an epilepsy model, Frontiers in Neuroscience. (2015) 9, 58–61, https://doi.org/10.3389/fnins.2015.00058, 2-s2.0-84928007262.
10.3389/fnins.2015.00058
PubMed Google Scholar
18 Pascualetti F., Zampieri S., and Bullo F., Pinning a complex dynamical network to its equilibrium, IEEE Transactions on Control of Network Systems. (2014) 1, no. 8, 40–52.
Google Scholar
19 Hamdan A. and Nayfeh A., Measures of modal controllability and observability for first- and second-order linear systems, Journal of Guidance, Control, and Dynamics. (1989) 12, no. 3, 421–428, https://doi.org/10.2514/3.20424, 2-s2.0-0024656967.
10.2514/3.20424
Web of Science® Google Scholar
20 Mieghem P. V., Graph Spectra for Complex Networks, 2011, Cambridge University Press, Cambridge, UK.
Google Scholar
21 Steinmetz N. A., Zatka-Haas P., Carandini M., and Harris K. D., Distributed coding of choice, action and engagement across the mouse brain, Nature. (2019) 576, no. 7786, 266–273, https://doi.org/10.1038/s41586-019-1787-x.
10.1038/s41586-019-1787-x
CAS PubMed Web of Science® Google Scholar
22 Tavor I., Jones O. P., Mars R. B., Smith S. M., Behrens T. E., and Jbabdi S., Task-free mri predicts individual differences in brain activity during task performance, Science. (2016) 352, 216–220, https://doi.org/10.1126/science.aad8127, 2-s2.0-84963545848.
10.1126/science.aad8127
CAS PubMed Web of Science® Google Scholar
23 Wang D. C., Vagnucci A. H., and Li C. C., Digital image enhancement: A survey, Computer Vision, Graphics, and Image Processing. (1983) 24, 363–381, https://doi.org/10.1016/0734-189x(83)90061-0, 2-s2.0-0020970570.
10.1016/0734-189X(83)90061-0
Web of Science® Google Scholar
24 Pecora L. M. and Carroll T. L., Master stability functions for synchronized coupled systems, Physical Review Letters. (1998) 80, no. 10, 2109–2112, https://doi.org/10.1103/physrevlett.80.2109, 2-s2.0-4243241129.
10.1103/PhysRevLett.80.2109
CAS Web of Science® Google Scholar
25 Jalili M., Askari Sichani O., and Yu X., Optimal pinning controllability of complex networks: Dependence on network structure, Physical Review E. (2015) 91, no. 1, 012803–012808, https://doi.org/10.1103/physreve.91.012803, 2-s2.0-84937141072.
10.1103/PhysRevE.91.012803
Web of Science® Google Scholar
26 Tang E. and Bassett D. S., Colloquium: Control of dynamics in brain networks, Reviews of Modern Physics. (2018) 90, no. 3, 031003–31011, https://doi.org/10.1103/revmodphys.90.031003, 2-s2.0-85053015156.
10.1103/RevModPhys.90.031003
Web of Science® Google Scholar
27 Sorrentino F., di Bernardo M., Garofalo F., and Chen G., Controllability of complex networks via pinning, Physical Review E. (2007) 75, no. 4, 046103–046108, https://doi.org/10.1103/physreve.75.046103, 2-s2.0-34147124485.
10.1103/PhysRevE.75.046103
CAS PubMed Web of Science® Google Scholar
28 Ortiz A., Munilla J., Alvarez-Illan I., Gorriz M., Ramirez J., and Alzheimer’s Disease Neuroimaging Initiative, Exploratory graphical models of functional and structural connectivity patterns for alzheimer’s disease diagnosis, Frontiers in Computational Neuroscience. (2015) 9, https://doi.org/10.3389/fncom.2015.00132, 2-s2.0-84948754192.
10.3389/fncom.2015.00132
PubMed Google Scholar
29 Liu Y. Y., Slotine J. J., and Barabasi A., Controllability of complex networks, Nature. (2011) 473, no. 7346, 167–173, https://doi.org/10.1038/nature10011, 2-s2.0-79955879494.
10.1038/nature10011
CAS PubMed Web of Science® Google Scholar
30 Schmidt M., Bakker R., Hilgetag C. C., Diesmann M., and van Albada S. J., Multi-scale account of the network structure of macaque visual cortex, Brain Structure and Function. (2018) 223, no. 3, 1409–1435, https://doi.org/10.1007/s00429-017-1554-4, 2-s2.0-85034227327.
10.1007/s00429-017-1554-4
PubMed Web of Science® Google Scholar
31 Li Q., Yao L., You W., Liu J., Deng S., Li B., Luo L., Zhao Y., Wang Y., Wang Y., Zhang Q., Long F., Sweeney J. A., Gu S., Li F., and Gong Q., Controllability of functional brain networks and its clinical significance in first-episode schizophrenia, Schizophrenia Bulletin. (2022) 493–501.
Google Scholar
32 Dann B., Muchaels A., Schaffelfofer S., and Scherberger H., Uniting functional network topology and oscillations in the fronto-parietal single unit network of behaving primates, Elife. (2016) 4.
Google Scholar
33 Bardella G., Pani P., Brunamonti E., Giarrocco F., and Ferraina S., The small scale functional topology of movement control: Hierarchical organization of local activity anticipates movement generation in the premotor cortex of primates, NeuroImage. (2020) 207, 116354–4, https://doi.org/10.1016/j.neuroimage.2019.116354.
10.1016/j.neuroimage.2019.116354
PubMed Web of Science® Google Scholar
34 Gal E., London M., Globerson A., Ramaswamy S., Reimann M. W., Muller E., Markram H., and Segev I., Rich cell-type-specific network topology in neocortical microcircuitry, Nature Neuroscience. (2017) 20, no. 7, 1004–1013, https://doi.org/10.1038/nn.4576, 2-s2.0-85021410469.
10.1038/nn.4576
CAS PubMed Web of Science® Google Scholar
35 Gu Y., Qi Y., and Gong P., Rich-club connectivity, diverse population coupling, and dynamical activity patterns emerging from local cortical circuits, PLoS Computational Biology. (2019) 15, 1006902–1006904, https://doi.org/10.1371/journal.pcbi.1006902, 2-s2.0-85064773872.
10.1371/journal.pcbi.1006902
CAS PubMed Web of Science® Google Scholar
36 Bardella G., Bifone A., Gabrielli A., Gozzi A., and Squartini T., Hierarchical organization of functional connectivity in the mouse brain: a complex network approach, Scientific Reports. (2016) 6, no. 1, 32060–32064, https://doi.org/10.1038/srep32060, 2-s2.0-84983335529.
10.1038/srep32060
CAS PubMed Google Scholar
37 Gopinath K., Krishnamurthy V., Cabanban R., and Crosson B., Hubs of anticorrelation in high-resolution resting-state functional connectivity network architecture, Brain Connectivity. (2015) 5, no. 5, 267–275, https://doi.org/10.1089/brain.2014.0323, 2-s2.0-84939222171.
10.1089/brain.2014.0323
PubMed Web of Science® Google Scholar
38 Liang Z., King J., and Zhang N., Anticorrelated resting-state functional connectivity in awake rat brain, NeuroImage. (2012) 59, no. 2, 1190–1199, https://doi.org/10.1016/j.neuroimage.2011.08.009, 2-s2.0-83055194504.
10.1016/j.neuroimage.2011.08.009
PubMed Web of Science® Google Scholar
39 Mastrandrea R., Piras F., Gabrielli A., Banaj N., Caldarelli G., Spalletta G., and Gili T., The unbalanced reorganization of weaker functional connections induces the altered brain network topology in schizophrenia, Scientific Reports. (2021) 11, no. 1, 15400–15404, https://doi.org/10.1038/s41598-021-94825-x.
10.1038/s41598-021-94825-x
CAS PubMed Google Scholar
40 Mastrandrea R., Gabrielli A., Piras F., Spalletta G., Caldarelli G., and Gili T., Organization and hierarchy of the human functional brain network lead to a chain-like core, Scientific Reports. (2017) 7, no. 1, 4888–4894, https://doi.org/10.1038/s41598-017-04716-3, 2-s2.0-85022081134.
10.1038/s41598-017-04716-3
PubMed Google Scholar

All articles

Controllability of Functional and Structural Brain Networks

Abstract

1. Introduction

2. Preliminary Controllability Concepts and Definitions

3. Average Controllability Based on Determining the Best Driver Set

4. Modal Controllability Based on Graph Distances

5. Discussion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Controllability of Functional and Structural Brain Networks

Abstract

1. Introduction

2. Preliminary Controllability Concepts and Definitions

3. Average Controllability Based on Determining the Best Driver Set

4. Modal Controllability Based on Graph Distances

5. Discussion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information