1. Introduction

In the research of spacecraft proximity collaborative tasks, such as rendezvous and docking, precision formation, space manipulation, and on-orbit assembly, many scholars have proposed the necessity of attitude-orbit coupling modeling [1–5]. Some scholars have applied the attitude-orbit coupling results to spacecraft guidance, navigation and control (GNC) [6, 7]. Liu et al. [8, 9] proposed various effective attitude-orbit coupling control methods. Obviously, in the field of spacecraft relative dynamics, navigation, and control, attitude-orbit coupling is not a new issue. However, to the author’s knowledge, there is no research that has clearly defined attitude-orbit coupling. It is specifically a mathematical problem, a physical phenomenon, or an engineering application problem arising only from practical processes, and there is still controversy.

Due to the unsystematic academic investigations on attitude-orbit coupling, the research results have little guiding significance for engineering applications. In terms of engineering practice, most space missions such as rendezvous and docking [10] and space manipulation technology demonstrations [11] have been successfully deployed on orbit and achieved highly accurate spacecraft cooperative operations without considering the impact of attitude-orbit coupling effect. In the above aerospace engineering tasks, Hill-Clohessy-Wiltshire (HCW) equations [12] are the most widely used relative dynamic model. Obviously, it is not an attitude-orbit coupling relative dynamic model.

The viewpoint proposed in Refs. [1–5] conflicts with the engineering application research in Refs. [10–12], which makes scientific aerospace engineers to wonder whether the research work on attitude-orbit coupling relative dynamic model is necessary, or under what circumstances it is necessary. In addition, in ground experiments, the spacecraft simulator’s relative attitude maneuver does not cause relative translational motion [13], which means that the attitude-orbit coupling phenomenon is not explicitly expressed in the physical level, if engineering errors such as inaccurate centroid identification of the spacecraft simulator are ignored.

This paper clarifies, at the first part, the confusion about mechanism and application of attitude-orbit coupling effect and gives a clear definition of attitude-orbit coupling effect. Then, a spiral theory–based attitude-orbit coupling relative dynamic model is developed, which describes the 6-DOF relative motion between spacecraft, whether the spacecraft is a rigid body or a rigid-flexible coupling system, with one equation by using six-dimensional spinor dual vector. Therefore, the spiral theory–based model is known as integrated model [14–16]. Finally, taking spacecraft flying formation as an example, the application value of attitude-orbit coupling relative dynamic model in precision collaborative mission is provided, and simulation results verify the engineering significance of the attitude-orbit coupling relative dynamic model.

2. Mechanism Analysis of Attitude-Orbit Coupling Effects

Aiming at the root cause of the attitude-orbit coupling effects in spacecraft proximity relative motion, taking mathematical representation as the context, the mechanism of attitude-orbit coupling effects originating from different mathematical representation is investigated.

2.1. Particle Model

Since the development of space station rendezvous and docking missions in the 1960s, spacecraft relative dynamic modeling technology has also evolved accordingly. The initial relative dynamic model is known as the particle model, which regarded the relative motion between spacecraft as the relative motion between two points with mass. As shown in Figure 1, the motion of particle f and particle l represents the orbital motion of the follower spacecraft and the leader spacecraft, respectively. R_e, $$, and $$ denote the relative position, relative velocity, and relative acceleration between two particles in terms along the inertial system, respectively. If the leader is orbiting on a near circular Earth orbit, the relative dynamics between two spacecraft is [17]

$$ ()

Equation (1) is derived based on Newton’s second law, wherein m_f and m_l denote the mass of the follower and leader, respectively, μ is the gravitational constant, and R_l is the position vector of the leader with respect to the inertial system. d_t = d_f − m_f/m_ld_l, where d_f and d_l denote the external interference forces acting on the follower and leader, respectively. F_t = F_f − m_f/m_lF_l, where F_f and F_l denote the control forces acting on the follower and leader, respectively. Note that the external interference forces and control forces are acting on the center of mass (COM) of spacecraft in Equation (1). Based on the particle model, the spacecraft body coordinate system is constructed with the particle as the origin, and the relative attitude dynamic equations between the follower and leader can be expressed as

$$ ()

Equation (2) is derived by using quaternion mathematical representation, wherein J_f is the moment of inertia of follower, ω_e denotes the angular velocity tracking error, and τ_f and d_f denote the control torque and external interference torque acting on the follower. Note that all vectors in Equations (1) and (2) are expressed with respect to the inertial coordinate system. The relative dynamic equation describing the relative 6-DOF motion between spacecraft can be obtained by combining Equations (1) and (2).

Equations (1) and (2) are derived with respect to the inertial system. This model is used for initial theoretical calculations. If the above equations are expressed in the orbit coordinate system of the leader, the relative dynamic model can be expressed as [18–21]

$$ ()

where n_l is angular velocity of the leader orbit. The physical meaning of other parameters is the same as those corresponding to Equations (1) and (2). The difference between Equation (3) and Equations (1) and (2) is that all the vectors are represented in orbit coordinate system of leader. Furthermore, if the leader is orbiting on a circular orbit, the angular velocity of the leader orbit n_l can be simplified to the constant mean motion, n_l, and Equation (3) can further be expressed in a simple form [10].

$$ ()

where R_e = [x y z]^T and $$. These above equations of motion are known as the HCW equations. The HCW equations have been used extensively since the 1960s for space cooperative mission modeling [22–24]. The above functions are mainly used for rendezvous and docking missions with orbital hovering and orbital orbiting, as the HCW equation is constructed based on the orbital coordinate system as the reference coordinate system.

Equations (1)–(4) are relative dynamic equations derived from particle model for different engineering applications. Under particle model mathematical framework, the orbital and the attitude motion of spacecraft are independent of each other, and there is no motion projection between the orbital and the attitude motion. Therefore, there is no coupling between the relative attitude and orbit motion between two spacecraft.

2.2. Extended Particle Model

Segal and Gurfil [25] believe that even under particle model mathematical framework, attitude-orbit coupling effect is still a key factor affecting the success of space collaborative tasks, such as rendezvous and docking and spacecraft formation flying (Figure 2). Their argument is that because the size of the spacecraft itself is much smaller than the scale of relative orbital motion, it can be considered as a particle when describing relative motion. However, for space collaborative tasks at ultraclose distances (typically less than 100 m), or for ultraclose stages of certain collaborative tasks, such as the close approximation stage and docking stage of rendezvous and docking mission, the size of the spacecraft can no longer be considered as an absolute small amount compared to the relative motion distance. And the docking point is not actually the COM of the spacecraft, but rather a point on the edge of the spacecraft. Therefore, for the engineering application of above tasks, it is necessary to build the relative dynamic model between the docking points on the spacecraft, instead of the relative dynamic model between COMs of spacecraft, assuming that i and j are the docking points of the follower and leader, respectively. The relative dynamic equations between i and j can be expressed as

$$ ()

where $$ is the relative position vector from docking point i to j, $$ is the position vector from the COM of the follower to docking point i, $$ denotes the position vector from the COM of the leader to docking point j, and $$ denotes the angular velocity tracking error.

In Equation (6), it can be found that the relative translational motion is affected by the relative angular velocity ω_e; that is, the spacecraft proximity relative motion is affected by attitude-orbit coupling. Through the simulation of precision formation and rendezvous and docking, Segal and Gurfil conclude that the larger the size of a rigid spacecraft, the stronger the impact of the attitude-orbit coupling effect on the relative motion.

According to the conclusions of the above research, the attitude-orbit coupling effect originates from the relative dynamics between two noncentroid points. It can be inferred that when the particle and COM coincide, the impact of attitude-orbit coupling on relative motion is zero, which is the same as the conclusion drawn in Section 2.1. Obviously, Equation (5) describes a special scenario, not a general equation.

2.3. Spiral Theory–Based Relative Dynamic Model

An attitude-orbit coupling relative dynamic model was provided in 2001 based on the Newton-Euler equations by Pan and Kapila [26], which is also the first publicly published theoretical achievement of attitude-orbit coupling relative dynamics that the authors can find.

$$ ()

where $$ and $$ are the real-time relative orbital velocity and desired relative orbital velocity between the leader and follower, respectively; m_l and m_f are the mass of the leader and follower, respectively; and f_el, f_dl, and f_l are the Earth’s gravity, external interference force, and control force acting on the leader, respectively. Equation (6) contains element, $$, which shows that the relative rotational motion has an impact on the relative translational motion.

Equation (6) describes the relative dynamics between the COMs of the spacecraft. However, the attitude-orbit coupling effect occurs. Obviously, this conclusion conflicts with the research conclusions of Equations (1)–(5). It is worth mentioning that Pan and Kapila did not explain the cause of attitude-orbit coupling in Ref. [26] but focused on studying the impact of spacecraft attitude motion caused by gravity gradient torque on relative orbital motion.

In response to the above contradictions, in recent years, Sun et al. [27–29] conducted a detailed study on the attitude-orbit coupling characteristics of relative motion between spacecraft. The attitude-orbit coupling relative dynamics based on spiral theory was obtained.

$$ ()

where $$ and $$ denote the relative dual velocity and dual force acting on the follower, respectively, $$ is the dual inertia operator of the follower, $$ is the relative dual quaternion, $$ is the conjugate of $$, and $$ is the dual velocity of the leader. Based on the spiral theory, each dual number can represent two separate real vectors with a dual unit ε, which makes the relative dynamic model representation to be in a compact form. According to Ref. [27], it can be found that Equation (7) contains the same coupling element, $$, as Equation (6).

Both Equations (6) and (7) describe the relative motion between the COMs of spacecraft, and the attitude-orbit coupling phenomenon occurs in both equations. Unfortunately, none of the above investigations focused on the mechanism of attitude-orbit coupling phenomenon, but rather on the trajectory offset caused by attitude-orbit coupling effects. It makes engineers wonder what is the root cause of attitude-orbit coupling and what is the difference between the application scenarios of attitude-orbit coupling models and attitude-orbit-independent models.

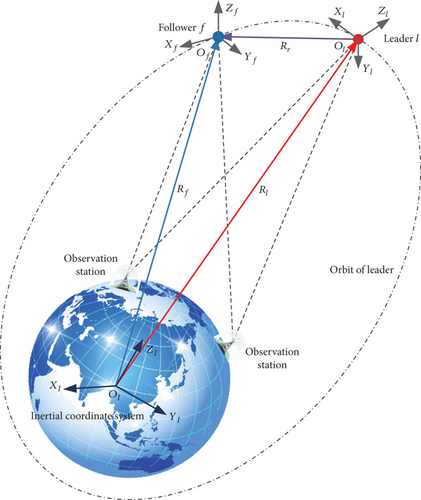
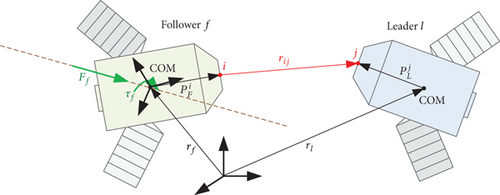
To clarify this confusion, by analyzing Equations (1)–(4) and Equations (6) and (7), it can be found that Equations (6) and (7) are attitude-orbit coupling relative dynamic model, Equations (1)–(4) are attitude-orbit-independent relative dynamic model, and the above equations all describe the relative motion between COMs of spacecraft. In addition to the mathematical representation, another one of the main differences of above equations is the reference coordinate system. In detail, the reference coordinate system of Equations (1) and (2) is the geocentric inertial coordinate system; the reference coordinate system of Equations (3) and (4) is the orbital coordinate system of leader; the reference coordinate system of Equations (6) and (7) is the body-fixed coordinate system of follower. Based on the above facts, we propose the following conjecture: attitude-orbit coupling effect between the COMs of spacecraft originates from the selection of reference coordinate system.

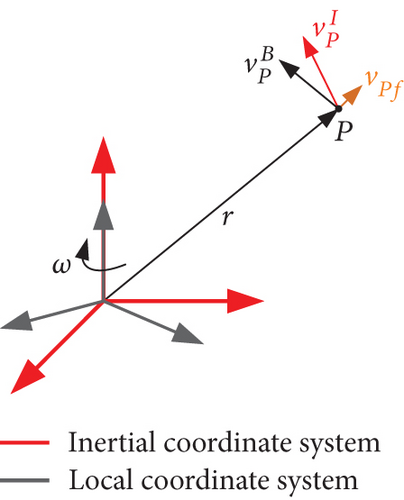
As shown in Figure 3, the position vector of a particle P in the inertial coordinate system is r, the velocity of particle P in the inertial coordinate system is $$, and the velocity of particle P in the local coordinate system is $$. The relationship between the two can be described as $$. Specifically, in the description of relative motion of spacecraft, the motion of the COM of leader relative to the COM of the follower is described using the body-fixed coordinate system of the follower as a reference system, thereby introducing relative rotational motion in relative translational motion, resulting in an attitude-orbit coupling characteristic. Therefore, the following inference can be obtained.

Ratiocination Definition 1. Attitude-orbit coupling is the physical phenomena that occur when describing the relative motion between the COMs of spacecraft with respect to a local coordinate system, namely, body-fixed coordinate system.

Ratiocination Definition 2. The dynamic equation also contains attitude-orbit coupling terms even if describing the 6-DOF motion of a single spacecraft with respect to the body-fixed coordinate system. Further, even if the origin of the body-fixed coordinate system coincides with the COM of this spacecraft, the centroid dynamics is also affected by attitude-orbit coupling effect.

3. Spiral Theory–Based Attitude-Orbit Coupling Relative Dynamics

Equation (7) is the spiral theory–based relative dynamics between two rigid spacecraft. Based on Equation (7), the relative dynamic model between two rigid-flexible spacecraft is provided. This model can solve the problem of motion description of spacecraft formation with rigid and flexible spacecraft investigated in Ref. [30].

3.1. Definition of the Coordinate Systems and Equation Assumptions

The mission scenario of this paper is designed to be a spacecraft formation flying task with a rigid spacecraft as the leader and a rigid-flexible coupling spacecraft as the follower. As shown in Figure 4, a simple rigid-flexible coupling spacecraft consists of a rigid base and a flexible appendage. All the coordinate systems are defined in Figure 4, and there are three coordinate systems in this paper.

• a.

  Earth-centered inertial coordinate system Ψ_I: the ECI frame is a classic frame for spacecraft dynamic analysis. It has the +z-axis pointing at the north pole, the +x-axis pointing at the vernal equinox, and +y completing the right-hand set.

• b.

  Body-fixed coordinate system of leader Ψ_A: it has the origin locating at the COM of leader, with +z-axis pointing at the working part, +x pointing the relative measuring sensor of leader, and +y completing the right-hand set.

• c.

  Body-fixed frame of follower Ψ_B: it has the origin locating at the COM of follower, with +z-axis pointing at the flexible appendages, +x pointing the relative measuring sensor of follower, and +y completing the right-hand set.

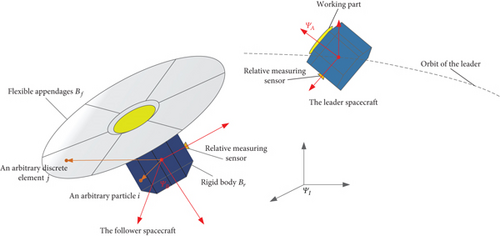
The following notations are employed: $$ denotes the components of x expressed in the body-fixed coordinate system of the follower, and $$ denotes the components of x expressed in the body-fixed coordinate system of the leader.

The derivation of relative dynamics requires the following three conditional assumptions.

Assumption 1. The position of COM and the moment of inertia of the rigid-flexible coupling spacecraft remain unchanged under the vibration of the flexible appendages.

Assumption 2. There is no relative rotation and translation between the flexible appendages and the rigid base; that is, the rigid-flexible spacecraft has a stable configuration.

Assumption 3. The elastic displacement of the flexible appendages is assumed to be small and yields to the linear elasticity theory.

4. Analysis of Engineering Application Advantages

5. Simulation and Results

In this section, the advantage of engineering application of the attitude-orbit coupling relative dynamics is verified by numerical simulation. The GNC system of the spacecraft in a spacecraft proximity mission is shown as Figure 5. Taking the measurement sensors (high-accuracy metrology sensor based on laser metrology) of the PROBA-3 mission as an example, measured results are the relative differentials with respect to the spacecraft body-fixed coordinate system of the follower and have 25 μm measurement accuracy, as shown in Figure 6.

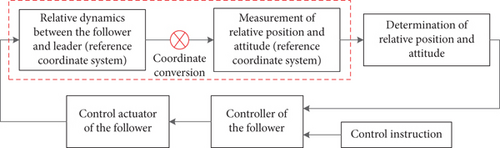
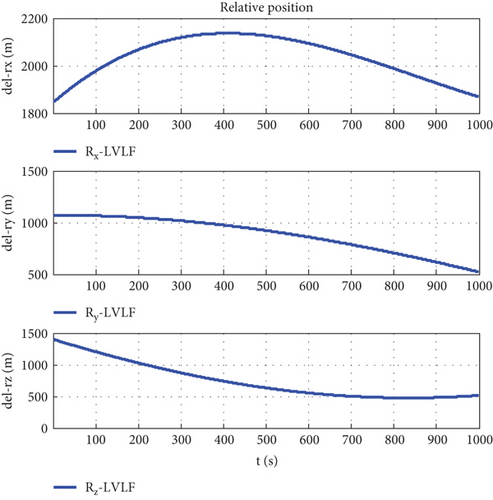
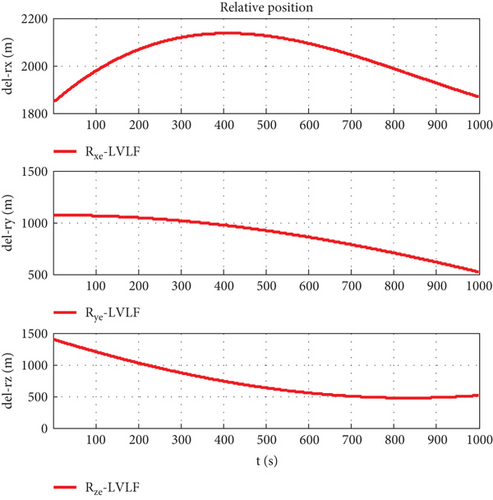
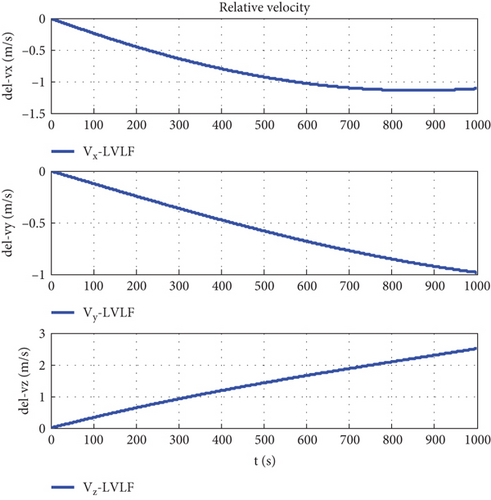
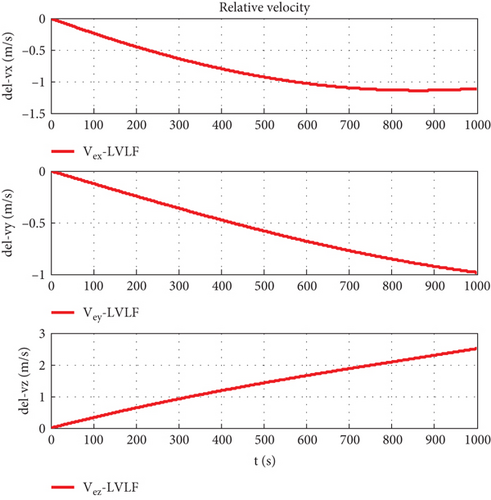
Taking the body-fixed coordinate system of the follower as the conference coordinate system and assuming that the orbit determination accuracy is Δr = 100 m, the simulation step length is 0.1 s, and the simulation time is 1000 s, and using the coordinate conversion matrix C_IO, the relative motion states are shown in Figures 7–16.

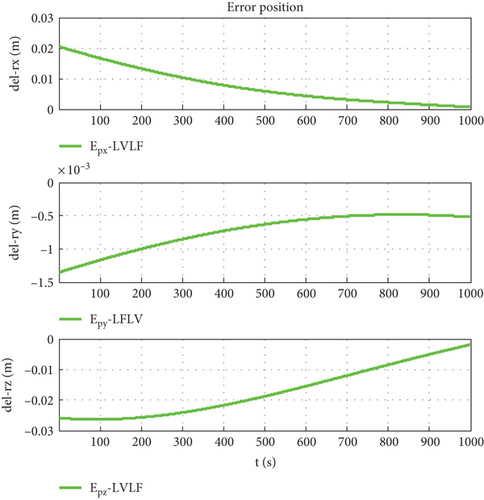
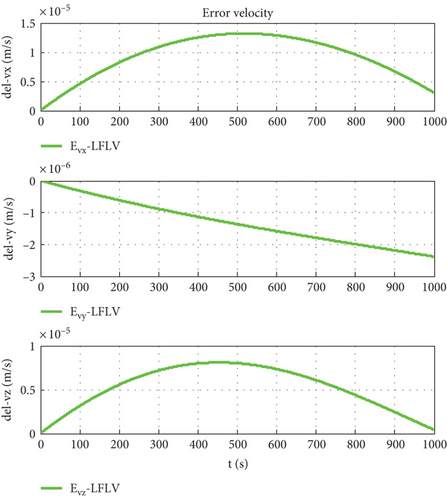
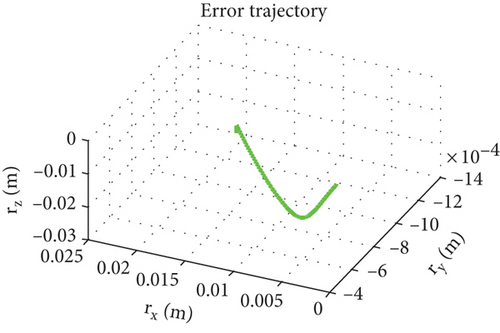
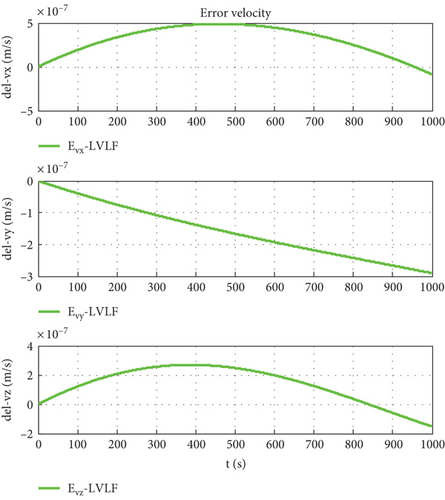
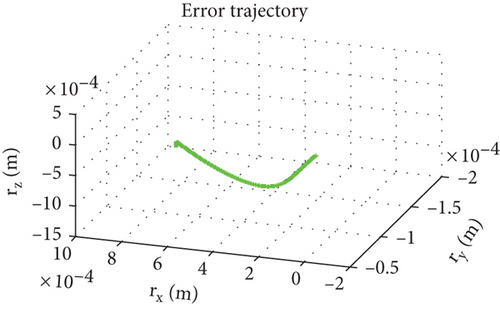
The orbit determination accuracy is set to Δr = 10 m, and other parameters remain unchanged. Simulation results are shown as Figures 17–19.

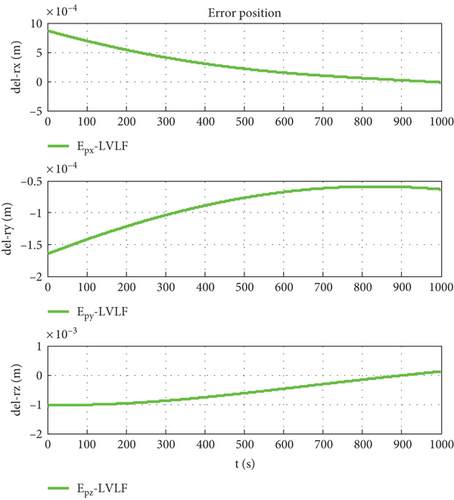
The orbit determination accuracy is set to Δr = 1 m, and other parameters remain unchanged. Simulation results are shown as Figures 20–22.

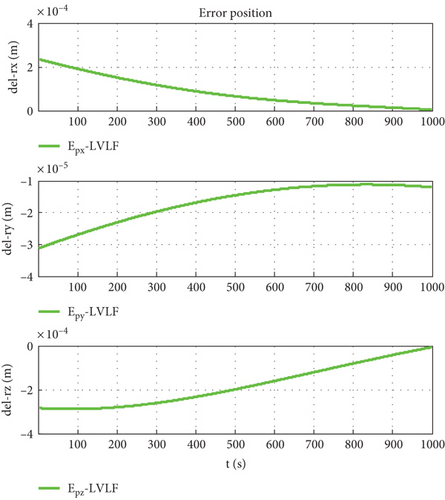
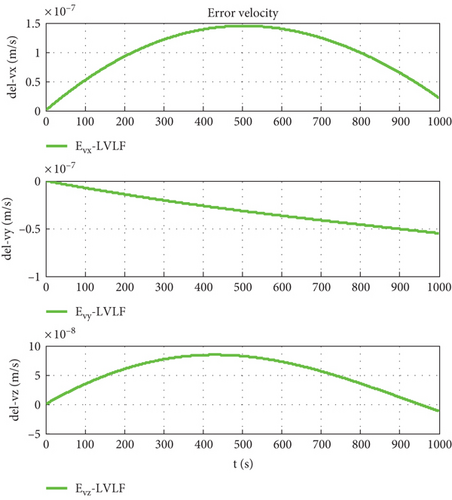
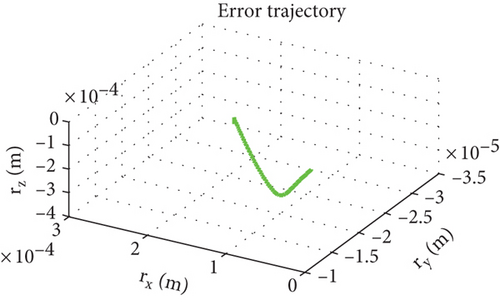
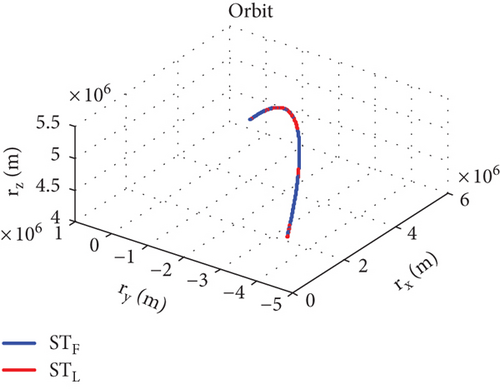
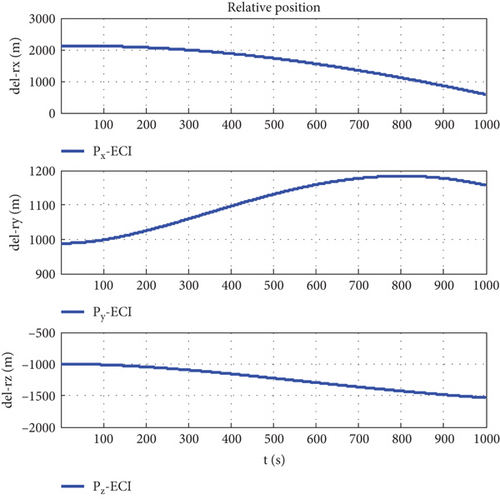
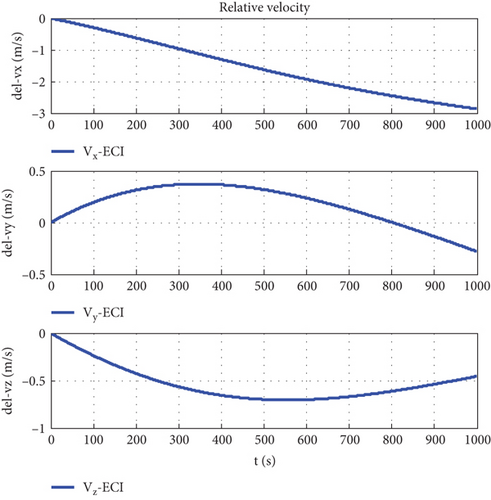
Figure 7 is the relative trajectory of two spacecraft in the inertial coordinate system, where the red line represents the trajectory of the leader and the blue line represents the trajectory of the follower. Figures 8 and 9 show the true values of the relative positions and velocities of two spacecraft in the inertial coordinate system, respectively. Figures 10 and 11 show the three-axis relative position curve between two spacecraft in the body-fixed coordinate system of the follower when orbit determination accuracy is zero and Δr, respectively. Figures 12 and 13 show the three-axis relative velocity curve between two spacecraft in the body-fixed coordinate system of the follower when orbit determination accuracy is zero and Δr, respectively. Figure 14 is the three-axis relative position error between two spacecraft due to coordinate conversion errors with respect to the body-fixed coordinate system of the follower, which is the difference curve between Figures 10 and 11. Figure 15 is the three-axis relative velocity error between two spacecraft due to coordinate conversion errors with respect to the body-fixed coordinate system of the follower, which is the difference curve between Figures 12 and 13. Figure 16 shows the relative motion trajectory error of two spacecraft due to coordinate conversion errors. Figures 17 and 20 is the three-axis relative position error between two spacecraft due to coordinate conversion errors with respect to the body-fixed coordinate system of the follower when Δr = 10 m and Δr = 1 m, respectively. Figures 18 and 21 is the three-axis relative velocity error between two spacecraft due to coordinate conversion errors with respect to the body-fixed coordinate system of the follower when Δr = 10 m and Δr = 1 m, respectively. Figures 19 and 22 show the relative motion trajectory error of two spacecraft due to coordinate conversion errors when Δr = 10 m and Δr = 1 m, respectively.

From Figure 14, we can conclude that when the orbit determination error is 100 m, the relative position description error caused by coordinate conversion errors is about 0.03 m, which indicates that, even if the relative data obtained by spacecraft using relative measurement sensors are absolutely accurate, the error caused by coordinate rotation can reach 0.03 m. This error even exceeds the measurement error of the sensor (25 μm). According to Figures 12, 13, and 15, the relative velocity description error caused by coordinate conversion error is about 0.015 mm/s. From Figures 14, 17, and 20, we found that the higher the orbit determination accuracy, the smaller the error caused by coordinate conversion, but it is still greater than the measurement error of the relative measurement sensor. From Figures 7–16, it can be seen that within 1000 s, the relative motion error between spacecraft caused by coordinate conversion increases as a whole over time. Considering the high efficiency characteristics of precision collaborative tasks such as precision spacecraft formation flying, the one-time working time of the spacecraft will not be too long. Therefore, the simulation duration of 1000 s is within a reasonable range, resulting in a relative motion description error of about centimeters, which basically exceeds the indicator requirements for precision collaborative tasks such as precision spacecraft formation flying.

6. Conclusions

This article mainly completes two innovative contents. First, through the study of attitude-orbit coupling dynamic mechanism and mathematical representation, we conclude that one of the main root causes of attitude-orbit coupling effects of spacecraft proximity relative motion is the selection of the reference coordinate system. Second, through extending the representation of dual spinors to flexible body, the attitude-orbit coupling dynamic model between a rigid-flexible coupling spacecraft and a rigid spacecraft is developed. Based on the above analysis and modeling work, the engineering application advantages of the attitude-orbit coupling relative dynamics is provided. Simulation results show that in GNC systems for precision collaborative missions, the use of attitude-orbit coupling relative dynamic model can reduce the errors and computational complexity caused by coordinate conversion. Our next work is aimed at investigating control methods based on attitude-orbit coupling dynamics, like model predictive control method [34] linear matrix inequality approach [9], and other control method [35–37].

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was supported by the Fundamental Research Funds for the Central Universities of China (No. 3072022JC0202), the project D030307.