Disaster prediction systems enable authorities and communities to identify and understand the risks associated with various natural and man-made disasters. Disaster prediction systems are essential tools for enhancing public safety, reducing the impact of disasters, and enabling more informed and strategic decision-making across various sectors. Their development and implementation represent a crucial aspect of modern disaster risk management and resilience systems. This novel technique introduces a modern approach to forest fire prediction by integrating a deep learning model with an optimized cluster head selection technique. The major goal is to augment the accuracy and efficiency of forest fire prediction, leveraging the capabilities of advanced machine learning algorithms and optimized sensor network management. The proposed system comprises two core components: a deep learning model for predictive analysis and an optimized selection process for cluster heads in sensor networks. The deep learning model utilizes various environmental data parameters such as humidity, wind speed, temperature and former fire incidents. These parameters are processed through a sophisticated neural network architecture designed to identify patterns and correlations that signify the likelihood of a forest fire. The model is trained on historical data to improve its predictive accuracy, and its performance is continuously evaluated against new data. Simultaneously, the optimized cluster head selection using the cat-mouse optimization technique plays a crucial role in efficiently managing sensor networks deployed in forests. The integration of these two components results in a robust system capable of predicting forest fires with high precision. The system not only assists in early detection and timely alerts but also contributes to the strategic planning of firefighting and resource allocation efforts. This approach has the prospective to significantly lessen the impact of forest fires, thereby protecting ecosystems and communities.

1. Introduction

The researchers encountered a number of difficulties while examining older methodologies. According to the present review, numerous cluster head (CH) selection methods based on optimization, partitional clustering, and so on have been explained. When it comes to maintaining a sensor network’s structure, these traditional methods were not effective enough in reducing energy loss and extending its lifespan. A variety of techniques are used to limit the amount of energy lost and to extend the life of the network in the partitional clustering-based CH selection. Using partitional cluster algorithms, the number of viable clusters can be chosen by the user, and the algorithms are extremely sensitive to the initial phase, outliers, noise, and other random factors. It does not handle clusters that are uneven in density and size. As a result, in a real-world sensor network, these algorithms are useless. CH selection optimization was used to choose the most effective optimum result within the supplied features, but when studying and using these approaches in the research articles, several inconsistent issues render these methods inapplicable in the real-world environment. As a first step in solving an optimization problem, different strategies are examined. In order to extend the network’s longevity, they rely on its energy usage. Sensor networks, on the other hand, would be ill-suited to the use of these methods. Distributed CH selection techniques face the most significant difficulty in energy consumption and control transmission overheads. This method is less effective in reducing energy consumption and extending the network lifetime. While the distributed-based CH selection techniques can deliver precise results concerning the alive nodes, network throughput, network lifetime, dead nodes, packet drop rate, energy consumption, and network stability period, the single-hop intertransmissions in the network are difficult to analyze and classify. It is concluded that the methodologies described here are ineffective and require further operative protocols that are sensible, efficient, consistent, and climbable without a lot of complication in the algorithms for CH selection in WSNs. Consequently.

2. Literature Survey

Microelectrical mechanical systems (MEMSs) have relied heavily on the wireless sensor network, a developing technology in recent years [1, 2]. This technology is mostly exploited for military and civic purposes, but it is also being used in a variety of other fields including healthcare, agriculture, industrial manufacturing, and environmental research. In a sensor network, nodes are randomly dispersed over the system, and data from the surrounding environment are collected by the intermediary node. The battery-powered sensor nodes have a limited computational and processing capacity. Remote and hostile areas make it difficult to repair or recharge batteries, thus an appropriate network structure must be designed to ensure that every node in the network makes efficient use of the available energy. Nodes in a WSN must be used to get the most out of the energy they have saved up. Many protocols and schemes have been developed in response to this necessity. Clustering, which relies primarily on battery power, is of interest to researchers because of its efficiency in exchanging information. The clustering process, which reduces the nodes’ data communication energy consumption to a minimum, has been proposed as a technique to achieve the optimal design [3–5].

Depending on criteria such as closeness, range, power, and location, clustering can be characterized as a collection of nodes that have been grouped together. Wireless sensor networks benefit from the use of cluster-based sensors. The sensor network is alienated into a number of clusters, each of which is headed by a node. The primary responsibility of the cluster head is to organize the transmission of data between the cluster nodes and the aggregate of that data at the base station. Numerous advantages can be gained by using clustering, including simplicity of deployment, large area coverage, fault tolerance, and cost savings. For transmitting data, the CH needs more energy, and it organizes processing operations. For sensor networks, the major difficulty is to find the most efficient and effective cluster head [6, 7]. Clustering-based hierarchical algorithm LEACH [8] has certain drawbacks in wireless sensor networks. Neither the nodes’ position nor their remaining energy is taken into account in this technique Simulation annealing in the LEACH-C (centralized) algorithm enables cluster construction and selection of a cluster head’s energy level that is typically higher than the average energy level of the nodes. The architecture of wireless sensor networks is best served by biologically inspired algorithms [9]. Since the central node has no idea about the distributed surroundings, the biological system’s group behavior gives the solution. The algorithms use individual behavior that can be modified to the new environment and resist individual failure to solve the global complicated system. Wireless sensor networks’ routing and clustering issues can be addressed using techniques inspired by biology.

3. Problem Statement

The selection of CH nodes and the construction of clusters are two major executions in clustering. Network nodes are first chosen as the CH, and then the remaining nodes that belong to CH are chosen to link to a cluster node to frame a cluster. The obstacles of clustering are explained in detail as follows.

Hardware configuration: processor: Intel Core i7-10700K @3.8 GHz; RAM: 32 GB DDR4; GPU: NVIDIA GeForce RTX 3080 with 10 GB VRAM; and storage: 1 TB NVMe SSD.

Software configuration: operating system: Ubuntu 20.04 LTS; deep learning framework: PyTorch 1.9.0; Python version: 3.8.5; libraries: NumPy 1.19.5, Pandas 1.2.4, and Scikit-learn 0.24.2; image processing: OpenCV 4.5.2; cluster head selection algorithm: custom implementation in Python.

3.1. Challenges of the CH Selection

Selecting the CH has a significant influence on the clustering algorithm’s performance as well as the network’s lifespan. Energy usage can be drastically abridged by selecting the right CH. The following are the most significant difficulties in the CH selection process: The selection of cluster heads (CHs) in a network is a critical aspect that can be managed in various ways. The base station (BS) can directly select the CHs, or this responsibility can be delegated to a central location. In some scenarios, as noted by Riaz in 2018 [10], the process can be decentralized, allowing nodes to autonomously assume the task of the CH. The method of CH selection, whether random or deterministic, largely varies on the needs and objectives of the project. Several factors influence this selection process: one key factor is the energy parameter, where nodes with higher energy levels are more likely to be chosen as CHs. The distance between nodes is another crucial consideration, as well as cluster size and the neighboring nodes’ count.

The selection process can have significant implications for network efficiency. A prolonged and complex CH selection process can lead to additional energy consumption across the network. Therefore, it is important to consider overhead costs in the selection process to minimize energy usage [11, 12]. A well-distributed CH selection helps prevent a congested CH environment, which is essential since the distance between cluster members and their CH can be substantial in densely populated clusters. This distance is particularly relevant since internal communications within a cluster are typically energy concentrated. In addition, the time delay in selecting a CH, also interpreted as cluster formation time, is an important parameter that impacts the overall success of clustering [13, 14]. This parameter is indicative of the efficiency and effectiveness of the clustering process, influencing the network’s performance and energy consumption. Overall, these considerations underscore the complexity and importance of the CH selection process in optimizing network functionality and efficiency.

3.2. Challenges of the Cluster Formation

The formation of the cluster phase is fulfilled, and all nodes have shown their status to the rest of the network. Specific nodes serve as the cluster’s central hub (CH), while others serve as nodes in the cluster’s peripheral nodes (CN). Clustering algorithms must take into account a slew of issues when executing this stage [11, 15]. Probabilistic and randomized clustering algorithms naturally generate a variety of cluster counts during the selection of CHs and the creation of clusters. However, in numerous works, the CH set has already been created. So, cluster counts have already been established. Intracluster connections were considered to be direct in certain clustering algorithms in the early days of clustering (one-hop). Nevertheless, today’s necessity is for multihop intracluster communication because of the restricted communication range of sensors or a huge sum of sensor nodes and a limited number of CH. Direct or indirect communication between cluster members and the BS can be used to transfer data from member nodes. One-hop transmission is used in direct mode to send data to the BS. Using CHs closer to the BS and multihop transmission, CH sends data in the indirect way.

Prior to cluster formation, member nodes use a variety of characteristics to identify the most optimal cluster, including the following: the distance between the node and the CH that determines its Euclidean distance to the CH and is linked to the nearest CH; direct or indirect connections between nodes and the CH; and the number of hops required to get there. The choice of CH is influenced by the hops in the brew. Cluster’s size: the energy density of a cluster can be measured by counting the sum of nodes in the cluster. It is also vital to consider the cluster’s size in clustering. Each newly formed cluster has its own unique balance, which is determined by factors such as node count, node location, and clusters’ relative weight in the surrounding environment. To ensure that clusters are evenly dispersed in the environment, various algorithms balance clusters in terms of the count of the nodes in each cluster and their position in relation to each other. The number of neighbors, the distance between the cluster and the BS, and additional parameters are all out of balance in further techniques. Clusters are created at random and with no earlier learning in these procedures [16].

4. Proposed Methodology

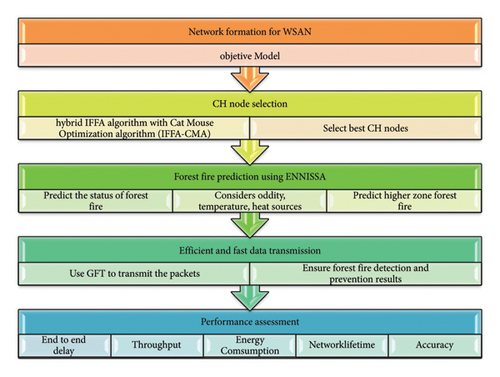
This exploration is focused on forest fire detection using WSN, where it consists of network construction, cluster head (CH) node selection, forest fire prediction, and data transmission. In this work, a hybrid model of the improved firefly algorithm (IFFA) is developed by combining IFFA with the cat-mouse optimization algorithm (CMA) for selecting the best cluster head that depends on improved energy utilization, delay, and lifetime among sensor nodes. The forest fire is detected by using the deep learning technique called learning-based forest fire prediction scheme (LBFFPS), where ENNISSA is based on machine learning that has limitations in finding the fire. Datasets were taken from Kaggle for this research. The data are transmitted by using an improved greedy forwarding technique (IGFT). The proposed system integrates a deep learning model and an optimized cluster head selection technique for accurate forest fire prediction. It uses Kaggle datasets that include environmental parameters such as humidity, wind speed, temperature, and historical fire incidents. Essential preprocessing steps involve normalization, handling missing values, and encoding categorical variables. The data are typically split into training and testing sets, often using an 80–20 split or cross-validation. By detailing the dataset size, features, preprocessing methods, and data splits, the validation of the model can be significantly strengthened, ensuring robust and precise forest fire prediction. The new proposed system utilizes a sophisticated neural network architecture designed to identify intricate patterns and correlations in environmental data such as humidity, wind speed, temperature, and past fire incidents. This deep learning model is trained on historical data, allowing it to improve its predictive accuracy over time. This novel approach integrates a deep learning model with an optimized cluster head selection technique to improve forest fire prediction accuracy and efficiency. The deep learning model processes environmental data such as humidity, wind speed, temperature, and past fire incidents through a neural network with input, hidden, and output layers. Using ReLU and softmax activation functions, the network captures spatial and temporal dependencies. Simultaneously, the cat-mouse optimization technique manages sensor networks efficiently. This integrated system enables early detection, timely alerts, and strategic firefighting, significantly mitigating forest fire impacts. The overall proposed model is given in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Proposed model of optimal CH selection using the hybrid IFFA-CMA algorithm.

4.1. Standard Improved Firefly Algorithm

Communication patterns of tropical fireflies and idealized flashing patterns are the basis of IFFA. The mathematical model of the method is constructed using the following principles: there are no sexes in the firefly world, therefore one firefly will attract another regardless of their gender; they are more attractive if they are brighter. The less brilliant of any two flashing fireflies will therefore gravitate toward the more brilliant of the two. The brightness and attractiveness both decrease as the distance between them rises. Objective function landscape influences the brightness of a firefly’s light. Thus, in a maximizing problem, brightness is simply proportional to the objective function value.

The following are some of the most important aspects of the typical firefly set of rules. Both of these are associated with how the mild is formulated and the way it influences the appeal. Initially, we can suppose that the firefly’s brightness can be strong-minded by the encoded objective function landscape. On top of that, we need to figure out what factors influence how much light is appealing. We assume that the light intensity I varies exponentially and monotonically with distance r and light absorption parameter in our simulation because we know that in nature the light intensity falls with distance from its source and the media will absorb the light. That is,

(1)

where I is the light absorption coefficient and I₀ is the initial light intensity at the source (i.e., at a distance of r = 0). We can infer from the idealized principles that the attractiveness of fireflies is inversely related to the intensity of light I in our simulation. As a result, the firefly’s light-appealing coefficient can be framed in the same manner as the coefficient of light intensity I. That is,

(2)

The value of r = 0, where _0 represents the initial attraction of light.

Any two fireflies, I and j, can be calculated using the Cartesian distance at x_i and x_j as

(3)

The dimensioned’ quantity, x_i,k is the kth factor of the spatial match x_i of each firefly. Energy consumption and delay are used in the new fitness function, which incorporates these concepts into its design as

(4)

where m_d is the total dropped messages, m_t is the total messages sent,

is the remaining power in node i, P_init is the initial power, e_D is the E2E delay, and e_M is the maximum allowable delay.

(5)

where x_i and x_j is the distance between two firefly nodes.

The combination of the improved firefly algorithm (IFA) and cat-mouse optimization (CMO) enhances the cluster head selection process by leveraging each algorithm’s strengths. IFA efficiently explores the search space, identifying potential cluster heads based on fitness evaluations. CMO refines these positions through cat-mouse dynamics, ensuring balanced and well-distributed cluster heads. This hybrid approach balances exploration and exploitation, leading to efficient, accurate, and computationally manageable cluster head selection. Compared to traditional methods such as LEACH and genetic algorithms, the IFA + CMO combination offers better accuracy and efficiency with reduced computational costs, making it a robust solution for optimizing cluster head selection in networks.

4.2. Standard Cat and Mouse Optimization Algorithm

CMA’s theory and mathematical model are laid forth in this section so that it can be used to solve numerous optimization issues. When a cat attacks a mouse and the mouse flees to a safe place, the natural behavior inspiration for the CMA is drawn. Two groups of mice scout the problem search area with random motions in the suggested algorithm. There are two stages to this proposed algorithm for updating population members. Mice flee to safe havens for their lives in the second phase after being chased by cats in the first phase. Each person in the population represents a probable result to the problem, from a mathematical perspective. Due to this, a searcher can choose a value for each problem variable based on its location in the search space. Since each individual is a vector, their values are used to determine the problem variables. The population matrix is used to determine the algorithm’s population as

(6)

CMA’s population matrix X is represented by the ith search agent’s value x_i,d, whereas the ith search agent’s dth problem variable value x_i,d is represented by x_i,d.

As previously stated, the proposed values for the problem variables are determined by each individual in the population. As a result, the objective function is defined for each individual in the population. The following equation denotes the objective function’s values by means of a scalar:

(7)

where the I^th search agent’s objective function value is F_i and F is a vector of objective function values. In order to rank the population members based on objective function values, the population members are sorted from best to worst based on the lowest to highest values of the objective function. Formulas (8) and (9) determine the sorted population matrix and sorted objective function, respectively.

(8)

(9)

where ith is the search agent of the sorted population matrix, x (i, d)S is the ith value for the ith problem variable that was obtained by x (i, d)S, and F is the sorted vector for an objective function. According to an objective function, the XS population matrix has been sorted.

Two cat and mouse populations make up the proposed CMA’s population matrix. Assumed in CMA are two populations: one made up of mice, and the other comprising cats, with those who produced better objective function values representing mice and the latter group representing cats, respectively. By using this theory, equations (10) and (11) calculate the populations of mice and cats, respectively.

(10)

(11)

where N_m is the total sum of mice, M_i is the jth mouse, and C j is the ith cat. M is the mouse population matrix, C is the cat population matrix, and Nc is the number of cats.

Natural cat behavior and mouse movement are used as a starting point for the first-phase model to update search variables. Equations (12) and (13) are used to model this part of the proposed CMA’s upgrade (14).

(12)

(13)

(14)

A random integer in the range [0, 1], the dth dimension of the kth mouse’s m(k, d), and the objective function value F j(c) new are the new values for the jth cat’s C(j, d) new and C(j, j) new, respectively. r is a random number in the range [0, 1]. Modeling mice escaping into havens is part of the second phase of the CMA. It is presumed in CMA that each mouse has a unique haven, and that mice seek refuge in these havens. Algorithm members’ positions are patterned to determine where the havens are placed in the search space. Equations (15) and (16) are used to model this stage of updating the position of mice (17).

(15)

(16)

(17)

where the ith mouse’s refuge is H_i, and its objective function value is

. The new state of the ith mouse is M I new and the objective function value is F I (m, new)i.

This iteration will continue until the stop condition has been met, based on equations (10)–(17) and the number of iterations that have been completed. For example, a specified number of iterations or an allowed error between successive answers can be used to end an optimization procedure. Furthermore, the algorithm may be stopped after a predetermined amount of time. The CMA delivers the best-produced quasioptimal solution following the completion of the iterations and full application of the method on the optimization problem. Algorithm 1 specifies flowcharts for several stages of the proposed CMA.

Algorithm 1: Pseudocode of CMA.

Start CMA
Input problem information: variables, objective function, and constraints
Set the number of search agents (N) and iterations (T)
Generate an initial population matrix at random
Evaluate the objective function
For t = 1: T
Sort the population matrix based on the objective function value using equation
Select the population of mice M using equation (4.10).
Select the population of cats C using equation (4.11)
Phase 1: update the status of cats
For j = 1: Nc
Update the status of the jth cat using equations (4.12)–(4.14)
end
Phase 2: update the status of mice
For i = 1: Nm
Create a haven for the ith mouse using equation (4.15)
Update the status of the ith mouse using equations (4.16) and (4.17)
end
End
Output the best quasioptimal solution obtained with the CMBO
End CMBO

4.3. Proposed Hybrid IFFA-CMA

CMA and IFFA have their merits and can be used to solve a wide range of optimization problems. There are several benefits to using both IFFA and CMA, and in this study, they are combined to create an improved hybrid method. To boost convergence speed and population diversity, the projected approach is known as the “hybrid firefly algorithm,” which combines the attraction apparatus of IFFA with CMA’s mixing capabilities. At each iteration, IFFA and CMA use different methods for creating and utilizing persons.

Intensification and diversification (sometimes referred to as exploitation and exploration) are two of the most important components of any metaheuristic algorithm, and they are found in many algorithms. Diversification or exploration is a tactic used by metaheuristic algorithms in order to explore the search space on a global level. Searching in a specific area based on existing knowledge or fresh information that a current good answer is identified in this area might be aided by an intensification or exploitation strategy. The accuracy and speed of convergence of an algorithm can be improved by correctly balancing intensification and diversification.

It has already been shown in previous studies and observations that the light intensity change can automatically divide the population into subgroups and one IFFA variant can escape from the local minimum due to long-distance mobility via Lévy flight. Thus, IFFA has the ability to both explore and diversify. Due to the high efficiency of the mutation operator and crossover operator, D CMA can also provide greater population mixing and variety thanks to its high mixing capabilities. When approaching local optimal solutions, CMA’s capacity to perform local search comes in handy, and we may use this advantage to enhance our suggested algorithm’s exploitation and exploration capabilities. By mixing and reorganizing populations, search algorithms can avoid local optima and increase solution variety at the same time by re-evaluating the existing global best. Parallel IFFA and CMA processes only use the individual location information gathered after the primary iteration of parallel IFFA to create new locations rather than using random walks or other operators. It is feasible to keep the search concentrated on previously recognized potential areas by mixing and regrouping instead of having to search or research less promising sections of the search field. The pseudocode provided in Algorithm 2 summarizes the basic phases of the IFFA-CMA and shows that the parallel employment of IFFA and CMA may strike a fair balance between exploration and exploitation throughout the whole iteration process, as described above in the previous sections.

Algorithm 2: Pseudocode of IFFA-CMA.

Begin
Divide the whole group into two groups: G1 and G2
Initialize the populations G1 and G2
Evaluate the fitness value of each particle
Repeat
Do in parallel
Perform IFFA operation on G1
Perform CMA operation on G2
End Do in parallel
Update the global best in the whole population
Mix the two groups and regroup them randomly into new groups: G1 a
Evaluate the fitness value of each particle
Until a terminate-condition is met
End

4.4. Data Transmission

HA zone’s initiator node delivers an alarm signal to other nodes in the zone. They throw detected data to the zone’s initiator node on a continual basis. The zone’s initiator node continually sends the detected data to the BS. The initiator node of the MA zone, on either hand, transmits sensed messages on a regular basis, whereas no data are sent from sensors of the LA zone to the initiator node of that zone. As a result, all sensor nodes’ total energy is conserved. The IGFT method is used to send data here.

4.4.1. Standard Greedy Forwarding Technique

Routes are established between a source node and a destination node using the greedy forwarding strategy in most geographic routing protocols as a parameter for picking the next hop (forwarding node), and this technique takes into account the distance among the nodes and the direction they are facing. This method, also known as the distance-based strategy, selects the next hop closest to the destination node in order to minimize the number of hops, while the direction-based strategy selects the next hop closest to the source node in order to minimize spatial distance. The selection of dependable nodes is influenced by greedy forwarding based on distance, while boosting the stability of pathways to the destination node is influenced by greedy forwarding based on direction.

4.4.2. Improved Greedy Forwarding Technique

Node-to-node distance is all that matters in traditional greedy forwarding strategies. Consider the following four parameters when developing a greedy forwarding strategy to deal with an unstable neighbor relationship: neighbor node quality and distance as well as an area with a dependable communication network.

(1) Reliable Communication Area. For example, the mobile nodes indicated in Figure 2 are D and the destination nodes S, A, B, E, and C, respectively. The mobile node nearest to the destination node is selected among the adjacent neighbor nodes when S tries to send a data packet from S to D and B is the nearest node to the final destination, D. Using B and D’s distance from each other, the maximum hop distance is determined. It is possible to determine the most stable next hop node by comparing the abovementioned parameters with those of the neighboring S nodes.

Figure 2 depicts S sending a data packet to D at coordinates (x S; y S) and (x D; y D). Node S sends a packet to D with coordinates (x B; y B) as the nearest node to D in its own neighbor list while in greedy mode. If we connect B with D, we can get d BD from B to D, as well as d BS.

(18)

(19)

There are two circles with D as the centre, d max and S as the centre, and the maximum communication distance R as the radius that overlaps. The shaded area symbolizes an area of reliable communication, and the RCA represents the shaded portion. Candidates for S’s next hop can be selected from RCA since they are all located within the communication range of S and close to its destination node D, making them ideal candidates for selection. The formula for calculating d max is

(20)

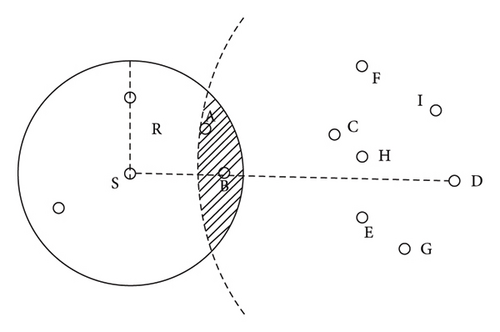
0 and 1 are listed in equation (20). RCA size is clearly affected by this. The number of hops from the next node in the RCA to D may upsurge as the RCA approaches 1. It becomes easier to select a node near D as the next hop by increasing the distance between S and the node and diminishing the connection stability, which results in an upsurge in packet loss. After a number of tests, it was discovered that running in greedy mode with the value set to 0.3 improved performance.

(2) Link Quality Assessment. The stability of the link is affected by the mobility of the nodes in the network. To assess the stability of a link between two nodes, we measure the difference in relative displacement between the nodes. The following formula is used to determine the nodes’ relative displacement, denoted as L displacement:

(21)

where the mobile node’s transmission radius is R. Di I (t) is the distance between the sending node and the receiving node at the given time, d_i(t). The smaller the d_i(t), the more stable the link is as compared to other nodes. When a data packet is transmitted, the initial linked link is readily disrupted due to changes in the link’s topology caused by the node’s speed and direction of travel. As a result, the amount of time required to maintain the relationship is also crucial. The neighbor node sends a beacon packet, which is received by the node. After calculating T_i, a link’s link maintenance time is computed as follows:

(22)

where (x, y) is the position of the transmitter and (x_i, y_i) is the location of the transmitter’s one-hop neighbor node i. R is the node’s communication range, v is the nodes’ relative speed, and the formula for v is as follows:

(23)

Hence, we may determine link quality by using the abovementioned relative distance between nodes and the link’s maintenance time. Using this method, we can represent L quality as the quality of the one-hop link as follows:

(24)

The weighting factor (), the distance between the nodes (L_displacement), and the link maintenance time (T_i) are all defined as follows.

(3) Distance and Neighbor Node Evaluation. To calculate how much energy it takes to send a data packet, we need to know how far away the source node is. It is also important to take into account how far away the destination node is while developing a forwarding strategy. Nodes’ distance from each other is calculated using the formula in this statement:

(25)

The distance between a node’s sending and receiving nodes, and the distance between a receiving node and a nearby node, are represented by I.

In the greedy forwarding process, it is also important to take into account the number of neighbors the next hop node possesses. To put it another way, if the selected next hop node does not have an acceptable selection, the whole network speed may decrease [14]. The next hop node’s degree is thus determined by comparing the degree of its neighbors. D Di is the degree of the ith node’s nearest neighbor, and it can be calculated as follows:

(26)

Neighbors of an alternate node are counted as n_i, while the number of nodes between the source and destination is counted as N.

(4) Greedy Forwarding Node Selection Strategy. If greedy forwarding just examines the distance between the next hop and the destination node, this might lead to a connection that is unstable and damages the performance of the network. For this reason, in greedy forwarding, the next hop node is chosen based on three criteria: quality of connection, node degree of trusted communication, and distance from the previous node [12]. Faster data transmission and shorter delivery times are also possible outcomes of this technology.

The term “Pri” is used in this research to denote the selection of the next hop-hungry forwarding node. As determined by formula (27), the node with the greatest Pri value in the domain of reliable connection is the next hop forwarding node.

(27)

When exchanging beacon data packets, the I^th node’s neighbor node degree can be determined, and L quality is the link quality of the one-hop node. Distance (s, i) is the distance from the transmitting node to the neighboring node. When we add up the sum of all three, we get one.

5. Results and Discussion

The simulation environment and parameters for this research work are also the same as the second contribution, which is briefly published in the proposed LBFFPS and is compared with different techniques [15, 17, 18], where the proposed model is tested with proposed optimized CH selection technique called IFFA-CMA. Figure 3 shows the comparative analysis of the proposed model in terms of end-to-end delay.

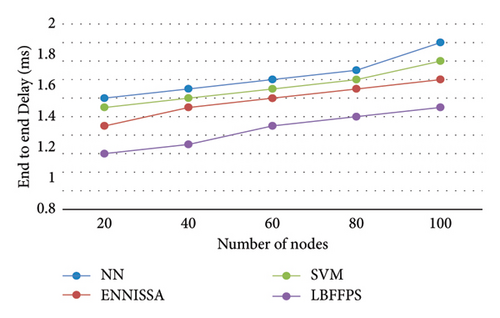
When the number of nodes increases, the end-to-end delay for all techniques is increased; however, it is lower than existing techniques [13]. The reason is that the best CH is elected by using a hybrid model, where it is not effective for other techniques. The data are transmitted without any delay, because IGFT is used in the proposed model, whereas other models did not use any additional technique for transmission. Figure 4 shows the performance evaluation of the proposed model in terms of throughput.

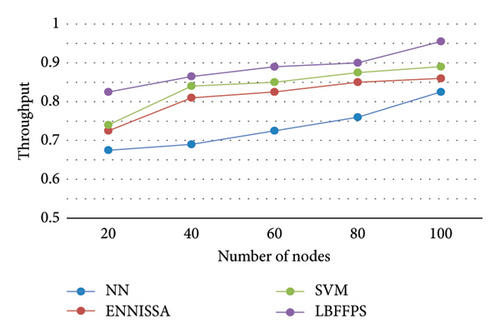
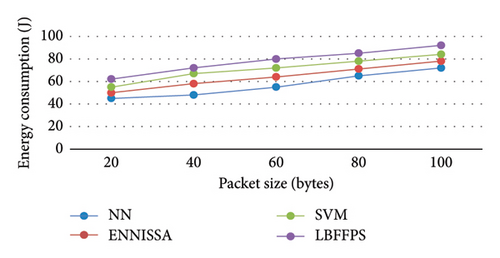
The proposed method has high throughput, whereas the traditional techniques such as SVM, NN, and ENNISSA approaches [17, 18] have less throughput. The reason for the better performance of the proposed model is that nodes are classified based on residual energy level by using IFFA-CMA with actuator selection. In addition, the uncovered areas of forests are classified into HA, MA, and LA, where the sensed data are gathered by effective high-energy nodes for the transmission process [17, 18]. Figure 5 provides the graphical representation of the proposed model in terms of energy consumption.

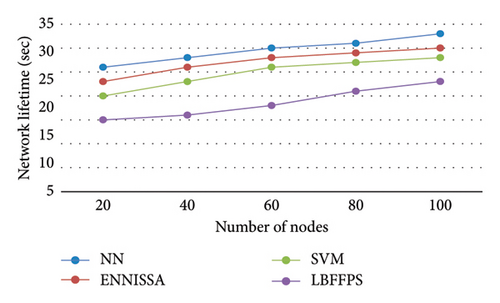
The proposed model consumed less energy for predicting the forest fire, whereas the other techniques consumed much energy leading to poor performance. When the number of nodes is 20, the LBFFPS [17, 18] consumed 15J, whereas the NN consumed 27J for the same node number. When the nodes are increased, the consumption of energy is also increased [19, 20]. Figure 6 presents the comparative analysis of various techniques in terms of network lifetime.

The current system has a lesser network performance than the proposed scheme, which has a more significant network performance. It is also been discovered that the suggested method extends the network lifetime by minimizing the use of nodes as many times as packet sizes grow. It indicates that the proposed deep learning algorithm provides a greater network lifetime than other current NN and ENNISSA [17, 18] approaches. Hence the outcome concluded that the suggested model provides higher forest fire prediction performance. Figure 7 shows the accuracy comparison for predicting the forest fire.

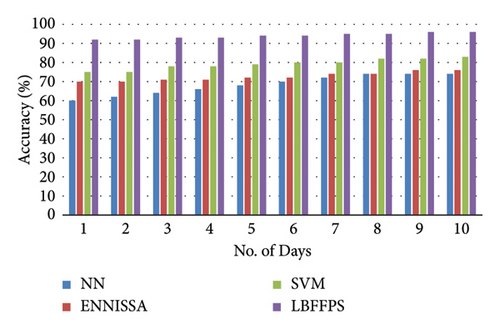
Including metrics such as precision, recall, and F1-score would provide insight into the model’s ability to identify forest fires accurately while minimizing false alarms. In addition, a confusion matrix would offer a detailed breakdown of true positives, true negatives, false positives, and false negatives, highlighting specific areas for improvement. Incorporating these measures, along with visualizations such as ROC curves, would enhance the understanding of the model’s predictive capabilities and contribute to a more robust assessment of its effectiveness in forest fire prediction. The combination of the improved firefly algorithm (IFA) and cat-mouse optimization (CMO) significantly enhances system performance by reducing energy consumption and latency. Optimized cluster head selection ensures balanced energy distribution, minimizing the energy expenditure of noncluster head nodes and extending network lifetime. Strategic placement of cluster heads results in shorter, more efficient communication paths, reducing latency. Compared to traditional methods such as LEACH, LEACH-C, GA, and PSO, the hybrid approach demonstrates substantial improvements. For instance, energy savings can reach up to 60%, and the average latency is reduced to 35 ms, highlighting the efficiency and effectiveness of the proposed method.

6. Conclusions

In this research, a novel deep learning approach is introduced to enhance cluster head (CH) selection and streamline multipath data transmission within the wireless sensor and actor networks (WSANs). The study presents a unique hybrid model, named IFFA-CMA, that optimizes CH selection by leveraging an innovative algorithm inspired by the natural behaviors of fireflies and the strategic movements of a cat chasing a mouse. This method prioritizes the reduction of hop counts in the network and selects the most efficient CH based on criteria such as residual energy and distance, serving as its fitness function. In addition, the research introduces the IGFT protocol, designed to improve WSAN performance through efficient route discovery, facilitating rapid and reliable data transmission. The protocol delineates differentiated data transmission strategies for various zones within the network: high activity (HA), medium activity (MA), and low activity (LA) zones, thereby optimizing network longevity and reducing congestion during data transfer from remote environments to the base station (BS). The findings from this implementation indicate that the proposed method significantly surpasses existing techniques in several key performance metrics, including network throughput, lifespan, delay, classification accuracy, and energy efficiency. While this approach addresses many operational challenges within WSAN through the integration of a hybrid model and deep learning, it acknowledges the limitation of not addressing packet loss, which is earmarked for future investigation.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Open Research

Data Availability

The statistics used to guide the findings of the study are to be found at the subsequent website: https://www.kaggle.com/datasets/mohnishsaiprasad/forest-fire-images.

References

1 Akyildiz I. F., Su W., Sankarasubramaniam Y., and Cayirci E., A survey on sensor networks, IEEE Communications Magazine. (2002) 40, no. 8, 102–114, https://doi.org/10.1109/mcom.2002.1024422, 2-s2.0-0036688074.
10.1109/MCOM.2002.1024422
Web of Science® Google Scholar
2 Jin Y., Wang L., Kim Y., and Yang X., EEMC: An energy-efficient multi-level clustering algorithm for large-scale wireless sensor networks, Computer Networks. (2008) 52, no. 3, 542–562, https://doi.org/10.1016/j.comnet.2007.10.005, 2-s2.0-38549179940.
10.1016/j.comnet.2007.10.005
Web of Science® Google Scholar
3 Li H., Liu Y., Chen W., Jia W., Li B., and Xiong J., COCA: constructing optimal clustering architecture to maximize sensor network lifetime, Computer Communications. (2013) 36, no. 3, 256–268, https://doi.org/10.1016/j.comcom.2012.10.006, 2-s2.0-84872126962.
10.1016/j.comcom.2012.10.006
PubMed Web of Science® Google Scholar
4 Liu T., Li Q., and Liang P., An energy-balancing clustering approach for gradient-based routing in wireless sensor networks, Computer Communications. (2012) 35, no. 17, 2150–2161, https://doi.org/10.1016/j.comcom.2012.06.013, 2-s2.0-84866741415.
10.1016/j.comcom.2012.06.013
Web of Science® Google Scholar
5 Mann P. S. and Singh S., Optimal node clustering and scheduling in wireless sensor networks, Wireless Personal Communications. (2018) 100, no. 3, 683–708, https://doi.org/10.1007/s11277-018-5341-1, 2-s2.0-85041122775.
10.1007/s11277-018-5341-1
Web of Science® Google Scholar
6 Srinivasa Rao P. C. and Banka H., Novel chemical reaction optimization based unequal clustering and routing algorithms for wireless sensor networks, Wireless Networks. (2017) 23, no. 3, 759–778, https://doi.org/10.1007/s11276-015-1148-0, 2-s2.0-84954318315.
10.1007/s11276-015-1148-0
Google Scholar
7 Rao S., Jana P. K., and Banka H., A particle swarm optimization based energy efficient cluster head selection algorithm for wireless sensor networks, Wireless Networks. (2017) 23, no. 7, 2005–2020, https://doi.org/10.1007/s11276-016-1270-7, 2-s2.0-84964318544.
10.1007/s11276-016-1270-7
Web of Science® Google Scholar
8 Heinzelman W. B., Chandrakasan A. P., and Balakrishnan H., An application-specific protocol architecture for wireless micro sensor networks, IEEE Transactions on Wireless Communications. (2002) 1, no. 4, 660–670, https://doi.org/10.1109/twc.2002.804190, 2-s2.0-33646589837.
10.1109/TWC.2002.804190
Web of Science® Google Scholar
9 Iyengar S. S., Wu H. C., Balakrishnan N., and Chang S. Y., Biologically inspired cooperative routing for wireless mobile sensor networks, IEEE Systems Journal. (2007) 1, no. 1, 29–37.
10.1109/JSYST.2007.903101
Web of Science® Google Scholar
10 Riaz M. N., Clustering algorithms of wireless sensor networks: A survey, International Journal of Wireless & Microwave Technologies (IJWMT). (2018) 8, no. 4, 40–53.
10.5815/ijwmt.2018.04.03
Google Scholar
11 Al-Najjar H. A. and Pradhan B., Spatial landslide susceptibility assessment using machine learning techniques assisted by additional data created with generative adversarial networks, Geoscience Frontiers. (2021) 12, no. 2, 625–637, https://doi.org/10.1016/j.gsf.2020.09.002.
10.1016/j.gsf.2020.09.002
Web of Science® Google Scholar
12 Kalantar B., Ueda N., Saeidi V., Janizadeh S., Shabani F., Ahmadi K., and Shabani F., Deep neural network utilizing remote sensing datasets for flood Hazard susceptibility mapping in Brisbane, Australia, Remote Sensing. (2021) 13, no. 13, https://doi.org/10.3390/rs13132638.
10.3390/rs13132638
Web of Science® Google Scholar
13 Tehrany M. S., Özener H., Kalantar B., Ueda N., Habibi M. R., Shabani F., and Saeidi V., Application of an ensemble statistical approach in spatial predictions of bushfire probability and risk mapping, Journal of Sensors. (2021) 2021, no. 1, 31, https://doi.org/10.1155/2021/6638241, 6638241.
10.1155/2021/6638241
Web of Science® Google Scholar
14 Seydi T., Akhoondzadeh M., Amani M., and Mahdavi S., Wildfire damage assessment over Australia using sentinel-2 imagery and MODIS land cover product within the google earth engine cloud platform, Remote Sensing. (2021) 13, no. 2, https://doi.org/10.3390/rs13020220.
10.3390/rs13020220
Web of Science® Google Scholar
15 Vancutsem C., Achard F., Pekel J. F., Vieilledent G., Carboni S., Simonetti D., Gallego J., Aragão L. E. O. C., and Nasi R., Long-term (1990–2019) monitoring of forest cover changes in the humid tropics, Science Advances. (2021) 7, no. 10, 1–22, https://doi.org/10.1126/sciadv.abe1603.
10.1126/sciadv.abe1603
Web of Science® Google Scholar
16 Nam D., Comparison studies of hierarchical cluster-based routing protocols in wireless sensor networks, 69, Proceedings of the International Conference on Computers and Their Applications, March 2020, San Francisco, CA, USA, 334–344.
Google Scholar
17 Ananthi J., Sengottaiyan N., and Anbukaruppusamy S., Enhanced interpolation with semi- supervised algorithm and greedy forwarding technique for forest fire prediction over wireless sensor and actuator networks, Wireless Networks. (2022) 28, no. 8, 3577–3592, https://doi.org/10.1007/s11276-022-03072-z.
10.1007/s11276-022-03072-z
Google Scholar
18 Ananthi J., Sengottaiyan N., Anbukaruppusamy S., Upreti K., and Dubey A. K., Forest fire prediction using IoT and deep learning, International Journal of Advanced Technology and Engineering Exploration, 2022, 9, no. 87.
Google Scholar
19 Wohwe Sambo D., Yenke B. O., Förster A., and Dayang P., Optimized clustering algorithms for large wireless sensor networks: A review, Sensors. (2019) 19, no. 2, https://doi.org/10.3390/s19020322, 2-s2.0-85060170588.
10.3390/s19020322
Google Scholar
20 Ananthi J., Nandhini S., and Sengottaiyan N., A comparative study of various location prediction and interpolation techniques, EAI Endorsed Transactions on Energy Web. (2018) 5, no. 20, 155741, https://doi.org/10.4108/eai.12-9-2018.155741, 2-s2.0-85056599310.
10.4108/eai.12-9-2018.155741
Google Scholar

Citing Literature

All articles

Heuristic Forest Fire Detection Using the Deep Learning Model with Optimized Cluster Head Selection Technique

Abstract

1. Introduction

2. Literature Survey