1. Introduction

With the rapid advancement of information technology, the level of intelligence continues to rise. In today’s world, fixed-wing unmanned aerial vehicles (UAVs) have garnered significant attention due to their high stability, long endurance, and remote operation capabilities. They are widely used in various fields such as military, agriculture, and exploration [1–5]. The fixed-wing UAV is equipped with advanced low-energy-consumption multiprocessors [6] and camera devices, enabling efficient collection of extensive geographical data. It performs multimodal tasks, utilized in environmental conservation sectors such as meteorological monitoring, natural disaster alerts, and forest fire surveillance [7]. In the agricultural sector, fixed-wing UAVs can fly along predetermined paths, collecting data on soil, vegetation, humidity, and other aspects. This data can be utilized to enhance crop yield and quality while minimizing resource wastage [8]. In the military field, the formation flight of drones [9] flying can effectively reconnaissance terrain, search, and rescue. As flight missions become increasingly complex, there is a growing demand for higher tracking and control performance in fixed-wing UAVs. Given that UAVs often operate at high altitudes and are frequently affected by wind fields, existing fixed-wing UAVs need to possess higher accuracy and robustness to meet these challenges.

In addressing the tracking control problem of UAVs, researchers have proposed many algorithms, such as PID control [10, 11], fuzzy control [12], sliding mode control [13], and ADRC control [14]. Traditional PID control is widely used due to its simplicity. It adjusts based on the UAV’s tracking error, providing good tracking accuracy. Li et al. [15] designed a controller based on quaternion error, combining fractional-order PID control and s-plane to enhance the wind disturbance resistance and tracking accuracy of quadcopter UAVs. Ullah et al. [16] propose integer and fractional adaptive robust schemes for trajectory tracking problem of quad-rotor with cable-suspended payloads. Houm et al. [17] applied nonlinear sliding surfaces to achieve fast convergence of state variables in the control of quadcopter UAVs. An improved supertwisting controller was utilized to suppress disturbances, ensuring robustness against external disturbances. Modern control methods include model predictive control [18] and deep learning [19]. Koo et al. [20] introduced model predictive control to the landing deck process of fixed-wing UAVs. By predicting the motions of the aircraft carrier deck and UAV, it calculates real-time optimal control input sequences within a certain time range, enhancing the UAV’s landing performance. Fang et al. [21] addressed the uncertainty and external disturbance issues of small unmanned helicopters and proposed a robust trajectory tracking controller. Zhang, Li, and Fei [22] combine radial basis function (RBF) neural networks with virtual parameter estimation algorithms to propose a neural network adaptive control scheme for UAVs.

Sliding mode control is fundamentally a special type of nonlinear control that can, during dynamic processes, slide the system state along a sliding surface by switching control laws, ensuring the invariance of the system against external disturbances. Davila, Fridman, and Levant [23] proposed a supertwisting sliding mode control (STSMC) where discontinuous switching functions are incorporated into the integral operation, ensuring the continuity of the control rate over time. This effectively suppresses sliding mode chattering. Matouk et al. [24] designed a control method for quadcopter UAVs based on the supertwisting algorithm, significantly enhancing the stability of the control system. Sami et al. [25] combined the properties of artificial intelligence with STSMC and applied it to the wind energy conversion system (WECS) of doubly fed induction generators (DFIGs), enhancing the anti-interference ability of STSMC. In sliding mode control, the chattering problem [26] is a primary obstacle for the practical application of variable structure control theory. Slotine and Sastry [27] proposed the quasisliding mode approach, introducing the concept of boundary layer and replacing the sign function with a saturation function to effectively mitigate chattering. Mechali et al. [28] presented a fixed-time nonswitching uniform nonsingular terminal sliding mode control method, which is applied to multirotor aircraft. This method effectively suppresses chattering in sliding mode control while addressing singularity issues. In various fields, fixed-wing UAVs often operate in harsh environments and strong wind conditions due to the influence of flight location terrain and climate. Therefore, the control systems of fixed-wing UAVs need to possess strong anti-interference capabilities and control precision, presenting a challenge for existing fixed-wing UAVs.

In this paper, we present the initial integration of the RBF neural networks with the STSMC algorithm into the control system of a fixed-wing UAV. We propose a control methodology that combines the RBF neural networks with the STSMC, leveraging the high robustness of the STSMC and the rapidity and stability of the RBF neural networks to achieve path tracking for fixed-wing UAVs. The main structure of this paper is outlined as follows: The modeling of fixed-wing UAVs is described in the second section. The third section presents the RBF neural network, STSMC, and controller design. The fourth section conducts simulation validation of the proposed controller.

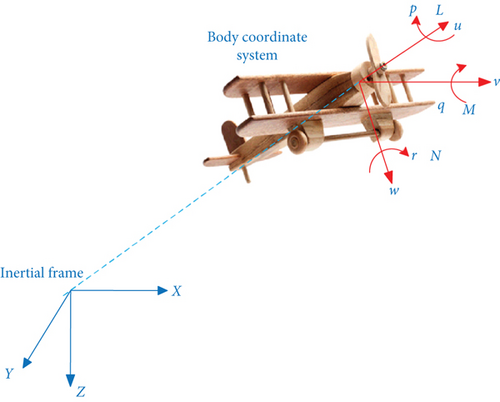
2. Dynamics Model of Fixed-Wing UAV

3. RBF-STSMC Controller

3.3. RBF-STSMC Controller

In the motion process, fixed-wing UAVs are often subject to wind disturbances. In this paper, we employ the combination of the STSMC and RBF controller to enhance the tracking accuracy of the UAV. RBF neural networks are utilized to compensate for unknown disturbances in the x, y, and z directions. Consider the first-order system represented in (10), where u represents the system input, f represents the unknown disturbance, and f_x, f_y, and f_z, respectively, denote disturbances acting on the UAV in the three directions.

$$ ()

For the x direction, the sliding mode function is set as

$$ ()

Combining the STSMC algorithm, the selected control algorithm is as follows:

$$ ()

where u_x represents the continuous control part to ensure that the system stays on the sliding mode surface and u_sta denotes the discontinuous part aimed at robust control against external disturbances and chattering reduction.

Taking the derivative of (12) and substituting (11) into (12) yield

$$ ()

Setting $$, then an equivalent control law can be obtained as

$$ ()

Supertwisting control exhibits strong robustness, enabling it to resist external disturbances and achieve convergence within a finite time. According to the theory described in (9), the control law for the x direction is designed as follows:

$$ ()

RBF neural networks are used to estimate and compensate for the disturbance f_x in (17).

$$ ()

In (17), set the radial basis vector of the RBF network to be h = [h₁, h₂ ⋯ h_m, ]. According to the chosen structure of the neural network, m = 5. And h_j is the Gaussian basis function, j represents the jth node of the hidden layer, and x is the network input.

$$ ()

where j represents the jth node of the hidden layer, f_x represents the unknown disturbance, W^∗ represents the ideal network weights, ε_x represents the approximation error and |ε_x| ≤ ε_N, and ε_N represents the upper bound of the approximation error.

$$ ()

$$ represents the estimated values of the ideal weights W^∗ in the neural network output layer, and $$ represents the weight error. Therefore, the disturbance error $$ in the x direction can be written as

$$ ()

The control law in (16) can be expressed as

$$ ()

Substituting (21) into (14), we obtain

$$ ()

Defining the Lyapunov function as

$$ ()

Then, the derivative of L with respect to time is

$$ ()

The adaptive law is given by

$$ ()

Assumption 1. $$, and K = k₁/2.

Substituting (25) into (24), we have

$$ ()

Because $$, the (26) can be rewritten as

$$ ()

When the network approximation error ε_x becomes sufficiently small, $$. Therefore, the global stability of the system can be ensured. According to LaSalle’s invariance principle, when L is always equal to zero, s is also always equal to zero.

Similarly, the sliding mode function and the control law for the y direction are given by (28) and (29), respectively:

$$ ()

$$ ()

The sliding mode function and the control law for the z direction are given by (30) and (31), respectively:

$$ ()

$$ ()

The structure of the RBF-STSMC controller is shown in Figure 2.

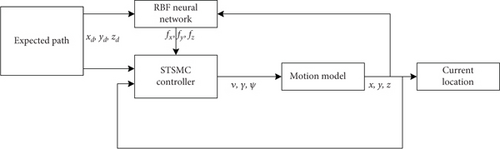
In Figure 1, the position coordinates of points on the expected path and the current position coordinates of the fixed-wing UAV are transmitted to the designed controller and the RBF neural network module. The RBF neural network estimates unknown disturbances and transmits them to the STSMC controller. Based on the error and its rate, the controller calculates the UAV’s speed, pitch angle, and heading angle under the influence of the control rates. These three control inputs are fed into the UAV motion model, obtaining the actual flight path coordinates of the fixed-wing UAV. Part of these coordinates is fed back to the STSMC controller for new control rate calculations, while the other part is transmitted back to the RBF neural network for disturbance estimation. By repeating these processes, the fixed-wing UAV can track the expected path accurately.

4. Simulation and Result Analysis

4.1. Simulation Experiment

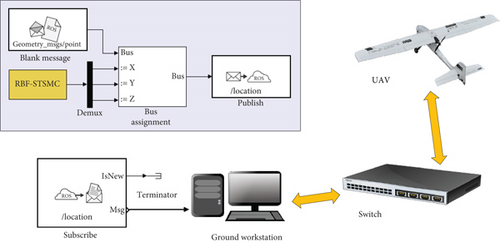
In order to test the control accuracy and anti-interference ability of the RBF-STSMC controller designed in this article, we used the hardware equipment shown in Figure 3 to form a simulation system. This mainly includes ROS simulation systems, ground workstations, switches, and drones. ROS communicates with ground workstations and drones through switches. Its working principle is to use the ROS toolbox to create a node network. Users will configure a module to send “geometry_msgs/Point” messages to the “/location” topic and create a blank ROS message. The RBF-STSMC controller designed in this article will input the tracked position coordinates into the ROS message and then update the ROS message to the ROS network. At this point, the subscription module will subscribe to the messages published in the ROS network, and then, the messages containing the coordinates of the location points will be transmitted to the ground workstation. The ground workstation will send control commands to the drone through the switch to control its flight.

The desired trajectory is set as a spiral, represented by (32). The initial position of the UAV is (0,0,0), and the tracking control time is set to 30 s. The initial parameter settings are shown in Table 1:

$$ ()

Table 1. Parameters in STSMC controller.

Parameter	c1	c2	c3	λ1	λ2	λ3	k1	k2	k3
Value	0.1	10	0.15	10	1.0	0.5	0.5	2.0	0.2

Meanwhile, we used the model equipped with the STSMC controller as a comparison condition. The control parameters for STSMC are set as λ_i = 0.15  and k_i = 0.5. The parameters for the neural network in the RBF-STSMC controller are shown in Table 2.

Table 2. Parameters in RBF neural networks.

Parameter	cij	bj	γi i = 1, 2, 3
Value	$$	10	50

4.2. Result Analysis

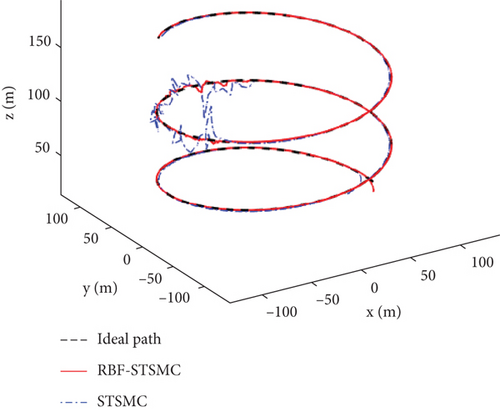
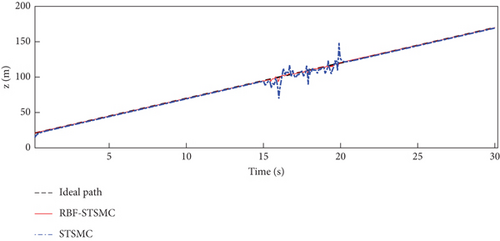
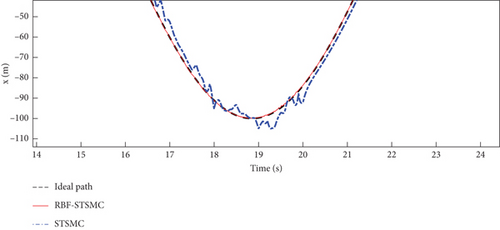
To thoroughly assess the performance of the designed controller in real flight scenarios, white noise was introduced between 15 and 20 s to simulate external disturbances experienced by the fixed-wing UAV. The simulation graph of the fixed-wing UAV flying along the spiral trajectory is shown in Figure 4.

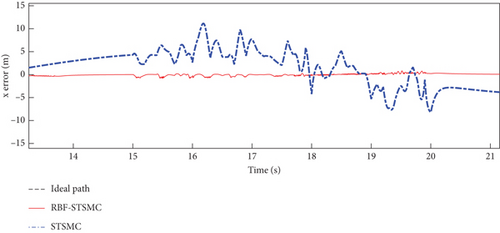
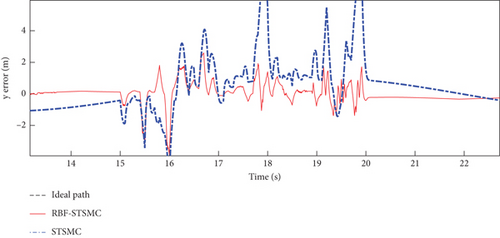
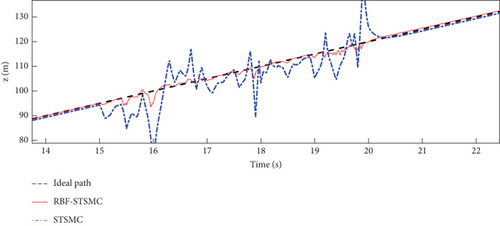
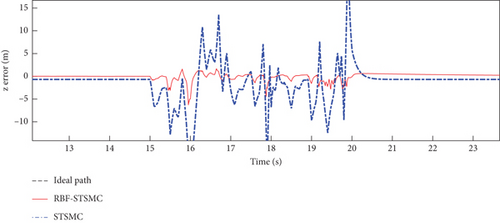
The trajectory tracking performance and errors of the fixed-wing UAV in the x, y, and z directions are shown in Figures 5, 6, and 7.

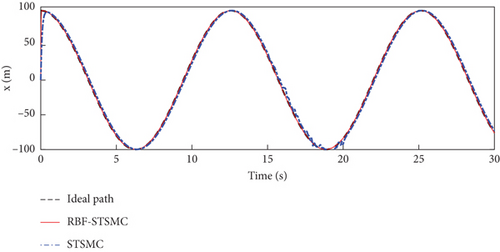
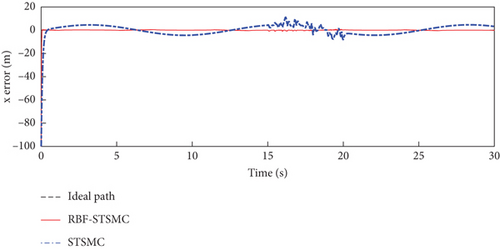
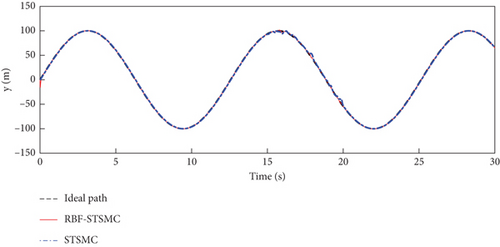
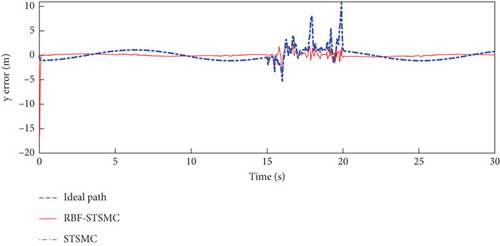
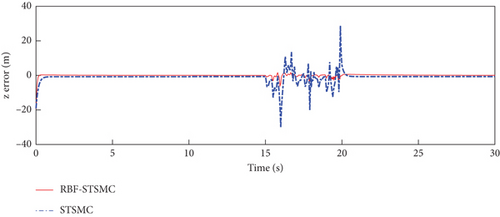
The maximum deviations in the x, y, and z directions are shown in Table 3.

Table 3. Maximum deviation values in three directions.

	x direction	y direction	z direction
STSMC	11.14	10.93	28.78
RBF-STSMC	−0.79	−3.84	−6.29

To study the characteristics of the designed controller, we utilized the error integral criterion to analyze the errors. As shown in Tables 4, 5, and 6, the analysis includes IAE (integrated absolute error), ISE (integrated squared error), and ITAE (integrated time absolute error), expressed as shown in (33).

$$ ()

Table 4. Performance indicator values calculated based on IAE.

IAE	x direction	y direction	z direction
STSMC	19.35	7.26	28.75
RBF-STSMC	5.867	7.612	8.012

Table 5. Performance indicator values calculated based on ISE.

ISE	x direction	y direction	z direction
STSMC	492.12	25	262.9
RBF-STSMC	85.16	12.75	21.8

Table 6. Performance indicator values calculated based on ITAE.

ITAE	x direction	y direction	z direction
STSMC	190.8	129.3	452.3
RBF-STSMC	57.86	108.5	119.1

IAE is the integral of the absolute value of error. The J_IAE in the x and z directions of RBF-STSMC is smaller than those of STSMC, so the system of RBF-STSMC has a better ability to suppress errors than STSMC.

ISE represents the integral of the squared error, which measures the sum of squared differences between the system output and the expected value. The J_ISE of RBF-STSMC in all directions is smaller than the J_ISE of STSMC, indicating that the deviation between the output of RBF-STSMC and the expected value is small, and the system has good stability.

ITAE comprehensively considers the absolute value of error and the integration of time, and to a certain extent, it weighted the duration of error. Therefore, when J_ITAE is small, the system has a better ability to quickly suppress errors. From the data in the table, it can be seen that the J_ITAE of RBF-STSMC is smaller than that of STSMC. Therefore, we believe that the RBF-STSMC system has a better ability to quickly suppress errors.

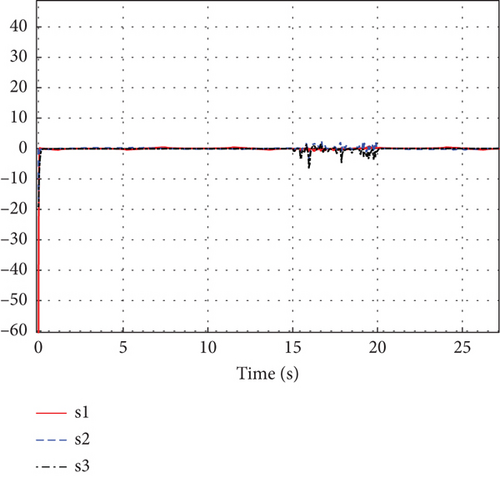
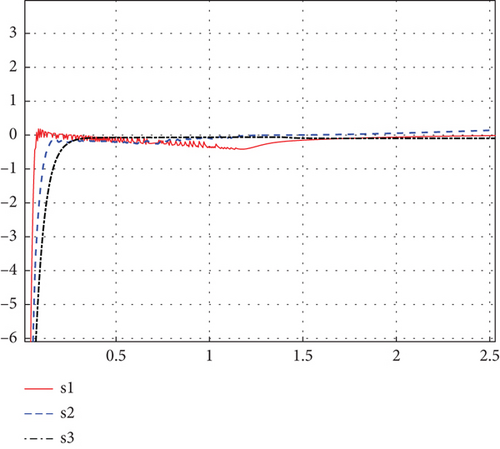
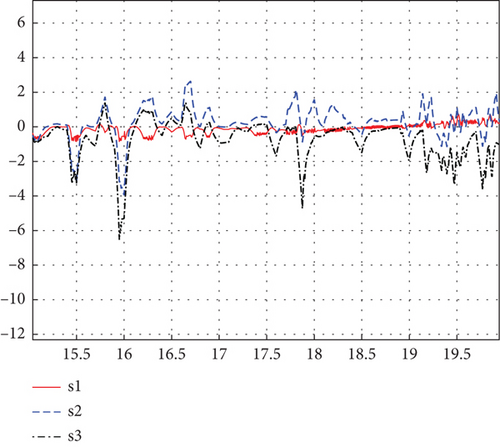
The simulation results of sliding surfaces s1, s2, and s3 are shown in Figures 8 and 9. Figures 9(a) and 9(b), respectively, represent the enlarged schematics of 0–3 s and 15–20 s from Figure 8.

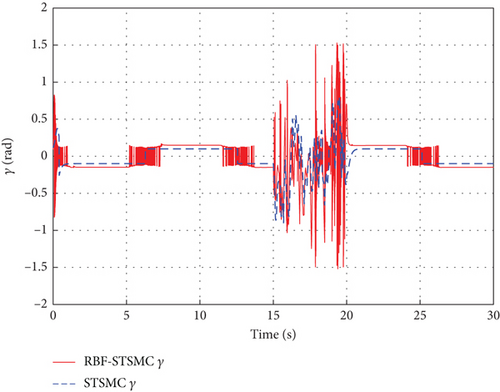
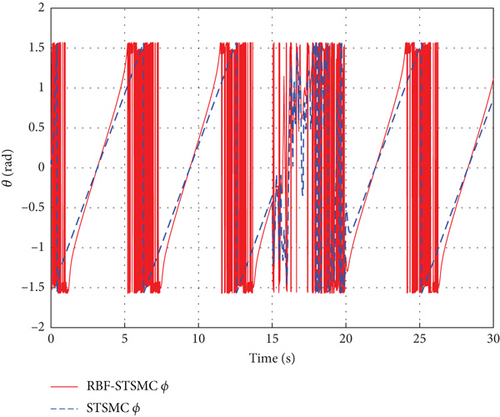
Figures 10 and 11, respectively, illustrate the variation curves of the UAV’s pitch angle and heading angle during the path tracking process. It can be observed that during the disturbance period from 15 to 20 s, although the UAV controlled by RBF-STSMC exhibits rapid angle variations, considering control accuracy, its disturbance rejection capability is stronger. In addition, by zooming in on the curves during the 15–20 s interval with added white noise, as shown in Figures 12, 13, and 14, it can be observed that the controller designed in this study exhibits stronger disturbance rejection capability and tracking accuracy when subjected to external disturbances.

5. Conclusions

This paper addresses the flight tracking control problem of fixed-wing UAVs in the presence of unknown disturbances. A controller combining the RBF neural network with the STSMC algorithm is proposed. This method reduces the impact of external disturbances on the UAV while mitigating the chattering phenomenon. Furthermore, its performance was verified through comparative experiments. Simulation results indicate that the novel controller, integrating neural networks with STSMC, outperforms the STSMC in terms of tracking accuracy. The results of this work can effectively suppress the external interference problems encountered during the flight of UAVs, which is helpful for the design and development of fixed-wing UAV flight control systems. In the future, we will further improve control algorithms to enhance the accuracy of flight control for fixed-wing UAVs.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work is supported by the National Natural Science Foundation of China (5190924562003314), the Key R&D Plan of Shanxi Province (202202020101001), and the 2023 Project Funding for Technological Initiatives at North University of China (20231975).