Multi-UAV Cooperative Search for Moving Targets With Impaired Communication Using Improved Gray Wolf Optimizer
Abstract
The study investigates the problem of collaborative target search by multiple unmanned aerial vehicles (UAVs) under the condition of communication information corruption. The problem involves the influence of target movement and environmental obstacles on the update of the UAV’s local target probability map (TPM), as well as communication information corruption among UAVs due to packet loss and resulting local information inconsistency. The objective is to efficiently plan paths for the UAV swarm to discover more targets. To address the above issues, this paper proposes the following methods. Firstly, an information diffusion model is introduced to simulate the TPM changes caused by target movement and the discovery of obstacles based on a two-dimensional Gaussian distribution, thereby correcting the real-time target information held by UAVs. Secondly, a radial basis function neural network (RBFNN) is employed to recover the corrupted information, and a weighted averaging method is used to fuse the information from multiple UAVs, achieving consensus among the UAVs. Lastly, the original gray wolf optimizer (GWO) is enhanced by incorporating strategies such as Levy flight and the nonlinear convergence factor. Subsequently, the improved GWO is integrated with the model predictive control (MPC) for UAV trajectory planning, enabling a more efficient search for optimal paths. Experimental results demonstrate that the proposed information recovery method outperforms the compared methods by 24.7% in terms of performance. The proposed comprehensive search approach shows higher efficiency in searching for more targets within a specified time, and it also exhibits advantages in terms of area coverage and other aspects.
1. Introduction
With the continuous advancement of technology, unmanned aerial vehicles (UAVs), as emerging aircraft, are playing an increasingly important role in tasks such as target search, tracking, interference, firepower, and effectiveness evaluation [1–3]. The technology of UAVs searching for multiple moving targets has wide applications in the military, security, rescue, environmental protection, and other fields. In the military domain, UAVs can provide real-time monitoring and tracking of enemy moving targets, offering precise information support for combat command. In the security field, UAVs can be used to monitor public areas, promptly detect suspicious moving targets, and enhance public safety. In the rescue field, UAVs can swiftly locate disaster areas, search for missing persons, and improve rescue efficiency. In the environmental protection sector, UAVs can monitor wildlife, contributing to biodiversity conservation. In target search missions in high-risk areas, using reconnaissance means such as satellites and radar may lead to resource wastage, while using vehicles may not be efficient for reconnaissance. In such scenarios, UAV target search holds significant value. Therefore, the main focus of this paper is on the collaborative search of moving targets by multiple UAVs.
For multi-UAV cooperative target search tasks, path planning based on environmental information held by the UAV is an important research topic. Path planning algorithms for UAV cooperative search are presented in detail in [4]. These algorithms are classified into three categories based on (1) global probability maps (GPMs), (2) model predictive control (MPC), and (3) intelligent optimization algorithms (IOAs). Among them, GPM algorithms have higher requirements on the a priori information of the environment, and MPC algorithms have higher computational costs and higher requirements on the UAV hardware. In contrast, IOA algorithms need modest prior data, effectively reducing the computational complexity through information updating rules. However, IOAs might lag in convergence and precision due to update limitations, risking local optimality. To address this issue, relevant enhancements have been made as follows:
Sun et al. [5] proposed an improved intelligent water drop optimization algorithm by introducing heterogeneous water drop populations and a coevolutionary mechanism with a stronger ability to jump out of local optima. Shao et al. [6] optimized the initial distribution of particles and acceleration coefficients and proposed a mutation strategy that improved the performance of the original algorithm. The immune genetic algorithm proposed by Zhou et al. [7] utilized an immune strategy to enable UAVs to search for targets more efficiently in uncertain environments. The above methods perform well when searching for unknown stationary targets; however, in real search tasks, the targets faced by UAVs are often moving targets in unknown environments. Therefore, path planning algorithms also need to have strong real-time performance. Pérez-Carabaza et al. [8] used an ant colony algorithm to plan feasible paths for UAVs in real time to minimize the search time, which considered constraints in terms of communication and obstacles. However, the method required more a priori information. Zhen et al. [9] considered four types of time-sensitive targets and proposed a hybrid artificial potential field and ant colony optimization method. To search for dynamic targets more efficiently, the target probability map (TPM) update was related to the motion of the target, but the obstacle information was known a priori. Reference [10] integrates the gray wolf algorithm with the differential evolution algorithm, resulting in a better balance between the exploration and exploitation phases. Compared to the original algorithm, the improved algorithm plans trajectories with shorter and smoother total lengths. Fei et al. [4] combined MPC with an improved sparrow search algorithm to establish a multi-UAV cooperative search algorithm whose planned implementation paths have high search accuracy and stability. In most previous research, the initial state probability distribution of the target in the updating process of the TPM has been used without considering the influence of obstacles. However, actual TPM updates should take into account the target motion and positions of obstacles. Additionally, the UAV swarm lacks real-time collaboration during the target search process, resulting in low search efficiency. To address these issues, a real-time path planning algorithm needs to be designed. This algorithm should be able to detect obstacle information in the environment in real time and consider the probability changes caused by target motion. Furthermore, it should improve the environmental adaptability and overall search efficiency of the multi-UAV target search. The issues laid out above are the primary motivation for the research work described in this paper.
During collaborative UAV missions, information inconsistency arises due to differing UAV detections. Factors such as enemy interference, adverse weather, and ambient noise can degrade communication channels, leading to packet loss in transmitting environmental data among UAVs. Therefore, information inconsistency is more common among multiple UAVs. Consistency among UAVs is also known as reaching group consensus, which can avoid many problems such as repeated searches of the same area due to information inconsistency among multiple UAVs. A group consensus can generally be reached through information fusion, which integrates the environmental information of each UAV to make the information consistent [11–13]. Khan, Yanmaz, and Rinner [14] considered a variety of constraints, analyzed the characteristics of transmitted information, and investigated the effect of multisource information fusion on search time in path planning. Basso et al. [15] used information filtering to merge environmental information between multiple UAVs and further processed the fused information to obtain coherent information regarding the region of interest. Saadaoui et al. [16, 17] employed the LPSO algorithm to perform collaborative search tasks with multiple UAVs. In the global communication method, each UAV sends local information and fuses the information received at each time step. Zhou et al. [18] identified UAVs by their range and fused feasible ones. Zhou et al. [19] considered constraints such as energy consumption and investigated the reasonable allocation of UAV computational resources in information transmission and fusion processes. However, real environments introduce challenges such as adverse weather or other factors not addressed in the previously mentioned studies. Li et al. [20] considered the issue of lost information in transmission and used an improved least squares method to compensate for the lost information and fuse the information from each UAV. However, the influence of obstacles was not accounted for in the recovery of lost data [20]. Additionally, previous researchers have rarely considered inconsistent environmental information among UAVs due to communication degradation in the transmission of environmental information in obstacle environments. Therefore, a method that takes into account the obstacle information during the process of recovering damaged data, which is then fused with the recovered information, must be designed. This topic was the second motivation for the research work reported in this paper.
- 1.
The problem of inconsistent UAV information owing to poor communication and other factors is addressed. This study proposes a data recovery and information fusion method using a radial basis function neural network (RBFNN) to unify the environmental information held by the UAVs and enable multiple UAV systems to reach a group consensus. The details of the RBFNN are covered in Section 4.1.
- 2.
The problem of target motion and obstacle detection affecting the local TPM distribution of UAVs is addressed. In this study, we utilized an information diffusion mechanism to model the changes in the TPM distribution at each time step for the aforementioned reasons.
- 3.
An improved gray wolf optimizer (IGWO) combined with MPC is proposed, which can solve the current optimal path for UAVs at each time step and solve the problem of real-time path planning optimization for multiple UAVs.
The remainder of this paper is organized as follows: Section 2 describes the problem and path-planning model. In Section 3, the mechanism for updating the UAV environmental information is described; we propose a new consistency strategy for environmental information and describe the real-time path planning algorithm of the UAV. Simulation results are presented in Section 4. Finally, Section 5 summarizes this study.
2. Problem Formulation and Models
The main focus of this study is the problem of cooperative target search by multiple UAVs in adverse communication environments. The problem can be described as follows. Each UAV has knowledge of the initial position of the target, but during the search process, the target is moving and the UAVs encounter obstacles in the environment. Both of these situations cause changes in the UAVs’ local TPMs, necessitating the design of a method to compensate for these changes. Additionally, the adverse communication environment can result in damaged information transmission between the UAVs. Therefore, it is necessary to employ certain methods to recover the damaged information and perform information fusion to achieve consensus within the UAV cluster. Once consensus is reached, the UAVs update their local environmental information through their own sensors and communication, make decisions, and execute actions based on the currently available environmental information. This ensures a low-cost search while maintaining efficient path planning.
2.1. Environmental Model
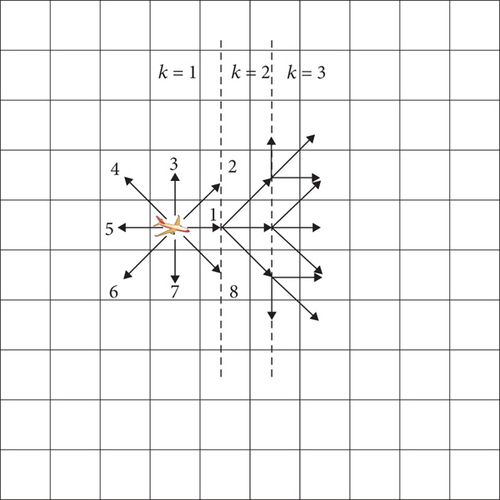
The rasterized method [21] is used to divide the search area into Lx × Ly cells; that is, the search area has Lx cells in each row and Ly cells in each column. The coordinates of the gth cell are denoted by g = (xg, yg), where xg ∈ {1, 2, ⋯Lx} and yg ∈ {1, 2, ⋯Ly}. It is assumed that multiple UAVs take off from the airport with the same flight attitude into the search environment for target search, that each UAV flies at a uniform speed at each time step, and that at each time step, the UAVs can only move one cell to an adjacent cell.
2.2. Environment-Aware Map Model
2.3. UAV Model
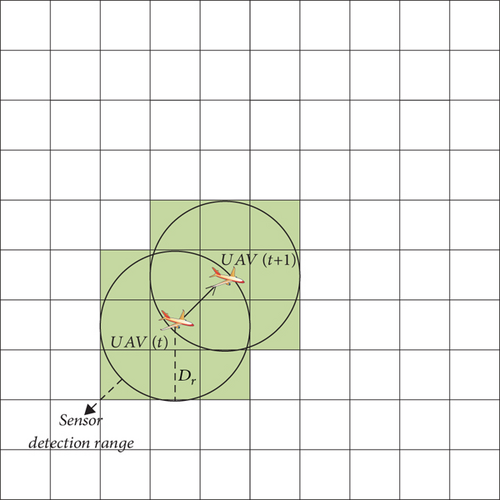
In this study, the sensor detection radius of the UAV is Dr, the TPM of the grids within the detection range, and χ is updated locally according to the detection update rule in Section 2.2. The TPM of the undetected grids is updated using information diffusion, which is described in detail in Section 3.1. As shown in Figure 2, the detection area of the UAV at each moment is indicated by the surrounding green square.
2.4. Target Model
- 1.
The maximum velocity of the target motion is less than or equal to the maximum velocity of the UAV motion;
- 2.
The motion of the target is independent of the UAV motion;
- 3.
The heading angle of the target at each moment can be selected from any of the eight directions described in Section 2.2.
2.5. Obstacle Avoidance Model
3. Method
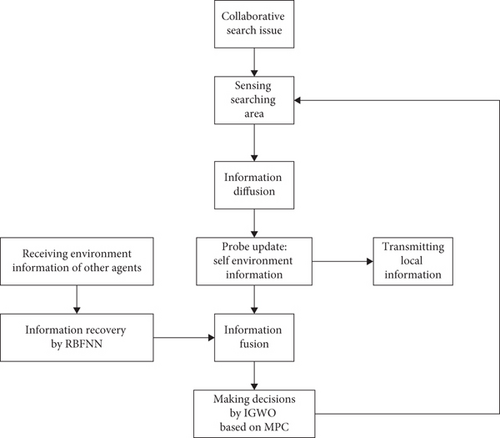
3.1. Collaborative Search Framework in Poor Communication Environments
In the aforementioned problem, the search area is divided into multiple grids using the grid-based approach. Assuming the initial position of the target is known but its movement direction is unknown, a normal distribution is used to describe the initial distribution of the target’s position. This distribution affects the update of the TPMs. During the actual search process, the target is moving and obstacles may be encountered. This is reflected in the TPM by increasing the target existence probability in the grid where the target is located and reducing the target existence probability to zero in the grids where obstacles are detected. Therefore, the initial target distribution cannot be used continuously to update the TPM. This paper adopts an information diffusion approach to compensate for the impact of the aforementioned issues and dynamically adjust the target information acquired by the UAVs.
The effectiveness of UAV decisions can be determined by a reward function, where the reward function Ji(Si(k), ui(k)) represents the reward obtained by UAVi when it is in the state Si(k) and takes control input ui(k). A higher value of Ji(Si(k), ui(k)) indicates better performance of ui(k). However, in adverse communication environments, when UAVs package and transmit their locally sensed environmental information to other UAVs, some data may be lost, leading to significant errors in the information fusion results between UAVs. As a result, consensus cannot be reached among the UAVs, and the decisions made may lead to mutual repetition or conflicts, thereby reducing the overall efficiency of cooperative search. Therefore, it is necessary to address the issue of inconsistent information among UAVs in a degraded communication environment. In this paper, we employ RBFNN to recover the damaged information and utilize a weighted averaging method to perform a multisource fusion of information between UAVs, ultimately achieving consensus among all UAVs in the group.
After addressing the aforementioned issues, UAVs make decisions based on the acquired environmental information, specifically in the context of path planning. In this paper, we propose the use of the MPC-based IGWO algorithm for path planning of the UAV cluster. MPC considers future states during the search process, enabling UAVs to adapt better to the environment and tasks. Additionally, compared to other algorithms, IGWO incorporates strategies such as Levy flight and nonlinear convergence factors, which enhance its ability to escape local optima. Figure 4 illustrates the framework of the multi-UAV cooperative search under adverse communication conditions.
3.2. Update of Environment-Aware Map
As described above, the process of updating the TPM is influenced by the distribution of the target’s position and the presence of obstacles detected in the environment. In this section, an information diffusion model is used to simulate the effects of target movement, and the discovered obstacle grid cells are subjected to specific operations to reduce the probability of the target’s existence to zero. Additionally, a revisiting mechanism is incorporated into the update process to address the issue of the target potentially moving into areas that have already been searched due to the extended search duration.
3.2.1. Update of TPM
In the process of the UAV searching for a target, the probability distribution of the target UAV will change owing to the target movement, so we cannot always use the initial distribution of the target to update the local TPM of the UAV. Thus, we must make a reasonable prediction of the target movement to improve accuracy when the TPM is updated.
For the initial distribution of information on the target, we adopted the information diffusion mechanism [23] to predict the change in the probability distribution of the target. This approach is similar to the gas diffusion mechanism, which mainly describes the phenomenon in which information will diffuse from the current grid to the surrounding neighboring grids. The information of the neighboring grids will also diffuse into the current grid, the information will diffuse from the high-probability grids to the low-probability grids, and the probability distribution of the target will converge to a uniform distribution after a long period of time.
Using the initial distribution information of the target and the above probability diffusion model, any grid target probability can be obtained at any time, and all UAVs have the same initial information and probability diffusion rules, which avoids the problem of inconsistent information among UAVs. In addition, using the predicted target probability distribution to update the target probability of the corresponding grids results in a higher level of confidence.
The above diffusion process corresponds to the case in which there are no obstacles in the search area. However, after detecting an obstacle through the sensors, the UAV needs to change the way in which the information diffuses in the obstacle area and its neighboring areas.
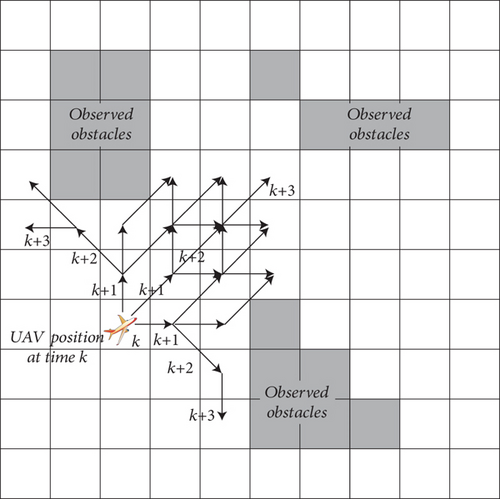
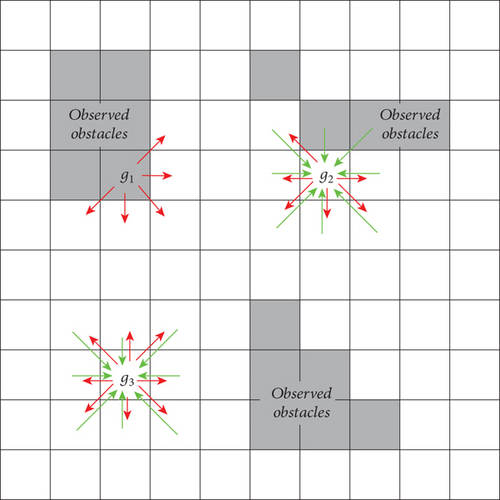
The direction of the diffusion of grid probabilities is shown in Figure 5, where g1 is the obstacle grid, g2 is the normal grid adjacent to the obstacle, and g3 is the normal grid. The red and green arrows show the direction of the probability of spreading outward and inward, respectively.
3.2.2. Uncertainty-Related Revisit Mechanisms
Because of the random movement of the target in the search area, it may travel back to the area that was previously detected by the UAV, and the UAV does not have an effective reobservation method for these already detected grids. Thus, a grid-revisit method is needed to solve the problem.
3.3. Group Consensus Among UAVs
The transmission of environmentally aware information in poor communication environments leads to partial data loss. As described in this section, we first compensate for the lost data and then fuse the UAV local information with the processed received information to make the environment-aware information consistent among all UAVs.
3.3.1. Information Recovery
Suppose that all information about grid g in the transmission message Ej(k) from UAVj is lost. The following methods were adopted to recover lost information from other UAVs. Regarding the target probability at grid g, firstly, owing to the local correlation of the transmission information, the target probability of the grids around grid g can be collected using the k-nearest neighbors algorithm [24] (KNNA), and then the collected data are fitted to the lost probability of grid g using the RBFNN [25]. Regarding the uncertainty of the loss χ of grid g, χig(k) can be set to one because the transmission information has been lost and the UAV knows nothing about the grid.
Figure 6 illustrates the neighborhood grid information collection at Ld = 1, with the loss probability grid in red and the neighboring grids within the distance threshold in green.
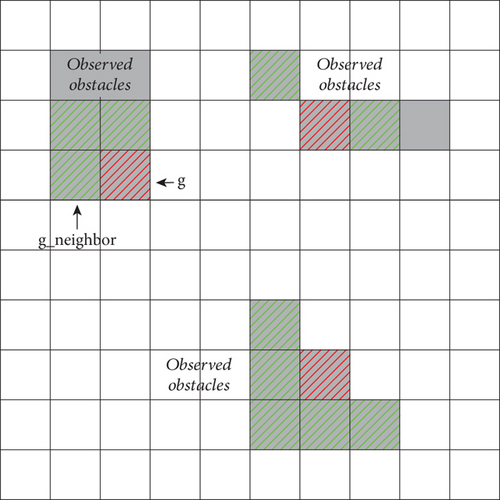
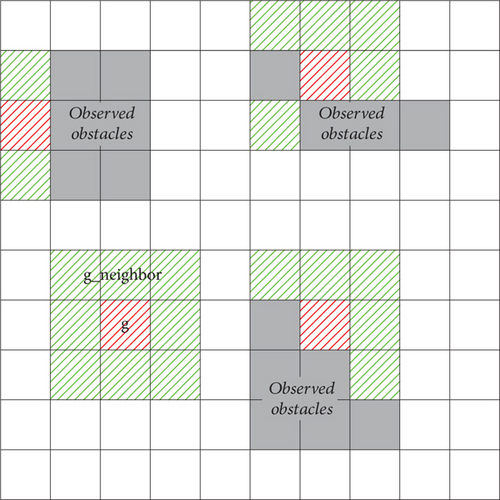
After collecting sufficient valid information using the KNNA, this information must be used to fit the missing values. Assuming the target probability in grid g from UAVj’s TPM is lost, because the information contained in the TPM consists of only the coordinates of the grid and the target probability, the fitting function can be designed as pjg(k) = frecover(xg, yg), where pjg(k) represents the target presence probability of grid g recovered at time k and frecover is a recovery function fitted using the coordinates and target presence probabilities of neighboring grids g−neighbor in UAVj. Because the RBFNN has the characteristics of a simple structure, fast learning speed, excellent approximation performance, and generalization ability, it was employed in this study to solve the above-fitting function.
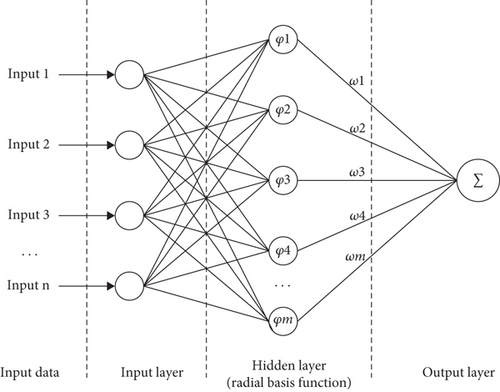
The RBFNN is a commonly used three-layer feedforward network, the three layers are the input, implicit, and output layers. The implicit layer has multiple radial basis activation functions, which are used to map the input vectors from low-dimensional m to high-dimensional n; thus, an indistinguishable low-dimensional linear space is converted into a distinguishable high-dimensional linear space. The RBFNN is a local approximation network in which only a few connection weights in the local region of its input space affect the output. Compared with backpropagation and other global approximation networks, an RBFNN has a faster learning speed, which is conducive to meeting the real-time requirements of searching for targets in UAVs. The input of the RBFNN consists of the coordinates of neighboring grids and the target probability, whereas the output consists of the target probability of the damaged grid. Gaussian functions are used as the radial basis functions. The structure of the RBFNN is illustrated in Figure 7.
The parameter that must be determined in the RBFNN training process is the spread speed d, which mainly serves to adjust the sensitivity of the hidden layer to the data. The lower the spread speed d, the higher the sensitivity of the implicit layer to the input, and the more accurate the function approximation; however, the approximation process will be poorly smoothed, resulting in average network performance. The higher the d is, the smoother the function fitting will be, but the approximation error will be correspondingly larger.
3.3.2. Information Fusion
The pseudocode for information recovery and fusion is shown in Algorithm 1.
-
Algorithm 1: Pseudocode for information recovery and merge.
-
1: Input Distance threshold for KNAA Ld, Spread speed of RBFNN d, Number of UAVs N
-
2: Restore the lost information of grid g
-
3: for n =1:N do
-
4: for x =1: Lx do
-
5: for y =1: Ly do
-
6: if L <Ldthen
-
7: Collect, and pjg_neighbor(k)
-
8: end if
-
9: end for
-
10: end for
-
11: Input , , pjg_neighbor(k) and (xg, yg) to RBFNN
-
12: Obtain the fitted value pjg(k)
-
13: end for
-
14: for each grid do
-
15: calculate the weighted matrix ωjg(k)
-
16: end for
-
17: calculate the final recovered target probability
3.4. Collaborative Target Search Algorithm
Section 3.3 presents UAV environment perception information with collective consensus. This section describes the combination of the MPC strategy with IGWO to find the optimal path for each UAV. Firstly, the UAVs exchange their respective environmental information such as position and target probability. Then, MPC is used to generate a set of feasible predicted paths for each UAV. Subsequently, IGWO evaluates the quality of each path using a path evaluation function and selects a path with a higher evaluation in each iteration. This newly generated path can be one of the original paths or a path generated by the algorithm. Through multiple iterations, the UAVs can achieve collaboration and obtain more efficient search paths.
3.4.1. Description of MPC
The basic idea of MPC is to predict the future dynamics of the UAV at each sampling moment, solve a finite-time open-loop optimization problem online, and consider the first element of the obtained control sequence as the decision of the UAV. This method of predicting the future state is helpful for enhancing the perception performance and adaptability to the environment of UAVs and for ensuring the optimality of the planned path to a certain extent; therefore, it is widely used in path planning problems.
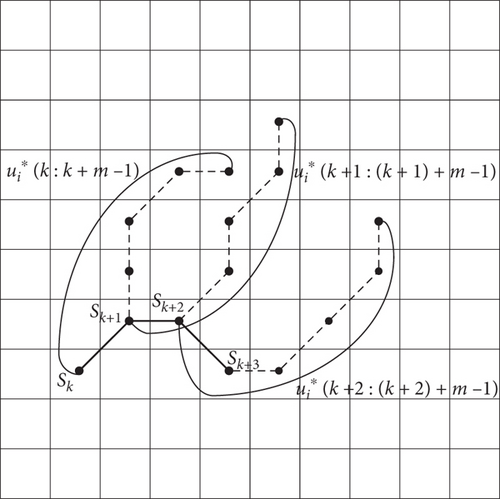
Considering the accuracy of the prediction, only the first term, that is, , is executed. When the moment steps to k + 1, the above process is repeated, and the optimal control input, , is obtained at moment k + 1. Figure 8 shows the three-step MPC prediction process for m = 6, with the dashed line indicating the predicted trajectory, and the bold solid line indicating the actual action taken.
3.4.2. IGWO
3.4.2.1. Gray Wolf Optimizer (GWO) Algorithm
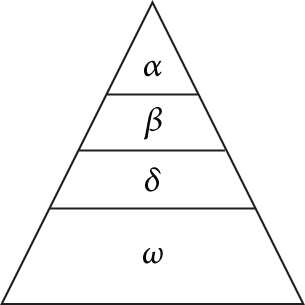
The GWO [26] is a classical and effective IOA that simulates the hunting behavior of gray wolves in nature, with the advantages of a simple structure and high solution accuracy. Gray wolves hunt in a hierarchy, as shown in Figure 9, where the lower ranked wolf ω is led by higher ranked wolves α, β, and δ to surround, approach, and capture prey.
3.4.2.2. Improvement Strategies
- 1.
Levy flight strategy: Levy flight is stochastic wandering with a heavy-tailed probability distribution of the step length, which has a high probability of jumping out of the current search area during the wandering process. It then explores a larger search space and thus is helpful for solving the problem of falling into the local optimal solution, which can be mathematically described as follows:
- 2.
Nonlinear convergence factor strategy: The convergence factor A determines the search strategy of the gray wolf, and the control parameter a in the convergence factor A is optimally set to regulate the relationship between global and local searches more effectively throughout the iteration process.
- 3.
Optimal individual information fusion strategy: To improve the ability of the community to find the optimal value in the global range further, the following strategy is designed such that the optimal individual in the kth iteration is αk, βk, and δk; α, β, and δ are the individuals with the optimal fitness values up to this iteration, which is briefly referred to as the global optimal individual. Because the risk of falling into local optimality increases in the late iterations of the algorithm, it is considered that the optimal individuals α, β, and δ (e.g., in the kth generation) and other stochastic individuals of this generation are integrated into the global optimal individuals in the form of differential evolution during the iteration process, which not only enhances the stochasticity and diversity of the community but also improves the solving efficiency of the algorithm. The mathematical description of this strategy is as follows
The pseudocode for IGWO is given in Algorithm 2.
-
Algorithm 2: Pseudocode for IGWO.
-
1: Input Population size Popsize, Number of iterations MAX, Search area
-
2: Calculate the fitness of all gray wolves in the kth iteration, and denote the top three individuals in fitness as αk, βk and δk
-
3: Update the global optimal individual position by using (24) and (25)
-
4: Update a and A by applying (23) and (19), update C according to Ref. [27]
-
5: Update all the individual positions by utilizing (16) and (17), apply Levy flight strategy to the individuals, and retain the optimal solution
3.4.3. Path Evaluation Function
The higher the uncertainty, the more likely a potential target exists in that grid.
4. Experiments
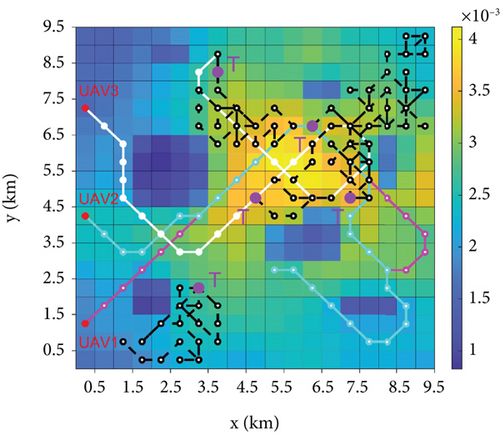
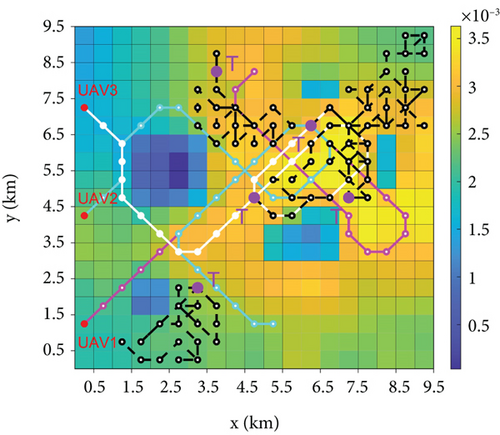
The simulation experiments were conducted in the MATLAB 2020a environment. Table 1 lists the symbols used in this study and their corresponding values. The number of grids that lost information at each moment when communication was performed between the UAVs was random, the initial placement position of the UAVs was on the boundary of the search area, and the number of UAVs was three. In Figure 10, the white, magenta, and purple lines are used to denote the motion path of the UAVs in their searching process, and the black line denotes the target movement path. The higher the target probability in the simulation results, the brighter the color of the grid, where blue and green represent the lower target probability and yellow represents the higher target probability. The obstacle region settings used in this study are shown in Figure 11.
| Notation | Description | Value |
|---|---|---|
| χig(0) | Initial uncertainty of the grid g | 1 |
| Popsize | Population size | 30 |
| MAX | Maximum number of IGWO iterations | 500 |
| N | Number of UAVs | 3 |
| Pis | Initial position of UAVi | / |
| λd | Diffusivity | 0.1 |
| Vi | Velocity interval of UAVi | 1 grid |
| d | Spread speed of RBFNN | 10 |
| Ld | Distance threshold for KNAA | 1 grid |
| Th | Time threshold for revisit | 50 s |
| m | MPC predicted steps | 6 |
| SMAX | Maximum number of exercise steps for UAVi | / |
| pd | Sensor detection probability for UAVi | 0.9 |
| pf | Sensor false alarm probability for UAVi | 0.1 |
| Dr | Detection radius of UAVi | / |

4.1. Information Recovery and Fusion Performance Testing
The search area was a rectangular area of 9.5 km × 9.5 km, which was divided into 19 × 19 grids, each with a length and width of 0.5 km, in which five targets existed with initial positions of 3.25 km and 2.25 km, 4.75 km and 4.75 km, 6.75 km and 4.75 km, 3.75 km and 8.25 km, and 6.25 km and 6.75 km; in this area, the speed was 50 m/s for horizontal or vertical flight, the speed was √2 times the horizontal for oblique flight, the decision time interval was 10 s (i.e., the UAV was at the center of any grid each time it made a decision), and the maximum number of movement steps was SMAX = 30; the information was lost during the transmission process, and the number of lost data grids was 10% of the total number of grids in the area.
Figure 12 shows a vertical view of TPM fusion for each UAV. Comparing Figures 12(a) and 12(b) demonstrates that numerous grids have significant missing data in the received information of UAV1, and the loss of these data hinders the subsequent decision-making process of UAV1. Figures 12(c) and 12(d) show the fused TPMs after recovering the target probabilities of the missing grids based on the strategies of RBFNN and [20] for UAV1, respectively. The RBFNN method of this study evidently has a better information recovery effect because [20] uses the least squares method for regression fitting, and the form of the fitting function used is generally adapted to the distribution of the target probability, whereas the RBFNN does not need to consider the form of the distribution of the fitting function. In addition, Li et al. [20] have a minimum restriction on the number of grids collected by the KNNA, but some of the grids that are at the boundaries of the obstacles are unable to collect enough information about neighboring grids. Figures 12(c) and 12(e) show the respective fused TPMs of the two UAVs, which are essentially the same as those of the fused TPM of the unlost data in Figure 12(a). The maximum value of the information error for the same grids in Figures 12(c) and 12(e) is 6.06 × 10−4, so that the information fusion strategy proposed in this study can enhance the consistency of information among UAVs and thus reach a better group consensus state.
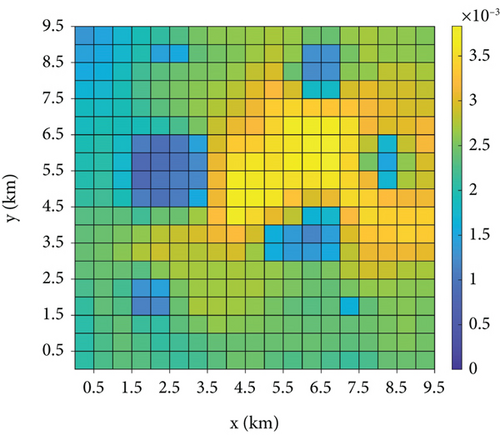
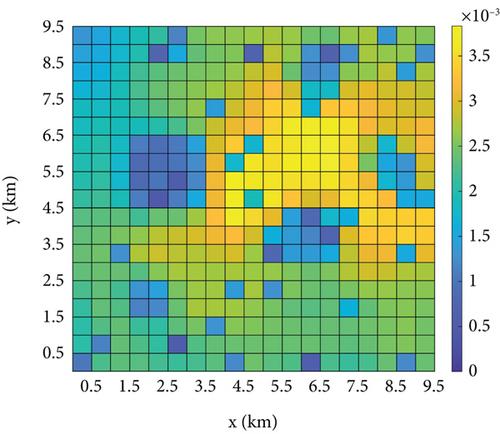
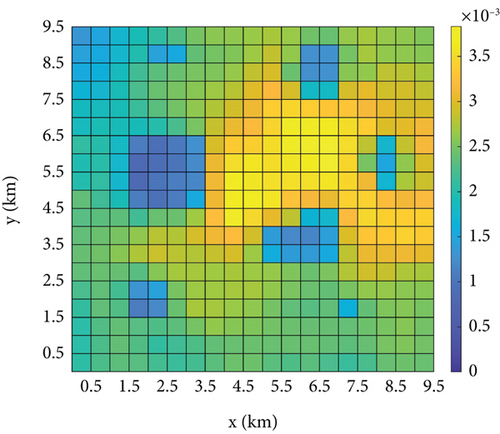
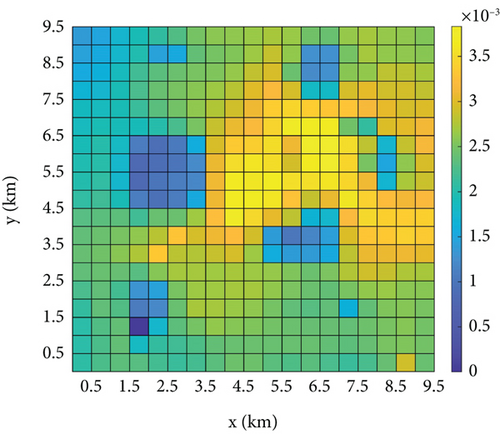
To compare the two methods further, the recovery error of each lost data grid is shown in Figure 13, where the total number of lost data grids is 40. The maximum recovery error of the strategy in [20] is 0.00223, and the maximum recovery error of the proposed strategy is 0.00168. Moreover, among the 40 grids with lost data, the recovery results of the strategy used in this study are better than those of [20] in 28 out of 40 grids. These recovery results are better than those of [20], and in most of the grids with better recovery results, the error is less than 3 × 10−4; thus, the recovered fusion TPM can be assumed to be equal to the state of the unlost data. Therefore, the information recovery method adopted in this study can be assumed to reduce the information error caused by the data loss significantly.
4.2. Effect of UAV Parameters on Search Performance
- •
Experiment 1: The UAV detection radius Dr was set to {0.5, 1, 1.5, and 2 km}. Figure 14(a) shows the number of search targets and the detection grid coverage for different UAV detection radii.
- •
Experiment 2: The number of UAVs was set to {2, 3, 4, 5}. Figure 14(b) shows the effect of the number of UAVs on the number of search targets and detection grid coverage.
- •
Experiment 3: The UAV sensor detection parameters were set to {pd = 0.6, pf = 0.4}, {pd = 0.7, pf = 0.3}, {pd = 0.8, pf = 0.2}, and {pd = 0.9, pf = 0.1}. Figure 14(c) demonstrates the sensitivity of the IGWO to the sensor performance.
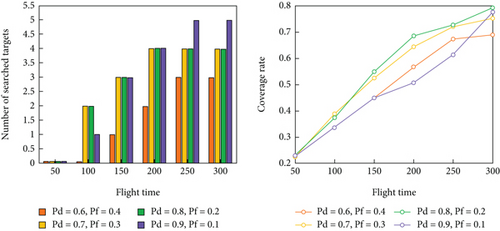
For all three experiments, each set of experiments was run independently 20 times, and the results were averaged.
From Figure 14(a), when Dr = 0.5 or 1 km, all targets cannot be found at the end of the search, and the UAV cluster finds all targets when Dr > 1.5 km. Only one target is found in the whole search process when Dr = 0.5 km. In addition, the grid coverage increases owing to the increase in the detection radius of the UAV. When Dr is small, the cluster search efficiency is poor; therefore, the algorithm in this study is more sensitive to the detection radius of the sensors used, and sensors with smaller detection radii cannot be used.
From Figure 14(b), when N = 2, the UAV cluster finally searches for four targets; when N > 2, the UAV cluster can find all targets, and the grid coverage also improves with an increase in the number of UAVs.
From Figure 14(c), the UAV cluster, only the sensor with {pd = 0.9, pf = 0.1}, finds all the targets, and the search efficiency is higher. The sensors with smaller pd and larger pf all increase the grid coverage in the middle and late iterations to jump out of the local optimum to find more targets. However, they are not successful. The {pd = 0.9, pf = 0.1} sensors can find more targets by covering fewer grids, indicating that the sensor performance significantly affects the search results, and UAVs can achieve good search results only when the sensor performance is excellent.
4.3. Performance Comparison of Different Search Algorithms
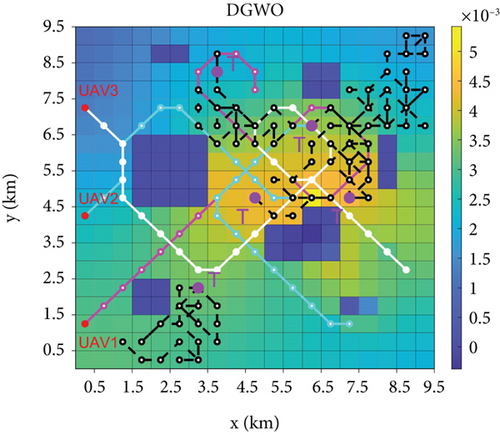
To test the performance of the search algorithm proposed in this study, simulation experiments were conducted using six search algorithms, including the algorithm proposed in this study: GWO, distributed gray wolf optimizer (DGWO) [28], motion-encode particle swarm optimization (MPSO) [29], greedy [19], distributed MPC (DMPC) [30], and IGWO. GWO, DGWO, and MPSO are popular IOAs that apply their respective rules for reasoning and solving to predict the optimal target grids for the next moment. DGWO divides all individuals in the wolf pack into several islands, with each island containing multiple candidate solutions. The islands update their positions according to the updating rules of GWO, and they exchange their candidate solutions with each other at a certain frequency; MPSO encodes the search trajectory into motion paths of the UAV, which vary with the particle positions in the PSO algorithm, preserving group cognition and global consistency. The greedy method favors grids with the largest target probability in the next moment. DMPC uses MPC for the next m-steps of the UAV, seeking optimal, high-efficiency paths, which is computationally costly.
The simulation scenario is the multitarget scenario described in Section 4.1, with three UAVs with initial departure positions at 0.25 km and 1.25 km, 0.25 km and 4.25 km, and 0.25 km and 7.25 km, respectively. The search radius Dr was 1.5 km. The number of targets searched for, time used for searching, and coverage of detection grids were used to analyze the strengths and weaknesses of the method. In addition, the overlap of the UAV search path with the grid of high-probability regions can aid in analyzing the performance of the algorithm.
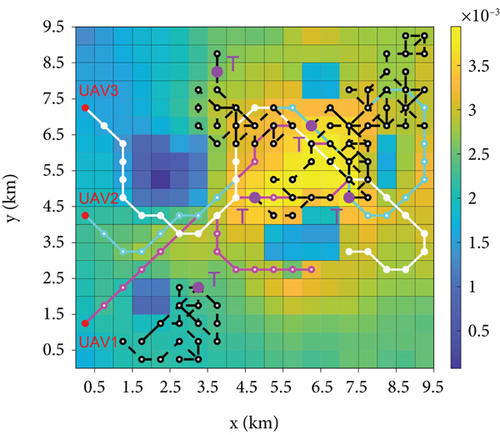
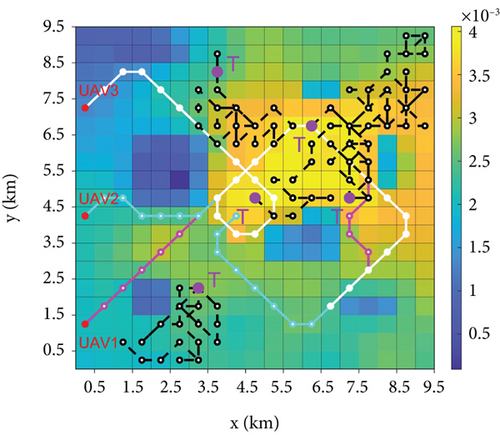
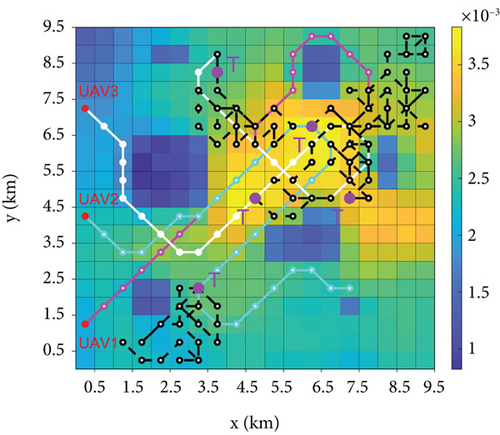
The comparison of the number of searched targets and the coverage of detected grids during the search process of the six methods is shown in Figure 15, which demonstrates that the IGWO algorithm outperforms the other algorithms in terms of the number of targets found, area coverage, and search efficiency. The performance of the IGWO is average in the presearch period, whereas the DMPC and DGWO have advantages in both the number of searched targets and coverage of detected grids because in the presearch period, UAVs have less information about the environment. In the DMPC method, the local information can be updated quickly by traversing all the predicted paths, whereas IOAs use their own updating rules for inference. Owing to the small difference in information between the grids, the degree of certainty of the grid information is low, which leads to a large error in the inference results. DGWO provides an additional exploration mechanism where the island model increases the probability of transforming low-quality candidate solutions on each island into better solutions. Compared to GWO, the computational complexity is significantly reduced, which is the reason for its efficient early-stage search. In the early stages of the search, IGWO directs UAVs toward high-probability areas. As the search progresses, each UAV begins to consider factors such as probability distribution and uncertainty, and based on their respective positions, they disperse their actions. The speed and quantity of target discoveries steadily increase, with all five moving targets found by 220 s. In contrast, other methods only found four targets by their maximum search time, demonstrating that the approach proposed in this paper has a stronger ability to escape local optima.
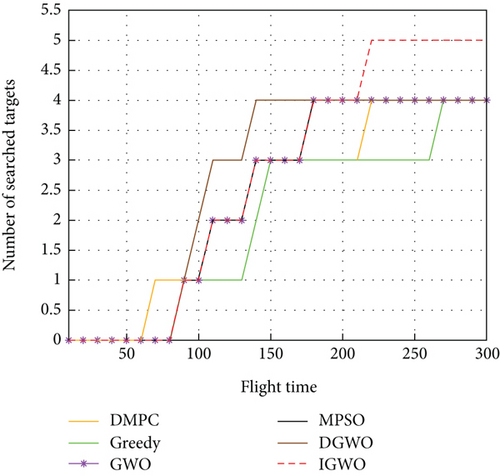

For the detection grid coverage, the proposed method maintains a low level in the first and middle periods. This occurs because the next moment of UAV travel to the grid predicted by this method has a higher reward value, which can accurately search for the target in a smaller detection area. This finding proves the feasibility of the strategy proposed in this study. At the late stage of the search, as the other methods get stuck in local optima, they fly around the local optimum for a long time, failing to find the last target, which slows the growth of coverage. However, the method proposed in this study promptly escapes local optima. After all the targets were found in 220 s, the UAV was unable to find the target each time it updated its position because the target disappeared; therefore, it continued to expand the search area to find the target, and the coverage rate increased rapidly in the process.
To demonstrate the superiority of the proposed method more intuitively, the comparison data of the six methods at different time periods are listed in Table 2. At t = 100 s, the number of targets searched by DGWO was two, while the other methods were all one, and the coverage of DMPC was higher than that of the remaining algorithms; at t = 150 s, the number of targets searched by DGWO was one, while the other methods were all one; at t = 200 s, IGWO and GWO can search four targets with lower coverage, whereas the greedy algorithm and DMPC only searched three targets, DGWO still only found four targets; at t = 250 s, only the IGWO searched all targets and the growth rate of its coverage was accelerated; and at t = 300 s, only the IGWO found all targets and achieved a coverage of 0.7875, which is higher than those of the other algorithms.
| Search time t (s) | 100 | 150 | 200 | 250 | 300 |
|---|---|---|---|---|---|
| GWO | |||||
| Number of targets searched | 1 | 3 | 4 | 4 | 4 |
| Coverage rate | 0.3375 | 0.4525 | 0.5450 | 0.6400 | 0.7625 |
| MPSO | |||||
| Number of targets searched | 1 | 3 | 4 | 4 | 4 |
| Coverage rate | 0.3825 | 0.5025 | 0.6075 | 0.6225 | 0.7125 |
| Greedy | |||||
| Number of targets searched | 1 | 3 | 3 | 3 | 4 |
| Coverage rate | 0.3350 | 0.4425 | 0.4975 | 0.5700 | 0.7225 |
| DMPC | |||||
| Number of targets searched | 1 | 3 | 3 | 4 | 4 |
| Coverage rate | 0.4100 | 0.5325 | 0.6425 | 0.7275 | 0.7475 |
| DGWO | |||||
| Number of targets searched | 2 | 4 | 4 | 4 | 4 |
| Coverage rate | 0.3900 | 0.5400 | 0.5775 | 0.5800 | 0.7600 |
| IGWO | |||||
| Number of targets searched | 1 | 3 | 4 | 5 | 5 |
| Coverage rate | 0.3375 | 0.4525 | 0.5100 | 0.6175 | 0.7825 |
The overall search process is shown in Figure 10, with the final TPM of UAV1 in the bottom panel (Section 4.1 demonstrates that the TPMs of all UAVs are consistent), where the darker areas are the obstacles detected by the UAVs and the red and violet dots are the starting points of the UAV and targets, respectively. Notably, the trajectories of IGWO and GWO were the same in the early stage; however, the advantages of the strategy developed in this study became effective after the UAV gathered a certain amount of environmental information and avoided the local optima to locate all the targets. DGWO shows high efficiency in the early stage of search but tends to get trapped in local optima in the mid to late stages. The MPSO and greedy methods focused on high-probability regions, leading to local optima entrapment and hampering search efficiency. DMPC can escape local optimum; however, it has limitations with updating rules, impacting the overall information utilization and resulting in inferior search efficiency compared to that of IGWO.
5. Conclusions and Future Works
In this study, we investigated collaborative target search methods for multiple UAVs in adverse communication environments. To recover damaged transmission information, a strategy based on KNNA, RBFNN, and multisource information fusion was developed. The simulation results indicated that this strategy effectively maintained consistency among all the information of all UAVs. Additionally, to mitigate the impacts of target motion and obstacles on the local TPMs of the UAVs, we employed an information diffusion mechanism for corresponding corrections. For UAV path planning, an algorithm combining the MPC and IGWO was designed. The simulation results demonstrate that IGWO outperforms the popular IOA and other algorithms in terms of optimization performance, significantly improving the search success rate and efficiency. The use of neural networks in recovering corrupted data in this study imposes a heavier computational burden on UAVs compared to classical methods. Additionally, IGWO requires UAVs to possess strong computational capabilities. Therefore, in scenarios with high real-time demands, corresponding improvements may be necessary. We did not consider factors such as flight altitude and adjustable speed and acceleration of the UAV, which will be the focus of our future research.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
The authors received no specific funding for this work.
Acknowledgments
The authors have nothing to report.
Open Research
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.




