Volume 2024, Issue 1 5772579

Research Article

Open Access

Structural, Electronic, Mechanical and Optical Properties of RhZrZ (Z = As, Sb) Half-Heusler Compounds: First-Principles Calculations

Adem Beriso Bejo,

Corresponding Author

Adem Beriso Bejo

[email protected]

orcid.org/0009-0005-5847-3606

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Megersa Wodajo Shura,

Megersa Wodajo Shura

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Mesfin Asfaw Afrassa,

Mesfin Asfaw Afrassa

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kumneger Tadele,

Kumneger Tadele

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Fekadu Tolessa Marem,

Fekadu Tolessa Marem

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kunsa Haho Habura,

Kunsa Haho Habura

Department of Physics , Arba Minch University , Arba Minch , Ethiopia , amu.edu.et

Search for more papers by this author

Adem Beriso Bejo,

Corresponding Author

Adem Beriso Bejo

[email protected]

orcid.org/0009-0005-5847-3606

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Megersa Wodajo Shura,

Megersa Wodajo Shura

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Mesfin Asfaw Afrassa,

Mesfin Asfaw Afrassa

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kumneger Tadele,

Kumneger Tadele

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Fekadu Tolessa Marem,

Fekadu Tolessa Marem

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kunsa Haho Habura,

Kunsa Haho Habura

Department of Physics , Arba Minch University , Arba Minch , Ethiopia , amu.edu.et

Search for more papers by this author

First published: 24 July 2024

https://doi.org/10.1155/2024/5772579

Citations: 2

Academic Editor: Upendra Kumar

Share a link

Email
Wechat
Bluesky

Abstract

In this study, density functional theory (DFT) as it is implemented in the Quantum Espresso simulation package was employed to investigate the structural, electronic, mechanical and optical properties of RhZrZ (Z = As, Sb) half-Heusler compounds. Results reveal that both the two compounds are most stable in α phase. Analysis of mechanical properties shows that the compounds are ductile in nature and mechanically stable. Calculations of band structure and density of states indicated that they are semiconductors with RhZrAs direct and RhZrSb indirect band gap. Furthermore, the investigation of the optical properties reveals that there is a high absorption coefficient and low electron energy loss in visible and some ultraviolet energy spectrum indicating that these compounds are potential candidates for optoelectronic applications.

1. Introduction

Since their discovery by German mining engineer and chemist, Heusler in 1903, the diverse properties of Heusler compounds have highly attracted the attention of different scientific communities [1]. Heusler compounds have very interesting properties including high spin-polarization, high Curie temperature, excellent mechanical stability, and half-metallicity [2]. Materials with high curie temperature have wide range of thermal stability and hence a wide range of applications, such as for high energy efficient devices [3, 4]. Half-metallic materials are materials that show metallic properties in one spin channel (e.g., spin up) around Fermi level but form band gap for another spin channel (e.g., spin down) around the Fermi level [5, 6]. Half-metallic materials can make 100% spin polarization at the Fermi level making them potential candidates for applications in spintronics [7, 8]. Half-metallic behavior was first predicted on half-Heusler compound NiMnSb by de Groot et al. [9]. Today, there are many half-Heusler compounds that exhibit half-metallic character. Possibility of band gap engineering as well as having high absorption coefficient in visible energy spectrum range also makes half-Heusler compounds attractive in optoelectronic applications [10].

Depending on their crystalline structures, Heusler compounds are mainly categorized into three classes: half, full, and quaternary Heusler compounds with their chemical formula XYZ, X₂YZ, and XX’YZ, respectively, where X, X’, and Y are transition metals and Z is nonmagnetic element from the III, IV, or V main groups [11, 12]. Full-Heusler compounds have two main categories, L2₁ (conventional) or the Cu₂MnAl type structure and XA (inverse) or the Hg₂TiCu type structure which both consist of four interpenetrating face-centered cubic (fcc) lattices [13]. If X has more valence band electrons than Y then the compound prefers L2₁ type structure but if X has less valence band electron than Y then the compound prefers XA type structure [14, 15]. The crystal structure of any half-Heusler (XYZ) compound is similar to the crystal structure of full-Heusler compounds (X₂YZ) but missing one X atom from half-Heusler compound [16].

Rhodium (Rh)-based half-Heusler compounds are members of half-Heusler compounds, where recently they have been investigated by some theoretical and experimental researchers to determine their different properties. Lone et al. [17] investigated the structural, electronic, and magnetic properties of half-Heusler compounds, XCrP (X = Pt, Rh) by using density functional theory (DFT). They predicted that all three compounds are most stable in the ferromagnetic state than that of the nonmagnetic and antiferromagnetic phases. Muhammad et al. [18] investigated the structural, mechanical, thermal, magnetic, and electronic properties of the RhMnSb half-Heusler alloy under pressure using first-principles calculations based on DFT, where pressure affects all the properties under their study. Meenakshi et al. [19] investigated the electronic structure, magnetic, optical, and transport properties of half-Heusler alloys RhFeZ (Z = P, As, Sb, Sn, Si, Ge, Ga, In, Al) using DFT by considering three phases: α, β, and γ. They reported that all the alloys in all three phases are mechanically stable, incompressible, ionic, and metallic in nature. Kadri et al. [20] studied structural, elastic, thermal, and transport properties of X (X = Co, Rh, and Ir) MnAs half-Heusler compounds with the help of DFT. Structurally, all three compounds are most stable when they are in ferromagnetic phase than in the nonmagnetic phase and they are also mechanically stable. Structural, mechanical, and thermoelectric properties of half-Heusler compounds RhBiX (X = Ti, Zr, and Hf) were investigated by Wei et al. [21] and they reported that the compounds are stable both mechanically and dynamically.

To the best of our knowledge, no experimental study has been conducted on both half-Heusler compounds under our study. Again, no any theoretical report is available on RhZrAs half-Heusler compound while few properties of RhZrSb half-Heusler compound were theoretically studied. Due to these reasons, we were motivated to investigate and analyze structural, electronic, mechanical, and optical properties of RhZrZ (Z = As, Sb) half-Heusler compounds for possible optoelectronic applications.

2. Theory

This section is devoted to mathematical relations that are used to calculate structural, electronic, mechanical, and optical properties of half-Heusler compounds under the current study. For optical property investigation, first, we start with complex dielectric function from which all other optical properties can be calculated. This complex dielectric function ε (ω) is expressed as follows:

(1)

where ε₁ (ω) is the real part of the dielectric function and ε₂ (ω) is the imaginary part of the dielectric function [22]. By using the real and imaginary parts of dielectric functions, other optical parameters such as the absorption coefficient (α (ω)), refractive index (n (ω)), extinction coefficient (k (ω)), reflectivity (R (ω)), and electron energy loss function (L (ω)) can be calculated as follows [23]:

(2)

(3)

(4)

(5)

(6)

Mechanical stability against deformation is checked from Born and Huang stability criteria for cubic structure which is given as follows [24]:

(7)

Birch–Murnaghan equation of state [25, 26] was used to calculate the equilibrium lattice constant (a_o), minimum volume (V_o), minimum energy (E_o), bulk modulus (B), and its first pressure derivative (B’) and is given as follows:

(8)

To analyze other mechanical properties such as anisotropy (A) [27], Cauchy’s pressure (CP) [28], bulk, shear, Voigt’s shear, Reuss’s shear, Young’s modulus, Poisson’s ratio, and hardness of a material [29], the following equations were used:

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

Finally, the melting temperature for materials under study was theoretically predicted in terms of the elastic constant, C₁₁ by the following equation [30]:

(18)

3. Computational Methods

First-principles calculations based on DFT using a quantum espresso simulation package (QE) were applied to calculate the structural, electronic, mechanical and optical properties of RhZrZ (Z = As, Sb) half-Heusler compounds. Generalized gradient approximation (GGA) with Perdew, Burke, and Ernzerhof of (PBE) functional type was used to treat exchange and correlation of electrons. The plane wave ultrasoft and norm-conserving pseudopotentials were used. Before calculations of all properties mentioned above, convergences for kinetic energy cutoff, k-points, and lattice constant were done. From kinetic energy cutoff convergence test, 100 Ry was obtained and used for both the two compounds property calculation. From k-points convergence test, 14 × 14 × 14 k-point mesh was obtained and used for the sampling of the irreducible Brillouin zone in k-space but for the study of partial density of states (PDOS) a denser 42 × 42 × 42 k-point was employed. Energy-strain method was used to calculate the mechanical properties of the half-Heusler compounds under our study. XCrySDen and VESTA software were used for crystal modeling, design, and visualization.

4. Results and Discussion

4.1. Structural Properties

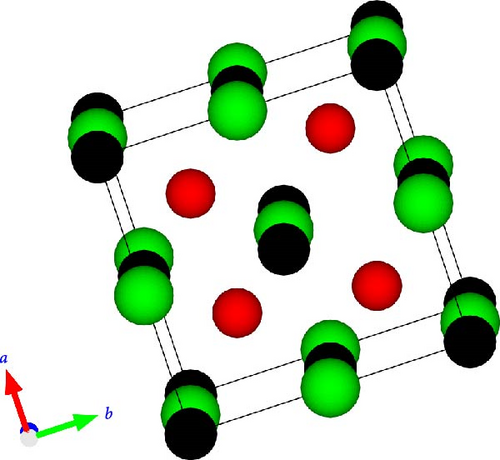
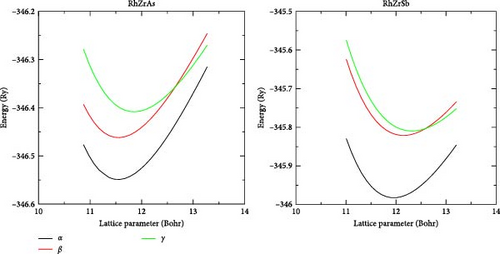
Figure 1 shows the RhZrZ (Z = As, Sb) half-Heusler compounds crystallize in fcc type crystal structure with space group F43m (No. 216). In this work, we first considered three types of phases, namely α, β, and γ to check in which phase the compounds are most stable. In the α phase, atoms are positioned as Rh (0.25; 0.25; 0.25), Zr (0.5; 0.5; 0.5), and Z (0.0; 0.0; 0.0). In the β phase, atoms are positioned as Rh (0.5; 0.5; 0.5), Zr (0.0; 0.0; 0.0), and Z (0.25; 0.25; 0.25), whereas in the γ phase, they are positioned as Rh (0.0; 0.0; 0.0), Zr (0.25; 0.25; 0.25), and Z (0.5; 0.5; 0.5). For all three phases, the equilibrium lattice constant (a₀), minimum volume (V₀), minimum energy (E₀), bulk modulus (B), and its pressure derivative (B’) were calculated from Birch–Murnaghan equation of state (Equation (8)) and are listed in Table 1. Lattice constant vs. energy for these three phases of the two compounds are drawn and shown in Figure 2. As can be observed from Table 1 and Figure 2, both half-Heusler compounds are most stable in the α phase because compared to other phases their energy is minimum in the α phase. Hereafter, we consider the most stable phase (α phase) for other properties calculations.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Alpha (α) phase half-Heusler RhZrZ (Z = As, Sb) generated by VESTA. The colors red, green, and black are for Rh, Zr, and Z = As, Sb, respectively.

Table 1. Phases of RhZrZ (Z = As, Sb) half-Heusler compounds with their corresponding minimum energy.

Half-Heusler compound	Phase	a₀ (Bohr)	V₀(Bohr³)	Minimum energy (Ry)	B (Gpa)	B^′
RhZrAs	α	11.5293	383.13	−346.54874	145.9	5.38
	β	11.5365	383.85	−346.46188	135.8	5.40
	γ	11.8512	416.12	−346.40785	107.4	4.53

RhZrSb	α	11.9552	427.18	−345.98118	137.8	4.64
	β	12.1538	448.82	−345.82081	110.2	4.42
	γ	12.3246	468.02	−345.80952	97.0	4.08

Lattice constant vs. energy for these three phases of the three compounds are also shown in Figure 2. As can be observed from Table 1 and Figure 2, all the three half-Heusler compounds are most stable in the α phase because compared to other phases their energy is minimum in the α phase. Hereafter, we consider the most stable phase (α phase) for other properties calculations.

4.2. Mechanical Properties

In order to discuss the mechanical stability of the Heusler compounds, whether they are ternary or quaternary compounds, the value of elastic constants must be first determined [31]. For simple geometrical system (cubic crystals) like half-Heusler compounds under our study, we need only three independent elastic constants C₁₁, C₁₂, and C₄₄ even though we can have many of these elastic constants in tensor form for other more complicated geometry [32]. After stability is determined, anisotropy, Cauchy’s pressure, bulk modulus, shear modulus, etc., can be applied to further see the mechanical properties of a given Heusler compound.

Anisotropy deals with the microcracks and defects in the material as it varies from the equilibrium value (A = 1). As the value of the anisotropy (A) increases above 1, the possibility of cracks and defects increase. Hence, RhZrAs compound has high possibility of cracks and defects compared to RhZrSb compound. The value of Cauchy’s pressure (CP) for both two compounds is positive indicating that the atomic bonding in these materials is ductile.

The three independent elastic constants C₁₁, C₁₂, and C₄₄ and other mechanical parameters for the two half-Heusler compounds in α phase are presented in Table 2. These elastic constants fullfill Born and Huang stability criteria (Equation (7)) and hence the compounds, RhZrZ (Z = As, Sb), are mechanically stable. RhZrAs has greater value of bulk modulus indicating that it is harder than RhZrSb. As we can see from Table 2, both the compounds under our study are ductile in nature because their Pugh’s and Poisson ratios are greater than the equilibrium values, 1.75 and 0.26 of Pugh’s and Poisson ratios, respectively. The Young’s modulus measures rigidity of materials. Thus, RhZrSb is more rigid than RhZrAs.

Table 2. Calculated values of elastic constants (C_ij (Gpa)), bulk modulus (B (Gpa)), Voigt modulus (G_V (Gpa)), Reuss modulus (G_R (Gpa)), shear modulus (G (Gpa)), Pugh’s ratio (B/G), Young’s modulus (Y (Gpa)), Poisson ratio (ν), hardness (H), anisotropy (A), Cauchy’s pressure (CP), and T_m (K) for RhZrZ (Z = As, Sb) half-Heusler compounds.

Mechanical parameters	RhZrAs	RhZrSb
C₁₁	208.32	277.62
C₁₂	118.145	69.40
C₄₄	50.56	38.594
B	148.21	138.81
G_V	48.38	64.80
G_R	48.23	51.57
G	48.31	58.19
B/G	3.07	2.39
Y	130.73	153.17
ν	0.35	0.32
H	5.21	3.9
A	1.12	0.37
CP	67.57	30.81
T_m ± 300 K	1,784.38	2,194.01

The melting temperature is an important factor for materials used in the heating system. The predicted values of melting temperature for the two compounds are presented in Table 2 with higher value for RhZrSb followed by RhZrAs. In general, these two compounds have high melting temperatures indicating that they are stable at high temperatures.

4.3. Electronic Properties

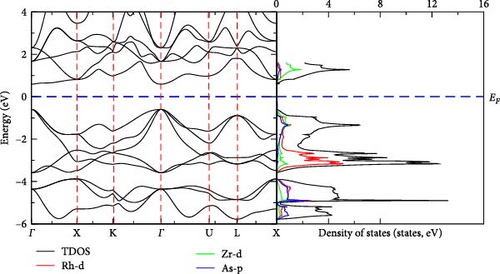
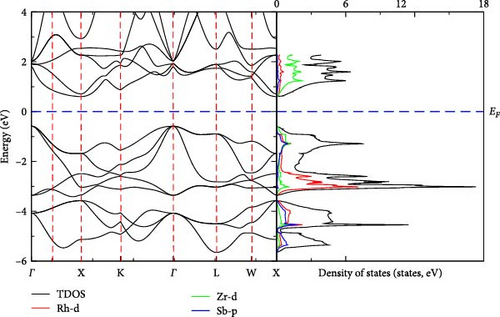
We have carried out calculation of electronic band structure of RhZrZ (Z = As, Sb) to predict their electronic nature by applying the GGA-PBE approach. As can be observed from Figures 3 and 4, RhZrAs and RhZrSb are semiconductor compounds. RhZrAs has a direct band gap at Γ→Γ (Figure 3) but RhZrSb has indirect band gap at Γ→X (Figure 4). The value of calculated band gap, optimized lattice constant, bulk modulus, and its pressure derivatives for the two compounds are presented in Table 3 along with some available previous works. DOS and PDOS for RhZrZ (Z = As, Sb) half-Heusler compounds are also computed and are shown in Figures 3 and 4. From these figures, it can be observed that there is an electronic band gap around Fermi level on both sides for RhZrAs and RhZrSb. This implies that there is a quite agreement between results of electronic band structure and density of states, as shown in Figures 3 and 4. Since the two compounds under the current study are semiconductor in α phase atomic arrangement, they promising candidates for optoelectronic applications.

Table 3. The computed electronic energy band gap, optimized lattice constant, bulk modulus (B), and its pressure derivatives (B′) for RhZrZ (Z = As, Sb) using GGA functional.

Compound	Method	E_g (eV)	a (Å)	B (Gpa)	B′
RhZrAs	Present work	1.1904	6.10	145.9	5.38
	Expt.	—	—	—	—
	Other	—	—	—	—

RhZrSb	Present work	1.1893	6.33	137.8	4.64
	Expt.	—	6.26 [33]	—	—
	Other [32]	1.17 [32]	6.33 [32]	138.03 [32]	4.47 [32]

Expt., experiment.

Both DOS and PDOS yield information about the influence of electronic properties of component atoms on their chemical bonding. Below the Fermi level, the main contribution comes from the Rh-d states while the states above the Fermi level are due to the Zr-d states. In both compounds, Rh-d states largely contribute to the total density of states.

4.4. Optical Properties

For possible optoelectronic applications, we studied the optical properties of the compounds RhZrZ (Z = As, Sb) by considering optical parameters that include dielectric function (both real and imaginary part), absorption coefficient, refractive index, extinction coefficient, reflectivity, and electron energy loss within photon energy range of 0–30 eV to investigate the reaction of these materials to solar energy radiation.

Dielectric function is the most fundamental optical parameter from which other optical parameters can be calculated [34]. The real part is related to the stored energy within the medium and the imaginary part is to the dissipation of energy within the medium [35]. The real and imaginary parts of the dielectric function, for the two compounds, are shown in Figures 5 and 6. For both compounds, there are two major peaks in the energy range of 0–4.5 eV for both dielectric components. From Figures 5 and 6, we can observe that the compounds RhZrAs and RhZrSb show maximum polarization of 46.69 and 47.51 at energies of 2.10 and 1.95 eV, respectively. For photon energies from 12 to 28 eV, the imaginary part of dielectric function goes to zero which shows that photons with higher energies pass through the materials without a huge loss of energy. The occurrence of peaks is due to the electronic transitions from the valence bands to the conduction bands. For both compounds, the value of real part of dielectric function is negative in the photon energy range of approximately 4–19 eV indicating that the compounds have a metallic character in these energy domains.

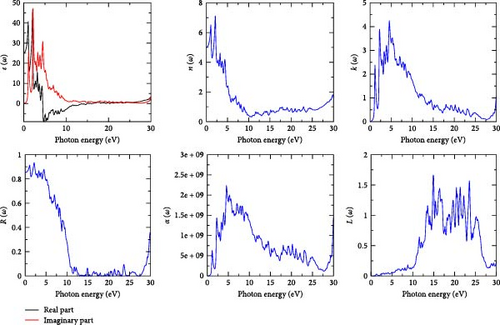
Refractive index, n (ω) which is the real part of reflectivity, determines how much light is bent or refracted when entering into a material [36]. From Figures 5 and 6, we see that the refractive indices of the compounds increase in the photon energy range 0–2 eV but after 2 eV they gradually decrease up to 23 eV and then gradually increase. Since the values of the refractive indices for both compounds are greater than one, the photons entering these materials are slowed down by the interactions with the electrons in the materials.

The imaginary part of reflectivity is the extinction coefficient, k (ω), and it indicates the amount of absorption energy loss of the electromagnetic waves when propagate throughout the material [37]. As we can see from Figures 5 and 6, there is a large amount of absorption energy loss approximately in photon energy range of 1–9 eV (in the whole visible and in some UV regions) for both two compounds.

Absorption coefficient is associated with transition between occupied and unoccupied bands due to light and electron interaction. It also indicates the ability of the material to absorb the incident photon of specific energy. It is one of the most important evaluation criteria to identify if the material is optically active or optoelectronic material [38]. It is illustrated in Figures 5 and 6 for the two compounds. Maximum absorption points for the compounds RhZrAs and RhZrSb are observed at photon energy of 4.56 and 4.16 eV, respectively. For both compounds, maximum absorption is observed in visible–ultraviolet region which tells us that the materials under the current study are potential candidates for optoelectronic applications.

Reflectivity, R (ω), which is the ratio of reflected photon energy to incident photon energy is indicated in Figures 5 and 6 for the two compounds; RhZrAs and RhZrSb with maximum peaks of 0.93 at 2.15 and 0.925 at 2.25 eV, respectively. The values of real part of dielectric function, refractive index, and reflectivity for both compounds at zero frequency are given in Table 4.

Table 4. The values of dielectric function ε₁, the refractive index n, and the reflectivity R for the RhZrZ (Z = As, Sb) compounds at zero frequency.

Compounds	ε₁(0)	n(0)	R(0)
RhZrAs	24.994579	4.9994599	0.85204162
RhZrSb	21.241835	4.6088869	0.82824450

As the external radiation incident on the material, some of the valence electrons may undergo inelastic scattering leading to loss of electron energy, L (ω), and it is an important quantity that describes the energy loss of a fast electron crossing into a given material [39]. From Figures 5 and 6, the highest peak for the two compounds corresponds to their plasma resonance frequency at which the material changes from metallic to dielectric properties. The highest peaks occur at 14.88 and 18.98 eV with values 1.66 and 1.69 for RhZrAs and RhZrSb compounds, respectively. In the photon energy range of 10–28 eV, there is high energy loss by electron for both compounds. For both compounds, there is very low energy loss in the low energy range (IR, visible, and in some UV ranges).

5. Conclusions

The structural, electronic, mechanical, and optical properties of RhZrZ (Z = As, Sb) half-Heusler compounds were predicted in this case. Calculations were performed by using quantum espresso code based on density functional theory (DFT). Our predictions suggest that both the compounds are structurally most stable in α phase and the three elastic constants for these compounds in α phase satisfy Born and Huang stability criteria indicating that the compounds are mechanically stable. Electronic properties are predicted from band structures and density of states (DOS) calculations. Our results suggest that both the compounds are semiconductors. From optical properties investigation, both the compounds under our study have high absorption coefficients and therefore, they can be considered as candidates for optoelectronic applications.

Conflicts of Interest

The authors have no conflicts of interest to disclose.

Acknowledgments

We acknowledge Madda Walabu University (MWU) and Adama Science and Technology University (ASTU) for their support during this work.

Open Research

Data Availability

The data that support the findings of this study are available within the article.

References

1 Yadav D. K., Bhandari S. R., and Kaphle G. C., Structural, elastic, electronic, and magnetic properties of MnNbZ (Z = As, Sb) and FeNbZ (z = Sn, Pb) semi-Heusler alloys, Materials Research Express, 2020, 7, no. 11, 116527.
Google Scholar
2 Graf T., Felser C., and Parkin S. S. P., Simple rules for the understanding of Heusler compounds, Progress in Solid State Chemistry. (2011) 39, no. 1, 1–50, https://doi.org/10.1016/j.progsolidstchem.2011.02.001, 2-s2.0-79955692690.
10.1016/j.progsolidstchem.2011.02.001
CAS Web of Science® Google Scholar
3 Anissa B., Radouan D., and Benaouda B., Optical and thermoelectric response of RhTiSb half-Heusler, International Journal of Modern Physics B. (2019) 33, no. 22, https://doi.org/10.1142/S0217979219502473, 2-s2.0-85072577785, 1950247.
10.1142/S0217979219502473
CAS Google Scholar
4 Chatterjee S., Chatterjee S., Giri S., and Majumdar S., Transport properties of Heusler compounds and alloys, Journal of Physics: Condensed Matter. (2021) 34, no. 1, https://doi.org/10.1088/1361-648X/ac268c, 013001.
10.1088/1361-648X/ac268c
Google Scholar
5 Andharia E., Alqurashi H., and Hamad B., Lattice dynamics, mechanical properties, electronic structure and magnetic properties of equiatomic quaternary Heusler alloys CrTiCoZ (Z = Al, Si) using first principles calculations, Materials, 2022, 15, no. 9, 3128.
Google Scholar
6 Feng L., Liu E. K., Zhang W. X., Wang W. H., and Wu G. H., First-principles investigation of half-metallic ferromagnetism of half-Heusler compounds XYZ, Journal of Magnetism and Magnetic Materials, 2014, 351, 92–97.
Google Scholar
7 Ahmad R. and Mehmood N., A density functional theory investigations of half-Heusler compounds RhVZ (Z = P, As, Sb), Journal of Superconductivity and Novel Magnetism. (2018) 31, no. 5, 1577–1586, https://doi.org/10.1007/s10948-017-4370-4, 2-s2.0-85030548407.
10.1007/s10948-017-4370-4
CAS Google Scholar
8 Galanakis I., Slater–Pauling behavior in half-metallic Heusler compounds, Nanomaterials. (2023) 13, no. 13, https://doi.org/10.3390/nano13132010.
10.3390/nano13132010
PubMed Google Scholar
9 Van Engen Ra De Groot P. G., Mueller F. M., and Buschow K. H. J., New class of materials: half- metallic ferromagnets, Physical Review Letters. (2024) 50, no. 25.
Google Scholar
10 Wei X.-P., Deng J.-B., Mao G.-Y., Chu S.-B., and Hu X.-R., Half-metallic properties for the Ti2YZ (Y = Fe, Co, Ni, Z = Al, Ga, In) Heusler alloys: a first-principles study, Intermetallics. (2012) 29, 86–91.
10.1016/j.intermet.2012.05.002
CAS Web of Science® Google Scholar
11 He J., Naghavi S. S., Hegde V. I., Amsler M., and Wolverton C., Designing and discovering a new family of semi-conducting quaternary Heusler compounds based on the 18-electron rule, Chemistry of Materials. (2018) 30, no. 15, 4978–4985.
10.1021/acs.chemmater.8b01096
CAS Web of Science® Google Scholar
12 Mostari F., Rahman M. A., and Khatun R., First principles study on the structural, elastic, electronic and optical properties of cubic ‘half-Heusler’ alloy RuVAs under pressure, International Journal of Mathematical Sciences. (2020) 2, no. 4, 51–63.
Google Scholar
13 Durukan I. K. and Ciftci Y. O., First-principles calculations of vibrational and optical properties of half-Heusler NaScSi, Indian Journal of Physics. (2021) 95, 2303–2312.
10.1007/s12648-020-01887-0
Google Scholar
14 Fadila B., Ameri M., Bensaid D., Noureddine M., Ameri I., Mesbah S., and Al-Douri Y., Structural, magnetic, electronic and mechanical properties of full-Heusler alloys Co₂YAl (Y = Fe, Ti): first principles calculations with different exchange-correlation potentials, Journal of Magnetism and Magnetic Materials. (2018) 448, 208–220.
10.1016/j.jmmm.2017.06.048
CAS Web of Science® Google Scholar
15 Nepal S., Dhakal R., and Galanakis I., Ab initio study of the half-metallic full- Heusler compounds Co2ZAl [Z = Sc, Ti, V, Cr, Mn, Fe]; the role of electronic correlations, Materials Today Communications. (2020) 25, 101498.
10.1016/j.mtcomm.2020.101498
CAS Google Scholar
16 Yang T., Hao L., Khenata R., and Wang X., Investigation of the structural competing and atomic ordering in Heusler compounds Fe₂NiSi and Ni₂FeSi under strain condition, Royal Society Open Science. (2019) 6, no. 9, https://doi.org/10.1098/rsos.191007, 2-s2.0-85073054844, 191007.
10.1098/rsos.191007
CAS PubMed Web of Science® Google Scholar
17 Lone I. U. N., Sirajuddeen M. M. S., and Rubab S., A comparison study of the structural, electronic and magnetic properties in zinc-blende PtXCr_1-xP and RhXCr_1-xP (x = 0.125, 0.25), and half-Heusler XCrP (X = Pt, Rh): first principles calculations, Materials Chemistry and Physics. (2019) 230, 151–161.
10.1016/j.matchemphys.2019.03.061
CAS Google Scholar
18 Muhammad I., Zhang J.-M., Ali A., Rehman M. U., and Muhammad S., Structural, mechanical, thermal, magnetic, and electronic properties of the RhMnSb half- Heusler alloy under pressure, Materials Chemistry and Physics. (2020) 251, 123110.
10.1016/j.matchemphys.2020.123110
CAS Web of Science® Google Scholar
19 Meenakshi R., Srinivasan R. A. S., Amudhavalli A., Rajeswara-palanichamy R., and Iyakutti K., Electronic structure, magnetic, optical and transport properties of half-Heusler alloys RhFeZ (Z = P, As, Sb, Sn, Si, Ge, Ga, In, Al)-a dft study, Phase Transitions. (2021) 94, no. 6–8, 415–435.
10.1080/01411594.2021.1944626
CAS Google Scholar
20 Kadri S., Mohamed T., Mahièddine B., Rabie A., and Zeyneb B., Study of structural, elastic, thermal and transport properties of ternary X (X = Co, Rh and Ir) MnAs obtained by dft, East European Journal of Physics. (2022) 1, 47–57.
10.26565/2312-4334-2022-1-07
Google Scholar
21 Wei J., Guo Y., and Wang G., Exploring structural, mechanical, and thermoelectric properties of half-Heusler compounds RhBiX (X = Ti, Zr, Hf): a first- principles investigation, RSC Advances. (2023) 13, no. 17, 11513–11524, https://doi.org/10.1039/d3ra01262j.
10.1039/D3RA01262J
CAS PubMed Google Scholar
22 Ahmad R. and Mehmood N., Theoretical investigations of properties of new half- Heusler compounds NiFeZ (Z = Si, Ge), Journal of Superconductivity and Novel Magnetism. (2018) 31, 1751–1759.
10.1007/s10948-017-4378-9
CAS Google Scholar
23 Khattab E.-S. R., Abd El Rehim S. S., Hassan W. M. I., and El-Shazly T. S., Band structure engineering and optical properties of pristine and doped monoclinic zirconia (m- ZrO₂): density functional theory theoretical prospective, ACS Omega. (2021) 6, no. 44, 30061–30068, https://doi.org/10.1021/acsomega.1c04756.
10.1021/acsomega.1c04756
CAS PubMed Web of Science® Google Scholar
24 Uto O. T., Adebambo P. O., Akinlami J. O., Kenmoe S., and Adebayo G. A., Electronic, structural, mechanical, and thermodynamic properties of CoYSb (Y = Cr, Mo, W) half-Heusler compounds as potential spintronic materials, Solids. (2022) 3, no. 1, 22–33.
10.3390/solids3010002
CAS Web of Science® Google Scholar
25 Katsura T. and Tange Y., A simple derivation of the Birch–Murnaghan equations of state (EOSs) and comparison with EOSs derived from other definitions of finite strain, Minerals. (2019) 9, no. 12, 745.
10.3390/min9120745
CAS Web of Science® Google Scholar
26 Amari D., Mokhtari M., Dahmane F., Belfarh T., Tabeti A., Elkeurti M., and Khenata R., A comparative study between Hg₂CuTi and Cu₂MnAl type structures for Zr₂CoZ (Z = Al, Ga, In) Heusler alloys, Chinese Journal of Physics. (2019) 60, 450–461.
10.1016/j.cjph.2019.05.024
CAS Web of Science® Google Scholar
27 Hossain M. A., Rahman Md T., Khatun M., and Haque E., Structural, elastic, electronic, magnetic and thermoelectric properties of new quaternary Heusler compounds CoZrMnX (X = Al, Ga, Ge, In), Computational Condensed Matter. (2018) 15, 31–41.
10.1016/j.cocom.2018.03.006
Web of Science® Google Scholar
28 Singh S. and Gupta D. C., Electronic structure, mechanical, thermoelectric, optical, and thermodynamic properties of yttrium-based Quaternary Heusler alloys, International Journal of Energy Research. (2019) 43, no. 14, 8633–8648.
10.1002/er.4860
CAS Web of Science® Google Scholar
29 Zerrouki T., Rached H., Rached D., Caid M., Cheref O., and Rabah M., First-principles calculations to investigate structural stabilities, mechanical and optoelectronic properties of NbCoSn and NbFeSb half-Heusler compounds, International Journal of Quantum Chemistry. (2021) 121, no. 8, e26582.
10.1002/qua.26582
CAS Web of Science® Google Scholar
30 Stinshof R., Nayak A. K., Fecher G. H., Balke B., Ouardi S., Skourski Y., Nakamura T., and Felser C., Completely compensated ferrimagnetism and sublattice spin crossing in the half-metallic Heusler compound Mn_1.5FeV_0.5Al, Physical Review B. (2017) 95, no. 6, 060410.
10.1103/PhysRevB.95.060410
Google Scholar
31 Rogl G., Grytsiv A., Gürth M., Tavassoli A., Ebner C., Wünschek A., Puchegger S., Soprunyuk V., Schranz W., Bauer E., Müller H., Zehetbauer M., and Rogl P., Mechanical properties of half-Heusler alloys, Acta Materialia. (2016) 107, 178–195.
10.1016/j.actamat.2016.01.031
CAS Web of Science® Google Scholar
32 Jubair M., Karim A. M. M. T., Nuruzzaman M., Roknuzzaman M., and Zilani M. A. K., Pressure dependent structural, elastic and mechanical properties with ground state electronic and optical properties of half-metallic Heusler compounds Cr₂YAl (Y = Mn, Co): first- principles study, Heliyon. (2021) 7, no. 12.
10.1016/j.heliyon.2021.e08585
PubMed Google Scholar
33 Dwight A. E., Alloying behavior of zirconium, hafnium and the actinides in several series of isostructural compounds, Journal of the Less Common Metals. (1974) 34, no. 2, 279–284.
10.1016/0022-5088(74)90170-2
CAS Google Scholar
34 Benzoudji F., Abid O. M., Seddik T., Yakoubi A., Khenata R., Meradji H., Ugur G., U§ur S., and Ocak H. Y., Insight into the structural, elastic, electronic, thermoelectric, thermodynamic and optical properties of MRhSb (M = Ti, Zr, Hf) half-Heuslers from ab initio calculations, Chinese Journal of Physics. (2019) 59, 434–448.
10.1016/j.cjph.2019.04.009
CAS Web of Science® Google Scholar
35 Almaghbash Z., Arbouche O., Dahani A., Cherifi A., Belabbas M., Zenati A., Mebarki H., and Hussain A., Thermoelectric and piezoelectric properties in half-Heusler compounds TaXSn (X = Co, Rh and Ir) based on ab initio calculations, International Journal of Thermophysics. (2021) 42, 1–19.
10.1007/s10765-020-02755-z
Google Scholar
36 Ahmad M., Naeemullah, Murtaza G., Khenata R., Bin Omran S., and Bouhemadou A., Structural, elastic, electronic, magnetic and optical properties of RbSrX (C, Si, Ge) half-Heusler compounds, Journal of Magnetism and Magnetic Materials. (2015) 377, 204–210, https://doi.org/10.1016/j.jmmm.2014.10.108, 2-s2.0-84908546319.
10.1016/j.jmmm.2014.10.108
CAS Web of Science® Google Scholar
37 Mehmood N. and Ahmad R., Structural, electronic, magnetic, and optical properties of half-Heusler alloys RuMnZ (z = P, As): a first-principles study, Journal of Superconductivity and Novel Magnetism. (2018) 31, no. 1, 233–239, https://doi.org/10.1007/s10948-017-4196-0, 2-s2.0-85021048401.
10.1007/s10948-017-4196-0
CAS Google Scholar
38 Surucu G., Candan A., Erkisi A., Gencer A., and Güllü H. H., First principles study on the structural, electronic, mechanical and lattice dynamical properties of XRhSb (X = Ti and Zr) paramagnet half-Heusler antimonides, Materials Research Express. (2019) 6, no. 10, https://doi.org/10.1088/2053-1591/ab4039, 2-s2.0-85072739525, 106315.
10.1088/2053-1591/ab4039
CAS Google Scholar
39 Chernov S., Lidig C., Fedchenko O., Medjanik K., Babenkov S., Vasilyev D., Jourdan M., Schönhense G., and Elmers H. J., Band structure tuning of Heusler compounds: spin-and momentum-resolved electronic structure analysis of compounds with different band filling, Physical Review B. (2021) 103, no. 5, https://doi.org/10.1103/PhysRevB.103.054407, 054407.
10.1103/PhysRevB.103.054407
CAS Web of Science® Google Scholar

Citing Literature

All articles

Structural, Electronic, Mechanical and Optical Properties of RhZrZ (Z = As, Sb) Half-Heusler Compounds: First-Principles Calculations

Abstract

1. Introduction

2. Theory

3. Computational Methods