1. Introduction

Many studies on electromagnetic (EM) surface waves have been conducted due to their fascinating applications (i.e., surface communication, optical sensing, chemical sensing, chiral sensing, spectroscopy, and near-field imaging) [1]. To control and manipulate the electromagnetic waves, different types of natural and artificial materials have been investigated, i.e., metamaterials [2], metasurfaces [3], near zero index materials [4], nanostructures [5], and graphene [6]. The EM surface wave concept (i.e., the EM surface wave travels along an interface of two different media and decays exponentially as the distance from the interface increases) was first introduced in 1907 [7–9]. Since then, it has gained the attention of numerous researchers due to its various potential applications, such as surface communication, surface-enhanced Raman scattering, chemical sensing, spectroscopy, near-field imaging, and biosensing [8]. Different EM surface waves (e.g., nonlinear surface waves and surface plasmon polaritons (SPPs), chiral surface waves, and Dyakonov surface waves (DSWs)) are supported depending on the interface type. That is, SPP waves propagate along metal and dielectric interfaces, DSWs propagate along uniaxially anisotropic and isotropic interfaces, and nonlinear surface waves propagate along nonlinear interfaces [9, 10]. By changing the sign of permittivity of a material when a metal is in contact with a dielectric, surface plasmons (SPs) are produced having applications in subwavelength resolution imaging, subdiffraction focusing, and signal filtering [11].

Almost three decades ago, the presence of a novel hybridized surface wave propagating along the interface of a transparent uniaxial medium and a dielectric medium was predicted theoretically by Dyakonov [12]. The experimental verification of these surface waves took more than 20 years [13]. The DSWs have been studied due to the change in symmetry between two media, at least one of which should be anisotropic in nature [14]. The study of DSWs with several anisotropic media (e.g., chiral materials [15], biaxial crystals [16], nonhomogeneous media [17], and hyperbolic metamaterials) has also been reported [18]. Typically, the propagation of an SPP wave occurs in a wide range of directions along an interface plane, while that of a DSW on an interface plane appears in a small angular existence domain. By changing the temperature, DSWs are switched into SPP waves due to the planar interface of the temperature-insensitive uniaxial material and temperature-sensitive isotropic material. This ability to tune the transformation of waves by controlling the temperature can potentially be used in temperature-sensing applications [19].

Uniaxial crystal is important due to its unique properties, such as its polarization-hybridized nature [20]. Moradi and Niknam considered the TiO₂ as rutile uniaxial crystal and carried out the theoretical study on the propagation of Dyakonov plasmon surface waves (DPSWs) supported by the plasma/TiO₂ interface [21]. However, they do not consider the temperature-dependent characteristics of plasma on the DPSWs. Some temperature-sensitive materials (TSMs) support surface waves. Due to their low electron density, high electron mobility, and lower effective mass, some narrow bandgap semiconductors such as indium antimonide (InSb) may be utilized as temperature-sensitive substances. InSb biosensors are utilized in infrared astronomy, temperature-dependent imaging cameras, and microorganism detection. The features of TSM materials can be tuned from insulator to conductor by the change of external temperature [22]. The structure of InSb is manufactured via artificial means by combining indium (In) and antimony (Sb). In the terahertz frequency region, the relative permittivity (ε_r) values of some isotropic dielectric media such as InSb due to the influence of temperature fluctuate from moderately dissipative dielectric crystals (Re (ε_r) > 0) to plasmonic matter (Re (ε_r) < 0). This fluctuation occurs at the temperature for which the value of the real part of relative permittivity is zero [19]. Owing to the transition features of temperature-dependent metal insulators, InSb and vanadium dioxide (VO₂) have been thoroughly investigated in the literature as temperature-dependent semiconductor materials [23, 24]. A multitude of studies have reported EM surface waves that are supported by TSMs. Specifically, Mackay and Lakhtakia used InSb and uniaxial materials to solve the canonical boundary value problem and examine the Dyakonov to SPP wave transition at a frequency range of 0.6 THz [19]. They continued to expand on their theoretical research on temperature-sensitive hyperbolic materials made of InSb and published their findings on the propagation of surface waves at 2 THz with negative phase velocity [25]. Fedorin conducted a numerical analysis to examine the impact of temperature on the planar surface interface across a nanocomposite porous material and a hypercrystal made of n-type layers of the semiconductor material (i.e., InSb). The results indicated that the temperature has an effect on the propagation length, effective mode index, and penetration depth. In addition, the dissipation elements influencing the propagation of hybrid and SP modes have been thoroughly examined. It has been found that the propagation frequency band and surface wave characteristics can be improved at a suitable level of temperature [26].

Applications such as temperature sensing and crystallographic phase detection have prompted theoretical research into the temperature-dependent propagation of SPP waves supported by the interface of silver/ VO₂. It has been discovered that the properties of an SPP wave are sensitive to the whole range of its thermal hysteresis [27]. Moreover, according to a theoretical temperature-dependent study of the EM surface wave propagation properties accompanied by graphene-packed semi-infinite InSb, in comparison to monolayer graphene, the graphene-InSb interface offers greater temperature-assisted versatility to the interfacial SP modes [28].

The present work studied the temperature-dependent DSWs supported by the uniaxial material-InSb interface. The primary motivation was to scrutinize the propagation of surface waves along the interface of uniaxial materials and TSMs such as InSb. It was hypothesized that the temperature may be varied to tune the propagation characteristics of surface waves. The influence of temperature and propagation angle on the dispersion curve, effective mode index, propagation length, and phase speed was analyzed. The remainder of the manuscript is organized as follows: the analytical formulation for the modeling of the problem is provided in Section 2, the numerical computations regarding the analytically derived dispersion equation for surface wave characteristics are given in Section 3, while the conclusions drawn from the numerical results are given in Section 4.

2. Analytical Formulation/Modeling of Problems

Here, the analytical formulation for the temperature-dependent hybrid EM surface waves along the uniaxial crystal-TSM interface is provided. The geometry of the problem is presented in Figure 1. The materials are stacked along the x-axis, where the region x < 0 contains TSMs with temperature-dependent permittivity (ε_T(ω, T)) and the region x > 0 is comprised of the uniaxial metamaterial crystal with the permittivity tensor $$ [29]. The uniaxial crystal-TSM interface is considered to be at x = 0. To secure the homogeneity at the interface, the optical axis (OA) of the crystal is assumed to be within the interface. The propagation of the surface wave is considered to be along the z-axis, at angle (φ) with the OA in the yz-plane, while the x-axis is orthogonal to the interface [29, 30].

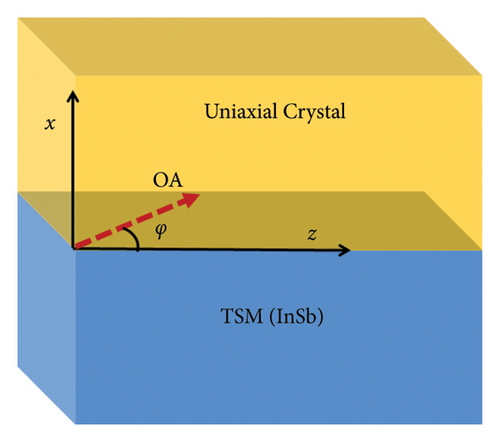
In the literature, such problems have been solved by using the different analytical methods, i.e., effective medium theory [31], transmission line model [32], equivalent circuit model [33], absorber model [34], and Dyadic green’s function [35]. However, in present, to simplify the problem, the waveguide model has been adopted to study the propagation of hybrid Dyakonov surface waves along the uniaxial crystal-InSb planar interface [20, 21].

This expression provides the analytical result for the propagation of surface waves supported by the uniaxial metamaterial crystal-TSM interface. To explore the possible propagation modes of the supporting DSWs by the proposed structure, the numerical results have been provided in the next section.

3. Results and Discussion

The plasma frequency is affected by the intrinsic carrier density “N(T),” electronic charge “q_e,” and mass of electron “m_e” (i.e., q_e = −1.6 × 10⁻¹⁹ C, m_e = 9.1 × 10⁻³¹ kg, and γ = π × 10¹¹ rad s⁻¹).The intrinsic carrier density “N” depends upon the temperature “T,” bandgap “E_g,” and Boltzmann constant “k_B” and can be calculated as N (T) = 5.76 × 10²⁰ T^(3/2) exp(−E_g/2k_BT)m⁻³ where the bandgap “E_g” and Boltzmann constant “k_B” values are 0.26 eV and 8.62 × 10⁻⁵ eV/K. As the intrinsic carrier density “N” depends upon the temperature “T,” we can say that the plasma frequency is also dependent upon the temperature. Therefore, by tuning the temperature of InSb, the plasma frequency can be adjusted. Thus, the relative permittivity of InSb can be controlled by varying the temperature parameters.

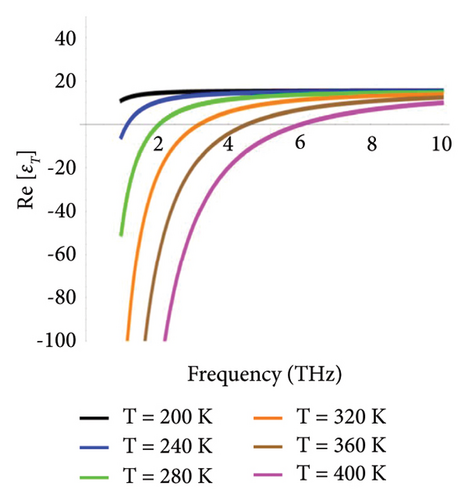
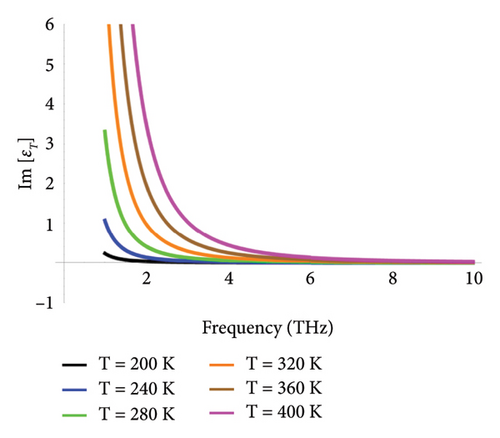
Figure 2 provides the functional analysis of the operational frequency and ambient temperature on the permittivity of InSb. As shown in Figures 2(a) and 2(b), the temperature can be changed to adjust the real and imaginary parts, respectively. As the temperature rises from 200 to 400 K up to the frequency range of 10 THz, Figure 2 shows that the real part of permittivity changes from positive to negative values, indicating the phase transition of InSb from the insulator to metallic phase. However, varying Re (ε_T) has no effect at frequencies exceeding 10 THz. Conversely, as illustrated by Figure 2(b), the imaginary component of permittivity rises with temperature up to a frequency range of 8 THz. It is evident that when T = 200 K, the temperature-dependent permittivity of (ε_T) behaves as an insulator, i.e., Re [ε_T] > 0; at T > 260 K, on the other hand, as indicated by [37], it behaves as a metal, i.e., Re [ε_T] < 0. The surface waves are only supported at the interface between neighboring materials when the actual permittivity of those materials is opposite in sign [27]. It is possible to infer from Figure 2 that the temperature-dependent InSb permittivity can enable the control over the surface wave propagation profile that the InSb interface permits. Thus, ε_T can be tuned by varying the temperature and adjusted according to the desired spectral regime.

3.1. Temperature-Dependent Characteristics of Surface Waves

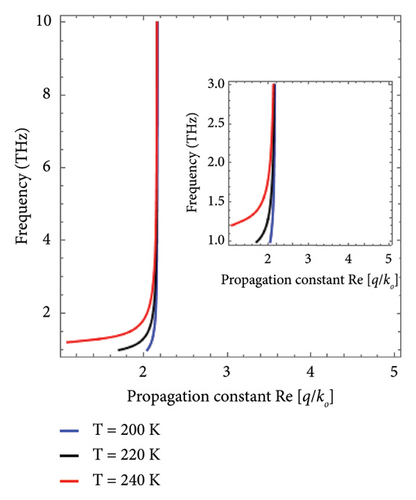
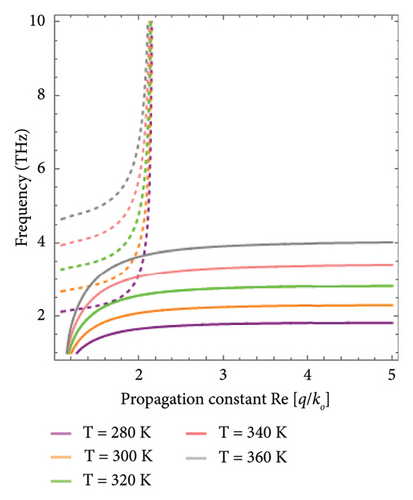
The numerical results regarding the propagation of hybrid Dyakonov waves on the uniaxial metamaterial-InSb interface were obtained under the two configurations (i.e., (i) for pure DSWs) (ε_‖ > ε_T > ε_⊥) and (ii) for hybrid Dyakonov SP waves (DPSWs) (0 > ε_T)), as reported in [29, 38]. To examine the nature and propagation characteristics of waves in media, the dispersion relation is a crucial tool [39]. Dispersion curves provide the response of a material against frequency (w and k relation). The dispersion relation enables the computation of the group velocity, frequency-dependent phase velocity, and characteristics of the propagating waves under a specific spectral range. Figure 3 presents the dispersion curves of hybrid DSWs with the variation of temperature at the propagation angle φ = 30^°. The dispersion curve analysis for pure DSWs supported by the uniaxial-InSb interface tuned via temperature as an external controlling agent is presented in Figure 3(a). For the temperature range (i.e., T ∈ [200, 240] K), InSb behaves as a dielectric material with Re[ε_T]>0 and satisfies the basic condition of pure DSWs (i.e., (ε_‖ > ε_T > ε_⊥)). On the other hand, Figure 3(b) illustrates the influence of temperature variation on the dispersion curve for the temperature range T ∈ [280, 360] K, and it can be inferred that the geometry supports the hybrid Dyakonov plasmon surface waves (DPSWs). The physical reason for the existence of such modes is the transition of InSb from the insulating phase to the conducting phase for the temperature range, as depicted in Figure 2, and the real part of permittivity of InSb becomes negative (i.e., Re [ε_T] < 0) and supports the hybrid DPSWs. The hybridized nature of dispersion curves with upper and lower frequency modes is presented in Figure 3(b). The figure shows that the resonance frequency increases with the temperature, as reported in [28, 29], as the plasma frequency of InSb depends upon the intrinsic carrier density (N), which can be varied by tuning the temperature according to equations (10) and (11). By increasing the temperature of InSb, the plasma frequency of InSb increases, which couples with the Dyakonov modes to excite the DPSWs at the InSb-uniaxial material interface for temperature range T ∈ [280, 360] K. The temperature-dependent InSb permittivity enables the control over the surface wave propagation profile that the InSb interface permits. Thus, ε_T can be tuned by varying the temperature and adjusted according to the desired spectral regime. It is evident that when T = 200 K, the temperature-dependent permittivity of (ε_T) behaves as an insulator, i.e., Re [ε_T] > 0; at T > 260 K, and it behaves as a metal, i.e., Re [ε_T) <0. So, the major driving transition factor is the transition of InSb as an insulator to metal which is responsible for the transition from the DSWs to DPSWs.

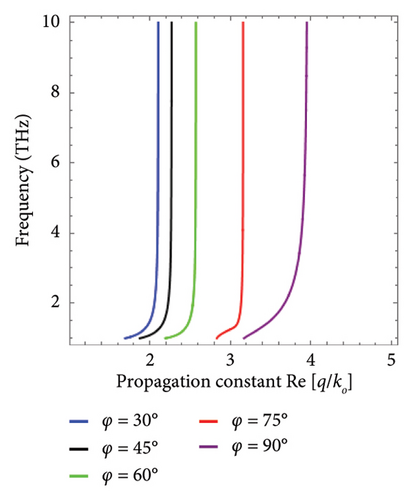
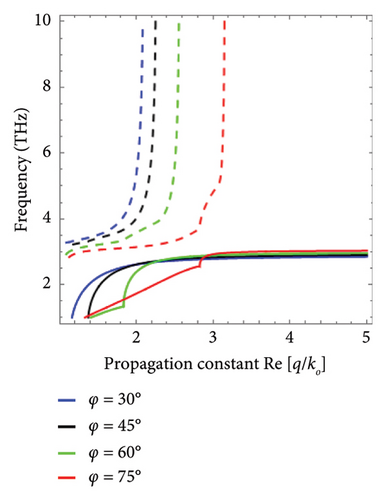
To study the direction dependence on the DSWs and DPSWs, the dispersion curve analysis is presented in Figure 4 for propagation angle variation (i.e., φ = 30^°, 45^°, 60^°, 75^°, and90^°). In Figure 4(a), the dispersion curve for DSWs is analyzed for the fixed temperature T = 200 K at which the InSb behaves as an insulator. It is clear that the characteristics of DSWs can be tuned by increasing the propagation angle. Moreover, for the temperature T = 300 K, InSb behaves as a metal, and the influence of the propagation angle φ = 30^°, 45^°, 60^°, and 75^° on the dispersion curves for DPSWs is presented in Figure 4(b). The figure shows that both the DSWs and DPSWs depend upon the propagation angle, which can be tuned and localized. The solid lines represent the dispersion curves for the DSWs while the dispersion curves for the DPSWs have been indicated by the dotted lines.

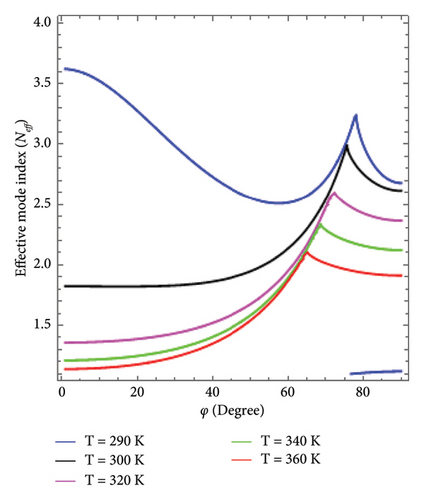
To estimate the confinement of the surface waves on the uniaxial-InSb interface, the effective mode index (i.e., N_eff = Re [q]/k_o) is computed and presented in Figure 5 under different temperature range values. Figure 5(a) presents the confinement of the DSWs against the propagation angle under temperature variation T ∈ [200, 220, 240] K. For T ∈ [200, 220, 240] K, the relative permittivity of InSb corresponds to 14.52 + i0.029, 13.02 + i0.066, and 10.31 + i0.134 at 2 THz. It is clear that the imaginary part of permittivity increases with the temperature, which is why the confinement of the surface waves decreases and the loss factor increases. Moreover, the basic condition for pure DSWs is secured by imposing the condition (i.e., (ε_‖ > ε_T > ε_⊥)), where ε_‖ and ε_⊥ have been fixed as (4.3)² and 1, respectively [29]. Figure 5(b) deals with the effective mode index of hybrid plasmons supported by the uniaxial material and metallic phase of InSb. For T ∈ [290, 300, 320, 340, 360] K at a frequency of 2 THz, InSb behaves as a metal with corresponding permittivity values of −5.35 + i0.52, −10.64 + i0.65, −24.02 + i0.99, −41.69 + i1.43, and  − 64.30 + i1.99, respectively [20]. The figure shows that the effective wave number of surface waves decreases as the temperature increases. Resultantly, the confinement of such surface waves supported by the uniaxial-loaded InSb THz slab also decreases for higher temperatures. One major physical reason for this trend could be that with an increase in temperature, the imaginary part of the permittivity of InSb increases. This increase in the imaginary part of permittivity leads to higher propagation losses, which consequently causes a decrease in the effective mode index.

The influence of temperature on propagation length (L_p) as a function of the propagation angle (φ) under different values of temperature is analyzed in Figure 6. The propagation length is normalized by free space wave number k₀ and computed by the expression L_p = 1/2 Im[q] [28]. Figure 6(a) presents the functional analysis between the normalized propagation length and propagation angle under temperature variation T = 200 K, 220 K, and 240 K at the frequency of 2 THz. Under these conditions, it depicts that the propagation length of DSWs decreases with increases in temperature. Moreover, the DSWs have a distinct angular existence as compared to the hybrid plasmons given in Figure 6(b). It can be concluded that with the increase in temperature, it shifts toward a lower angle range. Furthermore, when the impact of temperature variation T = 290 K, 300 K, 320 K, 340 K, and 360 K on the propagation length for the hybrid plasmons is analyzed, it remains the same for the T > 300 K under angle variation. Moreover, it is obvious from these figures that the pure DSWs have higher propagation lengths than the hybrid plasmon modes with distinct angular dependence.

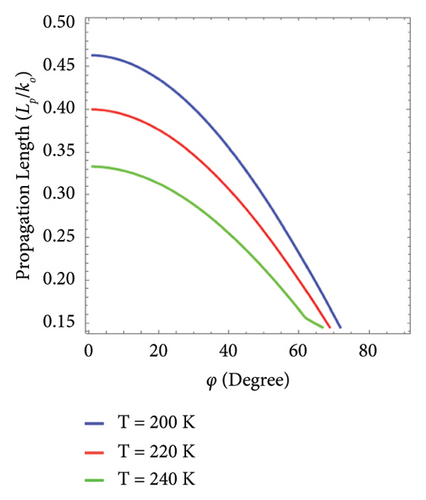
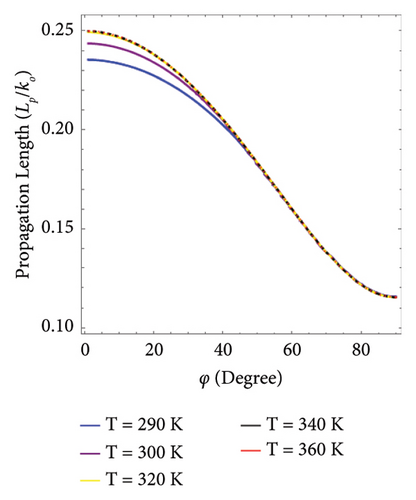
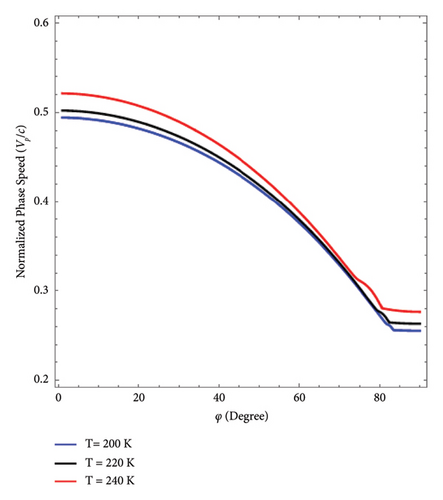
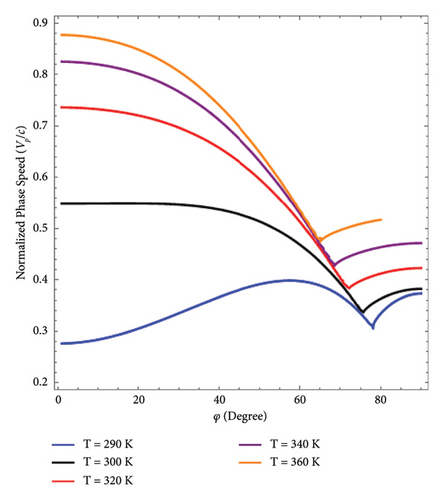
Figure 7 shows the influence of temperature on the normalized phase velocity graphically. The normalized phase speed is computed as V_p = k₀/Re[β]. It is clear from Figure 7 that the phase speed increases with temperature and can be tuned by adjusting the temperature for both cases. For the pure DSWs, the phase speed is higher for the lower angles and lower for the higher angles, while for the hybrid plasmons, the phase speed shows a nonlinear response against the temperature variation, as depicted in Figures 7(a) and 7(b), respectively. Moreover, Figure 7(b) shows the phase speed for the two hybrid modes as a function of each mode’s propagation angle. The upper modes are the faster modes, while the lower modes are the slower modes, as depicted in Figure 7(b).

For the sake of device fabrication, the uniaxial material can be deposited on the indium antimonide substrate via physical vapor deposition (PVD) technique [40, 41]. However, to excite the surface waves at the interface, the appropriate phase matching conditions can be adopted as reported in different works [42, 43].

4. Concluding Remarks

The study focused on temperature-assisted hybrid DSWs supported by the uniaxial material-InSb interface. The surface wave propagation properties—including the dispersion curve, effective mode index, phase velocity, and propagation length profile for the uniaxial-loaded InSb—are shown to be sensitive to external temperature. The numerically obtained results suggested that the temperature, which serves as an external variable, actively regulates the surface wave propagation properties, such as the dispersion relation, surface wave confinement, phase speed, and propagation length. The uniaxial material-loaded TSM (InSb) interface provides the opportunity to excite different types of surface waves. Regarding the future recommendation, the thermal effects can be explored to study the surface characteristics, i.e., surface electric currents [44], surface magnetic currents [45], and graded index metasurfaces [46]. The calculated numerical results in this work could find a use in the design of thermo-optical waveguides, near-field thermal imaging, THz photoemission temperature-assisted communication systems, and thermo-optical sensor design.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

Tahseen Sana and Muhammad Zeshan Yaqoob wrote the main manuscript and derived analytical expressions. Majeed A. S. Alkanhal and Abdul Ghaffar edited the manuscript and reviewed the numerical analysis. Ahtisham Ali Hafeez Ullah and Yasin proposed the methodology and were involved in analysis of results and discussion in the given study. All authors reviewed the manuscript before submission.