Volume 2024, Issue 1 5561911

Research Article

Open Access

Exploring Solution Strategies for Volterra Integro-Differential Lane–Emden Equations in Astrophysics Using Haar Scale 3 Wavelets

Ratesh Kumar,

Ratesh Kumar

Department of Mathematics , Lovely Professional University , Phagwara , 144411 , India , lpu.in

Search for more papers by this author

Sabiha Bakhtawar,

Sabiha Bakhtawar

Department of Mathematics , Lovely Professional University , Phagwara , 144411 , India , lpu.in

Search for more papers by this author

Homan Emadifar,

Corresponding Author

Homan Emadifar

[email protected]

orcid.org/0000-0002-8034-1475

Department of Mathematics , Saveetha School of Engineering , Saveetha Institute of Medical and Technical Science , Saveetha University , Chennai , 602105 , Tamil Nadu , India , saveetha.com

MEU Research Unit , Middle East University , Amman , 11831 , Jordan , meu.edu.jo

Department of Mathematics, Hamedan Branch , Islamic Azad University of Hamedan , Hamedan , Iran , iauh.ac.ir

Search for more papers by this author

Ratesh Kumar,

Ratesh Kumar

Department of Mathematics , Lovely Professional University , Phagwara , 144411 , India , lpu.in

Search for more papers by this author

Sabiha Bakhtawar,

Sabiha Bakhtawar

Department of Mathematics , Lovely Professional University , Phagwara , 144411 , India , lpu.in

Search for more papers by this author

Homan Emadifar,

Corresponding Author

Homan Emadifar

[email protected]

orcid.org/0000-0002-8034-1475

Department of Mathematics , Saveetha School of Engineering , Saveetha Institute of Medical and Technical Science , Saveetha University , Chennai , 602105 , Tamil Nadu , India , saveetha.com

MEU Research Unit , Middle East University , Amman , 11831 , Jordan , meu.edu.jo

Department of Mathematics, Hamedan Branch , Islamic Azad University of Hamedan , Hamedan , Iran , iauh.ac.ir

Search for more papers by this author

First published: 09 July 2024

https://doi.org/10.1155/2024/5561911

Academic Editor: Zengtao Chen

Share a link

Email
Wechat
Bluesky

Abstract

The current research introduces a novel approach to address the computational challenges associated with solving the Lane–Emden-type equations by transforming them from their conventional differential form to the corresponding integro-differential form. These equations have wide-ranging applications in physical sciences, including modeling diffusion phenomena and thermal gradients. We utilize the Volterra integro-differential (VID) form to resolve computational challenges due to singularity issues. Through the Scale 3 Haar Wavelet (S3-HW) algorithm, we transform the VID equations into algebraic form and obtain solutions using the Gauss-elimination method. The quasilinearization technique is implemented whenever a nonlinearity is encountered. Comparative analysis against various techniques demonstrates the superior accuracy and efficiency of our method. Despite challenges such as the discontinuity of Scale 3 Haar Wavelets and singularity issues of Lane–Emden-type equations, our algorithm paves the way for extending its application to a wide range of physical problems.

1. Introduction

The study of stellar structures has become a major subject in stellar astrophysics since its origin [1]. The number of attempts have been made to estimate the radial profiles of the density of the star, mass of the star, and also the pressure of the star, and the major finding of all these attempts is the Lane–Emden equation (LE-E). LE-E represents the thermal gradient of a spherical cloud of gas based on laws of basic thermodynamics as well as the mutual attraction among its particles. The polytrophic theory of stars is based on thermodynamic considerations that address the problem of energy transmission via material transfer among multiple levels of the star. These mathematical equations are fundamental to the theory of stellar structure and have also become the subject of numerous research [2, 3]. Mathematically, LE-E is an ordinary differential equation of the second order having singularity at the origin. To derive the basic model of the Lane–Emden equation, consider a spherical gas cloud as presented in Figure 1 [4, 5].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A spherical gas cloud.

Let P(r) represents the sum of the pressures exerted at a radius “r” from the center of a spherical gas cloud. Standard gas pressure and the impact of radiation together create the total pressure:

(1)

where a represents the radiation constant, T represents the absolute temperature, R represents the gas constant, and ν represents the specific volume [1, 6]. Now assume that the spherical mass is denoted by M(r), the gravitational potential is denoted by “ϕ,” and acceleration due to gravity is denoted by g. The following is the equilibrium equation for the system configuration:

(2)

(3)

where G is the universal gravitation constant and ρ is the density of the star at a distance r from the center of the spherical star. Eliminating the value of M(r) from the abovementioned equations gives rise to an equation. It is important to notice that this equation is an analogous form of the Poisson equation [1]:

(4)

The density and pressure of a degenerated electron gas are proportional to one another. The mathematical relation which describes their relation is “

.” Moreover, on the assumption that a relation of this kind does exist for other states of the star, we are compelled to hypothesize a relation of the type

, where K and m are constants. By using this relation in the abovementioned equation of hydrostatic equilibrium, we came to a conclusion:

(5)

where λ corresponds to the central density of the star and ζ represents the nondimensional quantity, both of which are associated with density ρ by the following expression [1]:

(6)

and introduce a new parameter c and define a relation between r and c:

and the value of

. By substituting the value of r, we obtain the basic Lane–Emden equation:

(7)

(8)

It is also essential to establish the boundary conditions according to the following boundary constraints for hydrostatic equilibrium and normalizing consideration of the additional new variables “ϰ” and “ζ”. The consequence of r = 0 is as follows:

(9)

(10)

Thus further, an additional constraint must still be incorporated to equally fulfill the above condition of r and ϰ:

(11)

Thus, to restate, here are the following restrictions:

(12)

The general structure of LE-E is as follows:

(13)

With the initial conditions:

(14)

where

is an analytical function while f(ϰ, ζ(ϰ)) is a continuous real-value function. The process of transforming a second-order ordinary differential equation of Lane–Emden type into Volterra integro-differential equations (VIDE) or simply Volterra integral equation can be summarized as follows. Initially, the highest order derivative in the equation is approximated as ζ^″(ϰ) = υ(ϰ). By integrating this equation, the values of ζ^′(ϰ) and ζ(ϰ) can be determined. These values are then substituted back into the original differential equation, resulting in the Volterra Integral form of the Lane–Emden equation. To obtain the corresponding integro-differential form, the integral form is differentiated. A more detailed explanation of this entire procedure can be found in [7]. The integro-differential form for the Lane–Emden Equation (13) is as follows:

(15)

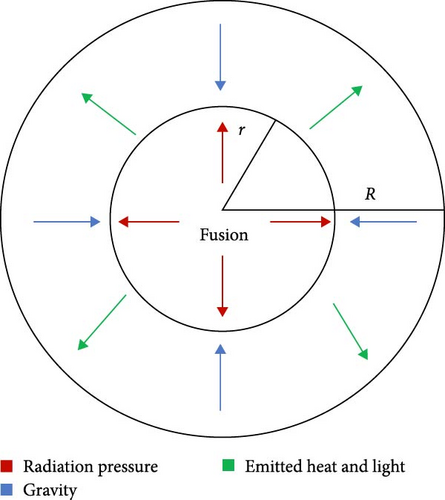
This equation has been used to explain various problems in physical sciences and cosmology, including stellar model theory, isothermal gas sphere, physical properties of a spherical cloud of gas, modeling of the cluster of galaxies, and thermionic current theory [8]. Some of the important real-world applications of the Lane–Emden equation are discussed in Table 1. Lane [13] was the first one to develop Lane–Emden equations, although Emden elaborated extensively in 1870. The Lane–Emden equation is a Poisson equation in astrophysics. This type of problem has received an enormous amount of attention from researchers. For further study on Lane–Emden equations, comprising their origin, modifications, and implementations, the researcher is gladly encouraged to read [1, 12, 13].

Table 1. Applications of Lane–Emden equations for different values of f(ϰ, ζ(ϰ)) in Equation (13) by considering

and k = 2.

Function type f(ϰ, ζ(ϰ))	Physical applications
ζ^m(ϰ)	This is the standard LE-E. The exact solution for this LE-E is available in the literature corresponding to m = 0, 1, and 5 only and the solutions are , respectively. This equation describes the thermal gradient of a spherical cloud of gas based on laws of basic thermodynamics as well as the mutual attraction among its particles [9]
e^ζ(ϰ)	This LE-E is the Poisson Boltzmann equation utilized to describe isothermal gas spheres [2, 10]
	This Lane–Emden equation arises in modeling of the thermal conduction in the human head [11]
	This Lane–Emden equation is called the white-dwarf (W-D) equation. This equation finds its application in the modeling of the gravitational potential of degenerate W-D stars [1]
	The study of steady-state gas diffusion in a spherical cell with Michaelis–Menten uptake kinetics leads to the development of this equation [12]

The LE-E generally does not have solutions that can be determined by analytical techniques. In practice, several real physical and mathematical problems are often very difficult to deal with. As a result, these problems are handled by using a variety of approximated and numerical techniques. Several researchers are working on the solution of LE-E. Parand and Hashemi [4] Dehghan and Shakeri [5] solved the LE-E using the variational iteration scheme. Wazwaz [14] solved the Lane–Emden type equations by using the Adomain decomposition method. Caglar and Caglar [15] implemented the B-splines for the approximation of the singular differential equation of the LE-E type. Yousefi [16] described the Legendre wavelets for finding the solution of the Lane–Emden equation. Ertürk [17] solved the Lane–Emden equations in differential form by utilizing the differential transform method. Ramos [18] approximated LE-E by utilizing a series approach. The author also discusses the comparability of the homotopy perturbation method with the series approach for solving Lane–Emden equations. Parand et al. [19] used a pseudospectral algorithm for the solution of Lane–Emden equations having nonlinearity in them on the semi-infinite domain. Vanani and Aminataei [20] presented a numerical method for LE-E of the nonlinear kind. Parand et al. [21] approximated the Lane–Emden equations by utilizing the hybrid collocation approach along with the Hermite function. Iqbal and Javed [22] applied the optimal homotopy asymptotic algorithm on Lane–Emden equations. Wazwaz et al. [23] used the Adomain decomposition method for solving the system of Lane–Emden equations by converting them into the corresponding Volterra integral equations. Taghavi and Pearce [24] applied the Tau technique for the approximation of Lane–Emden equations of differential form. Yüzbaşı and Sezer [25] constructed the Bessel collocation approach for the solution of Lane–Emden equations. Wazwaz and Khuri [26] solved the integrodifferential form of Lane–Emden equations with the aid of the variational iteration method. Asadpour et al. [27] solved the integral form of Lane–Emden equations by using the least square method. Parand and Hashemi [4] and Dehghan and Shakeri [5] employed a novel numerical approach to examine widely recognized categories of Lane–Emden type equations, which are nonlinear ordinary differential equations defined on the semi-infinite domain. The author employs the radial basis function differential quadrature (RBF-DQ) method, a meshless technique. Each technique has its own advantages and limitations, which makes it important to explore and develop new methods to improve the accuracy, efficiency, and robustness of the numerical solutions. Wavelet methods offer several advantages over other numerical methods when it comes to solving integral and integro-differential equations.

Wavelets are modernistic orthonormal functions with the ability to dilate and translate. These characteristics allow wavelet-based numerical algorithms to exhibit a qualitative improvement over other techniques. In literature, Lane–Emden equations have been solved by using numerous wavelets like, Legendre multiwavelets [28], Bernoulli wavelet [29], Chebyshev wavelet [30], Haar scale 2 wavelets [31], Morlet wavelet [32], and Taylor wavelet [33]. Among all wavelet families with analytic expression, the Haar wavelet is the simplest. Haar wavelet technique has superseded the other numerical techniques because of its mathematical simplicity, high levels of efficiency, and primarily its applicability to the problems to acquire more reliable results for a small number of nodal points. The Haar wavelet has been utilized in the literature to address a variety of equations, including the Burgers’ equation [34] and hyperbolic type wave equations [35]. In literature, the most commonly used wavelets are dyadic wavelets. These wavelets have a dilation factor that increases in powers of 2, creating two daughter wavelets. However, Chui and Lian [36] introduced a new class of wavelets called nondyadic (Scale 3 Haar) wavelets through a multiresolution analysis process. More recently, Mittal and Pandit [37, 38, 39] applied scale 3 Haar wavelets to solve various types of differential equations and observed that the scale 3 Haar wavelets exhibit a faster rate of convergence as compared to the dyadic wavelets. Despite this advancement, the scale 3 Haar wavelet-based technique has not been tested on any scientific models governed by integro-differential equations. Moreover, specifically, the scale 3 Haar wavelet method has not been used to investigate the characteristics of solutions to the integro-differential form of the Lane–Emden equation. This knowledge gap motivates us to develop a new technique utilizing scale 3 Haar wavelets for the analysis of system behavior governed by the integro-differential form of Lane–Emden equation.

The current manuscript involves the development and implementation of scale 3 Haar wavelets along with collocation method [40, 41, 42, 43, 44, 45, 46, 47, 48, 49] to solve the Lane–Emden equations in integro-differential form. The paper is organized as follows: in Section 2, a brief study about the Quasilinearization technique is included. The basic structure of scale 3 Haar wavelets and the structure for calculating the integrals of scale 3 Haar wavelets is discussed in Section 3. Section 4 contains the scale 3 Haar wavelet (S3-HW) collocation algorithm. The convergence analysis is provided in Section 5 of the manuscript. For the validation of the S3-HW algorithm, some applications of Lane–Emden equations are discussed in Section 6. Finally, the conclusion is discussed in Section 7 of the article.

2. The Quasilinearization Approach

Bellman and Kalaba [42] and D’Hondt [43] first proposed the idea of the quasilinearization approach for resolving nonlinear functional equations in 1965. The quasilinearization approach is basically the Newton–Raphson algorithm in generalized form. The key motivation for using this approach is that numerous nonlinear functional equations cannot be solved analytically, irrespective of the fact that solving these equations is a requirement of the researcher. To understand the procedure and working rule of the quasilinearization technique, consider a nonlinear ordinary differential equation of second order:

(16)

having the following boundary conditions:

(17)

where φ(ζ(ϰ), ϰ) is nonlinear in ϰ and ζ. Now, consider an initial approximation for ζ(ϰ) as ζ₀(ϰ) = ζ(a) = α₁, then by using the Taylor expansion (up to the first two terms) of φ(ζ(ϰ), ϰ) about ζ₀(ϰ):

(18)

By using Equation (18) in Equation (16):

(19)

Solving the Equation (19) for ζ(ϰ), the next approximation ζ₁(ϰ) would be obtained. By applying the Taylor expansion on φ(ζ(ϰ), ϰ) about ζ₁(ϰ) as explained:

(20)

Solving the Equation (20) for ζ(ϰ), next approximation ζ₂(ϰ) would be obtained. In order to obtain the desired efficiency, continuing the preceding technique and using the following recurrence relation as a generalization of the above technique:

(21)

having the following boundary conditions:

(22)

Again, considering a differential equation (nonlinear) of the following form:

(23)

where φ(ζ^′(ϰ), ζ(ϰ), ϰ) is nonlinear in ϰ, ζ, and ζ^′. Repeating the preceding technique, we have attained a recurrence relation of the following form:

(24)

The quasilinearization technique is generalized for higher order nonlinear functional equations. The obtained recurrence relation is given as follows:

(25)

where φ is the nonlinear function in

is nth order, linear differential operator. In order to calculate ζ_m+1(ϰ), the value of ζ_m(ϰ) is already known at each step. The quasilinearization algorithm will start from the initial approximation ζ₀(ϰ) resulting in the solution of a nonlinear functional equation following a series of convergent functions with order of convergence two.

3. Scale 3 Haar Wavelets

The wavelet family is an orthonormal subfamily of l²(R). From a fixed function known as the mother wavelet, all other functions in the wavelet family are constructed via translations and dilations. In Haar scaling 2 wavelets, a single mother wavelet provides the entire wavelet family, meanwhile, in Haar scale 3, two mother wavelets construct the extended wavelet family. The structure of the wavelet family for the Haar scale 3 along with their integrals is presented in this section [36, 44].

Haar scaling function:

(26)

Symmetric Haar wavelet:

(27)

Antisymmetric Haar wavelet:

(28)

where

(29)

For this wavelet family, the wavelet number is represented by i, the dilation factor is represented by j, and the translation parameter is represented by k. For the computation of wavelet number i following relations are used. i − 1 = 3^j + 2k (for even values of wavelet number) and i − 2 = 3^j + 2k (for odd values of wavelet number). The whole wavelet family would be constructed by utilizing the abovementioned expressions for various translations and dilations of ψ₂(ϰ) and ψ₃(ϰ). ψ₂(ϰ) and ψ₃(ϰ) are considered mother wavelets, and the remaining wavelets formed from these two parent wavelets are referred to as daughter wavelets. The graphs for the first six members of the wavelet family are shown in Figure 2. The primary distinction between the Haar scale 2 and Haar scale 3 wavelets is that the Haar scale 2 uses a single mother wavelet to generate all subsequent wavelets, whereas the Haar scale 3 uses two mother wavelets with different factors as well as different shapes to produce the wavelet family. As a result of this advantage, the Haar scale 3 wavelet accelerates the rate at which solutions converge.

Using the formula provided, one can efficiently evaluate the integrals of Equations (26), (27), and (28) over the interval [c, d] the desired number of times:

(30)

When we compute the above integrals, we get the following equation:

(31)

q_δ,i(ϰ)^′s for i = 2, 4, 6, 8, ⋯, 3p − 1 are given by the following equation:

(32)

q_δ,i(ϰ)^′s for i = 3, 5, 7, 9, ⋯, 3p are given by the following equation:

(33)

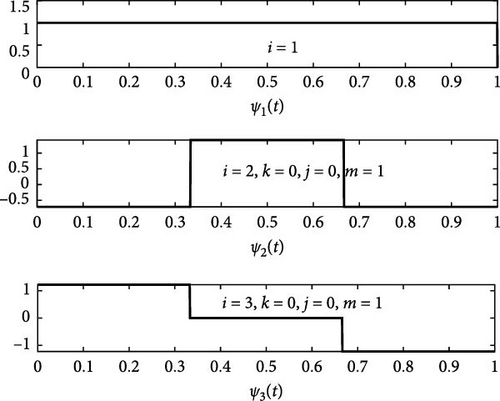
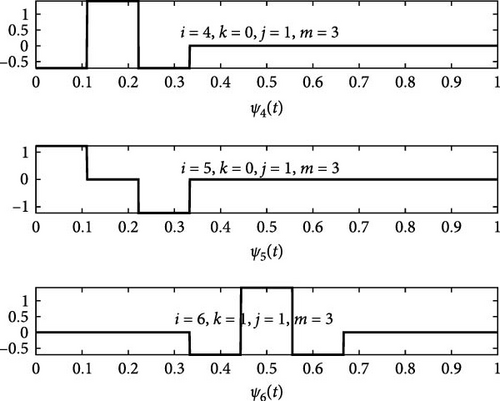
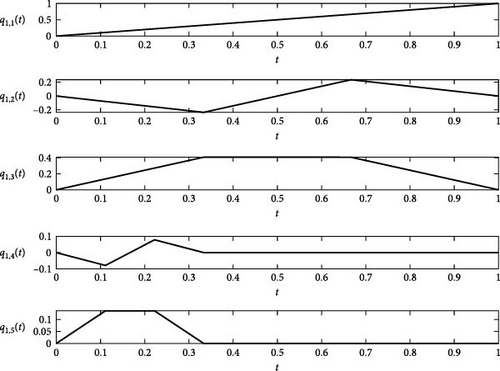
The graphs for the first integrals of the first five members of scale 3 Haar Wavelets are shown in Figure 3.

The Haar wavelet collocation points for the interval [c, d] are obtained by the following relation:

(34)

4. Construction of Scale 3 Haar Wavelet Algorithm

In this section, a novel algorithm is presented for the solution of Lane–Emden equations of VID form. We constructed a scale 3 Haar wavelet algorithm for the interval [0, 1]. In the proposed algorithm, the first-order derivative υ^′(ϰ) involved in the Lane–Emden equation is approximated by scale 3 Haar functions, and then by integrating, the value of unknown υ(ϰ) is obtained. Furthermore, the integrals involved are determined by using the formula given in Lemma 1.

Lemma 1. If υ(ϰ) is any function belonging to the family of l₂(R), the space of square-integrable function over the interval (a, b) in such a way that , then the integral of υ(ϰ) on (a, b) is given as follows:

(35)

Proof. See Kumar and Bakhtawar’s [45] study.

4.1. Proposed Methodology

Consider the Lane–Emden equation of the following form:

(36)

Consider the following equation:

(37)

Integrating Equation (37) from 0 to ϰ, we obtain the following equation:

(38)

Equation (38) is the approximate solution of the Lane–Emden Equation (36). Using Equations (37) and (38) in Equation (36), we obtain the following equation:

(39)

By applying the result of Lemma 1 for calculating the integrals and putting the collocation points, we get the following equation:

(40)

where

After putting the collocation points, a system of 3p × 3p algebraic equations has been obtained which can easily be reduced to the matrix form of the following type:

(41)

Any iterative method could be utilized to determine the solution to these equations. For the solution of this linear system, the Gauss elimination method has been implemented. For the nonlinear equations, quasilinearization is used. By solving these algebraic equations, the unknown Haar coefficient has been obtained. Finally, by substituting these Haar coefficients in Equation (38) solution at collocation points has been obtained.

5. Convergence Analysis

To establish the convergence of the proposed method, consider the approximated solution Equation (38) as given:

(42)

Now the convergence of the theorem will be proved with the help of Lemma 2.

Lemma 2. Let υ(ϰ)ɛL²(R)be any square-integrable function such that |υ^m(ϰ)| ≤ M, ∀ϰɛ(0, 1) and . Then, .

Proof. Let be the exact solution and be the approximated solution. Now the error at the Jth level of resolution is given by the following equation:

(43)

(44)

By applying the mean value theorem of integral, we get ε₁ ∈ (ρ₁(i), ρ₂(i)), ε₂ ∈ (ρ₂(i), ρ₃(i)), ε₃ ∈ (ρ₃(i), ρ₄(i)) such that:

(45)

Now equation becomes:

(46)

Now by using the Caputo definition of fractional derivatives in the above equations, we get the following equations:

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

Theorem 1. If υ(ϰ) represents the exact solution and υ_3p(ϰ) represents the non-Dyadic wavelet-based approximated solution, then:

(55)

Proof. At jth level of resolution, error estimation for the solution is given by the following equations:

(56)

(57)

(58)

(59)

(60)

(61)

Using Lemma 2 in the above equation, we get the following equation:

(62)

Take

(63)

(64)

(65)

It is clear from the above equations that error bound is inversely proportional to the level of resolution which means that with the increase in the level of resolution, error bound decreases, i.e., j → ∞⇒‖E_j‖⟶0. This proves the convergence of solution and ensures the stability of the solutions.

6. Numerical Examples

In this section, we examine several applications of Lane–Emden equations having initial or boundary conditions to analyze the efficiency and relevance of the presented algorithm. We compared the acquired results to existing numerical approaches used in the literature. Different errors have been calculated at collocation points by utilizing MATLAB software. All calculations are performed using an Intel Core i3-3rd generation processor with 8 GB of RAM. If υ_s3 represents the S3-HW solution and υ_x represents the true solution, then absolute error, l₂ − error, l_max − error, l_∞ − error and order of convergence p are computed by the given mathematical relation:

(66)

(67)

(68)

Example 1. Consider the second-order linear Lane–Emden differential equation of the form [14]:

(69)

having the following initial conditions:

(70)

Corresponding VID Lane–Emden equation is as follows:

(71)

The exact solution for Example 1 is ζ(ϰ) = ϰ² + ϰ³, and the approximated solution by using the presented algorithm is

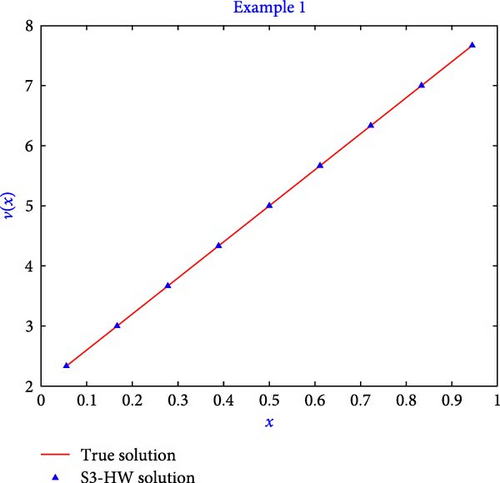
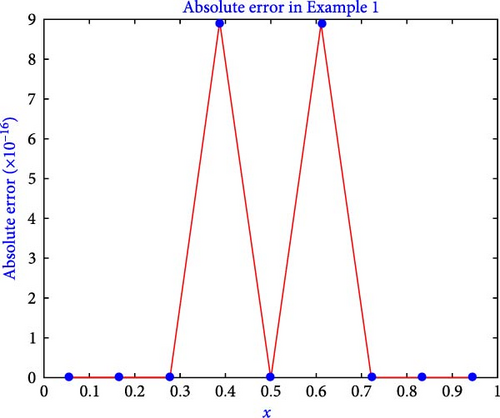
The computation of the true solution and S3-HW solution of Example 1 are given in Table 2 for the level of resolution 1. The results shown in the table demonstrate that the method generates accurate solutions in terms of absolute error (AE) having an error of 10⁻¹⁶. In Table 3, the computation of l₂ − error, l_max − error, and l_∞ − error is presented. Table 3 illustrates that by increasing the value of j, the error becomes lesser. The comparison of S3-HW errors with that of the Adomain decomposition method and Chebyshev wavelet is given in Table 4, which clearly depicts that our results are better than the previous one. Furthermore, the suggested algorithm has been shown to produce high-accuracy outcomes even with a small number of grid points. Figure 4 also shows the S3-HW solution and true solutions for the level of resolution j = 1. The figure shows that the resulting S3-HW solution coincides well with the true solution. Figure 5 shows the graph of absolute error for Example 1 when j = 1. Moreover, the presented algorithm took only 0.24 s of CPU time to execute the program written for this example.

Table 2. Comparability of true solution with S3-HW solution for Example 1 along with absolute error.

ϰ	True solution	S3-HW solution	AE
0.055555555556	2.333333333333	2.333333333333	0
0.166666666667	3.000000000000	3.000000000000	0
0.277777777778	3.666666666667	3.666666666667	0
0.388888888889	4.333333333333	4.333333333333	8.88178E − 16
0.500000000000	5.000000000000	5.000000000000	0
0.611111111111	5.666666666667	5.666666666667	8.88175E − 16
0.722222222222	6.333333333333	6.333333333333	0
0.833333333333	7.000000000000	7.000000000000	0
0.944444444444	7.666666666667	7.666666666667	0

Table 3. Computation of multiple errors for different levels of resolution for Example 1.

j	l₂ − error	l_max − error	l_∞ − error
0	0.00000E + 00	0.00000E + 00	0.00000E + 00
1	7.91776E − 17	1.25607E − 15	8.88178E − 16
2	0.00000E + 00	0.00000E + 00	0.00000E + 00
3	9.32507E − 17	4.44089E − 15	8.88178E − 16
4	8.63088E − 17	7.11929E − 15	1.77636E − 15
5	8.27657E − 17	1.18248E − 14	1.77636E − 15
6	1.07181E − 16	2.65229E − 14	1.77636E − 15

Table 4. Comparison of l₂ − error and l_∞ − error for Example 1.

Errors	Chebyshev wavelet method [30]	Adomian decomposition method [14]	S3-HW method
l₂ − error	5.66647E − 14	1.30900E − 12	8.27657E − 17
l_∞ − error	2.02061E − 14	1.28586E − 12	1.77636E − 15

Example 2. Next, we have solved the nonlinear Lane–Emden differential equation of the form [46]:

(72)

having the following boundary conditions:

(73)

The corresponding VID Lane–Emden equation is as follows:

(74)

The exact solution for Example 2 is , and the approximated solution by using the presented algorithm is

We have compared the value of absolute error for Example 2 obtained by using the S3-HW algorithm with that of Verma and Tiwari [46] in Table 5. This clearly depicts that the S3-HW algorithm is providing better results. Table 6 demonstrates the order of convergence of presented algorithm using an error table.

Table 5. Comparison of absolute error for Example 2.

ϰ	Absolute error for HWQA [46]	Absolute error for S3-HW
0.2	2.90983E − 05	5.4250E − 10
0.3	2.33723E − 05	2.4290E − 09
0.4	1.72621E − 05	6.5520E − 09
0.6	1.16388E − 05	2.2080E − 08
0.7	6.90631E − 06	3.2627E − 08
0.8	3.12139E − 06	4.3902E − 08
0.9	1.62325E − 07	5.5151E − 08

Table 6. Order of convergence of presented algorithm using error table.

Δx	0.333333	0.111111	0.037037	0.012346	0.0041152	0.0013717	0.0004572
j	0	1	2	3	4	5	6
l₂ − error	2.45E − 03	2.23E − 04	2.44E − 05	2.71E − 06	3.01E − 07	3.34E − 08	3.71E − 09
Order of convergence	—	2.18E + 00	2.01E + 00	2.00E + 00	2.00E + 00	2.00E + 00	2.00E + 00

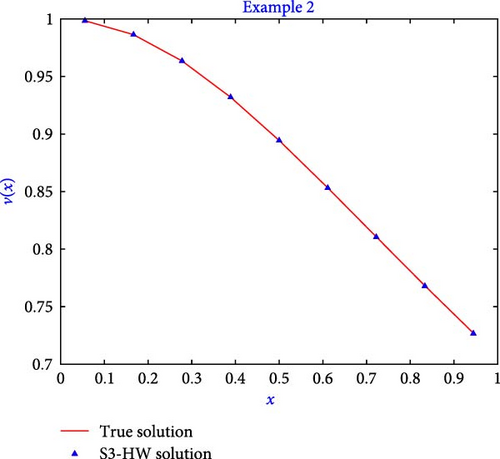
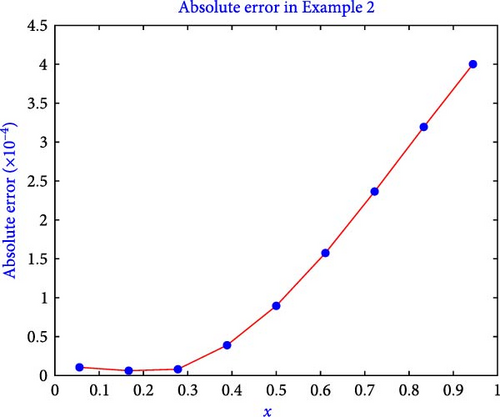
This equation originates in the analysis of isothermal gas sphere equilibrium. The computation of the true solution and S3-HW solution is given in Table 7 for Example 2. The results shown in the table demonstrate that the method generates accurate solutions in terms of absolute error. In Table 8, computation of l₂ − error, l_max − error, and l_∞ − error is presented. Table 8 illustrates that by increasing the value of j, the error becomes lesser. Figure 6 shows the S3-HW solution and true solutions for the level of resolution j = 1. The figure shows that the resulting S3-HW solution coincides well with the true solution. Figure 7 shows the graph of absolute error for Example 2 when j = 1. Furthermore, the presented algorithm executed the program for this example in just 0.228 s of CPU time.

Table 7. Comparability of true solution with S3-HW solution for Example 2 along with absolute error.

ϰ	True solution	S3-HW solution	AE
0.055555555556	0.998460353205	0.998470899829	1.05466E − 05
0.166666666667	0.986393923832	0.986400125001	6.20117E − 06
0.277777777778	0.963517909630	0.963509847025	8.06260E − 06
0.388888888889	0.932004671541	0.931965702446	3.89691E − 05
0.500000000000	0.894427191000	0.894337637786	8.95532E − 05
0.611111111111	0.853281833652	0.853124378302	1.57455E − 04
0.722222222222	0.810679228400	0.810442731760	2.36497E − 04
0.833333333333	0.768221279597	0.767901826959	3.19453E − 04
0.944444444444	0.727013152550	0.726612960465	4.00192E − 04

Table 8. Computation of multiple errors for different levels of resolution for Example 2.

j	l₂ − error	l_max − error	l_∞ − error
0	2.45168E − 03	3.76885E − 03	3.51118E − 03
1	2.23333E − 04	5.93868E − 04	4.00192E − 04
2	2.44184E − 05	1.12448E − 04	4.66187E − 05
3	2.70847E − 06	2.16029E − 05	5.27484E − 06
4	3.00884E − 07	4.15668E − 06	5.89792E − 07
5	3.34308E − 08	7.99937E − 07	6.56716E − 08
6	3.71453E − 09	1.53948E − 07	7.30203E − 09

Example 3. Consider the Lane–Emden equation with boundary conditions [15, 25]:

(75)

having the following boundary conditions:

(76)

The corresponding Volterra integral Lane–Emden equation is as follows:

(77)

The exact solution for Example 3 is .

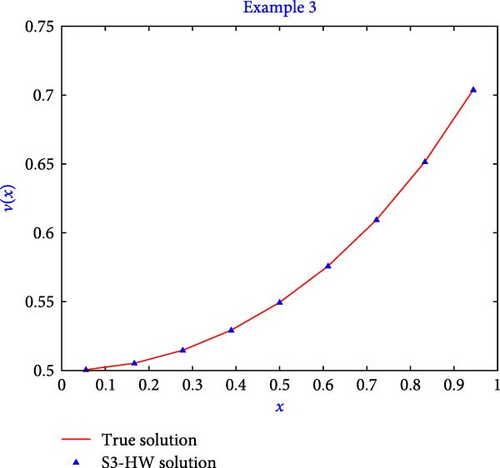
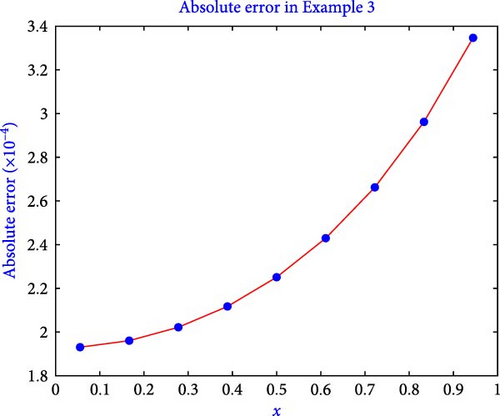
The computation of the true solution and S3-HW solution is given in Table 9 for Example 3. In Table 10, computation of l₂ − error, l_max − error, and l_∞ − error is presented. Table 11 illustrates that by increasing the value of j, the error becomes lesser. The error obtained for Example 3 in [15] is 10⁻⁶, in [27] the error is 10⁻⁸, and by using the presented algorithm the error obtained is 10⁻⁹ at the level of resolution 6, as shown in Table 11. Table 12 demonstrates the order of convergence of presented algorithm using error table.

Table 9. Comparability of true solution with S3-HW solution for Example 3 along with absolute error.

ϰ	True solution	S3-HW solution	AE
0.055555555556	0.500579076014	0.500386025849	1.93050E − 04
0.166666666667	0.505238621326	0.505042573279	1.96048E − 04
0.277777777778	0.514703340426	0.514501165202	2.02175E − 04
0.388888888889	0.529274148817	0.529062443064	2.11706E − 04
0.500000000000	0.549427679501	0.549202599104	2.25080E − 04
0.611111111111	0.575849911585	0.575606964558	2.42947E − 04
0.722222222222	0.609487186781	0.609220963206	2.66224E − 04
0.833333333333	0.651621391086	0.651325197151	2.96194E − 04
0.944444444444	0.703980101848	0.703645447854	3.34654E − 04

Table 10. Computation of multiple errors for different levels of resolution for Example 3.

j	l₂ − error	l_max − error	l_∞ − error
0	3.77842E − 03	3.74378E − 03	2.63404E − 03
1	4.26631E − 04	7.35990E − 04	3.34654E − 04
2	4.74912E − 05	1.41987E − 04	3.89216E − 05
3	5.27789E − 06	2.73329E − 05	4.39131E − 06
4	5.86446E − 07	5.26038E − 06	4.90422E − 07
5	6.51608E − 08	1.01236E − 06	5.45843E − 08
6	7.24009E − 09	1.94830E − 07	6.06836E − 09

Table 11. Comparison of absolute error for different collocation points for Example 3.

ϰ	Absolute error in [15] for	Absolute error in [15] for	Absolute error in [25]	Absolute error obtained by using HS 3-W
0.025	—	6.0E − 06	—	3.26E − 09
0.050	2.0E − 05	6.0E − 06	—	3.27E − 09
0.075	—	6.0E − 06	—	3.27E − 09
0.100	2.7E − 05	6.0E − 06	—	3.28E − 09
0.200	2.6E − 05	6.0E − 06	1.5665E − 06	3.34E − 09
0.300	2.5E − 05	5.0E − 06	—	3.45E − 09
0.400	2.4E − 05	4.0E − 06	1.5577E − 06	3.60E − 09
0.500	2.2E − 05	3.0E − 06	—	3.81E − 09
0.600	1.9E − 05	2.0E − 06	1.5524E − 06	4.08E − 09
0.700	1.5E − 05	2.0E − 06	—	4.42E − 09
0.800	1.1E − 05	1.0E − 06	1.551E − 06	4.85E − 09
0.900	6.0E − 05	1.0E − 06	—	5.39E − 09
1	0	0	1.6198E − 16	—

Table 12. Order of convergence of presented algorithm using error table for Example 3.

Δx	0.33333	0.111111	0.037037	0.012346	0.004115	0.001372	0.000457
j	0	1	2	3	4	5	6
l₂ − error	3.78E − 03	4.27E − 04	4.75E − 05	5.28E − 06	5.86E − 07	6.52E − 08	7.24E − 09
Order of convergence	—	1.99E + 00	2.00E + 00	2.00E + 00	2.00E + 00	2.00E + 00	2.00E + 00

Figure 8 shows the S3-HW solution and true solutions for the level of resolution j = 1. The figure shows that the resulting S3-HW solution coincides well with the true solution. Figure 9 shows the graph of absolute error for Example 3 when j = 1. Moreover, the presented algorithm successfully executed the program for the second example in a mere 0.213 s of CPU time.

Example 4. Last, consider the following Lane–Emden equation. This equation finds its application in stellar structure. The equation is basically originating in the differential form as follows [47]:

(78)

where k = 2, m = 5, and having the following conditions

. The true solution for this Lane–Emden equation is available only for three different values of m = 0, 1, and 5 are

, and

respectively.

The integro-differential equations of Equation (78) are of the following form:

(79)

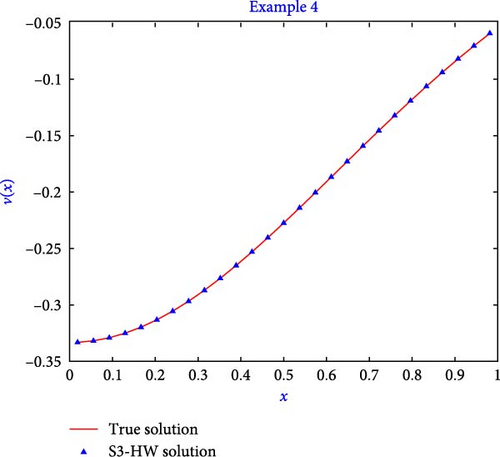
The computation of true solution and S3-HW solution for Example 4 corresponding to m = 5 is given in Table 13. In Table 14, computation of l₂ − error and l_∞ − error is presented. We have also compared the values l₂ − error and l_∞ − error with that of the method presented in [48]. The value of l_∞ − error and l₂ − error for j = 6 in [48] is 8.92E−06 and 7.28E−06, while in the presented S3-HW algorithm, the errors are 1.16153E−08 and 2.93359E−08, respectively, which shows that the presented algorithm provides much better results. Table 14 illustrates that by increasing the value of j, error becomes lesser. In Table 15, we have compared the absolute error for the level of resolution six obtained by using the presented method with that of existing results, and this can be observed that the presented method works more efficiently. Table 16 demonstrates the order of convergence of presented algorithm using an error table.

Table 13. Comparability of true solution with S3-HW solution for Example 4 along with absolute error when m = 5.

ϰ	True solution	S3-HW solution	AE
0.055555555556	−0.331793425541	−0.332479068763	6.85643E − 04
0.166666666667	−0.319708364572	−0.320345947060	6.37582E − 04
0.277777777778	−0.296736635324	−0.297284503406	5.47868E − 04
0.388888888889	−0.265048420258	−0.265476353156	4.27933E − 04
0.500000000000	−0.227400928481	−0.227692828367	2.91900E − 04
0.611111111111	−0.186702699731	−0.186856672356	1.53973E − 04
0.722222222222	−0.145630818194	−0.145657044820	2.62266E − 05
0.833333333333	−0.106368557497	−0.106285801027	8.27565E − 05
0.944444444444	−0.070483367951	−0.070315068968	1.68299E − 04

Table 14. Computation of multiple errors for different levels of resolution for Example 4 when m = 5.

j	l₂ − error	l₂ − error [48]	l_∞ − error	l_∞ − error
0	1.66492E − 02	—	6.14990E − 03	—
1	1.74408E − 03	—	6.85643E − 04	—
2	1.92617E − 04	4.71E − 04	7.62052E − 05	1.97E − 03
3	2.13876E − 05	1.65E − 04	8.46751E − 06	4.91E − 04
4	2.37623E − 06	5.84E − 05	9.40838E − 07	1.23E − 04
5	2.64023E − 07	2.06E − 05	1.04538E − 07	3.12E − 05
6	2.93359E − 08	7.28E − 06	1.16153E − 08	8.92E − 06

Table 15. Comparison of absolute error for different collocation points for Example 4.

ϰ	Error in [33]	Error in [40]	Error in [41]	Error obtained by using presented method
0.1	6.46E − 06	6.27E − 03	3.10E − 03	1.1282E − 08
0.2	6.30E − 06	6.12E − 03	2.90E − 03	1.0327E − 08
0.3	6.05E − 06	5.87E − 03	2.60E − 03	8.8434E − 09
0.4	5.70E − 06	5.53E − 03	2.20E − 03	6.9841E − 09
0.5	5.30E − 06	5.09E − 03	1.80E − 03	4.9334E − 09
0.6	4.84E − 06	4.53E − 03	1.40E − 03	2.8448E − 09
0.7	4.33E − 06	3.82E − 03	9.84E − 04	8.7770E − 10
0.8	3.86E − 06	2.88E − 03	6.07E − 04	8.5490E − 10
0.9	3.24E − 06	1.64E − 03	2.77E − 04	2.2772E − 09
1	1.45E − 13	0	3.49E − 08	3.3691E − 09

Table 16. Order of convergence of presented algorithm using error table for Example 4.

Δx	0.333333	0.111111	0.037037	0.0123457	0.0041152	0.0013717	0.0004572
j	0	1	2	3	4	5	6
l₂ − error	1.66E − 02	1.74E − 03	1.93E − 04	2.14E − 05	2.38E − 06	2.64E − 07	2.93E − 08
Order of convergence	—	2.05E + 00	2.01E + 00	2.00E + 00	2.00E + 00	2.00E + 00	2.00E + 00

Figure 10 shows the S3-HW solution and true solutions for the level of resolution j = 1. The figures show that the resulting S3-HW solution coincides well with the true solution. Figure 11 shows the graph of absolute error for Example 4 when j = 1. The algorithm also took only 0.212 s to execute the fourth example program.

7. Conclusions

In the present work, the basic Lane–Emden type equations of differential form have been converted to the corresponding integro-differential form. The LE-E has been utilized to describe different problems in physical sciences, including diffusion of oxygen in a spherical cell, shallow membrane cap deformation, and thermal gradients in the human head. VID form of Lane–Emden type equations reduces calculation and resolves the problem of singularity at x = 0. By applying the S3-HW algorithm, VID equations have been transformed into the corresponding algebraic equations. The Gauss-elimination method is then applied to the solution of the system of algebraic equations. The quantitative result obtained by the S3-HW algorithm is compared to those acquired by the other techniques, including the Chebyshev wavelet method, Adomain decomposition method, Haar scale 2 wavelets, and also the true solution. To demonstrate the applicability as well as the validity of the S3-HW algorithm, several applications have been presented. Tables and graphs illustrate that the presented algorithm provides less error. The following is a summary of the main advantages of the method:

(1)
Convergence and error reduction: as the level of resolution increases, the errors decrease, demonstrating the convergence of the S3-HW solution toward the exact solution.
(2)
Higher accuracy with fewer grid points: the proposed method achieves a higher level of accuracy even with a small number of grid points, highlighting the reliability of this approach.
(3)
High precision: the solution obtained through the method exhibits a level of accuracy up to 10⁻¹⁶ which can be further improved by increasing the level of resolution.
(4)
Computational support and compatibility: the computational work seamlessly supports the proposed algorithm. Common subprograms can be utilized for calculating wavelet matrices and integrals of wavelets for all problems.
(5)
Efficiency and low computation cost: the matrices associated with Haar Scale 3 wavelet collocation method, including wavelet matrices and their integrals, exhibit significant sparsity, resulting in faster computations and reduced computational costs.
(6)
Effectiveness for linear and nonlinear equations: the S3-HW algorithm proves equally effective for both linear and nonlinear Lane–Emden equations.
(7)
Superior performance: comparative numerical experiments reveal that the proposed method outperforms various other methods, establishing its superiority in terms of accuracy and efficiency.
(8)
Potential for extension: the rapid convergence and high accuracy achieved by the proposed method provide a strong foundation for extending its application to solve a wide range of physical problems governed by fractional integro-differential equations and integral equations.

The primary drawback of the scale 3 Haar wavelet family is its discontinuity at the partition points, which renders the derivative approach inapplicable in the initial stage, which we tackled by converting the given differential model into the corresponding integral model. Additionally, the computational cost rises as the level of resolution increases. But the given method exhibits good accuracy at the initial level of resolution. The increase in the level of resolution requires for more complex problems, where one can compromise the computational cost to obtain good accuracy.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors are grateful to Lovely Professional University for providing the infrastructure needed to conduct their research.

Appendix

MATLAB Code for First Nine Members of Scale 3 Haar Functions

function o = nhaar (i)

o = zeros(size (i));

o (i > = 0) = 1;

o (i = = 1) = 0;

end

function o = haar2 (i)

o = zeros(size (i));

o (i > = 0) = −1/sqrt (2);

o (i > = 1/3) = sqrt (2);

o (i > = 2/3) = −1/sqrt (2);

o (i >1) = 0;

end

function o = haar3 (i)

o = zeros(size (i));

o (i > = 0) = sqrt (3/2);

o (i > = 1/3) = 0;

o (i > = 2/3) = -sqrt (3/2);

o (i >1) = 0;

end

function o = haar4 (i)

o = zeros(size (i));

o (i > = 0) = -1/sqrt (2);

o (i > = 1/9) = sqrt (2);

o (i > = 2/9) = -1/sqrt (2);

o (i >1/3) = 0;

end

function o = haar5 (i)

o = zeros(size (i));

o (i > = 0) = sqrt (3/2);

o (i > = 1/9) = 0;

o (i > = 2/9) = -sqrt (3/2);

o (i >1/3) = 0;

end

function o = haar6 (i)

o = zeros(size (i));

o (i > = 3/9) = -1/sqrt (2);

o (i > = 4/9) = sqrt (2);

o (i > = 5/9) = -1/sqrt (2);

o (i >2/3) = 0;

end

function o = haar7 (i)

o = zeros(size (i));

o (i > = 3/9) = sqrt (3/2);

o (i > = 4/9) = 0;

o (i > = 5/9) = -sqrt (3/2);

o (i >2/3) = 0;

end

function o = haar8 (i)

o = zeros(size (i));

o (i > = 6/9) = -1/sqrt (2);

o (i > = 7/9) = sqrt (2);

o (i > = 8/9) = -1/sqrt (2);

o (i >1) = 0;

end

function o = haar9 (i)

o = zeros(size (i));

o (i > = 6/9) = sqrt (3/2);

o (i > = 7/9) = 0;

o (i > = 8/9) = -sqrt (3/2);

o (i >1) = 0;

end

close all;

x = 0 : 0.000001 : 1;

figure (1)

subplot (3,1,1) % add first plot in 2 x 2 grid

plot (x,nhaar (x),’k’,’LineWidth’,2)

txt = ’i = 1’;

text (0.5,0.5,txt,’FontSize’,14)

axis([0 1 0.0 1.5])% line plot

%title (’First nine members of haar wavelet family h1 to h9 ’)

xlabel (’h_{1} (t)’,’FontSize’,14)

fprintf (’\n\n’)

subplot (3,1,2) % add first plot in 2 x 2 grid

plot (x, haar2 (x),’k’,’LineWidth’,2)

txt = {’i = 2,k = 0,j = 0,m = 1 i = m + 2k + 1’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{2} (t)’,’FontSize’,14)

subplot (3,1,3) % add first plot in 2 x 2 grid

plot (x,haar3 (x),’k’,’LineWidth’,2)

txt = {’i = 3,k = 0,j = 0,m = 1 i = m + 2(k + 1)’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{3} (t)’,’FontSize’,14)

figure (2)

subplot (3,1,1) % add first plot in 2 x 2 grid

plot (x,haar4 (x),’k’,’LineWidth’,2)

txt = {’ i = 4,k = 0,j = 1,m = 3 i = m + 2k + 1’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{4} (t)’,’FontSize’,14)

subplot (3,1,2) % add first plot in 2 x 2 grid

plot (x,haar5 (x),’k’,’LineWidth’,2) % line plot

txt = {’i = 5,k = 0,j = 1,m = 3 i = m + 2(k + 1)’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{5} (t)’,’FontSize’,14)

figure (2)

subplot (3,1,3) % add first plot in 2 x 2 grid

plot (x,haar6 (x),’k’,’LineWidth’,2) % line plot

txt = {’i = 6,k = 1,j = 1,m = 3 i = m + 2k + 1’};

text (0.3,0.5,txt,’FontSize’,14)

xlabel (’h_{6} (t)’,’FontSize’,14)

figure (3)

subplot (3,1,1) % add first plot in 2 x 2 grid

plot (x,haar7(x),’k’,’LineWidth’,2) % line plot

txt = {’i = 7,k = 1,j = 1,m = 3 i = m + 2(k + 1)’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{7} (t)’,’FontSize’,14)

subplot (3,1,2) % add first plot in 2 x 2 grid

plot (x, haar8 (x),’k’,’LineWidth’, 2) % line plot

txt = {’i = 8,k = 2,j = 1,m = 3 i = m + 2k + 1’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{8} (t)’,’FontSize’,14)

subplot (3,1,3) % add first plot in 2 x 2 grid

plot (x,haar9 (x),’k’,’LineWidth’,2) % line plot

txt = {’i = 9,k = 2,j = 1,m = 3 i = m + 2(k + 1)’};

text (0.45,0.5,txt,’FontSize’,14)

xlabel (’h_{9} (t)’,’FontSize’,14)

Open Research

Data Availability

The data underlying the results presented in the study are available within the manuscript.

References

1 Mccrea W. H., An introduction to the study of stellar structure, Nature. (1939) 144, no. 3638, 130–131, https://doi.org/10.1038/144130a0.
10.1038/144130a0
Google Scholar
2 Wazwaz A.-M., A new algorithm for solving differential equations of Lane–Emden type, Applied Mathematics and Computation. (2001) 118, no. 2-3, 287–310, https://doi.org/10.1016/S0096-3003(99)00223-4, 2-s2.0-0040926145.
10.1016/S0096-3003(99)00223-4
Web of Science® Google Scholar
3 Bedient P. E. and Davis H. T., Introduction to nonlinear differential and integral equations, The American Mathematical Monthly. (1964) 71, no. 9, https://doi.org/10.2307/2311950, 1056.
10.2307/2311950
Google Scholar
4 Parand K. and Hashemi S., RBF-DQ method for solving non-linear differential equations of Lane–Emden type, Ain Shams Engineering Journal. (2018) 9, no. 4, 615–629, https://doi.org/10.1016/j.asej.2016.03.010, 2-s2.0-85048737081.
10.1016/j.asej.2016.03.010
Web of Science® Google Scholar
5 Dehghan M. and Shakeri F., Approximate solution of a differential equation arising in astrophysics using the variational iteration method, New Astronomy. (2008) 13, no. 1, 53–59, https://doi.org/10.1016/j.newast.2007.06.012, 2-s2.0-34548509029.
10.1016/j.newast.2007.06.012
Web of Science® Google Scholar
6 Agarwal R. P. and O’Regan D., Second order initial value problems of Lane–Emden type, Applied Mathematics Letters. (2007) 20, no. 12, 1198–1205, https://doi.org/10.1016/j.aml.2006.11.014, 2-s2.0-35348841427.
10.1016/j.aml.2006.11.014
Google Scholar
7 Wazwaz A.-M., Linear and Nonlinear Integral Equations Methods and Applications, 2011, Springer.
10.1007/978-3-642-21449-3
Google Scholar
8 Richardson O. W., The emission of electricity from hot bodies, Journal of the Röntgen Society. (1922) 18, no. 72, 150–150, https://doi.org/10.1259/jrs.1922.0041.
10.1259/jrs.1922.0041
Google Scholar
9 Roul P., Madduri H., and Agarwal R., A fast-converging recursive approach for Lane–Emden type initial value problems arising in astrophysics, Journal of Computational and Applied Mathematics. (2019) 359, 182–195, https://doi.org/10.1016/j.cam.2019.03.037, 2-s2.0-85064385652.
10.1016/j.cam.2019.03.037
Google Scholar
10 Singh H., An efficient computational method for the approximate solution of nonlinear Lane–Emden type equations arising in astrophysics, Astrophysics and Space Science. (2018) 363, no. 4, https://doi.org/10.1007/s10509-018-3286-1, 2-s2.0-85043465722.
10.1007/s10509-018-3286-1
Google Scholar
11 Duggan R. C. and Goodman A. M., Pointwise bounds for a nonlinear heat conduction model of the human head, Bulletin of Mathematical Biology. (1986) 48, no. 2, 229–236, https://doi.org/10.1007/BF02460025, 2-s2.0-0022448239.
10.1016/S0092-8240(86)80009-X
CAS PubMed Web of Science® Google Scholar
12 Hadian-Rasanan A. H., Rahmati D., Gorgin S., and Parand K., A single layer fractional orthogonal neural network for solving various types of Lane–Emden equation, New Astronomy. (2020) 75, https://doi.org/10.1016/j.newast.2019.101307, 101307.
10.1016/j.newast.2019.101307
Google Scholar
13 Lane H. J., On the theoretical temperature of the Sun, under the hypothesis of a gaseous mass maintaining its volume by its internal heat, and depending on the laws of gases as known to terrestrial experiment, American Journal of Science. (1870) s2-50, no. 148, 57–74, https://doi.org/10.2475/ajs.s2-50.148.57.
10.2475/ajs.s2-50.148.57
Google Scholar
14 Wazwaz A.-M., A new method for solving singular initial value problems in the second-order ordinary differential equations, Applied Mathematics and Computation. (2002) 128, no. 1, 45–57, https://doi.org/10.1016/S0096-3003(01)00021-2, 2-s2.0-0037052586.
10.1016/S0096-3003(01)00021-2
Web of Science® Google Scholar
15 Caglar N. and Caglar H., B-spline solution of singular boundary value problems, Applied Mathematics and Computation. (2006) 182, no. 2, 1509–1513, https://doi.org/10.1016/j.amc.2006.05.035, 2-s2.0-33751540078.
10.1016/j.amc.2006.05.035
Web of Science® Google Scholar
16 Yousefi S. A., Legendre wavelets method for solving differential equations of Lane–Emden type, Applied Mathematics and Computation. (2006) 181, no. 2, 1417–1422, https://doi.org/10.1016/j.amc.2006.02.031, 2-s2.0-33750454785.
10.1016/j.amc.2006.02.031
Web of Science® Google Scholar
17 Ertürk V. S., Differential transformation method for solving differential equations of Lane–Emden type, Mathematical and Computational Applications. (2007) 12, no. 3, 135–139, https://doi.org/10.3390/mca12030135.
10.3390/mca12030135
Google Scholar
18 Ramos J. I., Series approach to the Lane–Emden equation and comparison with the homotopy perturbation method, Chaos, Solitons and Fractals. (2008) 38, no. 2, 400–408, https://doi.org/10.1016/j.chaos.2006.11.018, 2-s2.0-43049098279.
10.1016/j.chaos.2006.11.018
Web of Science® Google Scholar
19 Parand K., Shahini M., and Dehghan M., Rational legendre pseudospectral approach for solving nonlinear differential equations of Lane–Emden type, Journal of Computational Physics. (2009) 228, no. 23, 8830–8840, https://doi.org/10.1016/j.jcp.2009.08.029, 2-s2.0-70349807582.
10.1016/j.jcp.2009.08.029
CAS Web of Science® Google Scholar
20 Vanani S. K. and Aminataei A., On the numerical solution of differential equations of Lane–Emden type, Computers & Mathematics with Applications. (2010) 59, no. 8, 2815–2820, https://doi.org/10.1016/j.camwa.2010.01.052, 2-s2.0-77950189652.
10.1016/j.camwa.2010.01.052
Web of Science® Google Scholar
21 Parand K., Dehghan M., Rezaei A. R., and Ghaderi S. M., An approximation algorithm for the solution of the nonlinear Lane–Emden type equations arising in astrophysics using Hermite functions collocation method, Computer Physics Communications. (2010) 181, no. 6, 1096–1108, https://doi.org/10.1016/j.cpc.2010.02.018, 2-s2.0-77950626787.
10.1016/j.cpc.2010.02.018
CAS Web of Science® Google Scholar
22 Iqbal S. and Javed A., Application of optimal homotopy asymptotic method for the analytic solution of singular Lane–Emden type equation, Applied Mathematics and Computation. (2011) 217, no. 19, 7753–7761, https://doi.org/10.1016/j.amc.2011.02.083, 2-s2.0-79955837803.
10.1016/j.amc.2011.02.083
Web of Science® Google Scholar
23 Wazwaz A.-M., Rach R., and Duan J.-S., A study on the systems of the volterra integral forms of the Lane–Emden equations by the Adomian decomposition method, Mathematical Methods in the Applied Sciences. (2014) 37, no. 1, 10–19, https://doi.org/10.1002/mma.2776, 2-s2.0-84890549157.
10.1002/mma.2776
Web of Science® Google Scholar
24 Taghavi A. and Pearce S., A solution to the Lane–Emden equation in the theory of stellar structure utilizing the Tau method, Mathematical Methods in the Applied Sciences. (2013) 36, no. 10, 1240–1247, https://doi.org/10.1002/mma.2676, 2-s2.0-84879416281.
10.1002/mma.2676
Web of Science® Google Scholar
25 YüzbaşI Ş. and Sezer M., An improved Bessel collocation method with a residual error function to solve a class of Lane–Emden differential equations, Mathematical and Computer Modelling. (2013) 57, no. 5-6, 1298–1311, https://doi.org/10.1016/j.mcm.2012.10.032, 2-s2.0-84873077054.
10.1016/j.mcm.2012.10.032
Web of Science® Google Scholar
26 Wazwaz A.-M. and Khuri S. A., The variational iteration method for solving the Volterra integro-differential forms of the Lane–Emden and the Emden-Fowler problems with initial and boundary value conditions, Open Engineering. (2015) 5, no. 1, 31–41, https://doi.org/10.1515/eng-2015-0006, 2-s2.0-84992025866.
10.1515/eng-2015-0006
Google Scholar
27 Asadpour S., Hosseinzadeh H., Yazdani A., Asadpour S., and Hosseinzadeh H., Numerical solution of the lane-emden equations with moving least squares method, Applications and Applied Mathematics: An International Journal (AAM). (2019) 14, no. 2, 762–776.
Google Scholar
28 Sahu P. Kumar, Numerical solutions for volterra integro-differential forms of lane-emden equations of first and second kind using legendre multi-wavelets, Electronic Journal of Differential Equations. (2015) 2015, no. 28, 1–11.
Google Scholar
29 Balaji S., A new bernoulli wavelet operational matrix of derivative method for the solution of nonlinear singular Lane–Emden type equations arising in astrophysics, Journal of Computational and Nonlinear Dynamics. (2016) 11, no. 5, https://doi.org/10.1115/1.4032386, 2-s2.0-84957916966.
10.1115/1.4032386
PubMed Google Scholar
30 Sahu P. K. and Ray S. S., Chebyshev wavelet method for numerical solutions of integro-differential form of Lane–Emden type differential equations, International Journal of Wavelets, Multiresolution and Information Processing. (2017) 15, no. 2, https://doi.org/10.1142/S0219691317500151, 2-s2.0-85008698092, 1750015.
10.1142/S0219691317500151
Google Scholar
31 Singh R., Shahni J., Garg H., and Garg A., Haar wavelet collocation approach for Lane–Emden equations arising in mathematical physics and astrophysics, The European Physical Journal Plus. (2019) 134, no. 11, https://doi.org/10.1140/epjp/i2019-12889-1.
10.1140/epjp/i2019-12889-1
Google Scholar
32 Sabir Z., Wahab H. A., Umar M., Sakar M. G., and Raja M. A. Z., Novel design of Morlet wavelet neural network for solving second order Lane–Emden equation, Mathematics and Computers in Simulation. (2020) 172, 1–14, https://doi.org/10.1016/j.matcom.2020.01.005.
10.1016/j.matcom.2020.01.005
Web of Science® Google Scholar
33 Gümgüm S., Taylor wavelet solution of linear and nonlinear Lane-Emden equations, Applied Numerical Mathematics. (2020) 158, 44–53, https://doi.org/10.1016/j.apnum.2020.07.019.
10.1016/j.apnum.2020.07.019
Web of Science® Google Scholar
34 Jiwari R., A Haar wavelet quasilinearization approach for numerical simulation of Burgers’ equation, Computer Physics Communications. (2012) 183, no. 11, 2413–2423, https://doi.org/10.1016/j.cpc.2012.06.009, 2-s2.0-84864445832.
10.1016/j.cpc.2012.06.009
CAS Web of Science® Google Scholar
35 Pandit S., Jiwari R., Bedi K., and Koksal M. E., Haar wavelets operational matrix based algorithm for computational modelling of hyperbolic type wave equations, Engineering Computations. (2017) 34, no. 8, 2793–2814, https://doi.org/10.1108/EC-10-2016-0364, 2-s2.0-85033403579.
10.1108/EC-10-2016-0364
Web of Science® Google Scholar
36 Chui C. K. and Lian J. A., Construction of compactly supported symmetric and antisymmetric orthonormal wavelets with scale = 3, Applied and Computational Harmonic Analysis. (1995) 2, no. 1, 21–51, https://doi.org/10.1006/acha.1995.1003, 2-s2.0-0029192321.
10.1006/acha.1995.1003
Google Scholar
37 Mittal R. C. and Pandit S., Sensitivity analysis of shock wave Burgers’ equation via a novel algorithm based on scale-3 Haar wavelets, International Journal of Computer Mathematics. (2017) 95, no. 3, 601–625, https://doi.org/10.1080/00207160.2017.1293820, 2-s2.0-85014439738.
10.1080/00207160.2017.1293820
Google Scholar
38 Mittal R. C. and Pandit S., Quasilinearized Scale-3 Haar wavelets-based algorithm for numerical simulation of fractional dynamical systems, Engineering Computations. (2018) 35, no. 5, 1907–1931, https://doi.org/10.1108/EC-09-2017-0347, 2-s2.0-85053014663.
10.1108/EC-09-2017-0347
Web of Science® Google Scholar
39 Mittal R. C. and Pandit S., New scale-3 haar wavelets algorithm for numerical simulation of second order ordinary differential equations, proceedings of the national academy of sciences india section A, Proceedings of the National Academy of Sciences, India Section A: Physical Sciences. (2019) 89, no. 4, 799–808, https://doi.org/10.1007/s40010-018-0538-y.
10.1007/s40010-018-0538-y
Google Scholar
40 Kanth A. S. V. R. and Aruna K., He’s variational iteration method for treating nonlinear singular boundary value problems, Computers & Mathematics with Applications. (2010) 60, no. 3, 821–829, https://doi.org/10.1016/j.camwa.2010.05.029, 2-s2.0-77955413071.
10.1016/j.camwa.2010.05.029
Web of Science® Google Scholar
41 Singh R. and Kumar J., An efficient numerical technique for the solution of nonlinear singular boundary value problems, Computer Physics Communications. (2014) 185, no. 4, 1282–1289, https://doi.org/10.1016/j.cpc.2014.01.002, 2-s2.0-84894622826.
10.1016/j.cpc.2014.01.002
CAS Web of Science® Google Scholar
42 Bellman R. E. and Kalaba R. E., Quasilinearization and nonlinear boundary-value problems, American Elsevier Publishing Company. (1966) 8, no. 3.
Google Scholar
43 D’Hondt T., Quasilinearization and nonlinear boundary value problems, Bulletin de la Classe des Sciences. (1977) 63, no. 1, 22–33, https://doi.org/10.3406/barb.1977.58179.
10.3406/barb.1977.58179
Google Scholar
44 Kumar R., Construction of non-dyadic wavelets family and their integral for multiscale approximation of unknown function, Journal of Emerging Technologies and Innovative Research. (2018) 5, no. 12.
Google Scholar
45 Kumar R. and Bakhtawar S., An improved algorithm based on Haar scale 3 wavelets for the numerical solution of integro-differential equations, Mathematics in Engineering, Science and Aerospace. (2022) 13, no. 3, 617–633.
Google Scholar
46 Verma A. K. and Tiwari D., Higher resolution methods based on quasilinearization and Haar wavelets on Lane–Emden equations, International Journal of Wavelets, Multiresolution and Information Processing. (2019) 17, no. 3, https://doi.org/10.1142/S021969131950005X, 2-s2.0-85057045419, 1950005.
10.1142/S021969131950005X
Web of Science® Google Scholar
47 Chawla M. M., Subramanian R., and Sathi H. L., A fourth order method for a singular two-point boundary value problem, BIT. (1988) 28, no. 1, https://doi.org/10.1007/978-3-0348-6303-2.
10.1007/BF01934697
Google Scholar
48 Singh R., Garg H., and Guleria V., Haar wavelet collocation method for Lane–Emden equations with Dirichlet, Neumann and Neumann–Robin boundary conditions, Journal of Computational and Applied Mathematics. (2019) 346, 150–161, https://doi.org/10.1016/j.cam.2018.07.004, 2-s2.0-85050292466.
10.1016/j.cam.2018.07.004
Web of Science® Google Scholar
49 Arora G., Kumar R., and Kaur H., A novel wavelet based hybrid method for finding the solutions of higher order boundary value problems, Ain Shams Engineering Journal. 9, no. 4, 3015–3031.
10.1016/j.asej.2017.12.006
Google Scholar

All articles

Exploring Solution Strategies for Volterra Integro-Differential Lane–Emden Equations in Astrophysics Using Haar Scale 3 Wavelets

Abstract

1. Introduction

2. The Quasilinearization Approach

3. Scale 3 Haar Wavelets

4. Construction of Scale 3 Haar Wavelet Algorithm

4.1. Proposed Methodology

5. Convergence Analysis

6. Numerical Examples

7. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

MATLAB Code for First Nine Members of Scale 3 Haar Functions

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exploring Solution Strategies for Volterra Integro-Differential Lane–Emden Equations in Astrophysics Using Haar Scale 3 Wavelets

Abstract

1. Introduction

2. The Quasilinearization Approach

3. Scale 3 Haar Wavelets

4. Construction of Scale 3 Haar Wavelet Algorithm

4.1. Proposed Methodology

5. Convergence Analysis

6. Numerical Examples

7. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

MATLAB Code for First Nine Members of Scale 3 Haar Functions

Open Research

Data Availability

References

Figures

References

Related

Information