International Journal of Energy Research

Volume 2024, Issue 1 5560003

Research Article

Open Access

Electricity Cogeneration Potential in Minas Gerais Cement Industry with Thermodynamic Cycles

Nathália de Assis Gomes

Pontifical Catholic University of Minas Gerais Department of Mechanical Engineering Av. Dom José Gaspar 500-30535-901 Belo Horizonte MG Brazil

Search for more papers by this author

Thais Martins Bernarde de Assis,

Thais Martins Bernarde de Assis

Pontifical Catholic University of Minas Gerais Department of Mechanical Engineering Av. Dom José Gaspar 500-30535-901 Belo Horizonte MG Brazil

Search for more papers by this author

Felipe Raul Ponce Arrieta,

Corresponding Author

Felipe Raul Ponce Arrieta

[email protected]

orcid.org/0000-0001-7107-4929

Pontifical Catholic University of Minas Gerais Department of Mechanical Engineering Av. Dom José Gaspar 500-30535-901 Belo Horizonte MG Brazil

Search for more papers by this author

Nathália de Assis Gomes,

Nathália de Assis Gomes

Pontifical Catholic University of Minas Gerais Department of Mechanical Engineering Av. Dom José Gaspar 500-30535-901 Belo Horizonte MG Brazil

Search for more papers by this author

Thais Martins Bernarde de Assis,

Thais Martins Bernarde de Assis

Pontifical Catholic University of Minas Gerais Department of Mechanical Engineering Av. Dom José Gaspar 500-30535-901 Belo Horizonte MG Brazil

Search for more papers by this author

Felipe Raul Ponce Arrieta,

Corresponding Author

Felipe Raul Ponce Arrieta

[email protected]

orcid.org/0000-0001-7107-4929

Pontifical Catholic University of Minas Gerais Department of Mechanical Engineering Av. Dom José Gaspar 500-30535-901 Belo Horizonte MG Brazil

Search for more papers by this author

First published: 22 May 2024

https://doi.org/10.1155/2024/5560003

Academic Editor: Chika Maduabuchi

Share a link

Email
Wechat
Bluesky

Abstract

To assess the electricity cogeneration potential in the Minas Gerais cement industry with thermodynamic cycles is the main purpose of this study. The potential was estimated based on Minas Gerais cement sector data. The Kalina cycle, the organic Rankine cycle, and the conventional Rankine cycle were technically and economically assessed. The technical evaluation considered the thermodynamic modeling with optimization including the mass, energy, entropy, and exergy balances and the heat transfer calculations for heat exchangers. The economic evaluation considered the economic modeling including the calculation of electric power generated specific cost, the total investment, cash flow, and payback. The result shows that the greatest irreversibilities are concentrated in the turbines and evaporators. The Kalina cycle confirmed more generated power and exergetic efficiency, but in terms of thermal efficiency, the values were very similar between the cycles. The three cycles can cover more than 35% of the energy demand, which means a considerable reduction in cement manufacturing costs. All cycles reveal a payback value lower than 3 years, a considerable value of cash flow, and high competitiveness in the current tariff scenario. The electricity cogeneration potential in the Minas Gerais cement industry is near 100 MW, and it is in the south-central region of Minas Gerais, where there is a greater population and energy demand concentration. This potential could save emissions of around 282,913 tCO₂/year.

1. Introduction

The cement industry consumes a huge amount of thermal energy, approximately 2% of the world’s energy [1], requiring between 90 and 150 kWh of electric energy per ton of produced cement [2]. The clinker production uses 90% of the total energy consumed [3], while for the whole process, 25% of the energy demand is electrical energy and 75% is thermal energy [4]. Nevertheless, in dependence of the age of the plant and details of the process, around 40% of input energy is heat loss [5], which represents a high potential for waste heat recovery (WHR) and electricity generation via bottoming cogeneration, which could be able to decrease the electric demand of the cement plant by up to 30%, without additional fuel consumption, and to decrease the electrical energy’s expenses [6], which represent about one-quarter of the cement factory’s operational costs [7]. On the other hand, the clinker production process generates a large amount of CO₂ in an approximate ratio of 0.927 tons of CO₂/ton of clinker [8], which could be reduced with the implementation of the WHR electricity cogeneration system in the cement industry [9].

In the bottoming cogeneration, the primary fuel produces high-temperature thermal energy (useful heat) upstream of the power production [10]. In the cement industries, useful heat is used for clinker production, while a WHR-bottoming electricity cogeneration system (from this point onwards, only a cogeneration system or just cogeneration) is used for power production. The cogeneration system is composed of heat recovery boilers, a power turbine, a condenser, and pumps. In the boilers, the waste heat is recovered from the cement production process for heating, evaporating, and superheating the working fluid, which is used in the turbine to produce mechanical power and electricity with a coupled generator. Later, the working fluid is condensed in the condenser, which is then pumped to the boiler, restarting the cycle [4]. The Kalina cycle, the organic Rankine cycle (ORC), and the conventional Rankine cycle could be applied to the WHR electricity cogeneration system in the cement industries [4]. These cycles are very similar, differing by the working fluid that they use. The first one uses an ammonia-water mixture as a working fluid, and its utilization in the cement industry is practically unexplored; however, some researchers show that the Kalina cycle is very efficient for this application [11]. The second one uses an organic fluid as a working fluid [12], and its utilization in the cement industry is little explored, although showing a great performance for heat sources with temperatures between 80 and 400°C. The last one uses water as a working fluid, and it is widely used for WHR electricity cogeneration in the cement industry [3] given its simple and cheap technology [5]. When it comes to the cogeneration of electricity from WHR, the conventional Rankine cycle is suggested when the temperature of the heat source is above 400°C. ORC is suggested when the temperature of the heat source is less than 300°C, whereas the Kalina cycle can be used over the entire temperature range of the heat source as long as the concentration of the ammonia-water mixture and the cycle setting is properly adjusted. These cycles have been widely studied for WHR electricity cogeneration.

The two-pressure Rankine cycle showed power (5.675 MW) and exergetic efficiency (48.03%) higher than the two-pressure ORC in a cogeneration application [13]. The thermodynamic performance of three Kalina cycle configurations using ammonia-water mixture mass concentration ranging from 0.60 to 0.95 for WHR cogeneration plant using cement kiln exhaust gases showed thermal and exergetic efficiency of 22.15% and 40.35%, respectively [14]. The conventional Rankine cycle produces less CO₂ (5.36 × 10⁴ ton/year), less payback (3.4 years), and saves more fuel (2.38 × 10⁷ m³/year) and money (2.1 × 10⁶ $/year) than an ORC with toluene [15]. A comparative study between the simple Rankine cycle and ORC indicated that the conventional Rankine presents a higher thermal efficiency (23.58%) and power production (6.26 MW) than the ORC (4.66 MW) [16]. In a study for WHR in the iron and steel industry, different thermal schemes of ORC and Kalina cycles were analyzed with lower product cost for the first, showing thermal efficiency ranging from 13.37 to 19.43 and 16.21 to 20.41, while exergetic efficiency reached 53.04–89.85 and 44.94–70.13 for ORC and Kalina cycles, respectively [17]. In other studies, the dual flash Rankine cycle can recover more heat and produce more electricity (9.4 MW) than the simple Rankine cycle (8.3 MW) because of its higher exergetic efficiency (41.08% vs. 36.30%) [18]. On the other hand, the simple Rankine exhibits a higher exergetic efficiency (42.1%) than the double-pressure Rankine and ORC [19]. The ORC has a higher thermal efficiency than the Rankine cycle, considering the same turbine inlet temperature when both operate coupled with low-temperature heat sources [20]. In general, the simple Rankine cycle has excellent performance at high source temperatures (>500°C) [4], suggesting the dual-flash Rankine cycle for WHR electricity cogeneration in the cement industry [21]. In cogeneration application with ORC, the largest exergetic losses are in the evaporation and condensation processes, while with simple and dual-pressure Rankine cycles, the largest exergetic losses are in the turbine expansion and condensation processes [22].

The comparative environmental impacts and emission reductions between the ORC and Kalina cycles for WHR, for a roller kiln, were completed. ORC basic, ORC regenerative, Kalina cycle 11, and Kalina cycle 34 (with ammonia-water mass concentration ranging from 0.65 to 0.85) were compared. The Kalina cycles showed better thermodynamic, economic, environmental, and water indicators than the ORCs considered [23]. An exergoeconomic comparison of WHR with thermodynamic cycles in a cement industry considers the Kalina cycle, ORC (trilateral flash), and ORC (recuperated). Several organic working fluids were studied in ORCs, and an ammonia-water mass concentration ranging from 0.70 to 0.90 was considered in the Kalina cycle. ORC showed better economic results in terms of cash flow and payback with higher generated power, while the Kalina cycle exhibits fewer irreversibilities and higher exergy efficiency [24]. The potential savings in the cement industry using WHR technologies in different Latin American countries show that although ORC and Kalina are almost mature technologies, a reduction potential of 1.8 million CO₂ tons/year is possible, avoiding between 36% and 58% of the energy requirement of a cement plant [25].

The main purpose of this study is to assess the electricity cogeneration potential in the Minas Gerais cement industry with thermodynamic cycles. Data from the Apodi cement plant are used for the calculation, based on mass, energy entropy, and exergy balances, and the heat transfer calculations for heat exchangers, of cycle thermal and exergetic efficiency, electricity generation, and energy covered from waste heat recovery, as well as the calculation of electric power generated specific cost, the total investment, cash flow, and payback. The potential electricity cogeneration was estimated considering Minas Gerais cement sector data and the attained thermal efficiencies. The novelty of this original research work is related to the following points: (i) the Kalina cycle, the ORC, and the conventional Rankine cycle were studied together and on the same basis for the first time from a thermodynamic and economic point of view aiming the electricity cogeneration potential in Minas Gerais cement sector taking into account the local energy scenario and (ii) it has shown that the electricity cogeneration in Minas Gerais cement sector is promising in terms of energy covered, electricity generation potential, geographic location, economic indexes, and indirectly avoid CO₂ emissions, making it unnecessary to install new thermal plants to generate electricity that, with cogeneration, is added to the grid by reducing consumption in cement plants.

2. Materials and Methods

In recent years, Brazil has been ranked among the 10 largest cement producers in the world [26]. In the country, Minas Gerais, which is the fourth largest state in land area [27] and has the second largest population [28], is the leader in cement production. Annual cement production in Minas Gerais is between 15 and 16 million tons [29]. The cement production process in Minas Gerais uses the dry path which is summarized in Figure 1. The process begins with the limestone extraction in the mine, then the crushing of raw materials, and finishes with the cement milling and storage in the cement silos.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Simplified scheme of dry path cement production process [2].

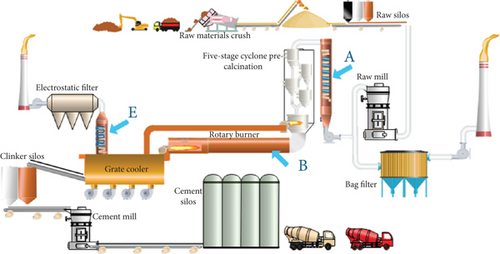
The intermediate stages of the process are interesting for this work because they are where there are points to heat recovery and, consequently, to generate electricity. The points for heat recovery are marked as A, B, and E [2]. Point B considers heat recovery from the heat transfer throughout the walls of the rotary kiln using phase change material, for example [30], and does not apply to this work. Points A and E represent the heat recovery steam generator (HRSG) for WHR and are the focus of this work aiming at electricity cogeneration. In HRSG shown in A and E, the thermal energy is recovered in the cyclone precalcination preheater exhaust gases and in hot air at the clinker grate cooler outlet, respectively.

Table 1 summarizes the data on the Minas Gerais cement sector. The data includes the name of the plant, the city where it is located, the number and type of furnaces, and the daily production capacity of each furnace. In addition, the main necessary data for the calculation of electricity generation from waste heat recovery are presented. This data includes the mass flow rate and the inlet and outlet temperatures of the HRSG. The outlet temperature of the HRSG of the cyclonic economizer is limited to 175°C by the subsequent use of the gas in the raw mill. Without heat recovery, the temperature of the gas is reduced to the values shown in Table 1. The outlet temperature of the clinker cooler HRSG is limited by the satisfactory operation of the electrostatic precipitator or bag filter (100-120°C). As can be seen in the table, there are some factories in which data for the waste heat recovery from the outlet of the clinker cooler are not shown. This is because, in these factories, the hot air at the clinker cooler outlet is injected directly into the rotary kiln. Therefore, in these factories, only the energy from exhaust gas from the cyclone preheater is available for heat recovery. That is, the focus is on those factories that have two points of thermal energy available for waste heat recovery. Cases where there is only one energy point available for waste heat recovery can be addressed with the methodologies provided in [11, 31] and will not be addressed here.

Table 1. Information of Minas Gerais cement sector and data for energy recovery.

Factory name	City	Kiln amount	Kiln type	Clinker production (t/day)	Data for energy recovery from cyclone precalcination preheater exhaust gases			Data for energy recovery from clinker grate cooler outlet
Factory name	City	Kiln amount	Kiln type	Clinker production (t/day)	(kg/s)	T_in (°C)	T_out (°C)	(kg/s)	T_in (°C)	T_out (°C)
Lafarge	Montes Claros	1	Rotative with grate cooler	2050	72.36	345	228	68.04	400	114

Lafarge	Matozinhos	1	Rotative with grate cooler	2050	72.36	345	228	68.04	400	114

LIZ	Vespasiano	1	Rotative with grate cooler	4600	84.04	345	228	39.83	400	114

Holcim	Pedro Leopoldo	2	Rotative with cooling air injection	5520	88.25	345	228	—	—	—
Holcim	Pedro Leopoldo	2	Rotative with cooling air injection	5520	88.25	345	228	—	—	—

InterCement	Pedro Leopoldo	1	Rotative with cooling air injection	2100	72.59	395	228	—	—	—

Lafarge	Arcos	1	Rotative with grate cooler	2050	72.36	345	228	68.04	400	114

Itaú de Minas	Itaú de Minas	3	Rotative with cooling air injection	1500	69.84	345	228	—	—	—
			Rotative with cooling air injection	1550	70.07	345	228	—	—	—
			Rotative with grate cooler	2800	75.79	345	228	59.74	400	114

Tupi	Carandaí	2	Rotative with grate cooler	3500	79.00	345	228	52.00	400	114
Tupi	Carandaí	2	Rotative with grate cooler	2700	75.34	345	228	60.85	400	114

Holcim	Barroso	2	Rotative with cooling air injection	5520	88.25	345	228	—	—	—
Holcim	Barroso	2	Rotative with cooling air injection	5520	88.25	345	228	—	—	—

InterCement	Ijaci	1	Rotative with grate cooler	5500	88.16	350	228	77.00	440	114

CSN	Arcos	2	Rotative with cooling air injection	2500	74.42	345	228	—	—	—
CSN	Arcos	2	Rotative with cooling air injection	6500	92.74	345	228	—	—	—

Brennand	Sete Lagoas	1	Rotative with grate cooler	3800	80.37	300	200	48.68	350	200

The data used for the calculation of electricity generation from waste heat recovery are shown in Table 2 and include at the inlet of the HRSGs the gas temperature, mass flow, and molar composition. This data is from the Apodi cement plant, located in Quixeré, Ceará, which is the only one with electricity cogeneration in Brazil. This plant has a daily clinker production capacity of 3500 t/day, operates for 8030 h/year, and has an annual electric energy consumption of 121 GWh/year [32].

Table 2. Energy availability data [32].

Parameter	Cyclone precalcination preheater exhaust gases	Clinker grate cooler outlet
T_in (°C)	310.0	440.0
(kg/s)	88.00	48.10
Molar composition (%-mass)
N₂	64.58	79.00
O₂	4.94	21.00
CO₂	26.30	—
H₂O	4.18	—

The data presented on the waste energy available for electricity generation allowed us to consider the use of Kalina, conventional Rankine, and organic Rankine cycles for waste heat recovery in this work. The description of these cycles, the thermodynamic modeling and optimization, and the cost modeling of them are presented below.

2.1. Kalina Cycle

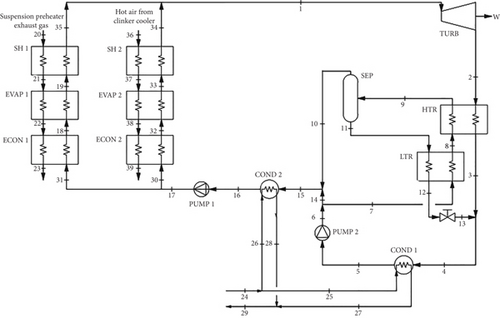
The working fluid of the Kalina cycle is an ammonia-water mixture with variable boiling temperatures at a given pressure, which reduces the irreversibility in the HRSG during the heat transfer process. Figure 2 shows the thermal scheme of the considered Kalina cycle. The choice of this Kalina cycle configuration is based on its better thermal and economic performance [31]. The suspension preheater exhaust gas from the cement production is used to produce superheated steam via heat transfer in the HRSG with SH 1 (20→21 to 19→35), EVAP 1 (21→22 to 18→19), and ECON 1 (22→23 to 31→18). The hot air from the clinker cooler is used to produce superheated steam via heat transfer in the HRSG with SH 2 (36→37 to 33→34), EVAP 2 (37→38 to 32→33), and ECON 2 (38→39 to 30→32). The superheated steam generated in the HRSGs is expanded through the turbine (TURB) to generate mechanical power (). The steam from the turbine exhaust goes into the high-temperature regenerator (HTR), and then it is mixed with an ammonia-water-poor mixture fluid (3→4 and 13→4). This poor mixture condenses through the condenser (COND 1) (4→5). Part of the working fluid is pumped to the low-temperature regenerator (LTR) (7→8), and part is mixed with the ammonia-water-rich mixture fluid from the separator (SEP) (10→15 and 14→15). The low- and high-temperature regenerators (LTR and HTR) heat the pumped fluid before it enters the separator (SEP), in which the vapor with the rich ammonia concentration goes up to COND 2 and the fluid with the poor ammonia concentration goes down to the LTR. This ammonia-water-poor mixture fluid is expanded in the valve to mix with the turbine exhaust steam. The mixture from the SEP and pump 2 condenses through COND 2 (15→16) and is pumped to the economizers ECON 1 and ECON 2, closing the cycle.

2.2. Organic Rankine Cycle Description

In this study, a regenerative organic Rankine cycle with superheating and working under subcritical conditions was evaluated. Regenerative components were included in the simple ORC to increase the cycle’s performance. These components raise the average thermodynamic temperature of the organic fluid during the heat addition process and increase the ORC thermal efficiency. The working fluid selected for this application was the isentropic fluid R11, based on the results given by Moreira and Arrieta [12]. Figure 3 illustrates the regenerative ORC thermal scheme.

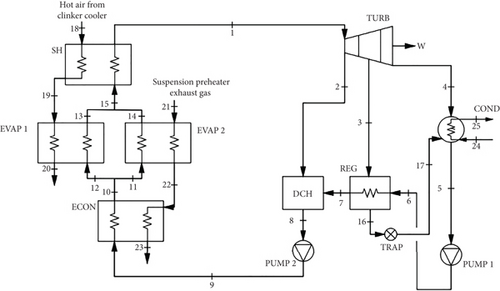
The suspension preheater exhaust gas from the cement production is used to produce saturated steam via heat transfer in the HRSG with EVAP 2 (21→22 to 11→14) and ECON (22→23 to 9→10). The hot air from the clinker cooler is used to produce superheated steam via heat transfer in the HRSG with SH (18→19 to 15→1) and EVAP 1 (19→20 to 12→13). The superheated steam generated in the HRSGs is expanded through the condensing extraction turbine (TURB) to generate mechanical power (). The extracted steam is used for regeneration in the direct contact heater (DCH) (2, 7→8) and regenerator (REG) (3→16 to 6→7). The turbine steam exhaust enters the condenser (COND) (4→5) along with the one that comes from the TRAP (16→17) for condensing to saturated liquid in 4, 17→5. At the COND outlet, the fluid is pumped for regeneration in PUMP 1 (5→6) and then pumped into the HRSG in PUMP 2 (8→9), closing the cycle.

2.3. Conventional Rankine Cycle Description

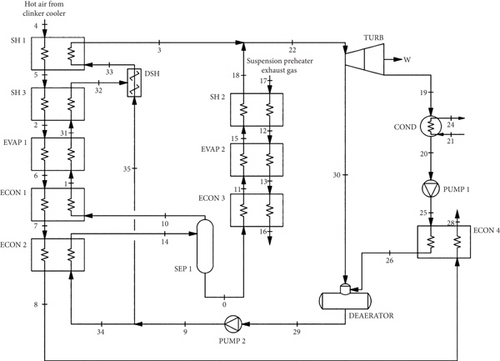
Figure 4 shows the thermal scheme of the considered conventional Rankine cycle. The suspension preheater exhaust gas from the cement production is used to produce superheated steam via heat transfer in the HRSG with SH 2 (17→12 to 15→18), EVAP 2 (12→13 to 11→15), and ECON 3 (13→16 to 0→11). The hot air from the clinker cooler is used to produce superheated steam via heat transfer in the HRSG with SH 1 (4→5 to 33→3), SH 3 (5→2 to 31→32), EVAP 1 (2→6 to 1→31), ECON 1 (6→7 to 10→1), and ECON 4 (8→28 to 25→26). The superheated steam generated in the HRSGs is expanded through the condensing extraction turbine (TURB) to generate mechanical power (). The extracted steam is used for regeneration in the DEAERATOR (30, 26→29). The turbine steam exhaust enters the condenser (COND) (19→20) for condensing to saturated liquid. At the COND outlet, the fluid is pumped for regeneration in PUMP 1 (20→25) and then pumped into the HRSGs in PUMP 2 (29→9), closing the cycle. After PUMP 2, the water is used for desuperheating in DSH (32, 35→33) and produces superheated steam in the HRSGs after SEP 1.

2.4. Thermodynamic Modeling

The thermodynamic modeling of Kalina, organic, and conventional Rankine cycles includes, for each component and the whole cycle, the mass, energy, entropy, and exergy (using the fuel () in kW and product () in kW approach [33]) balances. General considerations for the calculations are steady state, all processes are adiabatic, the variation of kinetic and potential energies is negligible, and the ideal gas behaviour is for the suspension preheater exhaust gas and the hot air from the clinker cooler. Table 3 shows the thermodynamic model for all cycles’ components in the form of generic equipment. This table also contains the generic equipment diagram for a better comprehension of the equations. The heat exchanger component represents in the Kalina cycle the SH 1, EVAP 1, ECON 1, SH 2, EVAP 2, ECON 2, HTR, and LTR; in the ORC the SH, EVAP 1, EVAP 2, ECON, and REG; and in the conventional Rankine cycle the SH 1, SH 3, EVAP 1, ECON 1, ECON 2, SH 2, EVAP 2, ECON 3, and ECON 4. The pump component represents PUMP 1 and PUMP 2 in all cycles. The separator represents SEP and SEP 1 in Kalina and conventional Rankine cycles, respectively, and it is not applicable to the ORC. Bifurcations are applicable for the ones existing in Kalina (bifurcations 6-7-14, 24-25-26, 17-30-31), ORC (10-11-12), and conventional Rankine (9-34-35) cycles. The desuperheater represents DSH in conventional Rankine cycles, and it is not applicable for ORC and Kalina cycles. Junctions are applicable for the ones existing in Kalina (junctions 13-3-4, 10-14-15, 34-35-1, and 27-28-29), ORC (13-14-15), and conventional Rankine (3-18-22) cycles. Condensers, turbines, direct contact heat, deaerators, valves, and traps are well specified in Table 3. The thermodynamic variables in Table 3 are the mass flow rate in a given state “i” () in kg/s, the specific enthalpy in a given state “i” (h_i) in kJ/kg, the specific entropy in a given state “i” (s_i) in kJ/kg.K, the entropy generation for a given cycle component () in kW/K, the specific exergy in a given state “i” (ex_i) in kJ/kg, the power consumed by the pump () in kW, and the power generated in the turbine () in kW.

Table 3. Thermodynamic model equations for all cycles’ components.

Component and diagram	Mass balance	Energy balance	Entropy balance	Fuel ()	Product ()
Heat exchanger

Condenser Kalina and Rankine

Condenser ORC

Pump

Turbine Kalina

Turbine ORC

Turbine Rankine

Separator or bifurcation

Junction or desuperheater

Direct contact heat exchanger and deaerator

Valve and trap

To perform the calculations, Kalina and ORC values of 0.70 and 0.85 are considered for pumps and turbines isentropic efficiencies [2, 19]. For conventional Rankine, the ones are 0.85 and 0.80, respectively, from GateCycle™ version 6.00 SP 4. Reference conditions are T₀ = 288.15 K and P₀ = 101.32 kPa for the specific exergy calculations, which include only thermomechanical exergy, except for some states in the Kalina cycle where the ammonia-water mixture composition changes. In these cases, the chemical exergy is added to the thermomechanical exergy given by equation (1). In this equation, h₀ and s₀ refer to the specific enthalpy, in kJ/kg, and specific entropy, in kJ/kg.K, respectively, at the reference condition. The chemical exergy is calculated considering the ammonia-water mass fraction (x) and the steam quality (q). This way, for q ≤ 0, the value is obtained using

or using

for other q values less than one [34]. In these equations,

, for ammonia and for the water

and

[35]. The irreversibility, in each control volume and for the whole cycle, is calculated by the difference between the fuel (

) and product (

), according to equation (2). The exergetic efficiency in each control volume is calculated by the ratio product (

)—fuel (

) and according to equation (3).

()

The cycle performance parameters like net electric power, considering 100% of electric generator efficiency, or just power (

), in MW; thermal efficiency (

), exergetic efficiency (

); annually energy generated (AEG), in GWh/year; and covered energy demand (CED), in %, are calculated with equations (4)–(8), respectively.

()

In equation (5), the heat input

, in MW, is calculated using equations (9)–(11) for Kalina, ORC, and conventional Rankine cycle, respectively.

()

In equation (6), the exergy input

, in MW, is calculated using equations (12)–(14) for Kalina, ORC, and conventional Rankine cycle, respectively.

()

The main heat exchangers of the thermodynamic cycles are the superheaters, evaporators, economizers, regenerators, and condensers. These are complex equipment, and several algorithms and methods have been discussed and proposed for their calculations [35–37]. For this equipment, in this work, the logarithmic mean temperature difference (LMTD) method [38] was used to calculate the heat transfer surface area (A), in m², according to equation (15). The heat transfer surface area is used for the heat exchanger cost estimation.

()

where

is the total heat transfer rate, in kW; U is the overall heat transfer coefficient, in kW/m².K; and ΔT_lm is the logarithmic mean temperature difference, in °C or K.

The adopted values for the overall heat transfer coefficient (U) shown in Table 4 for Kalina, ORC, and Rankine cycles were taken from [39] and kept fixed during the calculations. The values presented are the average values suggested in the reference mentioned in accordance with the fluid and the type of interaction presented in Table 4.

Table 4. Adopted values of the overall heat transfer coefficient for each heat exchanger.

Component	Type of interaction	Kalina cycle	ORC	Rankine cycle
Component	Type of interaction	U (kW/m².K)
SPH	Gas-gas	0.2601	0.0800	0.0227
ECO/EVAP	Liquid-gas	0.1150	0.0900	0.0397
REG	Liquid/gas-liquid	—	0.4000	—
HTR	Liquid-liquid	0.9500	—	—
LTR	Liquid-vapor	1.3000	—	—
COND	Liquid/gas-liquid	1.3000	0.3500	0.7093

For the thermodynamic calculations, the EES (Engineering Equation Solver version V10.836-3D) was used for the Kalina cycle and ORC, while the GateCycle™ version 6.00 SP 4 was used for the conventional Rankine cycle.

2.5. Optimization

The optimization of the cycles was performed to maximize the power generated considering independent parameters presented in Table 5 based on previous studies [12, 40, 41], performed for the Kalina, organic, and Rankine cycles, respectively. These parameters are related to the mass and energy balance calculation, including the effectiveness, which is the ratio of Q/Qmax. In ECON 1 and SH 3 of the Rankine cycle, the effectiveness is used in GateCycle™ to compute the water outlet temperature. In the Kalina cycle, the steam flow produced in the HRSGs ( and ) are used as independent parameters for better numerical performance of the Kalina cycle EES model, while in the ORC and Rankine cycles, the steam flow produced in the HRSGs results as maximum as possible according to the calculation of the mass and energy balance. The additional data adopted during the calculations that are kept fixed can be inferred from the optimization results that are shown later. The optimization was performed by employing the existing genetic algorithm tool in the EES for the Kalina cycle and the ORC and using the Excel GateCycle™ supplement for the case of the Rankine cycle. The constraint variables are related to the second law of thermodynamics, specifically that the entropy generation in each component must be equal to or higher than zero.

Table 5. Parameter range values for optimization.

Kalina cycle		ORC		Rankine cycle
Parameter	Range value	Parameter	Range value	Parameter	Range value
P₁ (kPa)	3000–8300	ΔT₁₀ subcooling (°C)	31-66	P₁₉ (kPa)	10.6–14.6
P₂ (kPa)	110-300	ΔT₁₉₋₁₃ (°C)	100–200	T₃ (°C)	437-439
x_1 (-)	0.45–0.70	ΔT₂₁₋₁₄ (°C)	100–200	T₁₈ (°C)	298-308
ΔT₂₀₋₃₅ (°C)	10-40	T₁ (°C)	200-250	T₁₄ (°C)	170-178
ΔT₃₆₋₃₄ (°C)	5–100	—	—	ΔT₁₃₋₁₁ (°C)	7–13
ΔT₂₋₉ (°C)	5-50	—	—	ΔT₁₂₋₁₅ (°C)	100-120
(kg/s)	1-12	—	—	ε_ECON 1 (-)	0.10–0.12
(kg/s)	1-12	—	—	ε_SH 3 (-)	0.60–0.90

2.6. Economic Modeling

For the economic modeling of the cycles, the electric power generated specific cost, the total investment, the cash flow, and the payback were calculated. This electric power generated specific cost depends on the total investment, the power generated, the amortization factor, the annual operating hours, and the operation and maintenance costs. The electric power generated specific cost C_g, in R$/kWh, was calculated using equation (16). In this equation, C_inv is the total investment cost, in R$;

is the net power generated, in kW; AF is the amortization factor, in year^-1; OH is the annual operation hours, in h/year; and C_O&M is the specific operation and maintenance cost, in R$/kWh, presented in Table 6 and adopted from [37]. The amortization factor is given by equation (17), in which i is the interest rate, in %, adopted from [42] and n is useful life of the cogeneration plant, in years. Equation (18) calculates the total investment cost, and E_C,x is the estimated cost of all cycle equipment in a year “x”, in R$, CC, FCF, CSD, CAB, and COS, are the dimensional cost factor of contingency, fees, site development, auxiliary buildings, and off-site facilities, respectively. The sum of the contingency costs and fees is 1.18, and the sum of the costs for site development, auxiliary building, and off-site facilities is 1.30. The estimated cost in a year “x” is determined by equation (19), in which E_C,1998/2004 is the cost in the year 1998 [43] or the cost in the year 2004 [44], CI_1998/2004 is the cost index for the year 1998 or 2004, CI_x is the cost index for the year “x”, and Tx_x is the dollar conversion rate of the year “x,” adapted from Ref. [45]. The cost indexes were obtained from Ref. [46]. Table 6 presents the main data required for the economic modeling of the cycles.

()

Table 6. Data for economic modeling.

Parameter	Kalina cycle	ORC	Rankine cycle
Specific O&M cost (R$/kWh)	0.072	0.02	0.072
Useful life (year)	20	20	20
Operation hours per year (h/year)	8,030	8,030	8,030
Interest rate per year (%)	7.0	7.0	7.0
Cost constant (-)	1.534	1.534	1.534
Cost indices for 1998	—	173	142
Cost indices for 2004	162	—	—
Current year	2020	2020	2020
Cost indices for the year x	121	121	100
Dollar conversion rate (R$/US$)	5.30	5.30	5.30

For each cycle of equipment, the cost is defined from the cost curves existing in [44, 46] in function of some parameters in dependence of the equipment. The main parameters of the turbines, heat exchangers, centrifugal pumps, cooling towers, vertical vessels, and horizontal vessels are the electric power generated, heat transfer surface area, volumetric flow, water mass flow, and total volume, respectively.

The cogeneration system implementation in a cement industry decreases the power consumption from electric energy companies, saving the energy purchase by the cogeneration power production. In this sense, the cash flow is the indicator responsible for measuring this financial saving after the cogeneration system implementation. The cash flow (CF), in R$/year, calculated with equation (20), is the multiplication of both previously described: net power generated by the cogeneration system and the annual operation hours, and the electricity tariff (Et), established in 430.74 R$/MWh according to [47]. The cash flow is important to compute the cogeneration system payback (PB), in year, calculated with equation (21).

()

3. Results and Discussion

The results of the thermodynamic modeling presented below focus on the optimal solution obtained. Table 7 shows the values of the independent parameters for the optimal condition. In Tables 8, 9, and 10, the main thermodynamic properties in each state of the cycle are shown for the Kalina cycle, ORC, and conventional Rankine cycle, respectively. The thermodynamic properties include the mass flow, pressure, temperature, specific enthalpy, entropy, exergy, and ammonia-water mass fraction in the case of the Kalina cycle.

Table 7. Parameter values after optimization.

Kalina cycle		ORC		Rankine cycle
Parameter	Optimum value	Parameter	Optimum value	Parameter	Optimum value
P₁ (kPa)	7214	ΔT₁₀ subcooling (°C)	65.00	P₁₉ (kPa)	10.6
P₂ (kPa)	125.42	ΔT₁₉₋₁₃ (°C)	145.00	T₃ (°C)	437
x_1 (-)	0.522	ΔT₂₁₋₁₄ (°C)	124.37	T₁₈ (°C)	301
ΔT₂₀₋₃₅ (°C)	10.82	T₁ (°C)	239.30	T₁₄ (°C)	175
ΔT₃₆₋₃₄ (°C)	50.82	—	—	ΔT₁₃₋₁₁ (°C)	10.7
ΔT₂₋₉ (°C)	18.53	—	—	ΔT₁₂₋₁₅ (°C)	115.8
(kg/s)	5.65	—	—	ε_ECON 1 (-)	0.12
(kg/s)	5.20	—	—	ε_SH 3 (-)	0.90

Table 8. Thermodynamic properties in Kalina cycle at optimum condition.

State	(kg/s)	P (kPa)	T (°C)	h (kJ/kg)	s (kJ/kg.K)	x (-)	ex (kJ/kg)
1	10.85	7214.00	345.39	2516.14	6.0035	0.522	990.04
2	10.85	125.42	84.77	1855.14	6.3311	0.522	234.63
3	10.85	125.42	76.57	1359.19	4.9319	0.522	141.87
4	23.43	125.42	61.43	595.42	2.4979	0.383	79.43
5	23.43	125.42	20.00	-134.29	0.1780	0.383	18.22
6	23.43	287.20	20.02	-134.02	0.1783	0.383	18.41
7	15.31	287.20	20.02	-134.02	0.1783	0.383	18.41
8	15.31	287.20	45.06	10.99	0.6480	0.383	28.07
9	15.31	287.20	66.24	362.41	1.7127	0.383	72.69
10	2.74	287.20	66.24	1508.41	5.5599	0.934	110.12
11	12.58	287.20	66.24	113.02	0.8755	0.262	64.54
12	12.58	287.20	25.05	-63.55	0.3209	0.262	47.79
13	12.58	125.42	25.06	-63.55	0.3215	0.262	47.62
14	8.11	287.20	20.02	-134.02	0.1783	0.383	18.41
15	10.85	287.20	41.63	280.25	1.5524	0.522	36.74
16	10.85	287.20	20.00	-149.81	0.1399	0.522	13.68
17	10.85	7214.00	21.26	-137.77	0.1522	0.522	22.16
18	5.20	7214.00	157.55	523.78	1.9848	0.522	155.67
19	5.20	7214.00	242.68	2192.25	5.4309	0.522	831.13
20	88.00	101.32	310.00	-3207.12	7.1215	0.000	96.35
21	88.00	101.32	300.01	-3217.98	7.1027	0.000	90.90
22	88.00	101.32	207.82	-3316.57	6.9152	0.000	46.34
23	88.00	101.32	170.42	-3355.67	6.8306	0.000	31.63
24	650.01	250.00	15.00	63.22	0.2244	0.000	202.35
25	510.63	250.00	15.00	63.22	0.2244	0.000	202.35
26	139.39	250.00	15.00	63.22	0.2244	0.000	202.35
27	510.63	250.00	23.00	96.70	0.3390	0.000	202.80
28	139.39	250.00	23.00	96.70	0.3390	0.000	202.80
29	650.01	250.00	23.00	96.70	0.3390	0.000	202.80
30	5.65	7214.00	21.26	-137.77	0.1522	0.522	22.16
31	5.20	7214.00	21.26	-137.77	0.1522	0.522	22.16
32	5.65	7214.00	157.55	523.78	1.9848	0.522	155.67
33	5.65	7214.00	242.68	2192.25	5.4309	0.522	831.13
34	5.65	7214.00	389.18	2645.06	6.2048	0.522	1060.95
35	5.20	7214.00	299.18	2376.08	5.7683	0.522	917.73
36	48.10	101.32	440.00	432.73	7.7891	0.000	172.26
37	48.10	101.32	390.78	379.55	7.7118	0.000	141.34
38	48.10	101.32	204.97	183.56	7.3657	0.000	45.08
39	48.10	101.32	129.38	105.85	7.1888	0.000	18.35

Table 9. Thermodynamic properties in ORC at optimum condition.

State	(kg/s)	P (kPa)	T (°C)	h (kJ/kg)	s (kJ/kg.K)	ex (kJ/kg)
1	97.23	3674.00	239.30	346.26	0.9048	90.59
2	7.22	950.38	170.43	318.88	0.9158	60.05
3	24.17	399.28	136.56	301.33	0.9234	40.30
4	65.84	117.13	94.98	277.87	0.9348	13.57
5	90.01	117.13	28.00	58.21	0.2187	0.26
6	90.01	950.38	29.11	59.18	0.2219	0.30
7	90.01	950.38	91.06	114.61	0.3874	8.05
8	97.23	950.38	107.16	129.78	0.4275	11.65
9	97.23	3764.00	112.24	134.67	0.4401	12.92
10	97.23	3764.00	120.36	144.67	0.4602	17.12
11	26.38	3764.00	120.36	144.67	0.4602	17.12
12	70.85	3764.00	120.36	144.67	0.4602	17.12
13	70.85	3764.00	185.36	287.95	0.7839	67.13
14	26.38	3764.00	185.36	287.95	0.7839	67.13
15	97.23	3764.00	185.36	287.95	0.7839	67.13
16	24.17	399.28	69.44	94.87	0.3321	4.24
17	24.17	117.13	28.00	94.87	0.3404	1.84
18	48.15	101.35	440.00	432.73	7.7890	172.26
19	48.15	101.35	330.36	315.00	7.6097	106.18
20	48.15	101.35	127.73	104.17	7.1845	17.88
21	88.03	101.35	310.00	-3254.42	7.1196	96.41
22	88.03	101.35	270.36	-3297.36	7.0434	75.45
23	88.03	101.35	260.09	-3308.39	7.0228	70.32
24	733.32	101.35	15.00	63.08	0.2244	3.46
25	733.32	101.35	20.00	84.01	0.2965	3.64

Table 10. Thermodynamic properties in conventional Rankine cycle at optimum condition.

State	(kg/s)	P (MPa)	T (°C)	h (kJ/kg)	s (kJ/kg.K)	ex (kJ/kg)
0	4.86	1000.00	175.00	741.10	2.0900	140.30
1	4.84	1000.00	176.80	749.10	2.1080	143.20
2	48.10	101.30	386.50	386.30	0.8570	139.20
3	4.85	1000.0	437.00	3343.00	7.5790	1160.00
4	48.10	101.32	440.00	444.00	0.9420	172.00
5	48.10	101.32	433.60	437.10	0.9320	168.00
6	48.10	101.32	189.90	178.70	0.4840	39.20
7	48.10	101.32	189.10	177.90	0.4830	38.90
8	48.10	101.32	127.30	114.20	0.3340	17.80
9	9.71	1000.0	102.50	430.40	1.3350	47.40
10	4.85	1000.0	175.00	741.30	2.0910	140.00
11	4.86	1000.0	179.20	759.60	2.1320	147.00
12	88.00	101.32	295.70	3318.00	0.6980	88.60
13	88.00	101.32	189.90	3431.00	0.4790	39.00
14	9.71	1000.00	175.00	741.30	2.0910	140.40
15	4.86	1000.00	179.90	2778.00	6.5860	881.60
16	88.00	101.32	188.90	3432.00	0.4770	38.65
17	88.00	101.32	310.00	3303.00	0.7250	96.39
18	4.86	1000.00	301.00	3053.00	7.1260	1001.00
19	9.63	10.60	46.98	2586.00	8.1280	245.40
20	9.63	10.60	46.98	196.60	0.6640	6.81
21	480.70	250.00	16.41	69.05	0.2450	0.16
22	9.711	1000.00	368.90	3197.00	7.3640	1077.00
23	480.70	101.32	16.40	68.87	0.2450	0.01
24	480.70	250.00	27.52	115.50	0.4020	1.25
25	9.63	250.00	47.00	197.00	0.6650	7.07
26	9.63	250.00	97.43	408.30	1.2780	41.7
27	9.63	250.00	97.43	408.03	1.2780	41.7
28	48.10	101.32	85.25	71.20	0.2210	7.50
29	9.71	250.00	102.40	429.40	1.3340	46.59
30	0.08	250.00	240.90	2950.00	7.5670	771.60
31	4.85	1000.00	179.90	2778.00	6.5860	881.60
32	4.85	1000.00	404.90	3274.00	7.4800	1120.00
33	4.85	1000.00	404.90	3274.00	7.4800	1120.00
34	9.71	1000.00	102.50	430.40	1.3350	47.41
35	0.00	1000.00	102.50	430.40	1.3350	47.41

Table 7 for the Kalina cycle shows that, in general, the optimal values of the independent parameters are located near the center of the studied range. This is explained by the fact that to maximize the generated power, the maximum steam generation is sought with a combination of temperature and pressure values at the turbine inlet that maximizes the enthalpy at the turbine inlet and the ammonia-water fraction to optimize the steam generation in the HRSGs. In the case of ORC, subcooling in ECON tended to the maximum value to maintain a gas outlet temperature in the state “23” of the order and 228°C, in accordance with Table 1. In the remaining parameters, the tendency was a value below the average value to maximize the steam generation in the HRSGs. In the conventional Rankine cycle, the optimization tended to bring most of the independent parameters to their extreme values in the range evaluated to maximize the power generated. Thus, the pressure at the outlet of the turbine adopted the minimum value, increasing the enthalpic variation in the turbine, and the temperature of the generated steam in the HRSG tended to have minimum values to increase the amount of generated steam. The approach temperatures in EVAP 2 and ECON 3 take mean values in the range to maintain a high steam generation without further increasing the heat transfer surface area in these equipment. The effectiveness of ECON and SH 3 is maximized to increase steam generation.

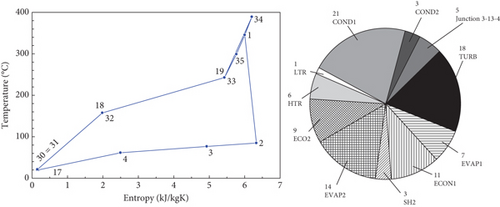
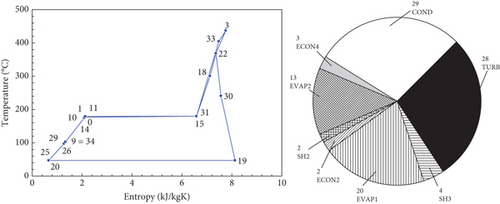
A summary of the exergetic analysis results is shown in Table 11. In this table, the fuel (), product (), irreversibility (), and exergetic efficiency (η_ex) are presented for each equipment of the cycle and the whole cycle. The irreversibility of the cycle includes the ones of the equipment plus the exergy dissipation in the condenser, which is the product of the condenser. This result must be explained together with Figure 5, in which the entropy—temperature diagram is shown and indicates the main irreversibilities by equipment, in percentage, in the considered cycles. As can be inferred from Table 11 and Figure 5, in equipment where there is more fuel, there is also more irreversibility. The turbines COND 1, EVAP 1 and 2, ECON 1 and 2, and TURB are where the greatest irreversibilities in the Kalina cycle are concentrated. In the SH, COND, EVAP 1 and 2, and TURB are where the greatest irreversibilities in the ORC are concentrated. In the conventional Rankine cycle, the greatest irreversibilities are concentrated in the COND, TURB, and EVAP 1 and 2. It is remarkable that if we sum the irreversibilities of evaporators, they are higher than the turbine ones, as reported in similar studies [2, 3, 6, 16]. In the turbines, the irreversibility is given by the efficiency of the expansion process. In the other equipment mentioned, which are heat exchangers, the irreversibility is due to the temperature differences existing in the heat transfer processes. The higher temperature differences in heat transfer processes are remarkable in ORC, if compared with the other cycles, given the low operation temperature of the organic fluid with respect to cement process gas temperature. This fact is compensated with a high flow rate of the working fluid, considering that the objective function aims to maximize the power generated. If the mass flow rate at the turbine inlet is considered, the ORC presents a working fluid mass flow rate greater than that of the Kalina and Rankine cycles, and between them, the flow value is of the same order, which is to be expected because both cycles operate at similar temperatures. In this equipment, the design, selection, operation, and maintenance should be focused on maintaining the efficiency of electricity cogeneration in the cement sector at the highest possible level. In terms of exergy efficiency, the Kalina cycle and ORC show the highest value, followed by the conventional Rankine. Despite a very similar cycle exergy efficiency value, the Kalina cycle extracts more exergy than the ORC from the cement process gas (note that the fuel in the Kalina cycle is greater than that of the ORC) and generates more power, which is explained by the particularity of the ammonia-water mixture of changing phase at variable temperature (as can be seen in the entropy—temperature diagram), causing a uniform temperature profile in the heat transfer process, reducing the irreversibility of the evaporators and condenser, as shown in Figure 5. Note in this figure that in the Kalina cycle, the irreversibility in these devices has a lower percentage weight than in the other cycles.

Table 11. Summary of exergetic analysis results.

Kalina cycle results					ORC results					Rankine cycle results
Equipment	(kW(	(kW)	(kW)	η_ex	Equipment	(kW)	(kW)	(kW)	η_ex	Equipment	(kW)	(kW)	(kW)	η_ex
TURB	8196.20	7171.92	1024.28	0.875	TURB	6506.89	5786.83	720.06	0.889	TURB	8036.66	6280.19	1756.48	0.781
SH 1	479.34	450.34	28.99	0.940	SH	3182.16	2281.15	901.02	0.717	SH 1	198.73	194.22	4.51	0.977
EVAP 1	3921.35	3512.37	408.98	0.896	EVAP 1	4251.9	3543.26	708.63	0.833	SH 3	1412.97	1160.08	252.89	0.821
ECON 1	1294.29	694.27	600.02	0.536	EVAP 2	1845.16	1319.24	525.92	0.715	EVAP 1	4810.16	3579.07	1231.09	0.744
SH 2	1487.00	1298.49	188.51	0.873	ECON	451.44	408.47	42.98	0.905	ECON 1	14.52	13.65	0.87	0.940
EVAP 2	4630.32	3816.32	813.99	0.824	DCH	349.53	323.7	25.83	0.926	ECON 2	1015.32	902.00	113.32	0.888
ECO2	1285.59	754.35	531.24	0.587	REG	871.48	697.33	174.15	0.800	SH 2	683.80	583.93	99.87	0.854
SEP	1113.03	1113.03	0.00	1.000	COND	915.07	131.62	783.45	0.144	EVAP 2	4362.56	3570.28	792.28	0.818
HTR	1006.51	683.22	323.29	0.679	PUMP 1	87.28	4.19	83.09	0.048	ECON 3	34.15	32.14	2.01	0.941
LTR	210.68	147.86	62.82	0.702	PUMP 2	475.49	123.69	351.79	0.260	ECON 4	495.46	334.46	161.01	0.675
COND 1	1433.86	232.93	1200.93	0.162	TRAP	102.52	44.48	58.05	0.434	SEP 1	1362.45	1362.45	0.00	1.000
COND 2	250.20	63.58	186.61	0.254	Bifurcation 10-11-12	1664.68	1664.68	0.00	1.000	DEAERATOR	58.73	46.20	12.53	0.787
PUMP 1	130.59	92.04	38.55	0.705	Junction 13-14-15	6527.18	6527.18	0.00	1.000	COND	2296.69	524.54	1772.14	0.228
PUMP 2	6.23	4.42	1.80	0.711	ORC plant	9730.66	5224.07	4506.6	0.537	PUMP 1	2.74	2.50	0.24	0.911
Valve	600.98	598.81	2.17	0.996	—	—	—	—	—	PUMP 2	8.96	7.96	1.00	0.889
Junction 3-13-4	2138.04	1860.77	277.27	0.870	—	—	—	—	—	DSH	5433.11	5433.11	0.00	1.000
Bifurcation 6-7-14	431.34	431.34	0.00	1.000	—	—	—	—	—	Junction 3-18-22	10495.82	10461.42	34.40	0.997
Junction 10-14-15	450.76	398.59	52.17	0.884	—	—	—	—	—	Bifurcation 9-34-35	460.45	460.45	0.00	1.000
Junction 34-35-1	10766.58	10741.94	24.64	0.998	—	—	—	—	—	Rankine Plant	13027.66	6280.19	6747.47	0.482
Bifurcation 17-30-31	240.43	240.43	0.00	1.000	—	—	—	—	—	—	—	—	—	—
Kalina plant	13097.89	7035.10	6062.79	0.537	—	—	—	—	—	—	—	—	—	—

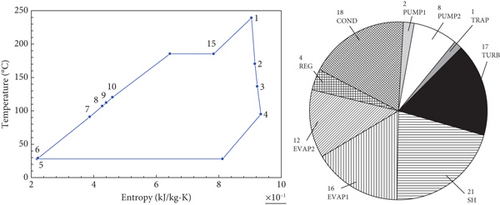
In Figure 6, the generated power, thermal efficiency, and exergetic efficiency are presented for the studied cycles at the optimum condition. The results are ordered by the function of the generated power presented in bar. The exergy efficiency is presented in dashed lines, and the thermal efficiency is in a continuous line. The highest value of generated power is observed in the Kalina cycle which can be explained by fewer irreversibilities and the high exergy absorption from the cement suspension preheater exhaust gas and the hot air clinker cooler in this cycle if compared to the other ones. As a means of validation, the thermal efficiency values are similar, or in the same range, to those found in other works [14] or [16], which show 23.58% for a conventional Rankine cycle, for example. An analogous fact is also applied to the exergy efficiency values [13, 17], or in other works. For example, in [12], the exergetic efficiency ranges from 35.7% to 52% in dependence on the ORC thermal scheme configuration and the operational parameter; in [2], the exergetic efficiency ranges from 50% to 60% as a function of the maximum pressure; in [3], it could reach 44%-60% in dependence of the evaporator pinch point; in [6], the conventional Rankine cycle exhibits 24.18% or 51.39% for thermal and exergetic efficiency, respectively. Note that in Table 11, the fuel () of the Kalina cycle has the highest value. In terms of thermal efficiency, the values are very similar, with the highest value for ORC explained by the lower heat input into the cycle. In terms of exergetic efficiency, the highest value for the Kalina cycle is explained by the higher power generated and the lower relative irreversibilities of the cycle if compared with the other ones.

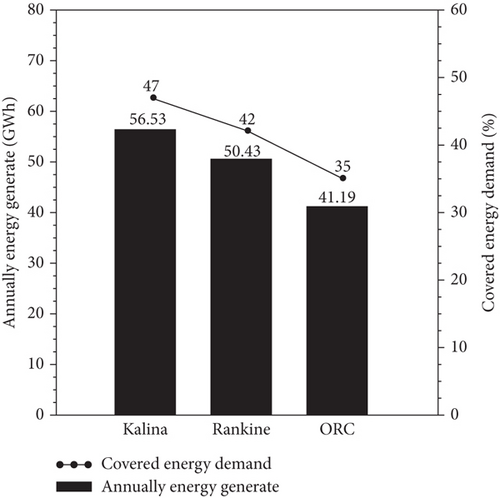
In Figure 7, the annually energy generated and the covered energy demand are presented for the studied cycles at the optimum condition. The results are ordered by the function of the annually energy generated presented in bar. The covered energy demand is presented in a continuous line. According to equation (7), annually energy generated for a fixed value of annual operation hours depends on the net power generated. This way, the Kalina cycle generates more energy annually than the other cycles. Considering the fixed value of 121 GWh of annual electric energy consumption of the Apodi plant, the Kalina cycle, as it annually generates more energy, will provide a greater covered energy demand than the other cycles studied. In any case, it is important to highlight that with the implementation of electricity cogeneration in the cement sector, the covered annual electric energy demand can be higher than 35%, which means a considerable reduction in cement manufacturing costs and electric energy consumption. With the reduction in electricity consumption at the cement plant, more electricity is available on the grid for other consumers and final use, avoiding the installation of new thermal power plants, which gives an environmental footprint to cogeneration in the cement sector.

In Figure 8, a summary of the economic results is presented for the studied cycles at the optimum condition. The total investment is presented in a black bar, while the payback is presented in a solid line bar, both could be read on the left axes. The cash flow is presented in a continuous line, while the electricity generation cost is presented in dashed lines, both could be read on the right axes.

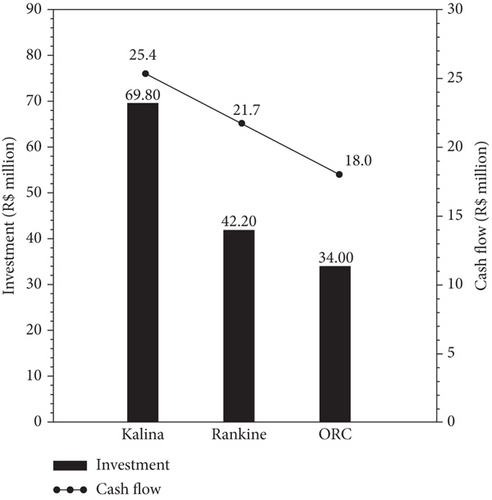
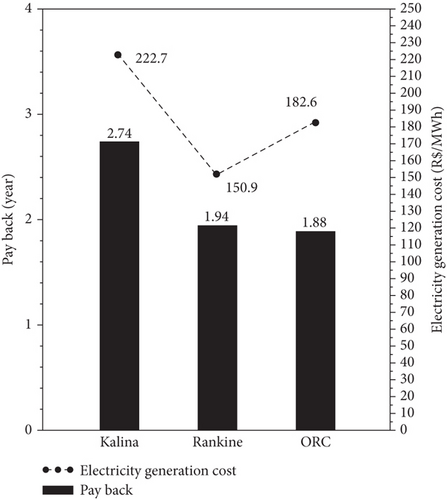
According to Figure 8, the implementation of the Kalina cycle costs R$ 69.80 million for a power generation of 7.04 MW (Figure 6), and an annually energy generation of 56.53 GWh able to cover 47% (Figure 7) of the considered 121 GWh energy demand. The cash flow determined with equation (20), shown in Figure 8, results in R$25.4 million, with which it is possible to achieve a payback of 2.74 years. The cogeneration electricity generation cost of 222.7 R$/MWh is very competitive in the existing electricity tariff scenario (430.74 R$/MWh).

In Figure 8, the implementation of a conventional Rankine cycle costs R$42.20 million with 6.28 MW of power generation (Figure 6) and 50.43 GWh of annually energy generation which is able to cover 42% (Figure 7) of the considered 121 GWh energy demand. For this cycle, the cash flow shown in Figure 8 is R$21.7 million which results in 1.94 years of payback. In the existing electricity tariff scenario (430.74 R$/MWh), the cogeneration electricity generation cost of 150.9 R$/MWh is highly attractive.

With the costs of R$ 34.00 for the implementation of ORC (Figure 8), it is possible to obtain 5.22 MW of power generation (Figure 6) with an annually energy generation of 41.19 GWh able to cover 35% (Figure 7) of the considered 121 GWh energy demand. With a cash flow of R$18.8 million, it is possible to achieve 1.88 years of payback. The cogeneration electricity generation cost of 222.7 R$/MWh is extremely competitive in the considered electricity tariff scenario (430.74 R$/MWh).

By way of comparison, it can be said that the Kalina cycle has a better thermodynamic performance than the other studied cycles. This is due to the higher power generated and exergy efficiency, while the energy efficiency presents very similar values between the cycles studied. In economic terms, the Kalina cycle requires the largest investment and the ORC the lowest, so in this respect, the ORC is the most attractive of the cycles. In terms of payback, it can be said that all cycles are very interesting because none exceed 3 years. From a cash flow point of view, the Kalina cycle is by far the most attractive because, after 2.74 years, it will have the greatest annual savings. Although the Kalina cycle has the highest cost of electricity generation and the conventional Rankine the lowest, it can be said that the three cycles studied are competitive in the current tariff scenario. In view of the above, it can be concluded that although all cycles are interesting for the cogeneration of electricity in the cement sector, the Kalina cycle has a better thermodynamic and suitable economic performance in terms of cash flow, payback, and electricity generation cost, which makes it promising for this purpose.

Based on the performance of the Kalina cycle, Table 12 and Figure 9 present the estimated potential for electricity cogeneration in Minas Gerais and its geographic distribution, respectively. To arrive at these results, the information in Table 1 is considered, specifically the mass flow values and the T_in and T_out temperatures of the two energy sources for waste heat recovery considered in this study. Based on this information, a for the cogeneration plant is estimated using a specific heat for the hot air from the clinker cooler and suspension preheater exhaust gas of 1.07 and 1.04 kJ/kg.K, respectively. Specific heat values were estimated using REFPROP with the molar composition presented in Table 2 and an average temperature of 257°C. Then, the value of the thermal efficiency of the Kalina cycle shown in Figure 6 is applied in equation (5) to obtain the potential estimation of power generated in each of the cement plants.

Table 12. Potential estimation.

Factory name	City	Clinker production (t/day)	Electricity cogeneration potential (MW)
Lafarge	Montes Claros	2050	7.80

Lafarge	Matozinhos	2050	7.80

LIZ	Vespasiano	4600	6.21

Holcim	P. Leopoldo	5520	3.51
Holcim	P. Leopoldo	5520	3.51

InterCement	P. Leopoldo	2100	3.85

Lafarge	Arcos	2050	7.80

Itaú de Minas	Itaú de Minas	1500	2.78
		1550	2.79
		2800	7.33

Tupi	Carandaí	3500	6.90
Tupi	Carandaí	2700	7.40

Holcim	Barroso	5520	3.51
Holcim	Barroso	5520	3.51

InterCement	Ijaci	5500	10.10

CSN	Arcos	2500	2.96
CSN	Arcos	6500	3.69

Brennand	S. Lagoas	3800	5.14

Total			96.61

As can be seen in Table 12, lower values of power generated are found in cement plants with rotative kilns with cooling air injection, while higher values are found in rotative kilns with grate coolers. This is explained by the fact that in plants with rotative kilns with cooling air injection, less waste heat is available for electricity cogeneration. In any case, the power-generating potential in Minas Gerais using cogeneration from waste heat is remarkable and close to 100 MW. This electricity generation potential, in addition to resulting in considerable energy savings in the cement manufacturing process and therefore reducing the cement production cost, can reduce CO₂ emissions in Minas Gerais. Considering an electricity generation potential of ~96 MW, an emission factor of 0.367 tCO₂/MWh [48], and 8030 h/year of operation, can be avoided 282,913 tCO₂/year with the installation of new natural gas-fired combined-cycle thermal power plants.

Figure 9 shows the electricity cogeneration potential distribution in Minas Gerais. As can be seen, the potential of electricity cogeneration from waste heat in the cement sector of Minas Gerais is concentrated in the south-central region of Minas Gerais, which is precisely where there is a greater population concentration and greater energy demand, which is also interesting to reduce electrical problems in the network and improve the energy quality.

4. Conclusions

From the study of the electricity cogeneration potential in the Minas Gerais cement industry with thermodynamic cycles, it is possible to conclude that

(i)
in general, for all cycles studied, the turbines and evaporators are where the greatest irreversibilities are concentrated. Despite a very similar cycle exergy efficiency value in the ORC and Kalina cycles, the last one generates more power between the studied cycles. In terms of thermal efficiency, the values are very similar, with the highest value for ORC
(ii)
the Kalina cycle generates more energy annually, but all cycles can cover more than 35% of the energy demand which means a considerable reduction in cement manufacturing costs
(iii)
all cycles are interesting for the cogeneration of electricity in the cement sector given the payback value lower than 3 years, the considerable value of cash flow, and the high competitiveness of the current tariff scenario
(iv)
the electricity cogeneration potential in the Minas Gerais cement industry is remarkable, ~96 MW, and could save emissions of around 282,913 tCO₂/year. Fortunately, the potential is concentrated in the south-central region of Minas Gerais, where there is a greater population and energy demand concentration

Nomenclature

COND:: Condenser
DCH:: Direct contact heater
DSH:: Desuperheater
ECON:: Economizer
EES:: Engineering equation solver
EVAP:: Evaporator
HRSG:: Heat recovery steam generator
HTR:: High temperature recuperator
LMTD:: Logarithmic mean temperature difference
LTR:: Low temperature recuperator
ORC:: Organic Rankine cycle
PUMP:: Pump
R$:: Brazilian reais
REG:: Regenerator
SEP:: Separator
SH:: Superheater
TURB:: Turbine
US$:: United States dollar
WHR:: Waste heat recovery.

Latin Symbols

:: Fuel (kW)
:: Product (kW)
:: Heat rate (kW)
:: Power (kW)
:: Mass flow (kg/s)
h:: Specific enthalpy (kJ/kg)
U:: Heat transfer global coefficient (kW/m².K)
A:: Heat transfer surface area (m²)
AEG:: Annually energy generated (GWh/year)
AF:: Capitalization factor (1/year)
C:: Cost (R$ or R$/kWh)
CAB:: Dimensional auxiliary buildings cost factor
CC:: Dimensional contingency cost factor
CED:: Covered energy demand (%)
CF:: Cash flow (R$/year)
FCF:: Dimensional fees cost factor
CI:: Cost index
COS:: Dimensional off-site facilities cost factor
CSD:: Dimensional site development cost factor
E:: Estimated cost (R$)
Et:: Electricity tariff (R$/MWh)
HO:: Operation hours (h/year)
P:: Pressure (kPa)
PB:: Payback (year)
T:: Temperature (K or °C)
Tx:: Reais to US dollar exchange rate (R$/US$)
ex:: Specific exergy (kJ/kg)
i:: Interest rate
n:: Useful life (year)
q:: Steam quality
s:: Specific entropy (kJ/kg.K)
x:: Ammonia mass fraction.

Greek Letters

:: Entropy generation rate (kW/K)
Δ:: Difference
ε:: Effectiveness
η:: Efficiency.

Subscripts

0:: Reference state
1, 2, …, 20:: States in the thermal schematics of cycle
1998:: 1998 year
C, x:: Cost in year x
ch:: Chemical
EX:: Exergetic
g:: Gas or generation
ger:: Generated
i:: State
in:: Inlet
inv:: Total investment
l:: Liquid
lm:: Logarithmic mean temperature difference
n:: Period numbers
O&M:: Operation and maintenance
out:: Outlet
p:: Pump
TH:: Thermal
turb:: Turbine
x:: Year x.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors thank FAPEMIG, FAPEMIG/CEMIG APQ-03422-12 research project, ANNEL Research and Developed Program (P&D) research project GT0554, CAPES—Financing Code 001 and CAPES grant PROAP 88881.888660/2023-01 and CNPq310727/2023-5 research project, and Pontifical Catholic University of Minas Gerais—PUC Minas for the financial support to this work. The authors wish to thank Mr. Colm Patrick Donnellan M.A. B.Ed. C.C.R.S. for the English review.

Open Research

Data Availability

The calculation data used to support the findings of this study are included within the article.

References

1 Institute for Industrial Productivity and IFC - International Finance Corporation - World Bank Group, Waste heat recovery for the cement sector: market and supplier analysis, 2014.
Google Scholar
2 Amiri Rad E. and Mohammadi S., Energetic and exergetic optimized Rankine cycle for waste heat recovery in a cement factory, Applied Thermal Engineering. (2018) 132, 410–422, https://doi.org/10.1016/j.applthermaleng.2017.12.076, 2-s2.0-85039985036.
10.1016/j.applthermaleng.2017.12.076
Web of Science® Google Scholar
3 Ozdil N. F. T., Segmen M. R., and Tantekin A., Thermodynamic analysis of an organic Rankine cycle (ORC) based on industrial data, Applied Thermal Engineering. (2015) 91, 43–52, https://doi.org/10.1016/j.applthermaleng.2015.07.079, 2-s2.0-84939839718.
10.1016/j.applthermaleng.2015.07.079
Web of Science® Google Scholar
4 Amiri A. and Vaseghi M. R., Waste Heat Recovery Power Generation Systems for Cement Production Process, IEEE Transactions on Industry Applications. (2015) 51, no. 1, 13–19, https://doi.org/10.1109/TIA.2014.2347196, 2-s2.0-84921477789.
10.1109/TIA.2014.2347196
Web of Science® Google Scholar
5 Ghalandari V., Majd M. M., and Golestanian A., Energy audit for pyro-processing unit of a new generation cement plant and feasibility study for recovering waste heat: a case study, Energy. (2019) 173, 833–843, https://doi.org/10.1016/j.energy.2019.02.102, 2-s2.0-85062698125.
10.1016/j.energy.2019.02.102
Web of Science® Google Scholar
6 Kizilkan O., Performance assessment of steam Rankine cycle and sCO2Brayton cycle for waste heat recovery in a cement plant: a comparative study for supercritical fluids, International Journal of Energy Research. (2020) 44, no. 15, 12329–12343, https://doi.org/10.1002/er.5138.
10.1002/er.5138
CAS Web of Science® Google Scholar
7 Nami H. and Anvari-Moghaddam A., Small-scale CCHP systems for waste heat recovery from cement plants: thermodynamic, sustainability and economic implications, 2020, 192, Elsevier Ltd.
Google Scholar
8 National Ready Mixed Concrete Association, Concrete CO 2 fact sheet, 2008, no. 2, Natl. Ready Mix. Concr. Assoc..
Google Scholar
9 Han T., Wang C., Zhu C., and Che D., Optimization of waste heat recovery power generation system for cement plant by combining pinch and exergy analysis methods, Applied Thermal Engineering. (2018) 140, 334–340, https://doi.org/10.1016/j.applthermaleng.2018.05.039, 2-s2.0-85047305774.
10.1016/j.applthermaleng.2018.05.039
Web of Science® Google Scholar
10 dos Reis E. P., Arrieta F. R. P., and Venturini O. J., General methodology and optimization for the analysis of bottoming cycle cogeneration, Energy Conversion and Management. (2023) 276, https://doi.org/10.1016/j.enconman.2022.116536.
10.1016/j.enconman.2022.116536
Web of Science® Google Scholar
11 Júnior E. P. B., Arrieta M. D. P., Arrieta F. R. P., and Silva C. H. F., Assessment of a Kalina cycle for waste heat recovery in the cement industry, 2019, 147, Elsevier Ltd.
10.1016/j.applthermaleng.2018.10.088
Google Scholar
12 Moreira L. F. and Arrieta F. R. P., Thermal and economic assessment of organic Rankine cycles for waste heat recovery in cement plants, Renewable and Sustainable Energy Reviews. (2019) 114, article 109315, https://doi.org/10.1016/j.rser.2019.109315, 2-s2.0-85070592079.
10.1016/j.rser.2019.109315
Web of Science® Google Scholar
13 Mohammadi A., Ashjari M. A., and Sadreddini A., Exergy analysis and optimisation of waste heat recovery systems for cement plants, International Journal of Sustainable Energy. (2018) 37, no. 2, 115–133, https://doi.org/10.1080/14786451.2016.1181067, 2-s2.0-84966701625.
10.1080/14786451.2016.1181067
Google Scholar
14 Mungyeko Bisulandu B. J. R., Ilinca A., Tsimba Mboko M., and Mbozi Mbozi L., Thermodynamic performance of a cogeneration plant driven by waste heat from cement kilns exhaust gases, Energies. (2023) 16, no. 5, https://doi.org/10.3390/en16052460.
10.3390/en16052460
PubMed Web of Science® Google Scholar
15 Sanaye S., Khakpaay N., Chitsaz A., Hassan Yahyanejad M., and Zolfaghari M., A comprehensive approach for designing, modeling and optimizing of waste heat recovery cycle and power generation system in a cement plant: a thermo-economic and environmental assessment, Energy Conversion and Management. (2020) 205, article 112353, https://doi.org/10.1016/j.enconman.2019.112353.
10.1016/j.enconman.2019.112353
Web of Science® Google Scholar
16 Karellas S., Leontaritis A. D., Panousis G., Bellos E., and Kakaras E., Energetic and exergetic analysis of waste heat recovery systems in the cement industry, Energy. (2013) 58, 147–156, https://doi.org/10.1016/j.energy.2013.03.097, 2-s2.0-84881107834.
10.1016/j.energy.2013.03.097
Web of Science® Google Scholar
17 Atashbozorg D., Arasteh A. M., Salehi G., and Azad M. T., Analysis of different organic Rankine and Kalina cycles for waste heat recovery in the iron and steel industry, ACS Omega. (2022) 7, no. 50, 46099–46117, https://doi.org/10.1021/acsomega.2c03922, 36570319.
10.1021/acsomega.2c03922
CAS PubMed Web of Science® Google Scholar
18 Varma G. V. P., Srinivas T., Pradeep Varma G. V., and Srinivas T., Design and analysis of a cogeneration plant using heat recovery of a cement factory, Case Studies in Thermal Engineering. (2015) 5, 24–31, https://doi.org/10.1016/j.csite.2014.12.002, 2-s2.0-84928336782.
10.1016/j.csite.2014.12.002
Web of Science® Google Scholar
19 Wang J., Dai Y., and Gao L., Exergy analyses and parametric optimizations for different cogeneration power plants in cement industry, Applied Energy. (2009) 86, no. 6, 941–948, https://doi.org/10.1016/j.apenergy.2008.09.001, 2-s2.0-60549084709.
10.1016/j.apenergy.2008.09.001
CAS Web of Science® Google Scholar
20 Paepe D. M., HEFAT2011 8 th International Conference on Heat Transfer, Fluid mechanics and thermodynamics organic Rankine cycle as efficient alternative to steam cycle for small scale power generation, 2011, Pointe Aux Piments.
Google Scholar
21 Nguyen T. Q., Slawnwhite J. D., and Boulama K. G., Power generation from residual industrial heat, Energy Conversion and Management. (2010) 51, no. 11, 2220–2229, https://doi.org/10.1016/j.enconman.2010.03.016, 2-s2.0-77953914608.
10.1016/j.enconman.2010.03.016
CAS Web of Science® Google Scholar
22 Madlool N. A., Saidur R., Rahim N. A., Islam M. R., and Hossian M. S., An exergy analysis for cement industries: an overview, Renewable and Sustainable Energy Reviews. (2012) 16, no. 1, 921–932, https://doi.org/10.1016/j.rser.2011.09.013, 2-s2.0-82355175264.
10.1016/j.rser.2011.09.013
Web of Science® Google Scholar
23 Wang Y., Yang H., and Xu K., Comparative environmental impacts and emission reductions of introducing the novel organic Rankine & Kalina cycles to recover waste heat for a roller kiln, Applied Thermal Engineering. (2021) 190, article 116821, https://doi.org/10.1016/j.applthermaleng.2021.116821.
10.1016/j.applthermaleng.2021.116821
Web of Science® Google Scholar
24 Fierro J. J., Hernández-Gómez C., Marenco-Porto C. A., Nieto-Londono C., Escudero-Atehortua A., Giraldo M., Jouhara H., and Wrobel L. C., Exergo-economic comparison of waste heat recovery cycles for a cement industry case study, Energy Conversion and Management: X. (2022) 13, https://doi.org/10.1016/j.ecmx.2022.100180.
10.1016/j.ecmx.2022.100180
Web of Science® Google Scholar
25 Marenco-Porto C. A., Fierro J. J., Nieto-Londoño C., Lopera L., Escudero-Atehortua A., Giraldo M., and Jouhara H., Potential savings in the cement industry using waste heat recovery technologies, Energy. (2023) 279, https://doi.org/10.1016/j.energy.2023.127810.
10.1016/j.energy.2023.127810
Web of Science® Google Scholar
26 Ore I., Pigments I. O., Rock P., Crystal Q., Earths R., and Ash S., Mineral commodity summaries 2021: nitrogen (fixed) - ammonia, 2021, U. S. Department of the Interior.
Google Scholar
27 De Jesus F. S., “No title,” Lista de Estados Brasileiros por extensão territorial, 2013, December 2023, https://www.geografiaopinativa.com.br/2013/09/lista-de-estados-brasileiros-por.html.
Google Scholar
28 Isabela Bolzani C. M. and Martins R., “No Title,” Censo 2022: Brasil tem 203 milhões de habitantes, 4,7 milhões a menos que estimativa do IBGE, 2023, December 2023, https://g1.globo.com/economia/censo/noticia/2023/06/28/censo-2022-brasil-tem-203-milhoes-de-habitantes-47-milhoes-a-menos-que-estimativa-do-ibge.ghtml#2.
Google Scholar
29 SNIC, SINDICATO NACIONAL DA INDUSTRIA DO CIMENTO-Relatório Anual, 2022, http://snic.org.br/assets/pdf/relatorio_anual/rel_anual_2022.pdf.
Google Scholar
30 Akram N., Moazzam M U., Hafiz M. A., Ajaz A., Saleem A., Kilic M., and Mobeen A., Improved waste heat recovery through surface of kiln using phase change material, Thermal Science. (2018) 22, no. 2, 1089–1098, https://doi.org/10.2298/TSCI170611301A, 2-s2.0-85047494821.
10.2298/TSCI170611301A
Web of Science® Google Scholar
31 da Costa Horta G. R., Barbosa E. P., Moreira L. F., Arrieta F. R. P., and de Oliveira R. N., Comparison of Kalina cycles for heat recovery application in cement industry, Applied Thermal Engineering. (2021) 195, article 117167, https://doi.org/10.1016/j.applthermaleng.2021.117167.
10.1016/j.applthermaleng.2021.117167
Web of Science® Google Scholar
32 APODI, WHRS-UTE CIMENTO APODI WASTE HEAT RECOVERY SYSTEM SISTEMA DE RECUPERAÇÃO DE CALOR, 2015, APODI, Quixeré-CE-Brazil.
Google Scholar
33 Lozano M. A. and Valero A., Theory of the exergetic cost, Energy. (1993) 18, no. 9, 939–960, https://doi.org/10.1016/0360-5442(93)90006-Y, 2-s2.0-0027656213.
10.1016/0360-5442(93)90006-Y
Web of Science® Google Scholar
34 Singh O. K. and Kaushik S. C., Energy and exergy analysis and optimization of Kalina cycle coupled with a coal fired steam power plant, Applied Thermal Engineering. (2013) 51, no. 1–2, 787–800, https://doi.org/10.1016/j.applthermaleng.2012.10.006, 2-s2.0-84868698745.
10.1016/j.applthermaleng.2012.10.006
Web of Science® Google Scholar
35 Kotas T. J., The Exergy Method of Thermal Plant Analysis, 1985, 1st edition, U. S. Geological Survey.
Google Scholar
36 Saldanha W. H., Arrieta F. R. P., Ekel P. I., Machado-Coelho T. M., and Soares G. L., Multi-criteria decision-making under uncertainty conditions of a shell-and-tube heat exchanger, International Journal of Heat and Mass Transfer. (2020) 155, article 119716, https://doi.org/10.1016/j.ijheatmasstransfer.2020.119716.
10.1016/j.ijheatmasstransfer.2020.119716
Web of Science® Google Scholar
37 Saldanha W. H., Arrieta F. R., Machado-Coelho T. M., dos Santos E. D., Maia C. B., Ekel P. I., and Soares G. L., Evolutionary algorithms and the preference ranking organization method for enrichment evaluations as applied to a multiobjective design of shell-and-tube heat exchangers, Case Studies in Thermal Engineering. (2020) 17, article 100564, https://doi.org/10.1016/j.csite.2019.100564.
10.1016/j.csite.2019.100564
Web of Science® Google Scholar
38 Incropera F. P. and DeWitt D. P., Fundamentals of Heat and Mass Transfer, Water. (2002) 6.
Google Scholar
39 Walas S. M., Chemical Process Equipment: Selection and Design, 2004, Butterworth-Heinemann, Newton.
Google Scholar
40 Júnior E. P., Arrieta M. D., Arrieta F. R., and Silva C. H., Assessment of a Kalina cycle for waste heat recovery in the cement industry, Applied Thermal Engineering. (2019) 147, 421–437, https://doi.org/10.1016/j.applthermaleng.2018.10.088, 2-s2.0-85055543016.
10.1016/j.applthermaleng.2018.10.088
Web of Science® Google Scholar
41 de Assis Gomes N., Assessment of a Rankine cycle for cogeneration in cement industries, 2021, no. 2020.
Google Scholar
42 FINEP, Comunicado sobre a Lei 13.483 de 21 de setembro de 2017, que institui a TLP, 2019, TJLP-Taxa de Juros de Longo Prazo, http://finep.gov.br/area-para-clientes/200-tjlp/4651-tjlp.
Google Scholar
43 Loh H. P., Lyons J., Charles I. I. I., and White W., “Process equipment cost estimation, final report,” Other Inf. PBD 1 Jan 2002, no. January, p. Medium: ED; Size: 410 Kilobytes, 2002, http://www.osti.gov/scitech//servlets/purl/797810-Hmz80B/native/.
Google Scholar
44 Ulrish G. D. and Vasudevan P. T., Chemical Engineering Process Design and Economics: A Practical Guide, 2004, 2nd edition, Process Publishing.
Google Scholar
45 B C do Brasil, Conversão de Moedas, 2019, https://www.bcb.gov.br/acessoinformacao/legado?url=https:%252F%252Fwww4.bcb.gov.br%252Fpec%252Fconversao%252Fconversao.asp.
Google Scholar
46 Bridges C., Equipment and fixtures index, percent good and valuation factors (AH581), 2017, https://www.boe.ca.gov/proptaxes/pdf/ah58116.pdf.
Google Scholar
47 Brasil, Ministério de Minas e Energia: Secretaria de Energia Elétrica, 2020, http://www.mme.gov.br/web/guest/secretarias/energia-eletrica.
Google Scholar
48 E de P E EPE, Apresentação da metodologia e dos fatores de emissão utilizados para as estimativas de emissão de GEE nos planos de energia, no BEN e demais produtos da EPE, 2022, https://www.epe.gov.br/sites-pt/areas-de-atuacao/estudos-socioambientais/SiteAssets/Paginas/Emissoes-de-Gases-de-Efeito-Estufa/InformativoTecnico_11-2022_fatoresdenSMA.pdf.
Google Scholar

All articles

Electricity Cogeneration Potential in Minas Gerais Cement Industry with Thermodynamic Cycles

Abstract

1. Introduction