An optimal configuration method for the combined heat and power (CHP) system considering demand response is proposed to scientifically and reasonably configure the parameters of the additional heat source and reduce unnecessary investment and construction costs. First, additional heat sources and demand response are utilized to decouple power generation and heating supply, enhancing the flexibility of the CHP system. Second, a multiobjective optimization configuration model of the CHP system is established, taking the system’s comprehensive satisfaction, economic cost, and wind power consumption capacity as the objectives, the unit output, and the capacity parameters of the additional heat source as the decision variables. Furthermore, an improved memetic algorithm (IMA) combined with a hierarchical sequence method is designed to solve the optimization model characterized by multiple objectives, hierarchical levels, and nonlinearity. The hierarchical sequence method solves problems sequentially based on the importance of optimization goals, ensuring the satisfaction of the configuration scheme. The IMA employs adaptive crossover and mutation probabilities, enhancing the algorithm’s convergence and quality. Finally, case analysis demonstrates that the CHP system achieves the best benefits when heat storage tanks and electric boilers are configured simultaneously. Moreover, compared to the MA, IPSO, and IABC algorithms, the IMA algorithm reduces the average economic cost by approximately 5.11%, 2.70%, and 8.43%, respectively.

1. Introduction

Energy and environmental issues have become critical bottlenecks for the development of today’s society. The choices for energy development are unavoidable: increasing the overall use of renewable energy, cutting carbon emissions, and improving energy use efficiency. A combined heat and power (CHP) system is a kind of efficient energy system that can not only produce electricity and heat as two forms of valuable energy but also realize the conversion and coordination of electricity and heat energy sources, effectively improving the economic performance and renewable energy consumption capacity of the system [1]. CHP has become the primary winter heating mode in China’s “Three North” regions, which are rich in wind power resources. Nevertheless, the single CHP system lacks flexibility because of the intricate coupling relationship between heat production and power generation, particularly after large-scale clean energy sources like wind power are connected to the grid. This could result in the inefficient use of clean energy and harm the system’s ability to improve the economy and the environment.

1.1. Literature Review

To solve the heat-electricity coupling problem of the CHP system, one effective method is to consider the impact of demand response [2] on the user side. Literature [3–5] proposed a demand response plan including interruptible/curtailable services, which enables energy consumers to rethink their energy consumption patterns based on incentive and punishment policies and effectively improves the economy of distribution systems. Users can adjust their heat or electric load according to the electricity market’s price signal or incentive mechanism to realize the coordinated optimization of the source-load side and enhance the system’s dependability and economics. This method’s benefit is that it can make full use of the potential resources on the user side, increasing the flexibility and regulation ability of the system. Still, the disadvantage is that it needs to consider the user’s satisfaction and comfort. Another effective method is adding heat sources, such as heat storage tanks and electric boilers, to the system to realize the heat-electricity decoupling and coordination and increase the system’s capability for wind power consumption and flexibility. To achieve the storage and regulation of heat energy and lower the costs associated with system operation and wind abandonment, the heat storage tank can store excess heat energy when the system’s heat energy is abundant and release the stored heat energy when the system’s heating is insufficient [6]. The electric boiler can use the excess wind power to produce heat energy when the wind power output is higher than the electric load and meets the demand of heat load, thus realizing the direct consumption of wind power and improving the system wind power utilization rate [7].

The current research on the optimal configuration method of the CHP system mainly focuses on the following aspects. Literature [8] proposed a two-stage optimal setup strategy for various distributed heat source types and a distributed heat source evaluation method based on the wind power curtailment rate. Literature [9] proposed a bilevel optimization model, which optimizes the CHP system’s main equipment capacity and annual load allocation simultaneously to balance the economic and environmental objectives. Literature [10] adopted a multiobjective optimization method to find the optimal configuration scheme of the system generator capacity, number, etc. Literature [11] proposed a mixed-integer linear programming (MILP) model for the optimal configuration of a complex distributed energy system based on different types of production units, which optimizes the size of various components in the system, the expansion of the solar field, and the heat storage capacity of the heat recovery. Literature [12] optimized the configuration of the CHP system integrated with the battery energy storage system that provides peak shaving service. Literature [13] considered the solid oxide fuel cell (SOFC), waste heat boiler, compressor intake cooling system, two combustion chambers, and two air preheaters (regenerators) to achieve the possible optimal configuration of the system. Literature [14] used the particle swarm optimization (PSO) algorithm to optimize the equipment size of the CHP system. Literature [15] analyzed the influence of the configuration parameters of the heating device required by the CHP system on the organic Rankine cycle. Literature [16] optimized the design parameters of the heat exchanger in the CHP system. Literature [17] analyzed the optimal system configuration of the CHP system under different unit numbers and returns water temperatures in detail and revealed the internal reasons for the system energy consumption change by analyzing the variation rules of the optimal key parameters under different conditions. Literature [18] optimized the size and number of various equipment in the CHP system according to the annual load demand. Literature [19] used the constrained programming method to optimize the optimal size of the CHP unit, auxiliary boiler, heat storage tank, and battery in the CHP system. Literature [20] optimized the configuration of the gas turbine in the CHP system. However, few studies consider the optimal configuration of the additional heat source, including the heat storage tank and the electric boiler in the CHP system. Table 1 presents an overview of the most essential reviewed papers.

Table 1. Review of recent relevant studies along with the present study.

Reference	Improvement strategy	Configured objects	Objective function	Solution strategy	Optimization algorithm
[5]	Demand response and energy storage	The operation scheme of the switches and the capacity of the capacitors	Energy loss, energy not supplied, and operational cost	Pareto-front	IPSO
[9]	Boiler and hot tank	Main components capacities and system annual load	Net present value and CO₂ emission	Pareto-front	NSGA-II
[11]	Boilers and compression chillers	The sizes of various components	The total annual cost	The commercial software X-press	—
[12]	Battery energy storage	Size and number of CHP gas engines and battery size	Simple payback period and primary energy savings	Pareto-front	MOGA-II
[13]	Gas turbine and SOFC	Design parameters of the system	Exergy efficiency and total cost rate	Pareto-front	NSGA-II
[14]	Energy storage	The devices size and hourly operation	The overall cost	—	PSO
[16]	Turbocharger	The design parameters of the heat exchanger	Thermal efficiency and overall electrical efficiency	—	GA
[18]	—	The size and number of various equipment	The operation cost	A mixed-integer linear programming	The branch and bound algorithm
[19]	Energy storage	The device’s size	The greenhouse gas emissions and annual costs	Pareto-front	Constraint programming
This paper	Demand response and additional heat source	The capacity of additional heat source	The quality, economic cost, and wind power consumption capacity of the optimal solution	The hierarchical sequence method	IMA

IPSO: improved particle swarm optimization; MOGA: multiobjective genetic algorithm.

1.2. Research Gaps and Contributions

Upon reviewing and analyzing the relevant studies on the optimization configuration of CHP systems, it is evident that previous research typically focused on incremental improvements to the CHP system, such as the addition of energy storage, electric boilers, or considering demand response on the load side, all aimed at enhancing the system’s flexibility and operational efficiency. The configuration objects of cogeneration systems are diverse, involving the system’s scale, equipment parameters, and even the system’s structure, all to achieve optimal operational status. The CHP system optimization configuration objectives have expanded from a single economic indicator to a multiobjective approach encompassing economy, emissions, and energy efficiency. Due to the multiobjective, nonlinear, and multi-decision-variable nature of the CHP system optimization configuration model, intelligent algorithms that do not require high demands on objectives and constraints are often used for solving. This study differs from previous research in that it implements a demand response mechanism on the load side, guiding users to change their energy usage habits to enhance the system’s economy. The optimization configuration focuses on the capacity of additional heat sources that can decouple the system’s electrical and thermal coupling, making it easier for the system to reach an optimal operational state. A satisfaction function for the optimization configuration scheme is defined in the objective function, ensuring the reliability and effectiveness of the optimization configuration scheme from the perspectives of objectives and constraints. The optimization objectives are set in order of importance, such as the quality of the optimization solution, economic cost, and wind power consumption capacity, which guide the optimization process. Based on the hierarchical nature of multiple objective functions, a multiobjective hierarchical sequence method is chosen as the solving strategy, which gradually optimizes multiple objectives while satisfying a series of complex constraints. The optimization algorithm selects an IMA algorithm that combines global and local searches with adaptive adjustment of critical parameters. Based on the above analysis, this paper proposes an optimal configuration method for the additional heat source of the CHP system, considering demand response. The main contributions of this study are as follows:

(1)
A cogeneration system optimal configuration model is constructed to optimize solution quality, system economy, and wind power absorption capacity. In this model, the satisfaction of the configuration scheme is quantified as the primary objective function to ensure the effectiveness of the configuration plan. The optimal capacity of additional heat sources, including thermal storage tanks and electric boilers, is configured using demand response in power generation and heating by combining time-of-use energy price with heating comfort on the demand side. The additional heat sources further decouple the system’s power generation and heat production, enhancing the system’s flexibility and promoting economic operation.
(2)
An improved memetic algorithm (IMA) combined with a multiobjective hierarchical sequence method is designed with the cogeneration system’s optimization features to identify the optimal setup and operation. Specifically, based on the MA algorithm, the IMA algorithm is designed for the initial solution generation process, constraint handling methods, global evolution, and local search strategies. Crossover and mutation parameters can be dynamically changed to suit the iteration process’s requirements, improving the search capability of the algorithm.

In summary, the rest of this paper is organized as follows. Section 2 introduces the structure and operation principle of the CHP system considering demand response and additional heat source; Section 3 establishes the optimal configuration model of the additional heat source of the CHP system considering demand response, defines the performance indicators and constraints, and gives the mathematical expressions and solution strategies; Section 4 designs the improved memetic algorithm to solve the system model and gives the specific design steps of the algorithm; Section 5 selects the appropriate case data and parameter settings, runs the algorithm to obtain the optimal configuration scheme, compares the economic performance and wind power consumption capacity of different configuration schemes, and verifies the effectiveness and superiority of the algorithm; Section 6 summarizes the main conclusions of the research.

2. Problem Description

The following features of a CHP system that consider demand response and add an extra heat source are shown in Figure 1: the power subsystem comprises electric loads, thermal power units, wind power units, CHP units, and electric boilers. The electric load incorporates the time-of-use energy price mechanism to fully leverage the potential of electric demand response to satisfy the regular load demand. The units that produce electric energy initially satisfy the electric load’s need. The electric boiler converts excess wind energy into heat energy, which stores or provides the heat load. Heat loads, storage units, and CHP units comprise the heat subsystem. In order to effectively utilize the potential of the heat demand response and satisfy the regular load requirement, the heat load introduces the comfort mechanism. The devices’ heat initially satisfies the need for heating.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structure diagram of the CHP system.

In this study, the additional heat sources are crucial for enhancing the economic efficiency of CHP systems with consideration of demand response. During the operation of CHP systems, heat storage tanks are used to store heat energy during low heating demand, while electric boilers provide necessary supplemental heat during peak demand periods. This configuration effectively addresses load demand fluctuations and optimizes energy utilization. However, it also introduces a series of economic challenges. In the actual operation of the system, the capacity configuration parameters of the additional heat source are often challenging to determine. The redundant capacity configuration can consume all the clean energy to the maximum extent, but the system’s economic performance is difficult to guarantee. The insufficient capacity configuration can reduce the investment and operation costs brought by the additional heat source configuration. Still, it may lead to much waste from clean energy sources such as wind power. Therefore, this study proposes an optimization problem for the capacity configuration of additional heat sources, aiming to establish mathematical models and optimization algorithms to analyze the economic impact of different configuration schemes, thereby finding the optimal solution. This will support cogeneration systems’ design and operational decision-making, driving energy systems towards greater efficiency and economy.

3. Mathematical Formulation

The optimal configuration of the additional heat source capacity parameters must balance the CHP system’s economic performance and wind power consumption capacity. The cost of the construction and operation of the additional heat source and each part of the system can reflect the economic performance of the CHP system; the total amount of wind power curtailment in a scheduling period can be used to describe the wind power consumption capacity of the system. Therefore, the performance indicators of the optimal configuration of the additional heat source of the system are as follows:

(1)
Coal cost
The coal cost of the system consists of the coal cost of the CHP units and the thermal power units.
(1)
The coal cost of the CHP units is expressed as follows:
(2)
where T represents the time frame for scheduling, T = 24; m represents the quantity of CHP units; a, b, and c represent the units’ coal consumption coefficients; c_v represents the decrease in power production brought on by heat extraction from the unit; P_e,i represents the CHP units’ electric output, MW; P_h,i represents the heat produced by the CHP units, MW.
The coal cost of the thermal power units is expressed as follows:
(3)
where n represents the quantity of thermal power units; P_e,j represents the electric output of the thermal power units, MW.
(2)
Average investment cost of additional heat source
The average investment cost of the additional heat source consists of the heat storage tank’s average investment cost and the electric boiler’s average investment cost. Generally speaking, the investment cost of the additional heat source is linearly related to the maximum capacity.
(4)
The average investment cost of the heat storage tank can be expressed as follows:
(5)
where C_ths represents the heat storage tank’s installed capacity (MWh); u_ths represents the capacity unit price of the heat storage tank construction (¥/MWh); r₀ represents the annual depreciation rate; l_ths represents the heat storage tank’s service life (years).
The average investment cost of the electric boiler can be expressed as follows:
(6)
where C_eb represents the electric boiler’s installed capacity (MWh); u_eb represents the capacity unit price of the electric boiler construction (¥/MWh); l_eb represents the service life of the electric boiler (years).
(3)
Operation cost of additional heat source
The extra heat source’s operational expenses include the heat storage tank’s operation and the electric boiler’s operation costs.
(7)
The operation cost of the heat storage tank is expressed as follows:
(8)
where s represents the heat storage tank’s operation cost coefficient, ¥/MWh; Q represents the heat value in the heat storage tank, MWh.
The operation cost of the electric boiler is expressed as follows:
(9)
where τ represents the operation cost coefficient of the electric boiler, ¥/MWh; P_eb represents the operation power of the electric boiler, MW.
(4)
Wind power curtailment penalty cost
(10)
where d represents the coefficient of wind power curtailment penalty, ¥/MWh; P_wl represents the wind power curtailment of the system, MWh.

The capacity configuration of the additional heat source needs to meet the following constraints:

(1)
Power balance constraint considering demand response
Following the user’s response to the time-of-use power pricing, the next relationship exists between the electric load demand and the price:
(11)

(12)
where γ_ij represents the price of electricity’s elasticity coefficient.
Furthermore, the following power balance constraint accounting for demand response is obtained:
(13)
where P_w represents the output of the wind power unit, MW; E_real represents the flexible electric load at time, MW.
(2)
Heat balance constraint considering demand response
To ensure the user’s thermal comfort, the heating constraint is obtained by conversion:
(14)

(15)
where k_up represents the coefficient of adjustment for heat load upward; k_down represents the coefficient of adjustment for heat load downward; T_fit,max represents the highest indoor temperature necessary to ensure thermal comfort; T_fit,min represents the lowest temperature required indoors to achieve thermal comfort; Q_fit,max represents the maximum heat load that can be met without compromising thermal comfort, MW; Q_fit,min represents the minimum heat load required to achieve thermal comfort, MW; Q_real represents the system’s actual heating, MW.
Additionally, the demand response considering heat balance limitation is obtained:
(16)

(17)
where η represents the electric-thermal conversion efficiency of the electric boiler; Q_ths represents the heat storage of the heat storage tank, MW.
(3)
CHP unit constraint
(18)
where represents the CHP unit’s lowest possible electric output, MW; represents the CHP unit’s maximum electric output, MW; represents the CHP unit’s lowest heat output, MW; represents the CHP unit’s maximum heat output, MW; k_i represents the CHP unit’s set heat-to-electricity ratio, MW; represents the CHP unit’s upward ramping power, MW; represents the CHP unit’s downward ramping power, MW.
(4)
Thermal power unit constraint
(19)
where represents the thermal power unit’s lowest electric output, MW; represents the thermal power unit’s maximum electric output, MW; represents the thermal power unit’s upward ramping power, MW; represents the thermal power unit’s downward ramping power, MW.
(5)
Wind power unit constraint
(20)
where P_w(t) represents the wind power unit’s output, MW; represents the upper limit of the wind power unit output, MW.
(6)
Additional heat source constraint
(21)
where C_ths represents the capacity of the heat storage tank, MW.
(22)
where C_eb represents the maximum power of the electric boiler, MW.

It can be seen that the optimal configuration of the additional heat source of the CHP system is a complex problem with multiple performance indicators and constraints. Sometimes, the optimization solution is not ideal, and it cannot meet each constraint condition strictly while achieving the expected goal of the system operation. Therefore, to quantify the quality of the optimization solution and obtain a higher quality optimization solution as much as possible, the concept of comprehensive satisfaction of the optimization solution is introduced.

3.1. Optimization Objective Satisfaction

In practice, optimizing the CHP system with wind power grid-connected consumption is usually based on the minimization of the system’s economic cost as the objective. When the optimization solution reaches the expected goal, the optimization objective satisfaction takes the maximum value of 1. Therefore, the aim of optimization satisfaction can be expressed as follows:

(23)

where F represents the objective value of the optimization solution; F_max represents the maximum objective value of all optimization solutions; F_min represents the minimum accurate value of all optimization solutions. The smaller the objective value of the optimization solution, the higher the optimization objective satisfaction.

3.2. System Constraint Satisfaction

The system constraint satisfaction is used to describe the closeness of the optimization solution and the system constraint. When the optimization solution fully satisfies all the constraints, the system constraint satisfaction takes the maximum value of 1. Therefore, the constraint satisfaction can be expressed as follows:

(24)

where H represents the sum of the constraint violation amounts of the optimization solution; H_max represents the maximum constraint violation amount of all optimization solutions. The smaller the constraint violation amount of the optimization solution, the higher the optimization constraint satisfaction.

3.3. Comprehensive Satisfaction of Optimization Solution

Considering that the optimization objective satisfaction and the system constraint satisfaction are both better when they are more prominent, and the quality of the optimization solution is higher when the difference between them is slight, this paper uses the product of the two to represent the comprehensive satisfaction of the optimization solution.

(25)

Therefore, the optimal configuration model of the additional heat source of the CHP system for wind power consumption is obtained:

Objective function 1: The quality of the optimization solution is the highest. That is, the comprehensive satisfaction is the highest.
(26)
Objective function 2: The system has the best economic performance. That is, the minimum comprehensive cost.
(27)
Objective function 3: The system has the maximum wind power consumption capacity and the minimum wind power curtailment.
(28)
Constraints: (13)–(22).
Decision variables: The electric output of the CHP units at each time P_e,i(t), the heat output of the CHP units at each time P_h,i(t), the electric output of the thermal power units at each time P_e,j(t), the output of the wind power units at each time P_w(t), the heat value of the heat storage tank at each time Q_ths(t), the output of the electric boiler at each time P_eb(t), the installed capacity of the heat storage tank C_ths, and the installed capacity of the electric boiler C_eb.
Solution strategy: The model has three objective functions, and the hierarchical sequence method is used to solve the multiobjective problem. The solution process is as follows: first, the optimal solution for objective function one is obtained, and all the optimal solutions are found and denoted R₁. Then, the optimal solution for objective function two is received within R₁, and the optimal solution set is denoted as R₂. Finally, the optimal solution for objective function three is obtained within R₂, which is the optimal configuration solution.

4. Solution Design

This paper uses the improved memetic algorithm to solve the optimal configuration model of the additional heat source of the CHP system considering demand response, and the specific steps are shown in Figure 2.

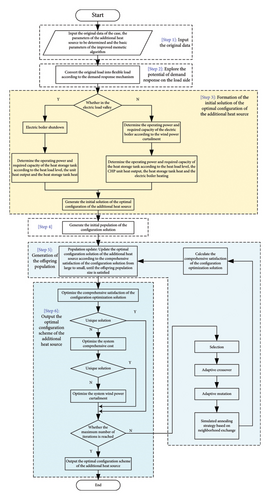
Step 1: Input of original data. We enter the primary data for optimization, including original electrical load data E_load, heat load data Q_load, wind power data Pwt, and parameters of the additional heat source with pending capacity. We set reasonable parameters such as population size popsize and maximum number of iterations setgen required for the improved memetic algorithm.
Step 2: Explore the potential of demand response on the load side. The load side introduces time-of-use electricity pricing and thermal comfort mechanisms to transform original load data into flexible load data.
Step 3: Formation of the initial solution of the optimal configuration of the additional heat source. Based on the level of flexible electrical load E_real, the electrical output level of each unit P_e, and the predicted wind power Pwt, it is determined whether there is wind curtailment in the cogeneration system. If there is no wind curtailment, the electric boiler is shut down, and the operating power P_ths and required capacity Q_ths of the heat storage tank are determined based on the level of flexible heat load, the heat output of the CHP units, and the heat quantity in the heat storage tank. If there is wind curtailment, the operating power P_eb and required capacity C_eb of the electric boiler are determined based on the amount of curtailed wind P_wl, and the operating power P_ths and required capacity C_ths of the heat storage tank are determined based on the level of flexible heat load Q_real, the heat output of the CHP units P_h, the heat quantity in the heat storage tank Q_ths, and the heating quantity Q_eb produced by the electric boiler.
Step 4: Generation of the initial population. The initial solutions for the optimization of additional heat sources generated in Step 3 are inserted into formula (26) to calculate the comprehensive satisfaction of the configuration solution, forming the initial population and recording the best individual from the initial solutions.
Step 5: Generation of the offspring population. The initial population undergoes global evolution, local search, and renewal to generate a new subsequent population. Individuals in the population after global evolution may not meet the set range; thus, a verification operation is required. If they meet the criteria, proceed to the following steps; if not, global evolution must be redone.
Step 6: Output of the optimal configuration scheme for additional heat sources. We determine whether the maximum number of iterations setgen has been reached. If not, we increment the iteration counter gen = gen + 1 and return to Step 5; if so, we exit the loop, output the record of the optimal individual, and obtain the optimal configuration scheme for additional heat sources based on the hierarchical sequence method.

The design of the global evolution, local search, and population update operations of the improved memetic algorithm is as follows:

(1)
Global evolution
Three subprocesses are involved in the population’s global evolution: crossover, mutation, and selection.
- (a)
  Selection operator design
- First, according to the comprehensive satisfaction function of the optimization solution (26), the fitness value of each individual (optimization solution) in the population is calculated. Second, two individuals are chosen randomly from the present population; their fitness values are then compared, and the one with the higher fitness value is kept. Lastly, keep doing this until the number of individuals kept equals the predetermined population size.
- (b)
  Crossover operator design
- The arithmetic crossover method guarantees that the crossover operation is effective.
  (29)
  where X and Y represent the new people that crossover has produced; A and B represent two distinct people that were chosen at random from the population based on the crossover probability; α represents the crossover factor and α = rand(0, 1).
- (c)
  Mutation operator design [21].
  (30)
  where X_m represents the newly created individual through mutation; X₀, X₁, and X₂ represent three people chosen at random from the population based on the probability of a mutation; K represents the mutation factor.
- (d)
  Adaptive crossover and mutation probability
  (31)
  where S represents the more considerable fitness value of the two individuals to be crossed; S_max represents the maximum fitness value in the current population; S_avg represents the average fitness value of the individuals in the current population.
  (32)
  where S^′ represents the fitness value of the mutated individual.
(2)
Local search
To optimize the population structure and improve the solution efficiency and quality during the population iteration, the local search algorithm is the simulated annealing algorithm that can jump out of the local optimum. Individuals with higher optimal values in the population following global evolution are chosen for simulated annealing to increase the effectiveness of local search even further.
Through the analysis of the characteristics of the CHP system optimization problem, it is observed that each unit’s output allocation exhibits time-sharing optimization features. In the local search for this problem, the exchange structure is a better neighborhood structure. The specific operation can be described as follows: first, we select a target individual for a simulated annealing operation. Within the scheduling period, we alternate the output allocation of various units at two separate times at random. And we obtain the values of each decision variable according to the predetermined optimization strategy. Then, according to the optimization solution’s comprehensive satisfaction function, we recalculate the individual’s fitness value after neighborhood exchange. Finally, we compare the fitness values and retain the individual with the more considerable fitness value.
(3)
Population update
In order to build a new population with the desired size, the individuals with fitness values ranging from significant to minor are preserved while a vast population is created by combining the new individuals created by local search and global evolution with the parent individuals.

5. Simulation Analysis

To thoroughly verify the effectiveness of the proposed optimal configuration method of the additional heat source of the CHP system considering demand response, three configuration schemes are designed for verification, as shown in Table 2.

Table 2. Design of optimal configuration schemes for additional heat source.

Configuration scheme	Additional heat source structure		Demand response	Objective and solution
Configuration scheme	Heat storage tank	Electric boiler	Demand response	Objective and solution
1	√	√	√	Objective: optimize solution quality, economic performance, and wind power consumption capacity; Solution strategy: multiobjective hierarchical sequence method
2		√	√
3	√		√

5.1. Original Data

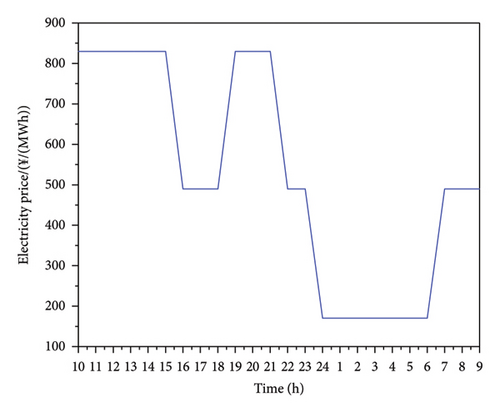
The CHP system used in this paper is an example of a grid-connected wind farm with four thermal power units (the specific parameters of the units are displayed in Table 3), a CHP unit (the specific parameters of the unit are displayed in Table 4), an electric boiler (the electric-thermal conversion efficiency is 0.8), a heat storage tank (the maximum operating power is 50 MW), and other components. The scheduling period is 24 h, the unit scheduling interval is one h, the time-of-use electricity price is shown in Figure 3, the additional heat source parameters are shown in Table 5, and the wind power prediction and load prediction values are shown in Table 6.

Table 3. Parameters of thermal power units.

Unit number	Maximum electric power (MW)	Minimum electric power (MW)	Upward ramp rate (MWh)	Downward ramp rate (MWh)	a	b	c
G1	200	60	100	100	0.0054	27.79	134.7
G2	200	60	100	100	0.0054	27.79	134.7
G3	150	60	75	75	0.00678	26.78	154.0
G4	100	30	50	50	0.00712	27.27	161.1

Table 4. Parameters of CHP unit.

Unit number	Electric power (MW)		Heat power (MW)		Coal consumption coefficient			Ramp rate (MWh)
Unit number	Maximum	Minimum	Maximum	Minimum	a	b	c	Upward	Downward
G5	300	75	400	100	0.00813	27.79	515.5	150	150

Table 5. Parameters of additional heat source.

Number	Additional heat source	Capacity installation unit price (¥·(MWh)⁻¹)	Annual depreciation rate (%)	Service life (years)	Operation cost coefficient (¥·(MWh)⁻¹)
THS	Heat storage tank	15000	5	20	3
EB	Electric boiler	720000	5	20	20

Table 6. Wind power prediction and load prediction values.

Time	Wind power (MW)	Electric load (MW)	Flexible electric load (MW)	Heat load (MW)	Flexible heat load (MW)
Time	Wind power (MW)	Electric load (MW)	Flexible electric load (MW)	Heat load (MW)	Upper limit	Lower limit
1:00	420	593	695	385	417	352
2:00	427	554	649	390	423	357
3:00	403	547	641	395	428	361
4:00	403	534	626	380	412	347
5:00	380	541	634	365	395	334
6:00	360	559	655	346	375	316
7:00	345	566	571	327	354	299
8:00	324	619	624	304	329	278
9:00	307	676	682	289	313	264
10:00	285	716	597	278	301	254
11:00	225	760	634	270	292	247
12:00	180	785	655	269	291	246
13:00	127	762	768	264	286	241
14:00	134	772	778	274	297	250
15:00	110	749	755	287	311	262
16:00	145	738	744	290	314	265
17:00	210	719	725	300	325	274
18:00	283	724	604	320	347	292
19:00	357	720	601	320	347	292
20:00	385	710	592	345	374	315
21:00	430	680	686	354	383	324
22:00	355	625	630	363	393	332
23:00	400	616	722	368	399	336
24:00	435	620	726	379	411	346

5.2. Parameter Setting

The basic parameters of the improved memetic algorithm (IMA) are as follows: population size is 150, iteration number is 300, initial annealing temperature is 500, final annealing temperature is 1, and annealing rate is 0.9. The parameters of the memetic algorithm (MA) [22], improved particle swarm algorithm (IPSO) [23], and improved artificial bee colony algorithm (IABC) [24] used for comparison are as follows:

Memetic algorithm: population size is 150, iteration number is 300, initial annealing temperature is 500, final annealing temperature is 1, annealing rate is 0.9, crossover probability is 0.8, mutation probability is 0.1; improved particle swarm algorithm: particle swarm size is 150, initial inertia weight coefficient is 0.9, final inertia weight coefficient is 0.4, learning factor is 2, iteration number is 300; improved artificial bee colony algorithm: bee swarm size is 150, iteration number is 300, honey source determined to be discarded times is 5.

5.3. Configuration Results

5.3.1. Configuration Scheme 1

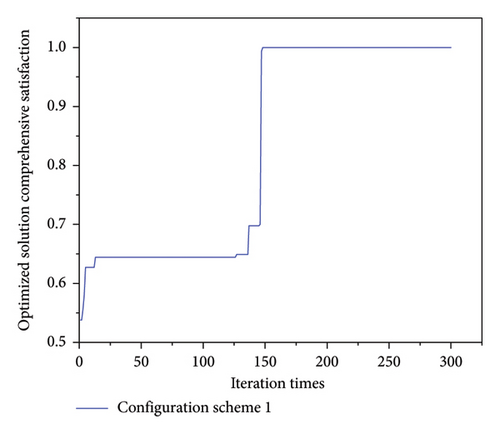
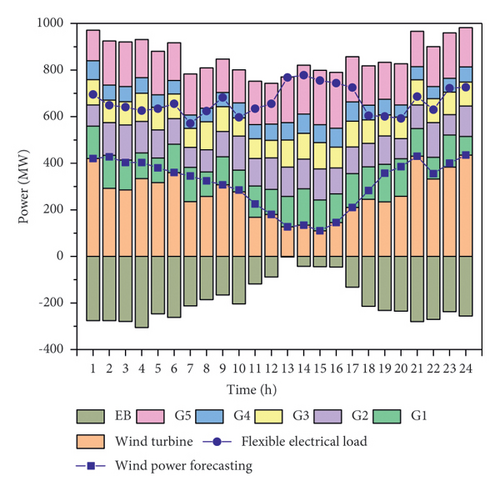
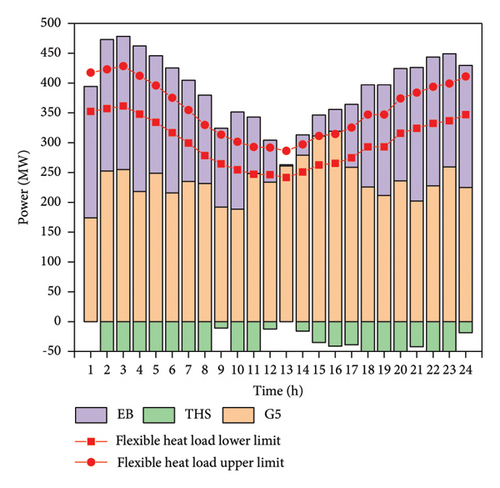
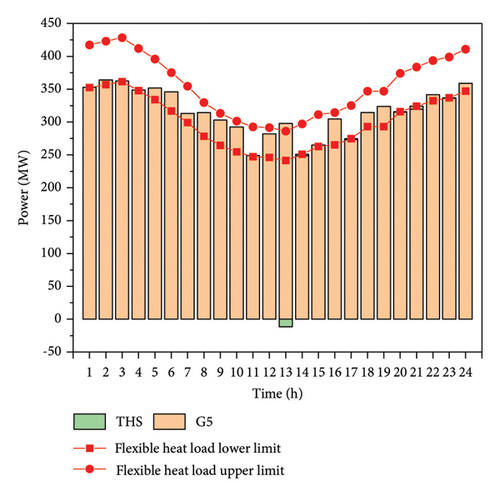
The system simultaneously configures the electric boiler and the heat storage tank. Figure 4 displays the system optimization solution’s comprehensive satisfaction convergence curve. The comprehensive satisfaction of the system optimization solution converges to 1.0 at about 150 generations, indicating that the system can find the optimal solution for the CHP system operation under the premise of satisfying all the constraints of the system under the operating conditions of simultaneously configuring the heat storage tank and the electric boiler. The best operation scheme of the system under configuration scheme one is shown in Figure 5. It can be seen that when the system is in the best operation state, the configuration power of the system electric boiler is 304 MW. The configuration capacity of the system heat storage tank is 915 MW.

5.3.2. Configuration Scheme 2

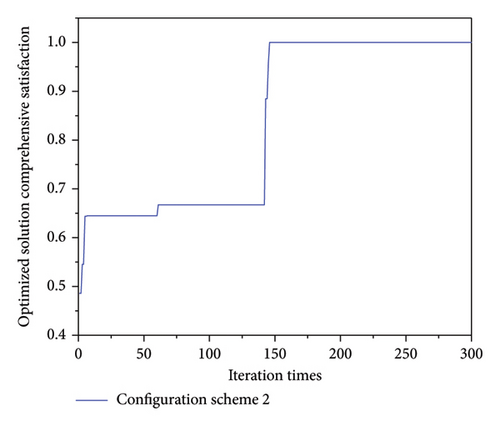
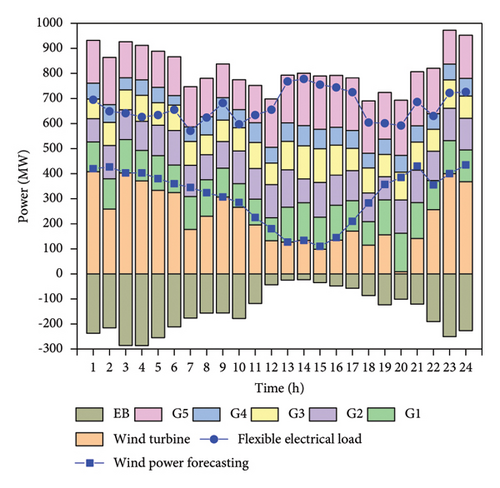
The system only configures the electric boiler. Figure 6 displays the system optimization solution’s comprehensive satisfaction convergence curve. The comprehensive satisfaction of the system optimization solution converges to 1.0 at about 150 generations, indicating that the system can find the optimal solution for the CHP system operation under the premise of satisfying all the system constraints under the operating condition of only configuring the electric boiler. Figure 7 displays the system’s optimal operation scheme under configuration scheme two. The configuration power of the system electric boiler is 286 MW when the system is operating at its peak efficiency.

5.3.3. Configuration Scheme 3

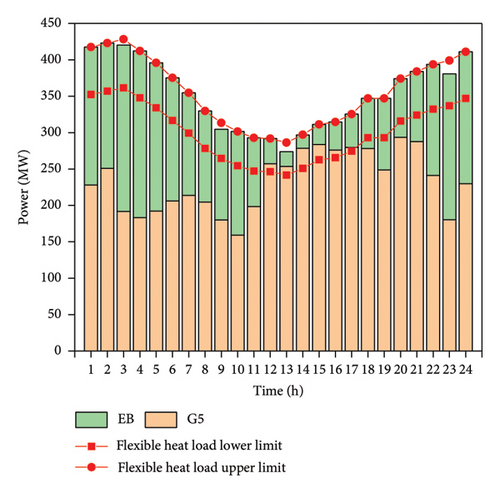
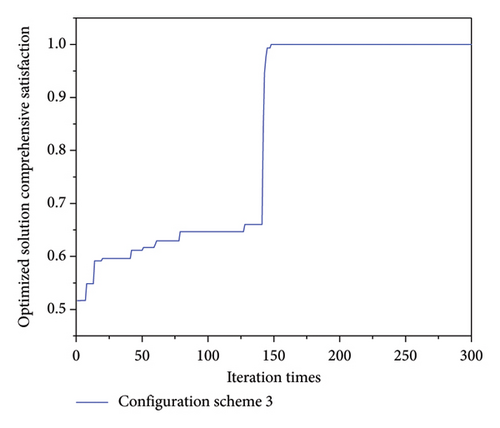
The system only configures the heat storage tank. Figure 8 displays the system optimization solution’s comprehensive satisfaction convergence curve. The comprehensive satisfaction of the system optimization solution converges to 1.0 at about 150 generations, indicating that the system is capable of determining the best way to operate the CHP system while meeting all of its constraints when it comes to just setting the heat storage tank. Figure 9 displays the system’s optimal operation plan under configuration scheme three. The system heat storage tank’s configuration capacity is 38 MW when operating at peak efficiency.

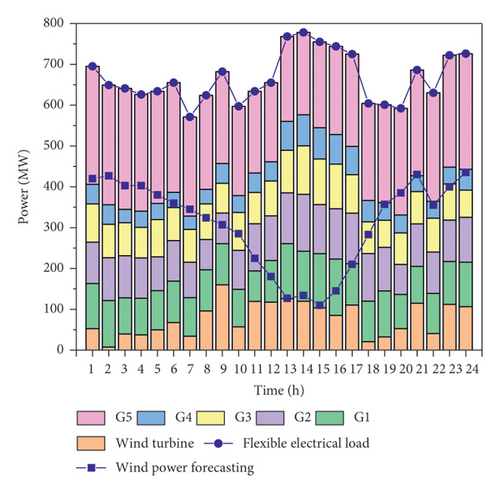
To further verify the impact of adding a heat storage tank and electric boiler to the CHP system’s wind power consumption capacity and economic performance, the wind power output and economic performance under different configuration schemes are compared, as shown in Figures 10 and 11. It is intuitively apparent from Figure 9 that the system has the least amount of wind power curtailment, that is, the most robust wind power consumption capacity, when the system is configured with scheme 1, that is, simultaneously configuring the heat storage tank and the electric boiler; the system has the most wind power curtailment, that is, the weakest wind power consumption capacity when the system is configured with scheme 3, that is, only configuring the heat storage tank. The economic performance of the system operation is also the same. Since configuration scheme 3 has the highest wind power curtailment cost, its economic performance is the worst, which further reflects that the configuration of the heat storage tank and the electric boiler can further improve the economic performance of the system operation.

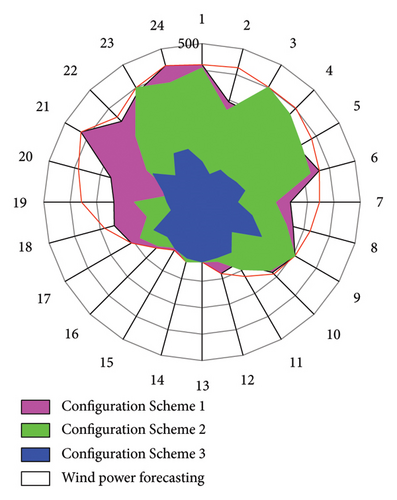
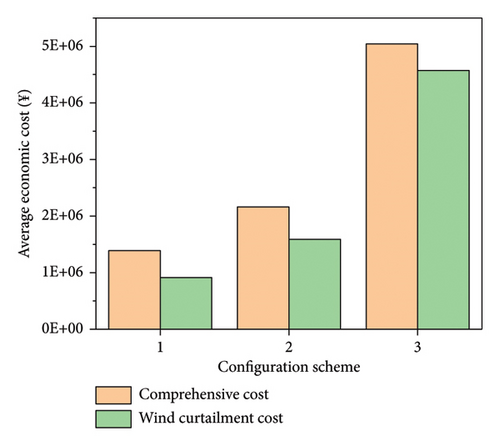
The above analysis shows that different configuration schemes can find the best operation scheme that satisfies the system objectives and constraints. Among them, when the system is configured with both a heat storage tank and an electric boiler, the system has the most robust wind power consumption capacity and the lowest comprehensive cost, indicating that this configuration scheme is the best; when the system is configured with only electric boiler, the system has a strong wind power consumption capacity and the lower comprehensive cost, indicating that this configuration scheme is the second best; when the system is configured with only heat storage tank, the system has the weakest wind power consumption capacity and the highest comprehensive cost, indicating that this configuration scheme is the worst.

5.4. Algorithm Effectiveness Verification

The economic performance of the system configuration under various algorithms is compared, as indicated in Table 7, to confirm the efficacy of the enhanced memetic algorithm for resolving the CHP system’s optimal scheduling problem. To make the comparison results more apparent, the relative percentage increase (RPI) [25] value is a gauge for the system’s operational economy. From Table 7, it can be seen that the improved memetic algorithm has the best configuration economic performance.

Table 7. Comparison of RPI values of system configuration economic performance under different algorithms.

Number of runs	IMA	MA	IPSO	IABC
1	3.3435	7.6900	2.4795	10.054
2	0.8604	5.8800	3.9208	10.650
3	1.4012	7.9182	3.2036	9.9476
4	2.3056	6.3031	4.3580	9.8470
5	0.5294	4.8074	5.2340	8.4051
6	0.0000	6.3834	4.8929	9.8547
7	0.5742	5.6839	3.6671	10.764
8	0.4504	7.4542	4.2028	9.0022
9	0.5760	5.8997	3.7291	8.2581
10	2.0261	5.1646	3.4456	9.6039
Mean	1.2067	6.3185	3.9133	9.6388

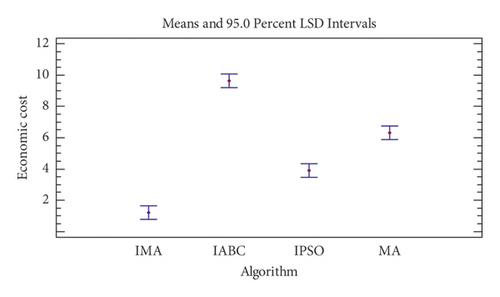
To further intuitively show the improved memetic algorithm’s excellent performance in solving the CHP system’s optimal scheduling problem, a multifactor analysis of variance [26] is performed on the data in Table 7. The kind of algorithm is the independent variable, and Figure 12 displays the research findings. It is evident from the figure that the median of the comprehensive satisfaction of the optimization solution of the improved memetic algorithm is the lowest. The distribution is more concentrated, indicating that the economic performance of the algorithm is the best and most stable.

6. Conclusions

This paper studies the optimal configuration method of the additional heat source of the CHP system, considering demand response. It proposes a multiobjective optimization model considering the system optimization solution’s quality, economic viability, and wind power consumption capacity. To solve the model effectively, this paper adopts the improved memetic algorithm combined with the hierarchical sequence method, introduces the adaptive crossover mutation operator and the simulated annealing strategy based on neighborhood exchange, and improves the search efficiency and quality of the algorithm. The proposed method’s effectiveness and superiority are verified through simulation experiments. The main conclusions are as follows:

(1)
Among the three configuration schemes of additional heat source, the satisfaction of all configuration schemes is optimal, and the system’s economy and wind power consumption capacity are the best when the heat storage tank and electric boiler are configured simultaneously. Electric boilers and heat storage tanks can increase the flexibility and wind power absorption capacity of the system and improve the overall economic performance of the system by removing the coupling between power generation and heating of the cogeneration system. At the same time, the demand response mechanism makes the original load flexible, releases the potential of demand response on the load side, enhances the flexibility and peak shaving ability of the system, and makes extra space for wind power consumption.
(2)
The multiobjective hierarchical sequence method can solve the problem one by one according to the importance order of the objectives and ensure the optimality of the essential goal of configuration scheme satisfaction. The improved memetic algorithm can dynamically modify the probability of crossover and mutation based on each individual’s fitness level, protect the suitable individuals, eliminate the poor individuals, use the simulated annealing strategy based on neighborhood exchange for local search, jump out of the local optimum, and improve the solution efficiency and quality. Under the same simulation conditions, compared with MA, IPSO, and IABC algorithms, the average economic costs of the IMA algorithm are reduced by about 5.11%, 2.70%, and 8.43%, respectively.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the Changsha Federation of Social Science (2022csskkt188) and the Natural Science Foundation of Liaoning Province of China (2023JH2/101700068).

Open Research

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Çakir U, Çomakli K., and Yüksel F., The role of cogeneration systems in sustainability of energy, Energy Conversion and Management. (2012) 63, 196–202, https://doi.org/10.1016/j.enconman.2012.01.041, 2-s2.0-84866981465.
10.1016/j.enconman.2012.01.041
Web of Science® Google Scholar
2 Liu C., Wang H., Wang Z.Y., Liu Z., Tang Y., and Yang S., Research on life cycle low carbon optimization method of multi-energy complementary distributed energy system: a review, Journal of Cleaner Production. (2022) 336, 130380.
10.1016/j.jclepro.2022.130380
Web of Science® Google Scholar
3 Lotfi H., Multi-objective energy management approach in distribution grid integrated with energy storage units considering the demand response program, International Journal of Energy Research. (2020) 44, no. 13, 10662–10681, https://doi.org/10.1002/er.5709.
10.1002/er.5709
Web of Science® Google Scholar
4 Lotfi H. and Ghazi R., Optimal participation of demand response aggregators in reconfigurable distribution system considering photovoltaic and storage units, Journal of Ambient Intelligence and Humanized Computing. (2021) 12, no. 2, 2233–2255, https://doi.org/10.1007/s12652-020-02322-2.
10.1007/s12652-020-02322-2
Web of Science® Google Scholar
5 Lotfi H. and Shojaei A. A., A dynamic model for multi-objective feeder reconfiguration in distribution network considering demand response program, Energy Systems. (2023) 14, no. 4, 1051–1080, https://doi.org/10.1007/s12667-022-00507-6.
10.1007/s12667-022-00507-6
Google Scholar
6 Saleh A., Hajabdollahi H., Ghamari V., and Shafiey Dehaj M., Evaluation of operational strategy of cooling and thermal energy storage tanks in optimal design of multi generation system, Energy. (2023) 284, 129256.
10.1016/j.energy.2023.129256
CAS Web of Science® Google Scholar
7 Deng B., Fang J., Hui Q., Zhang T., Chen Z., Teng Y., and Xi X., Optimal scheduling for combined district heating and power systems using subsidy strategies, CSEE Journal of Power and Energy Systems. (2019) 5, no. 3, 399–408.
Web of Science® Google Scholar
8 Yi Z., Xu Y., and Li Z., Optimal configuration of distributed heat source to promote the wind power penetration in combined heat and power system, Journal of Renewable and Sustainable Energy. (2019) 11, no. 3, https://doi.org/10.1063/1.5088004, 2-s2.0-85067827762, 036302.
10.1063/1.5088004
Web of Science® Google Scholar
9 Ding Z., Hou H., Duan L., Francesco Frate G., Zhang N., and Desideri U., Study on the capacity-operation collaborative optimization for multi-source complementary cogeneration system, Energy Conversion and Management. (2021) 250, 114920.
10.1016/j.enconman.2021.114920
Web of Science® Google Scholar
10 Gimelli A. and Muccillo M., Optimization criteria for cogeneration systems: multi-objective approach and application in an hospital facility, Applied Energy. (2013) 104, 910–923, https://doi.org/10.1016/j.apenergy.2012.11.076, 2-s2.0-84872245072.
10.1016/j.apenergy.2012.11.076
Web of Science® Google Scholar
11 Buoro D., Pinamonti P., and Reini M., Optimization of a distributed cogeneration system with solar district heating, Applied Energy. (2014) 124, 298–308, https://doi.org/10.1016/j.apenergy.2014.02.062, 2-s2.0-84897389892.
10.1016/j.apenergy.2014.02.062
Web of Science® Google Scholar
12 Gimelli A., Mottola F., Muccillo M., Proto D., Amoresano A., Andreotti A., and Langella G., Optimal configuration of modular cogeneration plants integrated by a battery energy storage system providing peak shaving service, Applied Energy. (2019) 242, 974–993, https://doi.org/10.1016/j.apenergy.2019.03.084, 2-s2.0-85063206903.
10.1016/j.apenergy.2019.03.084
Web of Science® Google Scholar
13 Hajabdollahi Z. and Fu P. F., Multi-objective based configuration optimization of SOFC-GT cogeneration plant, Applied Thermal Engineering. (2017) 112, 549–559, https://doi.org/10.1016/j.applthermaleng.2016.10.103, 2-s2.0-84992386833.
10.1016/j.applthermaleng.2016.10.103
CAS Web of Science® Google Scholar
14 Stoppato A., Benato A., Destro N., and Mirandola A., A model for the optimal design and management of a cogeneration system with energy storage, Energy and Buildings. (2016) 124, 241–247, https://doi.org/10.1016/j.enbuild.2015.09.036, 2-s2.0-84944097340.
10.1016/j.enbuild.2015.09.036
Web of Science® Google Scholar
15 Habka M. and Ajib S., Determination and evaluation of the operation characteristics for two configurations of combined heat and power systems depending on the heating plant parameters in low-temperature geothermal applications, Energy Conversion and Management. (2013) 76, 76996–81008, https://doi.org/10.1016/j.enconman.2013.08.046, 2-s2.0-84884875270.
10.1016/j.enconman.2013.08.046
Web of Science® Google Scholar
16 Amirante R. and Tamburrano P., Novel, cost-effective configurations of combined power plants for small-scale cogeneration from biomass: feasibility study and performance optimization, Energy Conversion and Management. (2015) 97, 111–120, https://doi.org/10.1016/j.enconman.2015.03.047, 2-s2.0-84925865993.
10.1016/j.enconman.2015.03.047
Web of Science® Google Scholar
17 Li W. and Li Y., Configuration optimization of the novel cogeneration heating system with multi turbine units, Energy Conversion and Management. (2020) 221, 113140.
10.1016/j.enconman.2020.113140
Web of Science® Google Scholar
18 Oh Si-D., Lee Ho-J., Jung J.-Y., and Kwak Ho-Y., Optimal planning and economic evaluation of cogeneration system, Energy. (2007) 32, no. 5, 760–771, https://doi.org/10.1016/j.energy.2006.05.007, 2-s2.0-33846276892.
10.1016/j.energy.2006.05.007
Web of Science® Google Scholar
19 Mohammadi H., Mohammadi M., and Ghasemi A., Optimal configuration planning of rule and optimization-based driven storage coupled micro cogeneration systems by the implementation of constraint programming, Journal of Energy Storage. (2022) 48, 103934.
10.1016/j.est.2021.103934
Web of Science® Google Scholar
20 Costea M., Feidt M., Alexandru G., and Descieux D., Optimization of gas turbine cogeneration systemfor various heat exchanger configurations, Oil & Gas Science and Technology–Revue d’IFP Energies nouvelles. (2012) 67, no. 3, 517–535, https://doi.org/10.2516/ogst/2011140, 2-s2.0-84863974444.
10.2516/ogst/2011140
Web of Science® Google Scholar
21 Pang X., Wang Y., Yu Y., and Liu W., Optimal scheduling of a cogeneration system via Q-learning-based memetic algorithm considering demand-side response, Energy. (2024) 300, 131513.
10.1016/j.energy.2024.131513
Web of Science® Google Scholar
22 Neri F. and Cotta C., Memetic algorithms and memetic computing optimization: a literature review, Swarm and Evolutionary Computation. (2012) 2, 1–14, https://doi.org/10.1016/j.swevo.2011.11.003, 2-s2.0-84855278833.
10.1016/j.swevo.2011.11.003
Web of Science® Google Scholar
23 Li Y. L., Shao W., You L., and Wang B.-Z., An improved PSO algorithm and its application to UWB antenna design, IEEE Antennas and Wireless Propagation Letters. (2013) 12, 1236–1239, https://doi.org/10.1109/lawp.2013.2283375, 2-s2.0-84886911721.
10.1109/LAWP.2013.2283375
Web of Science® Google Scholar
24 Chen W. and Xiao Y., An improved ABC algorithm and its application in bearing fault diagnosis with EEMD, Algorithms. (2019) 12, no. 4, https://doi.org/10.3390/a12040072, 2-s2.0-85064198289.
10.3390/a12040072
PubMed Web of Science® Google Scholar
25 Yu H., Li J. q, Chen X. l, Niu W., Sang H. y, Niu W., and Sang H.-yan, An improved multi-objective imperialist competitive algorithm for surgical case scheduling problem with switching and preparation times, Cluster Computing. (2022) 25, no. 5, 3591–3616, https://doi.org/10.1007/s10586-022-03589-0.
10.1007/s10586-022-03589-0
PubMed Web of Science® Google Scholar
26 McHugh M. L., Multiple comparison analysis testing in ANOVA, Biochemia Medica. (2011) 21, no. 3, 203–209, https://doi.org/10.11613/bm.2011.029.
10.11613/BM.2011.029
CAS PubMed Web of Science® Google Scholar

All articles

Optimal Configuration of Additional Heat Source for CHP System considering Demand Response Based on Comprehensive Benefits

Abstract