We find that in the upstream status of global value chain, country effects are relatively stronger than industry effects; industry effects dominate country effects downstream of the global value chain. During financial crisis, downstream in the value chain, the influence of industry effects waned and country effects rose. Moreover, for developed countries, the negative impact of the upstream status of value chain weakened considerably; the impact of upstream status strengthened for emerging markets after the subprime mortgage crisis. For tradable industries, the negative impact of global value chain upstream status on pure industry-specific returns strengthens significantly.

1. Introduction

The benefits of international portfolio diversification may be attributed to the imperfectly integrated equity markets resulting from country-specific economic policies and institutional regimes and/or differences in the various industrial compositions. The relative strengths of country and industry effects in international portfolio diversification are important for global equity investment activities. Several early studies on the changing roles of countries versus industries were provided by Grinold, Rudd, and Stefek [1]; Heston and Rouwenhorst [2]; Rouwenhorst [3]; and Cavaglia, Brightman, and Aked [4]. They postulated that security prices are determined by a global equity market factor, country effects, industry effects, and common firm characteristics such as size and value.

More specifically, it would be beneficial for portfolio managers to assess the gains from international diversification to figure out the degree of risk reduction derived from diversification across countries versus diversification across industries. Identifying the changing roles of country and industry effects in international portfolio diversification will help investors construct portfolios that maximize the return-to-risk trade-offs among underlying influencing factors. If country effects dominate industry effects, then diversification across countries is more effective in reducing portfolio risks; conversely, if industry effects are more important, then diversification across industries has more merits for risk reductions.

Marceloa, Quirós, and Martins [5] summarized the theoretical framework for investigating the role of country and industry factors. In principle, the existing literature identifies that the degree of a country’s market segmentation plays an essential role in the magnitude of the country effect, and the role of global industry effects depends on the degree of capital market integration and the externality of original technology development across various industries. Campa and Fernandes [6] revealed that the importance of country and industry factors is correlated with measures of international economic and financial integration and development.

Many previous studies, such as Drummen and Zimmermann [7]; Beckers, Connor, and Curds [8]; and Kuo and Satchell [9]; achieved similar results and emphasized the dominance of the country effect over the industry effect. In relatively recent years, a growing number of studies have documented the importance of industry effects [4, 10]. Galati and Tsatsaronis [11] found that 50% of European portfolio managers in 1997 believed that the country effect was the dominant factor; however, in 2001, approximately 75% of managers believed that investment strategies based on industry diversification were superior to geographic strategies. Brooks and Del Negro [12] explored this issue on a global scale from different research perspectives. In a firm-specific investigation, Bai and Green [13] provided additional evidence in the debate over country and industry effects and the implications for portfolio diversification.

Moreover, Isakov and Sonney [14] studied a sample of European countries and found that the relative importance of the industry effect and its impact on equity returns has grown significantly over the period 1997–2000. Ferreira and Ferreira [15] also found similar results for 11 countries in the Economic and Monetary Union. In examining the issue of portfolio diversification and assessing the differences between development economies and emerging markets, Serra [16] and Chen, Bennett, and Zheng [17] documented the high prevalence of country effects in emerging markets and showed that the trend around the industry effect growth is more often observed in developed markets. Bhargava, Dania, and Malhotra [18] clarified that, given the increase in correlation among markets around the world in recent years, diversification across industries is one strategy to achieve risk reduction. Marceloa, Quirós, and Martins [5] examined the behavior of country and industry effects during high (low) volatility periods and posited that industry diversification may provide relatively more protection in crisis. Ali, Sensoy, and Goodell [19] identified diversification benefits among Asian equity markets in the COVID-19 era. They found that such benefits among Asia-Pacific markets changed considerably during the pandemic, and most changes were persistent; in most cases, any of the sample equities had at least one safe-haven protection.

The aims of this study are to introduce a new perspective to analyzing this subject and investigate the impact of global value chain status on the changing roles of country and industry effects in international equity portfolio diversification (Portfolio diversification is an investment strategy that seeks to reduce an investor’s risk and increase his or her return, usually by having a variety of investments. In this study, we employed the indicators of diversification potential, factor correlation, and mean absolute deviation to measure the strength of country and industry factors regarding international portfolio diversification, which have been defined in details at the beginning of the following “Methodology” section). We believe that the re-examination of this issue continues to be legitimized. Strengthening economic ties among countries worldwide has given rise to increasing production fragmentation across various regions. Because of these countries’ industrial proximity to each other and the declining costs of international communication and coordination, opportunities for regional multistage production have been increasing. Production processes are fragmented into several sequential stages that can be distributed across multiple countries [20]. This situation is characterized by vertical specialization in international production networks, which gives prominence to the role of the global value chain.

Porter [21] originally proposed the idea of the value chain in which the process of enterprise value creation is composed of a series of interconnected activities, including research and development, design and trial production, raw material and equipment procurement, product production, transportation, storage, marketing, and services that form a complete chain structure. Furthermore, as defined by the United Nations Industrial Development Organization, the global value chain is a global inter-enterprise network organization connecting the processes of production, sales, and recycling to realize the added value of goods or services and involves the entire process from raw material collection and transportation, production and distribution of semifinished products, finished products to final consumption, and recycling. The global value chain reflects a production network of vertical specialization. Timmer, Erumban, Los, Stehrer, and Vries [22]; Kwon and Ryou [23]; Chen [24]; Miroudot and Ye [25]; and Sone and Ko [26] discussed the multifaceted influence of global value chain status on international market segmentation, integration, and industrial technology overflows.

Due to the potential impacts of global value chain status on countries’ market segmentation, the extent of involvement in capital market fluctuations for various industries, and the ranges of technology gradient transfer across industries, our analysis in this study focused on the impact of the status of the global value chain on the changing roles of country and industry effects.

Our empirical results show that in the upstream status of the global value chain, country effects are relatively stronger than industry effects. In contrast, in most cases, industry effects dominate country effects downstream of the global value chain. While the influence of industry and country effects increased overall during the global financial crisis, downstream in the global value chain, the influence of industry effects waned and country effects rose but country effects continued to dominate upstream in the global value chain. Additionally, the symmetric influence of value chain upstream status on the country and industry-specific returns implies that the country effects have a more important role in explaining the gains from international portfolio diversification in the upstream of the global value chain, while industry effects are more important in the downstream.

Moreover, for developed countries, the negative impact of value chain upstream status weakened considerably; conversely, the impact of upstream status strengthened for emerging markets after the subprime mortgage crisis. The findings may reflect an increase in economic and financial integration across developed countries in the upstream value chain and the efforts of emerging markets to engage in the differentiated improvement of the production structure after a subprime crisis. In addition, for nontradable industries, a upstream status in the global value chain has an insignificant effect on pure industry-specific returns, while the negative impact strengthens for tradable industries. It has been documented that the nontradable industries tend to be more stable and are barely influenced by global fluctuations compared with tradable industries.

Our study contributes to the literature on country and industry effects in international portfolio diversification by exploring a new perspective on the global value chain. We identify status in the value chain as a determinant of the changing roles of country and industry effects. Vertical specialization has become prevalent in international production networks, but thus far, little is known about the role of the status of the global value chain in international portfolio diversification, which is deeply embedded in our study. Finally, our results are very relevant to the debate concerning the changing strengths of country and industry effects in portfolio diversification.

The remainder of this study is structured as follows. In Section 2, we describe our sample data, variable definitions, and the methodology used in this study. Section 3 reports our main empirical results. Section 4 presents additional robustness analyses that further confirm our main results. Section 5 concludes this study.

2. Data and Methodology

2.1. Sample Data

The data used in this study were collected from the Wind, MSCI, and WIOD (World Input-Output Database) databases. As the market leader in China’s financial information services industry, Wind provides accurate and real-time information, as well as sophisticated communication platforms for financial professionals. The Wind financial database is the most comprehensive and powerful tool for financial professionals who need complete information on international stocks, bonds, funds, futures, exchange rates, and global economies. MSCI Inc. is a leading provider of investment decision support tools to investors worldwide, including asset managers, banks, hedge funds, and pension funds. MSCI products and services include global indices, portfolio risk and performance analytics, and governance tools. The data of our dependent variables and control variables were extracted and processed from Wind and MSC.

WIOD (https://www.wiod.org/home) provides annual time series of world input-output tables and underlying data. These tables have been constructed in a clear conceptual framework based on the system of national accounts. They are based on officially published input-output tables merged with national accounts data and international trade statistics. The WIOD has proved very useful in analyses of international trade. It has been used to describe trends in global chain trade and research into the formation of regional production clusters in the world economy [27]. Our global chain status indicators are drawn and constructed based on data from this database.

Our sample dataset covers 28 countries, including 18 developed countries, such as Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Italy, Japan, the Netherlands, Norway, Portugal, Spain, Sweden, Switzerland, the United Kingdom, and the United States, as well as 10 emerging markets, such as Russia, South Korea, the Czech Republic, Turkey, Greece, China, India, Indonesia, Brazil, and Poland. Additionally, the dataset covers 24 industries according to the MSCI second-level industry classification, including tradable industries and nontradable industries. We classified the 56 subdivided industries involved in WIOD into the above 24 MSCI industries.

All the downloaded data is reported in U.S. dollars on a monthly basis, but may be annualized according to the requirements of the following analysis. To remove the influence of outliers on our empirical results, we winsorized the data of continuous variables at intervals of 5% and 95%. Finally, all data of value variables were inflation-adjusted to eliminate the impact of price fluctuations (our sample goes from January 2000 to December 2014 because the WIOD dataset was not updated after 2015, and the global value chain experienced a significant shock attributed to a tide of antiglobalization when Donald Trump was elected the 45th president of the U.S. on November 9, 2016).

2.2. Methodology

2.2.1. Indicators Measuring the Strength of Country and Industry Factors

In this study, we focused on the relative evolutions and determinants of industry and country factors in global equity markets over time. Following Rouwenhorst [3]; Phylaktis and Xia [28]; Campa and Fernandes [6]; Menchero and Morozov [29]; and Marcelo, Quirós, and Martins [5]; we employed the indicators of diversification potential, factor correlation, and mean absolute deviation to measure the strength of country and industry factors regarding international portfolio diversification.

(1) Diversification Potential. Following Menchero and Morozov [29]; full-investment pure factor portfolios were constructed because an important measure of diversification is the volatility ratio between a pure factor portfolio fully invested in a single country or industry and one that is diversified across the entire world. We obtained an industry neutral portfolio that is 100 percent net long the particular country and a country neutral portfolio that is 100 percent long the particular industry. The return

of the full-investment pure factor is as follows:

(1)

where f_k is the return of the zero-investment pure factor; f_k = ∑_nΩ_knr_n, Ω_kn is the weight of stock n in country/industry-factor portfolio k; r_n is excess stock returns; and f_w is the return of the world factor. The variance of the full-investment factor portfolio is given by

(2)

where σ_w is volatility of the world factor; σ_k is volatility of the zero-investment factor; and ρ_kw is the correlation between the zero-investment factor and the world factor.

The diversification potential for a single country k is defined as the volatility ratio

, which measures the reduction in volatility that can be achieved by diversifying the portfolio across the world instead of concentrating within a single country. Additionally, the diversification potential for countries is obtained by a weighted average of the individual diversification potentials across countries where w_k is the weight of country k:

(3)

Diversification potential for industries (Dpi) can be similarly defined, which is comparable with Dpc to measure the relative strength of the two effects.

(2) Factor Correlation. Factor correlation is another important indicator of the strength of country/industry factors.

is the correlation between the full-investment factor

(country/industry) and the world factor f_w and can be aggregated across countries:

(4)

The factor correlation for industries follows a similar expression. If the correlation is fairly small, then a high volatility for the zero-investment factor leads to a low correlation , which implies attractive diversification opportunities.

(3) Mean Absolute Deviation. The mean absolute deviation (Mad) is a measure of the relative strength of countries versus industries, as proposed by Rouwenhorst [3]. Heston and Rouwenhorst [2] employed a dummy variable approach that assumes the return of an index of industry i and country k at time t is given by

(5)

where α_t is a common factor at time t, β_i,t is the global industry i factor, γ_k,t is the country k factor, and ε_ik,t is the idiosyncratic disturbance. Following Campa and Fernandes [6], for each month t, we estimated the common factor, global industry factors, and country factors based on the regression of all the indices on country and industry dummies:

(6)

where r_ik is the return on the value-weighted index of industry i in country k. I and C are the industry and country dummies. Furthermore, to gauge the importance of each national or industrial factor, we used the mean absolute deviation (Mad) metric:

(7)

Mad_γ(t) measures the weighted mean absolute deviation of country effects; the higher it is, the more dispersed the country returns around the world are. Mad_β(t) measures the weighted mean absolute deviation of industry effects; the higher this value is, the more dispersed the industry returns are in that period. The w_i/w_k are the weights of the industries/countries.

Furthermore, following Campa and Fernandes [6], to examine the determinants of the evolution of country/industry-specific returns (Counb/Indr) in world financial markets, we used the estimates of the monthly industry and country (β and γ) factors from the above section and aggregated them to obtain yearly values for the pure country and industry factors. For each country/industry, we took the average of the absolute country/industry factor during a year. These yearly aggregate measures (Counb/Indr) are employed in the regression analysis as the dependent variables because some of the exogenous control variables, such as certain elements in the vector of country and industry characteristics, and are only available on a yearly basis.

2.2.2. Global Chain Status Indicators

In this study, the global chain status indicator was used as our primary explanatory variable. According to Koopman et al. [30]; Wang et al. [31]; and Timmer et al. [32], we constructed indicators measuring status in the global value chain for various countries and industries. More specifically, these indicators (Gvcposition_coun/Gvcposition_ind) are calculated as follows:

(8)

where IV is a country/industry’s value-added embodied as intermediate inputs in third countries/industries’ gross exports; FV is the value-added from foreign sources embodied in a particular country/industry’s gross exports; and E is all gross exports. Gvcposition_coun is the log ratio of a country sector’s supply of intermediates used in other countries’ exports to the use of imported intermediates in its own production. Additionally, an industry-level index for the position in the global value chain, Gvcposition_ind, has a similar connotation (more details of the constructions of Gvcposition_coun/Gvcposition_ind can be found in the studies of Koopman et al. [30] and Wang et al. [31].

The Gvcposition_coun and Gvcposition_ind are additive. Higher values of these indicators imply that the country-sector/industry lies upstream in a value chain. Of course, two countries/industries can have identical values of the Gvcposition_coun/Gvcposition_ind while having slightly different degrees of participation in the global value chain. Therefore, the global value chain participation index for countries/industries can be defined following Koopman et al. [30] and used in our robustness tests.

2.2.3. Control Variables for Investigating the Determinants of Pure Country/Industry Factors

To examine the determinants of the evolution of country/industry-specific returns (Counb/Indr) in world financial markets, we related these pure factors with several fundamental country/industry characteristics. Following Rouwenhorst [3]; Campa and Fernandes [6]; and Chong et al. [33]; the control variables were set at the country and industry levels, respectively.

The country level control variables include one-year lagged return index of a country (Lagcounret) because if there is a momentum in stock returns, then higher current returns in a given country may lead to a positive country shock in the next period, and vice versa; turnover (Counturnover), a proxy for the degree of liquidity and trading activity, which is defined as the number of shares traded divided by the number of outstanding shares; the log of market capitalization (end-period), which is used as a measure of size in explaining the country factors (Counsize) because larger countries are perceived to be more stable and thus would be better off in weathering crises, resulting in lower shocks; the industrial market value concentration of a country regarding the magnitude of country shocks (Counhhi) in that higher industrial concentration would increase country factors; the share of the number of listings of a country in the U.S. (Scounusa), which is a proxy for the degree of financial market integration; country openness variable (Copenness), which is calculated as a ratio of the sum of export and import values to the GDP of a country in a year. Finally, we also controlled for the GDP growth rate (Gdpgrowth) and the logarithm of GDP per capita of a country (Lngdpp).

Additionally, at the industry level, we employed the analog control variables of one-year lagged return (Lagindret), liquidity and trading activity (Indturnover), industry size (Indsize), and industry concentration (Indhhi), reflecting the extent to which the listed stocks in a market disperse across industries, and the degree of financial integration from the perspective of various industries (Sindusa), which is the share of the number of overseas enterprise listings of an industry in the US.

3. Empirical Results

3.1. Descriptive Analysis

In Figures 1-3, we illustrated the evolutions of diversification potential, factor correlation, and mean absolute deviation during our sample period. The diversification potential and factor correlation are mirror images of one another. It is shown that the industry effect dominated the country effect during 2000–2006. With the onset of the U.S. subprime mortgage crisis in 2007, however, the country effect began to dominate the industry effect for a few years. Since 2009, country and industry effects have been roughly comparable. After 2011, as the international financial crisis faded away, the industry effect returned to a higher position again.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Evolution over time of the diversification potential of country and industry effects.

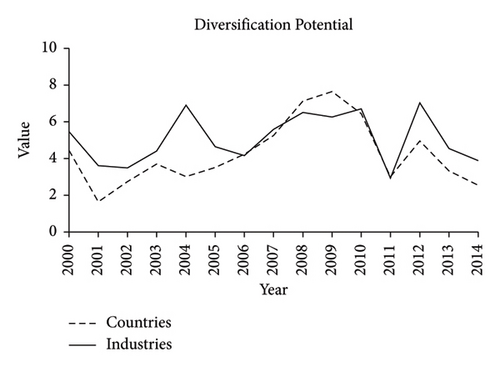
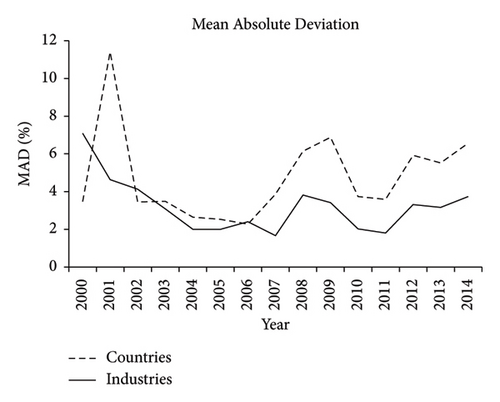
Moreover, mean absolute deviation provides additional history compared to risk-based measures and complements the diversification potential and factor correlation indicators (A little difference in the evolution pattern between Figures 1 and 3 is a common phenomenon according to Rouwenhorst [3]; Phylaktis and Xia [28]; Campa and Fernandes [6]; Menchero and Morozov [29]; and Marcelo et al. [5]. In Figure 3, we found that except for a short period between 2001 and 2002, the results are roughly consistent with Figure 1, namely, the country effect does not dominate industries before 2007, with the situation reversing after 2007. Since then, the two effects have been close and comparable, although the country effect appears to retain a slight advantage. In addition, Figure 3 shows that since both country and industry factors were quite weak between 2003 and 2005, the high diversification potential during this period in Figure 1 was more likely caused by a low-volatility world factor rather than strong country and industry factors.

Additionally, Figure 4 reports the annual changes in the global value chain position indices for countries and industries. Both indices have a highly similar annual change pattern, which may be because they all mirror the position distribution dynamics of all countries and industries in a given global value chain. The annual maximum drawdown appeared during 2007-2008, which reflected a significantly negative shock to the global value chain. Analogous dynamics of the global value chain participation indices for countries and industries can also be found.

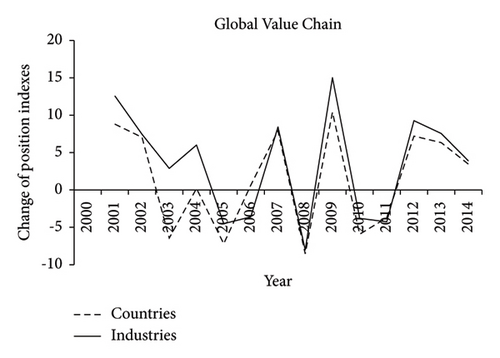
Table 1 shows the fundamental descriptive statistics of the annual changes in the global value chain position indices across countries and industries with different properties, such as emerging markets/developed countries and nontradable/tradable industries. The average annual changes in the global value chain position indices are higher for emerging markets than for developed countries and nontradable industries than for tradable industries.

Table 1. Brief statistics for the annual changes of the global value chain position indices.

	Mean	Std. dev.
Emerging markets	2.7905	18.8662
Developed countries	1.3762	15.9924
Tradable industries	2.9383	17.4593
Nontradable industries	4.4266	13.1597

Finally, Table 2 reports the summary statistics of the main control variables used in the analysis on the determinants of pure country and industry effects. Panel A provides the statistics for the country sample; Panel B reports the statistics for the industry sample. The test result value of the condition number and the mean variance inflation factors (VIFs) all imply that high multicollinearity between the explanatory and control variables was not found.

Table 2. Summary statistics for the main control variables for the analysis on pure country and industry effects.

	Mean	Std. dev.	Minimum	Maximum
Panel A: country control variables
Lagcounret	0.0026	0.0038	−0.0040	0.0101
Counturnover	0.7330	1.5391	0.00002	5.1055
Counsize	18.0328	2.6801	13.4339	24.6275
Counhhi	0.2956	0.2816	0.0733	0.8977
Scounusa	0.0521	0.1901	0.0000	0.8227
Copenness	0.5534	0.2622	0.2022	1.2552
Gdpgrowth	2.0514	2.9760	−4.0573	8.4913
Lngdpp	10.3103	0.8191	7.8988	11.1912
Panel B: industry control variables
Lagindret	0.0012	0.0023	−0.0032	0.0050
Indturnover	3.5039	3.8685	0.0042	15.5211
Indsize	18.2279	2.3737	14.6755	25.4562
Indhhi	0.4102	0.2165	0.1469	0.9144
Sindusa	0.1645	0.0937	0.0571	0.3836

The results of ANOVA between the pure country effect and country-level index of position in the global value chain shows that the mean of the variance square sum of a dummy variable equal to one if the value of Gvcposition_coun is above the median Gvcposition_coun is 0.0144, and the value of F test statistic is 6.02, which implies that there is a significant difference (at 5% significance level) the mean value of pure country-specific returns (Counb). Moreover, we found that the mean of the variance square sum of a dummy variable equal to one if the value of Gvcposition_ind is above the median Gvcposition_ind is 0.0030, and the value of F test statistic is 9.45, which implies that there is a significant difference (at 1% significance level) in the mean value of pure industry-specific returns (Indr).

3.2. Global Value Chain Status and the Strength of Country and Industry Factors

The general country and industry effects comparative analysis does not account for the impacts of the value chain status. In fact, the relative strength of country and industry effects with respect to different value chain statuses may vary. We divided our sample into two classifications based on the medians of Gvcposition_coun and Gvcposition_ind, namely, the group of countries in the upstream of a value chain and the group of countries in the downstream of a value chain. The results of the analysis with respect to the indicator differences between country effects and industry effects are illustrated in Figures 5-7.

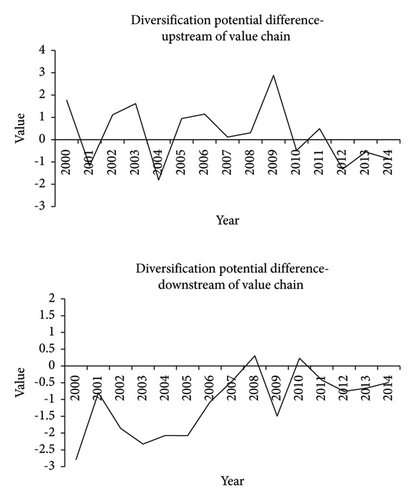
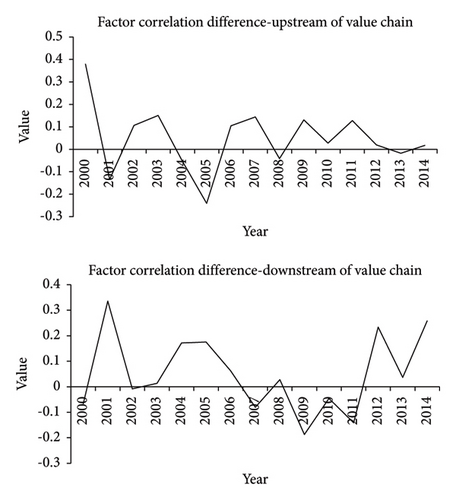
The empirical results showed that in sharp contrast to the evolution over time of the diversification potential differences between country and industry effects corresponding to the downstream of global production value chain, in the upstream status, the polyline that fluctuates up and down around the horizontal axis implies that country and industry effects were intertwined during 2000–2006. In the meantime, the industry effects actually dominated the country effects in the downstream of the global value chain because the polyline is below the horizontal axis. With the onset of the U.S. subprime mortgage crisis in 2007, the country effect began to dominate the industry effect for several years in the upstream of the global value chain, however only for a very short period of time for the downstream group. The increase in total country effects illustrated in Figure 1 is primarily due to the surge in country effects in the upstream of the global value chain. After 2011, as the international financial crisis faded away, compared to country effects, the industry effects returned to a higher position again. Additionally, the results of the heterogeneity investigation for the diversification potential difference and factor correlation difference are mirror images of one another.

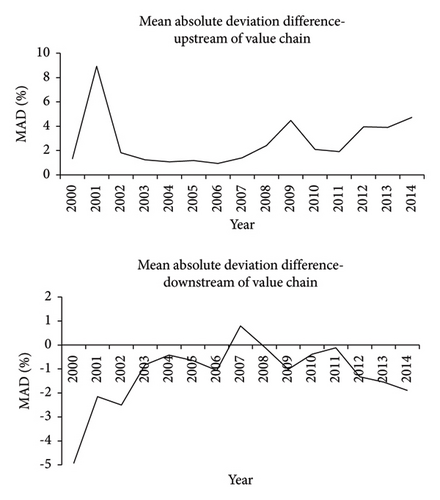
Moreover, the mean absolute deviation complements the diversification potential and factor correlation indicators again. In Figure 7, we found that except for a short period between 2007 and 2008, the industry effects were always higher than the country effects in the downstream of the global production value chain. The results are primarily consistent with Figure 5. The dynamic shapes of the relative strengths of country and industry effects in Figure 3 are mainly driven by the subsample from the upstream of the global value chain. In summary, global value chain status has an obvious impact on the relative strengths of country and industry factors in international portfolio returns.

Overall, in the upstream of the global value chain, on average, country effects are stronger than industry effects. Conversely, in most cases, industry factors dominate country factors in the downstream of the global value chain. Additionally, for a few years during the global financial crisis, the influence of industry effects declined and country effects rose in the downstream of the global value chain while country effects dominated in the upstream of the global value chain.

In light of the individual features, heterogeneity, and relative independence characterized by the activities in the value chain upstream, such as R&D, creative designs, and technology innovations across countries, country diversification remains more effective than industry diversification, which we derived from the lower correlations across countries corresponding to the upstream of the global value chain. The synchronicity of fluctuations of various industries in the upstream is relatively higher because these industries are more dependent on a global capital market and driven by the externality of new industrial transformation [6]. However, downstream of the value chain, industry factors dominate country factors because of the wave of economic globalization, and the standardization of economic activities such as processing, production and retail across countries. Meanwhile, specific industries lacking externalities from a common driving force, such as some core technology development, give rise to loose correlations between industries. In this situation, the gains from industry diversification are larger than those from country diversification.

Additionally, in times of high volatility, such as the global financial crisis spreading into international trade or rising country protectionism corresponding to the downstream of the value chain, the correlation among countries decreases, in which case the country effects rise and the industry effects fall as a result of increased fluctuation synchronicity of different industries in a global crisis. On the other hand, in the upstream of the value chain, country and industry effects may enhance one another during a crisis period due to the ascending segmentations across countries and industries despite the dominance of country effects. Except for the conjoint externality and integrated capital markets of various industries in high value-added production activities still leading to a relatively high association across industries, the fluctuation synchronicity of countries decreases even more due to asymmetric shocks to the economies upstream in the value chain, which are larger than the shocks at the industrial level.

3.3. Variation in Country- and Industry-Specific Returns Based on Regression Results

Furthermore, to examine the determinants of the evolution of country/industry-specific returns (Counb/Indr) in world financial markets, we related these pure effects with several fundamental country/industry characteristics, which are defined as the control variables following Campa and Fernandes [6]; Menchero and Morozov [29]; and Marcelo et al. [5]. We investigated why some countries have such high deviations from the world market, which would imply strong country effects, and why some industries deviate so much from the average industry, which would imply strong industry effects.

To maintain consistency with our above ANOVA and graphical analysis, the dummy variables Gvcpositiond_coun and Gvcpositiond_ind were defined as our primary explanatory variables for pure country returns and industry returns, respectively. Gvcpositiond_coun equals one if the value of Gvcposition_coun is greater than its median and zero otherwise; Gvcpositiond_ind equals one if the value of Gvcposition_ind is higher than its median.

For the baseline regressions, we employ the fixed-effects models with Driscoll–Kraay standard errors that are robust to very general forms of cross-sectional (“spatial”) and temporal dependence when the time dimension becomes large. Table 3 reports the empirical results. The negative estimates of the coefficients of our main explanatory variables imply that the average pure country- and industry-specific returns are reduced by approximately 1.07% and 1.35%, respectively, corresponding to the upstream of the global value chain. The negative impacts on country- and industry-specific returns are fairly symmetric. The difference between them is more than 26%.

Table 3. Results of baseline regressions regarding pure country and industry effects.

	Counb				Indr
	(1)	(2)	(3)		(1)	(2)	(3)
Gvcpositiond_coun	−0.0116 ^∗∗∗(0.0040)	−0.0111 ^∗∗(0.0045)	−0.0107 ^∗∗(0.0048)	Gvcpositiond_ind	−0.0142 ^∗∗∗(0.0033)	−0.0136 ^∗∗∗(0.0031)	−0.0135 ^∗∗∗(0.0036)
Lagcounret	1.0372 (1.4351)	0.8729 (1.6077)	1.1209 (1.4743)	Lagindret	0.9851 ^∗(0.5439)	0.8215 (0.5556)	0.7592 (0.6378)
Counturnover	−0.0048 (0.0049)	−0.0050 (0.0049)	−0.0063 (0.0049)	Indturnover	−0.0011 ^∗∗∗(0.0003)	−0.0009 ^∗(0.0005)	−0.0010 (0.0007)
Counsize		−0.0007 (0.0012)	0.0006 (0.0010)	Indsize			−0.0003 (0.0014)
Counhhi	0.1202 ^∗∗(0.0513)	0.1163 ^∗∗(0.0553)	0.0690 ^∗∗(0.0294)	Indhhi		0.0296 (0.0181)	0.0282 ^∗(0.0164)
Scounusa	0.2211 (0.1323)	0.2314 ^∗(0.1218)	0.5581 ^∗(0.2998)	Sindusa	−0.1369 (0.0889)	−0.0641 (0.0513)	−0.0606 (0.0374)
Copenness			−0.0479 (0.0369)
Gdpgrowth			−0.0008 (0.0017)
Lngdpp			−0.0777 (0.0515)
County dummies	Yes	Yes	Yes	Industry dummies	Yes	Yes	Yes
Constant	−0.1052 (0.0859)	−0.0970 (0.0967)	0.5213 (0.3577)	Constant	0.0650 ^∗∗∗(0.0185)	0.0405 ^∗∗∗(0.0085)	0.0457 (0.0321)
Obs.	221	221	221	Obs.	345	345	345
P value of F test	≤0.01	≤0.01	≤0.01	P value of F test	≤0.01	≤0.01	≤0.01

The dependent variables are Counb and Indr. As our primary explanatory variables, Gvcpositiond_coun equals one if the value of Gvcposition_coun is greater than its median and zero otherwise; Gvcpositiond_ind equals one if the value of Gvcposition_ind is higher than its median. Fixed-effects models with Driscoll–Kraay standard errors were employed. ^∗, ^∗∗, ^∗∗∗ denote statistical significance at the 10%, 5%, and 1% levels, respectively. Corresponding standard errors are reported in parentheses.

Pure country-specific returns are smaller for countries upstream of the global value chain, which implies that country-specific returns are large relative to the world market portfolio when the production and services of these countries are downstream of the value chain and subject to specific shocks to these countries’ markets to a greater degree. Additionally, we found that a higher status (upstream) in the global value chain in the economic activity of an industry is correlated with lower pure industry-specific returns, which significantly decreases the magnitude of industry shocks. Thus, industry-specific returns in the lower status (downstream) of the global value chain are more vulnerable to industry shocks.

The symmetric influences of the higher value chain status on the country/industry-specific returns implies that comparatively speaking, country effects have a more important role in explaining the gains from international portfolio diversification in the upstream of global value chain while the industry effects are more important downstream, which is also mostly consistent with our above graph analysis results for the changing relative strengths of country and industry effects (It is worth noting that the relationship between global value chain status and the relatively changing roles of country and industry effects is the observed key point of our study).

We then investigated the heterogeneous impacts of Gvcpositiond_coun/Gvcpositiond_ind on the pure country- and industry-specific returns (Counb and Indr) across various country- and industry-groups before and after the U.S. subprime mortgage crisis, respectively. The results in Table 4 report that before the subprime mortgage crisis, the significant estimate of the coefficient of Gvcpositiond_coun for the developed countries was. −0.1097, which is a larger negative effect than that for the emerging market group (the corresponding coefficient estimate is −0.0149) at the 5% significance level based on the test of the difference between two groups. However, after 2007, Gvcpositiond_coun had an insignificant impact on Counb in the developed country group; in contrast, the significantly negative impact for emerging markets strengthened (It is also shown that the number of observations in Column (1) for Counb is relatively small because of the missing values in the context of our refined research sample. Nevertheless, according to existing literature, such as Acemoglu and Restrepo [34]; our results are still conceivable, especially as an augmented analysis for our primary empirical results). Meanwhile, the negative impacts of Gvcpositiond_ind on Indr for nontradable industries was always insignificant; the magnitude and significance of the coefficient estimates of Gvcpositiond_ind all rose after 2007 for the subgroup of tradable industries.

Table 4. Results of subgroup regressions regarding pure country and industry effects.

	Counb					Indr
	Before 2007		After 2007			Before 2007		After 2007
	(1)	(2)	(3)	(4)		(1)	(2)	(3)	(4)
Gvcpositiond_coun	−0.0149 ^∗∗∗(3.53e − 11)	−0.1097 ^∗∗(0.0389)	−0.0397 ^∗∗∗(0.0083)	−0.0054 (0.0041)	Gvcpositiond_ind	−0.0065 ^∗(0.0033)	−0.0024 (0.0056)	−0.0214 ^∗∗∗(0.0064)	−0.0044 (0.0024)
All country-level control variables	Yes	Yes	Yes	Yes	All industry-level control variables	Yes	Yes	Yes	Yes
County dummies	Yes	Yes	Yes	Yes	Industry dummies	Yes	Yes	Yes	Yes
Obs.	12	48	42	119	Obs.	120	64	105	56
P value of F test	≤0.01	≤0.01	≤0.01	≤0.01	P value of F test	≤0.01	≤0.01	≤0.01	≤0.01

The dependent variables are Counb and Indr. As our primary explanatory variables, Gvcpositiond_coun equals one if the value of Gvcposition_coun is greater than its median and zero otherwise; Gvcpositiond_ind equals one if the value of Gvcposition_ind is higher than its median. When the dependent variable is Counb, in Columns (1) and (3), our sample covers emerging economies; Columns (2) and (4) correspond to developed countries. When Indr is the dependent variable, the sample includes tradable industries in Columns (1) and (3) and nontradable industries in Columns (2) and (4). Fixed-effects models with Driscoll–Kraay standard errors were employed. ^∗, ^∗∗, ^∗∗∗ denote statistical significance at the 10%, 5%, and 1% levels, respectively. Corresponding standard errors are reported in parentheses.

For developed countries, the negative impact of Gvcpositiond_coun weakens considerably and conversely strengthens for emerging markets. Meanwhile, for the nontradable industries, Gvcpositiond_ind had an insignificant effect on pure industry-specific returns, while this negative impact strengthens for tradable industries. The former may reflect an increase in economic and financial integration across developed countries upstream in the value chain after the subprime mortgage crisis and the efforts of emerging markets to engage in the differentiated improvement of the production structure. The latter documents that nontradable industries tend to be more stable and are barely influenced by global fluctuations compared with tradable industries.

4. Robustness Analysis

To verify our regression results, we conducted several robustness tests. Since status in a global value chain primarily depends on the factors of resource endowment, production structure, geographical location, and historical path dependence, the reverse relationship between the explanatory variables and explained indicators may not be a serious concern. Therefore, to address the potential endogeneity problem, we implemented sensitivity analysis to omitted variables, as described in Cinelli, Ferwerda, and Hazlett [35].

The sensitivity analysis to omitted variables proposed by Cinelli, Ferwerda, and Hazlett [35] in Table 5 shows that the unadjusted coefficient estimate for Gvcpositiond_cou was −0.003 when the dependent variable is Counb and the unadjusted estimate for Gvcpositiond_ind was −0.005 when the dependent variable is Indr. Additionally, we found that even the potentially omitted variables with more than triple explanation power compared with the benchmark variables such as Counturnover or Indturnover still cannot reverse the negative signs of the estimates to influence our baseline regression results. Therefore, our results are robust because Counturnover and Indturnover, which reflect trading activities, are the relatively important influencing factors identified in the existing literature [36, 37].

Table 5. Results of sensitivity analysis to omitted variables.

	Counb	Indr
Gvcpositiond_coun	−0.0030
Gvcpositiond_ind		−0.0050

The benchmark variables used in the sensitivity analysis to omitted variables, compared to potentially unobserved confounders, are Counturnover and Indturnover corresponding to the explained variables such as Counb and Indr, respectively. Our main control variables are all included.

Second, we employed the estimation in difference-in-differences (DID) designs with multiple groups and periods as proposed by de Chaisemartin and D’Haultfoeuille [38] to confirm our main regression results, which can be used to estimate the effect of a treatment on an outcome, using group-level panel data with multiple groups and periods. In this study, the outcome variables are Counb and Indr. The group is classified by country or industry; the time period variable is calendar year. The treatment variable is Gvcpositiond_coun or Gvcpositiond_ind. With the full control variables defined as above, the estimation results are summarized in Table 6. It is shown that the parallel trends assumptions are supported because the placebo estimates for the coefficient of our explanatory variables are all positive and the 95% confidence intervals include zero. However, the estimated average treatment effects on the outcome variables are all negative at the 5% significance level.

Table 6. Estimation results of DID with multiple groups and periods.

	Counb	Confidence interval		Indr	Confidence interval
Gvcpositiond_coun	−0.0063	(−0.0112, −0.0009)	Gvcpositiond_ind	−0.0073	(−0.0138, −0.0007)
Placebo estimate	0.0031	(−0.0257, 0.0320)	Placebo estimate	0.0010	(−0.0096, 0.0116)

The DID estimators of the dynamic treatment effects and of placebo tests of the parallel trends assumption are used. The estimators are robust to heterogeneous effects and to dynamic effects. The placebo estimators compare the outcomes of those who switched for the first time and those who have not yet switched. The corresponding 95% confidence intervals are reported in parentheses. Our main control variables are all included.

Finally, because two countries/industries may have identical values of Gvcposition_coun/Gvcposition_ind while having slightly different degrees of participation in the global production value chain, the global value chain participation index for countries/industries can be defined as an alternative explanatory variable following Koopman et al. [30]. Even so, we found that our primary empirical results still hold. Additionally, to address the concern that the movements in stock prices in the information and technology industries accounted for a large part of the fluctuations in industry effects [12], we refined the research sample excluding these industries and perform our analysis again. The empirical results remain robust to this adjustment.

5. Conclusion

Previous studies have focused on the relative strength of country versus industry effects, which is of major importance to global equity portfolio managers. To identify the appropriate diversification strategy, we may need to take other considerations such as geographic factors, macroeconomic uncertainties, and market competition into account. In this study, we investigated the changing roles of country and industry effects in international portfolio diversification from the perspective of global value chain status.

Our empirical evidence shows that in the upstream of the global value chain, country effects are stronger than industry effects. In contrast, in most cases, industry effects dominate country effects in the downstream of the global value chain. For a short period during the global financial crisis, while the industry effects declined and country effects rose up downstream of the global value chain, industry effects and country effects increased overall and country effects dominated in the upstream.

Additionally, we found that the symmetric influences of the higher value chain status on the country/industry-specific returns imply that comparatively speaking, country effects have a more important role in explaining the gains from international portfolio diversification in the upstream of global value chain; meanwhile, industry effects are more important in the international diversified investments in the downstream status of global production value chain. Our empirical results are fairly robust.

Moreover, for developed countries, the negative impact of global value chain upstream status weakened considerably and, conversely, strengthened for emerging markets after the subprime mortgage crisis. The findings may reflect an increase in economic and financial integration across developed countries in the upstream value chain and the efforts of emerging markets to engage in the differentiated improvement of the production structure after the subprime mortgage crisis. Meanwhile, for nontradable industries, an upstream status in the global value chain has an insignificant effect on pure industry-specific returns, while this negative impact strengthens for tradable industries, which documents that nontradable industries tend to be more stable and are barely influenced by global fluctuations compared with tradable industries.

Our analysis has obvious implications for portfolio management. Status in the global value chain also appears to be an essential determinant of the relative roles of country and industry effects in international portfolio diversification. A high value should be placed on global asset allocations. Global equity investment management will increasingly need to take into account the changing roles and heterogeneous impacts of country and industry effects corresponding to value chain statuses in different time periods and in countries at differentiated development stages. Finally, for the future research, further investigations on whether the changing roles of country and industry effects in international portfolio diversification would be confined or manifested in other turmoil periods, such as in the COVID-19 era, can be an interesting future agenda.

Additional Points

AI-Software Usage Statement. The authors declare that no AI-software was used to prepare our manuscript.

Disclosure

All errors remain the authors’ responsibility.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

We greatly appreciate the enlightenment, comments, and suggestions given by Kong-lin Ke, Wei Jing, Maoyong Cheng, Rui Li, and the seminar participants at the School of Economics and Finance of Xi’an Jiaotong University. Financial support from the research funding entitled “Research on Industrial Agglomeration and Upgrading of Taizhou Small and Micro Enterprises Based on Financial and Credit Big Data” is gratefully acknowledged.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Grinold R., Rudd A., and Stefek D., Global factors: fact or fiction?, Journal of Portfolio Management. (1989) 16, no. 1, 79–89.
10.3905/jpm.1989.409232
Web of Science® Google Scholar
2 Heston S. L. and Rouwenhorst K. G., Industry and country effects in international stock returns, Journal of Portfolio Management. (1995) 21, no. 3, 53–58, https://doi.org/10.3905/jpm.1995.409523.
10.3905/jpm.1995.409523
Web of Science® Google Scholar
3 Rouwenhorst K. G., European equity markets and the EMU, Financial Analysts Journal. (1999) 55, no. 3, 57–64, https://doi.org/10.2469/faj.v55.n3.2272.
10.2469/faj.v55.n3.2272
Google Scholar
4 Cavaglia S., Brightman C., and Aked M., The increasing importance of industry factors, Financial Analysts Journal. (2000) 56, no. 5, 41–54, https://doi.org/10.2469/faj.v56.n5.2389, 2-s2.0-0002078352.
10.2469/faj.v56.n5.2389
Google Scholar
5 Marcelo J. L. M., Quirós J. L. M., and Martins J. L., The role of country and industry factors during volatile times, Journal of International Financial Markets, Institutions and Money. (2013) 26, 273–290, https://doi.org/10.1016/j.intfin.2013.06.005, 2-s2.0-84881243898.
10.1016/j.intfin.2013.06.005
Web of Science® Google Scholar
6 Campa J. M. and Fernandes N., Sources of gains from international portfolio diversification, Journal of Empirical Finance. (2006) 13, no. 4-5, 417–443, https://doi.org/10.1016/j.jempfin.2006.01.001, 2-s2.0-33747338725.
10.1016/j.jempfin.2006.01.001
Google Scholar
7 Drummen M. and Zimmermann H., The structure of European stock returns, Financial Analysts Journal. (1992) 48, no. 4, 15–26, https://doi.org/10.2469/faj.v48.n4.15.
10.2469/faj.v48.n4.15
Google Scholar
8 Beckers S., Connor G., and Curds R., National versus global influences on equity returns, Financial Analysts Journal. (1996) 52, no. 2, 31–39, https://doi.org/10.2469/faj.v52.n2.1978, 2-s2.0-0002918409.
10.2469/faj.v52.n2.1978
Google Scholar
9 Kuo W. and E Satchell S., Global equity styles and industry effects: the pre-eminence of value relative to size, Journal of International Financial Markets, Institutions and Money. (2001) 11, no. 1, 1–28, https://doi.org/10.1016/s1042-4431(00)00033-0, 2-s2.0-0011372690.
10.1016/S1042-4431(00)00033-0
Google Scholar
10 Baca S. P., Garbe B. L., and Weiss R. A., The rise of sector effects in major equity markets, Financial Analysts Journal. (2000) 56, no. 5, 34–40, https://doi.org/10.2469/faj.v56.n5.2388, 2-s2.0-0002727182.
10.2469/faj.v56.n5.2388
Google Scholar
11 Galati G. and Tsatsaronis K., The impact of the Euro on Europe’s financial markets, Financial Markets, Institutions & Instruments. (2003) 12, no. 3, 165–222, https://doi.org/10.1111/1468-0416.00064, 2-s2.0-0142219307.
10.1111/1468-0416.00064
Google Scholar
12 Brooks R. and Del Negro M., A Latent Factor Model with Global, Country, and Industry Shocks for International Stock Returns, 2005, International Monetary Fund Working Paper.
Google Scholar
13 Bai Y. and Green C. J., International diversification strategies: revisited from the risk perspective, Journal of Banking & Finance. (2010) 34, no. 1, 236–245, https://doi.org/10.1016/j.jbankfin.2009.07.026, 2-s2.0-70350216018.
10.1016/j.jbankfin.2009.07.026
Web of Science® Google Scholar
14 Isakov D. and Sonney F., Are practitioners right? On the relative importance of industrial factors in international stock returns, Journal of Economics and Statistics. (2004) 140, no. 3, 355–379.
Google Scholar
15 Ferreira M. A. and Ferreira M. A., The importance of industry and country effects in the EMU equity markets, European Financial Management. (2006) 12, no. 3, 341–373, https://doi.org/10.1111/j.1354-7798.2006.00324.x, 2-s2.0-33845772435.
10.1111/j.1354-7798.2006.00324.x
Web of Science® Google Scholar
16 Serra A. P., Country and industry factors in returns: evidence from emerging markets’ stocks, Emerging Markets Review. (2000) 1, no. 2, 127–151, https://doi.org/10.1016/s1566-0141(00)00007-8, 2-s2.0-0034259686.
10.1016/S1566-0141(00)00007-8
Google Scholar
17 Chen J., Bennett A., and Zheng T., Sector effects in developed vs. emerging markets, Financial Analysts Journal. (2006) 62, no. 6, 40–51, https://doi.org/10.2469/faj.v62.n6.4352, 2-s2.0-33845805694.
10.2469/faj.v62.n6.4352
PubMed Web of Science® Google Scholar
18 Bhargava V., Dania A., and Malhotra D. K., Industry effects and volatility transmission in portfolio diversification, Journal of Asset Management. (2012) 13, no. 1, 22–33, https://doi.org/10.1057/jam.2011.17, 2-s2.0-84855481529.
10.1057/jam.2011.17
Google Scholar
19 Ali F., Sensoy A., and Goodell J. W., Identifying diversifiers, hedges, and safe havens among Asia Pacific equity markets during COVID-19: new results for ongoing portfolio allocation, International Review of Economics & Finance. (2023) 85, 744–792, https://doi.org/10.1016/j.iref.2023.02.015.
10.1016/j.iref.2023.02.015
Web of Science® Google Scholar
20 Lin S. M. and Dinh H. L., Value chain transition in east Asian production network, Journal of International Logistics And Trade. (2015) 13, no. 3, 7–42, https://doi.org/10.24006/jilt.2015.13.3.002.
10.24006/jilt.2015.13.3.7
Google Scholar
21 Porter M., Competitive Advantage, 1985, The Free Press, New York, NY, USA.
Google Scholar
22 Timmer M. P., Erumban A. A., Los B., Stehrer R., and de Vries G. J., Slicing up global value chains, The Journal of Economic Perspectives. (2014) 28, no. 2, 99–118, https://doi.org/10.1257/jep.28.2.99, 2-s2.0-84903120036.
10.1257/jep.28.2.99
Web of Science® Google Scholar
23 Kwon T. and Ryou J., Global value chains of east Asia: trade in value added and vertical specialization, Asian Economic Journal. (2015) 29, no. 2, 121–143, https://doi.org/10.1111/asej.12051, 2-s2.0-84931839175.
10.1111/asej.12051
Web of Science® Google Scholar
24 Chen Y., Intra-industry fragmentation: bilateral value added in electronics exports, Economics Letters. (2016) 138, 22–25, https://doi.org/10.1016/j.econlet.2015.11.015, 2-s2.0-84949257303.
10.1016/j.econlet.2015.11.015
Web of Science® Google Scholar
25 Miroudot S. and Ye M., Multinational production in value-added terms, Economic Systems Research. (2019) 32, no. 3, 395–412, https://doi.org/10.1080/09535314.2019.1701997.
10.1080/09535314.2019.1701997
Web of Science® Google Scholar
26 Sone E. and Ko J. H., Global value chain of Korea’s automobile industry in the global economy, Korea International Trade Research Institute. (2020) 16, no. 5, 1–17, https://doi.org/10.16980/jitc.16.5.202010.1.
10.16980/jitc.16.5.202010.1
Google Scholar
27 Baldwin R. and Lopez-Gonzalez J., Supply-chain trade: a portrait of global patterns and several testable hypotheses, CEPR Discussion Paper 9421. (2013) .
Google Scholar
28 Phylaktis K. and Xia L., The changing roles of industry and country effects in the global equity markets, The European Journal of Finance. (2006) 12, no. 8, 627–648, https://doi.org/10.1080/13518470500460202, 2-s2.0-33845199429.
10.1080/13518470500460202
Google Scholar
29 Menchero J. and Morozov A., The Relative Strengths of Industry and Country Factors in Global Equity Markets, 2011, Social Science Electronic Publishing, https://ssrn.com/abstract=1915233.
Google Scholar
30 Koopman R., Powers W., Wang Z., and Wei S. J., Give Credit where Credit Is Due: Tracing Value Added in Global Production Chains, 2010, National Bureau of Economic Research.
10.3386/w16426
Google Scholar
31 Wang Z., Wei S. J., and Zhu K., Quantifying International Production Sharing at the Bilateral and Sector Levels, 2013, National Bureau of Economic Research.
10.3386/w19677
Google Scholar
32 Timmer M. P., Dietzenbacher E., Los B., Stehrer R., and de Vries G. J., An illustrated user guide to the world input–output database: the case of global automotive production, Review of International Economics. (2015) 23, no. 3, 575–605, https://doi.org/10.1111/roie.12178, 2-s2.0-84937163467.
10.1111/roie.12178
Web of Science® Google Scholar
33 Chong T. T. L., Hooy C. W., and Lee M. H., The sources of country and industry variations in ASEAN stock returns, MPRA Paper 80574. (2013) University Library of Munich, Germany.
Google Scholar
34 Acemoglu D. and Restrepo P., Demographics and automation, The Review of Economic Studies. (2022) 89, no. 1, 1–44, https://doi.org/10.1093/restud/rdab031.
10.1093/restud/rdab031
Web of Science® Google Scholar
35 Cinelli C., Ferwerda J., and Hazlett C., SENSEMAKR: stata module to provide sensitivity tools for OLS, Statistical Software Components. (2020) S458773.
Google Scholar
36 Easley D. and O′Hara M., Price, trade size, and information in securities markets, Journal of Financial Economics. (1987) 19, no. 1, 69–90, https://doi.org/10.1016/0304-405x(87)90029-8, 2-s2.0-0010940821.
10.1016/0304-405X(87)90029-8
Web of Science® Google Scholar
37 Stoll H., Presidential address: friction, The Journal of Finance. (2000) 55, no. 4, 1479–1514, https://doi.org/10.1111/0022-1082.00259.
10.1111/0022-1082.00259
Web of Science® Google Scholar
38 de Chaisemartin C. and D′Haultfoeuille X., Two-way fixed effects estimators with heterogeneous treatment effects, The American Economic Review. (2020) 110, no. 9, 2964–2996, https://doi.org/10.1257/aer.20181169.
10.1257/aer.20181169
Web of Science® Google Scholar

All articles

Global Value Chain and the Changing Roles of Country and Industry Effects in International Portfolio Diversification

Abstract

1. Introduction