Volume 2024, Issue 1 5517265

Research Article

Open Access

Global Fixed-Time Stability of General Stochastic Nonlinear Systems

Liandi Fang,

Liandi Fang

orcid.org/0000-0001-8347-791X

College of Mathematics and Computer Science , Tongling University , Tongling , 244061 , China , tlc.edu.cn

Search for more papers by this author

Daohong Zhu,

Corresponding Author

Daohong Zhu

[email protected]

orcid.org/0009-0008-9447-1079

Anhui Engineering Research Center of Intelligent Manufacturing of Copper-based Materials , Tongling University , Tongling , 244061 , China , tlc.edu.cn

Search for more papers by this author

Zhenzhen Long,

Zhenzhen Long

orcid.org/0009-0003-2322-4875

School of Mathematics and Statistics , Anhui Normal University , Wuhu , 241005 , China , ahnu.edu.cn

Search for more papers by this author

Liandi Fang,

Liandi Fang

orcid.org/0000-0001-8347-791X

College of Mathematics and Computer Science , Tongling University , Tongling , 244061 , China , tlc.edu.cn

Search for more papers by this author

Daohong Zhu,

Corresponding Author

Daohong Zhu

[email protected]

orcid.org/0009-0008-9447-1079

Anhui Engineering Research Center of Intelligent Manufacturing of Copper-based Materials , Tongling University , Tongling , 244061 , China , tlc.edu.cn

Search for more papers by this author

Zhenzhen Long,

Zhenzhen Long

orcid.org/0009-0003-2322-4875

School of Mathematics and Statistics , Anhui Normal University , Wuhu , 241005 , China , ahnu.edu.cn

Search for more papers by this author

First published: 16 August 2024

https://doi.org/10.1155/2024/5517265

Academic Editor: Chih Chiang Chen

Share a link

Email
Wechat
Bluesky

Abstract

In this article, the fixed-time stabilization issue is investigated for a kind of general p-norm stochastic nonlinear systems. The feature of the considered systems is that all powers are any positive rational numbers, which means this type of systems includes many previously considered systems. Firstly, a higher accurate upper bounded estimation of settling time is given by applying an ingenious variable transformation and the definition of Gamma function, thereby obtaining an improved stochastic fixed-time stability theorem. Then a continuous state-feedback controller is designed for the general p-norm stochastic systems by using the adding a power integrator method, and the designed controller is proved to ensure the fixed-time stability of the considered systems in light of stochastic fixed-time stability theorem. Finally, numerical simulation results of fixed-time stabilizer and finite-time stabilizer indicate the effectiveness of the developed scheme.

1. Introduction

Because of faster convergence, higher accuracy, and better robustness [1, 2], the finite-time stability of nonlinear systems has attracted a matter of great concern. Compared to deterministic nonlinear systems, finite-time stabilization problems of stochastic nonlinear systems were considered relatively later. Reference [3] first proposed a clear definition of finite-time stable in probability and established stochastic Lyapunov finite-time stability theorem. After that, many problems of finite-time stability/control have been addressed for various stochastic nonlinear systems. References [4, 5] have, respectively, investigated the characteristics of stochastic finite-time stability and the design of finite-time output-feedback stabilizing controller for stochastic nonlinear systems. The finite-time stabilization has been studied for switched and hybrid stochastic nonlinear systems in [6–8], successively. Notably, the upper bounded estimation of the settling time in finite-time convergence relies on the initial state. However, the initial conditions are usually unknown or not easily gained firsthand for many real systems. This implies that the practical applications of finite-time stability may be limited.

To overcome above obstacle, the fixed-time stability theorem was established [9], which shows that the upper bounded estimation of settling time would become independent of the initial condition. Subsequently, the fixed-time stabilization/control of various deterministic nonlinear systems has been studied in [10–16]. More specifically, references [10, 11] have considered fixed-time stabilization/tracking control for nonholonomic systems and multiagent ones, while fixed-time stabilization or HOSM controller has been addressed for output-constrained nonlinear systems and sliding mode systems in [12–14]. Whereas, the theorem about fixed-time stable in probability was just reported in [17] recent year. Subsequently, references [18, 19] have, respectively, investigated the fixed-time stability for switched stochastic nonlinear systems and stochastic multiagent ones. References [15, 16, 20] have provided new fixed-time Lyapunov criteria or improved methods for estimating the upper bounded function of the settling time in fixed-time convergence. But in contrast to deterministic nonlinear systems, the studies on fixed-time stability of stochastic nonlinear systems are still inadequate and not deep. Moreover, although having nothing with the initial condition, the upper estimation of settling time proposed in existing results yet may be relatively conservative owing to overamplification.

On the other hands, the p-norm stochastic nonlinear systems have attracted great attention because of their more general form and wilder application of which can model many complex systems, for instant the underactuated and weakly coupled mechanical system [21, 22]. For a class of p-norm stochastic nonlinear systems with powers being equal to or greater than 1 (called as stochastic high-order nonlinear systems), references [23–26] have investigated asymptotic/finite-time stabilization issues based on state feedback and output feedback. Meanwhile, the finite-time stabilizers have been developed for a kind of p-norm stochastic nonlinear systems, called as stochastic low-order nonlinear systems, every power of which is equal to or less than 1 [27–29]. Reference [30] has addressed finite-time stability of p-norm stochastic systems in a general form, in which every power is any positive odd rational numbers. In the aforementioned systems, the powers however are either only high-order or only low-order positive odd rational numbers. Two questions naturally arise. (i) Can the restriction on the powers of the p-norm system be further relaxed? (ii) The issue of fixed-time stability of p-norm stochastic systems is not considered and still open. How to arrive the fixed-time stability for p-norm stochastic nonlinear systems?

Motivated by above analyses, this note will find a higher accurate upper estimation of the settling time and consider the fixed-time stabilization issue for kinds of p-norm stochastic nonlinear systems in a more general form. The main contributions of this paper can be summarized as follows:

(i)
Applying a subtle variable substitution and the properties of Gamma/Beta functions, one finds a higher accurate upper estimation of the settling time, which is less than the values in [17, 18]. On this basis, a corollary is provided for the stochastic fixed-time stability theorem.
(ii)
The considered systems are more general than the systems in [23–30]. Significantly, the powers of the systems considered by references [23–30] are either only high-order positive odd rational numbers or only low-order positive ones. Specifically, the powers of systems in [23–26] are positive odd rational numbers and equal to or greater than 1, while the powers of systems in [27–29] are equal to or less than 1. Reference [30] has relaxed the restriction on the powers, which were required to be any positive odd rational numbers. Oppositely, all powers of the considered systems in this paper are any positive rational numbers, which can be any ratios of arbitrary positive odd or even numbers. In other words, the system considered here includes all the systems mentioned above. Meanwhile, a weaker restriction on system nonlinearities is provided and an appropriate Lyapunov function is presented.
(iii)
The global fixed-time stability is studied for the more general p-norm stochastic nonlinear systems based on the improved stochastic fixed-time stability theorem for the first time.

2. Preliminaries

Consider the following stochastic systems:

(1)

where x ∈ Rⁿ and ω, respectively, represent the system state and an m-dimension Brownian motion process on (Ω, F, P) and g(x) and φ(x) denote continuous system functions with g(0) = 0 and φ(0) = 0.

Some definitions and lemmas are provided in the following for preliminaries.

Definition 1 (see [4].)For any provided W(x) ∈ C²(Rⁿ) of system (1), the second-order differential operator is defined as

(2)

Definition 2 (see [17].)For system (1), the origin x = 0 of system (1) is allowed to be globally fixed-time stable in probability, if the following two conditions are addressed: (i) for ∀x₀ ∈ Rⁿ, the origin is globally finite-time stable in probability; (ii) the settling time function T(x₀, ω) satisfies , where is a constant independent of initial conditions.

Lemma 3 (see [17].)For system (1), if there is a positive definite and radially unbounded Lyapunov function W(x) ∈ C²(Rⁿ) and positive real numbers λ, μ, α ∈ (1, +∞), and γ ∈ (0, 1), such that

(3)

then the origin of system (1) is globally fixed-time stable in probability, and the settling time T(x₀, ω) fulfills

(4)

Lemma 4 (see [12].)For ∀ m > 0 and variables Z_j ∈ R, j = 1, …, N, one gets

(5)

with C = max{1, N^m−1}.

Lemma 5 (see [12].)Let m₁, m₂ ∈ R⁺ with m₁ ≥ 1. For any variables Z₁, Z₂ ∈ R, one has

(6)

where

Lemma 6 (see [26].)For any constants ϱ₁ > 0, ϱ₂ > 0 and variables Z₁, Z₂ ∈ R, one has

(7)

3. Main Results

3.1. Problem Description

In this paper, we consider a class of p-norm stochastic nonlinear systems described as

(8)

where

and ω are defined as system (1) and u ∈ R denotes control input; for i = 1, …, n,

, the nonlinearities g_i : Rⁱ⟶R and φ_i : Rⁱ⟶R^m are continuous and satisfy g_i(0) = 0 and φ_i(0) = 0, and every fractional power q_i ∈ R⁺.

Note that the fractional powers q_i’s can take any positive real numbers, which indicates systems (8) contain all previously considered p-norm systems. For example, if q_i’s are ratios of any two positive odd real numbers and satisfy q_i ≥ 1, then systems (8) become high-order p-norm nonlinear systems. In other words, systems (8) can be regarded as a generalized p-norm stochastic nonlinear system.

Assumption 7. For ∀k = 1, …, n, there exist known smooth functions and such that

(9)

where s₁ = 1, s_k ≥ 1, θ ∈ (0, 1), and (q_k/^sk + 1) = θ + (1/^sk) − 1.

Remark 8. Of note, all of q_i’s in system (8) are ratios of any positive real numbers, which means q_i’s not only can take both odd and even rational numbers but also can be equal to or greater than or less than 1. In other words, system (8) is a more general class of p-norm systems than the considered p-norm systems with q_i ≥ 1 in [23–26] and the ones with q_i ≤ 1 in [27–29]. Besides, condition (9) is originated from reference [30]. Nevertheless, reference [30] has just considered the case of q_i taking any odd rational numbers and the finite-time stability.

Now, this paper aims to find a higher accurate upper bounded estimation of the settling time and then construct a state-feedback controller to enable that the origin of system (8) is globally fixed-time stable in probability.

3.2. A Corollary

Definition 9 (see [31].)Let c > 0; then a Gamma function Γ(c) is defined as follows:

(10)

Definition 10 (see [32].)Let a > 0, b > 0; then a Beta function B(a, b) is defined as follows:

(11)

Now, we will provide a corollary of Lemma 3 in the following.

Corollary 11. For system (1), if there exists a positive definite and radially unbounded Lyapunov function W(x) ∈ C²(Rⁿ) and real numbers λ > 0, μ > 0, α ∈ (1, +∞), and γ ∈ (0, 1), such that

(12)

then the origin of system (1) is globally fixed-time stable in probability, and the settling time T(x₀, ω) fulfills

(13)

Proof. Let ; then it is easy to get W = (μ/λ((1/z) − 1))^{(1/γ − α)} and dW = ((μ/λ)^{(1/γ − α)}/Z²(α − γ))((1/z) − 1)^{((1/γ − α) − 1)}dZ. For ∀0 < ε < +∞, we can deduce

(14)

Since (1 − γ/α − γ) − 1 = −(α − 1/α − γ), (α − 1/α − γ) = −(1 − γ/γ − α) and (1 − γ/α − γ) + (α − 1/α − γ) = 1, it can be deduced from Definitions 9 and 10 that

(15)

In light of equations (14) and (15), equation (13) is proved.

Remark 12. Notably, Lemma 3 from [17] has shown the settling time [T(x₀, ω) satisfying , while [T(x₀, ω) in [15] satisfies . To get higher accurate estimation of settling time, one should choose a suitable estimation method. Unlike the estimating methods in [15, 17], both of which are simultaneously amplifying integral intervals and integrand, we only amplify integral intervals but keep integrable function unchanged in the proof of Corollary 11. Applying an ingenious variable transformation and the definitions of Gamma/Beta functions, we obtain a higher accurate upper-bounded estimation of the settling time. It is obvious to gain and .

3.3. Controller Design

In this part, one will apply the adding a power integrator method to explicitly construct a continuous state-feedback controller.

Step 1. Let , where the constant σ is taken as 0 < σ ≤ 1/2. Define the Lyapunov function W₁(x₁) as

(16)

Apparently, W₁(x₁) is positive definite and C².

Using Definition 1 and Assumption 7, we can directly obtain

(17)

where the function

is a smooth one.

Then, one can design the virtual variable η₂ as

(18)

where

, λ₁ ≥ 0, μ₁ ≥ 0, and τ ≥ 0 are constant parameters to be selected later.

Substituting (18) into (17) yields

(19)

Step k (2 ≤ k ≤ n − 1). Suppose at step k − 1, one finds a C² and positive definite Lyapunov function and constructs k virtual control variables η₁, η₂, …, η_k as

(20)

with

, such that

(21)

Then, a proposition can be provided in the following.

Proposition 13. Select the Lyapunov function as with

(22)

Thus, is C² and positive definite. Then, there exists a virtual controller such that

(23)

where

with the smooth function

The proof of above proposition will be given in Appendix.

Step n. Let x_n+1 = u. According to above steps, the overall Lyapunov function W_n(x) can be defined as

(24)

with

(25)

and the last virtual variable η_n+1 is constructed as

(26)

where

. Then one easily gains

(27)

Hence, the actual controller can be naturally designed as

(28)

which yields

(29)

Heretofore, the actual controller is completely established for system (8).

3.4. Stability Analysis

Firstly, we provide a theorem to display the main results of this note.

Theorem 14. Suppose system (8) fulfills Assumption 7; then the designed actual controller (28) with virtual ones (20) can guarantee that the origin of system (8) is globally fixed-time stable in probability.

Proof. In light of the expression of W_n(x), one can easily get that W_n(x) is positive definite and radially unbounded. Further, using the integral mean value theorem and Lemma 5 infers that

(30)

for all k = 1, …, n, where 0 < δ = σ(1 − θ) < 1.

Then, one gains

(31)

Here, we choose the constant parameter τ > δ, and it is clear that 0 < (4/4 + δ) < 1 and (4+τ)/(4 + δ) > 1. Therefore, one obtains from (31) and Lemma 4 that

(32)

(33)

In view of equations (29), (32), and (33), it is easy to get

(34)

Now, let λ = 2^{(−4/4 + δ)}λ₁ > 0, μ = 2^{(−4 − τ/4 + δ)}n^{(δ − τ/4 + δ)}μ₁ > 0, 0 < γ = (4/4 + δ) < 1, and α = (4+τ)/(4+δ) > 1. According to (34), one has

(35)

Thus, we can conclude from (35) and Lemma 3 that controller (28) can make the origin of system (8) globally fixed-time stable in probability.

From Corollary 11, one can get that the settling time T(x₀, ω) satisfies

(36)

with

(37)

Remark 15. Compared to the finite-time stabilizers of p-norm stochastic nonlinear systems in references [25–30], we design fixed-time stabilizers by adding a function into the controller gain in this paper. Because of this, the designed fixed-time controller guarantees that the system converges to the equilibrium point at a faster speed than the convergence rate under the finite-time controller. At the same time, we can obtain the upper estimation of settling time independent of initial conditions.

4. Simulation

To illustrate the application of Theorem 14, the following stochastic nonlinear system is considered:

(38)

Clearly, q₁ = (8/9) < 1, q₂ = (9/7) > 1, g₁(x₁) = φ₁(x₁) = 0, , and .

Choose s₁ = 1 and θ = 2/3. Then, it can be obtained that s₂ = q₁/θ = 4/3, s₃ = (q₂/(θ + 1/s₂ − 1)) = 108/35. Further, one gets q₂s₁/s₃ = 5/12, s₁/2s₃(q₂ + (s₃/s₂)) = 17/24, s₂/2s₃(q₂ + (s₃/s₂)) = 7/9. Consequently, it is easy to deduce and , which means that Assumption 7 holds with ϕ₁(x₁) = ψ₁(x₁) = 0, and . We select σ = 1/2. According to design process, one defines and constructs the virtual variable . Furthermore, define .

Apparently, controller u of system (38) can be designed as

(39)

We can select constant parameters as τ = 1, λ₁ = 1, μ₁ = 1. Two initial values are chosen arbitrarily, that is, x₀ = (1, 2)^T and x₀ = (15, 30)^T, respectively. Figures 1 and 2 indicate the curves of x(t) with different initial conditions under controller (39). From Figures 1 and 2, one also can easily observe that system (38) under controller (39) always is fixed-time stable with the different initial states and the stochastic settling time function fulfills T(x₀, ω) ≤ 2.3 for every given initial value x₀. Meanwhile, calculating by Matlab can render

(40)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Trajectory of x(t) with x₀ = (1, 2)^T under fixed-time controller.

Besides, we can calculate

, that is,

(41)

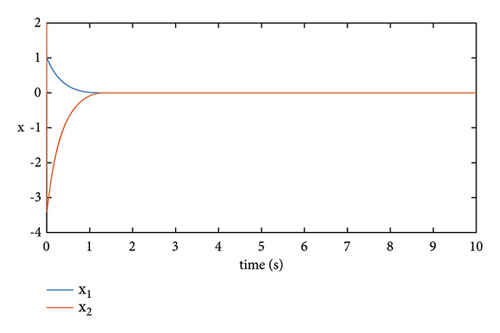
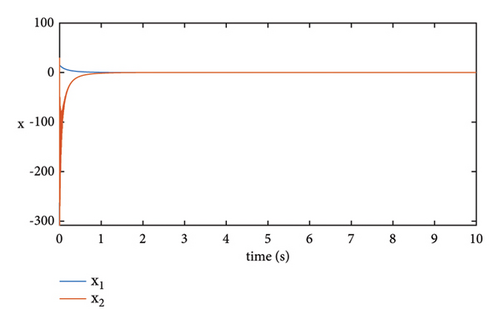
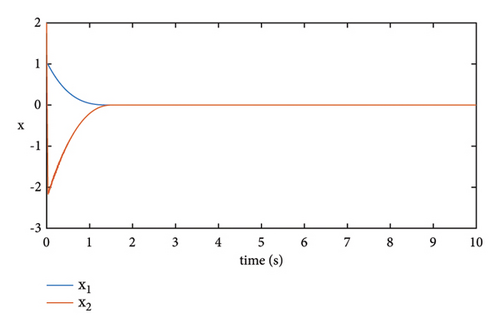
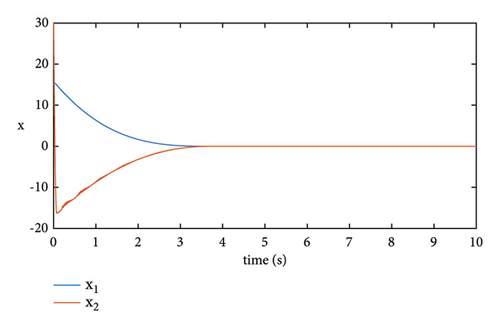
On the other hand, we note that controller (39) would become a finite-time stabilizer if μ₁ = 0. To compare fixed-time stability with finite-time stability, we also present Figures 3 and 4 to show the simulation result of system (38) under the finite-time stabilizing controller. From the two figures, we can find the finite-time stabilizing controller is effective, too. However, the fixed-time stabilizing controller not only can ensure independence between the upper hound estimation of the settling time and initial conditions but also can provide faster convergence rate than the finite-time one. Thus, the results of simulating demonstrate the validity of the presented scheme.

5. Conclusion

The problem on fixed-time stability is addressed for kinds of more general p-norm stochastic nonlinear systems, in which all powers are any positive rational numbers, instead of only odd numbers. Firstly, a subtle variable substitution is defined, and the Gamma function is next applied to amplify the integral and derive the upper bounder. Unlike the previous method, our technique performs only one amplification, which can derive a higher accurate upper bounded estimation of the settling time. Then a new theorem of fixed-time stable in probability is provided. Based on the new theorem, one has developed the fixed-time stabilizing control strategy for the general p-norm stochastic nonlinear systems. Then, both the mathematical analysis and simulation results illustrate the effectiveness of the developed strategy.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (62103306) and Scientific Research Project of Anhui Higher Education Institutions (2022AH020094 and 2023AH051661). Talent Research Launch Fund Project of Tongling University (2023tlxyrc40) also supported this work.

Appendix

Proof of Proposition 13. In view of equation (22), one can get

(A.1)

for i, j = 1, …, k − 1.

Furthermore, we can infer from Definition 1 and equations (21) and (22) that

(A.2)

where

In what follows, the upper bounded estimations of every right-hand side in (A.2) will be provided. To this end, one gives four subpropositions.

Proposition 16. There are smooth functions , such that

(A.3)

(A.4)

Proof. It is obviously easy to get

(A.5)

for j = 2, …, k.

Thus,

(A.6)

where

and

are smooth functions satisfying

(A.7)

and

(A.8)

Proposition 17. There is a constant D_k1 ≥ 0 such that

(A.9)

Proof. Since q_k−1σ/s_k ≤ 1, by Lemma 5, we have

(A.10)

By using (A.10) and Lemma 6, one can easily derive

(A.11)

with D_k1 ≥ 0 being a constant. Clearly, equation (A.9) is obtained.

Proposition 18. There is a smooth function D_k2(⋅) ≥ 0 such that

(A.12)

Proof. Using Proposition 16 and Lemma 6, one easily obtains that

(A.13)

where

is a nonnegative and smooth function.

Proposition 19. There is a smooth function D_k3(⋅) ≥ 0 such that

(A.14)

Proof. As stated in [12], any continuous function has at least a smooth upper bound. Thus, for ∀j = 1, …, k − 1, there exist smooth functions and , such that

(A.15)

By Lemma 5, one has

(A.16)

Since q_jσ/^sj + 1 = (θ + (1/^sj) − 1)σ and q_kσ/s_k+1 = (θ + (1/^sk) − 1)σ, it follows from (A.15) and (A.16) that

(A.17)

with

being a nonnegative and smooth function.

Letting can render equation (A.14) directly.

Proposition 20. There is a smooth function D_k4(⋅) ≥ 0 such that

(A.18)

Proof. Note that

(A.19)

First of all, it is not difficult to get

(A.20)

where

is a nonnegative and smooth function. Combining above equation with Proposition 16 and Lemma 6 results in

(A.21)

where

is a nonnegative and smooth function. Clearly, we have

(A.22)

where

Secondly, if i ≠ j and i < j, one can derive that

(A.23)

where

and

are nonnegative and smooth functions. According to symmetry of x_i and x_j, equation (A.23) still holds while i ≠ j and i > j.

Hence, for ∀1 ≤ i ≠ j ≤ k − 1, utilizing equations (A.15) and (A.23) and Lemma 6 can draw that

(A.24)

where

is a nonnegative and smooth function.

Then, one has

(A.25)

where

. In almost the same way as inferring (A.25), applying (A.15), Proposition 16, and Lemma 6, we get

(A.26)

(A.27)

where

and

are nonnegative and smooth functions.

Let , Substituting (A.22) and (A.25)–(A.27) into (A.19) yields (A.18) directly.

Combining Propositions 16–20 with (A.2) indicates that

(A.28)

where function

is smooth.

According to (A.28), one constructs the virtual variable η_k+1 as

(A.29)

with

Then, substituting (A.29) into (A.28) renders

(A.30)

Hence, we can gain that equations (A.29) and (A.30) hold for all k = 2, 3, …, n. That is, Proposition 13 has been well proved.

Open Research

Data Availability

No data were used to support this study.

References

1 Jiang M., Xie X., and Zhang K., Finite-time stabilization of stochastic high-order nonlinear systems with FT-SISS inverse dynamics, IEEE Transactions on Automatic Control. (2019) 64, no. 1, 313–320, https://doi.org/10.1109/tac.2018.2827993, 2-s2.0-85045740684.
10.1109/TAC.2018.2827993
Web of Science® Google Scholar
2 Ma L., Cheng C., Guo J., Shi B., Ding S., and Mei K., Direct yaw-moment control of electric vehicles based on adaptive sliding mode, Mathematical Biosciences and Engineering. (2023) 20, no. 7, 13334–13355, https://doi.org/10.3934/mbe.2023594.
10.3934/mbe.2023594
PubMed Web of Science® Google Scholar
3 Yin J., Khoo S., Man Z., and Yu X., Finite-time stability and instability of stochastic nonlinear systems, Automatica. (2011) 47, no. 12, 2671–2677, https://doi.org/10.1016/j.automatica.2011.08.050, 2-s2.0-81155139623.
10.1016/j.automatica.2011.08.050
Web of Science® Google Scholar
4 Khoo S. Y., Yin J. L., Man Z., and Yu X., Finite-time stabilization of stochastic nonlinear systems in strict-feedback form, Automatica. (2013) 49, no. 5, 1403–1410, https://doi.org/10.1016/j.automatica.2013.01.054, 2-s2.0-84876682872.
10.1016/j.automatica.2013.01.054
Web of Science® Google Scholar
5 Zha W., Zhai J., Fei S., and Wang Y., Finite-time stabilization for a class of stochastic nonlinear systems via output feedback, ISA Transactions. (2014) 53, no. 3, 709–716, https://doi.org/10.1016/j.isatra.2014.01.005, 2-s2.0-84899649820.
10.1016/j.isatra.2014.01.005
PubMed Web of Science® Google Scholar
6 Huang S. and Xiang Z., Finite-time stabilization of switched stochastic nonlinear systems with mixed odd and even powers, Automatica. (2016) 73, 130–137, https://doi.org/10.1016/j.automatica.2016.06.023, 2-s2.0-84986573180.
10.1016/j.automatica.2016.06.023
Web of Science® Google Scholar
7 Song Z. and Zhai J., Global finite-time stabilization for switched stochastic nonlinear systems via output feedback, Journal of the Franklin Institute. (2019) 356, no. 3, 1379–1395, https://doi.org/10.1016/j.jfranklin.2018.12.004, 2-s2.0-85059162772.
10.1016/j.jfranklin.2018.12.004
Google Scholar
8 Zhong S., Zhang W., and Jiang X., Finite-time stability and asynchronous H∞Finite-time stability and asynchronous H∞ control for highly nonlinear hybrid stochastic systemscontrol for highly nonlinear hybrid stochastic systems, Information Sciences. (2023) 637, https://doi.org/10.1016/j.ins.2023.118985, 118985.
10.1016/j.ins.2023.118985
Google Scholar
9 Polyakov A., Nonlinear feedback design for fixed-time stabilization of linear control systems, IEEE Transactions on Automatic Control. (2012) 57, no. 8, 2106–2110, https://doi.org/10.1109/tac.2011.2179869, 2-s2.0-84864747003.
10.1109/TAC.2011.2179869
Web of Science® Google Scholar
10 Defoort M., Demesure G., Zuo Z., Polyakov A., and Djemai M., Fixed-time stabilisation and consensus of non-holonomic systems, IET Control Theory and Applications. (2016) 10, no. 18, 2497–2505, https://doi.org/10.1049/iet-cta.2016.0094, 2-s2.0-85006736354.
10.1049/iet-cta.2016.0094
Web of Science® Google Scholar
11 Fu J. and Wang J., Fixed-time coordinated tracking for second-order multi-agent systems with bounded input uncertainties, Systems and Control Letters. (2016) 93, 1–12, https://doi.org/10.1016/j.sysconle.2016.03.006, 2-s2.0-84962393990.
10.1016/j.sysconle.2016.03.006
Web of Science® Google Scholar
12 Chen C. and Sun Z., Fixed-time stabilization of high-order nonlinear systems with an asymmetric output constraint, Nonlinear Dynamics. (2023) 111, no. 1, 319–339, https://doi.org/10.1007/s11071-022-07839-z.
10.1007/s11071-022-07839-z
Google Scholar
13 Mei K. and Ding S., Fixed-time HOSM controller design for constrained sliding mode systems with mismatched terms, Information Sciences. (2022) 585, 366–381, https://doi.org/10.1016/j.ins.2021.11.032.
10.1016/j.ins.2021.11.032
Web of Science® Google Scholar
14 Ma L., Mei K., Ding S., and Pan T., Design of adaptive fuzzy fixed-time HOSM controller subject to asymmetric output constraints, IEEE Transactions on Fuzzy Systems. (2023) 31, no. 9, 2989–2999, https://doi.org/10.1109/tfuzz.2023.3241147.
10.1109/TFUZZ.2023.3241147
Web of Science® Google Scholar
15 Min H., Xu S., Zhang B., Ma Q., and Yuan D., Fixed-time Lyapunov criteria and state-feedback controller design for stochastic nonlinear systems, IEEE/CAA Journal of Automatica Sinica. (2022) 9, no. 6, 1005–1014, https://doi.org/10.1109/jas.2022.105539.
10.1109/JAS.2022.105539
Google Scholar
16 Long Z., Zhou W., Fang L., and Zhu D., Fixed-time stabilization of a class of stochastic nonlinear systems, Actuators. (2023) 13, no. 1, 3–22, https://doi.org/10.3390/act13010003.
10.3390/act13010003
Google Scholar
17 Yu J., Yu S., Li J., and Yan Y., Fixed-time stability theorem of stochastic nonlinear systems, International Journal of Control. (2019) 92, no. 9, 2194–2200, https://doi.org/10.1080/00207179.2018.1430900, 2-s2.0-85044095315.
10.1080/00207179.2018.1430900
Web of Science® Google Scholar
18 Song Z., Li P., Zhai J., Wang Z., and Huang X., Global fixed-time stabilization for switched stochastic nonlinear systems under rational switching powers, Applied Mathematics and Computation. (2020) 387, https://doi.org/10.1016/j.amc.2019.124856, 124856.
10.1016/j.amc.2019.124856
Web of Science® Google Scholar
19 Yu J., Yu S., and Yan Y., Fixed-time stability of stochastic nonlinear systems and its application into stochastic multiagent systems, IET Control Theory and Applications. (2021) 15, no. 1, 126–135, https://doi.org/10.1049/cth2.12040.
10.1049/cth2.12040
Web of Science® Google Scholar
20 Min H., Shi S., Xu S., Guo J., and Zhang Z., Fixed-time Lyapunov criteria of stochastic nonlinear systems and its generalization, IEEE Transactions on Automatic Control. (2023) 68, no. 8, 5052–5058, https://doi.org/10.1109/tac.2022.3218592.
10.1109/TAC.2022.3218592
Google Scholar
21 Fang L., Ding S., Park J. H., Park L., and Ma L., Adaptive fuzzy control for stochastic high-order nonlinear systems with output constraints, IEEE Transactions on Fuzzy Systems. (2021) 29, no. 9, 2635–2646, https://doi.org/10.1109/tfuzz.2020.3005350.
10.1109/TFUZZ.2020.3005350
Web of Science® Google Scholar
22 Fang L., Ding S., Park J. H., and Ma L., Adaptive fuzzy control for nontriangular stochastic high-order nonlinear systems subject to asymmetric output constraints, IEEE Transactions on Cybernetics. (2022) 52, no. 2, 1280–1291, https://doi.org/10.1109/tcyb.2020.3000920.
10.1109/TCYB.2020.3000920
PubMed Web of Science® Google Scholar
23 Li W., Xie X., and Zhang S., Output feedback stabilization of stochastic high-order nonlinear systems under weaker conditions, SIAM Journal on Control and Optimization. (2011) 49, no. 3, 1262–1282, https://doi.org/10.1137/100798259, 2-s2.0-79960367156.
10.1137/100798259
Web of Science® Google Scholar
24 Li W., Liu X., and Zhang S., Further results on adaptive state-feedback stabilization for stochastic high-order nonlinear systems, Automatica. (2012) 48, no. 8, 1667–1675, https://doi.org/10.1016/j.automatica.2012.05.035, 2-s2.0-84864452619.
10.1016/j.automatica.2012.05.035
Web of Science® Google Scholar
25 Fang L., Ma L., Ding S., and Park J. H., Finite-time stabilization of high-order stochastic nonlinear systems with asymmetric output constraints, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2021) 51, no. 11, 7201–7213, https://doi.org/10.1109/tsmc.2020.2965589.
10.1109/TSMC.2020.2965589
Web of Science® Google Scholar
26 Fang L., Ma L., Park J. H., and Ding S., Finite-time stabilization for a class of stochastic output-constrained systems by output feedback, International Journal of Robust and Nonlinear Control. (2022) 32, no. 3, 1256–1271, https://doi.org/10.1002/rnc.5879.
10.1002/rnc.5879
Web of Science® Google Scholar
27 Liu L., Xu S., and Zhang Y., Finite-time output feedback control for a class of stochastic low-order nonlinear systems, International Journal of Control. (2017) 90, no. 7, 1457–1465, https://doi.org/10.1080/00207179.2016.1209563, 2-s2.0-84980329047.
10.1080/00207179.2016.1209563
Web of Science® Google Scholar
28 Zhao Y. and Zhao P., Global finite-time stabilization by state-feedback for a class of stochastic nonlinear systems, Journal of Systems ence and Mathematical ences. (2014) 34, no. 12, 1604–1612.
Google Scholar
29 Fang L., Ding S., Ma L., and Zhu D., Finite-time state-feedback control for a class of stochastic constrained nonlinear systems, Journal of the Franklin Institute. (2022) 359, no. 14, 7415–7437, https://doi.org/10.1016/j.jfranklin.2022.07.025.
10.1016/j.jfranklin.2022.07.025
Google Scholar
30 Jiang M. and Xie X., Adaptive finite-time stabilization of stochastic nonlinear systems with the powers of positive odd rational numbers, International Journal of Adaptive Control and Signal Processing. (2019) 33, no. 9, 1425–1439, https://doi.org/10.1002/acs.3040, 2-s2.0-85069654028.
10.1002/acs.3040
Web of Science® Google Scholar
31 Bateman H., Higher Transcendental Functions, 1955, McGraw-Hill, New York, NY, USA.
Google Scholar
32 Erd elyi A., Magnus M., Oberhettinger F., Tricomi F. G., and Bateman H., Higher Transcendental Functions, 1953, McGraw-Hill, New York, NY, USA.
Google Scholar

All articles

Global Fixed-Time Stability of General Stochastic Nonlinear Systems

Abstract

1. Introduction

2. Preliminaries

3. Main Results

3.1. Problem Description

3.2. A Corollary

3.3. Controller Design

3.4. Stability Analysis

4. Simulation

5. Conclusion

Conflicts of Interest

Acknowledgments

Appendix

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Global Fixed-Time Stability of General Stochastic Nonlinear Systems

Abstract

1. Introduction

2. Preliminaries

3. Main Results

3.1. Problem Description

3.2. A Corollary

3.3. Controller Design

3.4. Stability Analysis

4. Simulation

5. Conclusion

Conflicts of Interest

Acknowledgments

Appendix

Open Research

Data Availability

References

Figures

References

Related

Information