Shell and tube-type crossflow heat exchangers with circular fins are widely used in various industries, including nuclear power plants. This study focuses on the sodium-to-air heat exchanger, which is one of the key safety features in sodium-cooled fast reactors. Tube alignment inside the heat exchanger is important because it directly determines the performance. Although heat exchangers are generally designed to have staggered tube alignment, inevitable inline-aligned zones exist. Therefore, this paper proposes a hybrid tube alignment modeling approach that considers both staggered and inline tube heat transfer phenomena. The results of the hybrid model calculations are verified and validated with liquid sodium experiments. The hybrid approach to the tube arrangement reduced the temperature deviation between experimental and calculated values to a difference of 4.55% and 7.38% for both sodium and air sides, respectively, while for the heat transfer, the difference was 15.12% and 9.06% for sodium and air sides, respectively. The results of this study can also be used as a basis for the safety evaluation of nuclear reactors and licensing processes for sodium-cooled fast reactors. In addition, this study is limited not only to sodium heat exchangers but also to any serpentine tube arrangement or crossflow heat exchanger under high-temperature systems, such as concentrated solar power and thermal energy storage industries.

1. Introduction

Crossflow heat exchangers with circular fins are among the most common single-phase heat transfer components and are widely used in various industries, including nuclear power plants. The nuclear power industry now prioritizes higher efficiency with a compact design in addition to safety. For both safety and efficiency, the key component is the heat exchanger. Conventional nuclear power plants use steam generators and employ water as a coolant. However, recently developing Generation IV reactors use various fluids to transfer heat. One of the most promising designs is a sodium-cooled fast reactor (SFR) [1, 2].

Although the designs of SFR differ, they generally have various heat exchangers that can be categorized by the coolants such as sodium-to-sodium, sodium-to-water, and sodium-to-air types [3]. The sodium-to-air heat exchanger is directly related to the safety of the overall plant [4–12]. However, the heat transfer characteristics of air are relatively unfavorable compared to those of liquid sodium. Many researchers have attempted to enhance the heat transfer rate through various designs while maintaining cost competitiveness. One such solution is a heat exchanger with circular fins. The fins provide a large surface area to enhance the heat transfer performance, and the characteristics change according to the layout of the tubes [13–17].

Tube alignment inside the heat exchanger is very important because it directly determines the performance [18–22]. Generally, a staggered alignment enhances heat transfer; thus, most crossflow heat exchangers adopt staggered tubes. However, several inevitable “inline tube zones” with nonnegligible effects exist. Previous studies on the modeling approach did not consider this aspect, and an appropriate methodology is required to accurately predict the heat transfer rate. Moreover, experimental verification is necessary to confirm and support the analytical results.

In this study, a hybrid tube alignment modeling approach is proposed. It considers both staggered and inline tube heat transfers with a weighting factor. The calculation results of the hybrid model were verified and validated using a liquid sodium experiment. This study focuses on the effect of the hybrid model on a finned-tube sodium-to-air heat exchanger (FHX), where sodium is on the tube side. Schematics of the FHX in the SFR and the general tube arrangement are shown in Figure 1 [23, 24].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic of FHX unit in SFR and finned tube arrangement [1, 2].

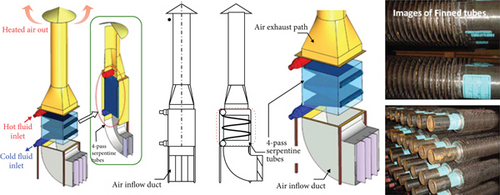
2. Modeling of Circular Fin Heat Exchanger

2.1. 1-D Analysis Model in FHXSA Code

The FHXSA code was originally developed by KAERI (Korea Atomic Energy Research Institute) to design a finned-tube crossflow sodium-to-air heat exchanger in SFR. It calculates both the heat transfer area for a given heat transfer and temperature/flow rates of the sodium/air inlet/outlet and the heat transfer rate for a given heat transfer area. It calculates the heat transfer rate of a single tube from the tube side to the air side (shell side), as well as the pressure drop on each side. The results of single-tube calculations can be expanded to estimate the total heat transfer rate. The model is evenly divided into several control volumes, and the correlations between heat transfer and pressure drop are used for each control volume. In the FHXSA code, the governing equations are expressed as follows.

2.1.1. Continuity Equation

The continuity equation can be simplified based on the steady-state condition.

(1)

where w_s and w_t denote the flow rates on the air (shell) and sodium (tube) sides, respectively.

2.1.2. Momentum Equation

The total pressure drop at each control volume i is defined as the sum of the acceleration, friction, and gravity terms:

(2)

(3)

(4)

(5)

where M, ρ,

, f, d, θ, L, and g are the mass flow, density, average density, friction factor, hydraulic diameter, inclination angle of the tube, length of the control volume, and gravitational acceleration, respectively.

2.1.3. Energy Equation

The detailed energy flow is shown in Figure 2, and heat transfer is expressed as follows:

(6)

(7)

(8)

(9)

(10)

where ΔQ, U, ΔA_o,w, T, w, and H are the heat transfer rate, total heat transfer coefficient, heat transfer area of the tube outside wall, temperature, sodium flow rate, and enthalpy, respectively. The subscripts t, s, in, and out denote tube, shell, inlet, and outlet, respectively. LMTD denotes the log mean temperature difference, and d_o,w is the outside diameter of the tube.

The total heat transfer coefficient U can be expressed as the sum of the convection of the air (shell) and sodium (tube) sides, conduction through the tube wall, and fouling at the inner and outer surfaces. The total heat transfer coefficient of the i-th control volume is expressed as follows:

(11)

Combining this equation with Eq. (6), U can be defined as

(12)

The η in Eq. (12) is the heat transfer enhancement factor and is defined as follows:

(13)

where A_fin and A_tot are the surface area of the fins and the total surface area including the fins, respectively. The η_f is the efficiency of a single fin and is one of the input parameters of the FHXSA code.

Therefore, the inner and outer wall temperatures are

(14)

(15)

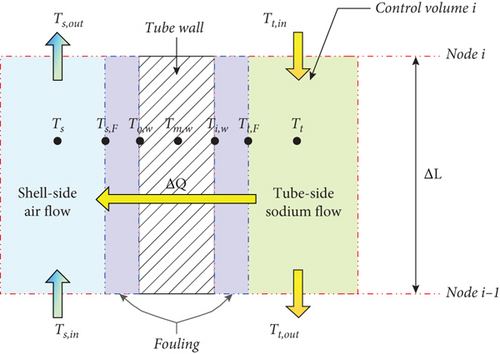
The fouling factor is generally applied to water or steam because the fouling effect is closely related to oxidation at the surface of the metal. However, in the case of sodium, oxygen and hydrogen are controlled and monitored using a cold trap and plugging meter to maintain a certain concentration. Therefore, the fouling on the sodium side is negligible, whereas fouling on the air side is considered, taking into account the humidity. In the FHX design, the fouling factor for compressed air (0.002 Ft² °F/Btu) was applied, and the corresponding h_s,F is approximately 2.841 kW/m².

2.2. Heat Transfer Modeling

2.2.1. Tube Side (Sodium)

The Lubarsky–Kaufman correlation was selected as the heat transfer correlation for the sodium side, which is expressed as a function of the Peclet number [25].

(16)

where Nu and Pe are the Nusselt number and Peclet number, respectively.

2.2.2. Shell Side (Air)

The heat transfer correlation for the air side was selected as that of Zukauskas, which is expressed as a function of the pitch-to-diameter ratio because heat transfer is most affected by the flow area and perimeter [11]. The finned tube layout and flow channel model are shown in Figure 3.

For staggered grid:

(17)

for 1 × 10² ≤ Re_f ≤ 2 × 10⁴.

(18)

for 2 × 10⁴ ≤ Re_f ≤ 2 × 10⁵, 1.1 ≤ a ≤ 4.0, 1.03 ≤ b ≤ 2.5, 0.07 ≤ h/d ≤ 0.715, and 0.06 ≤ s/d ≤ 0.36.

(19)

for 2 × 10⁵ ≤ Re_f ≤ 1.4 × 10⁶, 2.2 ≤ a ≤ 4.2, 1.27 ≤ b ≤ 2.2, 0.125 ≤ h/d ≤ 0.6, and 0.125 ≤ s/d ≤ 0.28.

(20)

(21)

(22)

For inline grid:

(23)

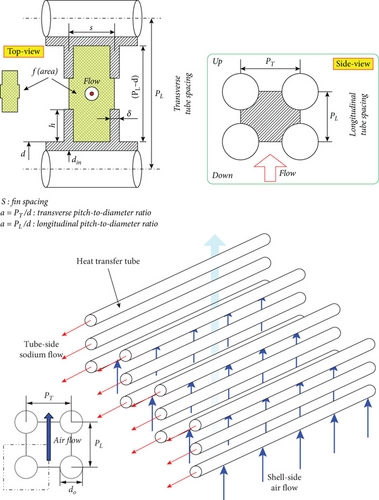
where f denotes the air crossflow area between the fins. The h, δ, s, d, and d_in are the fin height, thickness, spacing between the fins, tube outer diameter, and tube inner diameter, respectively. The V_max, used to calculate Re_f, is the maximum air velocity and is expressed as a function of the geometrical information of P_T and P_L. V is the frontal velocity before entering the tube. The R_A,flow is defined as the ratio of the flow area reduction owing to the fin area. The ε is the surface extension ratio. The coefficients used in the correlation are based on the tube alignment of the staggered or inline grid.

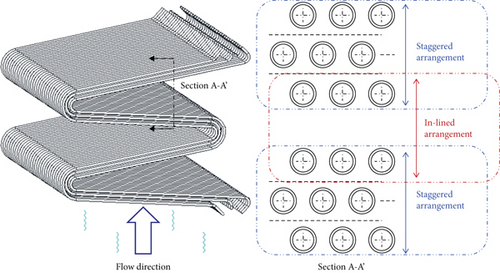
2.3. Detailed Tube Alignment

Figure 4 shows the detailed tube layout inside the FHX. The tube alignment in the airflow direction is neither staggered nor inline. The last tubes in the path are aligned with the tubes in the next path, whereas the tubes within the path are in a staggered position. The flow pattern in several rows before the tube bank is different from the tube rows in the stabilized flow region. Therefore, Zukauskas’s correlation for a staggered grid applies to a fully stabilized flow. However, in this case, the flow does not stabilize sufficiently for the case of only 3 rows. Therefore, a correction factor is required. In the code, a weighting method was applied to handle the hybrid tube layout. The final Nusselt number was calculated by adding that of each staggered and inline configuration, weighted by 1/3 and 2/3, respectively.

2.4. Pressure Drop Modeling

2.4.1. Tube Side (Sodium)

The pressure drop on the tube side, caused by friction, is calculated using the correlation expressed as a function of the Reynolds number. The friction factor is obtained from the Darcy factor and interpolated for the transition zone. The pressure drop is then calculated by the following equation:

(24)

(25)

where f, L, d_h, ρ, v, and i are friction factor, flow length, hydraulic diameter, density, velocity, and control volume, respectively.

2.4.2. Shell Side (Air)

For the air side, the friction factor is calculated using the Gunter-Shaw correlation as follows [26]:

(26)

Either Gunter-Shaw or Zukauskas correlation can be used to calculate the pressure drop. Here, the Zukauskas correlation was used.

(27)

where f, G, g, μ_w, μ, D_v, L, and ρ are friction factor, mass flow, gravity, kinematic viscosity at tube wall, air viscosity, volumetric hydraulic diameter, flow length, and air density, respectively.

(28)

(29)

(30)

(31)

(32)

(33)

(34)

where N_L is the number of tube layers and c₂ is the value determined by the tube arrangement.

3. Experiments

3.1. Test Facility

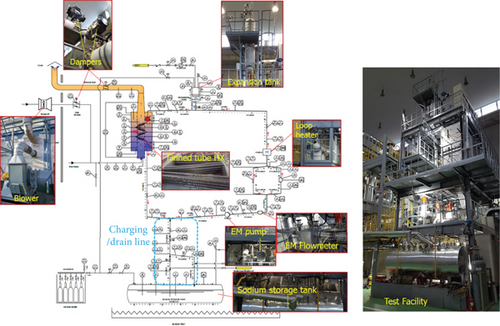
The test facility consists of a main test loop, a gas supply, and related auxiliary systems. The main sodium-side (tube side) components are the test section, model heat exchanger (M-FHX), electromagnetic pump, electric loop heater, flow meters, expansion tank, and sodium storage tank. The air-side (shell side) components are the blower and dampers. The P&ID and images of the test facility are shown in Figure 5. The designed maximum temperature of the facility is 500°C, and the designed power capacity of the main heater is 650 kW. The entire heat exchanger test facility employs pipes with a 2-inch diameter and Sch20 classification [13], and the expected operation flow range is 0.99–4.38 kg/s on the tube side and 0.12–3.4 kg/s on the air side. The maximum available flow rates of the electromagnetic pump and blower are approximately 6 and 5 kg/s, respectively. Appropriate instruments were used to measure the flow rates, temperatures, and pressure differences.

3.2. Test Section—Model FHX

For the experimental verification, an M-FHX was designed, fabricated, and installed in the facility. To have a clear connection with the actual reactor, FHX in the prototype Gen IV sodium-cooled fast reactor (PGSFR), developed by KAERI, was selected as the reference design because sufficient data is publicly available. In Table 1, detailed design parameters of the M-FHX are listed. Each bend of its tube has a thermocouple with a thermowell to measure the temperature of the sodium inside. Twenty multipoint thermocouples with five different measurement points in each sensor (i.e., a total of 100 measurement points) were installed on the air side to measure the temperature of the air.

Table 1. Key parameters of M-FHX.

Design parameters	Model HX
Thermal duty (MWt)	0.3125
No. of tube columns	4
No. of tubes	12
Tube pitch to diameter (P/OD), P_L & P_T	2.05 & 2.5
Tube material	STS304
Bare tube (OD/ID) (mm)	34.0/30.7
Thickness (mm)	1.65
Finned tube length (total, m)	7.722
Fin height (mm)	15.0
Fin thickness (width, mm)	1.5
Tube inclined angle (degree)	7.2
No. of fin (per unit length, m)	157.48
Spacing between fins (mm)	4.85
Total heat transfer area with fin surface (m²)	82.04
Total number of fins per single tube (ea)	1216
Flow region size (W × D, m)	1.984 × 0.3825
Tube side (sodium)
Flow rate (kg/sec)	2.19
Inlet/outlet temp. (°C)	335/224.18
Pressure drop (Pa)	512
Shell side (air)
Flow rate (kg/sec)	1.70
Inlet/outlet temp. (°C)	20.0/213.9
Pressure drop (Pa)	47

3.3. Test Matrix and Procedure

The test conditions of M-FHX were set to verify and validate the code model discussed in the previous section. In Table 2, the test matrix for the 17 test groups is shown.

Table 2. M-FHX test matrix.

Test group no.	Tube side (sodium)		Shell side (air)
Test group no.	Flow rate (kg/s)	Inlet temperature (°C)	Flow rate (kg/s)	Inlet temperature (°C)
(1)	0.99	187	0.12	Atmospheric temperature (uncontrolled)
(2)	1.06	380	0.11
(3)	1.50	366	0.37
(4)	1.50	366	0.61
(5)	1.50	366	1.14
(6)	2.19	335	1.14
(7)	2.19	335	1.66
(8)	2.19	335	2.08
(9)	2.19	480	1.66
(10)	2.19	480	2.08
(11)	2.74	335	1.14
(12)	2.74	335	1.66
(13)	2.74	335	2.08
(14)	2.74	335	2.49
(15)	3.29	480	1.66
(16)	3.29	480	2.08
(17)	3.29	335	2.49

The experiment starts with sodium charging. After charging the main test loop from the storage tank, sodium was circulated until the target temperature was reached. Simultaneously, the airflow rate was adjusted. Eventually, the sodium flow rate, sodium inlet temperature, and airflow rate were maintained at the target values for a steady state. Table 3 lists the criteria for the steady-state conditions of the measurements, and the measured data are the average values over 10 min.

Table 3. Criteria of steady-state condition.

Parameter	Steady-state condition
Sodium inlet temperature	(Avg. ±1%)
Sodium outlet temperature	(Avg. ±1%)
Air inlet temperature	(Avg. ±1%) or (Avg. ±1°C)
Air outlet temperature	(Avg. ±1%) or (Avg. ±1°C)
Sodium flow rate	(Avg. ±1%) or (Avg. ±1 kg/s)
Airflow fate	(Avg. ±1%) or (Avg. ±1 kg/s)

4. Results and Discussion

4.1. Test Results

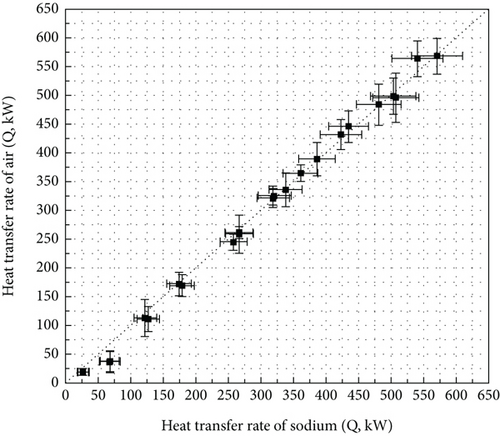
A total of 25 tests were conducted along with the uncertainty analysis results. Additionally, the heat-transfer rates of sodium and air were compared in terms of the enthalpy changes to ensure data reliability (Figure 6). The individual heat-transfer rates from sodium to air were calculated. The specific heat was obtained by averaging the inlet and outlet data. The vapor enthalpy of air was also considered, and the water vapor pressure was obtained using the Buck equation.

4.2. Uncertainty Analysis

The uncertainty is estimated by the sum of error components. The error components are defined as follows: notation “B” means bias error and “P” means precision error.

(35)

For the sodium temperature measurements, the bias error components are related to the measurement system. B_ST1 and B_ST2 were estimated to be ±1.5°C from calibration results and ±1.0°C by additional signal transmission tests, respectively. B_ST3 was statistically obtained using Student’s t-distribution table. B_ST4 was conservatively defined as ±0.5°C by separately conducted experiments, and B_ST5 was considered a negative error after the heat loss tests. The precision errors were quantified using a statistical approach. P_ST1 was calculated by taking conservative degrees of freedom from the measured values obtained over 5 min, and P_ST2 was deduced from four separate experiments performed on different days.

For air temperature measurements, the error components are defined as follows: B_AT1 and B_AT2 had the same values as sodium. B_AT3 was obtained in the same manner using a statistical approach. P_AT1 and P_AT2 were calculated in the same manner as for sodium.

For sodium flow rate measurements, Coriolis and electromagnetic flow meters were used. The corresponding error components are defined as follows. B_SF1 and B_SF2 were considered to be ±0.0125 and ±0.001 kg/s, respectively. B_SF3 denoted the transfer error from the current signal to the physical instrument, and its value was ±0.0005 kg/s. P_SF1 and P_SF2 were quantified using statistical approaches.

For airflow rate measurements, the installation uncertainty was considered. All the other measurements were performed using the same procedure. Moreover, the measurement error of air humidity was considered. Consequently, 3.5 and 0.112% R.H. for the bias and precision error, respectively, were used in the uncertainty analysis.

The relative influence of each error component is summarized in Tables 4 and 5.

Table 4. Bias (system) error component influence.

Description of the bias error component	Influence
Calibration error for used instruments	Moderate
Data acquisition error on transmitting process	Small
Data recording error on the HMI program	Small
Error due to manufacturing tolerance	Moderate
Error due to spatial variation	Large

Table 5. Precision (random) error component influence.

Description of the precision error component	Influence
Random error of measured values	Moderate
Random error for repeated tests (on different days)	Moderate

4.3. Comparison with Code Calculation

4.3.1. Temperature

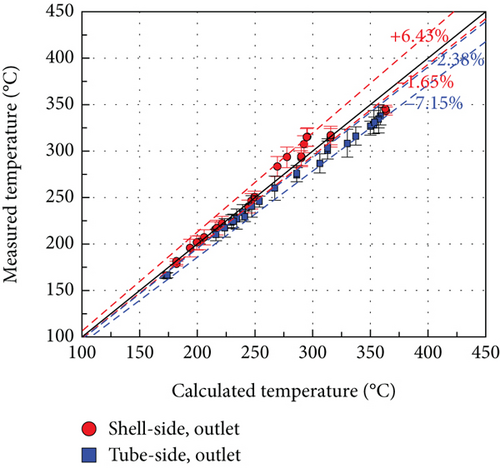
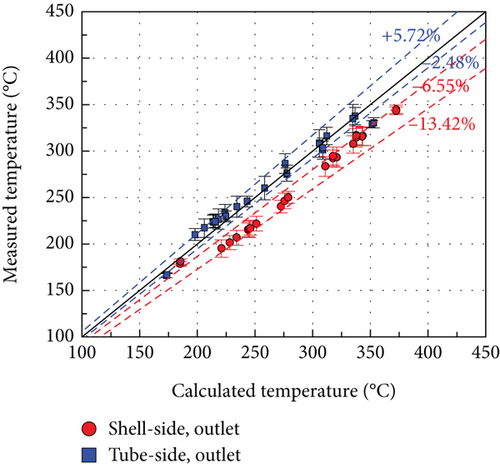
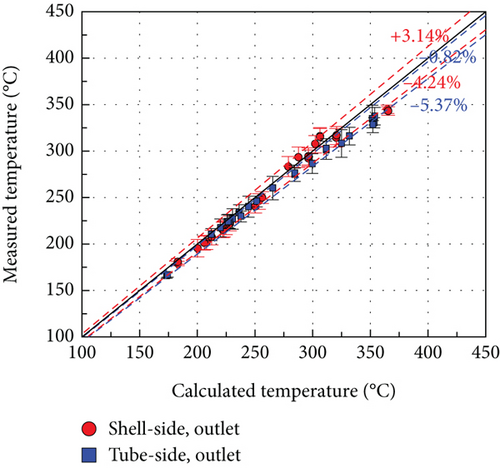
The test results were compared with the code calculations shown in Figures 7, 8–9. For a clear distinction of the hybrid models, the inline- and staggered-only results are also depicted. The hybrid model predicts more accurately than the inline-only and staggered-only models. The inline-only model shows larger differences on the tube side, whereas the staggered-only model shows larger differences on the air (shell) side. The hybrid approach reduced these differences for both tube and shell sides, resulting in 4.55% and 7.38% differences, respectively.

4.3.2. Heat Transfer

The heat transfer comparison results are shown in Figures 10, 11–12. Similar to the temperature comparison cases, the heat transfer was compared with the inline-only and staggered-only calculations. Both the inline-only and staggered-only models exhibited larger differences on the tube side. The results of the hybrid model for tube and shell sides exhibited differences of 15.12% and 9.06%, respectively.

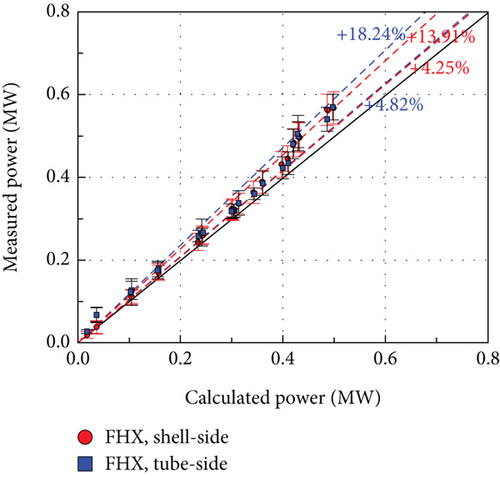
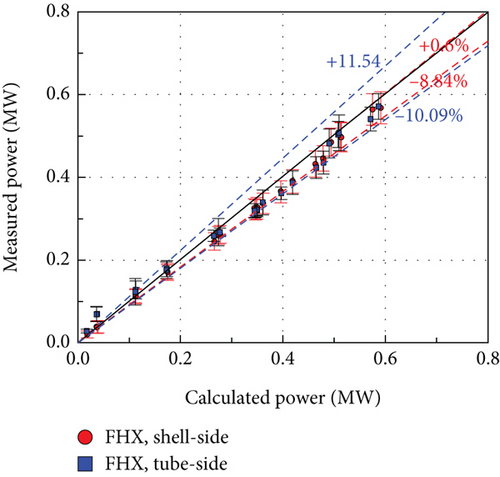
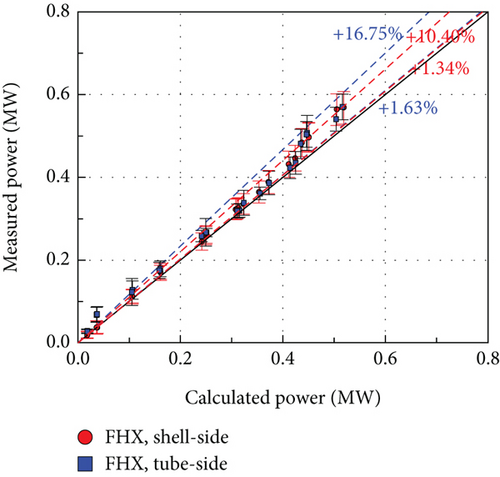
The FHX tube arrangement in this study looks staggered if only 3 tubes are considered. However, the tubes at the top and bottom of the serpentine structure can be considered as an inline arrangement. In this case, the correlation for each arrangement (staggered-only or inline-only) cannot predict the heat transfer accurately. Therefore, the hybrid model was applied to solve the problem with reasonable results, especially for the abnormally arranged tubes.

5. Conclusions

To ensure safety in modern nuclear reactors, heat exchangers play a crucial role, with staggered-arrayed serpentine tubes featuring circular fins being a critical component of SFR. Tube alignment in the heat exchanger directly influences its performance, and the FHX has both staggered and inline tube zones. A hybrid modeling approach is proposed, and the calculation results are verified and validated using a liquid sodium experiment. In applying the correlation equation, the hybrid approach to the tube arrangement reduced the temperature deviation between experimental and calculated values to a difference of 4.55% and 7.38% for both sodium and air sides, respectively, while for the heat transfer, the difference was 15.12% and 9.06% for sodium and air sides, respectively. In this study, a total of 25 tests were conducted, and the data uncertainty was evaluated quantitatively. Consequently, significant improvements in the temperature prediction and heat transfer rate were achieved. The sodium experiment enabled an appropriate evaluation of air-side heat transfer correlation at high temperatures (over 500°C) while keeping the minimum heat resistance issue. The result of this study is limited not only to sodium heat exchangers but also to any serpentine tube arrangement or crossflow heat exchanger under high-temperature conditions, such as the concentrated solar power (CSP) and thermal energy storage (TES) industries. The results of this study can also be used as a basis for the safety evaluation of nuclear reactors and licensing processes for sodium-cooled fast reactors by verifying the performance of the final heat sink in the decay heat removal system (DHRS).

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Research Foundation (NRF) and National Research Council of Science & Technology (NST) grant funded by the Korea government (MSIT) (Nos. 2021M2E2A2081063, 2023M2D2A1A01074092, and CAP20034-000).

Open Research

Data Availability

The data is available upon request.

References

1 Yoo J., Chang J., and Joo H.-K., Overall reactor system description of prototype gen-IV sodium cooled fast reactor, Transactions of the American Nuclear Society. (2016) 114.
Google Scholar
2 Yoo J., Chang J., Lim J.-Y., Cheon J.-S., Lee T.-H., Kim S. K., Lee K. L., and Joo H.-K., Overall system description and safety characteristics of prototype gen IV sodium cooled fast reactor in Korea, Nuclear Engineering and Technology. (2016) 48, no. 5, 1059–1070, https://doi.org/10.1016/j.net.2016.08.004, 2-s2.0-84992436190.
10.1016/j.net.2016.08.004
Web of Science® Google Scholar
3 Wang H. and Kissick S. M., Modeling and simulation of a supercritical CO2-liquid sodium compact heat exchanger for sodium-cooled fast reactors, Applied Thermal Engineering. (2020) 180, article 115859, https://doi.org/10.1016/j.applthermaleng.2020.115859.
10.1016/j.applthermaleng.2020.115859
Web of Science® Google Scholar
4 Kim H. K., Yoon K. H., Lee Y. H., Lee H. S., and Cheon J. S., Mechanical design of a sodium cooled fast reactor fuel assembly in Korea: normal operation condition, Nuclear Engineering and Design. (2019) 346, 67–74, https://doi.org/10.1016/j.nucengdes.2019.03.009, 2-s2.0-85062730210.
10.1016/j.nucengdes.2019.03.009
CAS Web of Science® Google Scholar
5 Caramello M., Gregorini M., Bertani C., De Salve M., Alemberti A., and Panella B., Thermal hydraulic analysis of a passively controlled DHR system, Progress in Nuclear Energy. (2017) 99, 127–139, https://doi.org/10.1016/j.pnucene.2017.05.015, 2-s2.0-85019564347.
10.1016/j.pnucene.2017.05.015
CAS Web of Science® Google Scholar
6 Planchon H. P., Sackett J. I., Golden G. H., and Sevy R. H., Implications of the EBR-II inherent safety demonstration test, Nuclear Engineering and Design. (1987) 101, no. 1, 75–90, https://doi.org/10.1016/0029-5493(87)90152-X, 2-s2.0-0023330732.
10.1016/0029-5493(87)90152-X
CAS Web of Science® Google Scholar
7 Bubelis E., Jaeger W., Bandini G., Alemberti A., and Palmero M., Assessment of the enhanced DHRS configuration for MYRRHA reactor, Nuclear Engineering and Design. (2016) 307, 181–187, https://doi.org/10.1016/j.nucengdes.2016.07.017, 2-s2.0-84984860242.
10.1016/j.nucengdes.2016.07.017
CAS Web of Science® Google Scholar
8 Hong J., Yeom S., Eoh J.-H., Lee T.-H., and Jeong J.-Y., Heat transfer performance test of PDHRS heat exchangers of PGSFR using STELLA-1 facility, Nuclear Engineering and Design. (2017) 313, 73–83, https://doi.org/10.1016/j.nucengdes.2016.11.035, 2-s2.0-85006508594.
10.1016/j.nucengdes.2016.11.035
CAS Web of Science® Google Scholar
9 Saraswat S. P., Munshi P., and Allison C., Linear stability analysis of RELAP5 two-fluid model in nuclear reactor safety results, Annals of Nuclear Energy. (2020) 149, article 107720, https://doi.org/10.1016/j.anucene.2020.107720.
10.1016/j.anucene.2020.107720
Web of Science® Google Scholar
10 Mascari F., D’Auria F., Bestion D., Lien P., Nakamura H., Austregesilo H., Moon S. K., Reventos F., Umminger K., Reyes J. N., and Rohatgi U. S., OECD/NEA/CSNI state-of-the-art report on scaling in system thermal-hydraulics applications to nuclear reactor safety and design (the S-SOAR), Nuclear Engineering and Design. (2024) 416, article 112750, https://doi.org/10.1016/j.nucengdes.2023.112750.
10.1016/j.nucengdes.2023.112750
Web of Science® Google Scholar
11 Zhao F., Zou S., Xu S., Wang J., Xu T., and Tang D., Safety analysis of marine nuclear reactor in severe accident with dynamic fault trees based on cut sequence method, Nuclear Engineering and Technology. (2022) 54, no. 12, 4560–4570, https://doi.org/10.1016/j.net.2022.08.014.
10.1016/j.net.2022.08.014
CAS Web of Science® Google Scholar
12 Pavlakovič B., Visiting nuclear reactors–safety and security aspects, International Journal of Thermofluids. (2022) 16, article 100241, https://doi.org/10.1016/j.ijft.2022.100241.
10.1016/j.ijft.2022.100241
Google Scholar
13 Kim M., Han C., Baek C., and Kim Y., Air-side heat transfer enhancement in fin-tube heat exchangers using forced vibrations under various conditions, International Communications in Heat and Mass Transfer. (2023) 144, article 106798, https://doi.org/10.1016/j.icheatmasstransfer.2023.106798.
10.1016/j.icheatmasstransfer.2023.106798
Web of Science® Google Scholar
14 Wang H., Fu T., Wang J., Zhang F., Zhang K., and Deng X., Study on heat transfer performance of fin-and-tube heat exchanger with elliptical fins, Journal of Energy Storage. (2022) 56, article 105956, no. Part B, https://doi.org/10.1016/j.est.2022.105956.
10.1016/j.est.2022.105956
Web of Science® Google Scholar
15 Liu X., Wang M., Liu H., Chen W., and Qian S., Numerical analysis on heat transfer enhancement of wavy fin-tube heat exchangers for air-conditioning applications, Applied Thermal Engineering. (2021) 199, article 117597, https://doi.org/10.1016/j.applthermaleng.2021.117597.
10.1016/j.applthermaleng.2021.117597
Web of Science® Google Scholar
16 Ko Y. M., Song J. Y., Lee J. W., Sohn S., Song C. H., Khoshvaght-Aliabadi M., Kim Y., and Kang Y. T., A critical review on Colburn j-factor and f-factor and energy performance analysis for finned tube heat exchangers, Energy. (2024) 287, article 129609, https://doi.org/10.1016/j.energy.2023.129609.
10.1016/j.energy.2023.129609
Web of Science® Google Scholar
17 Maghsoudali Y., Rastegarkoutenaei A., Sahami M., and Bandpy M. G., Investigation of the effect of using the finned tubes on the performance of shell and tube heat exchanger by 3D modeling, Journal of Energy Storage. (2022) 56, article 106031, https://doi.org/10.1016/j.est.2022.106031.
10.1016/j.est.2022.106031
Web of Science® Google Scholar
18 Zukauskas A. and Karni J., High-Performance Single-Phase Heat Exchangers, Revised and Augmented Edition, 1989, Hemisphere Publishing Corp..
Google Scholar
19 Bahiraei M. and Gharagozloo K., Experimental investigation of hydrothermal characteristics for flow within a circular tube equipped with twisted conical strip inserts under different alignments, Journal of the Taiwan Institute of Chemical Engineers. (2020) 114, 24–35, https://doi.org/10.1016/j.jtice.2020.09.002.
10.1016/j.jtice.2020.09.002
CAS Web of Science® Google Scholar
20 Nia M. F., Farzad H., Ansari A. B., Ghodrat M., Nassab S. A. G., and Behnia M., Performance improvement of a tubular heat exchanger by tube arrangement optimization using simulated annealing algorithm and blocked-off method, Thermal Science and Engineering Progress. (2023) 40, article 101793, https://doi.org/10.1016/j.tsep.2023.101793.
10.1016/j.tsep.2023.101793
Google Scholar
21 Deeb R., New correlations for predicting convective heat transfer of single and multi-row heat exchangers employing staggered drop-shaped tubes, International Journal of Heat and Mass Transfer. (2023) 202, article 123689, https://doi.org/10.1016/j.ijheatmasstransfer.2022.123689.
10.1016/j.ijheatmasstransfer.2022.123689
Web of Science® Google Scholar
22 Wu Z., You S., Zhang H., and Zheng W., Experimental study on thermal and flow performance of staggered tube-bundle heat exchanger for seawater source heat pump, Sustainable Cities and Society. (2020) 59, article 102195, https://doi.org/10.1016/j.scs.2020.102195.
10.1016/j.scs.2020.102195
Web of Science® Google Scholar
23 Lee H. Y., Kim H., Kim J. B., and Jeong J. Y., Design and integrity evaluation of a finned-tube sodium-to-air heat exchanger in a sodium test facility, ASME Journal of Pressure Vessel Technology. (2017) 139, no. 3, article 031203, https://doi.org/10.1115/1.4035038, 2-s2.0-84994578216.
10.1115/1.4035038
Web of Science® Google Scholar
24 Kim H., Yoon J., Lee H. Y., Eoh J., Jeong J. Y., and Lee J., Design and thermal-hydraulic evaluation of the finned-tube type sodium-to-air heat exchanger in sodium test facility, Nuclear Engineering and Design. (2020) 366, article 110755, https://doi.org/10.1016/j.nucengdes.2020.110755.
10.1016/j.nucengdes.2020.110755
Web of Science® Google Scholar
25 Lubarsky B. and Kaufman S. J., Review of Experimental Investigations of Liquid-Metal Heat Transfern, 1955, NCSA Tech. Note 3336.
Google Scholar
26 Gunter A. Y. and Shaw W. A., A general correlation of friction factors for various types of surfaces in crossflow, Journal of Fluids Engineering. (1945) 67, no. 8, 643–656, https://doi.org/10.1115/1.4018353.
10.1115/1.4018353
Google Scholar

All articles

Heat Transfer Performance Tests of a Circular-Fin Sodium-to-Air Heat Exchanger for Sodium-Cooled Fast Reactors

Abstract

1. Introduction