International Journal of Aerospace Engineering

Volume 2024, Issue 1 5266773

Research Article

Open Access

A Finite-Time Fractional-Order Error Extended State Observer for Hypersonic Vehicle

Mingfei Zhao,

Mingfei Zhao

School of Astronautics , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Jia Song,

Jia Song

School of Astronautics , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Yunlong Hu,

Corresponding Author

Yunlong Hu

[email protected]

orcid.org/0009-0007-6501-1690

School of Astronautics , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Wenling Li,

Wenling Li

orcid.org/0000-0002-9130-5736

School of Automation , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Mingfei Zhao,

Mingfei Zhao

School of Astronautics , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Jia Song,

Jia Song

School of Astronautics , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Yunlong Hu,

Corresponding Author

Yunlong Hu

[email protected]

orcid.org/0009-0007-6501-1690

School of Astronautics , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

Wenling Li,

Wenling Li

orcid.org/0000-0002-9130-5736

School of Automation , Beihang University , Beijing , 100191 , China , buaa.edu.cn

Search for more papers by this author

First published: 11 July 2024

https://doi.org/10.1155/2024/5266773

Academic Editor: Jinchao Chen

Share a link

Email
Wechat
Bluesky

Abstract

To address the challenges posed by strong coupling, nonlinearity, and rapid time-varying dynamics in hypersonic vehicle (HV), this study presents an active disturbance rejection control (ADRC) scheme based on finite-time fractional-order error extended state observer (FTFOEESO). To begin, a control-oriented HV model is established. Subsequently, the FTFOEESO is developed to accurately estimate and compensate for strong disturbances and uncertainties. Unlike traditional FOESO, this observer does not alter the physical interpretation of the estimated variables or introduce unknown disturbances. Furthermore, this approach has demonstrated significant potential in mitigating high-frequency noise. Theoretical analysis has confirmed that the observation error of FTFOEESO is uniformly bounded. Finally, this paper conducts experiments using both conventional simulation and semiphysical simulation systems. Simulation studies and comparisons have revealed that the ADRC based on FTFOEESO possesses superior anti-interference and antinoise capabilities.

1. Introduction

The rapid development of hypersonic vehicle (HV) technology has attracted widespread attention from researchers due to its exceptional speed, maneuverability, and wide flight envelope [1–3]. However, the complex dynamics of HV, characterized by strong nonlinearity, coupling, and fast time-varying dynamics, pose significant challenges to the safety and reliability of flight [4, 5]. Moreover, exposure to radiation and mechanical vibration during flight can introduce measurement noise, further impacting the reliability of the vehicle [6]. Therefore, the adoption of advanced flight control laws is crucial to ensuring the safe operation of HV.

To date, various advanced control theories have been utilized in the design of control systems for HVs. These include robust control [7, 8], sliding mode control [9, 10], model predictive control [11], and backstepping control [12, 13]. Although significant progress has been made in the control methods of HV, these methods have limitations in their practical application due to their reliance on models [14] or chattering near equilibrium points [15].

Active disturbance rejection control (ADRC), introduced by Professor Han [16], has gained significant traction across various domains owing to its model-independent nature and robust anti-interference capabilities [17–20]. As a typical control framework, ADRC utilizes extended state observer (ESO) estimation and compensation for disturbances [21], combined with feedback control to effectively improve the system’s disturbance rejection performance. To further enhance control performance, many studies have made improvements to ADRC [22–24], and one effective method is to introduce FOPID into the framework. Gao et al. have effectively integrated the merits of FOPID and ADRC to devise the fractional-order ADRC (FOADRC) approach for HV [25]. Simulation results demonstrate that FOPID-based ADRC outperforms traditional PID-based ADRC in terms of speed, accuracy, and robustness.

Recent developments in FOPID suggest that the potential for combining fractional-order operators with state observers is enormous. For example, Naderolasli, Hashemi, and Shojaei have proposed the fuzzy fractional-order state observer to estimate the unavailable states, which can converge the tracking error to around the origin without the need to measure all the system’s states [26]. Meanwhile, several studies have investigated the use of fractional-order ESO (FOESO) to explore the potential to significantly improve error estimation performance [27, 28]. Chen et al. have successfully used FOESO to compensate for total disturbances in an integral-order system, achieving better performance than traditional integral-order ESO [28]. However, most of these studies have focused on applying FOESO to fractional-order systems, and its potential for integral-order systems remains largely unaddressed. And it should be noted that traditional FOESO alters the physical meaning of total disturbance, introducing complex dynamics into the estimation results.

As an advanced aircraft with exceptionally high dynamic performance, the control system of HV needs to rapidly converge to meet stringent task requirements. Therefore, studying finite-time FOESO for HV is of significant importance. In this context, Naderolasli, Shojaei, and Chatraei utilize the terminal sliding mode disturbance observer on the basis of traditional sliding mode observers to estimate the speed of the leader in the formation, achieving finite-time convergence [29]. However, it should be noted that as the initial state of the system grows infinitely, the convergence time of TSMO also tends to infinity, thereby somewhat restricting its practical applicability [30]. Moreover, the team also has studied high gain state observers, which can effectively reduce convergence time and estimation errors by combining finite-time stability terms [31]. Nevertheless, all the aforementioned studies do not consider the finite-time convergence of FOESO.

Building upon the aforementioned discussions, this paper introduces an approach called finite-time fractional-order error ESO (FTFOEESO) for hypersonic aircraft attitude control systems, aiming to achieve finite-time convergence. Drawing inspiration from the concept of finite-time control, we incorporate time-varying functions into the FOEESO to facilitate rapid convergence of estimation errors. The contributions of this paper are summarized as follows:

1.
Compared with the traditional FOESO proposed in Ref. [27, 28], the proposed FTFOEESO preserves the physical interpretation of the estimated variables and the integral sequence structure, ensuring finite-time system convergence without introducing new unknown disturbances.
2.
This paper utilizes the new FTFOEESO to estimate and compensate for the coupling term between the three channels of HVs, achieving complete decoupling of the aircraft. And compared with Ref. [6], it improves the convergence speed of the control system.
3.
Successfully applied the FTFOEESO algorithm to a semiphysical simulation system, achieving effective suppression of high-frequency noise in engineering.

The structure of the remaining sections is as follows: Section 2 establishes a control-oriented HV model; the third section introduces the design of FTFOEESO and proves that the observer can achieve finite-time convergence of errors; Section 4 presents the comparison and verification of the algorithm’s control performance; finally, the conclusion can be found in Section 5.

2. Problem Formulation

This study centers around the winged-cone HV model initially proposed by Shaughnessy. To meet the specific research objectives, certain modifications have been made to the mass, rotary inertia, and geometric characteristics of the vehicle. The adjusted parameters are listed in Ref. [6].

2.1. Nonlinear HV Model

The system dynamics of HV can be described as follows [6]:

()

where η refers to the velocity and g represents the gravitational acceleration. ω_γ, ω_ψ, and ω_θ correspond to the angular rates. α, β, and γ_c denote aerodynamic angle. θ and ψ represent path angle and azimuth angle, respectively. The variables ε_r, ε_e, and ε_i represent the position in the inertial coordinate system. I_xx, I_yy, and I_zz refer to the moments of inertia. The variables l, m, and n denote the roll, yaw, and pitch moment, respectively. T_x, L_y, and N_z represent the aerodynamic forces, and they can be expressed as follows:

()

where q = 0.5ρη² represents dynamic pressure and ρ is the atmospheric density. The aerodynamic moment can be written as

()

The aerodynamic moment coefficient can be expressed as

()

2.2. Linearized HV and Disturbance Model

Utilizing the nominal nonlinear HV model and considering the aerodynamic forces and moments, we establish the linearized HV attitude model.

Define

, and

, and the system can be expressed as follows:

()

where f_α, f_β, and

are ignored while linearization.

()

Define the system parameters of the linearized HV model as

()

where ΔC_l,p, ΔC_m,r, ΔC_m,β,

, ΔC_n,q, ΔC_D,α,

, and ΔC_Z,β represent modeling error. Define

()

and the control system can be represented as follows:

()

where ΔA_ε denotes the system uncertainty and f_ε represents unmodelled dynamic and external disturbance.

Apparently, the linearized HV attitude control system can be divided into three individual second-order subsystems. And each subsystem will be impacted by multisource interference.

3. FTFOEESO-ADRC-Based HV Attitude Control System

The main goal of this section is to develop an ADRC controller for HV based on FTFOEESO. In order to ensure the stability of the HV’s attitude dynamics, the control variables, namely, the angle of attack, sideslip angle, and velocity roll angle, are carefully selected and incorporated into the control design. The control scheme is visually depicted in Figure 1, providing a comprehensive overview of the proposed ADRC-based control architecture for HV attitude control.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The control system of HV based on FTFOEESO. The linearized HV attitude control system is divided into three individual second-order subsystems: α subsystem, β subsystem, and γ_c subsystem.

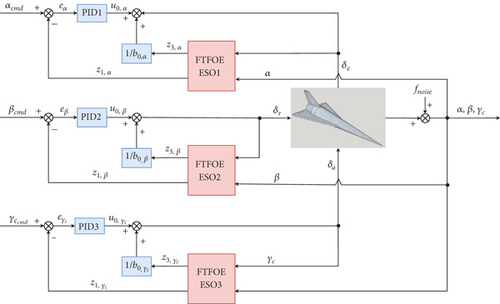
3.1. Some Definition and Lemmas

Lemma 1 (see [30].)The system is said to be finite-time input-to-state stable (FT-ISS) in a finite-time T with respect to δ, where ‖δ‖ ≤ σ, if the inequality for functions f₁ and f₂ is guaranteed for any t ≥ t₀ + T:

()

Definition 1 (see [32].)The gamma function is defined as

()

The fractional-order parameter α ∈ (0, 1).

Definition 2 (see [32].)The Mittag-Leffler function is defined as

()

And the k-th order derivative of the Mittag-Leffler function can be represented as

()

Definition 3 (see [33].)The Caputo fractional derivative is defined as

()

3.2. FTFOEESO Design

As demonstrated in Section 2, the second-order system of HV model can be written as

()

where

. And the internal and external disturbances are described as lumped disturbance Φ = (0 ϕ)^T.

The differential equations of general ESO can be described as

()

where β_i(e₁, t), i = 1, 2, 3 are gain functions, e₁ = x₁ − z₁, e₂ = x₂ − z₂, e₃ = ϕ − z₃.

According to the definition of error, the differential equation of estimation error can be expressed as follows:

()

For FTFOEESO, β_i indicates functions including fractional calculus operators:

()

where k is a positive integer.

Suppose

()

is a lower triangular matrix.

Select the gain functions as follows:

()

where

, and ω_e denotes the observer bandwidth. k₂₁, k₃₁, and k₃₂ should meet the following constraints:

()

At this point, FTFOEESO has been designed and completed.

3.3. Asymptotic Convergence Analysis

Let

; the ,System (24) can be written as

()

where

()

Theorem 1. The FTFOEESO observation error converges to zero under constant total disturbance if and only if γ > 2/3.

Proof 1. For System (32), the transfer function matrix can be obtained via the Laplace transformation:

()

where

. The transfer function matrix of

can be expressed as

()

where

()

Rearranging and analyzing Equation (31), we find

()

Since the observation error can only converge to zero if the integral order of the pole polynomial is higher than that of the zero polynomial, which ensures that the observation error can approximate a constant signal when the total disturbance changes slowly, we have

()

Thus, when γ > 2/3, the observation error can converge to zero and the System (32) is stable.

Theorem 2. Define q = 1/(1 − γ). If q is integer, the System (22) is stable.

Proof 2. Since q = 1/(1 − γ), can be expanded as follows:

()

We can get

()

The extra states are the fractional-order differential of integral-order states. Therefore, the transfer function matrix of τ can be expressed as

()

where

()

Since System (38) is derived from a linear transformation of System (32) and System (32) is stable, System (38) is also stable.

The relationship between and τ can be expressed as follows:

()

where

()

The solution of Equation (38) can be expressed as

()

where

and

. We can get

()

Combining the above transformations, we can get

()

Then, the FTFOESO is applied to HV control system, which is an integral-order differential system. The fractional-order differential states are obtained by numerical method. Therefore, the initial states of fractional order can be considered as zero. The inequality (42) can be expressed as follows:

()

Based on the transformation , one obtains

()

Thus, based on Lemma 1, the stability of System (22) has been proven.

3.4. Analysis of the Influence of Parameters

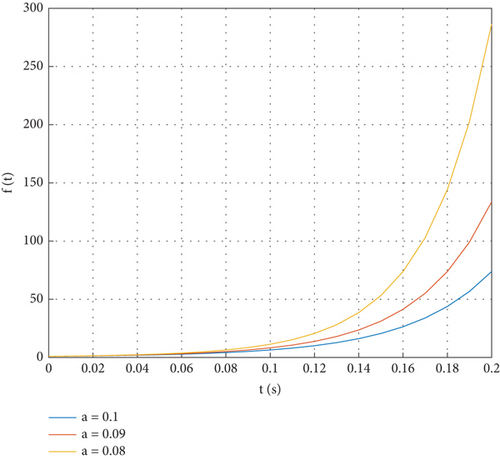
As shown in Figure 2, the smaller the value of the adjustment parameter a is, the greater the rate of increase in the time-varying function f(t), resulting in a swifter convergence speed for FTFOEESO.

For the system shown in Equation (24), the measurement noise is defined as x_1,N, and the differential equation system of observation error can be expressed as

()

And it can be written as follows:

()

where

. If the Laplace transform is applied to both ends of Equation (48), the noise transfer function can be expressed as

()

It should be noted that for FOEESO, the noise transfer function of the system is

()

The observation error of the state transformation after noise excitation can be expressed as

()

Substituting Equation (50) into Equation (51) while considering the inverse state transformation

, the state observation error of noise excitation can be expressed as

()

By organizing Equation (52), the transfer function matrix of state observation error under noise excitation can be obtained:

()

In practical applications, HV tends to generate periodic vibration noise signals with distinct frequencies. To mitigate the potentially serious adverse effects of this noise, it is generally advisable to attenuate the amplitude of the noise response beyond a specified frequency threshold. Within the FTFOEESO framework, it is desirable that under the excitation of noise, the response amplitude of z₃ above a specific frequency can be less than a certain degree. For the specific frequency ω_p and the amplitude frequency function,

()

the design parameters μ and ω_e can be used to make |G_NE,3(jω_p)| ≤ A_p and maximize the design bandwidth, where A_p is the noise suppression amplitude that meets the design requirements.

4. Simulation and Experimental Analysis

In this section, simulation comparative experiments are conducted to verify the control performance based on FTFOEESO under nominal conditions, disturbance conditions, and high-frequency noise conditions. To ensure fairness in comparison, all control system parameters are kept consistent, and the controller parameters are designed using a nonlinear parameter optimization method [25]. The expecting amplitude margin and phase margin are set as 8 dB and 45°, respectively. The controller parameter design is presented in Table 1.

Table 1. The parameters of controllers.

Parameters	Roll channel	Pitch channel	Yaw channel
k_p	82.13	198.68	74.94
k_i	10.14	1.65	0
k_d	20.09	19.39	17.39

Additionally, the initial state of the HV control system is V = 15 Ma, y = 33, 500 m, and γ_c = 1^°, while all other states are zero. The reference signal of attack angle and speed roll angle is set as 5°. And the desired sideslip angle is zero.

4.1. Nominal Conditions

The gain functions are defined as follows:

()

and the FTFOEESO degenerates into FOEESO. The bandwidth is set as ω_e = 100 rad/s, and the fractional coefficient is selected as μ = 1.2. The transform function is set as

, where a = 0.01.

Given the requirement for HV to have rapid response capabilities, the simulation duration for experimentation was set to 2 s. The corresponding results are illustrated in Figures 3, 4, and 5.

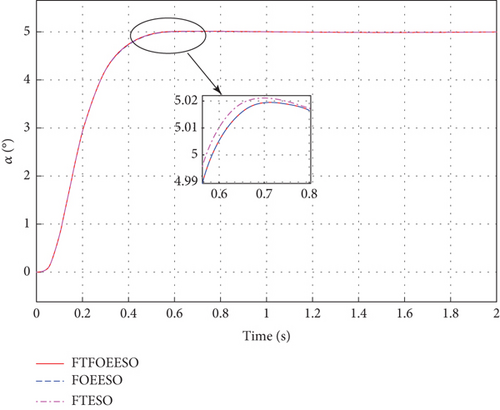
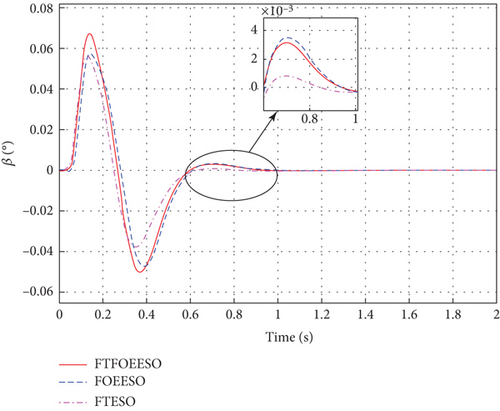
Based on Figures 3, 4, and 5, it is evident that the FTFOEESO-based ADRC system achieves stable control of HV successfully. While the control performance may be slightly lower compared to traditional FOEESO, there is a slight improvement in convergence speed, thereby validating the convergence capabilities of the proposed FTFOEESO to some extent. However, despite the advantages of the proposed method, the performance of FTESO remains more favorable under nominal conditions.

4.2. Disturbance Conditions

To validate the robustness of the system, the external disturbance is applied.

The rest of the conditions remain unchanged, and the results are showcased in Figures 6, 7, and 8.

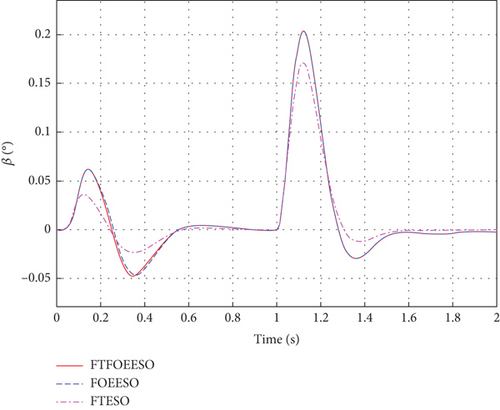
From the observations in Figures 6, 7, and 8, it is evident that the FTFOEESO-based ADRC system effectively mitigates the effects of disturbances on the system, thereby ensuring the stability of hypersonic aircraft attitude. Due to the strong coupling within the aircraft, even though disturbances are introduced only in the pitch channel, disturbances of varying magnitudes are generated in both the roll and yaw channels. However, ESO enables rapid compensation for these disturbances. Furthermore, FTFOEESO exhibits a slightly improved convergence speed compared to FOEESO.

4.3. High-Frequency Noise Conditions

The simulation conditions are consistent with those mentioned above. Besides, a sine wave f_n = 0.1^°sin40πt is applied to pitch channel as measurement noise. Figures 9, 10, and 11 display the simulation results.

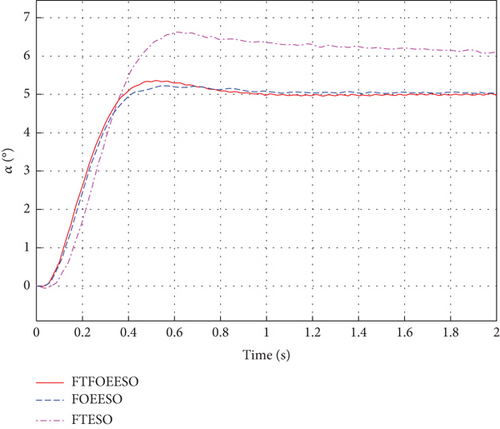
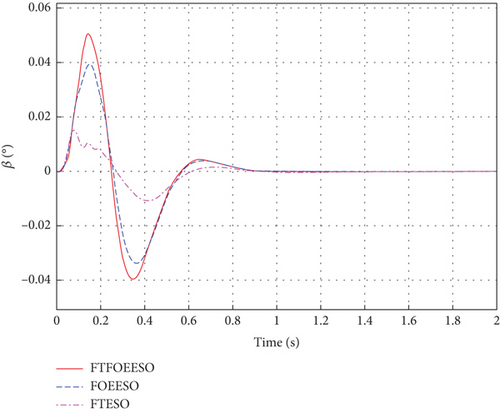
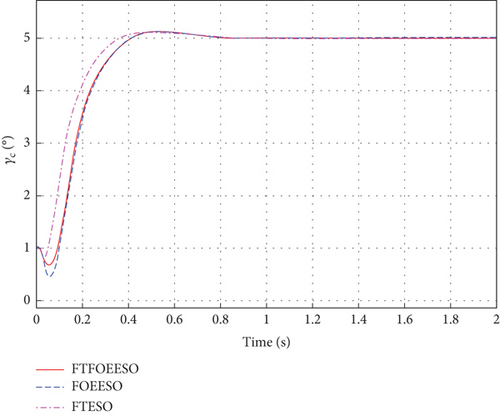
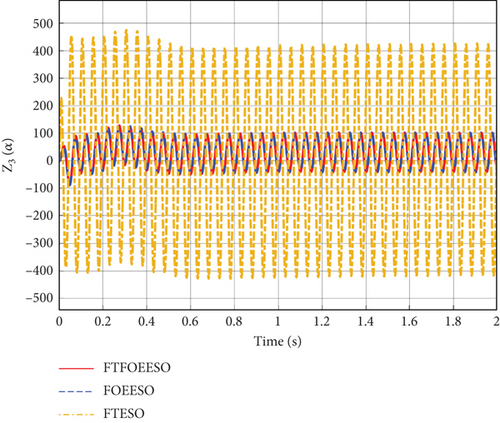
As depicted in Figure 9, the closed-loop control system of HV utilizing FTFOEESO-ADRC and FOEESO-ADRC exhibits enhanced resilience against high-frequency noise, shorter stability time, and reduced steady-state error when compared to FTESO-ADRC. The steady-state error is 80% smaller than that of FTESO. Additionally, Figures 9, 10, and 11 illustrate that FTFOEESO demonstrates a faster convergence speed than FOEESO, indicating its advantages in terms of noise resistance and convergence speed.

The estimation of the lumped disturbance is presented in Figure 12. It is evident that FTFOEESO successfully mitigates the influence of measurement noise on the total disturbance estimation. And it can be concluded that FTNFOESE exhibits superior anti-interference and antinoise capabilities compared to FTESO.

4.4. Semiphysical Simulation Verification

As shown in Figure 13, the hardware in the loop simulation system consists of onboard sensor, onboard autopilot, three-axis turntable, and real-time simulation computer.

The control period of the flight control is 0.001 s, and the parameters of the controller are set according to Table 2.

Table 2. The parameters of controllers in the loop simulation system.

Parameters	Roll channel	Pitch channel	Yaw channel
k_p	35.6616	45.4184	17.5936
k_i	0.8764	1.1374	0
k_d	9.4103	11.731	4.3911

To verify the robustness of FTFOEESO, a high-frequency noise as mentioned earlier is applied to the system. Experiments have revealed that during the hardware-in-the-loop simulation process, FTESO is prone to divergence when the noise amplitude is large. To ensure a more equitable comparison in the experiment, the amplitude of the noise is reduced to prevent the divergence of FTESO. And the experiment is shown in Figure 14.

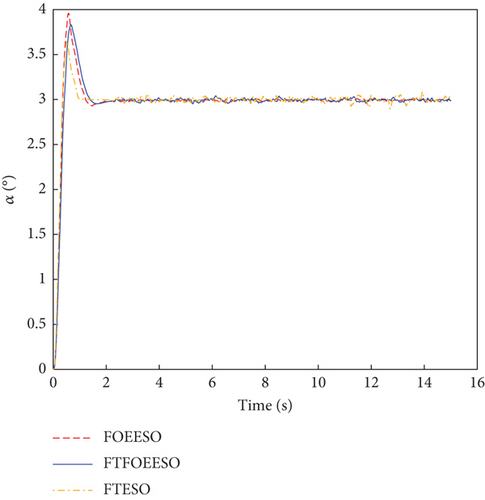
Based on the observation from Figure 14, it is evident that while FTESO exhibits fast convergence with minimal overshoot, it falls significantly short in terms of noise suppression compared to FTFOEESO and FOEESO. Conversely, the ADRC utilizing FTFOEESO showcases superior performance in terms of faster convergence speed and smaller overshoot, without a significant difference in noise suppression ability compared to FOEESO.

To further ascertain the observer’s performance, the mean error was employed as a metric to evaluate the noise suppression capability of each observer after introducing noise. The corresponding results are presented in Table 3.

Table 3. The mean error of controllers in the loop simulation system.

	FTFOEESO	FOEESO	FTESO
Mean error	0.0095	0.0126	0.0198

It is observed from Table 3 that the noise resistance of FTFOEESO has experienced a reduction of 34.4% in comparison to FOEESO. However, this decrease in noise resistance has only resulted in a marginal increase of 0.0031 in the overall mean error. Consequently, this increment can be considered negligible. Therefore, it can be concluded that FTFOEESO enhances the system’s convergence speed and dynamic performance while making only a minor sacrifice in terms of noise resistance performance.

In conclusion, this implies successful achievement of stable control for HV through hardware-in-the-loop simulation, signifying the practicality and applicability of the algorithm in engineering scenarios.

5. Conclusion

This paper introduces an ADRC method based on FTFOEESO to address the high dynamics and fast time-varying characteristics of HV. Firstly, the three channels of the HV are simplified and decoupled, dividing them into three second-order subsystems for easier control system design. Subsequently, FTFOEESO is designed and incorporated into the ADRC framework, and a controller is designed for HV, demonstrating the uniform boundedness of FTFOEESO. Lastly, in addition to the conventional simulation, the paper also employs a hardware-in-the-loop simulation system to demonstrate the effectiveness of the proposed algorithm. Compared to the traditional FTESO and FOEESO, simulation results indicate that although FTFOEESO’s dynamic performance is slightly lower than FTESO’s, it ensures stable attitude in noisy conditions. Additionally, it enhances FOEESO’s convergence speed without compromising noise resistance. Therefore, adopting FTFOEESO can effectively enhance the system’s performance in complex environments. Furthermore, the design of FTFOEESO and its degenerate form, FOEESO, utilizes only two free parameters. In future research, we aim to further explore the potential performance of FOEESO.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by Key Laboratory of Spacecraft Design Optimization and Dynamic Simulation Technologies, Ministry of Education, Beihang University.

Acknowledgments

The authors thank the colleagues for their constructive suggestions and research assistance throughout this study.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Ding Y. B., Yue X. K., Chen G. S., and Si J. S., Review of control and guidance technology on hypersonic vehicle, Chinese Journal of Aeronautics. (2022) 35, no. 7, 1–18, https://doi.org/10.1016/j.cja.2021.10.037.
10.1016/j.cja.2021.10.037
Web of Science® Google Scholar
2 Mu C., Ni Z., Sun C. Y., and He H. B., Air-breathing hypersonic vehicle tracking control based on adaptive dynamic programming, IEEE Transactions on Neural Network Learning System. (2016) 28, no. 3, 584–598, https://doi.org/10.1109/TNNLS.2016.2516948, 2-s2.0-84957645179.
10.1109/TNNLS.2016.2516948
PubMed Web of Science® Google Scholar
3 Li Z. H., He B., Wang M. H., Lin H. S., and An X. B., Time-coordination entry guidance for multi-hypersonic vehicles, Aerospace Science and Technology. (2019) 89, 123–135, https://doi.org/10.1016/j.ast.2019.03.056, 2-s2.0-85064001823.
10.1016/j.ast.2019.03.056
Web of Science® Google Scholar
4 Sziroczak D. and Smith H., A review of design issues specific to hypersonic flight vehicles, Progress in Aerospace Sciences. (2016) 84, 1–28, https://doi.org/10.1016/j.paerosci.2016.04.001, 2-s2.0-84964329418.
10.1016/j.paerosci.2016.04.001
Web of Science® Google Scholar
5 Sun J. G., Song S. M., and Wu G. Q., Fault-tolerant track control of hypersonic vehicle based on fast terminal sliding mode, Journal of Spacecraft and Rockets. (2017) 54, no. 6, 1304–1316, https://doi.org/10.2514/1.A33890, 2-s2.0-85035013597.
10.2514/1.A33890
Web of Science® Google Scholar
6 Zhao M. F., Hu Y. L., and Song J., Improved fractional-order extended state observer-based hypersonic vehicle active disturbance rejection control, Mathematics. (2022) 10, no. 23, https://doi.org/10.3390/math10234414.
10.3390/math10234414
PubMed Web of Science® Google Scholar
7 Liang S., Xu B., and Ren J., Kalman-filter-based robust control for hypersonic flight vehicle with measurement noises, Aerospace Science and Technology. (2021) 112, article 106566, https://doi.org/10.1016/j.ast.2021.106566.
10.1016/j.ast.2021.106566
Web of Science® Google Scholar
8 He N. B., Gao Q., Gutierrez H., Jiang C. S., Yang Y. F., and Bi Y. C., Robust adaptive dynamic surface control for hypersonic vehicles, Nonlinear Dynamics. (2018) 93, no. 3, 1109–1120, https://doi.org/10.1007/s11071-018-4248-4, 2-s2.0-85045285993.
10.1007/s11071-018-4248-4
Web of Science® Google Scholar
9 Sagliano M., Mooij E., and Theil S., Adaptive disturbance-based high-order sliding-mode control for hypersonic-entry vehicles, Journal of Guidance, Control and Dynamics. (2017) 40, no. 3, 521–536, https://doi.org/10.2514/1.G000675, 2-s2.0-85015077204.
10.2514/1.G000675
Web of Science® Google Scholar
10 Ding Y. B., Wang X. G., Bai Y. L., and Cui N. G., An improved continuous sliding mode controller for flexible air-breathing hypersonic vehicle, International Journal of Robust and Nonlinear Control. (2020) 30, no. 14, 5751–5772, https://doi.org/10.1002/rnc.5114.
10.1002/rnc.5114
Web of Science® Google Scholar
11 Guo J. G., Peng Q., and Zhou J., Disturbance observer–based nonlinear model predictive control for air-breathing hypersonic vehicles, Journal of Aerospace Engineering. (2019) 32, no. 1, https://doi.org/10.1061/(ASCE)AS.1943-5525.0000948, 2-s2.0-85054258288.
10.1061/(ASCE)AS.1943-5525.0000948
Web of Science® Google Scholar
12 Sun J. L., Yi J. Q., Pu Z. Q., and Tan X. M., Fixed-time sliding mode disturbance observer-based nonsmooth backstepping control for hypersonic vehicles, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2018) 50, no. 11, 4377–4386, https://doi.org/10.1109/TSMC.2018.2847706, 2-s2.0-85049323956.
10.1109/TSMC.2018.2847706
Web of Science® Google Scholar
13 Yu C. J., Jiang J., Zhen Z. Y., Bhatia A. K., and Wang S., Adaptive backstepping control for air-breathing hypersonic vehicle subject to mismatched uncertainties, Aerospace Science and Technology. (2020) 107, article 106244, https://doi.org/10.1016/j.ast.2020.106244.
10.1016/j.ast.2020.106244
Web of Science® Google Scholar
14 Liu J. J., Chen Z. Q., Sun M. W., and Sun Q. L., Practical coupling rejection control for Herbst maneuver with thrust vector, Journal of Aircraft. (2019) 56, no. 4, 1726–1734, https://doi.org/10.2514/1.C035338, 2-s2.0-85071278603.
10.2514/1.C035338
Web of Science® Google Scholar
15 Sumantri B., Uchiyama N., and Sano S., Least square based sliding mode control for a quad-rotor helicopter and energy saving by chattering reduction, Mechanical Systems and Signal Processing. (2016) 66-67, 769–784, https://doi.org/10.1016/j.ymssp.2015.05.013, 2-s2.0-84955721210.
10.1016/j.ymssp.2015.05.013
Web of Science® Google Scholar
16 Han J. Q., From PID to active disturbance rejection control, IEEE Transactions on Industrial Electronics. (2009) 56, no. 3, 900–906, https://doi.org/10.1109/TIE.2008.2011621, 2-s2.0-63149185343.
10.1109/TIE.2008.2011621
Web of Science® Google Scholar
17 Wang G. L., Liu R., Zhao N. N., Ding D. A., and Xu D. G., Enhanced linear ADRC strategy for HF pulse voltage signal injection-based sensorless IPMSM drives, IEEE Transactions on Power Electronics. (2018) 34, no. 1, 514–525, https://doi.org/10.1109/TPEL.2018.2814056, 2-s2.0-85043467392.
10.1109/TPEL.2018.2814056
Web of Science® Google Scholar
18 Tao J., Sun Q. L., Tan P. L., Chen Z. Q., and He Y. P., Active disturbance rejection control (ADRC)-based autonomous homing control of powered parafoils, Nonlinear Dynamics. (2016) 86, no. 3, 1461–1476, https://doi.org/10.1007/s11071-016-2972-1, 2-s2.0-84980022883.
10.1007/s11071-016-2972-1
Web of Science® Google Scholar
19 Patelski R. and Dutkiewicz P., On the stability of ADRC for manipulators with modelling uncertainties, ISA Transactions. (2020) 102, 295–303, https://doi.org/10.1016/j.isatra.2020.02.027, 32151392.
10.1016/j.isatra.2020.02.027
PubMed Web of Science® Google Scholar
20 Wu Z. L., Gao Z. Q., Li D. H., Chen Y. Q., and Liu Y. H., On transitioning from PID to ADRC in thermal power plants, Control Theory and Technology. (2021) 19, no. 1, 3–18, https://doi.org/10.1007/s11768-021-00032-4.
10.1007/s11768-021-00032-4
CAS Google Scholar
21 Hu Y. L., Wu M., Zhao K., Song J., and He B. J., ADRC-based compound control strategy for spacecraft multi-body separation, Aerospace Science and Technology. (2023) 143, article 108686, https://doi.org/10.1016/j.ast.2023.108686.
10.1016/j.ast.2023.108686
Web of Science® Google Scholar
22 Liu B. Y., Hong J. W., and Wang L. C., Linear inverted pendulum control based on improved ADRC, Systems Science and Control Engineering. (2019) 7, no. 3, 1–12, https://doi.org/10.1080/21642583.2019.1625081, 2-s2.0-85067192281.
10.1080/21642583.2019.1625081
Web of Science® Google Scholar
23 Yang Z. B., Jia J. J., Sun X. D., and Xu T., An enhanced linear ADRC strategy for a bearingless induction motor, IEEE Transactions on Transportation Electrification. (2021) 8, no. 1, 1255–1266, https://doi.org/10.1109/TTE.2021.3112972.
10.1109/TTE.2021.3112972
Web of Science® Google Scholar
24 Cao H. Y., Deng Y. T., Zuo Y. F., Li H. W., Wang J. L., Liu X. F., and Lee C. H. T., Improved ADRC with a cascade extended state observer based on quasi-generalized integrator for PMSM current disturbances attenuation, IEEE Transactions on Transportation Electrification. (2023) 10, no. 1, 2145–2157, https://doi.org/10.1109/TTE.2023.3286889.
10.1109/TTE.2023.3286889
Web of Science® Google Scholar
25 Gao K., Song J., Wang X., and Li H. F., Fractional-order proportional-integral-derivative linear active disturbance rejection control design and parameter optimization for hypersonic vehicles with actuator faults, Tsinghua Science and Technology. (2020) 26, no. 1, 9–23, https://doi.org/10.26599/TST.2019.9010041.
10.26599/TST.2019.9010041
Web of Science® Google Scholar
26 Naderolasli A., Hashemi M., and Shojaei K., Approximation-based adaptive fault compensation backstepping control of fractional-order nonlinear systems: an output-feedback scheme, International Journal of Adaptive Control and Signal Processing. (2020) 34, no. 3, 298–313, https://doi.org/10.1002/acs.3084.
10.1002/acs.3084
Web of Science® Google Scholar
27 Doostdar F. and Mojallali H., An ADRC-based backstepping control design for a class of fractional-order systems, ISA Transactions. (2022) 121, 140–146, https://doi.org/10.1016/j.isatra.2021.03.033, 33838876.
10.1016/j.isatra.2021.03.033
PubMed Web of Science® Google Scholar
28 Chen P. C., Luo Y., Zheng W. J., Gao Z. Q., and Chen Y. Q., Fractional order active disturbance rejection control with the idea of cascaded fractional order integrator equivalence, ISA Transactions. (2021) 114, 359–369, https://doi.org/10.1016/j.isatra.2020.12.030, 33422333.
10.1016/j.isatra.2020.12.030
PubMed Web of Science® Google Scholar
29 Naderolasli A., Shojaei K., and Chatraei A., Terminal sliding-mode disturbance observer-based finite-time adaptive-neural formation control of autonomous surface vessels under output constraints, Robotica. (2023) 41, no. 1, 236–258, https://doi.org/10.1017/S0263574722001266.
10.1017/S0263574722001266
Web of Science® Google Scholar
30 Razmjooei H., Palli G., and Abdi E., Continuous finite-time extended state observer design for electro-hydraulic systems, Journal of the Franklin Institute. (2022) 359, no. 10, 5036–5055, https://doi.org/10.1016/j.jfranklin.2022.04.030.
10.1016/j.jfranklin.2022.04.030
Web of Science® Google Scholar
31 Naderolasli A., Shojaei K., and Chatraei A., Finite-time velocity-free adaptive neural constrained cooperative control of Euler–Lagrange systems, Transactions of the Institute of Measurement and Control. (2023) no. article 014233122311546, https://doi.org/10.1177/01423312231154625.
10.1177/01423312231154625
Web of Science® Google Scholar
32 Jin B., Fractional Differential Equations, 2021, Springer International Publishing, Cham, Switzerland, https://doi.org/10.1007/978-3-030-76043-4.
10.1007/978-3-030-76043-4
Google Scholar
33 Luchko Y., Fractional derivatives and the fundamental theorem of fractional calculus, Fractional Calculus and Applied Analysis. (2020) 23, no. 4, 939–966, https://doi.org/10.1515/fca-2020-0049.
10.1515/fca-2020-0049
Web of Science® Google Scholar

All articles

A Finite-Time Fractional-Order Error Extended State Observer for Hypersonic Vehicle

Abstract

1. Introduction

2. Problem Formulation

2.1. Nonlinear HV Model

2.2. Linearized HV and Disturbance Model

3. FTFOEESO-ADRC-Based HV Attitude Control System

3.1. Some Definition and Lemmas

3.2. FTFOEESO Design

3.3. Asymptotic Convergence Analysis

3.4. Analysis of the Influence of Parameters

4. Simulation and Experimental Analysis

4.1. Nominal Conditions

4.2. Disturbance Conditions

4.3. High-Frequency Noise Conditions

4.4. Semiphysical Simulation Verification

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Finite-Time Fractional-Order Error Extended State Observer for Hypersonic Vehicle

Abstract

1. Introduction

2. Problem Formulation

2.1. Nonlinear HV Model

2.2. Linearized HV and Disturbance Model

3. FTFOEESO-ADRC-Based HV Attitude Control System

3.1. Some Definition and Lemmas

3.2. FTFOEESO Design

3.3. Asymptotic Convergence Analysis

3.4. Analysis of the Influence of Parameters

4. Simulation and Experimental Analysis

4.1. Nominal Conditions

4.2. Disturbance Conditions

4.3. High-Frequency Noise Conditions

4.4. Semiphysical Simulation Verification

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information