Orbit Determination of China’s Space Station Using Real ISL Measurements of the Tianzhou-6 Spacecraft
Abstract
Under most circumstances, the current studies related to precision orbit determination (POD) using intersatellite link (ISL) measurements are limited to ISL ranging components. In this article, we would like to discuss the idea of jointly using the GNSS observations and ISL ranging and orientation measurements of the Tianzhou-6 (TZ-6) spacecraft to generate the orbit solutions of China’s space station (CSS). Motivated by the requirement of mission implementation, the data processing procedure of the ISL orientation measurements is introduced based on the TZ-6 spacecraft attitude. The partial derivatives and the differential correction approach in a batch least squares estimator are elaborated on. This combined POD method concentrates on the connection between orbit determinations performed on the TZ-6 spacecraft using GNSS observations and on CSS using ISL ranging and orientation measurements, respectively. Realistic force, ISL measurements, and reference frame models are utilized to account for additional major error sources. Finally, the estimated solutions then are compared to the precision orbit ephemerides (POEs) of CSS. The statistical results demonstrate the effectiveness of the combined POD method.
1. Introduction
China’s Tianzhou-6 (TZ-6) cargo spacecraft was launched by the Long March 7 (LM-7) rocket from the coastal Wenchang Satellite Launch Centre at 9:22 p.m. (Beijing Time) on 10th May 2023. In around 10 min after the LM-7 rocket lift-off, the TZ-6 spacecraft entered its planned low Earth orbit with semimajor axis a = 6646.5 km and inclination i = 42.5° in the Earth-centred inertial frame. At 5:16 a.m. on 11th May, the TZ-6 spacecraft docked at the rear docking port of China’s Tianhe space station core module according to the China Manned Space Agency (CMSA) [1]. In the course of the Launch and Early Orbit Phase (LEOP), the orbital manoeuvre of the TZ-6 spacecraft was consistent with flight transitions of approaching, rendezvous, and docking.
For navigation, the TZ-6 spacecraft was equipped on board with a third-generation GNSS receiver of China’s BeiDou Navigation Satellite System (BDS-3). By July 2020, BDS-3 has completed the deployment of a hybrid constellation including 3 satellites in geostationary orbit (GEO), 3 satellites in inclined geosynchronous orbit (IGSO), and 24 satellites in medium orbit (MEO) [2]. To its intended purpose as a navigation aid, BDS-3 was capable of providing accurate positioning service for the TZ-6 spacecraft. For guidance, the TZ-6 spacecraft was equipped with laser radar and optical camera devices to provide ISL ranging and orientation measurement data of China’s space station (CSS). On the basis of such prerequisites, the objective of this study is to generate the orbit solutions of CSS through jointly using the real GNSS observations and ISL measurements on board the TZ-6 spacecraft.
Research related to the orbit determination using ISL ranging measurements from different observation sources has been studied in depth in the past decades. The US researchers, in the course of developing GPS, first proposed the autonomous navigation describing the capabilities of GPS satellites to navigate with the aid of using ISL ranging measurements between satellites in the GPS constellation [3]. Crosslink ranging measurements would be used by onboard computers to update the stored navigation messages that were based on trajectories predicted over an extended period of time through ground-based processing of tracking data [4]. ISL ranging measurements were also used by the Iridium satellites for estimating the clock offsets with accuracy at the 200-ns level [5]. In the meantime, the European researchers on GPS carried out relevant studies using ISL ranging measurements to improve the capabilities of GPS satellites. The research supported by one of the exploratory projects of the European Space Agency used intersatellite ranging and intersatellite communication links to bring potential improvements on a GNSS system navigation determination and the enhancement of the orbit and clock prediction accuracy [6]. The orbit determination approach was investigated by combining the ISL measurements and the L-band ground-based code/phase measurements to assess the accuracy of the future GPS constellation through using simulation data [7, 8]. A precision orbit determination (POD) method was tested by using GNSS and simulated ISL measurements to evaluate various ISL connectivity schemes and to assess the required quality of the ISL measurements in POD on the basis of simulations [9].
In addition to the US and European researchers above, the researchers in China also retained a keen interest in orbit determination using ISL measurements. Particularly in the course of developing China’s BDS-3 for the past 10 years, domestic researchers jointly processed ground-based tracking observations and ISL ranging measurements between satellites in the BDS-3 constellation in order to achieve the enhancement of the navigation capabilities. The autonomous broadcast ephemeris improvement methods using intersatellite ranging measurements were proposed in [10]. A method of correcting the pseudorange error up to 37%–76% in the batch least squares processing of the 4-day ground-based tracking data with the aid of ISL observation devices on board experimental BDS-3 satellites was discussed in [11]. The analysis was made on the orbit determination of six experimental BDS-3 satellites using ISL measurements and priori orbits with different levels of precision. As the ground-based observations are limited by the regional distribution of tracking stations, studies and experiments have been carried out with the processing of ISL measurements to achieve a high level of orbit precision for the BDS-3 satellite constellation. The batch processing and extended Kalman filtering (EKF) of intersatellite ranging measurements applied to the autonomous navigation of the BDS showed that the result of the orbit determination was 0.1 m in the radial direction and better than 1 m in three-dimensional (3D) directions, and the POD accuracy using EKF was better than 1.5 m in 3D with a priori information of clock bias [12]. The ISL-enhanced orbit determination was analyzed for eight BDS-3 satellites, using 10 domestic stations in China, and the result showed that the 3D position RMS was reduced from 1 to 0.5 m and the 24-h orbit prediction was also improved from 2 to 0.7 m, which was even better than the result of using the tracking data from 13 GNSS Monitoring and Assessment System (iGMAS) overseas stations [13]. Through processing 30-day ISL ranging measurements of 18 MEO satellites of BDS-3, the orbit error of POD was 3.40 m in 3D with the predicted EOP parameters [14]. A novel ISL-enhanced orbit determination strategy was proposed for the BDS-3 precise point positioning (PPP). The SLR validations of the BDS-3 satellite orbits demonstrated that the orbit accuracy was better than 10 cm in the radial direction [15].
All the studies and research work mentioned above on orbit determination using ISL measurements comprise exploratory studies. Only GPS Block IIR satellites have put satellite-to-satellite crosslink measurements and autonomous orbit determination into practice so far [16]. ISL space technology plays an important role in the enhancement of orbit determination to a high level of accuracy in contrast to that attained by the data processing of ground-based tracking sensors. Due to the fact that the ISL system potentially establishes links outside the atmosphere, the ISL measurements are not affected by atmospheric delays and they are also less impacted by multipath and interference than GNSS ground measurements [17]. Scalar radiometric ranging measurements taken along the line of sight between two satellites, that is, the space-observing satellite and the observed satellite, such as range or Doppler, would be a relatively easy way of obtaining tracking data, but these do not usually provide information on the absolute orientation of the orbits [18]. In particular, it needs to be pointed out that these investigations of the orbit determination methods utilized only the ranging components of ISL measurements in nearly all aerospace engineering scenarios. There are several aspects to be considered in simultaneously applying both ISL ranging and orientation measurements. Because the TZ-6 spacecraft has the capacity of providing the ranging and orientation measurement data on board, the present study would propose a combined POD method.
In this article, we would like to discuss the idea of jointly using the GNSS observations and the ISL ranging and orientation measurements obtained on board the TZ-6 spacecraft to generate the orbit solutions of CSS. In what follows, we shall primarily focus on several aspects in the present study. Firstly, the procedure of the intersatellite orientation data processing is introduced on the basis of the attitude determination of the TZ-6 spacecraft. Secondly, partial derivatives of observation components and the differential correction of a batch least squares estimator are elaborated on. Thirdly, the actual GNSS observations and ISL measurements on board the TZ-6 spacecraft are utilized to determine the CSS orbit. Realistic force, ISL measurement, and reference frame models are used in the orbit determination to account for additional major error sources. Finally, the accuracy of the combined POD method is then assessed by comparing the orbit solutions to the precision orbit ephemerides (POEs) of CSS.
2. Data
There are two exclusive BDS-3 receivers on board CSS and the TZ-6 cargo spacecraft, respectively. Each exclusive BDS-3 receiver is dedicated to flight guidance, trajectory positioning, and corrections in manoeuvre. To CSS, the B1/B2 code pseudorange, the B1/B2 carrier phase, and Doppler frequency measurements to BDS-3 satellites are acquired and transmitted to a ground telemetry tracking and control (TT&C) station. To the TZ-6 cargo spacecraft, due to the high dynamic feature of the spacecraft trajectory and the computational complexity, the B1/B2 code pseudorange and the carrier phase data are not used in the orbit determination. Alternatively, the broadcast ephemeris data processed on board the TZ-6 spacecraft are adopted in the orbit determination to assist flight transitions. And the accuracy of the orbit determination is up to 1.0~3.0 m. Each BDS-3 receiver works with a 1-s data sampling rate.
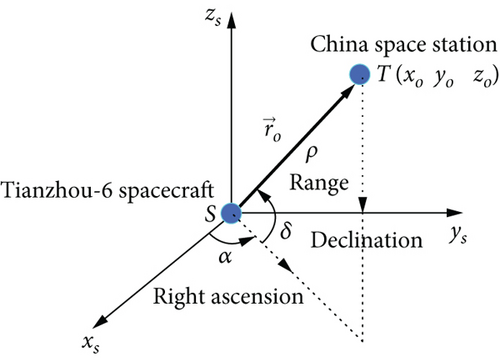
Multiple tracking and guidance devices are mounted on board the GNC subsystem of the TZ-6 spacecraft, including the laser radar and optical camera devices to provide the intersatellite measurement data from the TZ-6 spacecraft to CSS. These devices help implement the action sequence of proximity approaching, rendezvous, and docking. The error of intersatellite ranging measurement is calibrated on ground to be 0.2 m. The orientation measurements of the TZ-6 spacecraft relative to CSS are made on the basis of the TZ-6 spacecraft attitude. The error of intersatellite orientation measurement is around 0.056°. The conversion process of intersatellite orientation measurements (azimuth A, elevation E) between the TZ-6 spacecraft body–fixed coordinate system and the TZ-6 spacecraft–centred J2000 inertial system (right ascension α, declination δ) is shown in Figure 1.

The orientation measurements, azimuth A and elevation E converted to right ascension α and declination δ, are used in the orbit determination of CSS. Due to independent observation mechanisms, ISL ranging and orientation measurements usually do not share the same epoch time. For the purpose of positioning at an epoch time, the interpolation method is applied to obtain ISL ranging and orientation measurements at the same epoch time. The system error of ISL ranging measurements would influence the precision of the orbit determination, and one calibration method is put forward through the processing of ISL measurements [19].
Two variations in the orbit determination procedure, namely, the attitude determination accuracy of the TZ-6 spacecraft and the system errors of the ranging and orientation, are stochastic in nature and therefore are very difficult to predict accurately. One variation is the system errors of ISL measurements. They are estimated with the analysis of simulation results. Typical on-orbit satellites and realistic dynamic models are assumed in simulating the scenarios. From simulated results, while the system error of ranging is about 1 m, the position error of the orbit determination will be about 5 m when the relative distance between two spacecrafts is about 5 km. And while the system error of the orientation is around 0.083°, the position error of the orbit determination will be about 25 m. The system error of the orientation is partly due to the attitude accuracy of the observing spacecraft. The orientation measurement processing is based on the accuracy of the attitude determination of the observing spacecraft. The simulation results show that the impact of the orientation system error is apparently more than that of ranging. Hence, the eliminating method of orientation system error would certainly enhance the precision level of the orbit determination.
The other variation is the attitude accuracy of the observing TZ-6 spacecraft. We would like to present the real attitude information of the TZ-6 spacecraft in the form of Euler angles, which specify the orientation of the TZ-6 spacecraft body–fixed frame of reference relative to the orbital frame of reference, as shown in Figures 2, 3, and 4.
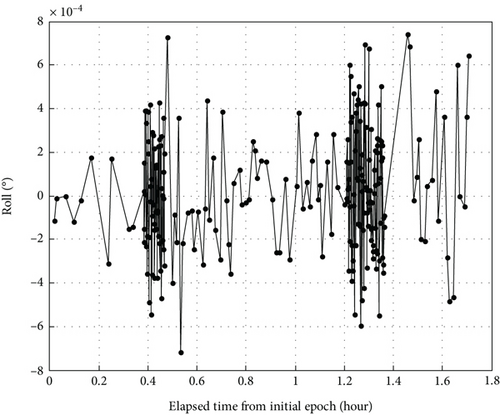
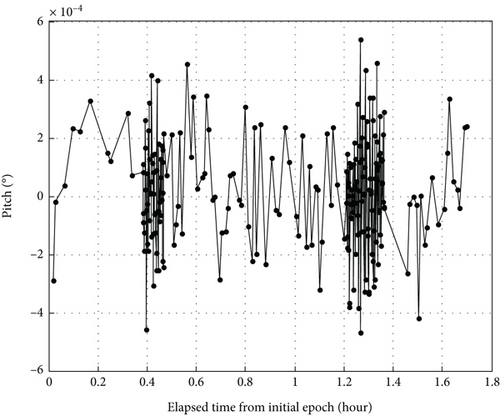
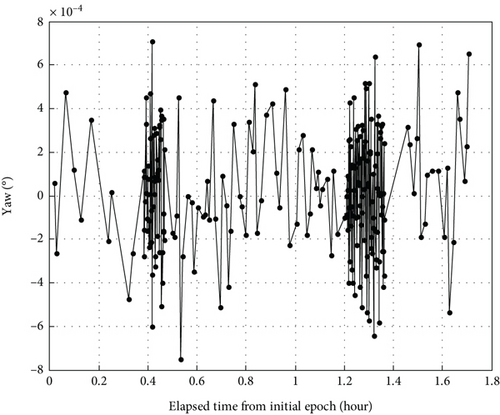
In Figures 2, 3, and 4, we could find that all the three Euler angles roll, pitch, and yaw are in the range of 0.0008°, very close to zero. In the arc of ISL measurements, the attitude control subsystem on board the TZ-6 spacecraft maintains the body-fixed frame of reference with the orbital frame of reference. Owing to such precision attitude determination, the orientation components of the ISL measurements could attain a relatively high level of accuracy.
Here, the two arcs of the GNSS observations and ISL ranging and orientation measurements downloaded from the TZ-6 spacecraft are listed in Table 1. The BDS-3 receiver on board works with the 1-s data sampling rate. And the laser radar and optical camera devices mounted on board the TZ-6 spacecraft provide the ISL measurements of CSS with the 3-s data sampling rate. In particular, the time length of each flight data arc is 1.6 h in terms of time, during which the TZ-6 spacecraft makes no manoeuvre.
| No. | Spacecraft ID | Observation type | Data arc (UTC) |
|---|---|---|---|
| 1 | TZ-6 | GNSS | 2023/05/10 18:41~20:17 |
| 2 | TZ-6 | ISL | 2023/05/10 18:41~20:17 |
To the orbit solutions of the TZ-6 spacecraft, both GNSS observations and ISL measurements will contribute to the differential correction of the orbit state of the TZ-6 spacecraft. Meanwhile, to the orbit solutions of CSS, the ISL measurements are to be used to generate the orbit of CSS on the basis of the precise positions of the TZ-6 spacecraft, expressed in a rectangular Cartesian inertial coordinate system, at each observation instance of time.
3. Method
- 1.
Download the GNSS observations and ISL ranging and orientation measurements and the attitude information through the telemetry receivers on board the TZ-6 spacecraft.
- 2.
Process the ISL ranging and orientation measurements on the basis of the attitude of the TZ-6 spacecraft. In particular, the orientation measurements are computed and transformed in frames of reference.
- 3.
Determine the orbits of the TZ-6 spacecraft and CSS jointly using the GNSS observations and the ISL ranging and orientation measurements of the TZ-6 spacecraft in a batch least squares estimator.
Realistic force, GNSS and ISL measurements, and reference frame models are utilized to account for additional major error sources. Because the arc length of the GNSS and ISL measurements is 1.6 h, we utilize a fixed atmospheric drag effect coefficient with a well-evaluated area/mass ratio. Considering the aerospace engineering application, the measurement noise is stochastic in nature. The GNSS and ISL measurements are jointly used and affected by observation errors. In order to evaluate the level of precision of the combined POD method, the estimated solutions then are compared to the POEs of CSS to overall reflect the influence degree of error sources.
3.1. Partial Derivative
In the geocentric J2000 inertial system, the observing TZ-6 spacecraft denoted as S and the observed CSS T are shown in Figure 5. At the epoch time t, the position of the observing TZ-6 spacecraft is and the position of the observed CSS is . The observation vector, from the observing TZ-6 spacecraft S to the observed CSS T, can be expressed in the form of vector as , and it is also expressed as.
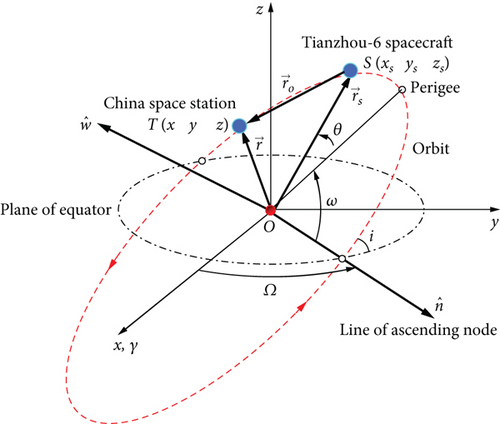
In the observing TZ-6 spacecraft–centred J2000 inertial system, the observation vector , which is from the observing TZ-6 spacecraft S to the observed CSS T, could also be expressed as . The observation vector is shown in Figure 6.
Meanwhile, the computed measurement components such as pseudorange ρc, right ascension αc, and declination δc are propagated by orbital dynamics models and transformed by measurement models.
At the initial epoch time t0, the observed CSS state is . At the observation epoch time t, the state is . The orbital state transition can be expressed as , and here Φ(t0, t) is the state transition matrix.
- a.
Where the pseudorange ρ is zero (ρ = 0) and does not carry any meaning.
- b.
Where the parameter κ is zero (κ = 0) and and do not carry any meaning.
The reason lies in the above-mentioned POD method using the downloaded ISL observations collected by the observing spacecraft, with the aim of obtaining the precise position information of the observed CSS. Therefore, it is unlikely to perform the POD method when and only when CSS is sufficiently close to the Zs axis direction of the observing TZ-6 spacecraft J2000 inertial system, that is, when CSS is hovering in the Zs axis direction of the observing TZ-6 spacecraft. However, it is possible to analyze the raw observations of CSS, so as to establish the relative position of CSS hovering in the Zs axis direction.
3.2. Differential Correction
The differential correction approach in a batch least squares mode is taken to generate the true solutions of the TZ-6 spacecraft and CSS, respectively. This approach uses the best available dynamic model and reference frame, given in Table 2. The major error sources of dynamical force models are considered to meet the accuracy requirements of the orbit solutions. The reference frame applied is following the IERS standards. The estimated parameters include position, velocity, and atmospheric drag effect.
| Force and reference type | Model and frame used in orbit determination |
|---|---|
| Earth’s gravity | JGM-3 model, truncated to 50 × 50 |
| Third-body perturbation | Jet Propulsion Laboratory Ephemerides, DE200 |
| Solid earth and tides | IERS Conventions 2010 |
| Ocean tides | IERS Conventions 2010 |
| Solid earth pole | IERS Conventions 2010 |
| Relativistic effects | IERS Conventions 2010 |
| Solar radiation pressure | Conical shadow model |
| Atmosphere drag | MSISE00 |
| Terrestrial frame | ITRF2014 |
| Earth orientation | Current EOP set |
| Estimated parameters | Position and velocity, atmosphere drag effect |
The GNSS observations and the ISL measurements are processed in a batch least squares mode to estimate the epoch conditions of the state vectors for the TZ-6 spacecraft and CSS. The state coordinates of the TZ-6 spacecraft and CSS are expressed in a rectangular Cartesian inertial coordinate system. The state vector consists of the spacecraft position and velocity. Due to the short observation arc, the scale parameter for the atmospheric drag is not solved. Alternatively, a constant of the scale parameter is utilized.
Using rigorous force models and frame, the orbit state of the TZ-6 spacecraft could be determined through the batch least squares method to an acceptable level of precision.
The residual in the course of differential correction could be computed as follows. At the epoch time tj (t > t0), the observation model gives ISL pseudorange ρo, right ascension α0, and declination δ0. The orbital dynamics models are extrapolated to give pseudorange ρc, right ascension αc, and declination δc, and the residuals of observation components at the epoch time tj could be expressed as Δρ = ρo − ρc, Δα = αo − αc, and Δδ = δo − δc.
According to the above derivation, we obtain the partial derivatives of the pseudorange ρo, the right ascension αo, and the declination δo with respect to the initial state of CSS T as Equation (2).
Similarly, we have the partial derivatives of pseudorange ρo, right ascension αo, and declination δo with respect to the initial state of the observing spacecraft S as Equation (4).
Through the above batch least squares recursive estimation, it is feasible to improve the estimated state vectors of the observing TZ-6 spacecraft S and that of the observed CSS T simultaneously. In the end, we could obtain the optimal solutions of the two sets of estimated state vectors, that is, and . Following the procedure, CSS and the TZ-6 spacecraft would have corrected solutions through the data processing of ISL ranging and orientation measurements.
3.3. Orbit Determination
As to the orbit determination using ISL measurements, it is needed to point out that there are currently three typical procedures. The first procedure is widely taken by use of only ISL ranging measurements, which requires fixing the state or ephemeris of one satellite to have the absolute orientation of the orbit solution to be observable. Because in the two-body problem, satellite-to-satellite tracking only provides information on the size, shape, relative orientation of the orbits, and the spacecraft positions along the orbits [22]. The second procedure is using only optical tracking and attitude information to find the direction vector between two spacecrafts and determine both orbits [23]. The third procedure is using crosslink range, attitude information, and an optical tracker to find the vector to another satellite and determine the orbits autonomously [24, 25]. Because the absolute orientation of the orbit solution is observable, it is not necessary to have the state of the observing satellite fixed. However, the attitude information of the observing satellite is essential to generate the ISL orientation components, which jointly indicate the vector direction from one satellite to another.
In this study, we would like to apply a combined POD method jointly using the GNSS and ISL ranging and orientation measurements downloaded from the TZ-6 spacecraft to obtain the orbit solutions of CSS. Motivated by the requirement of the TZ-6 spacecraft implementation, the combined POD method concentrates on the connection between the batch least squares estimators simultaneously performed on the TZ-6 spacecraft using the GNSS observations and on CSS using the ISL ranging and orientation measurements. In each iteration run, the epoch state of CSS is improved by processing the whole set of ISL measurements, while the epoch state of the TZ-6 spacecraft is corrected by processing the whole GNSS observations and the ISL measurements. For reference, Equation (2) gives the partial derivatives of the ISL measurement components with respect to the epoch state of CSS, and Equation (4) gives the partial derivatives of the ISL measurement components with respect to the epoch state of the TZ-6 spacecraft. It is noted that the combined POD method has not taken the state or ephemeris of the TZ-6 spacecraft as fixed. So, the GNSS observations and ISL ranging and orientation measurements of the TZ-6 spacecraft are jointly used to generate the orbit solutions of the TZ-6 spacecraft and CSS.
For validation, the actual flight data acquired on board the TZ-6 spacecraft have been utilized to test the combined POD method. To the present study, the flight data are composed of the GNSS observations and the ISL ranging and orientation measurements. In addition, the actual flight data are provided by the Xi’an Satellite Control Centre (XSCC) in China.
4. Results and Analysis
4.1. Orbit Determination Results
The GNSS observations and ISL measurements are jointly processed to determine the CSS orbit for the navigation and guidance of the TZ-6 spacecraft. In the aerospace engineering circumstance, the arc length of the ISL measurements is covering one period of orbital movements of CSS.
The 3D position residuals of the orbit determination of the TZ-6 spacecraft by use of the GNSS observations are depicted in Figure 7.
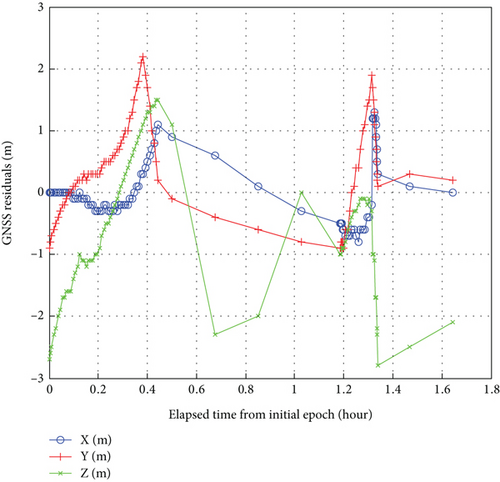
In Figure 7, it is shown that the GNSS residuals of the batch least squares estimator for the TZ-6 spacecraft are below 3.0 m. The state or ephemeris of the TZ-6 spacecraft could be considered an acceptable level of precision for the intersatellite observation applications. Taken as an observation station in space, the TZ-6 spacecraft obtains the ISL ranging and orientation measurements of CSS.
The residuals of the ISL measurement components in the orbit determination of CSS are shown in Figures 8, 9, and 10.
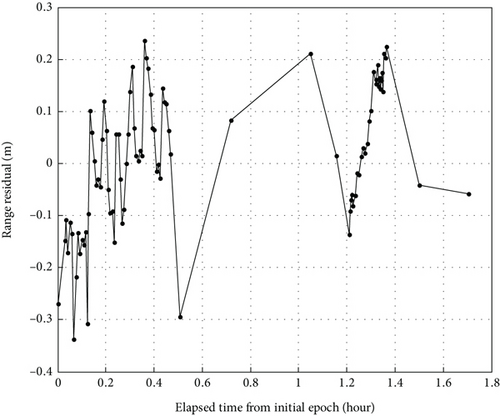
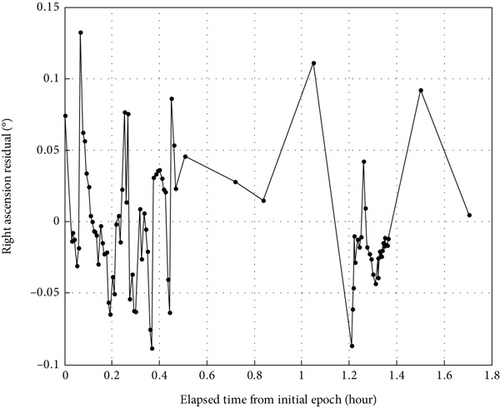
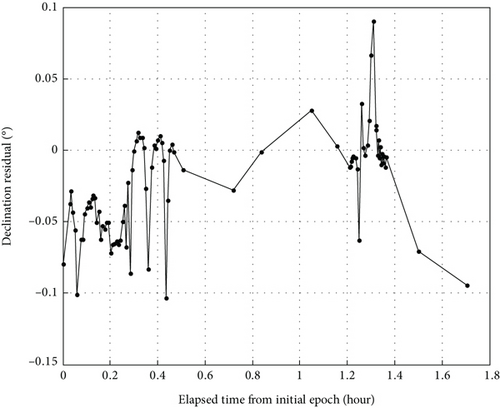
In Figures 8, 9, and 10, we could see the residuals of the pseudorange, right ascension, and declination components of the ISL measurements in the orbit determination of CSS. Figure 8 illustrates that the residuals of the pseudorange component using the real ISL measurements obtained on board the TZ-6 spacecraft are below 0.35 m. As depicted in Figure 9, the residuals of the right ascension component are below 0.15°. Also, as depicted in Figure 10, the residuals of the declination component are below 0.12°.
The orbit determinations are performed on the TZ-6 spacecraft and CSS. The statistical results listed in Table 3 are the RMS values of the batch least squares estimator using the GNSS observations and the ISL measurements, respectively.
| No. | Spacecraft and data type | Observation component | RMS of fit | Drag eff. |
|---|---|---|---|---|
| 1 |
|
Coordinate x | 1.51 m | 2.1 |
| Coordinate y | 1.89 m | |||
| Coordinate z | 2.48 m | |||
| 2 |
|
Pseudorange ρ | 0.16 m | 2.1 |
| Right ascension α | 0.04° | |||
| Declination δ | 0.04° | |||
In Table 3, one finds that the fitting RMS values of the GNSS observations processing are 1.51 m, 1.89 m, and 2.48 m for the coordinate components x, y, and z, respectively. Furthermore, the results of the ISL measurement processing reveal that the fitting RMS values are 0.16 m, 0.04°, and 0.04° for the ISL measurement components pseudorange, right ascension, and declination, respectively. Considering the aerospace engineering application, there commonly exist stochastic noise and even system bias in the 1.6-h ISL observation. Fortunately, owing to the accuracy of the ISL measurements, there is no system error involved, or any very small errors which can be neglected. Due to the short arc of ISL measurements, we could then use a fixed atmospheric drag effect coefficient 2.1 with a well-evaluated area/mass ratio.
4.2. Precision Assessment
To assess the precision of the combined POD method using the GNSS observations and ISL measurements, the orbit solutions are compared to the POEs of CSS. It is the true orbit solution of CSS, which is provided by the State Key Laboratory of Astronautic Dynamics (ADL) in China. The ADL processes more than 24-h GNSS observations and ground-based observations collected from the TT&C system to guarantee the high precision by use of rigorous orbit dynamics and frame systems. The GNSS observations of CSS in the form of broadcast ephemeris from the BDS-3 satellites are collected continuously from five fixed stations distributed in China. More than 24-h observations are collected from the TT&C system. In addition, the TT&C system is composed of four tracking stations in China and three tracking stations abroad.
By comparing the orbit solutions to the true solutions, namely, the CSS POEs, one finds the differences in the radial, along-track (ATRK), and cross-track (CTRK) directions and in the absolute position and velocity. The mean and maximum differences are listed in Table 4. It is noted that the velocity differences are listed in cm·s−1.
| Spacecraft (data type) | Residual | Radial | ATRK | CTRK | Pos./Vel. |
|---|---|---|---|---|---|
| TZ-6 (ISL measurements) | Mean position (m) | 1.53 | 2.56 | 0.37 | 3.00 |
| Max. position (m) | 2.16 | 3.80 | 0.67 | 3.80 | |
| Mean velocity (cm·s−1) | 0.18 | 0.13 | 0.04 | 0.22 | |
| Max. velocity (cm·s−1) | 0.26 | 0.20 | 0.07 | 0.27 |
In Table 4, it is clear that the mean difference of the position is 3.00 m and the maximum difference is 3.80 m, which is mainly in the ATRK direction followed by the radial direction. Likewise, in Table 4, one finds that the mean difference of the velocity is 0.22 cm·s−1 and the maximum difference is 0.27 cm·s−1, which is mainly in the radial direction followed by the ATRK direction.
For the further reference in detail, the orbit differences are shown in the following diagrams. The position differences are depicted in Figure 11, the velocity differences depicted in Figure 12, and the semimajor axis differences depicted in Figure 13.
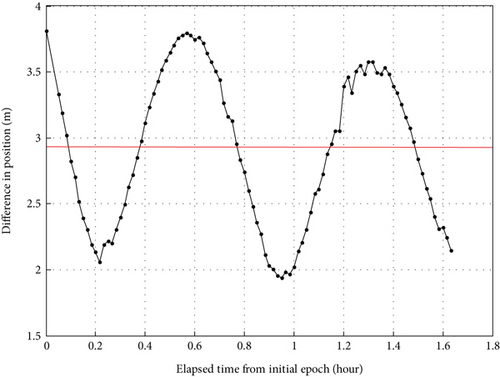
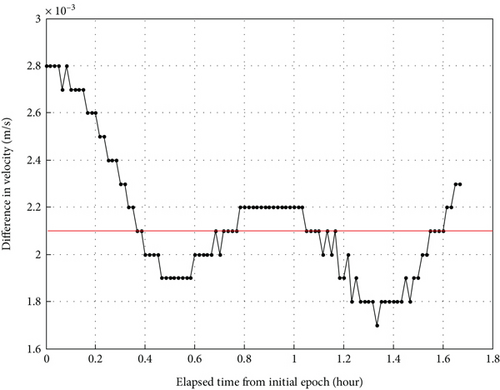
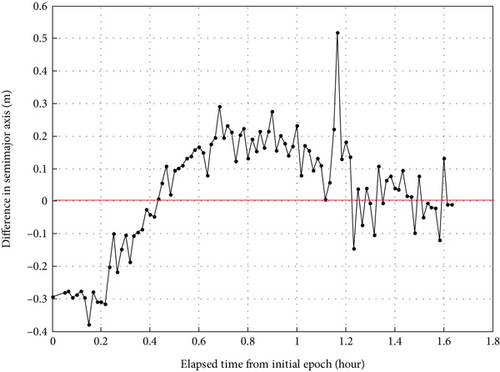
From the position difference diagram in Figure 11, it can be seen clearly that the position solutions attain the order of several meters in the radial, ATRK, and CTRK components of the orbit. Likewise, from the velocity difference diagram in Figure 12, one finds the velocity accuracy to be of the order of tenths of a centimeter per second in the radial, ATRK, and CTRK components of the orbit. And furthermore, it is clear that the mean difference of the semimajor axis component is zero, which is depicted in Figure 13.
5. Conclusions
A method of the combined orbit determinations is studied to generate the orbit solutions of CSS using the real GNSS observations and ISL measurements of the TZ-6 spacecraft. Under the aerospace engineering scenarios, the TZ-6 spacecraft is equipped on board with the BDS-3 receiver and laser radar and optical devices. The TZ-6 spacecraft has the capacity to provide the GNSS observations for itself and the ISL ranging and orientation measurements for CSS. Due to these prerequisites, the combined POD method reported in this article concentrates on the connection between the orbit determinations performed on the TZ-6 spacecraft using the GNSS observations and on CSS using the ISL measurements, respectively. The partial derivatives of observation components and the differential correction approach in the combined POD method are elaborated on. Realistic force, GNSS and ISL measurements, and reference frame models were utilized in the orbit determinations to account for additional major error sources.
According to the results of the batch least squares estimator using the real GNSS observations, the fitting RMS values are 1.51, 1.89, and 2.48 m for the coordinate components x, y, and z, respectively. And the fitting RMS values of the real ISL measurements are 0.16 m, 0.04°, and 0.04° for the measurement components pseudorange, right ascension, and declination, respectively. For validation, the estimated solutions of CSS are then compared to the true solutions in order to evaluate the precision level. Compared with the CSS POEs provided by the ADL, the mean difference of the position is 3.00 m and the maximum difference is 3.80 m, which is mainly in the ATRK direction followed by the radial direction. The mean difference of the velocity is 0.22 cm·s−1, and the maximum difference is 0.27 cm·s−1, which is mainly in the radial direction followed by the ATRK direction. And the mean difference of the semimajor axis is zero.
In conclusion, the evaluation results show that the combined POD method using the real GNSS observations and ISL measurements of the TZ-6 spacecraft could achieve an acceptable level of precision for the orbit solutions of CSS. Considering the observation complexity under the aerospace engineering scenarios, the orbit solutions are acceptable for the navigation and guidance of the TZ-6 spacecraft. Furthermore, since the processing of the orientation data on the basis of the spacecraft attitude is difficult to be very accurate, the high precision of the orbit determination using GNSS observations and ISL measurements would be met based on all kinds of more accurate data.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work is supported by the National Natural Science Foundation of China (NSFC, Grant No. 42074025).
Acknowledgments
Thanks go to the ADL for the professional technical support through the study and to iGMAS for the Earth orientation parameters downloaded from its website (http://www.igmas.org/). Further, the authors wish to acknowledge assistant engineers Shuang Chen and Zhenzhen Lu for their helpful instructions in the writing of this article. This work is supported by the National Natural Science Foundation of China (NSFC, Grant No. 42074025).
Open Research
Data Availability Statement
The flight data used in this contribution including GNSS observations and ISL measurements are provided by the Xi’an Satellite Control Centre, China. And the precision orbit ephemerides (POEs) of China’s space station (CSS) are provided by State Key Laboratory of Astronautic Dynamics (ADL) in China.




