Organic-inorganic heterojunction perovskite solar cells (PSCs) are of high interest due to their low manufacturing cost and higher power conversion efficiency (PCE). Hence, we study the opto-electro-thermal (OET) characteristics and investigate the optical and carrier transport and thermodynamic behaviors on the PSC. In this research, optical and electrical coupled behavior is investigated, and the results of this simulation are in the optimal state for nanoparticles (NPs) with a diameter of 50 nm: the short-circuit current (J_sc) of 18.05 mA/cm², the open-circuit voltage (V_oc) of 0.9406 V, and PCE of 14.15% were obtained. Then, by adding thermal behavior to optical and electrical physics, thermal effects and power losses in the solar cell were obtained. In this case, 221.5 W/m² Joule heat, 154 W/m² thermal heat, 123 W/m² Peltier heat, and 92.3 W/m² nonradiative heat waste power were achieved. Under these losses, the electrical parameters decrease. The parameters are J_sc = 21.74 mA/cm², V_oc = 0.94 V, and PCE = 13.53%. The best case is obtained for the structure without NPs.

1. Introduction

Today, with the progress of humans in various fields, dependence and necessity for energy is increasing more and more due to its high demand. This energy demand has been shown in different ways [1–5]. In recent years, a new generation of solar cells called perovskite solar cells (PSCs) has been able to occupy a special place compared to new generations of solar cells, so that the power conversion efficiency (PCE) of these solar cells has increased from 3% to 23% in a short period [6–12]. These cells have been noticed due to relatively simple and cheap construction as well as high PCE. Another advantage of these cells over previous generation of solar cells is that they respond to sunlight at more wavelengths, which causes high carrier mobility, high open-circuit voltage (V_oc), and long emission length [13–20]. For this reason, researchers are looking for PSCs to obtain more profit in solar cells [21–25]. One of these ways is to utilize the plasmonic effects of metal nanoparticles (NPs) in the structure of solar cell for increasing the PCE value [26–28]. Noble nanometals such as gold (Au), silver (Ag), and copper (Cu) have been considered due to their high plasmon resonance in the visible region [29]. By using them, the absorption capacity of light is increased, which increases the energy generation in the system and increases the PCE in the cell. To increase the PCE value, the short-circuit current (J_sc) and V_oc should be increased, where for optimizing the value of J_sc, the carrier generation rate can be increased and the recombination rate of the system can be reduced, which this has a direct effect on J_sc. In order to increase the rate of carrier generation, the amount of the absorption layer (i.e., perovskite) can be increased, which, in addition to increase the manufacturing cost [30–32], causes the carriers generated in the active layer (AL) to recombine before reaching the lower metal contact due to the lengthening of the diffusion path and increase the recombination [33–35]. For this purpose, to reduce the cost and increase the PCE, researchers use metal NPs, which this reduces the thickness of the AL, while the PCE of the cell does not decrease [36]. With the presence of metal NPsin the AL, the amount of electric field in this layer and absorption increases. Naturally, the generation rate decreases, but the presence of metal NPs and the increase of the electrical field in the AL compensate for this decrease in absorption and generation. There is another method to reduce the cost and improve the PCE by trapping the light, which allows the PSC structure to absorb sunlight with an AL thinner than the intrinsic absorption length of the material. It reduces the thickness of the perovskite layer and thus reduces the cost of cell manufacturing. Also, light trapping improves the cell PCE because a thinner cell increases the value of V_oc due to the creation of better optical charge carriers [37]. In plasmonic structures, using metal NPs such as Au, Ag, and Cu and creating surface plasmon resonance (SPR), they absorb and trap more sunlight. LSPR excitation and its characteristics are affected by electrical properties, dimensions, shape, and temperature properties of NPs as well as the dielectric material around them [38–41]. Increasing the distance from the surface of metal NPs decreases the amount of electromagnetic field, which in this process increases the electromagnetic field due to radiation effects and the scattering of light in the near field and far field [42–45]. In the near field, by coupling the plasmonic dipole field and the dipole field of the AL, they increase the interaction of light and materials together and enhance the electric field around the NP [46, 47]. The stability of PSCs can be influenced by the addition of plasmonic NPs. The incorporation of plasmonic NPs in perovskite materials can influence various factors such as electrical conductivity, surface roughness, perovskite crystal quality, and surface passivation, all of which are crucial for the PCE and stability of PSCs [48]. Plasmonic NPs can enhance the optical and electrical characteristics of PSCs, leading to improve device performance and stability [49, 50]. Additionally, the presence of plasmonic NPs may favor the chemical stability of the perovskite material, further contributing to the stability of the solar cells [29]. Therefore, the addition of plasmonic NPs holds promise for enhancing the PCE and stability of PSCs.

Among the features of surface plasmonic NPs, we can mention the enhancement of absorption and scattering and the increase of the electromagnetic field to facilitate the transport of the carrier to improve the electrical properties [51]. As we know, the perovskite (CH₃NH₃PbI₃) absorption range is less than 650 nanometers; that is why we use plasmonic NPs to improve the absorption in infrared wavelengths near the sun’s spectrum [52, 53]. In one of the studies, the amount of plasmon in the AL can be adjusted by changing the size, geometry, location, and type of material, and the plasmon in the wavelengths of 650 to 800 nm, which we had a loss in the AL, was increased by metal NPs [54–56]. The change in the plasmonic properties of Ag is due to the favorable conditions in its metal oxidation [57].

In the past years, the PCE in PSCs has reached 25%. Perovskite light absorbers have unique advantages, including high absorption coefficient, long carrier emission length, and low exciton binding energy [58–60]; the intrinsic (or lightly doped) perovskite layer is sandwiched between the hole transport layer (HTL) and the electron transport layer (ETL) so that a pair of heterojunctions is formed, which ensures the separation and efficient transport of photocarriers. In SCs, there are important thermal effects and losses in the system that lead to an increase in the cell temperature and affect the stability of the cell. Among the thermal losses can be heating, Joule, and Peltier heat, which causes a decrease in stability in the system [57, 61–63].

Recently, 3D simulation platforms have been presented with detailed models that can couple optical-electrical-thermal modules. Although solar cells are thermodynamic devices, the heat generation and dissipation mechanisms in these devices have rarely been investigated, specifically through modeling or simulation analysis. Also, in solar cells, the heat in the cell itself can be heated and affect the PCE of the cell, including this thermal heat can refer to self-heating and heating from light [64, 65]. In solar cells, a large part of the sun’s energy absorbed by the cell is converted into heat in various ways, increasing the cell temperature and reducing the cell’s PCE [8]. So, thermal losses play a significant role in the operation of solar cells, which have been rarely examined in the articles. Therefore, photovoltaic solar cells are also conventional thermodynamic systems in addition to optical and electrical systems [66, 67]. In previous studies, the working conditions of ideal cells were mainly assumed (air mass index 1.5, solar radiation Ps = 1000 W/m², and ambient temperature T_amb = 25^°C), and it was assumed that the operating temperature of the cells (T) is equal to T_amb [67, 68]. On the other hand, when the solar cell is exposed to sunlight, the temperature of the cell increases, and it affects the PCE of the cell. In this model of research, Maxwell’s equations are used to perform optical studies counting absorption, generation, and transfer of reflection carriers. Then, we obtain the different mechanisms of surface and mass recombination and carrier diffusion caused by the carrier concentration gradient, examine the cell electrically, and calculate and examine the cell temperature. All the energy absorbed in the solar cells cannot be used in the electrical part of the structure, because in the system, part of this energy is converted into heat (Joule heat, Peltier heat, etc.) or in the form of photons through optical recombination and it will be wasted. After the optical and electrical investigations, solar cells are thermodynamically analyzed, including heat generation (due to heating, Joule heat, Peltier heat, and recombination heat) and heat loss (such as convective and radiative cooling) [69]. In the previous articles, attempts were made to investigate optical and electrical physics, but in some paper, reports about the OET system have also been reported. In recent years, opto-electro-thermal (OET) modeling has been investigated in some studies, in which radiation cooling technology has been investigated in the effective cooling of systems. In this model, a silicon-based (SC) radiative cooling solar cell was investigated (OET), in which the effects of radiative cooling, thermodynamic and electrodynamic behaviors of carriers, temperature effects, and physical and thermodynamic analysis parameters were investigated. In this model, solar cells with radiation cooling and without radiation cooling have been compared, which shows that the temperature of the silicon-based solar cell can decrease to 10%, and for this reason, the PCE of the solar cells can be increased by 0.45% [69, 70].

Figure 1 shows the simulation structure which has been optimized in recently reported work [13] in which the top interface is indium tin oxide (ITO) with a thickness of 50 nm. An ETL of titanium dioxide (TiO₂) with a thickness of 50 nm, an AL of perovskite (CH₃NH₃PbI₃) with a thickness of 200 nm, an HTL of copper thiocyanate (CuSCN) with a thickness of 600 nm, a bottom metal interface made of gold (Au) with a thickness of 100 nm, and a metal (Ag) NP with the diameters of 5 to 100 nm in the middle of the AL are formed. TiO₂ has a suitable energy band, and the process of manufacturing and layering is easier in it. Also, this material reduces recombination and increases shunt resistance and acts as a hole-blocking layer [70–72].The AL of this structure consists of perovskite (CH₃NH₃P_bI₃), which has easier manufacturing and synthesis, higher PCE, lower production cost, high absorption of the sunlight spectrum, stability of the energy band, and more carrier emission. The HTL is made of a structure consisting of copper thiocyanate (CuSCN), which is an inexpensive mineral. Other features of this material include better hole transport, a large bandgap, and an easier manufacturing and synthesis process. The matching of its energy levels with perovskite reduces carrier recombination and improves carrier extraction, thus improving the fill factor (FF) and the PCE in a solar cell [73].

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Structure of the simulation in the planar structure and the dimensions and components of the layers of the solar cell. (b) Structure of the solar cell when Ag NPs with different diameters are placed in the middle of the perovskite layer.

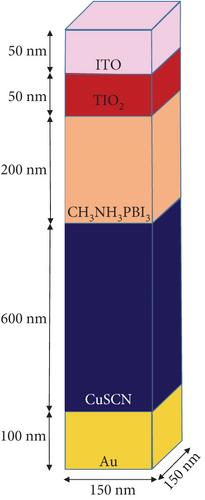
In this work, we must obtain the results of optical, electrical and thermal simulations through finite element method (FEM). Our simulation is done in three parts: optical, electrical and thermal. The material parameters for simulation are given in Table 1 [74, 75]. The optical part is used to find the absorption, reflection, and transmission parameters obtained by obtaining the distribution of the electromagnetic field through the solution of Maxwell’s equations. Then, using the obtained results, the electrical part of the solar cell is obtained, which is solved in the electrical theory of the coupled electron/hole transport equations and the Poisson equation for the electrostatic potential. In the thermal part, the thermodynamic equations of the carrier and thermal diffusion or generation processes and macroscopic heat loss are obtained through heat diffusion equations under the principle of conservation of energy.

Table 1. Electrical parameters utilized in solar cell simulation where the unit of temperature is Kelvin (K) [71, 72]. The parameters used in this table are as follows: μ_e0 = 6.5 cm²/V·s, μ_h0 = 3.8 cm²/V·s, τ0 = 2530 ns, A₀ = 1.1 × 10⁻²⁹ cm⁶/s, and B₀ = 5 × 10⁻¹³ cm³/s.

Parameter	TiO₂	CuSCN	CH₃NH₃PbI₃
ε_r	9	10	6.5
N_C (cm^-3)	1 × 10¹⁹	1.79 × 10¹⁹	1.66 × 10¹⁹
N_v (cm^-3)	1 × 10¹⁹	2.51 × 10¹⁹	5.41 × 10¹⁹
μ_n/μ_p (cm²/V·s)	20/10	25/25	50/50
X (eV)	4	1.9	3.93
E_g (eV)	3.2	3.4	1.55
N_A (cm^-3)	—	5 × 10¹⁸	5 × 10¹³
N_D (cm^-3)	5 × 10¹⁸	—	—
τ_n/τ_p (ns)	5/2	5/5	8/8
N_t (cm^-3)	1 × 10¹⁵	1 × 10¹⁴	1 × 10¹¹-10¹⁷
A_n/A_p	—	—	2.85786 × 10⁻²⁶
B	—	—	2.82 × 10⁻⁹

Here, we start using Maxwell’s equation to analyze the characteristics of light:

()

where E and H are the electric and magnetic field intensities, respectively, ε is the permittivity, μ is the permeability, and σ is the electrical conductivity.

The maximum energy of sunlight in a vacuum is 300 nm. In these solar cells, light absorption reaches zero after the wavelength of 800 nm because the bandgap of perovskite material is equal to 1.55 eV; in a result, the input light power will be Am1.5, and our simulation spectrum is in the range of 300 to 800 nm.

The carrier generation rate per arbitrary wavelength is calculated through the electric field intensity obtained from the above equations, as

()

where ℏ is the reduced Planck’s constant and ε^′ is the imaginary part of the relative permittivity defined as ɛ_r (λ) = (n(λ) − i k (λ))² as a function of wavelength. Now, to obtain the voltage-current characteristic curve (I-V) and carrier density, we must get the electrical characteristics, which are obtained here by simultaneously solving the Poisson equation and the electron and hole continuity equations:

()

denoting the electron charge with q, the electrostatic potential with φ, and the vacuum permittivity with ε₀. The recombination rates of electrons and holes are U_n and U_p, respectively. J_n and J_p are the current density of electrons and holes in order, and G_n and G_p are the total generation rate of electrons and holes, respectively. The assumption is G_n = G_p = G_tot. The charge density ρ is obtained from the following formula:

()

where n and p are the electron and hole concentrations and N_A and N_D are the electron acceptor and electron donor densities, respectively. Here, the carriers generated in the optical part are used as input to calculate the electron and hole densities in the electrical model. In solar cells, the relationship between current and voltage in the electrical model is calculated as follows:

()

where J_dark is a parameter that does not depend on the carriers of the AL but depends on the voltage applied to the cell, while J_sc is the opposite of the dark current and depends on the carriers of the AL and the current is in the presence of sunlight and is independent of voltage. The amount of gain in solar cells is obtained by calculating J_sc and V_oc.

()

where G_opt is the carrier generation rate that is the radiative process, and R_total is the recombination mechanism of the nonradiative process.

1.1. Plasmon

May’s theory can be used in analyzing the behavior of metal NPs exposed to sunlight. When the NPs are small, the field is created a little around them. But while the large NPs fall into the AL, the lights are scattered in different directions after colliding with the NPs [76].

The parts of lighting and absorption of light are as follows:

()

In this equation, ε_p is the particle dielectric function, V is the volume of the particle, and ε_m is the dielectric function of the embedding medium. It can be seen that the particle polarization becomes very large when ε_p = −2ε_m. It is known as the exacerbation of the surface plasmon resonance (SPR). In SPR, the cross-sectional cross-section can exceed the geometric cross-section of the particle [77].

1.2. OET Theory

Now we examine thermal physics. To solve the equations in the thermal state, we add the thermodynamics to the structure, but should note that the optical, electrical and thermal responses are examined simultaneously. After solving the Maxwell equations for the optical part and using them as inputs to the electrical part, also solving the Poisson equations, we can obtain the electron/hole transport characteristics. For thermal physics, carrier thermodynamic equations and simultaneous heat emissions must now be dissolved to calculate the energy absorption of carrier heat and relaxation under the principle of energy survival. The purpose of calculating the losses in this work is to bring the simulation results closer to reality and find destructive factors in the cell PCE.

Table 2 shows the thermal parameters related to different parts of the solar cell structure used for the simulation [78–80].

Table 2. Thermal parameters of various sections for the simulation of solar cell structure [80].

Parameter	ITO	TiO₂	CH₃NH₃PbI₃	CuSCN	Au
ρ	5560	3900	4286.4	2840	19300
K	31	4.8	0.59	2.39	129
C_m	128	683	308	800	318

The OET model can be expressed as follows [81–84]:

()

where k₀ is the wave vector in free space (vacuum), ε_c is the frequency-dependent complex permittivity, g (x, y, z, λ) is the light generation rate of the carriers at a specific wavelength λ at the position (x, y, z), n(p) is the electron (hole) concentration, D_n (D_p) is the electron (hole) diffusion coefficient, and

(

) is the electron (hole) thermal diffusion coefficient. N_c (N_v) is the conduction valence) band effective density of states, μ_n (μ_p) is the electron (hole) mobility, U is the total mass recombination, Φ is the electrostatic potential, ε₀ (ε_r) is the vacuum (relative) permittivity, C is the impurity concentration, κ is the thermal conductivity, T is the space-dependent temperature inside the device, and H is the heat source in the PSC at a steady state.

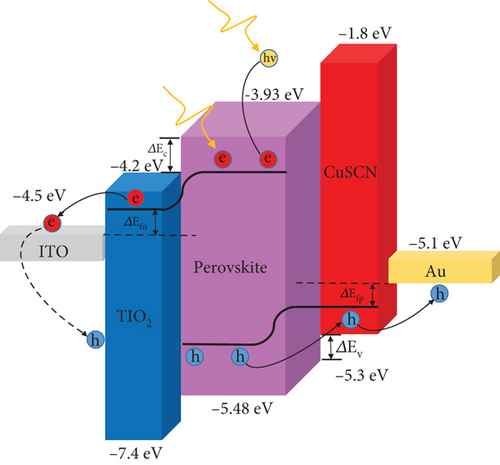
As we know, the carrier transfer equations are temperature-dependent because the network temperature gradient acts as an additional force to move the carriers. The diagram in Figure 2 shows the schematic of microscopic processes in photovoltaic systems and the energy band in SCs, where the incident photons deliver energy to the carriers and release light current and heat.

1.3. Heat Producing Factors

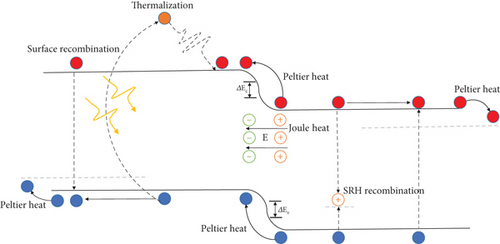
In this work, after performing optical calculations and obtaining its parameters with the help of the electrical model, we take the current-voltage characteristics, and by pairing it with the thermal module, we obtain the thermal losses. Figure 3 shows the heat generation factors in the system and how heat is released; in the following, we will examine each one separately.

There are 5 factors in heat generation in thermodynamic systems as follows:

(i)
Thermalization: when the energy of the incoming photon is greater than the bandgap, hot electrons are generated in the conduction band (created by hot photons (h_v > E_g)); due to creating their instability at this level, they tend to reach stability, that is why the electrons, the hot ones, come down from the edge of the conduction band and release their energy in the form of heat.

()

where G_tot (x, y, z) is the overall light generation rate for each wavelength in the solar spectrum and T_room is the room temperature

(ii)
Joule heat (H_Joule): which is generated due to the movement of carriers under the electric field and the flow of light in the discharge area where the electric field is strong:

()

where J_ph is the total light flux.

(iii)
Nonradiative recombination heat (H_non-rad): which is obtained from the sum of nonradiative recombination such as the SRH recombination and Augur recombination. Nonradiative recombination generates heat after electron recombination to midgap defects and energy exchange between carriers, respectively.

()

where n₀ and p₀ are the initial concentrations of electrons and holes in the equilibrium state, n_i is the intrinsic carrier concentrations, and C_n/p and S_n/p are the Auger recombination coefficients and the surface recombination rate of electrons and holes

(iv)
Surface recombination: which occurs due to heat generation on the surface of traps/defects due to recombination:

()

(v)
Peltier heat: it occurs when electrons (holes) fall from the conduction band (valence band) to the quasi-Fermi surface before being collected by the external circuit, producing heat.

()

Note that H_th, H_Joule, and H_non-rad are volumetric heat components with units of watts/volume (W/m³), while

, H_surf, and

are defined with units of watts/area (W/m²). The boundary thermal factors are applied at the top and bottom boundaries of the cell. To validate the structure of the PSC in the thermal part, different thermal parameters from previous works are listed in Table 3

Table 3. The solar cell structure for the thermal part [8].

	Thermalized heat	Joule heat	Peltier heat	Total recombination heat
Power density (W/m²)	131.9	37.05	83.23	16.79

To validate this work with past articles, the simulation results in past articles are given in Tables 4 and 5 [50, 57, 69, 77].

Table 4. Heating parameters of simulation.

	Thermalized heat	Joule heat	Peltier heat	Total recombination heat
Power density (W/m²) [69]	248.83	83.20	53.93	34.73
Power density (W/m²) [57]	156.68	121.29	31.02	14.32

Table 5. Electrical parameters of solar cell simulation.

	PCE	FF	J_sc	V_oc
Values of electrical parameters [77]	14.77	84.04	18.3	0.96
Values of electrical parameters [50]	14.83	69.9	21.48	1.00

1.4. Heat Dissipation Pathways

Solar cells must be in thermal interaction; for this reason, as mentioned above, the mechanisms mentioned above cause an increase in the temperature in the cells, so the cell must be in thermodynamic equilibrium, so the heat also passes through several paths called convective and radiative cooling, which, given by the following equations, diffuses from the cell:

()

where e, s, h, and T are surface emissivity, Boltzmann’s constant, convective heat coefficient, and device temperature, respectively. We set e_ITO = 0.2 [50].

1.5. Simulation Procedure

Our simulations consist of two stages; in the first stage, optical simulations are performed to obtain the light generation rate (G_tot) that is used as input for the electrical module to provide the current-voltage (I-V) characteristics, as well as the temperature of the semiconductor. At this stage, the PSC is optimized by changing the NP radiation and the effect of plasmonic effects. When the Ag NP with a radius of 25 nm is located in the AL, the PCE has the highest value. In the second stage, the temperature distribution calculated in the coupled modules of the first stage is calculated.

2. Results and Discussion

Figure 4 shows the absorption diagrams and generation profiles in the solar cell for wavelengths from 300 to 800 nm. The absorption diagram is shown in Figures 4(a) and 4(b), and the generation rate is demonstrated in Figures 4(c) and 4(d) for wavelengths from 300 to 800 nm in the structure. At wavelengths around 300 nm, more incident light is generated by the ITO and TiO₂ layers. As the wavelength increases, the absorption rates in these two layers will be decreased, where the AL (CH₃NH₃PbI₃) absorbs light at wavelengths between 300 and 800 nm. At the same time, from 550 nm onwards, the amount of absorption in this layer gradually decreases, and at the wavelength of about 750, this decrease becomes more intense.

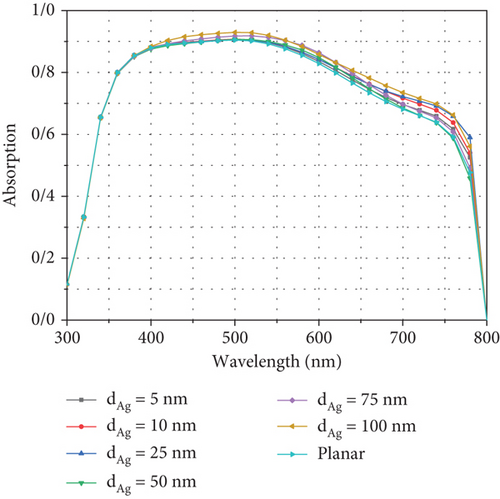
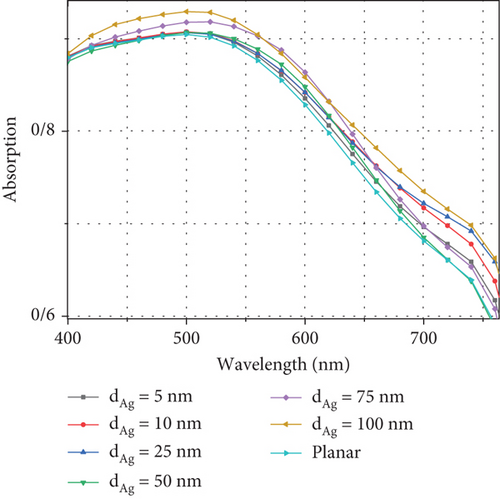
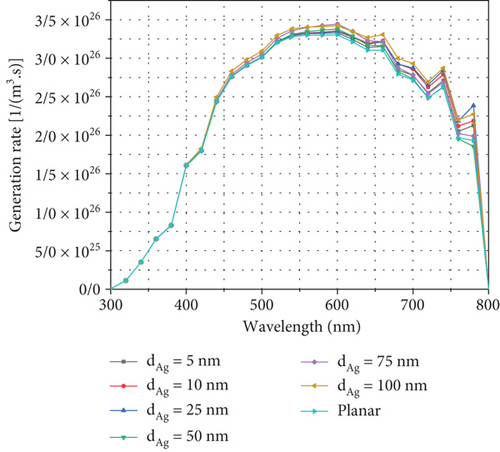
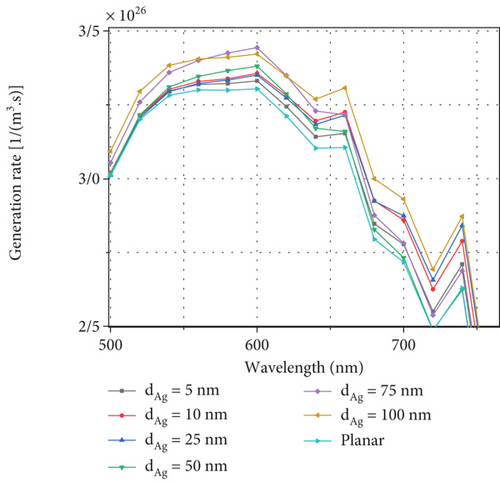
We experience a decrease in absorption in the perovskite layer at wavelengths of 550 nm, and later, the CuSCN layer begins to absorb light, but because this layer cannot generatecarriers, it does not affect the current characteristics.

One of the ways to increase the absorption in the AL is the use of metal NPs and plasmonic stimulation. In this article, we are trying to improve the absorption in this layer by adding NPs to the perovskite layer continuously and periodically. We placed Ag NPs with different diameters in the perovskite layer and investigated the effect of absorption and generation. We know that the Ag plasmon is in the wavelength region of 500 nm, so according to Figures 4(a) and 4(b), with the increase in the diameter of the Ag NPs, the number of absorptions increases from the region of about 550 to 650 nm. In addition, nanostructures cause a change in the electric field in the cell, somehow that of the incoming light, after hitting the NP that scatters the light in different directions and increases its movement path in the active area and increases absorption. For this reason, this causes the light at higher wavelengths, which have less energy, to go to the lower layer, i.e., CuSCN, and also increases the field in the AL, and therefore, the absorption of light for wavelengths of 550 nm and later increases compared to the planar state. For wavelengths of 700 nm and later, due to the reduction of the field and the reduction of the carrier generation, the amount of absorption in the cell decreases drastically. Figures 4(c) and 4(d) show the generation rate in the system. Because the field and absorption factor have a direct effect on the generation rate equations, for this reason, the behavior of the generation rate for different wavelengths will be the same as absorption so that at low wavelengths with high energy, the light incident on the cell is absorbed by the ITO and TiO₂ layers. As the wavelength increases and the energy decreases, the absorption of the first two layers decreases, and the absorption in the perovskite AL (MAPI₃) increases in wavelengths longer than 550 nm due to the plasmon phenomenon and the presence of Ag NPs; the generation rate increases. As can be seen, like absorption at wavelengths higher than 700 nm, the generation rate decreases drastically due to the reduction of the field in the recite layer.

Figure 5(a) shows the diagram of the electric field in the PSC structure with Ag NPs with the diameter of 50 nm at wavelengths of 400, 600, 500, and 800 nm. As the wavelength of light entering the PSC increases and approaches the Ag plasmonic wavelength, the plasmon electric field increases in the AL and around the NP, which improves absorption and generation in this wavelength, according to Figure 5.

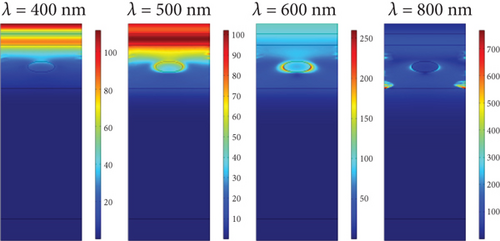
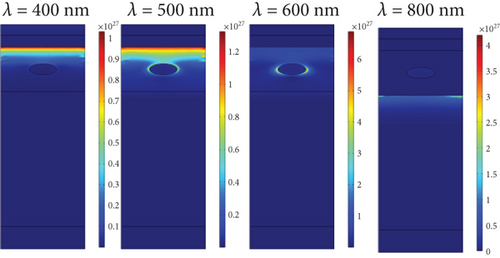
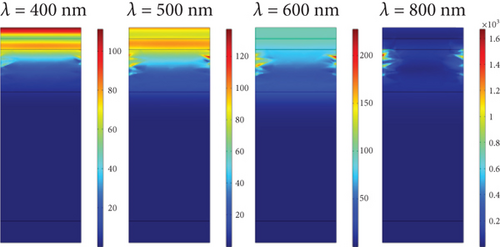
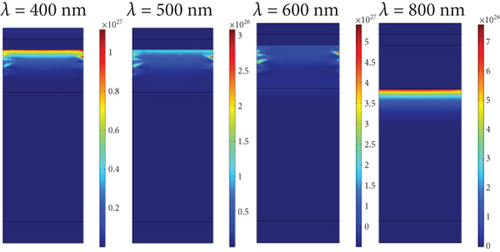
Figure 5(b) shows the generation rate diagram in the PSC with Ag NPs with the diameter of 50 nm at wavelengths 400, 600, 500, and 800 nm. By increasing the wavelength of the light entering the cell and approaching the Ag plasmonic wavelength, the electron-hole generation rate in the AL and around the plasmonic NP increases, which, according to Figure 5, leads to an improvement in the generation rate at this wavelength.

Figure 5(c) shows the electric field distribution in the PSC structure without Ag NPs at wavelengths 400, 600, 500, and 800 nm. At higher wavelengths, the amount of absorption improves due to increased light transmission in the upper layers of perovskite. Figure 5(d) shows the distribution of the generation rate in the solar cell without Ag NPs at wavelengths 400, 600, 500, and 800 nm.

At higher wavelengths, due to increased absorption, the generation speed improves. The distribution of the electric field at the wavelength of 500 nm is shown for the planar state, where the distribution of the electric field in the ITO and TiO₂ layers is greater than that of perovskite. It means that the perovskite layer absorbs the generated field, and according to the shape of the absorption rate in the cell, it has the highest value compared to other wavelengths. In this regard, Figure 5(d) shows the generation rate at a wavelength of 500 nm.

ITO and TiO₂ layers cannot produce carriers; that is why the generation rate in this layer is zero, but in the AL, due to the increased absorption and generation of electron-hole carriers, the generation rate has increased compared to the two higher layers. Figure 5(a) shows the profile of the electric field when we place a Ag NP with the diameter of 50 nm right in the center of the perovskite layer.

This figure shows that the Ag plasmon caused the field around the NP to increase significantly compared to the planar structure, and this, according to Figures 5(a) and 5(b), shows that the absorption rate and the generation rate compared to the planar structure during different waves have increased. Figure 5(c) also shows the profile of the generation rate when the 50 nm Ag NP is in the center of the AL, which shows that the generation rate has increased in this state compared to the planar structure.

Figure 6(a) shows the diagram of the dark current in the system, that is, when there is no carrier in the solar cells and light does not enter the solar cell. The dark current represents the amount of recombination in the system, so that by adding Ag NPs to the perovskite layer and increasing its diameter from 2.5 to 50 nm,the recombination increases according to the dark current diagram. Increasing the amount of recombination in the system reduces V_oc and J_sc because recombination is directly related to the resistance of the AL. Therefore, it can be concluded that the presence of metal NPs sometimes causes damage to the cell. Figure 6(b) shows the recombination rate diagram in the system at wavelengths of 300 to 800 nm. From 2.5 to 50 nm, it can be seen that it increases with the recombination rate. When the light enters the active area, as the diameter of the NP increases, the amount of light hitting the NP increases and causes more light to scatter in unusual directions in the perovskite layer and the length. The increased light path, therefore, increases the amount of carrier absorption and generation. With the increase in carrier generation, the recombination ratio also increases.

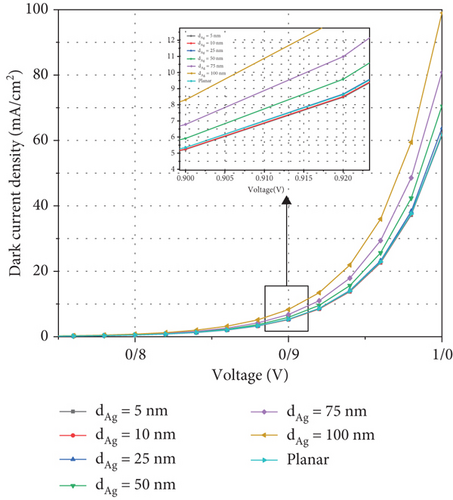
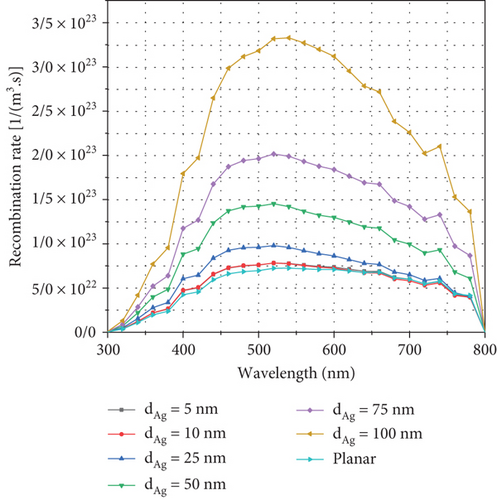
Figure 7(a) shows the current density versus voltage plot for the solar cell, showing the behavior of V_oc and J_sc for the planar structure and when we put NPs of different diameters in the middle of the perovskite layer. Figure 7(b) shows the changes in V_oc behavior with the addition of NPs in the AL, which increases the resistance and creates defects in the perovskite layer, which causes hardening and increases the resistance in the transport of carriers in the AL.

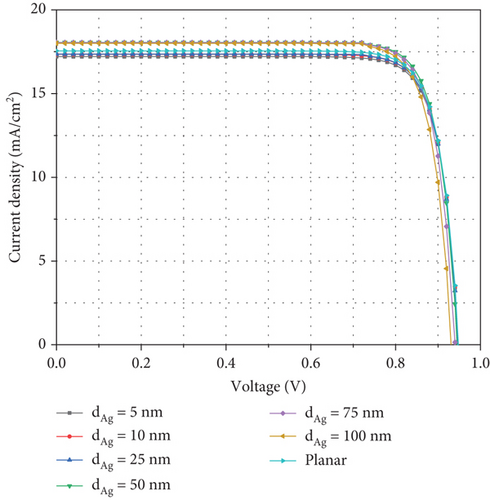
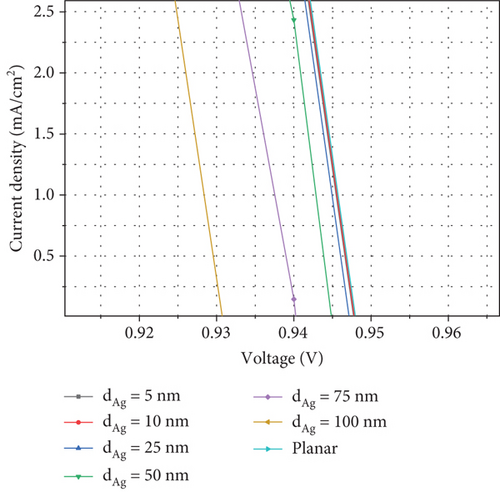
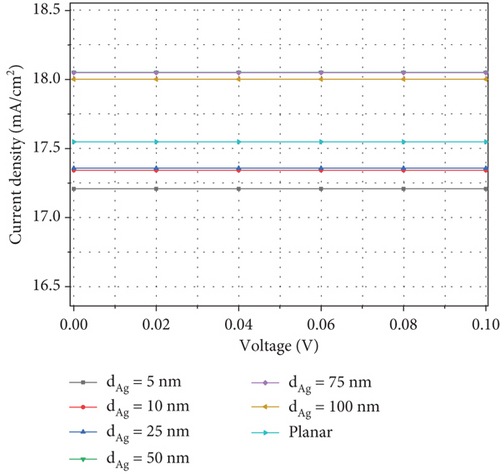
The behavior of V_oc is directly related to J_sc and the current recombination density (J₀) so that V_oc = (kT/q) ln (J_sc/J₀ + 1), where k is the Boltzmann constant, T is the temperature, and q is the charge of electrons. Therefore, according to the small changes of J_sc, V_oc indicates the recombination in the system. With the increase of recombination in the solar cell according to Figure 7(b), the value of V_oc in the planar structure is slightly less than 0.95 V, which by adding Ag NPs to the perovskite layer and increasing the diameter of V_oc to 0.93 V decreases. Figure 7(c) also shows the behavior of J_sc in the system, which according to Eq. (6) depends on the compromise between the generation and recombination rates. As shown in this figure, with the addition of NPs to the system, the current begins to increase from 5 nm and continues up to when the diameter of NP reaches 75 nm. But from this diameter onwards, due to the preponderance of recombination rate, the increase in current is reduced. However, J_sc decreases when the diameter of NP is 100 nm compared to when the diameter is 75 nm.

Table 6 shows the changing trend of PCE, FF, V_oc, and J_sc, for various values of Ag NP diameter placing in the AL. As is known, the PCE behavior is affected by the current and voltage values. Based on these results, the best performance in the solar energy of this cell occurs when the Ag NP with the diameter of 50 nm is placed in the perovskite layer, which has increased the PCE of PSC by 2.64% compared to the planar structure. The overall behavior of the FF is similar to V_oc and is affected by the recombination behavior in the system.

Table 6. Electrical parameters of the PSC for the planar structure when Ag NPs with the diameter of 5 to 100 nm are placed in the AL.

	PCE (%)	FF (%)	V_oc (V)	J_sc (mA/cm²)
Planar	13.789	82.39	0.9480	17.54843
d_Ag = 5 nm	13.532	82.47	0.9478	17.20868
d_Ag = 10 nm	13.644	82.5	0.9478	17.34264
d_Ag = 25 nm	13.65	82.53	0.9472	17.35771
d_Ag = 50 nm	14.1537	82.49	0.9447	18.05188
d_Ag = 75 nm	14.0435	82.22	0.9406	18.04917
d_Ag = 100 nm	13.8525	79.53	0.9307	18.00173

2.1. Heat

In practice and construction, we have effects such as recombination and temperature effects in the system, which affect the PCE and consequently the performance of the cell, while they are less considered in the simulations. In this article, we tried to simulate solar cells by considering the actual effects and bringing them closer to reality. In the last part, the results of the optical and electrical simulations were calculated in the standard mode, which included SRH recombination. The thermal analysis is performed along with the addition of new physics to the simulation. Consider that adding thermal physics to the simulation structure as well as temperature effects has a negligible effect on the refractive index of the material and the real and imaginary parts. This means that the addition of this physics does not affect the optical analysis and the generation and absorption rates in the cell. For this reason, we give up the optical analysis in thermal physics and consider them according to the previous analysis.

Figure 8 shows the dark current-voltage plot for the planar structure with Ag NPs of different diameters in thermally coupled physics. The dark current indicates the amounts of recombination rate and V_oc in the system, so here due to the increase in the recombination rate and the calculation of radiative and nonradiative recombination of the dark current compared to the previous case where only SRH recombination was calculated (as shown in Figure 4), attention has increased. An increase in the recombination rate in a solar cell reduces the value of V_oc, which this in turn reduces the PCE of the cell.

Figure 9 shows the graph of current density in terms of voltage, which shows the change in the behavior of V_oc and J_sc for the planar structure and when we put NPs of different diameters in the middle of the perovskite layer. Manufacturing and recombination parameters affect the value of J_sc. Therefore, with the stability of the generation rate compared to the state and the increase of the recombination rate in the system, we see a significant decrease in J_sc for increasing the NP diameter. Furthermore, this increase in recombination has led to a reduction in V_oc. When we start adding silver NPs to the structure, with the increase in diameter, it becomes harder to transport the carriers, and it causes an increase in the resistance in the cell in addition to V_oc, which reduces J_sc.

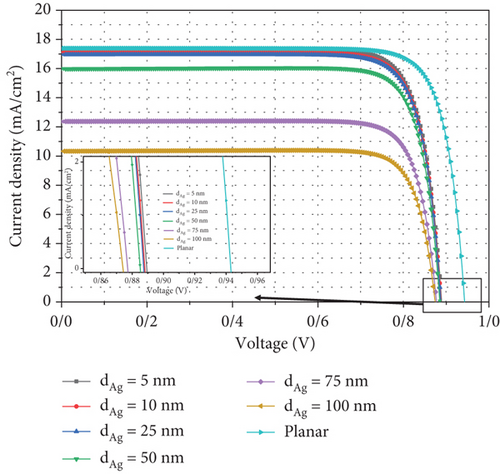
Table 7 shows the variations of electrical parameters, i.e., PCE, FF, V_oc, and J_sc, for various values of Ag NP diameter. The thermal physics is coupled to the system, as well as the effect of temperature and optical and nonradiative recombination in the system both in the planar structure and when Ag NPs with different diameters are added to the AL. As a result, we see a decrease in the PCE, so the profit from 13.53% in the planar state reaches about 7.51% when we have NPs with a diameter of 100 nm. In Table 1, the PCE in the planar structure was equal to 13.78%; with the addition of Ag NPs in the AL, the PCE increases. With NPs of 100 nm diameter, the PCE is not calculated, since the heat loss from the NP is flatter.

Table 7. Changes of electrical parameters (PCE, FF, V_oc, and J_sc) for different diameters of Ag NPs, when thermal physics is coupled with optical and electrical physics.

	PCE (%)	FF (%)	V_oc (V)	J_sc (mA/cm²)
Planar	13.5394	0.82	0.943	17.4
d_Ag = 5 nm	12.6347	0.81	0.89	17.339
d_Ag = 10 nm	12.4401	0.814	0.888	17.09
d_Ag = 25 nm	12.3487	0.815	0.887	16.96
d_Ag = 50 nm	11.6985	0.822	0.885	15.98
d_Ag = 75 nm	8.9641	0.81	0.877	12.4
d_Ag = 100 nm	7.51	0.82	0.874	10.33

Figure 10 shows the optimization of 25 nm Ag NP as the size of the structure increases from 100 to 175 nm; we see an increase in the values of V_oc and J_sc, which is due to the decrease in the density of the metal NP and increasing the density of perovskite in the system. By increasing the size of the structure to values greater than 175 nm, we see a decrease in the current in the solar cell, which affects the PCE of the PSC. The electrical parameters of optimizing cell structure dimensions are listed in Table 8.

Table 8. Changes of electrical parameters (PCE, FF, V_oc, and J_sc) of the PSC in the presence of silver NPs with the diameter of 25 nm, for different lengths and widths of the cell structure.

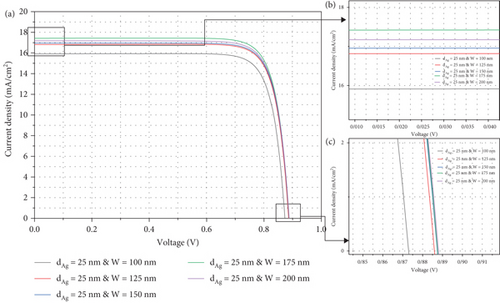
	PCE (%)	FF (%)	V_oc (V)	J_sc (mA/cm²)
W = 100 nm	1.4212	0.8175	0.873	15.9061
W = 125 nm	12.2623	0.8381	0.886	16.4142
W = 150 nm	12.3487	0.815	0.887	16.96
W = 175 nm	12.6868	0.8206	0.8875	17.4186
W = 200 nm	12.4773	0.8182	0.8879	17.1721

2.2. Thermal Parameters

Here, we examine the thermal characteristics by coupling optical, electrical and thermal physics. In Figure 11, the three significant factors of heat generation in the solar cell, i.e., Joule heat, thermalized heat, and nonradiative heat, are shown at two voltages V = V_oc and V = 0 V indicated. The biggest thermal effect in the cell is related to the nonradiative recombination heat and thermalized heat that occurs at the boundary of the two layers of MAPI/TIO₂. The reason for the increase of H_{Thermalization} and H_Nonradiative at V = V_oc is the increase of recombination in the system, while H_Joule has reached zero at the V_oc voltage regardless of recombination. According to Eq. (10), H_Joule has a direct relationship with optical current, so according to the diagram in Figure 7, the value of J_sc at V = V_oc is equal to zero. Due to the presence of discharge areas and their voltage dependence, most thermal effects occur at the boundary between two layers that have discharge areas and dependence on voltage. For a better understanding of this issue, a three-dimensional map of the overall thermal behavior is obtained from

()

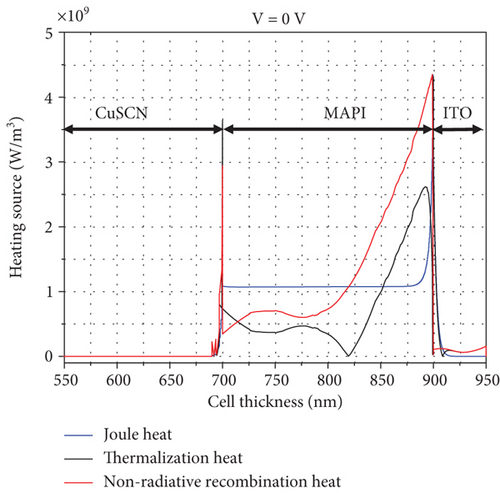
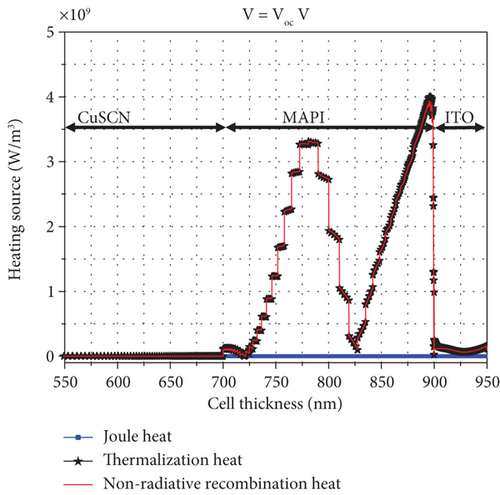
Figures 12(a) and 12(b) show the three-dimensional map of the total heat generated at two voltages V = V_oc and V = 0 V, respectively, using Eq. (19). Like Figure 8, this figure also shows that the most heat generated at the boundary between the two layers of it is active and ITO.

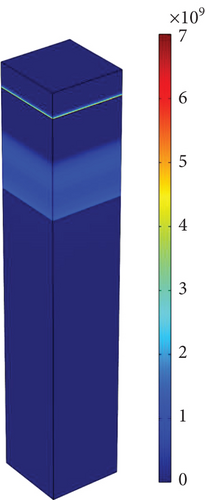
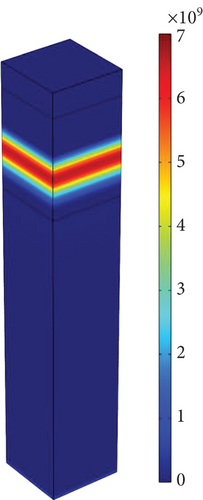
We also calculated H_surf and H_Peltier using Eqs. (13) and (15). Meanwhile, we neglected H_surf at the boundary between the top and bottom layers, i.e., ITO/TIO₂ and CuSCN/Au, because the recombination rate on the surface between these layers is insignificant. After all, near the bottom junction, which is made of Au, the hole-to-electron density ratio is higher, so the recombination rate is little.

Now, to compare the heat losses generated, the thermal power density in the system is shown in Figure 13, where Joule and thermal power density are the most effective in the system. In the V_oc voltage, due to the decrease of the field and the natural decrease of the H_Joule voltage, it gradually decreases.

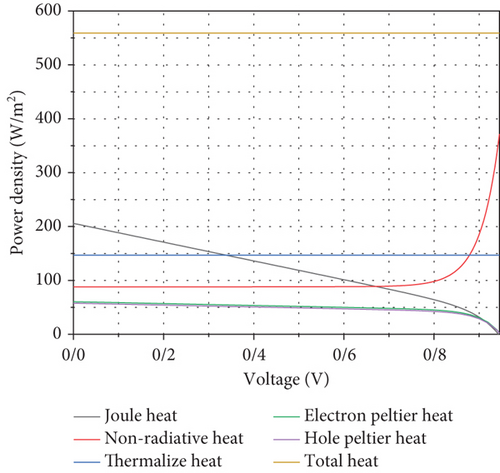
Also, at this voltage, the current density is equal to zero. That is why the H_Peltier gradually decreases and reaches zero. H_total is the total loss density in the system, and P_cell is the power density of the cell.

Now we examine how temperature behaves and its effect on current and voltage parameters. Figure 14 shows the current-voltage variation diagram for temperatures from 25 to 75°C. As we know, the temperature has a great effect on material properties (lifetime, bandgap, etc.), so temperature changes affect the cell performance and so the PCE. Therefore, we investigate the effect of temperature on the parameters and properties of solar cell materials. An increase in temperature causes an increase in the equilibrium population of the concentration of intrinsic carriers, which leads to an increase in the dark current density and, as a result, an increase in the recombination rate and a decrease in V_oc. It also decreases slightly with an increase in the bandgap. An increase in temperature leads to a reduction in V_oc and J_sc. It can reduce the amount of interest in the cell.

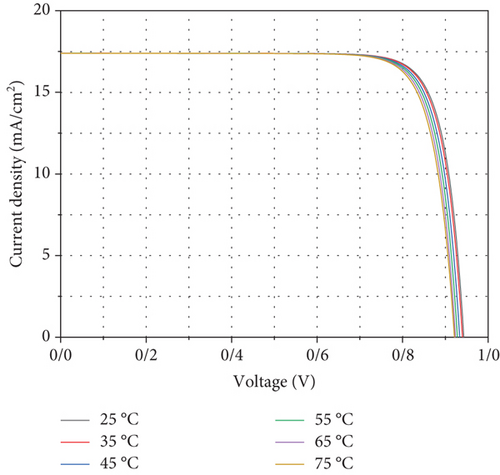
Table 9 displays changes in the values of J_sc, V_oc, FF, and PCE for different temperatures in the cell. As mentioned, with the increase in temperature from the ambient temperature (25°C) to 75°C, the value of V_oc has reduced a lot, and J_sc has decreased slightly, which causes a decrease in the PCE and the saturation coefficient in the cell.

Table 9. Variations of J_sc, V_oc, FF, and PCE with different temperature values.

	PCE (%)	FF (%)	V_oc (V)	J_sc (mA/cm²)
25°C	13.5394	0.8202	0.943	17.4
35°C	13.4815	0.8195	0.94	17.3944
45°C	13.378	0.8188	0.9336	17.3941
55°C	13.2877	0.8180	0.9282	17.3937
65°C	13.1972	0.8165	0.9237	17.3931
75°C	13.1073	0.813	0.9213	17.3923

3. Conclusion

Here, we study the opto-electro-thermal (OET) characteristics, as well investigate carrier transport and thermodynamic behaviors inthe perovskite solar cell (PSC) structure. Aganoparticles (NPs) have been utilizedas plasmonic NPs in the structure of perovskite. This workexamines the thermal effects of NPs in the PSC structure. When the PSC is studied with two optical-electrical physics, the electrical parameters and the power conversion efficiency (PCE) are improved. Then, thermal physics has been applied in the simulation process, and the electrical parameters and the PCE were calculated. When Ag NP is not present in the structure, the values of J_sc, V_oc, and PCE are 17.4 mA/cm², 0.943 V, and 13.54%, respectively. When the NP was added to the system and its diameter increased, J_sc decreases from 17.33 to 10.33 mA/cm², V_oc reduces from 0.89 to 0.874 V, and the PCE in the system is decreased from 12.63 to 7.5%. The thermal investigation of the PSC with Ag NPs of different dimensions has shown that by increasing the diameter of NPs more than 50 nm, the presence of the NPs increases the thermal losses in the cell and creates destructive effects in the system. This causes that the construction of these cells in the real world is not recommended.

Conflicts of Interest

The authors declare no conflict of interest.

Authors’ Contributions

M.B did the simulations and wrote the draft and prepared the figures. D.F and M.E defined the project and prepared the final manuscript. D.F supervised the project and the presented results. D.F and M.E edited the manuscript. All authors reviewed the manuscript.

Open Research

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Bhattarai S., Hossain M. K., Farhat L. B., Marzouki R., Hossain I., Ansari M. Z., Madan J., and Pandey R., Performance enhancement using an embedded nano-pyramid in a perovskite solar cell with TaTm as a hole transport layer, New Journal of Chemistry. (2023) 47, no. 39, 18332–18340, https://doi.org/10.1039/D3NJ03665K.
10.1039/D3NJ03665K
CAS Web of Science® Google Scholar
2 Bhattarai S., Hossain M. K., Toki G. I., Pandey R., Madan J., Samajdar D., Ezzine S., Farhat L. B., Ansari M. Z., Ahammad S. H., and Rashed A. N. Z., Efficiency enhancement of perovskite solar cell devices utilizing MXene and TiO₂ as an electron transport layer, New Journal of Chemistry. (2023) 47, no. 38, 17908–17922, https://doi.org/10.1039/D3NJ03548D.
10.1039/D3NJ03548D
CAS Web of Science® Google Scholar
3 Bhattarai S., Pandey R., Madan J., Tayeng S., Kalita P., Ansari M. Z., Farhat L. B., Amami M., and Hossain M. K., Comparative study of distinct halide composites for highly efficient perovskite solar cells using a SCAPS-1D simulator, RSC Advances. (2023) 13, no. 38, 26851–26860, https://doi.org/10.1039/D3RA04134D, 37692356.
10.1039/D3RA04134D
CAS PubMed Web of Science® Google Scholar
4 Fahimi M. J., Fathi D., and Ansari-Rad M., Accurate analysis of electron transfer from quantum dots to metal oxides in quantum dot sensitized solar cells, Physica E: Low-dimensional Systems and Nanostructures. (2015) 73, 148–155, https://doi.org/10.1016/j.physe.2015.05.030, 2-s2.0-84931271157.
10.1016/j.physe.2015.05.030
Web of Science® Google Scholar
5 Fahimi M. J., Fathi D., Eskandari M., and Das N., Marcus theory and tunneling method for the electron transfer rate analysis in quantum dot sensitized solar cells in the presence of blocking layer, Micromachines. (2023) 14, no. 9, https://doi.org/10.3390/mi14091731, 37763894.
10.3390/mi14091731
PubMed Web of Science® Google Scholar
6 Dai X., Xu K., and Wei F., Recent progress in perovskite solar cells: the perovskite layer, Beilstein Journal of Nanotechnology. (2020) 11, no. 1, 51–60, https://doi.org/10.3762/bjnano.11.5, 31976196.
10.3762/bjnano.11.5
CAS PubMed Web of Science® Google Scholar
7 Qiu L., He S., Ono L. K., and Qi Y., Progress of surface science studies on ABX3-based metal halide perovskite solar cells, Advanced Energy Materials. (2020) 10, no. 13, https://doi.org/10.1002/aenm.201902726.
10.1002/aenm.202003594
Web of Science® Google Scholar
8 An Y., Wang C., Cao G., and Li X., Heterojunction perovskite solar cells: opto-electro-thermal physics, modeling, and experiment, ACS Nano. (2020) 14, no. 4, 5017–5026, https://doi.org/10.1021/acsnano.0c01392, 32255622.
10.1021/acsnano.0c01392
CAS PubMed Web of Science® Google Scholar
9 Dadashbeik M., Fathi D., and Eskandari M., Design and simulation of perovskite solar cells based on graphene and TiO₂/graphene nanocomposite as electron transport layer, Solar Energy. (2020) 207, 917–924, https://doi.org/10.1016/j.solener.2020.06.102.
10.1016/j.solener.2020.06.102
CAS Web of Science® Google Scholar
10 Bhattarai S., Pandey R., Madan J., Sahoo G. S., Hossain I., Wabaidur S. M., and Ansari M. Z., Numerical investigation of toxic free perovskite solar cells for achieving high efficiency, Materials Today Communications. (2023) 35, https://doi.org/10.1016/j.mtcomm.2023.105893.
10.1016/j.mtcomm.2023.105893
Web of Science® Google Scholar
11 Bhattarai S., Hossain M. K., Pandey R., Madan J., Samajdar D., Rahman M. F., Ansari M. Z., and Amami M., Perovskite solar cells with dual light absorber layers for performance efficiency exceeding 30%, Energy & Fuels. (2023) 37, no. 14, 10631–10641, https://doi.org/10.1021/acs.energyfuels.3c01659.
10.1021/acs.energyfuels.3c01659
CAS Web of Science® Google Scholar
12 Bhattarai S., Kalita P., Hossain I., Alsubaie A. S., Mahmoud K. H., Ansari M. Z., and Janicek P., Designing an efficient lead-free perovskite solar cell through a computational method, Crystals. (2023) 13, no. 8, https://doi.org/10.3390/cryst13081175.
10.3390/cryst13081175
Web of Science® Google Scholar
13 Mohammadi M. H., Fathi D., and Eskandari M., Light trapping in perovskite solar cells with plasmonic core/shell nanorod array: a numerical study, Energy Reports. (2021) 7, 1404–1415, https://doi.org/10.1016/j.egyr.2021.02.071.
10.1016/j.egyr.2021.02.071
Web of Science® Google Scholar
14 Bhattarai S., Mohammed M. K., Madan J., Pandey R., Ansari M. Z., Zaki Rashed A. N., Amami M., and Hossain M. K., Performance improvement of perovskite solar cell design with double active layer to achieve an efficiency of over 31%, Sustainability. (2023) 15, no. 18, https://doi.org/10.3390/su151813955.
10.3390/su151813955
Web of Science® Google Scholar
15 Bhattarai S., Jayan D., Yousfi A., Chowdhury M., Rahman M. F., Pandey R., Madan J., Ansari M. Z., and Hossain M. K., Novel double graded perovskite materials for performance increment of perovskite solar cell using extensive numerical analysis, Physica Scripta. (2023) 98, no. 9, article 095507, https://doi.org/10.1088/1402-4896/aceb97.
10.1088/1402-4896/aceb97
Web of Science® Google Scholar
16 Bayles A., Carretero-Palacios S., Calió L., Lozano G., Calvo M. E., and Míguez H., Localized surface plasmon effects on the photophysics of perovskite thin films embedding metal nanoparticles, Journal of Materials Chemistry C. (2020) 8, no. 3, 916–921, https://doi.org/10.1039/C9TC05785D.
10.1039/C9TC05785D
CAS Web of Science® Google Scholar
17 Mohammadi M. H., Fathi D., and Eskandari M., NiO@GeSe core-shell nano-rod array as a new hole transfer layer in perovskite solar cells: a numerical study, Solar Energy. (2020) 204, 200–207, https://doi.org/10.1016/j.solener.2020.04.038.
10.1016/j.solener.2020.04.038
CAS Web of Science® Google Scholar
18 Tooghi A., Fathi D., and Eskandari M., Numerical study of a highly efficient light trapping nanostructure of perovskite solar cell on a textured silicon substrate, Scientific Reports. (2020) 10, no. 1, article 18699, https://doi.org/10.1038/s41598-020-75630-4, 33122757.
10.1038/s41598-020-75630-4
PubMed Web of Science® Google Scholar
19 Mohammadi M. H., Eskandari M., and Fathi D., Improving the efficiency of perovskite solar cells via embedding random plasmonic nanoparticles: optical-electrical study on device architectures, Solar Energy. (2021) 221, 162–175, https://doi.org/10.1016/j.solener.2021.04.038.
10.1016/j.solener.2021.04.038
CAS Web of Science® Google Scholar
20 Majdi M., Eskandari M., and Fathi D., Textured HTM-free perovskite/PbS quantum dot solar cell: optical and electrical efficiency improvement by light trapping control, Solar Energy. (2021) 230, 618–627, https://doi.org/10.1016/j.solener.2021.10.008.
10.1016/j.solener.2021.10.008
CAS Web of Science® Google Scholar
21 Aliyariyan M., Fathi D., Eskandari M., and Mohammadi M. H., Simulation and investigation of perovskite/nano-pyramidal GeSe solar cell: realizing high efficiency by controllable light trapping, Solar Energy. (2021) 214, 310–318, https://doi.org/10.1016/j.solener.2020.11.063.
10.1016/j.solener.2020.11.063
CAS Web of Science® Google Scholar
22 Fooladvand P., Eskandari M., Fathi D., and das N., Single-walled carbon nanotube as hole transport layer in perovskite solar cell: efficiency enhancement, Energy Reports. (2023) 10, 3652–3664, https://doi.org/10.1016/j.egyr.2023.10.020.
10.1016/j.egyr.2023.10.020
Web of Science® Google Scholar
23 Park N.-G., Miyasaka T., and Grätzel M., Organic-Inorganic Halide Perovskite Photovoltaics, 2016, Springer, Cham, Switzerland, https://doi.org/10.1007/978-3-319-35114-8, 2-s2.0-85032850336.
10.1007/978-3-319-35114-8
Google Scholar
24 Gao P., Grätzel M., and Nazeeruddin M. K., Organohalide lead perovskites for photovoltaic applications, Energy & Environmental Science. (2014) 7, no. 8, 2448–2463, https://doi.org/10.1039/C4EE00942H, 2-s2.0-84904544997.
10.1039/C4EE00942H
CAS Web of Science® Google Scholar
25 Laska M., Krzemińska Z., Kluczyk-Korch K., Schaadt D., Popko E., Jacak W., and Jacak J., Metallization of solar cells, exciton channel of plasmon photovoltaic effect in perovskite cells, Nano Energy. (2020) 75, article 104751, https://doi.org/10.1016/j.nanoen.2020.104751.
10.1016/j.nanoen.2020.104751
Web of Science® Google Scholar
26 Askari F., Fathi D., and Eskandari M., Copper sulfide/cuprous selenide as a new counter electrode for quantum-dot-sensitized solar cells, Journal of Materials Science: Materials in Electronics. (2020) 31, 1789–1796, https://doi.org/10.1007/s10854-019-02695-x.
10.1007/s10854-019-02695-x
CAS Web of Science® Google Scholar
27 Vafapoor B., Fathi D., and Eskandari M., ZnS/Al₂S₃ layer as a blocking layer in quantum dot sensitized solar cells, Journal of Electronic Materials. (2018) 47, 1932–1936, https://doi.org/10.1007/s11664-017-5993-8, 2-s2.0-85037734923.
10.1007/s11664-017-5993-8
CAS Web of Science® Google Scholar
28 Dlamini M. W., Hamed M. S., Mbuyise X. G., and Mola G. T., Improved energy harvesting using well-aligned ZnS nanoparticles in bulk-heterojunction organic solar cell, Journal of Materials Science: Materials in Electronics. (2020) 31, 9415–9422, https://doi.org/10.1007/s10854-020-03481-w.
10.1007/s10854-020-03481-w
CAS Web of Science® Google Scholar
29 Carretero-Palacios S., Jiménez-Solano A., and Míguez H., Plasmonic nanoparticles as light-harvesting enhancers in perovskite solar cells: a user’s guide, ACS Energy Letters. (2016) 1, no. 1, 323–331, https://doi.org/10.1021/acsenergylett.6b00138, 2-s2.0-85032348570, 28066822.
10.1021/acsenergylett.6b00138
CAS PubMed Web of Science® Google Scholar
30 Juarez-Perez E. J., Ono L. K., Uriarte I., Cocinero E. J., and Qi Y., Degradation mechanism and relative stability of methylammonium halide based perovskites analyzed on the basis of acid–base theory, ACS Applied Materials & Interfaces. (2019) 11, no. 13, 12586–12593, https://doi.org/10.1021/acsami.9b02374, 2-s2.0-85063546665, 30848116.
10.1021/acsami.9b02374
CAS PubMed Web of Science® Google Scholar
31 Das A., Kumar K., and Dhawan A., Plasmonics-enhanced organic solar cells with complex metallic nanoparticles, In Photonics for Solar Energy Systems VIII, 2020, 11366, SPIE, 15–20.
10.1117/12.2555583
Google Scholar
32 Tooghi A., Fathi D., and Eskandari M., High-performance perovskite solar cell using photonic-plasmonic nanostructure, Scientific Reports. (2020) 10, no. 1, https://doi.org/10.1038/s41598-020-67741-9, 32647193.
10.1038/s41598-020-67741-9
PubMed Web of Science® Google Scholar
33 Makableh Y. F., Awad I. A., Hassan W., and Aljaiuossi G., Enhancement of the thermal properties of heterojunction perovskite solar cells by nanostructured contacts design, Solar Energy. (2020) 202, 204–209, https://doi.org/10.1016/j.solener.2020.04.002.
10.1016/j.solener.2020.04.002
CAS Web of Science® Google Scholar
34 Blackburn J. L., Zhu K., Yang M., Dowgiallo A.-M., and Ihly R. R., Nanostructure-Containing Organic-Metal Halide Perovskites, 2020, U.S. Patent and Trademark Office, Washington, DC.
Google Scholar
35 Liu S., Liang L., Meng L., Tian X., Zhang Z., Yu Y., Lan Z., Wu J., Zhang J., and Gao P., Synergy of plasmonic silver nanorod and water for enhanced planar perovskite photovoltaic devices, Solar Rrl. (2020) 4, no. 2, article 1900231, https://doi.org/10.1002/solr.201900231.
10.1002/solr.201900231
Web of Science® Google Scholar
36 Mohsen A. A., Zahran M., Habib S., and Allam N. K., Refractory plasmonics enabling 20% efficient lead-free perovskite solar cells, Scientific Reports. (2020) 10, no. 1, https://doi.org/10.1038/s41598-020-63745-7, 32317720.
10.1038/s41598-020-63745-7
PubMed Web of Science® Google Scholar
37 Yu Z., Raman A., and Fan S., Fundamental limit of nanophotonic light trapping in solar cells, Proceedings of the National Academy of Sciences. (2010) 107, no. 41, 17491–17496, https://doi.org/10.1073/pnas.1008296107, 2-s2.0-78049314257, 20876131.
10.1073/pnas.1008296107
CAS PubMed Web of Science® Google Scholar
38 Erwin W. R., Zarick H. F., Talbert E. M., and Bardhan R., Light trapping in mesoporous solar cells with plasmonic nanostructures, Energy & Environmental Science. (2016) 9, no. 5, 1577–1601, https://doi.org/10.1039/C5EE03847B, 2-s2.0-84970967853.
10.1039/C5EE03847B
CAS Web of Science® Google Scholar
39 Kumar K., Das A., Kumawat U. K., and Dhawan A., Plasmonic metal-oxide core-shell nanoparticles for enhanced power conversion efficiency of organic solar cells, In Organic Electronics and Photonics: Fundamentals and Devices II, 2020, 11365, SPIE, 28–34.
Google Scholar
40 Eli D., Onimisi M., Garba S., Gyuk P., Jamila T., and Boduku H., Improved power conversion efficiency in perovskite solar cell using silver nanoparticles modified photoanode, In IOP Conference Series: Materials Science and Engineering. (2020) 805, no. 1, article 012005, https://doi.org/10.1088/1757-899X/805/1/012005.
10.1088/1757-899X/805/1/012005
Google Scholar
41 Kumar R. P., Venkatesh A., and Moorthy V., Large area and low-cost nanoholes-based plasmonic back reflector fabricated by a simple nanofabrication technique for photovoltaics applications, Nano-Structures & Nano-Objects. (2020) 21, article 100406, https://doi.org/10.1016/j.nanoso.2019.100406.
10.1016/j.nanoso.2019.100406
Google Scholar
42 Zhang W., Saliba M., Stranks S. D., Sun Y., Shi X., Wiesner U., and Snaith H. J., Enhancement of perovskite-based solar cells employing core–shell metal nanoparticles, Nano Letters. (2013) 13, no. 9, 4505–4510, https://doi.org/10.1021/nl4024287, 2-s2.0-84884257868, 23947387.
10.1021/nl4024287
CAS PubMed Web of Science® Google Scholar
43 Lakowicz J. and Radiative R., Radiative decay engineering 3. Surface plasmon-coupled directional emission, Analytical Biochemistry. (2004) 324, no. 2, 153–169, https://doi.org/10.1016/j.ab.2003.09.039, 2-s2.0-0346278795, 14690679.
10.1016/j.ab.2003.09.039
CAS PubMed Web of Science® Google Scholar
44 Lakowicz J. R., Radiative decay engineering 5: metal-enhanced fluorescence and plasmon emission, Analytical Biochemistry. (2005) 337, no. 2, 171–194, https://doi.org/10.1016/j.ab.2004.11.026, 2-s2.0-13244251098, 15691498.
10.1016/j.ab.2004.11.026
CAS PubMed Web of Science® Google Scholar
45 Chen H., Ming T., Zhao L., Wang F., Sun L.-D., Wang J., and Yan C.-H., Plasmon-molecule interactions, Nano Today. (2010) 5, no. 5, 494–505, https://doi.org/10.1016/j.nantod.2010.08.009, 2-s2.0-78049231307.
10.1016/j.nantod.2010.08.009
CAS Web of Science® Google Scholar
46 Kehr S. C., Liu Y. M., Martin L., Yu P., Gajek M., Yang S.-Y., Yang C.-H., Wenzel M., Jacob R., and Von Ribbeck H.-G., Near-field examination of perovskite-based superlenses and superlens- enhanced probe-object coupling, Nature Communications. (2011) 2, no. 1, https://doi.org/10.1038/ncomms1249, 2-s2.0-79953125980, 21427720.
10.1038/ncomms1249
PubMed Web of Science® Google Scholar
47 Lévêque G. and Quidant R., Channeling light along a chain of near-field coupled gold nanoparticles near a metallic film, Optics Express. (2008) 16, no. 26, 22029–22038, https://doi.org/10.1364/OE.16.022029, 2-s2.0-58149139943, 19104637.
10.1364/OE.16.022029
CAS PubMed Web of Science® Google Scholar
48 Ai B., Fan Z., and Wong Z. J., Plasmonic-perovskite solar cells, light emitters, and sensors, Microsystems & Nanoengineering. (2022) 8, no. 1, https://doi.org/10.1038/s41378-021-00334-2, 35070349.
10.1038/s41378-021-00334-2
PubMed Web of Science® Google Scholar
49 Zhao D.-W., Yu M.-Y., Zheng L.-L., Li M., Dai S.-J., Chen D.-C., Lee T.-C., and Yun D.-Q., Enhanced efficiency and stability of planar perovskite solar cells using a dual electron transport layer of gold nanoparticles embedded in anatase TiO₂ films, ACS Applied Energy Materials. (2020) 3, no. 10, 9568–9575, https://doi.org/10.1021/acsaem.0c00276, 33134879.
10.1021/acsaem.0c00276
CAS PubMed Web of Science® Google Scholar
50 Omrani M., Keshavarzi R., Abdi-Jalebi M., and Gao P., Impacts of plasmonic nanoparticles incorporation and interface energy alignment for highly efficient carbon-based perovskite solar cells, Scientific Reports. (2022) 12, no. 1, https://doi.org/10.1038/s41598-022-09284-9, 35354864.
10.1038/s41598-022-09284-9
PubMed Web of Science® Google Scholar
51 Nevruzoğlu V., Bal Altuntaş D., and Tomakin M., Cold substrate method to prepare plasmonic ag nanoparticle: deposition, characterization, application in solar cell, Applied Physics A. (2020) 126, 1–9.
10.1007/s00339-020-3433-8
Google Scholar
52 Zhao D., Yu Y., Wang C., Liao W., Shrestha N., Grice C. R., Cimaroli A. J., Guan L., Ellingson R. J., Zhu K., Zhao X., Xiong R. G., and Yan Y., Low-bandgap mixed tin-lead iodide perovskite absorbers with long carrier lifetimes for all-perovskite tandem solar cells, Nature Energy. (2017) 2, no. 4, 1–7, https://doi.org/10.1038/nenergy.2017.18, 2-s2.0-85016324194.
10.1038/nenergy.2017.18
Web of Science® Google Scholar
53 Palik E. D., Handbook of Optical Constants of Solids, 1998, Academic press.
10.1016/B978-0-08-055630-7.50017-1
Web of Science® Google Scholar
54 Pathak N. K. and Sharma R., Study of broadband tunable properties of surface plasmon resonances of noble metal nanoparticles using Mie scattering theory: plasmonic perovskite interaction, Plasmonics. (2016) 11, no. 3, 713–719, https://doi.org/10.1007/s11468-015-0097-x, 2-s2.0-84944704166.
10.1007/s11468-015-0097-x
CAS Web of Science® Google Scholar
55 Stratton J. A., Electromagnetic Theory, 2007, John Wiley & Sons.
Google Scholar
56 Roopak S., Ji A., Parashar P. K., and Sharma R., Light incoupling tolerance of resonant and nonresonant metal nanostructures embedded in perovskite medium: effect of various geometries on broad spectral resonance, Journal of Physics D: Applied Physics. (2017) 50, no. 33, article 335105, https://doi.org/10.1088/1361-6463/aa783e, 2-s2.0-85026755540.
10.1088/1361-6463/aa783e
Web of Science® Google Scholar
57 Shang A. and Li X., Photovoltaic devices: opto-electro-thermal physics and modeling, Advanced Materials. (2017) 29, no. 8, article 1603492, https://doi.org/10.1002/adma.201603492, 2-s2.0-85006980531, 27990695.
10.1002/adma.201603492
PubMed Web of Science® Google Scholar
58 Lin Q., Armin A., Nagiri R. C. R., Burn P. L., and Meredith P., Electro-optics of perovskite solar cells, Nature Photonics. (2015) 9, no. 2, 106–112, https://doi.org/10.1038/nphoton.2014.284, 2-s2.0-84923125095.
10.1038/nphoton.2014.284
CAS Web of Science® Google Scholar
59 Dong Q., Fang Y., Shao Y., Mulligan P., Qiu J., Cao L., and Huang J., Electron-hole diffusion lengths > 175 μm in solution-grown CH₃NH₃PbI₃ single crystals, Science. (2015) 347, no. 6225, 967–970, https://doi.org/10.1126/science.aaa5760, 2-s2.0-84923886273, 25636799.
10.1126/science.aaa5760
CAS PubMed Web of Science® Google Scholar
60 Miyata A., Mitioglu A., Plochocka P., Portugall O., Wang J. T.-W., Stranks S. D., Snaith H. J., and Nicholas R. J., Direct measurement of the exciton binding energy and effective masses for charge carriers in organic-inorganic tri-halide perovskites, Nature Physics. (2015) 11, no. 7, 582–587, https://doi.org/10.1038/nphys3357, 2-s2.0-84934863500.
10.1038/nphys3357
CAS Web of Science® Google Scholar
61 Milot R. L., Eperon G. E., Snaith H. J., Johnston M. B., and Herz L. M., Temperature-dependent charge-carrier dynamics in CH₃NH₃PbI₃ perovskite thin films, Advanced Functional Materials. (2015) 25, no. 39, 6218–6227, https://doi.org/10.1002/adfm.201502340, 2-s2.0-84944279831.
10.1002/adfm.201502340
CAS Web of Science® Google Scholar
62 Tress W., Domanski K., Carlsen B., Agarwalla A., Alharbi E. A., Graetzel M., and Hagfeldt A., Performance of perovskite solar cells under simulated temperature- illumination real-world operating conditions, Nature Energy. (2019) 4, no. 7, 568–574, https://doi.org/10.1038/s41560-019-0400-8, 2-s2.0-85068047030.
10.1038/s41560-019-0400-8
CAS Web of Science® Google Scholar
63 Domanski K., Alharbi E. A., Hagfeldt A., Grätzel M., and Tress W., Systematic investigation of the impact of operation conditions on the degradation behaviour of perovskite solar cells, Nature Energy. (2018) 3, no. 1, 61–67, https://doi.org/10.1038/s41560-017-0060-5, 2-s2.0-85039790996.
10.1038/s41560-017-0060-5
CAS Web of Science® Google Scholar
64 Broderick L. Z., Albert B. R., Pearson B. S., Kimerling L. C., and Michel J., Design for energy: modeling of spectrum, temperature and device structure dependences of solar cell energy production, Solar Energy Materials and Solar Cells. (2015) 136, 48–63, https://doi.org/10.1016/j.solmat.2014.12.034, 2-s2.0-84921334176.
10.1016/j.solmat.2014.12.034
CAS Web of Science® Google Scholar
65 Ghani F., Rosengarten G., Duke M., and Carson J., On the influence of temperature on crystalline silicon solar cell characterisation parameters, Solar Energy. (2015) 112, 437–445, https://doi.org/10.1016/j.solener.2014.12.018, 2-s2.0-84921047297.
10.1016/j.solener.2014.12.018
CAS Web of Science® Google Scholar
66 Raman A. P., Anoma M. A., Zhu L., Rephaeli E., and Fan S., Passive radiative cooling below ambient air temperature under direct sunlight, Nature. (2014) 515, no. 7528, 540–544, https://doi.org/10.1038/nature13883, 2-s2.0-84923069443, 25428501.
10.1038/nature13883
CAS PubMed Web of Science® Google Scholar
67 Zhu L., Raman A., Wang K. X., Abou Anoma M., and Fan S., Radiative cooling of solar cells, Optica. (2014) 1, no. 1, 32–38, https://doi.org/10.1364/OPTICA.1.000032, 2-s2.0-84930024430.
10.1364/OPTICA.1.000032
CAS Web of Science® Google Scholar
68 Benvenuti A., Coughrau W., and Pinto M. R., A thermal-fully hydrodynamic model for semiconductor devices and applications to III-V HBT simulation, IEEE Transactions on Electron Devices. (1997) 44, no. 9, 1349–1359, https://doi.org/10.1109/16.622585, 2-s2.0-0031235338.
10.1109/16.622585
Web of Science® Google Scholar
69 An Y., Sheng C., and Li X., Radiative cooling of solar cells: opto-electro-thermal physics and modeling, Nanoscale. (2019) 11, no. 36, 17073–17083, https://doi.org/10.1039/C9NR04110A, 2-s2.0-85072509410, 31506658.
10.1039/C9NR04110A
CAS PubMed Web of Science® Google Scholar
70 Li X., Hylton N. P., Giannini V., Lee K. H., Ekins-Daukes N. J., and Maier S. A., Multi-dimensional modeling of solar cells with electromagnetic and carrier transport calculations, Progress in Photovoltaics: Research and Applications. (2013) 21, no. 1, 109–120, https://doi.org/10.1002/pip.2159, 2-s2.0-84873718878.
10.1002/pip.2159
CAS Web of Science® Google Scholar
71 Ren H., Yu R., Qi J., Zhang L., Jin Q., and Wang D., Hollow multishelled heterostructured anatase/TiO₂ (B) with superior rate capability and cycling performance, Advanced Materials. (2019) 31, no. 10, article e1805754, https://doi.org/10.1002/adma.201805754, 2-s2.0-85059902242, 30633398.
10.1002/adma.201805754
PubMed Web of Science® Google Scholar
72 Yang Y., Jin Q., Mao D., Qi J., Wei Y., Yu R., Li A., Li S., Zhao H., and Ma Y., Dually ordered porous TiO₂-rGO composites with controllable light absorption properties for efficient solar energy conversion, Advanced Materials. (2017) 29, no. 4.
Web of Science® Google Scholar
73 Yang Y., Pham N. D., Yao D., Fan L., Hoang M. T., Tiong V. T., Wang Z., Zhu H., and Wang H., Interface engineering to eliminate hysteresis of carbon-based planar heterojunction perovskite solar cells via CuSCN incorporation, ACS Applied Materials & Interfaces. (2019) 11, no. 31, 28431–28441, https://doi.org/10.1021/acsami.9b07318, 2-s2.0-85071035790, 31311262.
10.1021/acsami.9b07318
CAS PubMed Web of Science® Google Scholar
74 An Y., Shang A., Cao G., Wu S., Ma D., and Li X., Perovskite solar cells: optoelectronic simulation and optimization, Solar RRL. (2018) 2, no. 11, article 1800126, https://doi.org/10.1002/solr.201800126.
10.1002/solr.201800126
Web of Science® Google Scholar
75 Foley B. J., Marlowe D. L., Sun K., Saidi W. A., Scudiero L., Gupta M. C., and Choi J. J., Temperature dependent energy levels of methylammonium lead iodide perovskite, Applied Physics Letters. (2015) 106, no. 24, https://doi.org/10.1063/1.4922804, 2-s2.0-84969627582.
10.1063/1.4922804
Web of Science® Google Scholar
76 Bohren C., Huffman D., and Kam Z., Scattered thoughts, Nature. (1983) 306, no. 5943, https://doi.org/10.1038/306625a0.
10.1038/306625a0
Google Scholar
77 Hosein Mohammadi M., Eskandari M., and Fathi D., Effects of the location and size of plasmonic nanoparticles (Ag and Au) in improving the optical absorption and efficiency of perovskite solar cells, Journal of Alloys and Compounds. (2021) 877, article 160177, https://doi.org/10.1016/j.jallcom.2021.160177.
10.1016/j.jallcom.2021.160177
Web of Science® Google Scholar
78 Qi Y., Li W., Liu S., and Ma X., Comprehensive design and simulation of a composite reflector for mode control and thermal management of a high-power VCSEL, JOSA B. (2020) 37, no. 11, 3487–3495, https://doi.org/10.1364/JOSAB.405735.
10.1364/JOSAB.405735
CAS Web of Science® Google Scholar
79 Qian X., Gu X., and Yang R., Lattice thermal conductivity of organic-inorganic hybrid perovskite CH₃NH₃PbI₃, Applied Physics Letters. (2016) 108, no. 6, https://doi.org/10.1063/1.4941921, 2-s2.0-84958213518.
10.1063/1.4941921
Web of Science® Google Scholar
80 Shen Y., Wang F. Q., and Wang Q., Ultralow thermal conductivity and negative thermal expansion of CuSCN, Nano Energy. (2020) 73, article 104822, https://doi.org/10.1016/j.nanoen.2020.104822.
10.1016/j.nanoen.2020.104822
Web of Science® Google Scholar
81 Maleki J., Eskandari M., and Fathi D., PbS-TBAI / MoSe₂-grating as new hole transport layer in perovskite solar cells: superior efficiency enhancement thru simulation and optimization, Journal of Alloys and Compounds. (2023) 960, article 170653, https://doi.org/10.1016/j.jallcom.2023.170653.
10.1016/j.jallcom.2023.170653
Google Scholar
82 Saha P., Singh S., and Bhattacharya S., Eco-friendly methyl-ammonium tin-based planar p–n homojunction perovskite solar cells: design and performance estimation, International Journal of Modern Physics B. (2023) 37, no. 17, article 22350169, https://doi.org/10.1142/S0217979223501692.
10.1142/S0217979223501692
Web of Science® Google Scholar
83 Saha P., Singh S., and Bhattacharya S., Efficient and lead-free perovskite solar cells based on defect-ordered methyl ammonium antimony iodide, IEEE Transactions on Electron Devices. (2023) 70, no. 3, 1095–1101, https://doi.org/10.1109/TED.2023.3235870.
10.1109/TED.2023.3235870
CAS Web of Science® Google Scholar
84 Saha P. and Bhattacharya S., Other applications, In Lithium Ion Glassy Electrolytes: Properties, Fundamentals, and Applications, 2022, Springer, 183–195.
10.1007/978-981-19-3269-4_17
Google Scholar

Citing Literature

All articles

Thermal Analysis of a Plasmonic Perovskite Solar Cell: Using Coupled Opto-Electro-Thermal (OET) Modeling

Abstract