1. Introduction

In 1972, Fujishima and Honda [1] reported that titanium dioxide (TiO₂) was used in a photoelectrochemical solar cell to split the water molecules into hydrogen and oxygen. After that, extensive studies have focused on anatase TiO₂ because of its high catalytic activity, good chemical stability, low cost, nontoxicity, and abundance. Moreover, it has wide applications in many fields, such as photocatalysis for pollutant degradation, biosensors, water treatment [2], lithium-ion batteries, and low-cost solar cells [3, 4].

The photocatalytic activity of TiO₂ depends on several factors such as crystal type, morphology, and the exposed surface facet [5]. TiO₂ exists in three crystalline phases: rutile, anatase, and brookite. In macrosize, the rutile phase has the highest thermodynamical stability compared to anatase and brookite under ambient conditions [6]. However, anatase is widely used as a photocatalyst due to its nanoparticle stability when its size is below 11 nm [7].

The photocatalytic process occurs when the photocatalyst is irradiated by light with sufficient energy that is equal to or larger than that of the band gap, and this will cause the excitation of electrons from the valence band (VB) to the conduction band (CB), creating electron-hole pairs. The created electron-hole pairs can reach the surface and induce chemical reactions by charge transfer from the catalyst to the adsorbate [8]. The band gap of bulk anatase TiO₂ is 3.2 eV, and this large band gap limits the photocatalytic activity of anatase to a small portion in the UV region which corresponds to about 4% of the incident solar energy [9, 10]. Thus, many experimental and theoretical studies have been conducted to enhance anatase TiO₂ photocatalytic activity by reducing its band gap to absorb light in both UV and visible regions and improving the distance between VB and CB.

These studies are based on ion implantation, doping, metal loading, and preparation of composite semiconductors [11, 12]. Studies show that metal doping can result in thermal instability, and transition metal ion doping lowers the photothreshold energy of TiO₂. The metal ions may also act as recombination centers for electrons and holes, resulting in reducing the activity of the photocatalyst. Many experimental studies reveal that nonmetal doping of TiO₂ increases its catalytic activity under visible light irradiation [10–13]. In particular, doping TiO₂ by substituting O sites with chalcogen atoms is a hot research topic due to the chalcogen’s peculiar electronic and optical properties [14–16]. Several studies demonstrated that the narrowing of the band gap was caused by the mixing of 2p O and dopant chalcogen states (3p S, 4p Se, and 5p Te) that generate induced energy levels above the VB [17–23]. Substitutional chalcogen doping for oxygen sites distorts the crystal structure of TiO₂ and increases its volume due to its large radius compared to that of O (for S, Se, and Te, respectively), leading to various applications in many fields [17]. Sulfur-doping TiO₂ has been extensively explored since it enhances photocatalytic activity by creating oxygen vacancies and reducing the band gap [18–20]. It was reported that S-doped TiO₂ exhibited superior photocatalytic activity under sunlight radiation [18]. Hebenstreit et al. [20] reported that 3p S appears in the band gap at S-doped TiO₂. Ksibi et al. reported that the optical response of anatase TiO₂ was shifted by S doping from the UV region to near-visible light according to UV–visible (UV–vis) spectroscopic analysis [15]. Moreover, the activity of S-doping TiO₂ is influenced by the concentration of S-doping. The increase in S concentration created additional energy states within the band gap that may act as recombination centers for electron-hole pairs and decrease the photocatalytic efficiency [21]. Gurkan and Cinar [14] performed a combination of experimental methods and density functional theory (DFT) calculations to determine the electronic, optical, and photocatalytic properties of Se-doped TiO₂. In the experimental part, they reported that the Se-doped TiO₂ band gap was modified and its absorption band gap extended from 420 to 650 nm. Also, Se-doped TiO₂ shows photocatalytic activity under the radiation from direct sunlight. In their DFT part, they used cluster modeling cutting from anatase TiO₂. They reported that 3p Se orbitals are responsible for inducing additional electronic states in the band gap that lead to the enhancement of photocatalytic activity. Harb theoretically investigated the electronic structure and optical absorption of Te-doped bulk anatase TiO₂. He reported that the TiO_(2−x)Te_x system displayed a narrower band gap of 1.12 eV compared with undoped TiO₂. The electronic structure analysis for that system revealed the existence of new occupied states in the band gap due to the contribution of 2p O with 5p Te orbitals [22].

The efficiency of doping TiO₂ is linked to the method of preparation, the size of the dopant, the surface area, and the structure of the TiO₂ matrix [22]. Mathew et al. [16], using X-ray photoelectron spectroscopy (XPS) and UV–vis diffuse reflectance (UV-DR) spectroscopy, investigated the effect of chalcogens (S, Se, and Te) on the anatase to the rutile phase transition of TiO₂. They demonstrated that the substitutionally doped TiO₂ has a red-shift light absorption and improved the anatase stability. Also, they reported that the Te-TiO₂–doped system has 100% disinfection under light irradiation, and it keeps the photocatalytic activity of TiO₂ even at 750°C due to the synergistic effects between Te and TiO₂.

Zheng et al. [24] performed ab initio calculations to explain the shift of absorption to visible light by chalcogen-doped TiO₂. They performed a 2 × 2 × 2 bulk TiO₂ supercell to investigate anionic, cationic, as well as interstitial chalcogen doping. They demonstrated that the absorption peak spectrum shifts toward a red shift as the atomic number of the chalcogen element increases due to the change in the electronic structure of the doped systems. The theoretical band gap values obtained were 1.21, 0.80, and 0.48 eV for S, Se, and Te, respectively.

The dimensionality and crystal structure as well as the surface thickness are crucial factors affecting a wide range of physical properties and influencing the doped system properties [25]. In this work, we investigated thin layers of TiO₂ (two layers [2L] or four layers [4L]) that can offer insights into surface phenomena and applications that differ from those of bulk materials. The properties of TiO₂ change significantly due to the increased surface-to-volume ratio. These ultrathin TiO₂ films exhibit unique electronic, optical, and catalytic properties that differ from bulk TiO₂ materials.

Thin sheets that contain several layers of atoms of TiO₂ got great attention [17, 26–30] in recent research. Liu, Zhou, and Wu reported that the band gap increased as the thickness of anatase (010) nanosheets decreased from seven to three layers of atoms [31]. Intensive experimental and theoretical studies about the extremely thin sheets of TiO₂ containing a few layers of atoms have been performed to reveal some properties of these thin sheets. Yang et al., using UV–vis absorption spectra and Raman spectra, examined the structural and spectral properties of ultrathin TiO₂ nanosheets. They derived the band gap for anatase TiO₂ nanosheets with 1.6 nm thickness from the cutoff wavelength of the absorbed light and obtained 3.23 eV, nearly equal to the band gap of bulk anatase TiO₂. They concluded that the size effect is not obvious for the electronic structure, and the band gap shows no changes even though the anatase nanosheet thickness becomes as thin as 1.0 nm [32].

While chalcogen-doped TiO₂ enhances photocatalytic activity, this improvement is combined with several obstacles, such as electron-hole recombination, which imposes limitations on the effective utilization of chalcogen-doped TiO₂ [33, 34]. An in-depth understanding of chalcogen-doped TiO₂ electronics, optical properties, and structure stability can open up the possibility of developing new photocatalytic materials. Furthermore, doping with heavy chalcogens (Se and Te) is a promising subject due to the semimetal effect of Se or Te on predicting superior optical and electronic properties. Herein, we present a DFT study of the energetic, structural, and electronic properties of thin even layers, namely, 2L or 4L of the anatase (101) TiO₂ surface. Moreover, the effects on the photocatalytic properties caused by doping of anatase (101) TiO₂ surfaces with chalcogens, namely, S, Se, or Te on 2L (4L), are investigated. The anatase (101) surface is constructed with an even number of slabs since (101) TiO₂ is organized as a stack of double layers of TiO₂ separated by a region of low density [27, 29, 35]. The DFT study can microscopically explain the doping method, the induced energy states by dopants in the band gap level, and the changes in the photocatalytic activity. Moreover, by comparing the effects of different chalcogens that have different radii and different coverages, we aim to gain an in-depth understanding of the enhancement of photocatalytic activity, which is helpful for applications in photocatalytic devices. It is interesting to model thin sheets with different thicknesses of TiO₂ and study the effect of interstitial chalcogen dopants and how they may affect the electronic structure across the chalcogen series with increasing atomic number (S, Se, and Te).

2. Methodology

All the calculations are done using Quantum Espresso code [36], with exchange-correlation potential described by using the generalized gradient approximation (GGA) based on the Perdew–Burke–Ernzerhof (PBE) functional [37]. Convergence tests are done for cutoff energy and k points. Plane-wave basis sets are employed with a 500 eV cutoff energy. The Monkhorst–Pack grids of (10 × 10 × 10) and (3 × 5 × 1) [38] are used to perform Brillouin zone integrations in the bulk and (101) (1 × 2) surfaces, respectively. The anatase structure is tetragonal with space group I41/amd. The obtained optimized (experimental [39]) bulk parameters are a = 3.785 (3.782) Å and c = 9.514 (9.502) Å, and the internal parameter is u = 0.206 (0.208). Generally, our results match the experimental [39, 40] and previous theoretical results [39–42], as shown in Table 1. The calculated band gap for bulk TiO₂ is 2.2 eV, which is less than the experimental value (3.2 eV; [40]). The underestimation of the gap is mainly due to the incomplete cancellation of the self-interaction for the exchange-correlation function at GGA [33]. However, the GGA band gap error is canceled as we aim to make trends from the obtained data for the effect of the doped chalcogens on the properties of TiO₂ (101) thin surfaces.

3. Results and Discussion

3.1. Clean TiO₂ Thin Surfaces

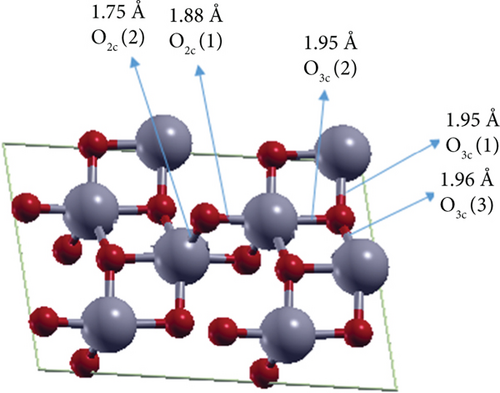
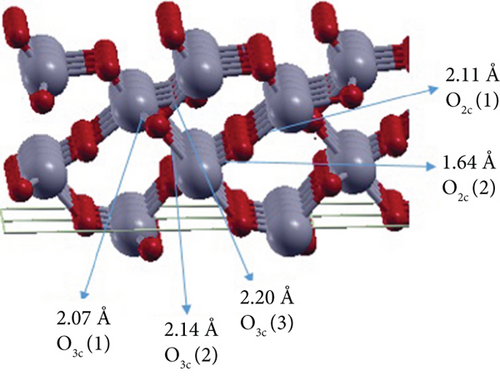
It is well known that the TiO₂ (101) surface is organized into a stack of double layers of TiO₂ with relatively low-density regions between them. The studied thin surface sheets are (1 × 2)- anatase (101) TiO₂ supercells with an even number of layers, 2L and 4L consisting of 24 and 48 atoms, respectively (see Figure 1). The (101) surface has twofold and threefold coordinated anion O atoms, which are O_2c and O_3c, respectively (see Figure 1). At the 2L surface, the bond lengths between Ti and O at O_2c are 1.88 and 1.75 Å, whereas the three bonds between Ti and O_3c have identical lengths (1.95 Å) (see Figure 1(a)). For the 4L (101) (1 × 2) TiO₂ surface, the bond lengths between Ti and O_2c are 2.11 and 1.64 Å, whereas the bond lengths between Ti and O_3c are 2.20, 2.14, and 2.07 Å. The calculated surface energies are 0.54 and 0.65 J/m² for 2L and 4L, respectively. These values are consistent with the literature values of 0.41 J/m² [29, 41] for 2L and 0.61 J/m² [44, 45] for 4L (101) TiO₂ surface. The surface energy of the 4L surface is higher than that of the 2L surface due to the peculiar structure of the “pentacoordinated nanosheet,” which is also reported by Vittadini and Casarin [29]. At this 4L anatase (101) TiO₂ surface, all Ti atoms are fivefold coordinated, and the central O atoms lower their coordination number from the chemically unfavored threefold to the favorable twofold coordination (see Figure 1(b)).

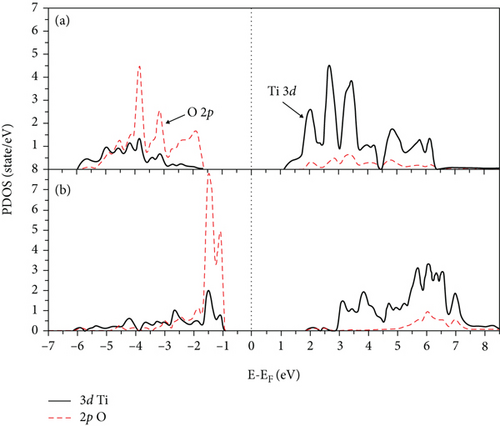
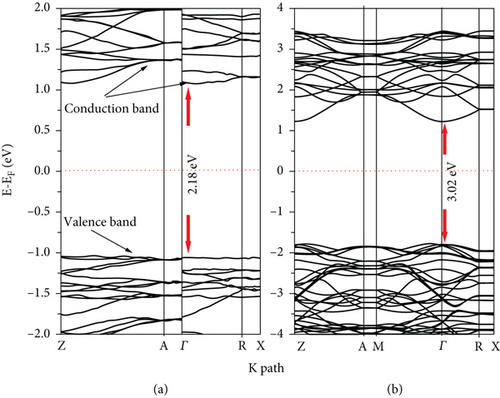
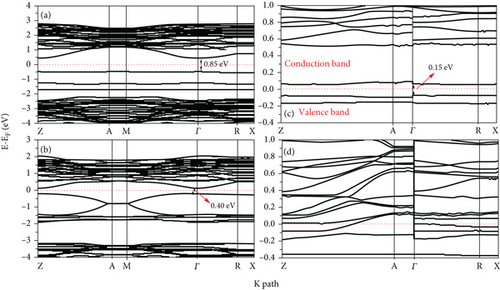
The partial densities of state (PDOS) for clean 2L and 4L anatase (101) TiO₂ surfaces are shown in Figures 2(a) and 2(b), respectively. The VB and CB consist of both 3d Ti and 2p O orbitals. At 2L (see Figure 2(a)), the CB is split into two parts: t_2g (lower part) below 4.2 eV and e_g states (upper parts) at higher energy [46]. The splitting between the two parts of CB at the 4L clean anatase (101) surface decreases due to the peculiar structure, and the 2p O orbital becomes more localized (see Figure 2(b)). The energy band structures for the 2L and 4L anatase TiO₂ (101) surfaces are shown in Figure 3, and the zero point energy is referred to as the Fermi energy (E_f). The band gaps between VB and CB at 2L and 4L surfaces are 2.18 and 3.02 eV, respectively. The band gap for the 2L surface is nearly identical to that we obtained for bulk TiO2 (2.2 eV). This means that the intrinsic band gap of TiO₂ is not affected by changing the size of TiO₂ [32]. The band gap for the 4L surface is 3.02 eV, which is greater than that for 2L due to the pentacoordinated effect at this surface.

3.2. Doped Systems

The chalcogen effects are investigated by replacing one (two) oxygen atom with one (two) chalcogen atom, namely, S, Se, or Te, at the topmost surface layer. The surface defect site is X (2X); (X = S, Se, and Te) corresponds to the substituted chalcogens (X) at 2L and 4L surfaces. The concentrations of doped-chalcogen in the TiO₂ (101) surface are 4.17, 8.33, 2.08, and 4.17 at percentages for 2L X, 2L 2X, 4L X, and 4L 2X, respectively (X = S, Se, and Te).

3.2.1. S-Doped TiO₂

The Ti-S bonds are always larger than the Ti-O bonds, as can be seen in Table 2. This result is expected since the substitution of O with larger atom radii causes the expansion of TiO₂ cell volume [46]. An ionic long bond formed between S and two Ti atoms with lengths of 2.32, 2.25, 2.33, and 2.25 Å at 2L 1S/TiO₂ and 2S/TiO₂ systems. The doped S atom has no common bond with the O atom in both 2L and 4L 1S/TiO₂ doped systems (see Table 2). However, in the 4L 2S/TiO₂ system, an irregular pentagon is formed with the bonds 2.28, 2.02, 2.09, 2.04, and 1.66 Å for Ti-S, Ti-O_3C (1), Ti-O_3C (2), Ti-O_2C (2), and O-S bonds, respectively.

Table 2. The structural properties for the studied doped systems. Ti-O_3C is the bond length between the Ti atom and three coordinated O atoms as can be seen in Figure 1, Ti-O_2C is the bond length between the Ti atom and two coordinated O atoms as can be seen in Figure 1, and O-X is the bond length between O and doped chalcogen atom.

System	Ti-O2C(1) Å	Ti-O2C(2) Å	Ti-X Å	Ti-O3C(1) Å	Ti-O3C(2) Å	Ti-O3C(3) Å	O-X
2L S/TiO2	1.76	1.85	2.32	1.96	2.01	1.95	—
			2.25
4L S/TiO2	1.62	2.07	2.18	2.03	1.96	2.08	—
2L 2S/TiO2	1.76	1.85	2.33	1.95	2.01	1.95	—
			2.25
4L 2S/TiO2	1.67	2.01	2.28	2.02	2.09	2.10	1.66
2L Se/TiO2	1.76	1.85	2.38	1.96	2.01	1.95
			2.45
4L Se/TiO2	1.62	2.08	2.22	2.05	1.99	2.07
2L 2Se/TiO2	1.76	1.85	2.46	1.95	2.01	1.94
			2.39
4L 2Se/TiO2	1.63	2.04	2.26	2.04	2.11	2.02
2L Te/TiO2	1.73	1.88	2.62	1.96	1.95	2.03
4L Te/TiO2	1.63	2.11	2.58	2.03	1.90	2.07
2L 2Te/TiO2	1.78	1.78	2.69	1.96	1.95	2.01
			2.69
4L 2Te/TiO2	1.68	1.68	2.66	2.11	2.06	2.09	2.11

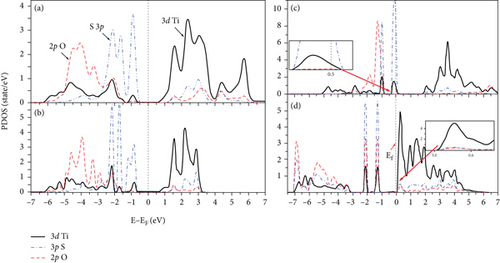
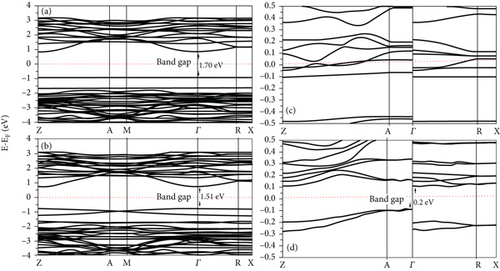
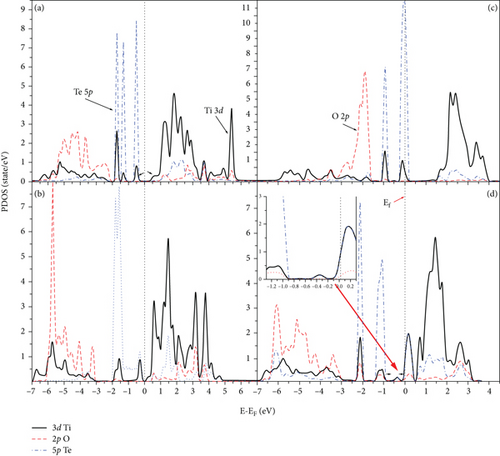
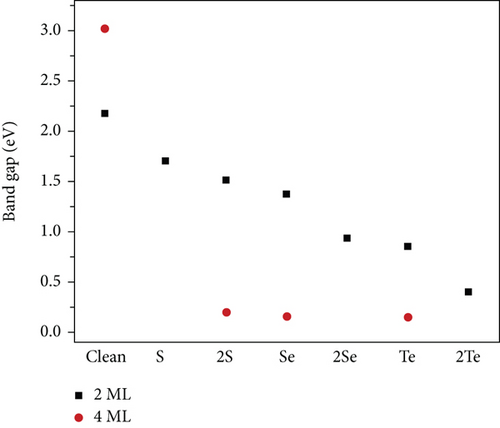
The PDOS of the S-doped TiO₂ is shown in Figure 4. There is a large hybridization between 3p S, 3d Ti, and 2p O at both the VB and the CB at all concentrations. 3p S is localized (delocalized) at VB (CB). Doping TiO₂ with S narrows the band gap due to the mixing of 2p O and 3d Ti states with the 3p S state and causes an increase in the width of the VB (see Figure 4). The band gap of the TiO₂ surface decreases at S-doping systems compared with its value at the clean TiO₂ surface, as can be seen in Figure 5. The band gap of S-doping TiO₂ is narrowed and becomes 1.70 and 1.51 eV at 2L 1S/TiO₂- and 2L 2S/TiO₂-doped systems with S atom concentrations of 4.17% and 8.33%, respectively. The large hybridization between 3p S and 3d Ti orbitals shifts the S state below Fermi energy in the band gap region (see Figure 4(c)) at the doped 4L 1S/TiO₂ system which predicts the modifications of the photoactivity of the TiO₂ surface. Moreover, the band gap has a large narrowing at the doped 4L 2S/TiO₂ system compared with a clean TiO₂ surface and becomes 0.2 eV (see Figure 5(d)). Moreover, the narrowing of the band gap at the doped 4L 2S/TiO₂ system (0.2 eV compared with 3.02 eV at the clean 4L surface) is greater compared with the 2L 1S/TiO₂ system (1.70 eV compared with 2.08 eV at the clean 2L surface), although the concentration of the doped S atom is the same at both systems (4.17%). These results predict that the narrowing of the band gap depends more on the thickness of the surface and the number of layers than on the concentration of S atoms [25]. Our results about the band gap narrowing due to S doping are consistent with previous results [15, 16, 24, 45, 46] that S-doping TiO₂ causes the shifts of the CB and VB and reduces the band gap of the samples at all S concentrations compared with its value at a clean TiO₂ surface. Umebayashi et al. found that the band gap of TiO_2-x S_x decreased to 1.4 eV compared with its value at a clean TiO₂ (2.3 eV) surface [46]. The narrowing of the band gap by doping S atoms depends on the concentration of S and the number of TiO₂ surface layers. In general, our results for the doped S/TiO₂ system relate the decrease in the band gap in the TiO₂ surface to the hybridization between the 3p S states and 3d Ti orbitals and the formation of new states in the band gap regions. These results predict an improvement in the photocatalytic properties of the TiO₂ surface [17, 46, 47].

3.2.2. Se-Doped TiO₂

The doped Se atom has two (one) bonds with Ti atoms at 2L (4L) Se/TiO₂ doped systems and has no common bond with the O atom, as seen in Table 2. In general, the Ti-Se bond length is larger than the Ti-S and Ti-O bonds due to the large radius of Se compared with the S and O radii.

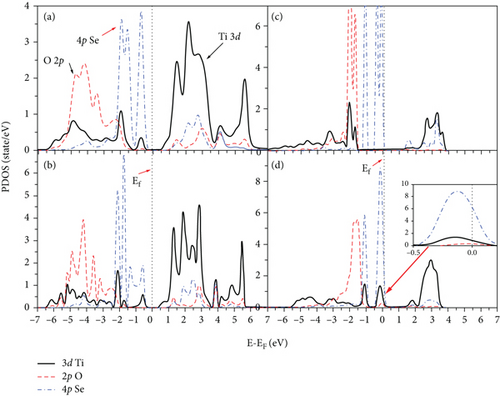
Figures 6(a) and 6(b) represent the PDOS for the 2L doped Se/TiO₂ system, while Figures 6(c) and 6(d) represent the 4L doped Se/TiO₂ ones. All Se-doped systems have a large hybridization between the 4p Se orbital and the 3d Ti band. This hybridization causes a decrease in the distance between VB and CB, as can be seen in Figure 6. The band gap decreases in Se-doped systems compared with its value at a clean TiO₂ system, as seen in Figure 7. The calculated band gaps are 1.37, 0.93, and 0.16 eV at 2L 1Se/TiO₂, 2L 2Se/TiO₂, and 4L 1Se/TiO₂ systems, respectively. The calculated band gaps decrease with increasing the number of layers, as can be seen in Figure 7. One can see in Figures 6(d) and 7(d) that the large hybridization between 3d Ti, 2p O, and 3p Se causes the shift of VB and arises new states in the band gap region which predicts the semimetallic features of the 4L 2Se/TiO₂ system. This new shallow state is beyond Fermi energy and not deep in the band gap region which predicts that it will not prevent photoactivity and will not act as an electron-hole recombination center [48]. These shallow states act as trapping centers for charge carriers and indicate the modification of the photoactivity of TiO₂ by the photogenerated charges [48, 49]. The decrease in the calculated band gap in Se-doped systems is consistent with previous experimental and theoretical studies [14, 16, 24, 34, 48, 50]. Similar results were reported by Mathew et al. [16] and H. Ibrahim, Mohamed, and I. Ibrahim [48] talked about the formation of intermediate energy states in the band gap of Se-doped anatase TiO₂ that extend the lifetime of the charge carriers and enhance the absorption of radiation in the visible region. Our results are compatible with the experimental results of Xie, Li, and Xu in that the band gap of TiO₂ is effectively narrowed by Se doping due to rising extra states in the band gap [34]. Moreover, the photoactivity of anatase TiO₂ is improved by Se doping according to the broadening in the absorbing range [14, 34, 40, 49]. Rockafellow et al. found evidence about the Se atoms trapping photogenerated electrons by using XPS on Se-doped TiO₂ [50]. They concluded that Se-doped TiO₂ photoactivity is greater than that of clean TiO₂ for visible light and is still capable of absorbing UV light at faster rates than undoped TiO₂ [50]. Our results are consistent with those of Zheng et al. [24], who found that the interstitial Se states extended more than S ones into the band gap and induced a peak caused by mixing 2p O and 3d Ti orbitals.

3.2.3. Te-Doped TiO₂

The bond lengths for doped Te systems are shown in Table 2. The bond lengths for X–Ti (X=S, Se, or Te) increase in the order S < Se < Te, and this is expected since the chalcogen ionic radius increases with increasing their atomic number. The Ti-Te bond lengths are longer than the Ti-O bond lengths on clean surfaces (see Table 2). All Te-doping atoms have no common bond with O atoms in all Te/TiO₂ systems except for the 4L 2Te/TiO₂ system. In the 4L 2Te/TiO₂ system, an irregular pentagon is formed with 2.66, 2.11, 2.06, 1.68, and 2.11 Å for Ti-Te, Ti-O_3C (1), Ti-O_3C (2), Ti-O_2C (2), and O-Te bonds, respectively.

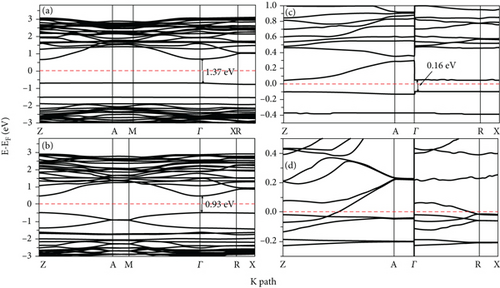
The PDOS of Te-doping anatase TiO₂ at 2L and 4L (1 × 2) surfaces is shown in Figure 8. There is a strong hybridization between 5p Te and 3d Ti in all Te-doped systems. The hybridization between 5p Te and 3d Ti appears at the top of VB. The strong hybridization between 5p Te and 3d Ti causes the shift of VB and CB near the Fermi level, and the band gap is 0.75 eV (0.15) at 2L 1Te/TiO₂ and 2Te/TiO₂ doped systems (see Figures 9(a) and 9(b)). Also, at the 4L 1Te/TiO₂ system, the strong hybridization between the 5p Te orbital and 3d Ti produces two peaks at the top of VB, and one of them extends beyond the Fermi level, as can be seen in Figure 8(c). The 5p Te orbital introduces new states in the band region of the 4L 1Te/TiO₂ system, and the calculated band gap is 0.15 eV, as shown in Figure 9(c). At the 4L 2Te/TiO₂ system, the CB passes beyond the Fermi level (see Figure 9(d)) which predicts the semimetal features [16]. Our results predict that heavier chalcogen doping is more effective in reducing the band gap of TiO₂ toward the visible region and has more effect on increasing the photoactivity of the anatase surface (see Figure 10). The trend of the decreasing of the band gap of TiO₂ by doping with chalcogen elements seen in this work is consistent with previous experimental [16] and theoretical [17, 24, 34, 47–49] works. Zheng et al. reported that anionic doping with heavy chalcogen elements such as Te and Se is more effective in narrowing the band gap of TiO₂ toward the visible light region [24]. Also, Mathew et al., by experimental investigation, found that the photoluminescence (PL) of Te-doped TiO₂ is lower than the other samples that were doped with lighter chalcogen [16]. The shifting of the absorption edge to the visible region is related to the introduction of new energy states caused by the p chalcogen orbital and the formation of semimetallic features [16, 24, 34, 48, 49]. Furthermore, similar results were reported by Zhang et al. that 5p Te orbitals are distributed in three occupied localized gap states, with the Fermi level positioned above these states which explains the visible light absorption.

4. Conclusions

The structural and electronic properties of substitution of one (two) chalcogen atoms, namely S, Se, and Te, with one (two) O atoms in anatase (101) TiO₂ thin surfaces are investigated by using DFT calculations. The structural and electronic properties of chalcogen-doped systems depend on the number of TiO₂ slab layers as well as the type of chalcogen. The band gap narrowing caused by chalcogen doping is explained by investigating the density of the state. The high hybridization between the p chalcogen orbital and 3d Ti as well as 2p O orbitals arises new states in the band gap region and reduces the band gap of the anatase TiO₂ surface. The effect of band gap narrowing increases with increasing the atomic number of the doped chalcogen and depends on the thickness of the surface.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was funded by Isra University with a grant number of 28-11/2020/2021.