Volume 2024, Issue 1 2327044

Research Article

Open Access

A Method of Constructing Superpotentials by Combining Two Functions Based on Shape Invariance

Wenxin Qiu,

Wenxin Qiu

orcid.org/0009-0008-0935-3853

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Yin Yin,

Yin Yin

orcid.org/0009-0004-9520-2824

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Wei Cheng,

Wei Cheng

orcid.org/0009-0009-0099-714X

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Yao Liu,

Yao Liu

orcid.org/0009-0008-7692-4927

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Guang Luo,

Corresponding Author

Guang Luo

[email protected]

orcid.org/0000-0002-3698-9311

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Wenxin Qiu,

Wenxin Qiu

orcid.org/0009-0008-0935-3853

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Yin Yin,

Yin Yin

orcid.org/0009-0004-9520-2824

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Wei Cheng,

Wei Cheng

orcid.org/0009-0009-0099-714X

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Yao Liu,

Yao Liu

orcid.org/0009-0008-7692-4927

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

Guang Luo,

Corresponding Author

Guang Luo

[email protected]

orcid.org/0000-0002-3698-9311

College of Physics and Electronic Engineering , Chongqing Normal University , Chongqing , 401331 , China , cqnu.edu.cn

Search for more papers by this author

First published: 08 October 2024

https://doi.org/10.1155/2024/2327044

Academic Editor: Antonio Scarfone

Share a link

Email
Wechat
Bluesky

Abstract

Supersymmetric quantum mechanics (SUSYQM) plays an important role in solving the Schrödinger equation, and it is also important to find more superpotentials that can be solved accurately. On the basis of studying the characteristics of existing superpotentials, the authors find a missing superpotential and put forward a method by combining two functions to construct all existing solvable superpotentials and prove the existence of the missing superpotential. First, based on the idea of SUSYQM, this paper studies the shape invariance of the partner potentials with the form of two functions and obtains the energy spectrum in many different cases. Second, according to the results of solving differential equations satisfied by two functions, the authors not only construct most existing solvable superpotentials successfully but also generate a missing solvable superpotential. Third, for the missing solvable superpotential, some discussions are made, such as the corresponding partner potentials, energy spectrum, ground state wave function, and excited state wave functions. Lastly, the summary is made, and the prospects are projected.

1. Introduction

In quantum mechanics, the solution of the Schrödinger equation with different potential constraints is a very core content, which is widely used in atomic physics, molecular chemistry, nuclear physics, nanostructure, and solid state physics [1–3]. The supersymmetric quantum mechanics (SUSYQM) method can accurately solve the energy and wave functions of quantum systems with certain potential, which brings new prospects for the development of quantum mechanics [4, 5].

In SUSYQM, one main research direction for supersymmetry is to utilize the Galois group theory method, focusing on the group symmetry satisfied by operators and to study from the perspective of Lie groups and Lie algebras in order to reveal more physical laws. This approach emphasizes the symmetry of the system and can also smoothly transition the research to the fields of quantum field theory, high-energy physics, and even cosmology [6, 7]. For instance, Acosta-Humanez [8] demonstrates that supersymmetry quantum mechanics problems can be analyzed and solved through differential Galois theory. Specifically, by studying the integrability of the Schrödinger equation, the author establishes a connection with the differential Galois group. These conclusions not only showcase the application of differential Galois theory in supersymmetry quantum mechanics but also provide a theoretical foundation and new research directions for future studies. In 2024, Contreras-Astorga, Escobar-Ruiz, and Linares [9] revisited the SUSY partner Hamiltonians of the quasi-exactly solvable sextic potential from a Lie algebraic perspective.

The other main research direction involves following the construction of quantum mechanical systems to solve the energy spectrum and wave functions of the Schrödinger equation under solvable potential constraints and to explore more exactly solvable potentials. In 1983, Gendenshtein proposed shape invariant potentials, which means two supersymmetric partner potentials that are similar in shape, differ by only a constant, and have the same intrinsic energy [10–12]. Then, Dutt, Khare, and Sukhatme [13] successfully constructed a dozen kinds of superpotentials whose energy spectrums and wave functions can be accurately solved by using supersymmetry and found that their partner potentials all belong to shape invariant potentials [14, 15]. In 2021, Benbourenane Jamal used shape invariance to solve a new superpotential and obtained an exact solution of the Schrödinger equation [9]. In the past 2 years, our team has also successfully proposed several new superpotentials, obtained energy spectrums and wave functions, and expanded the number of superpotentials that can be accurately solved [16–18]. At present, there are only a dozen superpotentials that can be solved by SUSYQM, including harmonic oscillator potential, Coulomb potential, and Morse potential [2, 15, 9, 17, 19, 20].

Further study of the existing superpotential shows that most of them are composed of two terms, and after derivation or squaring of these two terms, there will be a certain relationship, such as similar terms. Therefore, based on this idea, we can also propose a superpotential composed of two arbitrary functions, obtain the differential or algebraic relationship between the functions according to the shape invariance satisfied by the partner potentials, and thus determine the two functions by solving the differential equation or algebraic equation. Based on this idea, this paper first briefly reviews the basic idea of SUSYQM. Second, we describe the method of constructing solvable superpotential by combining two functions. This method not only constructs all existing solvable superpotentials but also finds a missing solvable superpotential. Third, we determine the energy spectrums in various cases according to the shape invariance. Fourth, we solve the solutions of the Schrödinger equation with the missing superpotentials, including partner potentials, ground state wave functions, and excited state wave functions. Finally, the full paper is summarized and prospected.

2. The Introduction of the SUSYQM

The one-dimensional steady state of the Schrödinger equation is as follows:

(1)

To simplify the calculation, set ℏ = 2m = 1, then the Hamiltonian of Equation (1) is as follows:

(2)

According to relevant studies [19, 21–23], introduce the superpotential W(x, a) to define the raising and lowering operators A^± as follows:

(3)

The potential V(x, a) of the system is replaced by the partner potentials V_±(x, a) [24] as follows:

(4)

And the partner potentials V_±(x, a) are satisfied with the shape invariance [17] as follows:

(5)

where R(a₀) is the additive constant, R(a₀) = g(a₁) − g(a₀), a₁ = f(a₀). The partner Hamiltonians of the system are as follows:

(6)

and there is [25]

(7)

It can be seen that the energy spectrums have the following relationship:

(8)

By using the iterative relationship, the eigen energies can be obtained as follows:

(9)

And the zero energy ground state wave function

is as follows:

(10)

where N is the normalized constant. Furthermore, by repeatedly applying A⁺ to

, the excited state wave functions are easily obtained as follows:

(11)

3. The Idea of Constructing Solvable Superpotentials

The specific expression of the existing superpotentials are shown in Table 1. Further study found that most superpotentials are composed of one or two terms, and there is always a certain correlation between terms. For example, the three-dimensional harmonic oscillator superpotential has two terms and is based on Equation (4), there will be a cross-term produced by squaring in its corresponding partner potentials. And the cross term is a constant term produced by and r. Another example is Scarf (hyperbolic) superpotential, and based on Equation (4), there are a derivative term and a cross term produced after the square in its corresponding partner potentials. The derivative of sech x is sech x tanh x, and the cross term of is also similar to sech x tanh x. These two terms can obviously be merged into similar terms.

Table 1. Existing solvable superpotentials.

Superpotentials	W
Harmonic oscillator	wx/2	nw
3D harmonic oscillator	wr/2 − (l + 1)/r	2nw
Coulomb
Morse	A − Be^−αx	A² − (A − αn)²
Eckart (I)
Scarf I (hyperbolic)	A tanh x + B sech x	A² − (A − n)²
Rosen–Morse (hyperbolic)
Scarf II (hyperbolic)	A coth x − B csch x	A² − (A − n)²
Scarf I (trigonometric)	A tan x − B secx	(A + n)² − A²
Rosen–Morse (trigonometric)
Scarf II (trigonometric)	A cotx + B csc⁡x	(A + n)² − A²
Posch–Teller 1 (trigonometric)	A tan x − B cotx	(A + B + 2n)² − (A + B)²
Posch–Teller 2 (hyperbolic)	A tanh x − B cothx	(A − B − 2n)² − (A − B)²
Matching with Rosen–Morse I (trigonometric)		—

Therefore, we can assume that the superpotential itself is composed of two functions, and there are some correlations between the two functions, such as differential relationship and algebraic relationship. Then, the relationship between the relevant parameters or coefficients can be determined according to the shape invariance that the corresponding partner potentials meet so as to achieve the purpose of solving the supersymmetric quantum mechanical system under the constraint of the potentials.

Furtherly, from Table 1, it can also be found that Scarf I (hyperbolic) superpotential A tanh x + B sech x is matched with Scarf II (hyperbolic) superpotential A coth x − B csch x,

Eckart (I) superpotential is matched with Rosen–Morse (hyperbolic) superpotential , Posch–Teller 2 (hyperbolic) superpotential A tanh x − B coth x is matched with Posch–Teller I (trigonometric) superpotential A tan x − B cotx, and so on. But there is no superpotential matched with Rosen–Morse (trigonometric) . The one that matches is . Although can be obtained by translating , we can still consider as a missed superpotential (similar to Scarf I [trigonometric] and Scarf II [trigonometric], which have the same translation relationship but are still different solvable superpotentials).

So, we assume that the superpotential is as follows:

(12)

where A, B, and C are arbitrary constants. f(x) and p(x) are two undetermined functions. Then,

(13)

and

(14)

And the partner potentials of Equation (4) are as follows:

(15)

According to the shape invariance, we can know

(16)

If the expression of f^′(x) or p^′(x) can be combined with f²(x), p²(x), f(x)p(x), or f(x), p(x), then by eliminating the term containing the unknown variable x in Equation (15), a system of equations can be established to determine the additive constant, and then the energy spectrum can be calculated using the iterative idea. Moreover, if the expression of f^′(x) or p^′(x) can be combined with f²(x), p²(x), f(x)p(x), or f(x), p(x), it means that some differential relationship can be established between f^′(x) (or p^′(x)) and f(x) (or p(x)) to form a differential equation or system of differential equations. By solving this differential equation or system of differential equations, we can obtain the expression of the functions f(x) and p(x), and thus determine the specific superpotential. Further, if we can also derive the missing superpotential, it will further illustrate the value of this method.

4. Determination of Energy Spectrums

Based on the above ideas, we simply assume that f^′(x) (or p^′(x)) and f(x) (or p(x)) satisfy the relationship as follows:

(17)

The reason we chose this relationship is because

and (secx)^′ = −tan x secx. Substituting Equation (17) into Equation (15), we can get the following:

(18)

To determine f(x) and p(x), and even finally determine the superpotential W(x), we must discuss according to the value of the parameters.

4.1. A = 0 and B ≠ 0

When A = 0 and B ≠ 0, then Equation (15) can be reduced to the following:

(19)

That is,

(20)

According to Equation (16), it is required that the coefficients which contain the unknown variable x must cancel each other, then it must,

(21)

1.
When B₁ = B₀ = B and k = 0, that is, p^′(x) = kf(x)p(x) + h = h, then the energy spectrum is as follows:
(22)
Then we can get p(x) = hx + c and W₁(x, B, C) = Bp(x) + C is the linear harmonic oscillator potential.
2.
When B₁ = −B₀ and C = 0, that is, p^′(x) = kf(x)p(x) + h = h. In this case, f(x) can be any function, which leads to , but the system has only one state, which will not be discussed here.

4.2. A ≠ 0 and B = 0

When A ≠ 0 and B = 0, because of the first expression of Equation (17), Equation (15) becomes the following:

(23)

There are two situations:

(G is a constant), then,

(24)

Because of the shape invariance of Equation (16), the coefficients containing the unknown variable x must be canceled by each other. And we can obtain the following:

(25)

We can obtain A₁ = −A₀ (which is not additive and will not be discussed) and A₁ = A₀ + s. Then, the energy spectrums are as follows:

(26)

Then f(x) can be further solved according to the first expression of Equation (17), with the following solutions:

1.
When se > 0, it can be solved as follows:
(27)
where c₁ is an arbitrary constant (c₁ and c₂ appeared in the following text are arbitrary constants).
- i.
  When and c₁ = 0 (),
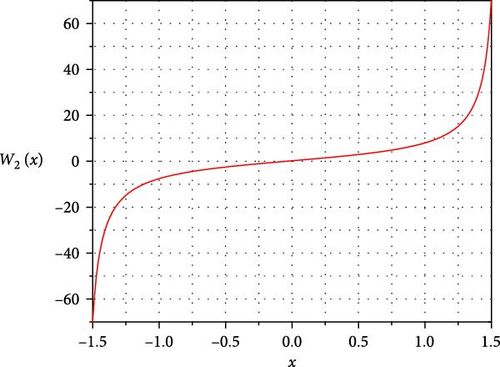
  (28)
  W₂(x, A, G) in Equation (28) happens to be the missing superpotential matched with .
- ii.
  When and . W₃(x, A, G) is Rosen–Morse (trigonometric) superpotential.
2.
When se < 0, the first expression of Equation (17) can be solved as follows:
(29)
or
(30)
- i.
  For Equation (29), when and is Rosen–Morse (hyperbolic) superpotential.
- ii.
  For Equation (30), when and is Eckart (I) (hyperbolic) superpotential.
3.
When s ≠ 0 and e = 0, the first expression of Equation (17) can be solved as follows:
(31)
When s = 1 and . And the Coulomb superpotential can be constructed.
4.
When s = 0 and e ≠ 0, the first expression of Equation (17) can be solved as follows:
(32)

In particular, when e = 1 and c₁ = 0, it is similar to the linear harmonic oscillator potential, but with only singlet states.

4.3. A ≠ 0 and B ≠ 0

When A ≠ 0 and B ≠ 0, Equation (15) becomes the following:

(33)

Because of the shape invariance of Equation (16), the coefficients containing the unknown variable x must be canceled by each other. We assume that f^′(x), p^′(x), f(x), and p(x) are all functions of non-normal numbers, then we have the following:

(34)

1.
C ≠ 0, according to Equation (19), there are s = 0 and k = 0, and then f^′(x) = e and f^′(x) = e. So we can solve for f(x) = ex + c₁ and p(x) = hx + c₂. Take them back into Equation (12) and we can get W₈(x, A, B) = (Ae + Bh)x + c, which is a linear harmonic oscillator potential with only a single state.
2.
C = 0, according to Equation (19), we can get the following:

(35)

Using the shape invariance, we have the following:

(36)

The system of Equation (36) has multiple solutions, but only A₁ = A₀ + s = A + s has additive, and it must satisfy that B₀ = B₁ = B and k = s. The energy spectrum is as follows:

(37)

The reason why the energy spectrum is such an expression is that the V_±(x) contains, which is noncancellable. According to a₁ = a₀ + s, the energy spectrum should conclude , and according to noncancellable constant terms ±bh, the energy spectrum should conclude 2nbh.

Next, we discuss the solution of Equation (17) with different values of the parameters s, e, h, and k on condition that A ≠ 0, B ≠ 0, and C = 0.

i.
When s = k ≠ 0 and se > 0, according to the first expression of Equation (17), we have

and

(38)

where c₁ is an arbitrary constant (and c₂ appearing in the following text is an arbitrary constant).

a.
When h = 0, substituting f₁(x) and f₂(x) of Equation (23) into the second expression of Equation (17) separately, we can obtain

and

(39)

The superpotentials are as follows:

(40)

and

(41)

For W₉(x), setting

, and c₁ = 0, we can get Scarf I (trigonometric) superpotential. For W₁₀(x), setting

, and c₁ = 0, we can get Scarf II (trigonometric) superpotential.

b.
When h ≠ 0, substituting f₁(x) and f₂(x) of Equation (23) into the second expression of Equation (17) separately, we can obtain the following:

(42)

and

(43)

The superpotentials are as follows:

(44)

and

(45)

If we choose

, and c₁ = 0, W₁₁(x) will become Scarf I (trigonometric) superpotential. And it can be consistent with W₉(x). By the same token, W₁₂(x) can be consistent with W₁₀(x).

ii.
When s = k ≠ 0 and se < 0, according to the first expression of Equation (17), we have

and

(46)

a.
h = 0, substituting f₁(x) and f₂(x) into the second expression of Equation (17) separately, we can get

and

(47)

The superpotentials are as follows:

(48)

and

(49)

Setting

, and c₁ = 0, we can get Scarf I (hyperbolic) superpotential according to W₁₃(x), and get Scarf II (hyperbolic) superpotential according to W₁₄(x).

b.
h ≠ 0, substituting f₁(x) and f₂(x) into the second expression of Equation (17) separately, we can obtain the following:

(50)

and

(51)

The superpotentials are as follows:

(52)

and

(53)

It is obvious that Scarf I (hyperbolic) superpotential and Scarf II (hyperbolic) superpotential can be obtained from W₁₅(x) and W₁₆(x) by selecting the parameters’ proper values.

iii.
When s ≠ 0 and e = 0, according to the first expression of Equation (17), we have the following:

(54)

a.
When h = 0, according to the second expression of Equation (17), it can be solved that

(55)

The superpotential in this case can be obtained as follows:

(56)

Because there is no constant term in Equation (56), substituting it into Equation (5), we will get the zero energy. It means that the system has only a single state.

b.
When h ≠ 0, according to the second expression of Equation (17), it can be solved as follows:

(57)

The superpotential can be obtained as follows:

(58)

For W₁₈(x), setting a = l, bc₂ − a = l + 1, bh = w and c₁ = 0, we can get 3D Oscillator superpotential.

iv.
When s = 0 and e ≠ 0, according to the first expression of Equation (17), we have the following:

(59)

a.
h = 0, according to the second expression Equation (17) it can be solved as follows:

(60)

The superpotential can be obtained

(61)

For W₁₉(x), setting

and ac₁ + bc₂ = 0, it has the same form as the harmonic oscillator potential, but the system has only a singlet state.

b.
h ≠ 0, according to the second expression of Equation (17), it can be solved

(62)

The superpotential can be obtained as follows:

(63)

For W₂₀(x), setting

and ac₁ + bc₂ = 0, it has the same form as the harmonic oscillator potential.

v.
if f^′(x) = 0, according to the first expression of Equation (17), we have

(64)

a.
When h = 0, substituting f₁(x) and f₂(x) into the second expression of Equation (17), we have

(65)

The superpotentials are as follows:

(66)

Obviously, Morse potential can be obtained by selecting appropriate parameter

, and

for W₂₁(x) in Equation (66).

b.
When h ≠ 0, according to the equation satisfied by p(x) in potential, it can be solved as follows:

(67)

The superpotential in this case can be obtained as follows:

(68)

It shows that they are almost the same and produce no new results by comparing W₂₃(x) with W₂₁(x).

Through the above discussions, we determine all of the existing solvable superpotentials, and also derive the previously missed superpotential. It shows that the method of determining superpotentials by combining the two functions that we proposed is feasible and effective.

Generally speaking, the energy spectrum of the above solvable superpotential has been given, but when it comes to specific functions, the relationship between functions is sometimes more complicated than the shape invariant relationship shown by Equation (18), and the energy eigenvalues of the Schrödinger equation may also change slightly. So it is necessary to further discuss the energy eigenvalues and the eigenwave functions of the Schrödinger equation with the derived missing superpotential.

5. Determinations of the Energy Eigenvalue and the Eigen Wave Function

From the previous section, it can be seen that the method by combining two functions can indeed construct the missing superpotential (to maintain consistency with the format in Table 1, we will change “G” to “B” in the following text), which is obviously a solvable potentials since it is obtained according to the shape invariant relationships. Because the superpotential is actually a deformation of the Rosen–Morse (trigonometric) superpotential, its application should also be similar to that of the Rosen–Morse (trigonometry) superpotential (the trigonometric Rosen–Morse potential has many applications in theoretical and mathematical physics [26]). Although for the missing solvable superpotential, it can be theoretically proven that translation does not cause changes in the energy spectrum, further research on it is still necessary. First, it is necessary to further study whether its energy spectrums change. Second, since it is a solvable superpotential, it means that the partner potentials, the ground states and the excited states need to be further determined. Third, Compean and Kirchbach [27] derived the trigonometric Rosen–Morse potential based on the form of the Eckart potential (here it is represented by Eckart I potential) and solved the Schrödinger equation using the Sturm Liouville technique. The energy spectrum and the eigenwave functions were obtained, and the triconometric Rosen–Morse superpotential was derived based on using the ground state wave function ψ₀(x). Due to the lack of shape invariance and the fact that the energy spectrum is not derived based on SUSYQM, the results are different from our current findings. Therefore, it is also necessary for us to study the solution of the Schrödinger equation under the constraint of the corresponding potential in this study. We will discuss those problems in the next.

According to W₂(x), we define

, and the partner Hamiltonians are as follows:

(69)

W₂(x)’s partner potentials are as follows:

(70)

where

, setting A = 5 and B = 1, we can plot the curves of the partner potentials V_±(x). The curves are shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Figures of the partner potentials V_±(x) of W₂(x).

Based on the shape invariance Equation (5),

(71)

i.e.,

(72)

Because R(A₀) is independent with x, A₀(A₀ − 1) = A₁(A₁ + 1). And one can obtain A₁ = A₀ − 1 or A₁ = −A₀. Setting a₀ = −A₀ and a₁ = −A₀ + 1, we can find that the shape invariance is satisfied (a₀ = −A₀ and a₁ = −A₀ + 1 satisfy the additivity. And a₀ = A₀ and A₁ = −A₀ do not satisfy the additivity and needs to be discarded). Then the energy spectrums are

. Since

, we can get

. And since n ≥ 0, A ≥ 0 is satisfied. The ground state wave function is as follows:

(73)

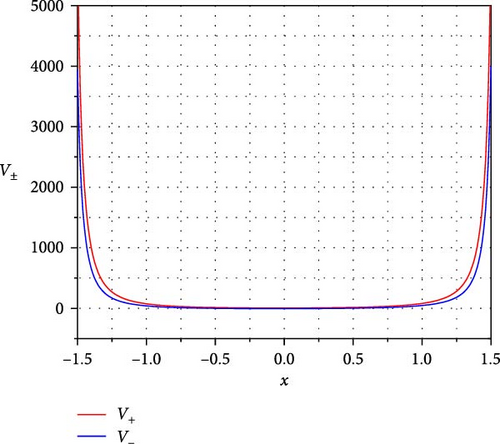
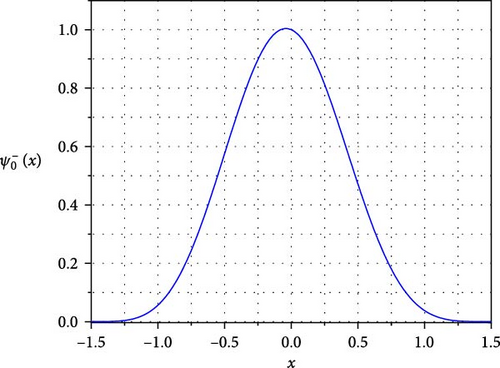
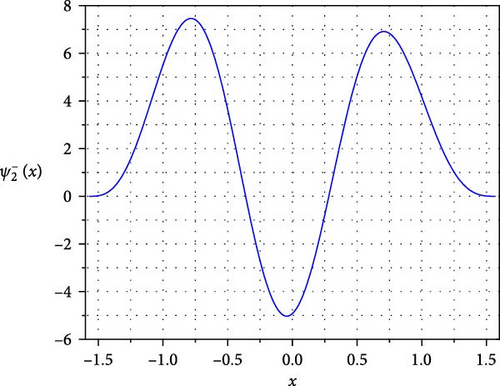
Setting A = 5 and B = 1, we can plot the curves of the superpotential and the ground state wave function as shown in Figure 2.

According to Equation (11), the first and second excited state wave functions can be obtained as follows:

(74)

(75)

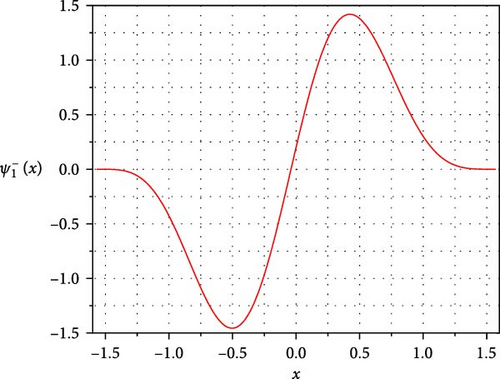
Setting A = 5 and B = 1, we have plotted the first and the second excited state wave functions in Figure 3.

6. Conclusion and Prospect

Based on the existing solvable superpotentials of SUSYQM, a missing superpotential is found according to the characteristics of existing superpotentials, and a method through combining two functions to construct a superpotential is proposed. By solving the differential equations satisfied by the two functions, the concrete forms of the functions are determined. According to the solutions, we not only reproduce all of the existing solvable superpotentials by assigning values to the parameters but more importantly, we also successfully obtain the missing solvable superpotentials. After comparing with the study of Compean and Kirchbach [27], we solve the energy spectrums, the ground state, and the excited state wave functions of the Schrödinger equation with the missing superpotentials. It shows that the method by combining two functions is a good way to construct solvable superpotentials effectively.

Combined with the previous research of our research group, we found that it is possible to find more solvable superpotentials based on SUSYQM, although this paper only analyzed and discussed in terms of a specific relationship between the two functions. In fact, in Table 1, there are still several types of superpotentials that have not been constructed, because the relationships between those two functions are not only described by Equation (17) in this article but also have many other forms of relationships. This method is proposed based on the shape invariance of SUSYQM and the solution idea of the Riccati equation without considering other solvable potentials that are not suitable for supersymmetric thinking and cannot be treated with shape invariance. However, there are many other solvable potentials, and further research is needed to determine whether similar methods are also feasible. Therefore, based on the method by combining two functions, it is still worthy to further study. We also expect to be able to construct more solvable superpotentials.

Consent

We confirm that any images, tables, figures, or text included in this paper have been obtained with the appropriate copyrights or permissions and are in compliance with copyright laws.

Disclosure

This research work represents our original contributions, and all research methods, data collection, analyses, and results presentation are our own work. We have not engaged in any form of plagiarism, replication, or unauthorized use of others’ research work or findings. Our research process has been conducted with honesty and integrity. We have not fabricated, manipulated, or altered any data, results, or experiments. The data and results presented are true and accurate.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Wenxin Qiu and Yin Yin are co-first authors.

Funding

No funding was received for this manuscript.

Open Research

Data Availability Statement

All relevant data are within the paper.

References

1 Schleich W. P., Greenberger D. M., Kobe D. H., and Scully M. O., Schrödinger Equation Revisited, Proceedings of the National Academy of Sciences. (2013) 110, no. 14, 5374–5379.
10.1073/pnas.1302475110
CAS PubMed Web of Science® Google Scholar
2 Benbourenane J. and Eleuch H., Exactly Solvable New Classes of Potentials with Finite Discrete Energies, Results in Physics. (2020) 17, https://doi.org/10.1016/j.rinp.2020.103034, 103034.
10.1016/j.rinp.2020.103034
Google Scholar
3 Falek M., Belghar N., and Moumni M., Exact Solution of Schrödinger Equation in (Anti-)de Sitter Spaces for Hydrogen Atom, the European Physical Journal Plus. (2020) 135, no. 3, https://doi.org/10.1140/epjp/s13360-020-00337-4, 335.
10.1140/epjp/s13360-020-00337-4
CAS Google Scholar
4 Barclay D. T. and Maxwell C. J., Shape Invariance and the SWKB Series, Physics Letters A. (1991) 157, no. 6-7, 357–360, https://doi.org/10.1016/0375-9601(91)90869-A, 2-s2.0-0041075098.
10.1016/0375-9601(91)90869-A
Google Scholar
5 Barclay D. T., Dutt R., Gangopadhyaya A., Khare A., Pagnamenta A., and Sukhatme U., New Exactly Solvable Hamiltonians: Shape Invariance and Self-Similarity, Physical Review A. (1993) 48, no. 4, 2786–2797, https://doi.org/10.1103/PhysRevA.48.2786, 2-s2.0-0001179402.
10.1103/PhysRevA.48.2786
CAS PubMed Google Scholar
6 Huang K., Shi S., and Yang S., Differential Galoisian Approach to Jacobi Integrability of General Analytic Dynamical Systems and Its Application, Science China Mathematics. 66, no. 7, 1473–1494.
10.1007/s11425-021-2015-6
Google Scholar
7 Lev F., Supersymmetry in Quantum Theory Over a Galois Field, Physics. (2002) 2, 246–268, https://doi.org/10.48550/arXiv.hep-th/0209229.
10.48550/arXiv.hep-th/0209229
Google Scholar
8 Acosta-Humanez P. B., Galoisian Approach to Supersymmetric Quantum Mechanics, https://doi.org/10.48550/arXiv.0906.3532.
10.48550/arXiv.0906.3532
Google Scholar
9 Contreras-Astorga A., Escobar-Ruiz A. M., and Linares R., The SUSY Partners of the QES Sextic Potential Revisited, Physica Scripta. (2024) 99, https://doi.org/10.1088/1402-4896/ad1913, 025223.
10.1088/1402-4896/ad1913
Google Scholar
10 Gendenshtein L. E. and Krive I. V., Supersymmetry in Quantum Mechanics, Uspekhi Fizicheskih Nauk. (1985) 146, no. 8, https://doi.org/10.3367/UFNr.0146.198508a.0553, 553.
10.3367/UFNr.0146.198508a.0553
CAS Google Scholar
11 Brunce A. J. and Steven D., Double-Graded Supersymmetric Quantum Mechanics, Journal of Mathematical Physics. (2020) 61, no. 6, 063503–018302, https://doi.org/10.1063/1.5118302.
10.1063/1.5118302
Google Scholar
12 Gangopadhyaya A., Bougie J., and Rasinariu C., Exactness of Semiclassical Quantization Rule for Broken Supersymmetry, Journal of Physics A: Mathematical and Theoretical. (2021) 54, no. 29, https://doi.org/10.1088/1751-8121/ac060a, 295206.
10.1088/1751-8121/ac060a
Google Scholar
13 Dutt R., Khare A., and Sukhatme U. P., Supersymmetry, Shape Invariance, and Exactly Solvable Potentials, American Journal of Physics. (1988) 56, no. 2, 163–168, https://doi.org/10.1119/1.15697.
10.1119/1.15697
Web of Science® Google Scholar
14 Cooper F., Ginocchio J. N., and Khare A., Relationship between Supersymmetry and Solvable Potentials, Physical Review D. (1987) 36, no. 8, 2458–2473, https://doi.org/10.1103/PhysRevD.36.2458, 2-s2.0-4244161498.
10.1103/PhysRevD.36.2458
CAS PubMed Web of Science® Google Scholar
15 Benbourenane J., Benbourenane M., and Eleuch H., Solvable Schrödinger Equations of Shape Invariant Potentials Having Superpotential W(x,A,B) = Atanh(px)+Btanh (6px), 2021.
Google Scholar
16 Xiong L., Tan X., Zhong S. K., Cheng W., and Luo G., A New Solvable Generalized Trigonometric Tangent Potential Based on SUSYQM, Symmetry. (2022) 14, no. 8, https://doi.org/10.3390/sym14081593, 1593.
10.3390/sym14081593
Google Scholar
17 Li M., Zhong S.-K., Dong L., Xiong L.-L., and Luo G., Shape Invariance of Solvable Schrödinger Equations with the Generalized Hyperbolic Pöschl-Teller Potential, Advances in Mathematical Physics. (2022) 2022, 4345342.
10.1155/2022/4345342
Google Scholar
18 Zhong S.-K., Xie T.-Y., and Dong L., et al.Shape Invariance of Solvable Schrödinger Equations with a Generalized Hyperbolic Tangent Superpotential, Results in Physics. (2022) 35, https://doi.org/10.1016/j.rinp.2022.105369, 105369.
10.1016/j.rinp.2022.105369
Google Scholar
19 Gangopadhyaya A., Mallow J., and Rasinariu C., Supersymmetric Quantum Mechanics: An Introduction, 2017, World Scientific Publishing Company, Singapore.
10.1142/10475
Google Scholar
20 Bougie J., Gangopadhyaya A., Mallow J. V., and Rasinariu C., Generation of a Novel Exactly Solvable Potential, Physics Letters A. (2015) 379, no. 37, 2180–2183, https://doi.org/10.1016/j.physleta.2015.06.058, 2-s2.0-84938741548.
10.1016/j.physleta.2015.06.058
CAS Web of Science® Google Scholar
21 Cooper F., Khare A., and Uday S., Supersymmetry and Quantum Mechanics, High Energy Physics Theory. (1994) 251, no. 5-6, 267–385.
Google Scholar
22 Liang H., Meng J., and Shen S., et al.Pseudospin Symmetry: Recent Progress with Supersymmetric Quantum Mechanics, Journal of Physics: Conference Series. (2014) 533, https://doi.org/10.1088/1742-6596/533/1/012020, 2-s2.0-84907916715, 012020.
10.1088/1742-6596/533/1/012020
CAS Google Scholar
23 Ushveridze A. G., Quasi-Exactly Solvable Models in Quantum Mechanics, 2017, Institute of Physics Pub.
10.1201/9780203741450
Google Scholar
24 Mallow J. V., Gangopadhyaya A., Bougie J., and Rasinariu C., Inter-Relations Between Additive Shape Invariant Superpotentials, 2019.
Google Scholar
25 Pursey D. L., Isometric Operators, Isospectral Hamiltonians, and Supersymmetric Quantum Mechanics, Physical Review. D, Particles and Fields. (1986) 33, no. 8, 22672279.
10.1103/PhysRevD.33.2267
Google Scholar
26 Chenaghlou A. and Faizy O., Gazeau-Klauder Coherent States for Trigonometric Rosen-Morse Potential, Journal of Mathematical Physics. (2008) 49, no. 2, https://doi.org/10.1063/1.2838316, 2-s2.0-40149101404, 022104.
10.1063/1.2838316
CAS Web of Science® Google Scholar
27 Compean C. B. and Kirchbach M., The Trigonometric Rosen-Morse Potential in the Supersymmetric Quantum Mechanics and Its Exact Solutions, Journal of Physics A: Mathematical and General. (2006) 39, no. 3, 547–557, https://doi.org/10.1088/0305-4470/39/3/007, 2-s2.0-29244454773.
10.1088/0305-4470/39/3/007
CAS Web of Science® Google Scholar

All articles

A Method of Constructing Superpotentials by Combining Two Functions Based on Shape Invariance

Abstract

1. Introduction

2. The Introduction of the SUSYQM

3. The Idea of Constructing Solvable Superpotentials