Volume 2024, Issue 1 1969686

Research Article

Open Access

Electron Spin Resonance Spin Probe Technique for Investigating Non-TEMPO Radicals Dispersed in Nanospaces of a Crystalline Zn Complex

Corresponding Author

Hirokazu Kobayashi

[email protected]

orcid.org/0000-0002-8643-1500

Faculty of Arts and Sciences at Fujiyoshida , Showa University , 4562 Kami-yoshida Yamanashi, Fuji-yoshida-shi , 403-0005 , Japan , showa-u.ac.jp

Search for more papers by this author

Kento Akiniwa,

Kento Akiniwa

Graduate School of Integrated Basic Sciences , College of Humanities and Sciences , Nihon University , 3-25-40 Sakura-jo-sui Setagaya-ku, Tokyo , 156-8550 , Japan , nihon-u.ac.jp

Search for more papers by this author

Fumiyasu Iwahori,

Fumiyasu Iwahori

Department of Chemistry , College of Humanities and Sciences , Nihon University , 3-25-40 Sakura-jo-sui Setagaya-ku, Tokyo , 156-8550 , Japan , nihon-u.ac.jp

Search for more papers by this author

Hidehiko Honda,

Hidehiko Honda

Faculty of Arts and Sciences at Fujiyoshida , Showa University , 4562 Kami-yoshida Yamanashi, Fuji-yoshida-shi , 403-0005 , Japan , showa-u.ac.jp

Search for more papers by this author

Masato Yamamoto,

Masato Yamamoto

Faculty of Arts and Sciences at Fujiyoshida , Showa University , 4562 Kami-yoshida Yamanashi, Fuji-yoshida-shi , 403-0005 , Japan , showa-u.ac.jp

Search for more papers by this author

Hirokazu Kobayashi,

Corresponding Author

Hirokazu Kobayashi

[email protected]

orcid.org/0000-0002-8643-1500

Faculty of Arts and Sciences at Fujiyoshida , Showa University , 4562 Kami-yoshida Yamanashi, Fuji-yoshida-shi , 403-0005 , Japan , showa-u.ac.jp

Search for more papers by this author

Kento Akiniwa,

Kento Akiniwa

Graduate School of Integrated Basic Sciences , College of Humanities and Sciences , Nihon University , 3-25-40 Sakura-jo-sui Setagaya-ku, Tokyo , 156-8550 , Japan , nihon-u.ac.jp

Search for more papers by this author

Fumiyasu Iwahori,

Fumiyasu Iwahori

Department of Chemistry , College of Humanities and Sciences , Nihon University , 3-25-40 Sakura-jo-sui Setagaya-ku, Tokyo , 156-8550 , Japan , nihon-u.ac.jp

Search for more papers by this author

Hidehiko Honda,

Hidehiko Honda

Faculty of Arts and Sciences at Fujiyoshida , Showa University , 4562 Kami-yoshida Yamanashi, Fuji-yoshida-shi , 403-0005 , Japan , showa-u.ac.jp

Search for more papers by this author

Masato Yamamoto,

Masato Yamamoto

Faculty of Arts and Sciences at Fujiyoshida , Showa University , 4562 Kami-yoshida Yamanashi, Fuji-yoshida-shi , 403-0005 , Japan , showa-u.ac.jp

Search for more papers by this author

First published: 04 August 2024

https://doi.org/10.1155/2024/1969686

Academic Editor: Massimiliano F. Peana

Share a link

Email
Wechat
Bluesky

Abstract

An ESR spin probe technique with non-TEMPO radicals, such as nitronyl nitroxide (NN), benzonitronyl nitroxide (BzNN), and iminonitroxide (IN) radicals, was used for a porous metal-organic framework (MOF), [(ZnI₂)₃(TPT)₂] (ZnTPT; TPT = tris(4-pyridyl)-1,3,5-triazine), at room temperature. The principal values of g and hyperfine coupling (A) tensors estimated from spectral reproduction were different from those for organic matrices for some of these radicals. These results indicate that host-guest interactions occur between the ZnTPT matrix and guest radicals. Thus, when using NN, BzNN, and IN radicals as spin probes for a porous MOF, the interaction between the metal atoms or organic ligands in host materials and guest radicals should be considered. The experimental ESR spectra for the derivatives of NN or BzNN radicals were reproduced only by the rigid-limit component in the ESR time scale. However, those for the derivatives of IN radicals were approximately reproduced only by rotational diffusion around the z-axis perpendicular to the plane in the IN group. Interestingly, this reproduction was not around the y-axis of the principal axes of the g tensors, parallel to the molecular long axis, as previously observed in a few organic matrices. The IN radicals dispersed in the ZnTPT matrix are expected to be accommodated in cylindrical or pseudocylindrical nanospaces sandwiched by the pyridyl or triazine rings of TPT in ZnTPT. These findings show that the ESR spin probe technique using non-TEMPO radicals can be used to investigate the chemical and biological structures of nanosized materials.

1. Introduction

Recent studies regarding various materials with tailored porous structures, sizes, and shapes, as well as interactions between host matrices and guest molecules, have grown remarkably. This has also accelerated the development of new functional materials using inclusion compounds (such as electric conductivity, [1] nonlinear optical property, [2] or magnetic property [3–5]), protection and storage of guest molecules (such as medical agents, [6] organic radicals, [7] or energetic materials [8]), and dynamics or mobility of guest molecules in a nanospace [9–12]. The detection or investigation of organic radicals confined in nanospaces or chemically decollated moieties by functional groups with unpaired electrons, such as N–O groups, requires the use of a powerful and unique technique, such as ESR spectroscopy. Using the ESR spin probe technique, the temperature dependence of the molecular dynamics of the organic radicals or moieties with unpaired electrons confined in the nanospace is studied to gain information on the structures, sizes, and shapes of the nanospaces present in organic [13–15] or inorganic porous materials [16], polymers [17, 18], peptide nanostructures [19], and biological membranes [20, 21].

The ESR spin probe technique is also used to investigate nanospaces formed in a variety of metal-organic frameworks (MOF) [11, 22, 23]. MOFs are expected to have applications such as adsorption or separation of small molecules on molecular sizes or host-guest interactions [11, 24] and catalysis for many chemical reactions [25]. Combinations of organic ligands and metals can lead to the development of various MOFs with unique pore sizes and shapes, as well as host-guest interactions. In many cases, derivatives of 2,2,6,6-tetramethyl-1-piperidinyloxyl (TEMPO) have been used as probe radicals. However, other radicals may be necessary in the future owing to the chemical diversity of the MOF pores in terms of the structures, sizes, shapes, and host-guest interactions between the MOF and guest radicals. For example, some TEMPO derivatives, such as 4-hydroxy-TEMPO (TEMPOL), introduced in MOF pores using the gas-phase sorption can be aggregated, resulting in the dipolar or exchange line-width modulation of ESR spectra [22]. In the impregnation method or encapsulation approach of probe radicals, the small spherical nitroxides, such as TEMPO, can be introduced into the narrow pore of the target materials, resulting in more complex ESR spectra due to the superposition of the spectra of the nitroxides in the narrow and large pores [18, 22].

The ESR spin probe technique has been used over the last decade to investigate non-TEMPO radicals such as 2-substituted nitronyl nitroxide (2-X-NN; 1–4; Figure 1(a)), 4-substituted phenyl benzonitronyl nitroxide (4-Y-PhBzNN; 5 and 6; Figure 1(b)), and 2-substituted-iminonitroxide (2-Z-IN; 7 and 8; Figure 1(c)), radicals for a nematic liquid crystalline phase [26]; organic 1D nanochannels such as 2,4,6-tris (4-chlorophenoxy)-1,3,5-triazine (CLPOT) or (o-phenylenedioxy) cyclotriphophazene crystals (TPP) [14, 27, 28]; or cylindrical cavities in polymethyl methacrylate (poly(methyl 2-methyl propenoate), PMMA) matrices [18]. The dipolar or exchange line-width modulation of ESR spectra for non-TEMPO radicals in nanospaces has not yet been reported [14, 18, 27, 28]. Moreover, the thin and long molecular shape of NN, PhBzNN, and IN radicals restricts their inclusion in excessively narrow pores. The principal values of g and hyperfine coupling (A) tensors of several NN or IN radicals had previously been studied, for example, in frozen organic matrices or cement [29, 30]. NN and IN radicals are important building blocks of porous films, vesicles, and nanoparticles [31], or ligands of magnetic metal complexes [32–34] as well as organic magnets [35]. In addition, NN and IN radicals are used as free radical scavengers to protect the peroxidation of cells [36] or as analgesic agents by selective binding with receptors [37]. Thus, NN or IN radicals have a potentially wide range of applications, particularly in the ESR spin probe technique. For instance, phenyl benzonitronyl nitroxide (PhBzNN) radicals [38, 39] can be used as spin probe radicals in two-dimensional (2D) sheet-type pores owing to their planar molecular shape [18].

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Chemical structures of guest radicals used in this study: (a) 2-X-NN (1–4); (b) 4-Y-PhBzNN (5 and 6); (c) 2-Z-IN (7 and 8).

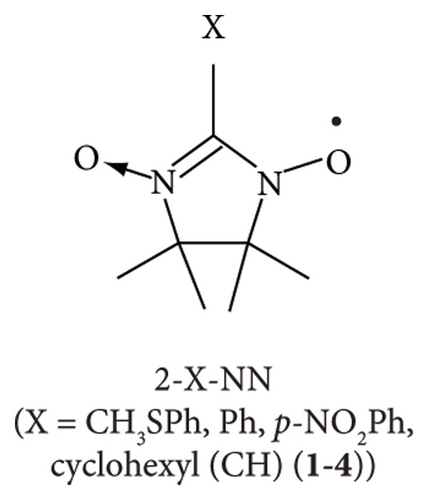
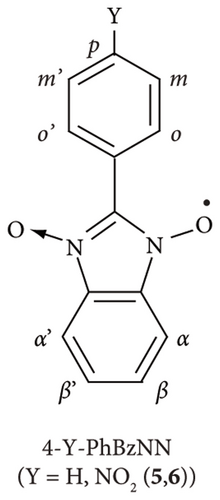
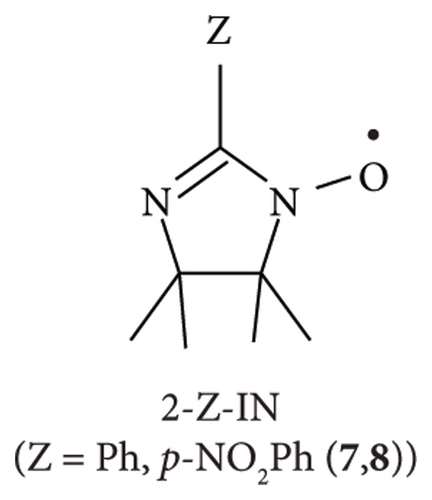
Herein, several 2-X-NN (X = Ph (2), p-NO₂Ph (3), or cyclohexyl (CH; 4); Figure 1(a)), 4-Y-PhBzNN (Y = H (5) or NO₂ (6); Figure 1(b)), and 2-Z-IN radicals (Z = Ph (7) or p-NO₂Ph (8); Figure 1(c)) were dispersed in the three-dimensionally networked cage framework of a zinc complex, [(ZnI₂)₃(TPT)₂] (ZnTPT; TPT = tris(4-pyridyl)-1, 3, 5-triazine) [24, 40–42]. The nanospace of ZnTPT shrinks or swells during the desorption or adsorption of guest molecules without destroying the crystal and is used to determine the structures of scarce target molecules, such as miyakosyne A (a marine natural product) or santonin (anthelmintic agent), using tiny crystals of [ZnTPT·(solvent molecule) (target molecule)] inclusion compounds (ICs) obtained by soaking ZnTPT in a solution of the target [24]. Electron-deficient panel-like TPT ligands in ZnTPT reduce the disorder of guest aromatics in the ZnTPT matrix. However, the preparation of single crystals of ZnTPT ICs is not always easy and it depends on the type of guest molecule. In addition, even if crystallization and determination of the crystal structure of ZnTPT ICs are successful, the pore structure of ZnTPT is dependent on the guest molecules, which are complex. In such cases, the ESR spin probe technique may be useful for determining the structures, sizes, shapes, and interactions between the pores of ZnTPT and the guest molecules. In addition, the MOF consisting of Zn(II) ion is suitable for the ESR measurement of adsorbed organic radicals because Zn(II) ion is nonmagnetic and gives no ESR signal. We conducted an ESR spin probe technique using non-TEMPO radicals with several NN, PhBzNN, and IN radicals in the nanospace of the ZnTPT. These studies have the potential to extend the reach of the application of the ESR spin probe technique and lead to the development of new magnetic materials formed by ordering magnetic molecules in nanospaces [4, 14, 43].

2. Experimental Details

2.1. Chemicals

ZnTPT [24, 40–42] and radicals 2–8 [44, 45] were synthesized following previously reported protocols. All the chemicals were used without further purification.

2.2. Sample Preparation

ZnTPT was synthesized as follows: 30 mg (9.6 × 10⁻² mmol) of TPT was dissolved in 25 mL of nitrobenzene, and the residue was filtered (ca. 3.8 × 10⁻³ mol L⁻¹; solution A). Concomitantly, 35 mg (0.11 mmol) of ZnI₂ was dissolved in 5 mL of methanol (2.2 × 10⁻² mol L⁻¹; solution B). One milliliter of solution B was layered onto 5 mL of solution A in a test tube, and a colorless crystal precipitated after 3 days. The color of the ZnTPT crystal changed to yellow after drying in air; it was kept in a cyclohexane solution until just before use. Radicals 2–8 were dispersed in ZnTPT together with cyclohexane [41, 42] as follows: ca. 10 mg (6 × 10⁻³ mmol) of ZnTPT crystals and 0.2 mg of radicals 2–8 (from 6 × 10⁻⁴ mmol to 9 × 10⁻⁴ mmol, depending on the molecular weight of radicals) were added in 0.5 mL of cyclohexane and stored for 3 days. The crystals were filtered and washed well with dichloromethane, then dried just before any characterization measurement. [ZnTPT·(cyclohexane)_x(guest radical)_y] has a color similar to that of the original guest radical. For example, the color of [ZnTPT· ] was red because of the red color of 7.

2.3. Instrumentation

The ESR spectra were recorded at room temperature using an X-band spectrometer (JES-FA300, JEOL) equipped with a TE₀₁₁ cylindrical cavity resonator. Colored crystals (2–3 mg) were packed in a commercial ESR tube (quartz glass; length: 270 mm; outer diameter: 5 mm). The X-band (e. g., 9.07 GHz) microwave power was set in the 0.001–1 mW range under nonsaturated conditions.

Single-crystal X-ray diffraction (XRD) analyses of [ZnTPT· and [ZnTPT· were conducted using a Rigaku Saturn diffractometer with graphite-monochromated Mo-Kα radiation (λ = 0.071075 nm) at 100 ± 1 K. For the determination of crystal orientation, plate-shaped crystals of the and (ca. 100 × 100 × 100 μm³) were placed at the bottom of a microtube and sealed with solvents. For the structure analysis, tiny crystals of [ZnTPT· and [ZnTPT· were mounted onto a single-crystal X-ray diffractometer while using a cryoloop, and diffraction data were collected. The crystal structures were solved and refined using SHELX97 software. The crystal structures of [ZnTPT· and gave rather poor factors because their crystal qualities were deteriorated after the adsorption of radical molecules; R = 0.1028 for [ZnTPT· and R = 0.2849 for [ZnTPT· , respectively.

Magnetic measurements for the [ZnTPT· (5.88 mg; 3.31 × 10⁻³ mmol) were performed with a Quantum Design MPMS-7 superconducting quantum interference device (SQUID) magnetometer. The sample was wrapped in a clean Al foil, and its magnetic susceptibilities were measured and subtracted separately. The magnetic curve for [ZnTPT· was measured in the magnetic field range of 0–50 kOe at 2 K. The static magnetic susceptibilities (χ) for [ZnTPT· were measured in the temperature range of 2.0–300 K at a magnetic flux density of 0.5 T. The diamagnetic contributions were calculated from Pascal’s constants (x_dia = −8.0 × 10⁻⁴ emu mol⁻¹).

Various core functions present in the EasySpin program package [46, 47] (version 5.2.35, ETH Zürich) such as garlic (for solution spectra), pepper (for solid-state spectra), and chili (for anisotropic slow-motion cw-ESR spectra) were used to simulate the spectra of radicals 2–8 dispersed in ZnTPT. Many parameters are required for spectral simulation. Therefore, high-speed calculations were performed in this study using parallel computing with a multicore computer. For example, computation with 12 cores was used to simulate the spectra using the step-by-step parameter variation technique, resulting in 12 reproductions within the time for a single calculation. Experiments and spectral simulations were performed with NN, PhBzNN, and IN radicals dispersed in ZnTPT. A personal computer (PC; RAM: <128 GB) was used to perform calculations to analyze the data using chili. The “Allocation” function of Opt was set as “Opt. Allocation = [4e7 2e5]” during the data analysis [46, 47].

2.4. Procedure to Obtain the Rigid-Limit or Rotational Diffusion ESR Spectra of the Radicals Dispersed in ZnTPT

The Hamiltonian functions reported in the literature were used to describe the radicals such as 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN dispersed in the matrices [14, 46–48]. The radicals in the matrices were characterized using the spin Hamiltonian:

()

where μ_B, B, g, A(N_i), A(H_j), μ_N, g_n(N_i), g_n(H_j),

, and

denote the Bohr magneton, laboratory magnetic flux density vector, electron spin g tensor, hyperfine tensor for the ith ¹⁴N nucleus of the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals (i = 1 or 2), superhyperfine tensor of jth ¹H nucleus of 4-Y-PhBzNN (j = α, β, o, m, or p; the protons at α and α′ and β and β′, o and o’, or m and m’ are equivalent due to molecular symmetry; Figure 1(b)), nuclear magneton, nuclear spin g tensor of the ith ¹⁴N nucleus of the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals, nuclear spin g tensor of the jth ¹H nucleus of 4-Y-PhBzNN, electron spin operator, and nuclear spin operator, respectively.

The principal axes of the g, A (N_i), and A (H_j) tensors of the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals were defined following previous reports [14, 18, 31]. The rigid-limit ESR spectra of the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals have been previously reported [14, 18]. Note that the initial values of each component of the g and A tensors of the 4-Y-PhBzNN radicals in ZnTPT were obtained from those of PMMA [18]. The final principal components of the g and A tensors of the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals were estimated using the step-by-step variation technique. Variations in the g and A tensor components, line-width parameters, and signal amplitudes were considered to minimize the sum of the squared differences between the data obtained from the experimental and simulated spectra.

Previously reported protocols used to determine the rotational axes of the radicals were followed to reproduce the spectra in cases where all or some of the radicals in the matrices underwent molecular motion (2-Z-IN radicals dispersed in ZnTPT in this study) [14, 18, 28]. The rotational axes of the radicals dispersed in ZnTPT were defined by the polar and azimuthal angles (θ and ϕ, respectively) relative to the principal axis of the g tensor of each radical [14, 48, 49]. The anisotropic rotational motion of each radical dispersed in ZnTPT can be described by a Markov process [49].

The simulation rate for the rigid-limit ESR spectra using the pepper (particularly for 4-Y-PhBzNN) increased manifold when the second-order perturbation theory (OPT method = “perturb2”) was used to carry out the calculations [47]. The line shape is expressed by a Voigt function [46, 48, 50].

3. Results and Discussion

3.1. Inclusion Amount of Guest Radicals in ZnTPT Matrix Estimated for [ZnTPT·(cyclohexane)_x (non-TEMPO radical)y] ICs

The ESR spectra for [ZnTPT· (cyclohexane)_x (non-TEMPO radical)_y] were reproduced by a single rigid-limit component in the cases of 2–6 (Figures 3 and 4; Sections 3.2 and 3.3) or uniaxial rotational diffusion components in the cases of 7 and 8 (Figure 5; Section 3.4). These results indicate that dimerization of guest radicals, in addition to interspin dipolar or exchange interactions between guest radicals, was rare. Therefore, each radical in the ZnTPT matrix was expected to be isolated. Several methods have been used to estimate the inclusion amount of guest radicals in the ZnTPT matrix, as shown below. We evaluated all methods used previously.

Single-crystal XRD analyses were conducted for [ZnTPT· and [ZnTPT· . Precise estimation of the crystal structure of [ZnTPT· (cyclohexane)_x (non-TEMPO radical)_y] was difficult because of the low crystallizability of the single crystals and high R values (see Section 2.3). However, the host-guest ratio for the and could be estimated; the upper limits of the inclusion amounts of cyclohexane used as solvent and guest radicals per formula unit in the unit cell of ZnTPT crystals were 1 and 0.5, respectively, for the and 1 for the . For radicals 3, 4, 5, 6, and 8, two cyclohexane molecules were observed per unit formula in the unit cell of the ZnTPT crystal. Therefore, only trace amounts of guest radicals 3, 4, 5, 6, and 8 may be included in the ZnTPT matrix.

Magnetic measurements were performed to the It should be considered that the interspin distance between radical 2 dispersed in the ZnTPT matrix was adequately long, and that each radical was isolated based on the ESR results (see Section 3.2). Therefore, the is expected to exhibit paramagnetism with an electron spin quantum number S = 1/2.

Figure 2(a) shows the magnetization curve for the powder sample of

at an external magnetic field H ranging from 0 to 50 kOe at a temperature of 2 K (cyan circles) and the theoretical magnetization curve of a paramagnet (magenta). The magnitude of the magnetization per unit volume, |M_Vol|, of a paramagnet is given as follows:

()

where N, g, μB^cgs, J, and B_J(x) denote the number of electron spins per unit volume (in this case, the number of radicals 2 per unit volume of the

), the electron g-factor, the CGS unit of the Bohr magneton, the total angular momentum quantum number (in this case, J = S = 1/2), and the Brillouin function:

()

where

, corresponding to the ratio of the Zeeman energy of the magnetic moment at the external field to the thermal energy [51];

and T denote the CGS unit of the Boltzmann constant and temperature, respectively. The magnitude of the molar magnetization |M_mol| of a paramagnet is given as follows:

()

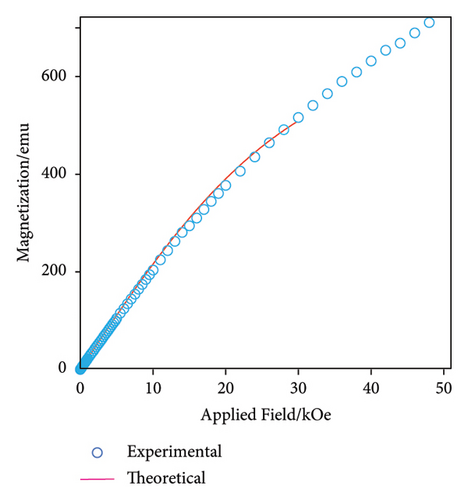
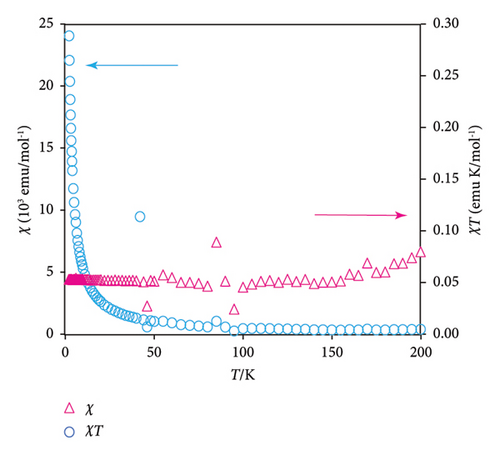
The sample mass, molecular weight, and Avogadro number are denoted by w, M, and N_A, respectively, and N is equal to MN_A/w. The occupancy of guest radicals per unit formula in the unit cell of the ZnTPT crystal is represented by p. The theoretical curve in the field range between 2 and 30 Oe, shown in Figure 2(a), demonstrates the case of p = 0.12, corresponding to y₂ in .

Figure 2(b) shows the χ–T and χT-T plots of the from 2 to 200 K (magenta triangles and cyan circles, respectively). Using Curie’s law for the N_A paramagnetic electron spins (S = 1/2), χT is estimated to be 0.375. In contrast, the experimental values of χT for were approximately constant at 0.05. The former corresponds to the case of x₂ = 1 and y₂ = 0.5 in the based on single-crystal XRD analyses, while the latter corresponds to x₂ = 1 and y₂ = 0.5p. p was estimated as 0.05/0.375 = 0.13. This value is consistent with the value of p estimated from the magnetization curve, as shown in Figure 2(a). In addition, the χ–T and χT-T plots of shown in Figure 2(b) were related to those of a typical paramagnet. These results demonstrate that the interspin interaction between the electron spins in the ZnTPT matrix is quite small, which is consistent with the ESR measurements (see below). Furthermore, similar or lower inclusion amounts of guest radicals are expected for radicals other than 2.

3.2. ESR Spectra of 2-X-NN Radicals Dispersed in ZnTPT Matrix

Figures 3(a)–3(d) show the ESR spectra recorded for 2-X-NN radicals (black) and the reproduced spectra (red); 2 (X = Ph; Figure 1(a)) dispersed in the PMMA matrix [16] and 2, 3 (X = p-NO₂Ph; Figure 1(a)), or 4 (X = CH; Figure 1(a)) in the ZnTPT matrix at room temperature. Five major hyperfine interaction lines associated with the equivalent nitrogen atoms having unpaired electrons in the NN groups are shown in Figure 3(a)–3(d) [14, 18, 27, 28]. Therefore, Figures 3(b)–3(d) display the typical spectra of the dispersed NN radicals, which were well reproduced based on a rigid-limit powder pattern of an NN radical dispersed in the matrix, i.e., 10⁻⁶ s < τ_R, where τ_R denotes the rotational diffusion correlation time of the radicals. The NN radicals were adequately isolated in the ZnTPT matrix, and their molecular motion was terminated on the ESR time scale. This is consistent with the magnetic results described in Section 3.1. The molecular motion of the NN radicals was potentially hindered and restricted by the TPT ligands coordinately bonded to the Zn atoms of the ZnTPT matrix. This may have resulted in the confinement of a part of the NN radicals in the nanospace of the ZnTPT matrix with a diameter of approximately 1.0 nm from the molecular-size perspective at the smallest estimate.

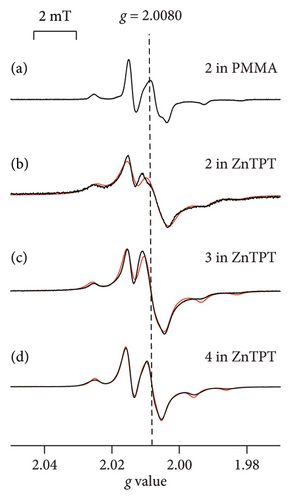
The spectra obtained for the 2-X-NN radical dispersed in the ZnTPT matrix (Figures 3(b)–3(d)) were simulated using the g and A tensor components listed in Table 1. The results of g and A tensor components for 2 agreed well with the results in which 2 was dispersed in various matrices [14, 18, 29, 30]. This indicates that few interactions between the ZnTPT matrix and dispersed radical 2 were observed. The g and A tensor components of 3 (or 4) in the Zn matrix are similar to those of 3 (or 4) in several other matrices (Table 1). However, the g_zz components of 3 (or 4) in the ZnTPT matrix were shifted to higher g values than those of the organic 1D nanochannels of CLPOT [32] or for an acrylic resin such as PMMA [18]. Such findings indicate that the interaction between the ZnTPT matrix and 3 (or 4) was not negligible, at least for some of the NN radicals. The local electric field around the Zn atoms or the pyridyl or triazine rings of the TPT ligands in the ZnTPT matrix [41] may be attributed to the nitroxide moieties present in the NN group of 3 (or 4).

Table 1. Tensor components of g and A of 2-X-NN (X = Ph (2), p-NO₂Ph (3), or CH (4)) radicals in various matrices.

Radicals	Matrices	g_xx	g_yy	g_zz	A_xx (N)	A_yy (N)	A_zz (N)
Radicals	Matrices	g_xx	g_yy	g_zz	/mT
2	Duco cement ^∗¹	2.0127	2.0068	2.0028	0.52	0.52	1.80
	Grassy toluene ^∗²	2.0100	2.0065	2.0021	—	—	1.86
	CLPOT ^∗³	2.0118	2.0075	2.0031	0.34	0.12	1.74
	TPP ^∗⁴	2.0107	2.0086	2.0031	0.01	0.01	2.13
	PMMA ^∗⁵	2.0105	2.0072	2.0031	0.33	0.04	1.74
	ZnTPT (this study)	2.0104	2.0079	2.0030	0.58	0.01	1.70

3	CLPOT ^∗³	2.0116	2.0076	2.0030	0.32	0.16	1.77
	PMMA ^∗⁵	2.0111	2.0071	2.0031	0.23	0.19	1.74
	ZnTPT (this study)	2.0105	2.0082	2.0040	0.01	0.02	1.73

4	PMMA ^∗⁵	2.0105	2.0070	2.0030	0.34	0.01	1.75
4	ZnTPT (this study)	2.0112	2.0083	2.0052	0.36	0.38	1.54

^∗¹Ref. 29; ^∗²Ref. 30; ^∗³Ref. 27; ^∗⁴Ref. 28; coinclusion with 7; ^∗⁵Ref. 18. Spacer molecules in the case of asterisks 3 and 4 were abbreviated.

The principal axis xx and yy components of the hyperfine coupling tensor, A_xx and A_yy, and (A(N)_iso = (1/3)(A_xx(N) + A_yy(N) + A_zz(N)); also in other A_iso’s or g_iso’s) for 3 in the ZnTPT matrix were smaller than those for 3 in other organic matrices (see Table 1). The (A(N))_iso for 4 in ZnTPT was almost the same as that for 4 in PMMA [18]. However, the principal axis zz component of the hyperfine coupling tensor, A_zz, for 4 in the ZnTPT matrix was smaller than that for 4 in PMMA, whereas the A_xx and A_yy for 4 were larger than those in PMMA [18]. These may be responsible for the host-guest interaction between the planar electron-deficient pyridyl or triazine rings of TPT ligands in the ZnTPT and the NO moieties present in the NN group of 3 (or 4) (see Section 3.3) [41].

3.3. ESR Spectra of 4-Y-PhBzNN Radicals Dispersed in the ZnTPT Matrix

Figures 4(a)–4(c) show the ESR spectra recorded for 4-Y-PhBzNN (black) and the reproduced spectra (red); 5 dispersed in PMMA (Y = H; Figure 1(b)), [18] and 5 and 6 (Y = p-NO₂; Figure 1(b)) dispersed in ZnTPT. The ESR spectra for 4-Y-PhBzNN radicals are more complex than those for 2-X-NN radicals due to the superhyperfine coupling between the unpaired electron and the protons in the annulated aromatic and aryl moieties in PhBzNN (see Figure 1(b) and Section 2.4). The superhyperfine coupling between the unpaired electron and protons in 4-Y-PhBzNN perturbed the characteristic rigid-limit powder pattern of the 2-X-NN radicals (see Section 2.4), resulting in five major hyperfine interaction lines associated with the equivalent nitrogen atoms having unpaired electrons in the BzNN groups (Figure 4(a)–4(c)), which are broader than the ESR spectra of the 2-X-NN radicals (Figures 3(a)–3(d)) [18]. The ESR spectra for 4-Y-PhBzNN in ZnTPT were similar to those for PMMA and could be reproduced using a rigid-limit powder pattern of the PhBzNN radical dispersed in a matrix, i.e., 10⁻⁶ s < τ_R [18]. The isolation of 4-Y-PhBzNN radicals in the ZnTPT matrix was confirmed, and the molecular motion of the PhBzNN radicals in the ZnTPT matrix was terminated on the ESR time scale. The molecular motion of the PhBzNN radicals was potentially hindered and restricted by the TPT ligands of the ZnTPT matrix. This may lead to the confinement of the BzNN radicals in the nanospace of the ZnTPT matrix, which has a diameter of approximately 1.2 nm from the molecular-size perspective at the smallest estimate.

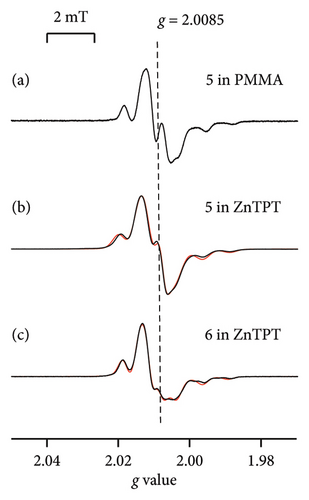
The spectrum recorded with 5 (or 6) dispersed in the ZnTPT matrix was simulated using the principal axes’ components of the g and A tensors, as shown in Table 2. They were relatively similar to those for 5 (or 6) in PMMA [18]. However, the principal axis components of the g tensor and g_iso estimated from the principal axes’ components of the g tensors of 5 (or 6) in the Zn matrix were totally shifted to a higher g value side than those for PMMA (Tables 2 and 3) [18]. This indicates that the interaction between the ZnTPT matrix and 5 (or 6) was not negligible. Furthermore, the local electric field around the Zn atoms or the electron-deficient pyridyl or triazine rings of the TPT ligands in ZnTPT [41] may be attributed to the nitroxide moieties present in the BzNN group of 5 (or 6), similar to the case of the 2-X-NN radicals in ZnTPT. The planar molecular configuration of 5 (or 6) may be influenced by the electron-deficient pyridyl or triazine ring of the TPT ligands in the ZnTPT.

Table 2. Tensor components of g, A_kk (N), and A_kk (H_j) (k = x, y, and z, and j = α, β, o, m, and p; Figure 1(b)) of 4-Y-PhBzNN (Y = Ph (5) or p-NO₂Ph (6)) dispersed in PMMA or ZnTPT.

Tensor components		States
Tensor components		5 in PMMA ^∗¹	5 in ZnTPT	6 in PMMA ^∗¹	6 in ZnTPT
g_xx		2.0121	2.0127	2.0118	2.0129
g_yy		2.0071	2.0078	2.0068	2.0084
g_zz		2.0032	2.0039	2.0028	2.0037

A_xx (N)	/mT	0.11	0.17	0.07	0.07
A_yy (N)		0.03	0.00	0.02	0.00
A_zz (N)		1.17	1.23	1.20	1.16
A_xx (H_α)		0.10	0.08	0.09	0.00
A_yy (H_α)		0.00	0.00	0.07	0.01
A_zz (H_α)		0.14	0.20	0.09	0.11
A_xx (H_β)		0.11	0.27	0.09	0.00
A_yy (H_β)		0.00	0.00	0.02	0.06
A_zz (H_β)		0.09	0.00	0.09	0.05
A_xx (H_o)		0.09	0.00	0.06	0.00
A_yy (H_o)		0.00	0.00	0.05	0.00
A_zz (H_o)		0.06	0.17	0.06	0.09
A_xx (H_m)		0.05	0.00	0.01	0.00
A_yy (H_m)		0.00	0.00	0.02	0.02
A_zz (H_m)		0.03	0.14	0.01	0.05
A_xx (H_p)		0.07	0.00	—	—
A_yy (H_p)		0.00	0.00	—	—
A_zz (H_p)		0.05	0.12	—	—

^∗¹Ref. 18.

Table 3. g_iso, (A(N))_iso, and (A(H_j))_iso (j = α, β, o, m, or p; Figure 1(c)) for 5 and 6 under various conditions.

States		g_iso	(A(N))_iso	(A(H_α))_iso	(A(H_β))_iso	(A(H_o))_iso	(A(H_m))_iso	(A(H_p))_iso
States		g_iso	/mT
5	In benzene solution ^∗¹	2.007	0.437	0.093	0.065	0.049	0.022	0.041
	The average of the principal axes’ components in PMMA ^∗²	2.0075	0.438	0.081	0.066	0.052	0.029	0.041
	The average of the principal axes’ components shown in Table 2 (this study)	2.0081	0.467	0.092	0.090	0.058	0.047	0.040

6	In benzene solution ^∗²	2.0068	0.432	0.078	0.064	0.057	0.010	—
	The average of the principal axes’ components in PMMA ^∗²	2.0072	0.434	0.083	0.067	0.058	0.012	—
	The average of the principal axes’ components shown in Table 2 (this study)	2.0083	0.409	0.042	0.039	0.030	0.024	—
	p-pyridinylBzNN ^∗¹	2.0072	0.426	0.091	0.073	0.041	0.020	—

^∗¹Ref. 38; ^∗²Ref. 18.

The estimation of (A(N))_iso and (A(H_j))_iso (j = α, β, o, m, and p) from the principal axis components of the A tensor components in ZnTPT differed from the isotropic values previously studied for 5 (or 6) in the solution-state or in PMMA (Table 3) [18, 38]. Those for 5 were relatively larger than the estimation based on the solution-state ESR spectra or the results in PMMA, whereas those for 6 were smaller. These could explain the difference in the resonant conditions between the solution- and solid-states. The other reason may be the plainer molecular shape of 4-Y-PhBzNN radicals (Figure 1(b)); the pyridyl or triazine rings of TPT ligands in the Zn matrix can potentially influence the unpaired electron density on the BzNN group or aryl moiety. The low (A(N))_iso and (A(H_j))_iso values for 6 may be associated with the electron-withdrawing NO₂ group on the nitrophenyl ring of 6 as in the case of 3 (see Section 3.2).

3.4. ESR Spectra Recorded with 2-Z-IN Radicals Dispersed in the ZnTPT Matrix

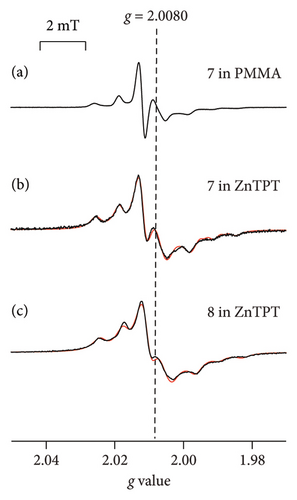
Figures 5(a)–5(c) show the ESR spectra recorded at room temperature for 2-Z-IN radicals (black), and the reproduced spectra (red); 7 (X = Ph; Figure 1(c)) dispersed in the PMMA matrix, [18] and 7 and 8 (X = p-NO₂Ph; Figure 1(c)) in the ZnTPT matrix. Seven major hyperfine interaction lines associated with the inequivalent nitrogen atoms having unpaired electrons in the IN groups are shown in Figures 5(a)–5(c) [14, 18, 28]. We attempted to reproduce the spectra of 7 (or 8) using a rigid-limit or anisotropic rotational diffusion component. The sum of the squared differences between the data obtained from the experimental and simulated spectra for the reproduction of anisotropic rotational diffusion component in 7 (or 8) was estimated to be as quarter of that of the rigid-limit component. The spectra could be more accurately reproduced using the rotational diffusion component of the dispersed IN radical than with rigid-limit components. The results revealed that 7 (or 8) in the ZnTPT matrix underwent anisotropic rotational diffusion in the cylindrical or pseudocylindrical nanospaces of the ZnTPT matrix. The spectra recorded with 7 (or 8) in the ZnTPT matrix (Figures 5(b) and 5(c), respectively) were simulated using the g and A tensor components, as shown in Table 4. The value of g_xx for 7 (or 8) in the ZnTPT matrix (also g_zz for 7) was larger than those for 7 (or 8) in other organic matrices, whereas those for g_yy were smaller. These may be responsible for the host-guest interaction between the Zn atoms or pyridyl or triazine rings of TPT ligands in the ZnTPT and the NO moieties present in the IN group of 7 (or 8).

Table 4. Tensor components of g, A (N₁), and A (N₂) corresponding to radicals 7 and 8 under various conditions.

Tensor components	States
	7				8
	In glassy toluene ^∗¹	In TPP ^∗²	In PMMA ^∗³	In ZnTPT (this study)	In PMMA ^∗³	In ZnTPT (this study)
g_xx	2.0093	2.0103	2.0098	2.0134	2.0098	2.0121
g_yy	2.0060	2.0050	2.0067	2.0048	2.0063	2.0045
g_zz	2.0022	2.0028	2.0023	2.0046	2.0022	2.0030
A_xx (N₁)	—	0.02	0.33	0.53	0.29	0.49
A_yy (N₁)	—	0.01	0.00	0.00	0.01	0.09
A_zz (N₁)	2.32	2.36	2.43	2.18	2.45	2.24
A_xx (N₂)	—	0.01	0.08	0.19	0.06	0.28
A_yy (N₂)	—	0.02	0.00	0.00	0.00	0.00
A_zz (N₂)	1.28	1.16	1.18	1.11	1.15	1.12

^∗¹Ref. 30; ^∗²Ref. 28; ^∗³Ref. 18.

The ESR spectra for 7 and 8 (Figures 5(b) and 5(c)) were simulated using a model that represents the anisotropic rotational diffusion of dispersed IN radicals (a slow-motion regime relative to the ESR time scale, i.e., 10⁻⁶ s > τ_R > 10⁻⁹ s). Rotational diffusion was assumed to occur around a tilted axis ((θ, ϕ) = (3°, 87°) for 7 and (θ, ϕ) = (12°, 87°) for 8) relative to the principal system of the g tensor with appropriate line-width components. The principal axes of the 2-Z-IN radicals are defined as follows: the z-axis is perpendicular to the molecular plane of the IN group, the y-axis is parallel to the bond between the 2-position carbon atom of the IN group and the phenyl ring, and the x-axis is perpendicular to the yz plane [28]. According to this definition, the rotational diffusion of 7 (or 8) dispersed in ZnTPT is expected to be approximately around the z-axis of the principal axes, that is, perpendicular to the IN plane. The θ and ϕ values for 7 (or 8) in the ZnTPT matrix were completely different from those for 7 (or 8) in organic 1D nanochannels of TPP [28] (caution: TPP is not to be confused with TPT) or in an acrylic resin, such as PMMA (Figure 5(a)) [18]. Such examples suggested rotational diffusion around the y-axis of the principal axis, which is parallel to the molecular long axis of 2-Z-IN radicals [14, 18, 28]. These results indicate the rarity of 2-Z-IN radicals exhibiting rotational diffusion around the principal z-axis. 2-Z-IN radicals could be used as spin probes if rotational diffusion can be performed not only around the y-axis of the principal axes of the g tensor (for example, as a spin probe for a nanochannel or nanosized cylindrical space from the viewpoint of the radical shape of 7 (or 8)) but also around the z-axis (for example, as a spin probe for a nanosized flat cylinder or 2D sheet-type pores), depending on the sizes and shapes of the nanospaces of host materials and the host-guest interactions between host materials and guest radicals. From the molecular-size perspective for 7 (or 8), the size of the nanospace in which 7 (or 8) is included is a flat cylinder or cylinder with a diameter of 1.0 nm and a height of 0.6 nm at the smallest estimate. In ZnTPT, 7 (or 8) is expected to be accommodated in flattened-cylindrical or pseudocylindrical nanospaces sandwiched between the pyridinyl or triazine rings of the TPT ligands of ZnTPT. A few examples have been reported for the case in which cyclohexane was used as a solvent and coincluded with other molecules in the nanospace of the ZnTPT matrix (the inclusion amount of cyclohexane per formula unit of ZnTPT complex was 1.0–2.5) [24, 41, 42]. In a previous report, the included cyclohexane molecules were accommodated in relatively large nanospaces in ZnTPT crystals, whereas coincluded plainer guest molecules, such as perylene, were stacked on the TPT ligands [42]. The nanospace in the ZnTPT matrix studied in this study by 7 (or 8) may be consistent with the space over the TPT ligands in previous studies rather than the large space in which cyclohexane was included.

The τ_R values corresponding to 7 and 8 dispersed in ZnTPT were estimated to be 1.1 × 10⁻⁷ s for 7 and 1.2 × 10⁻⁷ s for 8. The molecular dynamics of 7 and 8 in ZnTPT were similar and were barely influenced by the substituent at the 4-position of the phenyl group present in the radicals. These τ_R values were comparable to those recorded for 7 or 8 in PMMA [18] and were 10² times higher than those for TPP organic 1D nanochannels at room temperature [28]. These findings can be attributed to the strong host-guest interaction between ZnTPT and guest radicals.

The ESR spectra of 7 (or 8) dispersed in ZnTPT indicate that the nanospaces in the ZnTPT matrix can be studied using 7 (or 8) as the ESR spin probe. Thus, 2-Z-IN radicals can be used as spin probe molecules for ZnTPT complexes as well as polymers such as PMMA [18], and probably for other MOFs with nanosized pores. In particular, the ESR spin probe technique can be used when the preparation of single crystals of MOFs is difficult or when the pore structure of MOFs is complex. Apparently, the precision for the estimation of pore size in the ESR spin probe technique is lower than the single-crystal XRD analyses due to the indirect measurement method. Therefore, the ESR spin probe technique for MOFs should be used as a complementary approach to the single-crystal XRD. Suitable organic radicals, such as 2-X-NN and 4-Y-PhBzNN, can be selected as probes depending on the pore structure, size, and the host-guest interaction of the MOF if the molecular dynamics of guest radicals are performed with increasing temperature without destroying the pores of the host MOF. However, the g, A, and superhyperfine tensor components for the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals often differ from those of the organic matrices. When non-TEMPO radicals are used as ESR spin probes for the pores of MOF, the host-guest interactions between the host MOF and guest radicals should always be considered.

4. Conclusion

The nanospaces in the ZnTPT matrix were examined by ESR spectroscopy. Some of the g, A, and superhyperfine tensor components for the 2-X-NN, 4-Y-PhBzNN, and 2-Z-IN radicals in the ZnTPT matrix were shifted when compared with the estimations for organic matrices. When using non-TEMPO radicals as ESR spin probes for porous MOF, the interactions between the host materials and guest radicals should be considered. The spectra corresponding to 2-Z-IN were reproduced using uniaxial rotational diffusion components around the principal g_zz axis. The ESR spectra and simulation results for the 2-Z-IN radicals indicate that ZnTPT had flattened-cylindrical or pseudocylindrical nanospaces. These results demonstrate that 2-Z-IN radicals could potentially be used as spin probes to study the characteristics of the nanospace of the ZnTPT matrix. The ESR spin probe technique using 2-Z-IN radicals can be used while considering the host-guest interactions between the host MOF and guest radicals in cases when the preparation of single crystals of MOFs is difficult or when the pore structure of the MOF is complex even if they consist of metal ions other than Zn(II). However, it is to be noted that the magnetic properties of the metal ions other than Zn(II) may affect the ESR signal. The signal of the molecular motion in 2-X-NN and 4-Y-PhBzNN (dispersed in ZnTPT) could not be determined using ESR spectroscopy. However, they can be used as spin probes for other MOFs if the structures, sizes, and shapes of the nanospaces in the MOF matrices are appropriate.

These findings show that the ESR spin probe technique can be used to investigate the chemical and biological structures of nanosized materials using samples containing non-TEMPO derivatives. Nanosized spaces containing imino or nitronyl nitroxide groups have only been reported in recent years. In particular, paramagnetic vesicles, nanoparticles, and porous films with NN radicals can be used in molecule-based magnetism, magnetic resonance imaging (MRI) contrast agents, biosensing, and drug delivery [31]. In many cases, the preparation of single crystals of these materials is difficult. Although the precision of the estimation of the pore size is always discussed, the results of this study can be used to develop novel systems. Our research group is currently conducting additional investigations on this topic, with the goal of expanding this field even further.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was partially supported by the Strategic Research Base Development Program for Private Universities of the Ministry of Education, Culture, Sports, Science, and Technology of Japan (MEXT), 2009–2013. We would like to thank Prof. S. Stoll, working at the University of Washington, for helping with the EasySpin calculations. We would like to thank Editage (https://www.editage.com/) for the English language editing.

Open Research

Data Availability

No underlying data were used to support the results of this study.

References

1 Hertzsch T., Budde F., Weber E., and Hulliger J., Supramolecular-wire confinement of I₂ molecules in channels of the organic zeolite tris(o-phenylenedioxy)cyclotriphosphazene, Angewandte Chemie International Edition. (2002) 41, no. 13, 2281–2284.
10.1002/1521-3773(20020703)41:13<2281::AID-ANIE2281>3.0.CO;2-N
CAS Web of Science® Google Scholar
2 Hertzsch T., Kluge S., Weber E., Budde F., and Hulliger J., Surface recognition of dipolar molecules entering channels of the organic zeolite tris(o-phenylenedioxy)cyclotriphosphazene, Advanced in Materials. (2001) 13, no. 24, 1864–1867.
10.1002/1521-4095(200112)13:24<1864::AID-ADMA1864>3.0.CO;2-O
CAS Web of Science® Google Scholar
3 Bureekaew S., Horike S., Higuchi M., Mizuno M., Kawamura T., Tanaka D., Yanai N., and Kitagawa S., One-dimensional imidazole aggregate in aluminium porous coordination polymers with high proton conductivity, Nature Materials. (2009) 8, no. 10, 831–836, https://doi.org/10.1038/nmat2526, 2-s2.0-70349327378.
10.1038/nmat2526
CAS PubMed Web of Science® Google Scholar
4 Soegiarto A. C., Yan W., Kent A. D., and Ward M. D., Regulating low-dimensional magnetic behavior of organic radicals in crystalline hydrogen-bonded host frameworks, Journal of Materials Chemistry. (2011) 21, no. 7, 2204–2219, https://doi.org/10.1039/C0JM03449E, 2-s2.0-79551615755.
10.1039/C0JM03449E
CAS Web of Science® Google Scholar
5 Nikolayenko V. I., Barbour L. J., Arauzo A., Campo J., Rawson J. M., and Haynes D. A., Inclusion of a dithiadiazolyl radical in a seemingly non-porous solid, Chemical Communications. (2017) 53, no. 82, 11310–11313, 11310, https://doi.org/10.1039/C7CC06678C, 2-s2.0-85031331048.
10.1039/C7CC06678C
CAS PubMed Web of Science® Google Scholar
6 Lin F., Yu S. B., Liu Y. Y., Liu C. Z., Lu S., Cao J., Qi Q. Y., Zhou W., Li X., Liu Y., Tian J., and Li Z. T., Porous polymers as universal reversal agents for heparin anticoagulants through an inclusion–sequestration mechanism, Advanced Materials. (2022) 34, no. 23, 2200549, https://doi.org/10.1002/adma.202200549.
10.1002/adma.202200549
CAS Web of Science® Google Scholar
7 Rinkevicius Z., Frecuş B., Murugan N. A., Vahtras O., Kongsted J., and Ågren H., Encapsulation influence on EPR parameters of spin-labels: 2,2,6,6-Tetramethyl-4-methoxypiperidine-1-oxyl in cucurbit[8]Uril, Journal of Chemical Theory and Computation. (2012) 8, no. 1, 257–263, https://doi.org/10.1021/ct200816z, 2-s2.0-84855660084.
10.1021/ct200816z
CAS PubMed Web of Science® Google Scholar
8 Li J., Wang Y., Lin K., and Luo Y., Recent application of porous materials in explosives: a mini-review, Fire Physics Chemistry, 2024, 4, no. 3, 264–275, https://doi.org/10.1016/j.fpc.2024.03.001.
10.1016/j.fpc.2024.03.001
Google Scholar
9 Kulasekharan R., Jayaraj N., Porel M., Choudhury R., Sundaresan A. K., Parthasarathy A., Ottaviani M. F., Jockusch S., Turro N., and Ramamurthy V., Guest rotations within a capsuleplex probed by NMR and EPR techniques, Langmuir. (2010) 26, no. 10, 6943–6953, https://doi.org/10.1021/la904196g, 2-s2.0-77952387359.
10.1021/la904196g
CAS PubMed Web of Science® Google Scholar
10 Ayhan M. M., Casano G., Karoui H., Rockenbauer A., Monnier V., Hardy M., Tordo P., Bardelang D., and Ouari O., EPR studies of the binding properties, guest dynamics, and inner-space dimensions of a water-soluble resorcinarene capsule, Chemistry-A European Journal. (2015) 21, no. 46, 16404–16410, 16404, https://doi.org/10.1002/chem.201502212, 2-s2.0-84946091348.
10.1002/chem.201502212
CAS PubMed Web of Science® Google Scholar
11 Moreau F., Kolokolov D. I., Stepanov A. G., Easun T. L., Dailly A., Lewis W., Blake A. J., Nowell H., Lennox M. J., Besley E., Yang S., and Schröder M., Tailoring porosity and rotational dynamics in a series of octacarboxylate metal–organic frameworks, Proceedings of the National Academy of Sciences. (2017) 114, no. 12, 3056–3061, https://doi.org/10.1073/pnas.1615172114, 2-s2.0-85016102050.
10.1073/pnas.1615172114
CAS PubMed Web of Science® Google Scholar
12 Zhao P., Fang H., Mukhopadhyay S., Li A., Rudić S., McPherson I. J., Tang C. C., Fairen-Jimenez D., Tsang S. C. E., and Redfern S. A. T., Structural dynamics of a metal–organic framework induced by CO₂ migration in its non-uniform porous structure, Nature Communications. (2019) 10, no. 1, https://doi.org/10.1038/s41467-019-08939-y, 2-s2.0-85062268159.
10.1038/s41467-019-08939-y
Google Scholar
13 Dzikovski B., Tipikin D., Livshits V., Earle K., and Freed J., Multifrequency ESR study of spin-labeled molecules in inclusion compounds with cyclodextrins, Physical Chemistry Chemical Physics. (2009) 11, no. 31, https://doi.org/10.1039/B903490K, 2-s2.0-68349130628.
10.1039/b903490k
PubMed Google Scholar
14 Kobayashi H., T. Onishi, Inter-spin interactions of organic radical chains in organic 1D nanochannels: an ESR study of the molecular orientations and dynamics of guest radicals, Theoretical Chemistry for Advanced Nanomaterials -Functional Analysis by Computation and Experiment. (2020) Springer, Singapore, 423–467.
10.1007/978-981-15-0006-0_12
Google Scholar
15 Lukešová M., Zgardzinska B., Švajdlenková H., Zaleski R., Charmas B., and Bartoš J., Spin probe dynamics in relation to free volume in crystalline organics from ESR and PALS: N-tridecane, Physica B: Condensed Matter. (2015) 476, 100–108, https://doi.org/10.1016/j.physb.2015.07.008, 2-s2.0-84938351723.
10.1016/j.physb.2015.07.008
CAS Google Scholar
16 Bartoš J., Vyroubalová M., and Švajdlenková H., Bulk and confined acetonitrile in mesoporous silica matrices by extrinsic probing via ESR technique: effects of pore topology, pore size and pore surface composition, Chemical Physics Letters. (2022) 807, 140073, https://doi.org/10.1016/j.cplett.2022.140073.
10.1016/j.cplett.2022.140073
CAS Google Scholar
17 Kovarskii A. L., Sorokina O. N., Shapiro A. B., and Nikitin L. N., A spin-probe study of the porous structure of cellulose treated with supercritical carbon dioxide, Polymer Science - Series A. (2015) 57, no. 3, 309–314, https://doi.org/10.1134/S0965545X15030074, 2-s2.0-84930194815.
10.1134/S0965545X15030074
CAS Google Scholar
18 Kobayashi H., Akiniwa K., Iwahori F., Honda H., Yamamoto M., Odanaka Y., and Inagaki M., Investigation of various organic radicals dispersed in polymethylmethacrylate matrices using the electron spin resonance spectroscopy technique, ACS Omega. (2021) 6, no. 32, 20855–20864, 20855, https://doi.org/10.1021/acsomega.1c02170.
10.1021/acsomega.1c02170
CAS PubMed Google Scholar
19 Jeong D., Han S., Lim Y. B., and Kim S. H., Investigation of the hydration state of self-assembled peptide nanostructures with advanced electron paramagnetic resonance spectroscopy, ACS Omega. (2019) 4, no. 1, 114–120, https://doi.org/10.1021/acsomega.8b02450, 2-s2.0-85059510653.
10.1021/acsomega.8b02450
CAS PubMed Web of Science® Google Scholar
20 Syryamina V. N., De Zotti M., Toniolo C., Formaggio F., and Dzuba S. A., Alamethicin self-assembling in lipid membranes: concentration dependence from pulsed EPR of spin labels, Physical Chemistry Chemical Physics. (2018) 20, no. 5, 3592–3601, https://doi.org/10.1039/c7cp07298h, 2-s2.0-85041642321.
10.1039/C7CP07298H
CAS PubMed Google Scholar
21 Chede L. S., Wagner B. A., Buettner G. R., and Donovan M. D., Electron spin resonance evaluation of buccal membrane fluidity alterations by sodium caprylate and L-menthol, International Journal of Molecular Sciences. (2021) 22, no. 19, 10708, https://doi.org/10.3390/ijms221910708.
10.3390/ijms221910708
CAS PubMed Web of Science® Google Scholar
22 Poryvaev A. S., Sheveleva A. M., Kolokolov D. I., Stepanov A. G., Bagryanskaya E. G., and Fedin M. V., Mobility and reactivity of 4-substituted TEMPO derivatives in metal–organic framework MIL-53(Al), Journal of Physical Chemistry C. (2016) 120, no. 19, 10698–10704, 10698, https://doi.org/10.1021/acs.jpcc.6b02966, 2-s2.0-84971233968.
10.1021/acs.jpcc.6b02966
CAS Google Scholar
23 Efremov A. A., Poryvaev A. S., Polyukhov D. M., Sagdeev R. Z., and Fedin M. V., Anisotropic rotation of TEMPO radical in the cavities of metal–organic framework ZIF-8 induced by guest solvents, Applied Magnetic Resonance. (2022) 54, no. 1, 93–105, https://doi.org/10.1007/s00723-022-01486-8.
10.1007/s00723-022-01486-8
Google Scholar
24 Inokuma Y., Yoshioka S., Ariyoshi J., Arai T., Hitora Y., Takada K., Matsunaga S., Rissanen K., and Fujita M., X-ray analysis on the nanogram to microgram scale using porous complexes, Nature. (2013) 495, no. 7442, 461–466, https://doi.org/10.1038/nature11990, 2-s2.0-84875621905.
10.1038/nature11990
CAS PubMed Web of Science® Google Scholar
25 Said M. Y., Kang C. S., Wang S., Sheffler W., Salveson P. J., Bera A. K., Kang A., Nguyen H., Ballard R., Li X., Bai H., Stewart L., Levine P., and Baker D., Exploration of structured symmetric cyclic peptides as ligands for metal–organic frameworks, Chemistry of Materials. (2022) 34, no. 21, 9736–9744, https://doi.org/10.1021/acs.chemmater.2c02597.
10.1021/acs.chemmater.2c02597
CAS PubMed Web of Science® Google Scholar
26 Collauto A., Zerbetto M., Brustolon M., Polimeno A., Caneschi A., and Gatteschi D., Interpretation of cw-ESR spectra of p-Methyl-thio-phenyl-nitronyl nitroxide in a nematic liquid crystalline phase, Physical Chemistry Chemical Physics. (2012) 14, no. 9, https://doi.org/10.1039/c2cp23079h, 2-s2.0-84856872606.
10.1039/c2cp23079h
PubMed Google Scholar
27 Kobayashi H., Morinaga Y., Fujimori E., and Asaji T., ESR study of molecular orientation and dynamics of nitronyl nitroxide radicals in CLPOT 1D nanochannels, Journal of Physical Chemistry A. (2014) 118, no. 27, 4907–4917, https://doi.org/10.1021/jp503681b, 2-s2.0-84904333375.
10.1021/jp503681b
CAS PubMed Google Scholar
28 Kobayashi H., Mori T., Morinaga Y., Fujimori E., Akiniwa K., and Iwahori F., Electron spin resonance study of molecular orientation and dynamics of phenyl imino and nitronyl nitroxide radicals in organic 1D nanochannels of tris(o-phenylenedioxy)cyclotriphosphazene, Journal of Physical Chemistry A. (2018) 122, no. 25, 5493–5502, https://doi.org/10.1021/acs.jpca.8b01806, 2-s2.0-85048355388.
10.1021/acs.jpca.8b01806
CAS PubMed Google Scholar
29 D’Anna J. A. and Wharton J. H., Electron spin resonance spectra of α-nitronylnitroxide radicals; solvent effects; nitrogen hyperfine tensor; anisotropy, The Journal of Chemical Physics. (1970) 53, no. 10, 4047–4052, https://doi.org/10.1063/1.1673877.
10.1063/1.1673877
CAS Web of Science® Google Scholar
30 Dikanov S. A., Gulin V. I., Tsvetkov Y. D., and Grigor’ev I. A., 2 mm electron paramagnetic resonance studies of the new types of imidazoline nitroxide radicals, Journal of the Chemical Society, Faraday Transactions. (1990) 86, no. 19, https://doi.org/10.1039/FT9908603201, 2-s2.0-37049072070.
10.1039/ft9908603201
Google Scholar
31 Hui P. and Chandrasekar R., Shape-defined and shape-shifting paramagnetic organic nano/microstructures derived from a doublet state nitronyl nitroxide radical, ChemPlusChem. (2012) 77, no. 12, 1062–1065, https://doi.org/10.1002/cplu.201200143, 2-s2.0-84872328356.
10.1002/cplu.201200143
CAS Web of Science® Google Scholar
32 Meng X., Shi W., and Cheng P., Magnetism in one-dimensional metal-nitronyl nitroxide radical system, Coordination Chemistry Reviews. (2019) 378, 3201–3205, https://doi.org/10.1016/j.ccr.2018.02.002, 2-s2.0-85042919739.
10.1016/j.ccr.2018.02.002
Google Scholar
33 Tichnell C. R., Shultz D. A., Popescu C. V., Sokirniy I., and Boyle P. D., Synthesis, characterization, and photophysical studies of an iron(III) catecholate-nitronylnitroxide spin-crossover complex, Inorganic Chemistry. (2015) 54, no. 9, 4466–4474, https://doi.org/10.1021/acs.inorgchem.5b00298, 2-s2.0-84929224041.
10.1021/acs.inorgchem.5b00298
CAS PubMed Web of Science® Google Scholar
34 Vaz M. G. F., Cassaro R. A., Akpinar H., Schlueter J. A., Lahti P. M., and Novak M. A., A cobalt pyrenylnitronylnitroxide single-chain magnet with high coercivity and record blocking temperature, Chemistry - A European Journal. (2014) 20, no. 18, 5460–5467, https://doi.org/10.1002/chem.201304852, 2-s2.0-84899540940.
10.1002/chem.201304852
CAS PubMed Web of Science® Google Scholar
35 Kinoshita M., Turek P., Tamura M., Nozawa K., Shiomi D., Nakazawa Y., Ishikawa M., Takahashi M., Awaga K., Inabe T., and Maruyama Y., An organic radical ferromagnet, Chemistry Letters. (1991) 20, no. 7, 1225–1228, https://doi.org/10.1246/cl.1991.1225.
10.1246/cl.1991.1225
Web of Science® Google Scholar
36 He S. M., Lei Y. H., Wang J. M., Geng L. N., Wang S. P., Zhao J., and Hou Y. F., The protective effect of nitronyl nitroxide radical on peroxidation of A549 cell damaged by iron overload, Materials Science and Engineering: C. (2020) 108, 110189, https://doi.org/10.1016/j.msec.2019.110189.
10.1016/j.msec.2019.110189
CAS PubMed Web of Science® Google Scholar
37 Zhao M., Li Z., Peng L., Tang Y. R., Wang C., Zhang Z., and Peng S., Novel 1-oxyl-2-substituted phenyl-4, 4, 5, 5-tetramethylimidazolines: synthesis, selectively analgesic action, and QSAR analysis, Bioorganic and Medicinal Chemistry. (2007) 15, no. 8, 2815–2826, https://doi.org/10.1016/j.bmc.2007.02.023, 2-s2.0-33947167863.
10.1016/j.bmc.2007.02.023
CAS PubMed Web of Science® Google Scholar
38 Dooley B. M., Bowles S. E., Storr T., and Frank N. L., Synthesis of neutral spin-delocalized electron acceptors for multifunctional materials, Organic Letters. (2007) 9, no. 23, 4781–4783, https://doi.org/10.1021/ol701725r, 2-s2.0-36349030374.
10.1021/ol701725r
CAS PubMed Web of Science® Google Scholar
39 Lahti P. M., Esat B., Liao Y., Serwinski P., Lan J., and Walton R., Heterospin organic molecules: nitrene–radical linkages, Polyhedron. (2001) 20, no. 11-14, 1647–1652, https://doi.org/10.1016/S0277-5387(01)00667-2, 2-s2.0-0035972414.
10.1016/S0277-5387(01)00667-2
CAS Web of Science® Google Scholar
40 Biradha K. and Fujita M., A springlike 3D-coordination network that shrinks or swells in a crystal-to-crystal manner upon guest removal or readsorption, Angewandte Chemie International Edition. (2002) 41, no. 18, 3392–3395.
10.1002/1521-3773(20020916)41:18<3392::AID-ANIE3392>3.0.CO;2-V
CAS PubMed Web of Science® Google Scholar
41 Inokuma Y., Kawano M., and Fujita M., Crystalline molecular flasks, Nature Chemistry. (2011) 3, no. 5, 349–358, https://doi.org/10.1038/nchem.1031, 2-s2.0-79955100409.
10.1038/nchem.1031
CAS PubMed Web of Science® Google Scholar
42 Ohmori O., Kawano M., and Fujita M., Crystal-to-Crystal guest exchange of large organic molecules within a 3D coordination network, Journal of the American Chemical Society. (2004) 126, no. 50, 16292–16293, 16292, https://doi.org/10.1021/ja046478a, 2-s2.0-11444258120.
10.1021/ja046478a
CAS PubMed Web of Science® Google Scholar
43 Kobayashi H., Takeuchi K., Morinaga Y., Honda H., Yamamoto M., Odanaka Y., and Inagaki M., Inter-spin interactions of 1D chains of different-sized nitroxide radicals incorporated in the organic 1D nanochannels of tris(o-phenylenedioxy)cyclotriphosphazene, Bulletin of the Chemical Society of Japan. (2022) 95, no. 6, 981–988, https://doi.org/10.1246/bcsj.20220062.
10.1246/bcsj.20220062
CAS Web of Science® Google Scholar
44 Ullman E. F., Call L., and Osiecki J. H., Stable free radicals. VIII. New imino, amidino, and carbamoyl nitroxides, Journal of Organic Chemistry. (1970) 35, no. 11, 3623–3631, https://doi.org/10.1021/jo00836a008, 2-s2.0-33947294622.
10.1021/jo00836a008
CAS Web of Science® Google Scholar
45 Hirel C., Vostrikova K. E., Pécaut J., Ovcharenko V. I., and Rey P., Nitronyl and imino nitroxides: improvement of ullman’s procedure and report on a new efficient synthetic route, Chemistry - A European Journal. (2001) 7, no. 9, 2007–2014.
10.1002/1521-3765(20010504)7:9<2007::AID-CHEM2007>3.0.CO;2-7
CAS PubMed Web of Science® Google Scholar
46 Stoll S. and Schweiger A., EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, Journal of Magnetic Resonance. (2006) 178, no. 1, 42–55, https://doi.org/10.1016/j.jmr.2005.08.013, 2-s2.0-28844486080.
10.1016/j.jmr.2005.08.013
CAS PubMed Web of Science® Google Scholar
47 easyspin, EasySpin, 2024, http://www.easyspin.org/.
Google Scholar
48 Birrell G. B., Van S. P., and Griffith O. H., Electron spin resonance of spin labels in organic inclusion crystals, Journal of the American Chemical Society. (1973) 95, no. 8, 2451–2458, https://doi.org/10.1021/ja00789a006, 2-s2.0-0015928976.
10.1021/ja00789a006
CAS PubMed Web of Science® Google Scholar
49 Freed J. H., L. J. Berliner, Theory of slow tumbling ESR spectra for nitroxides, Spin Labeling, Theory and Applications. (1976) Academic Press Inc., New York, NY, USA.
10.1016/B978-0-12-092350-2.50008-4
Google Scholar
50 Bruce S. D., Higinbotham J., Marshall I., and Beswick P. H., An analytical derivation of a popular approximation of the Voigt function for quantification of NMR spectra, Journal of Magnetic Resonance. (2000) 142, no. 1, 57–63, https://doi.org/10.1006/jmre.1999.1911, 2-s2.0-0033630513.
10.1006/jmre.1999.1911
CAS PubMed Web of Science® Google Scholar
51 Pake G. E., Estle T. L., and Benjamin W. A., The Physical Principles of Electron Paramagnetic Resonance, 1973, 2nd edition, Academic Press Inc, Massachusetts, MA, USA.
Google Scholar

All articles

Electron Spin Resonance Spin Probe Technique for Investigating Non-TEMPO Radicals Dispersed in Nanospaces of a Crystalline Zn Complex

Abstract

1. Introduction