Oscillation and Asymptotic Behavior of Three-Dimensional Third-Order Delay Systems
Abstract
In this paper, oscillation and asymptotic behavior of three-dimensional third-order delay systems are discussed. Some sufficient conditions are obtained to ensure that every solution of the system is either oscillatory or nonoscillatory and converges to zero or diverges as t goes to infinity. A special technique is adopted to include all possible cases for all nonoscillatory solutions (NOSs). The obtained results included illustrative examples.
1. Introduction
Differential equations are one of the most important topics in applied mathematics due to their multiple applications; for example, see [1–3]. Among these equations are delay differential equations (DDEs). DDE is an important type of differential equation in which the derivative of a function depends not only on the current value of the function but also on its past values with a finite time delay. Therefore, ordinary differential equations (ODEs) are a special case of DDEs. The effect of the presence of delay or not affects in one way or another the behavior of solving differential equations; for example, it is not possible to obtain an oscillating solution for ODEs of the first order, but in DDEs, this is possible.
Oscillation theory is an important branch of the applied theory of differential equations related to the study of oscillating phenomena in technology and the natural and social sciences. This interest is heightened by the existence of time delays. The presence or absence of oscillatory solutions is one of the most important topics in oscillatory theory for a given equation or system [4]. In the 1840s, the development of oscillation theory for ODEs began when Sturm’s classic work appeared, in which oscillation comparison theorem were proved for solutions of homogeneous linear second-order ODE equations [5]. In 1921, the first paper on oscillating functional differential equations was written by Fite [6]. In 1987, Ladde et al. [7] presented their book’s oscillation theory of differential equations with deviating arguments. In 1991, Győri et al. [8] presented one of the most important books on oscillation theory in DDE, which included many applications, followed by several books specializing in oscillation; for example, see Bainov and Mishev [9]. Numerous research studies and theses have been written about the oscillation and asymptotic behavior of DDEs with various orders. The reader can see these research studies in [10–18] and the references cited therein. However, there are few studies (books or papers) that discuss the concept of oscillation for solving delay equations such as Ladde et al. [7, 19], Foltynska [20], Agarwal et al. [21], Mohamad and Abdulkareem [22], Abdulkareem et al. [23], Akın-Bohner et al. [24], Špániková [25], and the references cited therein.
Up to our knowledge, there is no research published dealing with the study of almost oscillation and asymptotic behavior of three-dimensional delay system (3D-DS) of the third order; this is the reason why we entered into this type of research.
- (i)
λ ∈ {1, −1},
- (ii)
for large t,
- (iii)
and Limt⟶∞τi(t) = ∞,
- (iv)
and Limt⟶∞τi(t) = ∞,
- (v)
αi > 0 is the ratio of two odd integers,
- (vi)
A solution is said to oscillate if at least one component is oscillatory. Otherwise, the solution is called nonoscillatory.
This paper consists of five sections; in the second and third sections, the nonoscillatory solutions (NOSs) to the system (1) are studied with certain conditions. In the fourth section, the system (1) oscillation is studied with certain conditions. Finally, we give some examples that illustrate the results.
2. NOS of System (1), Case λ = 1
In this section, we study the asymptotic behavior of NOS with λ = 1, which we use in the following sections.
Lemma 1. Suppose that X(t) is a NOS to the system (1) with λ = 1, and
Then there are only K1‒K8 possible classes:
Proof. Suppose that X(t) is an eventual positive solution to the system (1) (the case X(t) is an eventually negative is similar). Then, from (1), it follows that
That means and are nondecreasing; hence, there exists t1 ≥ t0 such that , and are eventually positive or eventually negative. So, eight cases can be discussed, which are as follows:
Now, we discuss the cases in Table 1 successively:
- (i)
Since and , then is positive nondecreasing, then there exists bi > 0, t2 ≥ t1 such that
(4) -
Integrating (4) from t to δ(t) for some continuous function δ(t) > t, we obtain
(5) -
We claim that for t ≥ t3 ≥ t2, otherwise if for t ≥ t3 ≥ t2, then (5) becomes
(6) -
Integrating (6) from t3 to t, we get
(7) -
Letting t⟶∞ the last inequality leads to Limt⟶∞yi(t) = −∞, which is a contradiction. Hence the claim was verified and and this case leads to Limt⟶∞yi(t) = ∞. That is (y1, y2, y3) ∈ K1.
- (ii)
Since and .
-
That is , is negative nondecreasing. So there are such that hence t ≥ t2 and so
(8) -
Integrating (8) from t to δ(t) yields
(9) -
We have two for :
- (a)
If . For t ≥ t3 ≥ t2, Then the last inequality becomes
(10) -
Integrating (10) from t3 to t yields
(11) -
As t⟶∞, it follows, either or yi(t) is bounded away from zero
- (b)
and leads to Limt⟶∞yi(t) = −∞, which is a contradiction,
-
which means X(t) ∈ K2.
- (a)
- (iii)
Since and that is, are negative nondecreasing, j = 1,2, there exists lj ≤ 0, such that Then, , thus
(12) -
Integrating (10) from t to δ(t) for some continuous function δ(t) > t, we obtain
(13)
We claim that for otherwise if and this implies to yj(t) < 0 and Limt⟶∞yj(t) = −∞ which is a contradiction. Hence, and . Now, and , so , is positive nondecreasing, then there exists b3 > 0 and t2 ≥ t1 such that
Integrating (14) from t to δ(t), we obtain
We claim that for t ≥ t3 ≥ t2, otherwise if for t ≥ t3 ≥ t2, then the last inequality becomes
Integrating (16) from t3 to t
Letting t⟶∞, then inequality (17) leads to Limt⟶∞y3(t) = −∞, which is a contradiction. Hence and , this case leads to Limt⟶∞y3(t) = ∞, and so X(t) ∈ K3. Analogously from the subcases (iv-viii), one can get X(t) ∈ Kn, n = 4,5, …, 8, respectively.
| (i) | |||
| (ii) | |||
| (iii) | |||
| (iv) | |||
| (v) | |||
| (vi) | |||
| (vii) | |||
| (viii) |
3. NOS of the System (1), Case λ = −1
In this section, we study the asymptotic behavior of NOS with λ = −1, which we use in the following sections.
Lemma 2. Assume that X(t) is NOS of (1) with λ = −1 and let (2) hold. Then there are only L1‒L8 possible classes.
Proof. Suppose that X(t) be an eventual positive solution of (1), then .
This means that is nonincreasing, so from Table 2, eight subcases can be discussed successively.
- (i)
.
-
Since is positively nonincreasing, there exists li ≥ 0, i = 1,2,3 such that, and then there exists t2 ≥ t1 such that , therefore,
(18) -
Integrating (18) from t to δ(t) for some continuous function δ(t) > t, we obtain
(19) -
We have two cases for .
- (ii)
-
then . Since , is negative nonincreasing, then there exists bi < 0, and t2 ≥ t1 such that for t ≥ t2, therefore,
(22) -
integrating (22) from t to δ(t), we obtain
(23) -
We claim that for ≥t3 ≥ t2 , otherwise if for t ≥ t3 ≥ t2, and implies that Limt⟶∞yi(t) = −∞, which is a contradiction, thus then (23) becomes
(24) -
Integrating (24) from t3 to t
(25) -
As ⟶∞ , it follows that Limt⟶∞yi(t) = ∞. Thus X(t) ∈ L2.
- (iii)
-
Then, and . Since , are negative and nonincreasing, then there exists bj < 0, and t2 ≥ t1 such that for t ≥ t2, therefore,
(26)
Integrating (26) from t to δ(t), we obtain
and we claim that for ≥t3 ≥ t2 , otherwise if for t ≥ t3 ≥ t2, and implies that Limt⟶∞yj(t) = −∞, which is a contradiction, thus then (27) becomes
Integrating the last inequality from t3 to t yields
As ⟶∞ , it follows that Limt⟶∞yj(t) = ∞, j = 1,2.
Concerning and nonincreasing, so there exists l3 ≥ 0, such that, then therefore
Integrating the last inequality from t to δ(t) leads to
we have two cases for .
- (a)
If for t ≥ t3 ≥ t2, and , it follows that Limt⟶∞y3(t) = ∞.
- (b)
If for t ≥ t3 ≥ t2, we claim that l3 = 0, otherwise l3 > 0, then (31) reduced to
(32) -
Integrating (32) from t3 to t
(33) -
As ⟶∞, it follows that Limt⟶∞y3(t) = −∞, which is a contradiction. Hence, (y1, y2, y3) ∈ L3. Analogously from the subcases (iv-viii), one can get X(t) ∈ Ln, n = 4,5, …, 8, respectively.
| Classes | Sign of | Behavior when t⟶∞ | |||||
|---|---|---|---|---|---|---|---|
| n | yi, i = 1,2,3 | ||||||
| L1 | + | + | + | + | + | + | yi⟶∞ |
| − | − | − | |||||
| L2 | + | + | + | − | − | − | yi⟶∞ |
| L3 | + | + | + | − | − | + | yi⟶∞ |
| + | + | − | yj⟶∞, j = 1,2, and | ||||
| L4 | + | + | + | − | + | − | yi⟶∞ |
| + | − | + | yj⟶∞, j = 1,3, and | ||||
| L5 | + | + | + | + | − | − | yi⟶∞ |
| − | + | + | yj⟶∞, j = 2,3, and | ||||
| L6 | + | + | + | + | + | − | yi⟶∞ |
| − | − | + | y3⟶∞ | ||||
| L7 | + | + | + | − | + | + | yi⟶∞ |
| + | − | − | y1⟶∞ | ||||
| L8 | + | + | + | + | − | + | yi⟶∞ |
| − | + | − | y2⟶∞ | ||||
4. Main Results of System (1)
In this section, some theorems and corollaries are established, which ensure that all bounded solutions of system (1) are either oscillatory or nonoscillatory and converge to zero as t⟶∞. On the other hand, all unbounded solutions of system (1) are either oscillatory or nonoscillatory diverge to infinity when t⟶∞.
Theorem 2. Suppose that λ = 1, and (2) holds in addition to
Then every bounded solution of system (1) oscillates.
Proof. Suppose that (1) has NOS X(t), so by Lemma 1, from Table 3, there is only the class K2, can occur for t ≥ t1 ≥ t0, that is,
Since y1(t), y2(t), y3(t), are increasing, so there exists ci > 0, i = 1,2,3 and t2 ≥ t1 such that yi(t) ≥ ci, t ≥ t2. Integrating the first equation of system (1) from t to δ(t) for some continuous function δ(t) > t, leads to
Integrating (36) from t to δ(t) yields
Then,
Integrating the above inequality from t2 to t, we get
As t⟶∞ concerning (34), it follows from (23) that Limt⟶∞y1(t) = ∞, which is a contradiction. Similarly, it can be shown that Limt⟶∞y2(t) = ∞, Limt⟶∞y3(t) = ∞, which is a contradiction.
This leads to the solution X(t) oscillates.
| Classes | Sign of | Behavior as t⟶∞ | |||||
|---|---|---|---|---|---|---|---|
| n | yi | ||||||
| K1 | + | + | + | + | + | + | yi⟶∞ |
| K2 | + | + | + | − | − | − | yi⟶∞ |
| K3 | + | + | + | − | − | + | j = 1,2y3⟶∞ |
| K4 | + | + | + | − | + | − | y2⟶∞,j = 1,3 |
| K5 | + | + | + | + | − | − | y1⟶∞, j = 2,3 |
| K6 | + | + | + | + | + | − | y1,2⟶∞ |
| K7 | + | + | + | − | + | + | y2,3⟶∞, |
| K8 | + | + | + | + | − | + | y1,3⟶∞, |
Theorem 3. Suppose λ = −1, (2) and (34) hold. Then every bounded solution of (1) oscillates or tends to zero as t⟶∞.
Proof. Suppose that system (1) has NOS X(t) so by Lemma 1, Table 2, there is only the possible case L1 to consider for t ≥ t1 ≥ t0:
Since y1(t), y2(t), y3(t), are positive and decreasing, so there exists li ≥ 0, i = 1,2,3 such that Limt⟶∞yi(t) = li, we claim that li = 0, otherwise li > 0 hence yi(t) ≥ li > 0 for t ≥ t2 ≥ t1.
Integrating the first equation of (1) from t to δ(t) yields:
Integrating (42) from t to δ(t), we get
Integrating (43) from t2 to t, we get
Corollary 4. Suppose that λ = 1, then (2) and (21) hold. Then every solution of system (1) is either oscillatory or Limt⟶∞|yi(t)| = ∞, i = 1,2,3.
Proof. Suppose that system (1) has a nonoscillatory solution X(t), let yi(t) > 0, t ≥ t0, i = 1,2,3. So by Lemma 1 and Table 3, there are only the possible classes K1 − K8 to consider for t ≥ t1 ≥ t0. If X(t) is bounded, then by Theorem 2, it follows that X(t) is oscillatory. Otherwise, X(t) is unbounded.
Case 1. Suppose that X(t) ∈ K1. By Lemma 1, it follows Limt⟶∞yi(t) = ∞, i = 1,2,3.
Case 2. Suppose that X(t) ∈ K2. By Theorem 2, Limt⟶∞yi(t) = ∞, i = 1,2,3..
Case 3. Suppose that X(t) ∈ K3. Since y1(t), y2(t), y3(t), are increasing, so there exists ci > 0, i = 1,2,3 and t2 ≥ t1 such that yi(t) ≥ ci, t ≥ t2.
Integrating the first equation of system (1) from t to δ(t) for some continuous function δ(t) > t, leads to
Integrating the (45) from t to δ(t), yields
Then,
Integrating the last inequality from t2 to t, we get
As t⟶∞ concerning (34), it follows from (30) that Limt⟶∞y1(t) = ∞.
Now, similarly, it can be shown that Limt⟶∞y2(t) = ∞, by Lemma 2.2, limt⟶∞y3(t) = ∞.
Other cases can be handled in the same way. The proof is complete.
Corollary 5. Suppose that λ = −1, i = 1,2,3, and (2), (40) are held. Then every solution of system (1) is either oscillatory or converges to zero or tends to infinity as t⟶∞.
Proof. Suppose that system (1) has a NOS X(t) so by Lemma 2 Table 2, there are only the possible cases L1 − L8 to consider for t ≥ t1 ≥ t0. If X(t) is bounded, then by Theorem 2, it follows that X(t) is either oscillatory or X(t)⟶0 as t⟶∞. If X(t) is unbounded, then from Table 2, we conclude that Limt⟶∞yi(t) = ∞, i = 1,2,3.
5. Examples
In this section, some examples illustrate the obtained results of the system (1).
Example 1. Consider the delay system as follows:
Obviously, to see that
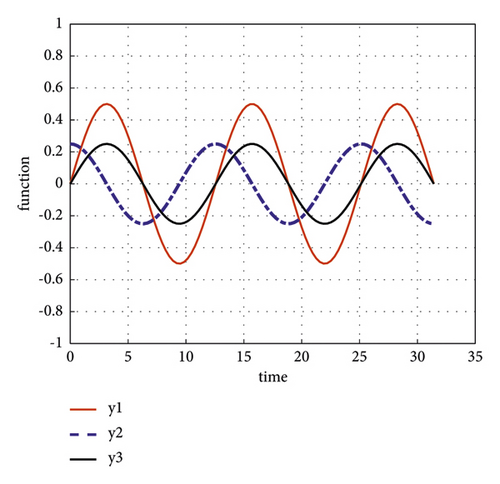
Hence all conditions of Theorem 2 are satisfied, so according to Theorem 2, every bounded solution of system (49) is oscillatory. For instance, (1/2sint/2, 1/4cost/2, 1/4sint/2)T, has an oscillatory solution, as shown in Figure 1.
Example 2. Consider the delay system as follows:
It is clear that
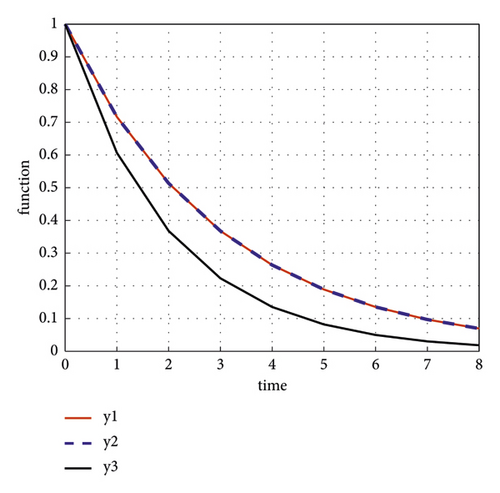
Hence all conditions of Theorem 3 satisfies, so according to Theorem 3, every bounded solution of (1) oscillates or tends to zero as t⟶∞. The solution has an nonoscillatory solution tends to zero as t⟶∞, as shown in Figure 2.
Example 3. Consider the delay system as follows:
It is clear that
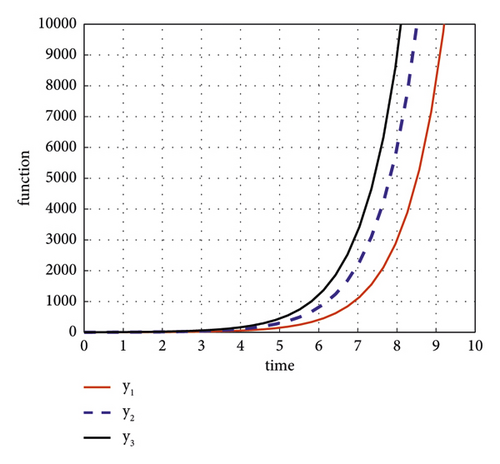
Hence all conditions of Corollary 5 satisfy, so according to Corollary 5, every solution of (1) oscillates or tends to zero or tends to infinity as t⟶∞. The nonoscillatory solution rose to infinity as t⟶∞. as shown in Figure 3.
6. Conclusions
- (i)
Knowing and calculating all possible cases of positive solutions of the third-order three-dimensional half-linear system with delay equations.
- (ii)
Oscillation: this trend revolves around studying and obtaining the necessary and sufficient conditions for obtaining the oscillation of positive solutions for a three-dimensional half-linear system with delay equations of the third order.
- (iii)
Asymptotic behavior: the required sufficient conditions were drawn in this direction to obtain the convergence to zero or divergence of all NOS of the half-linear systems of DDEs in the third order when t⟶∞. All the obtained results are included with illustrative examples.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Open Research
Data Availability
The data used in this study are available upon reasonable request to the corresponding author.




