Volume 2023, Issue 1 8892122

Research Article

Open Access

A Bottom-Up Approach to PV System Design for Rural Locality Electrification: A Case Study in Burkina Faso

Corresponding Author

Dominique Bonkoungou

[email protected]

orcid.org/0000-0003-3480-0025

Laboratoire de Matériaux et Environment (LAME), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Sosthène Tassembédo,

Sosthène Tassembédo

orcid.org/0000-0001-9697-6566

Laboratoire de Matériaux et Environment (LAME), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Sidiki Zongo,

Sidiki Zongo

orcid.org/0000-0002-1530-845X

Laboratoire de Physique et de Chimie de l’Environnement (LPCE), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Zacharie Koalaga,

Zacharie Koalaga

orcid.org/0000-0002-7819-9705

Laboratoire de Matériaux et Environment (LAME), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Dominique Bonkoungou,

Corresponding Author

Dominique Bonkoungou

[email protected]

orcid.org/0000-0003-3480-0025

Laboratoire de Matériaux et Environment (LAME), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Sosthène Tassembédo,

Sosthène Tassembédo

orcid.org/0000-0001-9697-6566

Laboratoire de Matériaux et Environment (LAME), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Sidiki Zongo,

Sidiki Zongo

orcid.org/0000-0002-1530-845X

Laboratoire de Physique et de Chimie de l’Environnement (LPCE), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

Zacharie Koalaga,

Zacharie Koalaga

orcid.org/0000-0002-7819-9705

Laboratoire de Matériaux et Environment (LAME), Université Joseph KI-Zerbo, Ouagadougou, BP 7021, Burkina Faso univ-ouaga.bf

Search for more papers by this author

First published: 27 May 2023

https://doi.org/10.1155/2023/8892122

Academic Editor: V. Ponnusami

Share a link

Email
Wechat
Bluesky

Abstract

This work evaluates the performance of optimal hybrid PV/battery and PV/diesel generator renewable energy systems for a remote village in Burkina Faso. Based on socioeconomic data and the household sample survey, a technoeconomic simulation and optimization model of electrical loading are presented. Ant colony optimization (ACO) and the loss of power supply probability (LPSP) algorithms were used for the search of the optimal hybrid power system. For the selected village location, the results have shown that the hybrid PV/battery system represents the best renewable energy solution due to abundant solar irradiation and carbon emission free compared to the conventional diesel generator (DG) or PV/DG system. To reach the estimated load power demand of 2150 kWh for the studied location, optimized PV/battery configuration sizing required 650 PV modules of 250 W and 715 batteries of 300 Ah. The economical evaluation reveals a cost investment of about 1,293 025.7 USD for a lifetime of 25 years in comparison of that of PV/DG and DG systems, which are 1,088 701.9 USD and 1,682 850.6 USD, respectively. However, environmental and atmospheric pollution is minimized with a saving of more than 17943 tons of CO₂. Therefore, the production of electricity from the PV/battery system leads to better competitiveness reliability for a socioeconomic development of studied remote villages.

1. Introduction

For the past three decades, the search for renewable energy resources has become a hot research topic for safe and clean energy production around the world [1]. However, the high investment costs remain a potential barrier, while conventional fossil fuels are sold at lower prices. As in most developing countries, accessibility to energy remains a major concern. Therefore, several papers reported on a low electricity access in sub-Sahara Africa [2–5]. In their investigation, Deborah et al. [5] indicated that only 48% have electricity access. Like the majority of sub-Saharan African countries, Burkina Faso is experiencing a high energy demand due to the rapid population growth, where the rate has doubled in less than two decades. Therefore, the energy coverage has become one of the national priorities. In addition to existing conventional energy sources (hydroelectric and diesel power plants), several solar power plants are being implemented across the country. Although these efforts, the energy access issue is more critical in rural areas [6]. To overcome this issue, strategies and programs such as rural electrification are initiated for an electricity coverage up to 100% by 2025, as indicated in the “Plan National de Développement Economique et Social (PNDES II)” [7]. For the socioeconomic development of remote villages, the promotion of hybrid renewable energy systems is proposed. The reliabilities of these systems have been reported in the literature. Thus, Enock Mulenga et al. [8], Kumar et al. [9], and Khan et al. [10] evaluated the technoeconomic analysis of hybrid power systems such as PV-Diesel, PV-Biomass, and PV-Hydrogen for the rural electrification plan. Other studies [11–14] focused on optimization techniques for the hybrid power system components sizing. Mishra et al. [15] described the design optimization approach for the grid-connected hybrid renewable system using discrete harmony search (DHS) algorithm. Mustafa Kamal et al. [16] discussed the optimal size for the standalone microgrid using the differential evolution (DE) algorithm to minimize the total cost of energy and the size of the system. Ali Saleh et al. [17] have developed an appropriate dispatching approach to analyze the stability, reliability, economic, and environmental performance of integrating PV with diesel-batteries power systems. Malla and Bhende [18] described an enhanced process of PV-diesel-battery system using Takagi–Sugeno (TS) fuzzy model for a maximum power extraction under changeable solar irradiation condition. In this process, the active power balance is kept through the PV system to avoid the diesel generator (DG) in running on/off frequently. Although the main objective in the operation of this system is achieved, the study does not mention the optimum assessment of various components.

Among diverse metaheuristic algorithms for optimization, ant colony optimization (ACO) algorithm is the most outstanding methods employed [19–23]. This algorithm refers to the behavior of ant colonies looking for food and connecting within one another through pheromone traces that are left behind [24]. In this study, the ACO and LPSP algorithms are used to optimally size a hybrid power system for a typical rural village of 4000 inhabitants. The ACO approach is developed to perform the LPSP algorithm by minimizing the total cost of investment in the system. We propose a PV system which eliminates the need for a DG system. Due to weather and partially or fully shading conditions, batteries are employed to form a hybrid PV-battery system. As in several references [25, 26], the yield of the storage system is greatly impacted by various factors such as state of charge (SOC), depth of discharge (DOD), and partial cycling temperature. Therefore, these parameters should be taken into account in the sizing of the storage system. The main contributions in this work refer to the following:

(1)
Proposing a reliable hybrid power system (PV-battery) for energy supply in a remote village with an abundant solar radiation
(2)
A developed bottom-up approach for energy load estimation in a village of 4000 people, based on socioeconomic data and household sample survey, while the assessment model is based on local climate and geographic data
(3)
A detailed mathematical approach for different components of the proposed system
(4)
Introducing ACO algorithm for optimizing the number of PV modules and batteries of the study system.

In addition to an introduction and conclusion, the paper is organized as follows: Section 2 describes the system as the main element of the design methodology. The optimization algorithms such as LPSP and ACO methods are described and introduced in Section 3 while the results of simulations and economic and environmental analysis are discussed in Section 4.

2. System Description

2.1. Remote Locality Description

The implementation of the hybrid system is carried out in the village of “Zerkoum” (12° 23′ N; 2° 04′ 39″ W) in Burkina Faso, with an estimated population of 600 households. The village is equipped with basic infrastructure, including schools, administration, health centre, and market. Due to its geographical position, “Zerkoum” is well irradiated and could take advantage of solar energy systems’ installation.

2.2. Load Profile Assessment

In this study, the load profile mainly deals with domestic power customers with basic facilities and devices, as presented in Table 1. The survey aimed to identify the power need while involving a total of 600 households subdivided into 3 groups as follows:

(1)
Group I: 50% of the population with very low incomes for their basic needs
(2)
Group II: 30% of the population with middle income and wish to use a TV, DVD player, and 1 or 2 appliances (fan, fridge, and flat iron)
(3)
Group III: 20% of the population with consistent income.

Table 1. Energy consumption needs in typical household.

Number of households (600)		Group I: 50%			Group II: 30%			Group III: 20%
Appliances	Rated power (W)	Number	Times (h)	Energy (Wh)	Number	Times (h)	Energy (Wh)	Number	Times (h)	Energy (Wh)
Lamp	18	03	03	162	06	04	432	08	04	576
Radio K7	15	02	06	180	02	07	210	02	04	120
TV color	80	…	…	…	01	04	320	02	05	800
Fridge	200	…	…	…	01	24	4800	01	24	4800
Freezer	150	…	…	…	…	…	…	01	10	1500
DVD player	50	…	…	…	01	04	200	01	03	150
Fan	60	…	…	…	01	08	480	01	01	60
Flat iron.	200	…	…	…	01	01	200	01	01	200
Phone charge	02	03	02	12	04	02	16	05	02	20

To obtain an accurate assessment of the methodology that describes the load pattern for all appliances, which are likely to be found in the village, a synthetic electric load shape was produced by employing an electrical local end approach. The technique is based on a bottom-up model, which uses some fundamental parameter data for the load profile. Based on some earlier works [27, 28, 29], an approximate appliance load profile for the village is established by using the statistical energy data on the number of households, abovementioned basic facilities, and commercial activities. The load is stochastically based on the hourly behavior of the customer. The daily load shape is simulated while considering the use of each appliance. The daily energy need for two people in different households is described in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Typical day availability model for two (2) individual persons in 2 different households.

From the figure, it can be clearly seen that the difference in the behavior of the two people results in a variation of the final electricity consumption which could be taken into account in the assessment model. The qualitative description of the hourly loadshape profile may be attributed to the presence of each person at home. From the hourly loadshape of different activities, the following equation can be formulated for each occupant [27]:

(1)

where d_ci is the daily presence of the i^th occupant at home during the simulated day, A_j is the j^th occupancy activity, α_i is the means of the i^th occupant, and β_ij is the propensity of the i^th occupant for j^th occupancy activity. Based on equation (1), different loadshapes are estimated for each activity and income source. Thus, the total energy required for the day is calculated through the expression in [27]:

(2)

where T_n and P_n are the duration of use and the nominal power, respectively, of the n^th appliance.

The contractual energy threshold of an individual household can be determined as follows [27]:

(3)

where P_Thres is the contractual power threshold.

In the case of energy use in a household, it can occur that when E_n≺E_Thres, then the remaining energy (E_rem) to power other appliances can be calculated as follows:

(4)

Similarly, the possible location time intervals of successive appliances are restricted to those for which E_n≺E_rem. Preferential time slots are defined for the use of appliance n, and this is based on daily usage patterns. Thus, the total power consumption of the household is defined as follows [27]:

(5)

where P_a is the total power of the active appliances during the considered day and is given by the following:

(6)

P_b defines the power consumption in which C_α and βC_α are automatic thermostat-controlled cyclic activation along the day and the electrical consumption resulting from the use of the appliance by an occupant of the household, respectively.

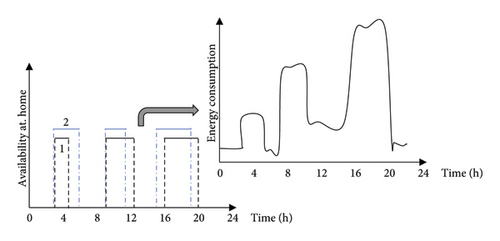
The global daily energy demand is therefore equal to the sum of individual households that include all activities with electricity consumption that must meet the electrical power system. Figure 2 illustrates the development of the bottom-up approach used in the studied locality loadshape assessment.

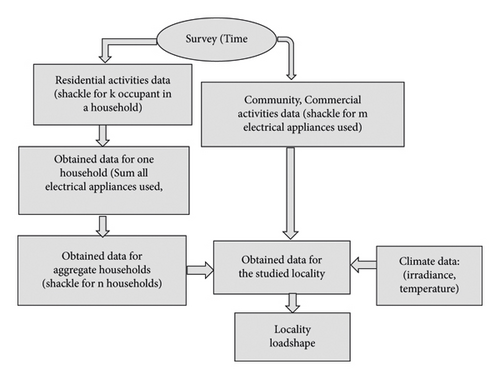
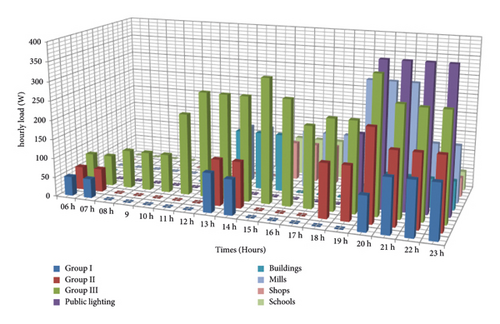
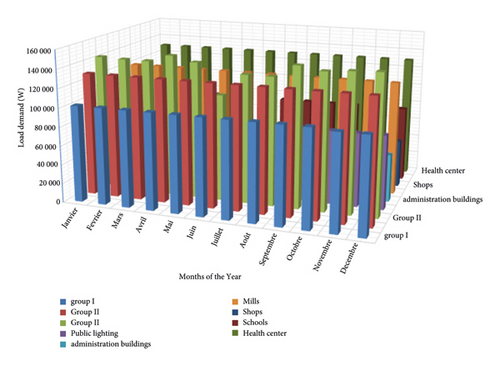
Figure 3(a) shows the hourly average load demand for various services in the locality for one day of operation. The evaluation of electrical energy consumption is carried out carefully by taking into account the peak consumption for all activities. It can be observed that the consumption peak is reached in the morning and evening. Indeed, these periods correspond to the moment where all residents are in their house and most domestic activities are carried out. On the other hand, the energy consumption is minimal at night when most people are less active at home as well as in the services. The total energy need for the village is estimated to be 2150 kWh per day with an average peak flow of 150 kW (load factor of 0 and 21) along the year, as shown in Figure 3(b). The maximum load value was recorded around 21:00 h. In this context, a PV module and a storage system could be an alternative in supplying the load to several houses in the absence of sun irradiation.

2.3. Solar Resource Assessment

Climatic data are measured over hourly intervals by the Research Laboratory of Energy under the direction of meteorology in Burkina Faso. The average annual solar irradiation obtained from the Ouagadougou meteorological station is evaluated at 5, 5 kWh/m² per day and direct sunshine is over 3000 hours per year [28]. These data obtained are used to characterize the climatic data of the village that contain diffuse, horizontal, and reflected radiation, relative humidity, and temperature. Figure 4 presents the daily solar radiation of the study locality for a year. From Figure 4, it is obvious that the village is well irradiated throughout the year. Since the hourly output of PV modules depends on the tilt angle and orientation of solar modules, some abovementioned climatic parameters were estimated accordingly from [29, 30]. Thus, the average energy output (E_PV) of the PV modules is estimated by using the following equation in [31]:

(7)

where S is the total solar modules area (m²), α is the solar modules efficiency (%), H is the annual average solar radiation on titled PV modules (kWh/m²), and P_r the coefficient for losses (range from 0, 5−0, 9 and default value is 0, 75).

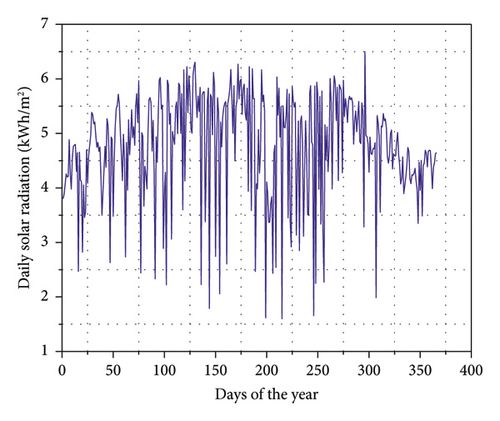
2.4. Components of the Hybrid PV/Battery System

The block diagram of the proposed PV/battery system is illustrated in Figure 5. It consists of a PV module system, storage system, converter, and different types of consumer’s electrical loads. In this diagram, the PV modules and storage systems are connected to a DC bus, while the electrical loads are linked to an AC bus via a DC/AC inverter. The maximum power point tracking (MPPT) procedure is used for the PV module generator to extract the maximum output power due to fluctuation of solar radiation under operating conditions. The storage system is loaded by the current generated by the PV module system where the control of their load is insured by a DC/DC controller. Since the PV system is autonomous, the presence of a storage device is essential to supply the load demands at any time. In this study, the basic relationship for computing PV modules’ output power is given by the following equation [32]:

(8)

where α_PV is the rated capacity of the PV modules (kW), β_PV is the rating coefficient (%), S_net represents the incident solar radiation (kW/m²), on the PV modules, S_net,STC is the incident solar irradiance at the standard test condition (STC: 1000 W/m²), γ is the temperature factor (%°C), and T defines the variation between the PV cell temperatures at normal (T_Cell) and STC (T_Cell,STC) given as T = T_Cell − T_cell,STC.

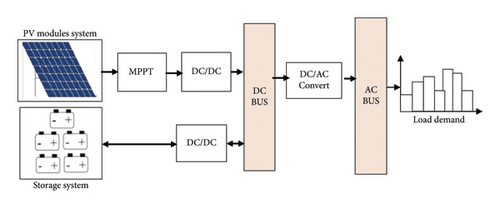
Taking into account that operating under a temperature parameter around 45°C in April, a monocrystalline solar module is considered. The main technical information about the PV module system is described in Table 2 [33].

Table 2. Technical information of PV module.

Parameters’ description	Values
Maximum power (P_mpp)	250 W
Open circuit voltage (V_oc)	37.4 V
Short circuit current (I_sc)	8.55 A
Temperature factor (γ)	−0.003865/°C
Life time	25 years
Ground reflection	20%
Efficiency	15.43%
Operating temperature	47°C
Capital cost ( ^∗)	0.67 USD/W
Replacement cost ( ^∗)	0.67 USD/W
Operation and maintenance (O&M) cost ( ^∗)	0.5 USD/kW/Year

( ^∗) These prices are derived from data obtained from local Burkinabe distributors and manufacturers.

2.5. Storage System Description

The storage system sizing for a hybrid renewable energy system is a key factor for the project over the lifetime. Thus, the battery bank should be optimum in size, while a proper selection of the storage system characteristics, such as the amp-hour (Ah) or Watt-hour (Wh) capacity, could play an important role in supplying the load requirements. In consideration of two cases, the state of charge (SOC) is computed by using (9) and (10) [34]:

(1)
Energy balance for storage system charging:
(9)
(2)
Energy balance for discharging the storage system:

(10)

where P_sto(t − 1) and P_sto(t) denote the storage system energy at the beginning and at the end of the interval t, respectively, P_Load(t) represents the load demand at the time t, P_PV(t) is the energy generated by the PV modules at the time t, σ is the self-discharge factor, and η_sto and η_con denote the storage system charging and the efficiency of the converter, respectively [34]. A lithium-ion technology is selected for this study, whose self-discharge factor (σ) is 2% per month, the battery charging efficiency (η_sto) is 85%, the converter efficiency (η_con) is 95%, and maximum battery capacity is 300 Ah.

2.6. Power Converter Model

The power converter is chosen based on the maximum load demand, whereas the performances of the inverters are chosen according to the power needs supply during peak hours. The capacity of the converter can be calculated using the following equation [35, 36]:

(11)

where C_con, L_ind, and L₀ denote the converter capacity, the total inductive loads, and other loads, respectively. The total inductive load consists of fridge, refrigerators, and fans, while TV, radio, DVD players, and so on belong to other load classes.

3. Optimization Approach

From the studied system, any other auxiliary energy source is excluded. Only the battery stores energy in the system. For this optimization approach, the loss of power supply probability (LPSP) presented in [39] is adopted to describe the reliability of power supply to load. The LPSP is defined as the proportion of the loss of power supply (LPS) to that required by the load during a given period and can be calculated through the following equation [34, 37]:

(12)

The optimization approach is divided in three steps: (i) estimation of the PV modules’ output based on one-year solar data; (ii) estimation of the yearly status of the battery storage which is done with the previous amount of stored energy, PV array output energy, battery efficiency, inverter efficiency, and load energy demand; and (iii) the LPSP is defined and then the optimization problem is formulated as follows:

(13)

where L_sys is the total cost of the system, L_pv is the size of a PV module, L_b is the capacity of a battery, L_other is the other total costs which are considered to be constant, and α and β are the unit costs of a PV module and a battery, respectively. The solution to this problem could be achieved by partially differentiating as follows:

(14)

Solving this equation could lead to the determination of the capacities of the PV module and the battery for a given LPSP.

4. Simulation Results and Discussion

4.1. Capacity of PV Module and Battery Optimization

In order to evaluate the performance of the system under various conditions, simulation studies have been carried out using load demand and real weather data of selected villages. Ant colony optimization (ACO) [20–42], as a probabilistic algorithm, is used to perform LPSP and system investment cost. ACO is swarm intelligence-based metaheuristic optimization algorithm that was inspired by the foraging behavior of ants [43]. ACO imitates the cooperative behavior of an ant colony to find the shortest path to a food source. In this approach, a combination of optimization issues with n sizing parameters is made as a multilayered diagram, as illustrated in Figure 6 [44]. The number of layers corresponds to the number of design parameters. Also, the number of nodes in each layer corresponds to the discrete values’ number allowed for the corresponding parameters. Therefore, each node in a particular location of the diagram is joined with an allowed discrete value of a design parameter. Artificial ants travel through this diagram, searching for good paths. An ant colony consists of N ants. The ants start at the nest node, walk through the different layers from the first layer to the last layer, and end at the destination node in each cycle or iteration. Each ant can choose only one node in each layer in accordance with the state transition rule given by metaheuristic information. The nodes selected along the path visited by an ant represent a candidate solution [44]. On the travelled path, the ant lays down some pheromone based on a local updating rule. In the start of the optimization process, all the edges or rays are initially carried out with the same amount of pheromone. Thus, in this first iteration, all the ants start from the home node and end at the food node by randomly choosing a node in each layer. Small quantities of pheromone are deposited during the construction phase, while larger amounts are deposited at the end of each iteration in proportion to solution quality. The optimization process is finished if any of the given termination conditions are satisfied. The values of the design parameters indicated by the nodes on the path with the largest amount of pheromone are considered as the components of the optimum solution vector. Overall, at the optimum solution, all ants walk along the same converged path. The most important characteristic of this algorithm is that it permits the best ant to update its pheromones.

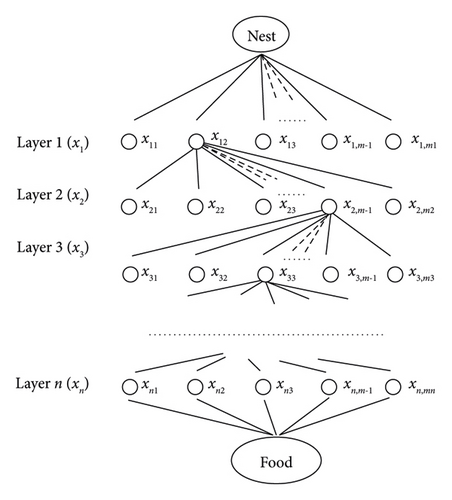
From its interest in complex system optimization, the ACO algorithm has been applied to several optimization problems including those related to renewable energy optimization.

Thus, Kumar et al. [45] employed ACO to optimize the sizing of wind turbines and PV arrays in a hybrid renewable energy system. The aim was to maximize the energy output of the system while considering the availability of wind and solar resource. ACO was used to determine the optimal dispatch of renewable sources to meet the demand for energy while minimizing the cost and emissions [46–48]. Moreover, ACO could easily be combined with other methods [45]. In our case, this optimization approach is employed to determinate the optimum capacities of PV modules and batteries for a minimized cost of the system. Two different loads are considered for this optimization: firstly, we consider a constant load, that is, the load energy demand remains almost the same along the year. Secondly, a variable load is considered; in this case, we incremented to 20% or 45% of the initial load demand over the year. The main aim is to maximize the energy output of the system while minimizing the cost. The flowchart of the ACO algorithm applied to optimize this hybrid power system can be described as follows:

(i)
Initialization: The initial solution is generated using the LPSP approach. This solution includes the initial sizes of the PV arrays and battery storage system.
(ii)
Pheromone update: In this step, the pheromone trails are updated based on the solutions generated in the previous iteration. If a solution generated in the previous iteration produced a higher energy output and lower cost, the pheromone is updated to reflect that.
(iii)
Solution generation: New solutions are generated on the basis of the updated pheromone trails and heuristics. The heuristics are rules that ensure the PV arrays and battery storage system are sized within the given constraints. These solutions represent different combinations of PV arrays and battery storage system sizes.
(iv)
Solution evaluation: solutions are evaluated on the basis of a predefined objective function. The objective function takes into account the energy output, cost, and other constraints such as the maximum allowed capacity of the battery storage system.
(v)
Termination: The algorithm terminates when a satisfactory solution is found.

As a result, the ACO algorithm will generate an optimal solution that represents the optimal sizing of the PV arrays and battery storage system to meet the energy demand of the studied location while minimizing the cost.

Thus, the optimization technique was carried out by taking into account the ACO parameters’ approach, as presented in Table 3. These parameters were estimated based on the work of Jiang et al. [41].

Table 3. Parameter values for ant colony algorithm.

Parameters	Values
No. of ants per iteration	4
Size of the problem	2
Size of the solution	10
Locality of the search process	0.45
Convergence speed	0.86

In the simulation process, the parameters (constant or variable) defined in Table 4 are considered. The lower and upper boundary stones of decided variables are assessed by the ACO program to concur with the optimal solution. The number of decided parameters that provide the best results is sorted by setting all possible values by trial and error.

Table 4. Constant and variable parameters used.

Constant parameters	Values
Converter efficiency (%)	95
Regulator efficiency (%)	99
Battery charging efficiency (%)	85
Connection loss factor	0.98
Other loss factor	1
α (US$/W_p) ^∗	0.67
β (US$/Ah) ^∗	1.08
Variable Parameters	Range
Number of PV modules	500–700
Number of batteries	500–725

^∗These prices are derived from data obtained from local distributors and manufacturers.

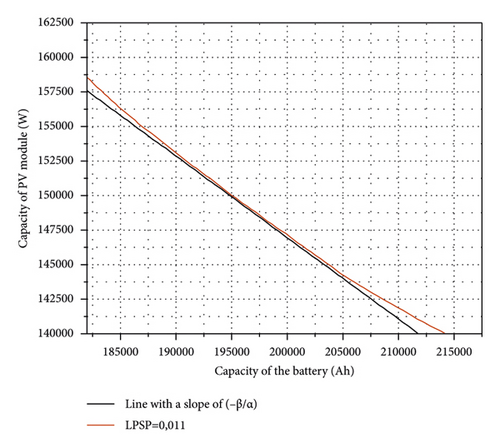
Using the ACO algorithm developed in MATLAB, the LPSP for various pairs of PV modules and batteries is determined, as shown in Figure 7(a). The optimum capacity arrangement of PV modules and batteries obtained for an LPSP is equal to 0, 011 (15, 70 min per day or 3, 98 days per year of blackout) and are roughly worth 150 000 W and 195 000 Ah, respectively, as observed in Figure 7(b).

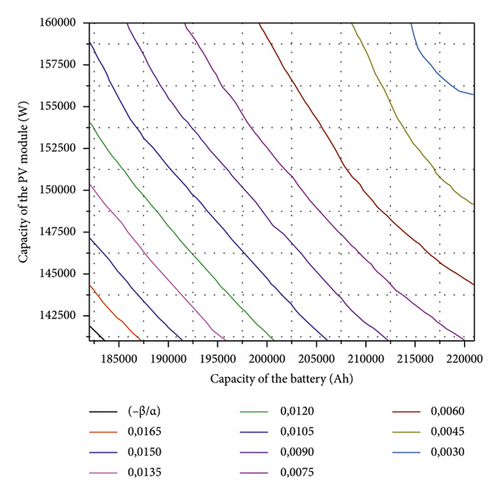
4.2. Cost Value of System Optimization

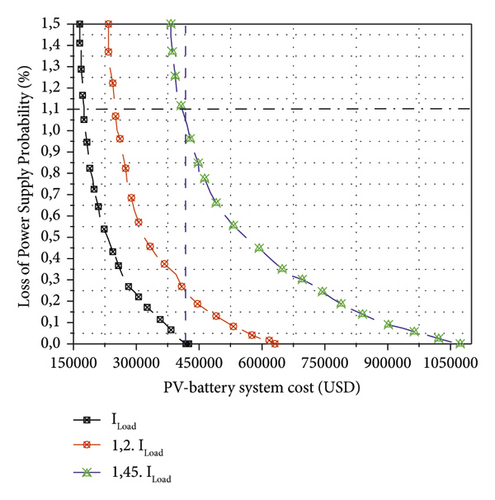
In this section, we discuss the optimal cost value of the PV/battery system for an optimal LPSP value. Three various load profiles such as initial load (I_load) and variables of load profile 1 (1,2 × I_load) and profile 2 (1,45 × I_load) are considered. The obtained Pareto limit profiles can be observed in Figure 8. The safety threshold was set at 1, 1% LPSP as a tolerable threshold for the local electricity supply, viz., up to 15, 70 min per day of failure. All points below the safety threshold are considered optimal points. These values are used to determine the cost of the system for a given LPSP value. The optimal values are those for which the 3 profiles are found in the defined safety threshold. From Figure 8, it can be observed that the optimum points correspond to a cost of 418764, 25 USD with a LPSP equals to 0, 0108. Referring to the aforementioned characteristics of commercially available PV module and battery, 650 PV modules of 250 W and 715 batteries of 300 Ah are sufficient to supply the load energy demand.

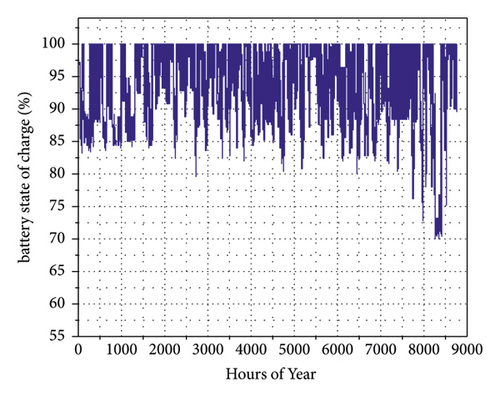
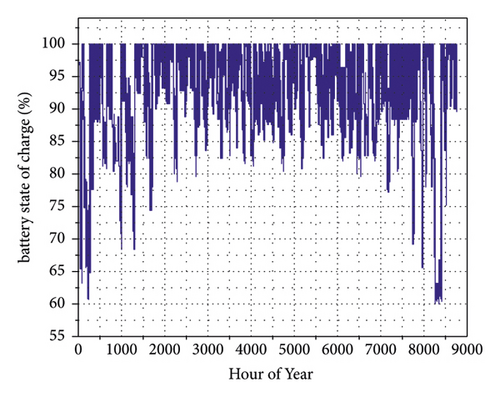
With the optimal arrangement, the SOC of the storage system is evaluated over one year, and the corresponding results are presented in Figure 9. In both cases (Figures 9(a) and 9(b)), the SOC oscillates between an allowed maximum value SOC_max (100%) and minimum value SOC_min (60% of SOC). These SOCs are greater than assumed minimum SOC of 40%. By adding variable load, the storage system is cycled in a fairly SOC large portion during the period November to March due to the higher energy consumption (Figure 9(b)). This allows a correlation between the demand and the storage system use. The higher the demand is, the higher the storage system use is. Therefore, the storage system is less used for the rest of the year as the demand is relatively low. The mean SOC vanishes between 80% and 92%. An increase in initial load could impact the SOC range and battery ageing as well. Figure 9 c shows the fluctuation of the energy level in a battery throughout one year with respect to the variable load profile. These are due to the overused energy per day of the storage system, which leads to an improper charge of batteries even during sunshine. However, all of these fluctuations could be controlled or reduced with proper strategic management.

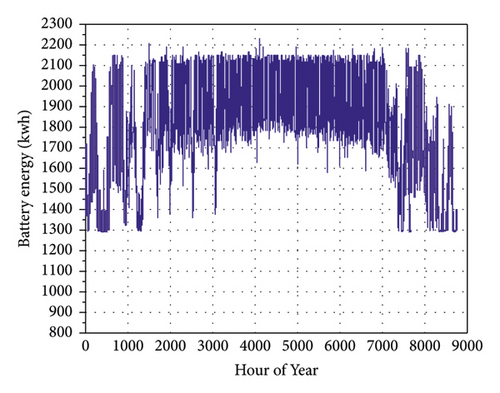
4.3. Comparison with Other Configurations and Environmental Analysis

This section presents an analysis of the economic feasibility and environmental impact of three different energy systems, namely DG only, PV/DG, and PV/battery systems for supplying the same load profile. As seen in Figure 3(b), the total daily need for energy needs presents a maximum power peak load of 150 kW and a minimum power peak of 60 kW.

(1)
Sizing of the DG system
In [49], a technoeconomic analysis of PV/DG hybrid system without storage was performed for a remote village in Burkina Faso. The authors found that the optimal functioning point of the DG is set at around 90% of its nominal power. Based on this work, it is suggested that the power that could be delivered by DG is 169, 5 kW for this investigation.
(2)
Sizing of the PV/DG system
In the present study, 30% of the PV maximum penetration is considered, as indicated in [50]. A PV array of 47 kW and 169.5 kW are required for a PV/DG system under the assumption that it will meet the load at low irradiation and night.

4.3.1. Economic Analysis Comparison

The economic evaluation is based on the life cycle cost (LCC). The calculations of cost efficiency of a typical system over the project duration include various costs, viz., initial capital cost (C_in, the recurring costs (M_op), and the nonrecurring costs (R_repl) in USD currency. The recurring costs represent the sum of all operating and maintenance (O&M) costs, while the nonrecurring costs denote the sum of equipment replacement cost. The expenses expected that could occur during the life cycle of the system are evaluated using the expression in [50, 51]:

(15)

The included technical data and assumptions on PV, DG, and battery units in this study are from [41, 52, 53]. According to the type of the system, an economic evaluation is presented. For the PV/DG system LCC analysis, we assumed that 8% of the energy consumed between 6:00 am and 5:00 pm is supplied by the PV generator. In this case, the DG should meet the peak load (150 kW) and runs 24 h per day. Thus, the total electrical load to be generated by these systems is about 19 618, 750 kWh over 25 years. Based on the same load demand over 25 years, the PV/DG system LCC (1 082, 701.9 USD) is found to be lower than the PV/battery system LCC (1 293 025.7 USD), which is also lower than that of the DG system LCC (1 682 850.6 USD). The life cycle cost breakdown for each selected energy system is shown in Figure 10.

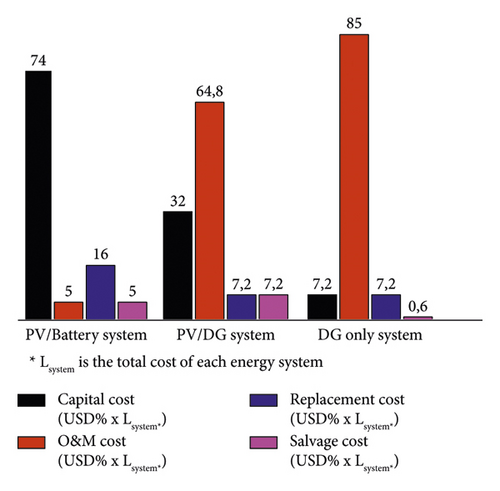
As expected, the investment cost of PV/battery systems is ten times higher than that of DG systems, while O&M costs remain lower, as replacement and salvage costs are minimal.

Indeed, the main issue in the DG system is related to the O&M and the increase in fuel prices. From these results, the PV/DG system is more economical and viable compared to the PV/battery and DG systems. Nevertheless, each system has to be considered on its merits, while taking into account the local conditions, the cost of alternatives, and other parameters such as environment. Although the PV/battery system has a high investment cost, it does not require fuel, high maintenance, and equipment replacement. Compared to hybrid PV/DG systems, the introduction of a DG in the PV/battery system could be a reliable option.

4.3.2. Environmental Analysis

Electrical energy in several remote localities in Burkina Faso is usually produced by the mean of DG. However, the production of energy through fossil fuels is a source of air pollution [54]. The environmental impacts of autonomous PV systems can only be evaluated properly if comparative study involves other energy supply systems. The life cycle impact assessment (LCIA) is used to perform the environmental analysis. Indeed, the LCIA is a crucial step in the life cycle assessment (LCA) methodology. It involves the evaluation and quantification of the environmental impacts of a product, process, or system throughout its entire life cycle, from raw material extraction to disposal or recycling. The LCIA provides a systematic approach to understand the significance of various environmental stressors and their effects on different impact categories.

Without a deep investigation, it can be admitted that PV systems in general are CO₂ emissions free. While a hybrid system involving diesel is a source of CO₂ emissions. The CO₂ emission rate (τ) is evaluated based on the demand and the quantity of fuel used by employing the following relation:

(16)

where LC is the total equivalent amount of CO₂ emitted over the life cycle of the PV system (kgCO₂), E is the overall annual energy supplied (kWh/year), and Ө is the lifetime of the PV system (year).

For a growing population and economical business activities in a remote village, an increase in CO₂ emission is expected while combining PV and DG for energy production. Some reports [55, 56] indicated that the emission factor considered for DG is 1.27 kg of CO₂/kWh. The value takes into account emissions during fuel combustion, fuel extraction and refining, the manufacturing of the DG itself, and transport (over 100 km). According to Fleck and Huot [57], the total emissions considered for the diesel fuel consumption is 3.15 kg of CO₂ per liter. During the life cycle of the DG system, about 1854 tons of CO₂ will be released in nature. Compared to the PV/DG system, about 3456 tons of CO₂ are saved over its life cycle while the PV/battery system has a CO₂ emission free. This later system allows the saving of 17943 tons of CO₂ compared to the DG system and 14487 tons of CO₂ compared to the PV/DG system. The mayor drawback in this system is the recycling of the batteries at the end of their lifetime because of lack of policies or regulations in most sub-Saharan African region [28]. From the abovementioned, it is clear that the PV/DG system presents advantages compared to PV/battery and DG in terms of cost and environmental pollution, respectively. However, attempts could be made in PV/DG systems to explore the benefits of the incorporation of short-term storage in terms of fuel savings, diesel running time, and storage systems of excess energy.

5. Conclusions

In this work, a bottom-up approach of energy load estimation for a typical village of 4000 people is proposed based on socioeconomic data and household sample survey. The behavior of the hybrid PV/battery system is studied, while considering a design of PV systems in respect of hourly global solar irradiance and real load demand profiles. An economic analysis is also carried out for an optimal size of different components such as PV modules, battery, controller, and inverter by using the ACO technique. The obtained results show that the PV/battery system is qualified to satisfy the load demand in the village location. Furthermore, the SOC analysis of the battery reveals the sustainability of the storage system for more than 20% of the initial load. The economic and environmental aspects of the PV/DG, PV/battery, and DG systems evaluation reveal that the proposed PV/battery system, consisting of 650 PV modules (250 W), 715 batteries (300 Ah), and a 139 kW inverter, is economically disadvantaged compared to the PV/DG system, but less expensive than the DG system. However, it remains environmentally advantageous at long-term exploitation because it releases free carbon emission.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors express their gratitude to the Laboratory of Materials and Environment (LA.M.E), University of Joseph KI-Zerbo, Burkina Faso, who permitted to realize the survey and experimental setup.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author on request.

References

1 Elia Campana P., Wästhage L., Nookuea W., Tan Y., and Yan J., Optimization and assessment of floating and floating-tracking PV systems integrated in on- and off-grid hybrid energy systems, Solar Energy. (2019) 177, https://doi.org/10.1016/j.solener.2018.11.045, 2-s2.0-85057745302.
10.1016/j.solener.2018.11.045
Web of Science® Google Scholar
2 Onyeji I., Morgan B., and Nussbaumer P., Contextualizing electricity access in sub-Saharan Africa, Energy for Sustainable Development. (2012) 16, no. 4, https://doi.org/10.1016/j.esd.2012.08.007, 2-s2.0-84869113757.
10.1016/j.esd.2012.08.007
Web of Science® Google Scholar
3 Moussa P. B. and Davies M., Electricity Access in Sub-saharan Africa: Uptake, Reliability, and Complementary Factors for Economic Impact, 2019, World Bank Group, Washington, DC, USA.
Google Scholar
4 International Energy Agency Iea, Africa energy outlook 2022, 2022, https://www.iea.org/reports/africa-energy-outlook-2022.
Google Scholar
5 Ramalope D., Reynolds C., Ganti G., Welder L., Fyson C., and Mainu M., Bill Hare « renewable energy transition in sub-saharan Africa, Climate Analytics November, 15.
Google Scholar
6 Iea (International Energy Agency), Electricity market report - july 2022: update, 2022a, https://www.iea.org/reports/electricity-market-report-july-2022.
Google Scholar
7 Marie C. J., Plan National de Développement Economique et Social 2021-2025 (PNDES II), Juillet. (2021) .
Google Scholar
8 Mulenga E., Kabanshi A., Henry M., Ndiaye M., Nyirenda E., and Mulenga K., Techno-economic analysis of off-grid PV-Diesel power generation system for rural electrification: a case study of Chilubi district in Zambia, Renewable Energy, 203, https://doi.org/10.1016/j.renene.2022.12.112.
10.1016/j.renene.2022.12.112
Google Scholar
9 Kumar R. and Kaur Channi H., A PV-Biomass off-grid hybrid renewable energy system (HRES) for rural electrification: design, optimization and techno-economic-environmental analysis, Journal of Cleaner Production. (2022) 349, 131347, https://doi.org/10.1016/j.jclepro.2022.131347.
10.1016/j.jclepro.2022.131347
Web of Science® Google Scholar
10 Khan T., Waseem M., Tahir M., Liu S., and Yu M., Autonomous hydrogen-based solar-powered energy system for rural electrification in Balochistan, Pakistan: an energy-economic feasibility analysis, Energy Conversion and Management. (2022) 271, 116284, https://doi.org/10.1016/j.enconman.2022.116284.
10.1016/j.enconman.2022.116284
CAS Web of Science® Google Scholar
11 Pandiyan P., Sitharthan R., Saravanan S., Natarajan P., Ramji Tiwari M., Chinnadurai T., Yuvaraj T., and Devabalaji K. R., A comprehensive review of the prospects for rural electrification using stand-alone and hybrid energy technologies, Sustainable Energy Technologies and Assessments. (2022) 52, 102155, https://doi.org/10.1016/j.seta.2022.102155.
10.1016/j.seta.2022.102155
Web of Science® Google Scholar
12 Raghav L. P., Rangu S. K., Dhenuvakonda K. R., and Singh A. R., Optimal energy management of microgrids-integrated nonconvex distributed generating units with load dynamics, International Journal of Energy Research. (2021) 45, no. 13, 18919–18934, https://doi.org/10.1002/er.6995.
10.1002/er.6995
Web of Science® Google Scholar
13 Raghav L. P., Kumar R. S., Raju D. K., and Singh A. R., Optimal energy management of microgrids using quantum teaching learning based algorithm, IEEE Transactions on Smart Grid. (2021) 12, no. 6, 4834–4842, https://doi.org/10.1109/TSG.2021.3092283.
10.1109/TSG.2021.3092283
Web of Science® Google Scholar
14 Ambekar P. and Sengar K. P., Cost analysis of a hybrid system by using an optimization technique, Int. J. Adv. Technol. Eng. Res.(2015) 5, 1–5.
Google Scholar
15 Mishra S., Saini G., Chauhan A., Upadhyay S., and Balakrishnan D., Optimal sizing and assessment of grid-tied hybrid renewable energy system for electrification of rural site, Renewable Energy Focus. (2023) 44, https://doi.org/10.1016/j.ref.2022.12.009.
10.1016/j.ref.2022.12.009
Google Scholar
16 Mustafa Kamal M., Ashraf I., and Fernandez E., Optimal sizing of standalone rural microgrid for sustainable electrification with renewable energy resources, Sustainable Cities and Society. (2023) 88, 104298, https://doi.org/10.1016/j.scs.2022.104298.
10.1016/j.scs.2022.104298
Web of Science® Google Scholar
17 Ali Saleh A., Naim Tajuddin M. F., Khalil Zidane T. E., Su C.-L., Kadhim Alrubaie A. J., and Alwazzan M. J., Techno-economic and environmental evaluation of PV/diesel/battery hybrid energy system using improved dispatch strategy, Energy Reports. (2022) 8, 6794–6814, https://doi.org/10.1016/j.egyr.2022.05.021.
10.1016/j.egyr.2022.05.021
Web of Science® Google Scholar
18 Malla S. G. and Bhende C. N., Enhanced operation of stand-alone “Photovoltaic-Diesel Generator-Battery” system, Electric Power Systems Research. (2014) 107, https://doi.org/10.1016/j.epsr.2013.10.009, 2-s2.0-84888183963.
10.1016/j.epsr.2013.10.009
Web of Science® Google Scholar
19 Dorigo M. and Stu¨tzle T., Ant Colony Optimization, 2004, The MIT Press, Cambridge, MA, USA.
10.7551/mitpress/1290.001.0001
Web of Science® Google Scholar
20 Abbaspour K. C., Schulin R., and van Genuchten M. T., Estimating unsaturated soil parameters using ant colony optimization, Advances in Water Resources. (2001) 24, 827–841.
10.1016/S0309-1708(01)00018-5
Web of Science® Google Scholar
21 Kaveh A. and Talatahari S., An improved ant colony optimization for constrained engineering design problems, Engineering Computations. (2010) 27, no. 1, https://doi.org/10.1108/02644401011008577, 2-s2.0-75949130675.
10.1108/02644401011008577
Web of Science® Google Scholar
22 Chandra Mohan B. and Baskaran R., A survey: ant Colony Optimization based recent research and implementation on several engineering domain, Expert Systems with Applications. (2012) 39, no. 4, https://doi.org/10.1016/j.eswa.2011.09.076, 2-s2.0-82255179246.
10.1016/j.eswa.2011.09.076
Web of Science® Google Scholar
23 Suresh V., Janik P., and Jasinski M., Metaheuristic approach to optimal power flow using mixed integer distributed ant colony optimization, Archives of Electrical Engineering. (2020) 69, no. 2.
Web of Science® Google Scholar
24 Gupta A. and Garg R., Load balancing based task scheduling with ACO in cloud computing, Proceedings of the 2017 International Conference on Computer and Applications (ICCA), September 2017, Doha, Qatar, 174–179, https://doi.org/10.1109/COMAPP.2017.8079781, 2-s2.0-85040020329.
10.1109/COMAPP.2017.8079781
Google Scholar
25 Keshan H., Thornburg J., and Ustun T. S., Comparison of lead-acid and lithium ion batteries for stationary storage in off-grid energy systems, Proceedings of the 4th IET Clean Energy and Technology Conference (CEAT 2016), November 2016, Kuala Lumpur, Malaysia, 1–7, https://doi.org/10.1049/cp.2016.1287.
10.1049/cp.2016.1287
Google Scholar
26 Krieger E. M., Cannarella J., and Arnold C. B., A comparison of lead-acid and lithium-based battery behavior and capacity fade in off-grid renewable charging applications, Energy. (2013) 60, https://doi.org/10.1016/j.energy.2013.08.029, 2-s2.0-84884588091.
10.1016/j.energy.2013.08.029
Web of Science® Google Scholar
27 Capasso A., Grattieri W., Lamedica R., and Prudenzi A., A bottom-up approach to residential load modeling, IEEE Transactions on Power Systems. (1994) 9, no. 2, 957–964, https://doi.org/10.1109/59.317650, 2-s2.0-0028426829.
10.1109/59.317650
Web of Science® Google Scholar
28 Azoumah Y., Ramdé E. W., Tapsoba G., and Thiam S., Siting guidelines for concentrating solar power plants in the sahel: a case study of Burkina Faso, Solar Energy. (2010) 84, 1545–1553.
10.1016/j.solener.2010.05.019
Web of Science® Google Scholar
29 Sidrach-de-Cardona M. and Mora L., A simple model for sizing stand-alone photovoltaic systems, Solar Energy Materials & Solar Cells. (1998) 55, 119–214.
10.1016/S0927-0248(98)00093-2
Web of Science® Google Scholar
30 Lena G., Rural electrification with PV-hybrid systems: overview and recommendation for further deployment, 2013, International Energy Agency, Paris, France, Report IEA-PVPS T9.
Google Scholar
31 Margaret Amutha W. and Rajini V., Cost benefit and technical analysis of rural electrification alternatives in southern India using HOMER, Renewable and Sustainable Energy Reviews. (2016) 62, 236–246, https://doi.org/10.1016/j.rser.2016.04.042, 2-s2.0-84965106480.
10.1016/j.rser.2016.04.042
Web of Science® Google Scholar
32 Adefarati T., Daniel Obikoya G., and Ambrose N., Design and analysis of a photovoltaic-battery-methanol diesel power system, Int Trans Electr Energ Syst. (2021) 31, e12800, https://doi.org/10.1002/2050-7038.12800.
10.1002/2050-7038.12800
Web of Science® Google Scholar
33 Thaleos, Panneaux photovoltaïques monocristallins 250 W, 2000, http://www.thaleos.com/files/produit/photovoltaique-file_prod_FR.pdf.
Google Scholar
34 Benavente F., Anders L., Elia Campana P., Zhang Y., Cabrera S., and Lindbergh G., Photovoltaic/battery system sizing for rural electrification in Bolivia: considering the suppressed demand effect, Applied Energy. (2019) 235, https://doi.org/10.1016/j.apenergy.2018.10.084, 2-s2.0-85056217184.
10.1016/j.apenergy.2018.10.084
Web of Science® Google Scholar
35 Krishan O. and Suhag S., Techno-economic analysis of a hybrid renewable energy system for an energy poor rural community, Journal of Energy Storage. (2019) 23, https://doi.org/10.1016/j.est.2019.04.002, 2-s2.0-85063968025.
10.1016/j.est.2019.04.002
Web of Science® Google Scholar
36 Akinyele D., Analysis of photovoltaic mini-grid systems for remote locations: a techno-economic approach, International Journal of Energy Research. (2018) 42, https://doi.org/10.1002/er.3886, 2-s2.0-85029440929.
10.1002/er.3886
Web of Science® Google Scholar
37 Diaf S., Diaf D., Belhamel M., Haddadi M., and Louche A., A methodology for optimal sizing of autonomous hybrid PV/wind system, Energy Policy. (2007) 35, no. 11, https://doi.org/10.1016/j.enpol.2007.06.020, 2-s2.0-34548825689.
10.1016/j.enpol.2007.06.020
Web of Science® Google Scholar
38 Nijhuis M., Gibescu M., and Cobben J. F. G., Bottom-up Markov chain Monte Carlo approach for scenario based residential load modelling with publicly available data, Energy and Buildings. (2016) 112, https://doi.org/10.1016/j.enbuild.2015.12.004, 2-s2.0-84950996585.
10.1016/j.enbuild.2015.12.004
Web of Science® Google Scholar
39 Paatero J. V. and Lund P. D., A model for generating household electricity load profiles, International Journal of Energy Research. (2006) 30, 273–290, https://doi.org/10.1002/er.1136, 2-s2.0-33645914413.
10.1002/er.1136
Web of Science® Google Scholar
40 Borowy B. S. and Salameh Z. M., Methodology for optimally sizing the combination of a battery bank and PV Array in a Wind/PV Hybrid System, IEEE Transactions on Energy Conversion. (1996) 11, no. 2.
10.1109/60.507648
Web of Science® Google Scholar
41 Jiang L. L., Maskell D. L., and Patra J. C., A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions, Energy and Buildings. (2013) 58, https://doi.org/10.1016/j.enbuild.2012.12.001, 2-s2.0-84872289297.
10.1016/j.enbuild.2012.12.001
Web of Science® Google Scholar
42 Ahmad M., Bhatia D., and Hassan Y., A novel ant colony optimization based scheme for substitution box design, Procedia Computer Science. (2015) 57, https://doi.org/10.1016/j.procs.2015.07.394, 2-s2.0-84944045002.
10.1016/j.procs.2015.07.394
Google Scholar
43 Dorigo M. and Di Caro G., Ant colony optimization: a new meta-heuristic, Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406). (1999) 2, IEEE.
10.1109/CEC.1999.782657
Google Scholar
44 Vassili V., A review on traditional and modern structural optimization: problems and techniques, Metaheuristic Applications in Structures and Infrastructures. (2013) Elsevier, Amsterdam, The Netherlands, https://doi.org/10.1016/B978-0-12-398364-0.00002-4, 2-s2.0-84882611231.
10.1016/B978-0-12-398364-0.00002-4
Google Scholar
45 Anil Kumar P. G., Aruna Jeyanthy P., and Devaraj D., Hybrid multi-objective method based on ant colony optimization and firefly algorithm for renewable energy sources, Sustainable Computing: Informatics and Systems. (2022) 36, 100810, https://doi.org/10.1016/j.suscom.2022.100810.
10.1016/j.suscom.2022.100810
Web of Science® Google Scholar
46 Suresh V., Janik P., Jasinski M., and Guerrero J. M., Zbigniew Leonowicz, Microgrid energy management using metaheuristic optimization algorithms, Applied Soft Computing. (2023) 134, 109981, https://doi.org/10.1016/j.asoc.2022.109981.
10.1016/j.asoc.2022.109981
Web of Science® Google Scholar
47 Li H. and Zhang H., Ant colony optimization-based multi-mode scheduling under renewable and nonrenewable resource constraints, Automation in Construction. (2013) 35, https://doi.org/10.1016/j.autcon.2013.05.030, 2-s2.0-84884501489.
10.1016/j.autcon.2013.05.030
Web of Science® Google Scholar
48 Vafaeipour M., Tran D.-D., Geury T., El Baghdadi M., and Omar H., Application of ant colony optimization for Co-design of hybrid electric vehicles, Intech Open Journal. (2021) https://doi.org/10.5772/Intechopen.97559.
10.5772/Intechopen.97559
Google Scholar
49 Tsuanyo D., Yao A., Aussel D., and Pierre N., Modeling and optimization of batteryless hybrid PV (photovoltaic)/Diesel systems for off-grid applications, Energy. (2015) 86, https://doi.org/10.1016/j.energy.2015.03.128, 2-s2.0-84931566187.
10.1016/j.energy.2015.03.128
Web of Science® Google Scholar
50 Azoumah Y. and Yamegueu D., Sustainable electricity generation by solar PV/diesel hybrid system without storage for off grids areas, IOP Conference Series: Materials Science and Engineering. (2012) 29, 012012.
10.1088/1757-899X/29/1/012012
Google Scholar
51 Lena G., Rural electrification with PV-hybrid systems: overview and recommendation for further deployment, 2013, International Energy Agency, Paris, France, Report IEA-PVPS T9.
Google Scholar
52 Yamegueu D., Azoumah Y., Py X., and Zongo N., Experimental study of electricity generation by Solar PV/diesel hybrid systems without battery storage for off-grid areas, Renewable Energy. (2011) 36, no. 6, https://doi.org/10.1016/j.renene.2010.11.011, 2-s2.0-78751704307.
10.1016/j.renene.2010.11.011
Web of Science® Google Scholar
53 Ghoneim A. A., Design optimization of photovoltaic powered water pumping systems, Energy Conversion and Management. (2006) 47, 1449–1463.
10.1016/j.enconman.2005.08.015
CAS Web of Science® Google Scholar
54 Ajan C. W., On the policy of photovoltaic and diesel generation mix for anoff-grid site: east Malaysian perspectives, Solar Energy. (2003) 74, 453–467.
10.1016/S0038-092X(03)00228-7
Web of Science® Google Scholar
55 Chedid R. and Chaaban F., Renewable-energy developments in Arab countries: a regional perspective, Applied Energy. (2003) 74, 211–221.
10.1016/S0306-2619(02)00148-4
Web of Science® Google Scholar
56 García-Valverde R., Miguel C., Martínez-Bejar R., and Urbina A., Life cycle assessment study of a 4.2 kWp stand-alone photovoltaic system, Solar Energy. (2009) 83, 1434–1445.
10.1016/j.solener.2009.03.012
CAS Web of Science® Google Scholar
57 Fleck B. and Huot M., Comparative life-cycle assessment of a small wind turbine for residential off-grid use, Renewable Energy. (2009) 34, 2688–2696.
10.1016/j.renene.2009.06.016
CAS Web of Science® Google Scholar

All articles

A Bottom-Up Approach to PV System Design for Rural Locality Electrification: A Case Study in Burkina Faso

Abstract

1. Introduction