The 6RUS parallel manipulator is a highly versatile and widely used robotic mechanism with six degrees of freedom. Its intricate kinematic structure and its capability to perform complex motion tasks have garnered significant research interest in recent years. The kinematic analysis of the 6RUS mechanism plays a crucial role in understanding its operational characteristics and optimizing its performance for various applications. In this paper, we present a state-of-the-art kinematic algorithm for the 6RUS parallel manipulator. Our algorithm is aimed at addressing the challenges associated with accurately determining the pose and motion of the end-effector relative to the base, considering the complexity of the mechanism’s architecture. By leveraging advanced mathematical modeling techniques and utilizing efficient computational algorithms, our proposed algorithm offers improved accuracy, efficiency, and robustness in determining the kinematic parameters of the 6RUS mechanism. The key contributions of this work include the development of a comprehensive forward and inverse kinematic model for the 6RUS parallel manipulator, incorporating the effects of joint constraints, singularities, and workspace limitations. We also present a detailed analysis of the algorithm’s performance in comparison to existing approaches, demonstrating its superiority in terms of computational efficiency and accuracy. The proposed kinematic algorithm holds significant potential for enhancing the design, control, and trajectory planning of 6RUS parallel manipulators. It provides a solid foundation for advanced applications such as robotic surgery, industrial automation, and virtual reality systems. The results presented in this paper contribute to the growing body of knowledge in parallel manipulator research and pave the way for future developments in the field.

1. Foreword

The solution of the positive kinematic problem starts from the simplified structure, and the special configuration is obtained by merging the joint points. Lin et al. completed the analysis of the 4-4 parallel mechanism [1]. In 1995, Innocenti obtained the positive solution of the 6-4 Stewart parallel mechanism [2]. Other Stewart platform topology simplification mechanisms include 3-6, 4-4, 4-5, 5-5 [3], and so on.

The 6RUS parallel manipulator, consisting of six revolute joints and a universal joint, has attracted significant research interest in recent years due to its versatile motion capabilities and potential applications in various fields. A mechanism model that considers the mechanism hinge parameters is shown in Figure 1. The kinematic analysis of the 6RUS mechanism plays a crucial role in determining its position, orientation, and motion. This section presents a comprehensive review of the recent research on kinematic algorithms for the 6RUS parallel manipulator, highlighting key advancements and contributions in this area.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

General 6R parallel mechanism.

1.1. Forward Kinematic Algorithms

The forward kinematic problem involves determining the position and orientation of the end-effector given the joint angles of the 6RUS mechanism. Several researchers have proposed efficient algorithms to solve this problem. Gutman derived a closed-form solution based on the geometric approach, providing explicit equations for calculating the end-effector pose [4]. Zhuang introduced an iterative method that iteratively refines the end-effector pose estimation using a geometric error minimization technique [5]. These algorithms enable accurate and computationally efficient computation of the forward kinematics of the 6RUS mechanism.

1.2. Inverse Kinematic Algorithms

The inverse kinematic problem of the 6RUS parallel manipulator involves determining the joint angles required to achieve a desired end-effector position and orientation. Researchers have developed various algorithms to address this problem. Praveen Kumar and Denis Ashok proposed an analytical approach based on the geometric relationship between the joint angles and the end-effector pose [6]. This algorithm provides closed-form solutions for the inverse kinematic problem of the 6RUS mechanism. Bai et al. introduced a numerical optimization-based method that utilizes a gradient descent algorithm to iteratively solve the inverse kinematic problem [7]. These algorithms offer efficient and accurate solutions for determining the joint angles of the 6RUS mechanism.

1.3. Singularity Analysis and Avoidance

Singularity analysis is crucial in studying the motion capabilities and performance limitations of the 6RUS parallel manipulator. Researchers have conducted extensive studies on singularity analysis and avoidance strategies for the 6RUS mechanism. Aginaga et al. presented a comprehensive analysis of singularities in the 6RUS mechanism [8], identifying critical configurations and providing guidelines for singularity avoidance. Dai et al. proposed a path planning algorithm that considers singularity avoidance to ensure smooth and continuous motion of the 6RUS manipulator [9]. These studies contribute to a better understanding of singularities and provide practical solutions to mitigate their adverse effects on the 6RUS mechanism’s performance.

1.4. Computational Techniques and Optimization Methods

Efficient computational techniques and optimization methods have been employed to enhance the performance and efficiency of kinematic algorithms for the 6RUS parallel manipulator. Symbolic computation techniques, such as those introduced by Yang et al., enable the derivation of closed-form solutions and simplify the kinematic analysis of the 6RUS mechanism [10]. Numerical optimization methods [11], such as the one proposed by Olaru et al., optimize the joint angles of the 6RUS mechanism to achieve a desired end-effector pose while considering practical constraints and performance criteria. These computational techniques and optimization methods contribute to improved accuracy, efficiency, and robustness of the kinematic algorithms for the 6RUS parallel manipulator.

1.5. Integration of Advanced Technologies

The integration of advanced technologies, such as machine learning, artificial intelligence, and computer vision, has shown great potential in advancing the kinematic analysis of the 6RUS parallel manipulator. Nabavi et al. proposed a machine learning-based approach to predict the kinematic behavior of the 6RUS mechanism [12], enabling real-time adaptation and optimization of its motion. Hodges et al. utilized computer vision techniques to enhance the accuracy and reliability of the forward and inverse kinematic algorithms [13] for the 6RUS manipulator (Figure 2). These integrations open up new possibilities for improved performance, adaptability, and automation of the 6RUS parallel manipulator.

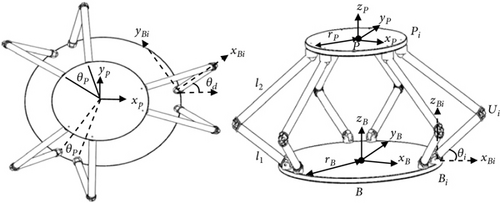
2. Kinematic Model of 6RUS Parallel Mechanism

The kinematics of a Stewart platform involve two main problems: inverse kinematics and forward kinematics. The inverse kinematic problem entails determining the position and posture of the moving platform based on the known values of the 6 drives. On the other hand, the forward kinematic problem involves obtaining the position and attitude of the moving platform when the values of the 6 drives are given.

Typically, a Stewart platform consists of 6 branch chains. In the context of inverse kinematics, these 6 branch chains can be treated as independent entities without any coupling. Consequently, the inverse kinematic solution for each branch chain is equivalent to that of a general 6R robot, where “6R” refers to a robot with 6 revolute joints [14].

By decoupling the branch chains, the inverse kinematic problem for a Stewart platform can be approached by considering the independent solutions for each individual branch chain. This simplifies the analysis by leveraging the well-established techniques and methodologies available for general 6R robots [15].

The kinematic model of the general 6RUS parallel mechanism is

(1)

indicates the position and posture of the moving platform. represents the transformation from the i − 1th coordinate system to the ith coordinate system on the jth branch. contains 4 parameters (θ_ji, s_ji, α_ji, and a_ji) include 3 constants and 1 variable. are a total of 24 parameters, θ_ji indicates the angle of rotation around the Z direction along the ith coordinate system on the jth branch chain. Only one variable is the active drive variable, and the remaining 5 are passive rotation variables. means the conversion from the 6th coordinate system to the M coordinate system of the moving platform on the jth branch chain, including 3 positions and 2 direction constants and a total of 5 parameters. The six branches include geometric structure parameters 34^∗6 = 204 items.

The position and posture of the moving platform are expressed by a dual quaternions, with 8 parameters.

(2)

Each branch chain contains 5 joint rotation angle variables θ_j2, θ_j3, θ_j4, θ_j5, and θ_j6, 6 branch chain variables, plus 8 unknown items on the moving platform, for a a total of 38 unknowns.

2.1. Elimination Processing

Multiply both sides of equation (1) by

at the same time to get

(3)

The left side of the branch chain equation includes 3 variables, θ_j2, θ_j3, and θ_j4. The right side includes 10 variables, θ_j6, θ_j5, b₀, b₁, b₂, b₃, e₀, e₁, e₂, and e₃.Take the left side of the j-branch (3) equation, and do the dual quaternion product and expand it.

(4)

The function of z(∗) on the right side of the equation is to treat dual quaternions as eight-dimensional vectors.

(5)

m_jk(k = 1…8) is a third-degree polynomial function with b₀, b₁, b₂, b₃, e₀, e₁, e₂, e₃, θ_j6, and θ_j5 as a variable. Because s_j3 > 0, B_j8×8 is an invertible matrix related to the structure and the known conditions_j3.

Simultaneous formulas (3), (4), and (5), we get

(6)

where

and y_jk, k = 1…8 are the third-degree polynomial functions with b₀, b₁, b₂, b₃, e₀, e₁, e₂, e₃, θ_j6, and θ_j5 as a variable, and

(7)

Consider the trigonometric constant formula.

(8)

Using (7) and (8) to calculate the Groebner basis and ignoring the higher-order identities, we can get

(9)

Substitute the third-degree polynomial of y_jk into the above 9 equations. From (9), we can get z_jk(θ_j5, θ_j6, b₀, b₁, b₂, b₃, e₀, e₁, e₂, e₃) = 0, j = 1.., 6; k = 1, ⋯, 9 is a 324-term algebraic polynomial with 10 variables up to 6th degree. The specific structure is as follows:

(10)

It contains 6 branches, each with 9 polynomials, for a total of 54 polynomials, where

is a 36-dimensional vector composed of the quadratic terms of 8 variables of the moving platform.

(11)

which is the coefficient matrix.

is a 9-dimensional vector. The two constraints of the mobile platform are

(12)

After the elimination process of the above-mentioned process, each branch has eliminated 3 variables, and a total of 18 variables have been eliminated. Now, the system of algebraic equations consists of only 20 variables.

2.2. Numerical Calculation and Solution

The positive solution of Stewart kinematics must satisfy a total of 56 algebraic polynomials (10) and (12). The optimization method is used here, and the objective function is

(13)

The solution of the 20-element nonlinear algebraic equation can be obtained

(14)

Judging by the value of the objective function corresponding to the obtained solution, if the value of the objective function is equal to or near 0, it means that b₀, b₁, b₂, b₃, e₀, e₁, e₂, and e₃ are the solution. Finally, substituting it into (15), the position and posture expressed by the homogeneous coordinate matrix can be obtained.

(15)

3. Example Calculation

In this study, the 6RUS Stewart platform is selected as the object of verification. During the design process, the rotating shafts of the branches are arranged to intersect vertically, with many structural parameters having nominal values of 0 and angle parameters set to 90 degrees. The proposed novel general algorithm in this paper addresses the challenge of nonequality between the actual structural parameters and their nominal values due to manufacturing errors. It is assumed that the length error is approximately 0.03 mm and the angle error is about 0.2 due to manufacturing variations.

The subsequent paragraph is aimed at validating the nominal structural parameters and then employing the assumed structural parameters to assess the performance of the general algorithm. Certain existing general 6R series algorithms are only applicable when the structural parameters are not equal to zero. They may encounter issues or yield significant computational errors when the structural parameters are zero or tend towards zero. However, the algorithm presented in this paper can be utilized for calculations involving both nominal and actual structural parameters.

3.1. Nominal Structural Parameters

Firstly, the branch coordinate system is established, and the components on the branch are sequentially numbered as 0, 1,…, 6 from the static platform to the moving platform. The local coordinate system fixed on each component is denoted as o_i − x_iy_iz_i, and it is referred to as the coordinate system. Moreover, coordinate systems o_B − x_By_Bz_B and o_P − x_Py_Pz_P are established at the center of the dynamic and static platforms, respectively. These coordinate systems are abbreviated as coordinate systems o_B − x_By_Bz_B and o_P − x_Py_Pz_P. Finally, the branch coordinate system of the parallel mechanism is established using the Denavit-Hartenberg (DH) method. The DH parameters for the branches are presented in Table 1.

Table 1. The DH parameters of each member at branched chain j.

Member no.	α_ji−1	s_ji	θ_ji
1	0	224.9757	θ_j1
2	90	0	θ_j2
3	90	s_j3 > 0	0
4	90	0	θ_j4
5	90	0	θ_j5
6	90	0	θ_j6

According to the definition of branched chain coordinate system, the transformation of branched chain J from coordinate system i-1 to coordinate system I is written by a dual quaternion, that is,

. According to Table 1, the data is substituted as follows:

(16)

Theoretically, all six branches are identical. However, due to engineering and manufacturing errors, each branch deviates from the ideal theoretical model. In this paper, a general algorithm is proposed to account for the variations in the DH parameters and engineering parameters of each individual branch. To conserve space, only one branch is analyzed in detail, but the remaining branches follow a similar approach.

Table 2 provides the position and directional parameters of the hinge points on the static platform. Table 3 provides the position and directional parameters of the hinge points on the Moving platform. Please refer to this table for detailed information.

Table 2. Position and direction in static platform coordinate system.

	x	y	z	X direction	Y direction	Z direction
Branched chain 1	-224.9757	-268.1156	0	0,0,1	0,1,0	-1,0,0
Branched chain 2	224.9757	-268.1156	0	0,0,-1	0,1,0	1,0,0
Branched chain 3	344.6827	-60.7769	0	0,0,1	-cos30°,-sin30°,0	sin30°,-cos30°,0
Branched chain 4	119.7071	328.8924	0	0,0,-1	-cos30°,-sin30°,0	-sin30°,cos30°,0
Branched chain 5	-119.7071	328.8924	0	0,0,1	cos30°,-sin30°,0	sin30°,cos30°,0
Branched chain 6	-344.6827	-60.7769	0	0,0,-1	cos30°,-sin30°,0	-sin30°,-cos30°,0

Table 3. Position and direction in moving platform coordinate system.

	x	y	z	X direction	Y direction	Z direction
Branched chain 12	0	-175.0000	0	1,0,0	0,1,0	0,0,1
Hinge 34	151.5544	87.5000	0	-sin30°,-cos30°,0	cos30°,-sin30°,0	0,0,1
Hinge 56	-151.5544	87.5000	0	-sin30°,cos30°,0	cos30°,-sin30°,0	0,0,1

The transformation from coordinate system B to coordinate system 0 on branched chain 1 is denoted as

, and the transformation from coordinate system 6 to coordinate system P is denoted as

(17)

The transformation from coordinate system B to coordinate system 0 on branched chain 2 is denoted as

, and the transformation from coordinate system 6 to coordinate system P is denoted as

(18)

The transformation from coordinate system B to coordinate system 0 on branched chain 3 is denoted as

, and the transformation from coordinate system 6 to coordinate system P is denoted as

(19)

The transformation from coordinate system B to coordinate system 0 on branched chain 4 is denoted as

, and the transformation from coordinate system 6 to coordinate system P is denoted as

(20)

The transformation from coordinate system B to coordinate system 0 on branched chain 5 is denoted as

, and the transformation from coordinate system 6 to coordinate system P is denoted as

(21)

The transformation from coordinate system B to coordinate system 0 on branch 6 is denoted as

, and the transformation from coordinate system 6 to coordinate system P is denoted as

(22)

It is known that

(23)

Calculate to get the posture of the moving platform

(24)

The result

of objective function is transformed into homogeneous coordinate matrix expression:

(25)

Substituting into the inverse solution of nominal structural parameters, it can see that the result of the positive solution is correct.

3.2. Algorithm Validation of General Structural Parameters

The branched structure of the parallel mechanism belongs to a general serial robot, and its inverse solution corresponds to the inverse solution of the general 6RUS serial robot. Initially, the inverse solution of the general 6RUS serial robot is obtained. The position and orientation of the moving platform with respect to the static platform are arbitrarily specified within the workspace, which is determined using the inverse solution algorithm of the general 6RUS serial robot. These values are then substituted into the forward solution program presented in this paper to calculate the position and orientation of the moving platform. For the purpose of this study, only certain parameters of branch 2 are modified, as indicated in Table 4, while the remaining branches remain unchanged.

Table 4. Assumed DH structure parameters of the branched chain 2.

Member no.	a_2i−1	α_2i−1	s_2i	θ_2i
1	0.01	0-0.1	224.9757 + 0.06	θ₂₁
2	0.02	90-0.2	0.05	θ₂₂
3	0.03	90-0.3	s₂₃ > 0	0.04
4	0.04	90-0.4	0.03	θ₂₄
5	0.05	90-0.5	0.02	θ₂₅
6	0.06	90-0.6	0.01	θ₂₆

The position and attitude of the moving platform are known and expressed by dual quaternion

(26)

From the inverse solution of the general 6RUS serial manipulator, it can be obtained that the actual drive of branched chain 2 is s₂₃ = 581.189.

The forward solution algorithm of the parallel mechanism is substituted into the driving parameters

(27)

Obtain the position and attitude of the moving platform

(28)

Be converted to homogeneous coordinate matrix expression

(29)

After calculation, the calculated position error is 0.0005 mm, and the accuracy can meet the needs of engineering practice.

4. Experimental Verification

Section 2.1 provides a verification of the forward solution algorithm using both theoretical data and a physical prototype. While theoretical data is used to validate the algorithm’s effectiveness, the real prototype (as depicted in Figure 3) is employed for practical verification purposes.

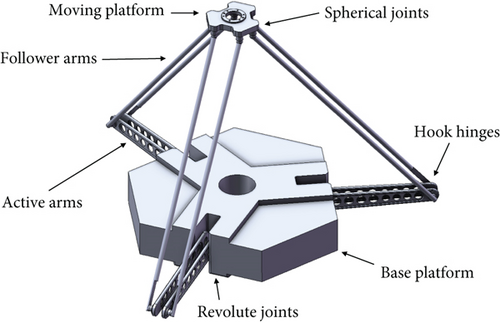
To account for measurement uncertainties, this experiment conducted a larger number of trials by generating 64 sets of postures. This approach is aimed at minimizing the influence of random factors. Given the infinite choices within the workspace, an orthogonal experiment was employed to select the 64 sets of postures evenly from the workspace for experimental purposes. The actual experimental prototype is shown in Figure 4.

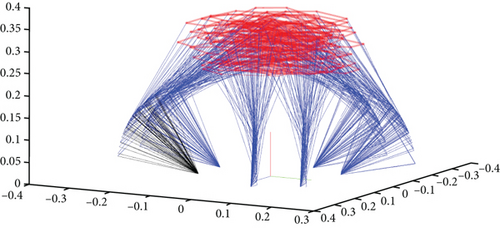
The specific methodology involved conducting an orthogonal test with eight levels and six factors on the moving platform of the parallel mechanism. This ensured that each factor spanned a wide range. The target data from Table 5 was used as input for the parallel mechanism, and each posture was measured using a laser tracker. Table 6 records a total of 64 poses. These posture data were expressed using a homogeneous coordinate matrix, with the accuracy sufficient to simultaneously record the corresponding driving parameters for each pose. This process is aimed at verifying the effectiveness of the forward-solution algorithm. The experimental results are shown in Figure 5.

Table 5. Eight levels and six factors (units in mm and degrees).

	X	Y	Z	A	B	C
1	-80	-80	250	5	3	3
2	-60	-50	260	3	2	2
3	-40	-20	280	1	1	1
4	-20	0	300	0	0	0
5	0	20	310	-1	-0.5	-0.5
6	20	40	320	-2	-1	-1
7	40	60	340	-4	-2	-2
8	80	80	350	-5	-3	-3

Table 6. L₆₄(8⁶) orthogonal test table.

	X	Y	Z	A	B	C
1	1	1	1	1	1	1
2	1	2	3	4	5	6
3	1	3	5	7	6	8
4	1	4	7	6	2	3
5	1	5	6	2	8	4
6	1	6	8	3	4	7
7	1	7	2	8	3	5
8	1	8	4	5	7	2
9	2	1	4	3	6	5
10	2	2	2	2	2	2
11	2	3	8	5	1	4
12	2	4	6	8	5	7
13	2	5	7	4	3	8
14	2	6	5	1	7	3
15	2	7	3	6	8	1
16	2	8	1	7	4	6
17	3	1	7	5	8	6
18	3	2	5	8	4	1
19	3	3	3	3	3	3
20	3	4	1	2	7	8
21	3	5	4	6	1	7
22	3	6	2	7	5	4
23	3	7	8	4	6	2
24	3	8	6	1	2	5
25	4	1	6	7	3	2
26	4	2	8	6	7	5
27	4	3	2	1	8	7
28	4	4	4	4	4	4
29	4	5	1	8	6	3
30	4	6	3	5	2	8
31	4	7	5	2	1	6
32	4	8	7	3	5	1
33	5	1	2	6	4	8
34	5	2	4	7	8	3
35	5	3	6	4	7	1
36	5	4	8	1	3	6
37	5	5	5	5	5	5
38	5	6	7	8	1	2
39	5	7	1	3	2	4
40	5	8	3	2	6	7
41	6	1	3	8	7	4
42	6	2	1	5	3	7
43	6	3	7	2	4	5
44	6	4	5	3	8	2
45	6	5	8	7	2	1
46	6	6	6	6	6	6
47	6	7	4	1	5	8
48	6	8	2	4	1	3
49	7	1	8	2	5	3
50	7	2	6	3	1	8
51	7	3	4	8	2	6
52	7	4	2	5	6	1
53	7	5	3	1	4	2
54	7	6	1	4	8	5
55	7	7	7	7	7	7
56	7	8	5	6	3	4
57	8	1	5	4	2	7
58	8	2	7	1	6	4
59	8	3	1	6	5	2
60	8	4	3	7	1	5
61	8	5	2	3	7	6
62	8	6	4	2	3	1
63	8	7	6	5	4	3
64	8	8	8	8	8	8

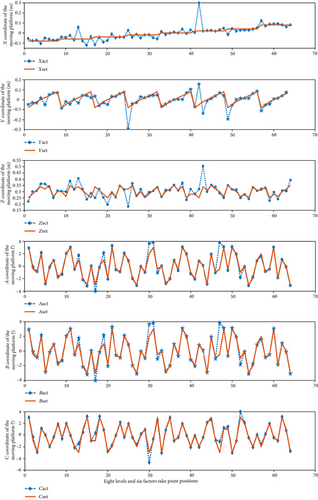
The experimental data consists of 64 groups, which record the six parameters of the parallel mechanism’s driving system and the pose parameters of the moving platform. For instance, in the 22nd group, the values 3, 6, 2, 7, 5, and 4 correspond to x = −0.1 m, y = 0.04 m, z = 0.26 m, A = −4 degrees, B = −0.5 degrees, and C = 0 degrees, respectively.

5. Conclusion

This paper focuses on the forward solution algorithm for the 6RUS parallel mechanism, which incorporates a Hooke hinge and a compound spherical hinge. The algorithm utilizes the D-H method and dual quaternion method, considering the pose parameters of the hinges and D-H parameters of all branch chains. It encompasses a total of 204 geometric parameters, providing a more accurate mathematical model compared to the conventional approach that considers only 42 geometric parameters. This algorithm enables the analysis of the geometric parameter influence on the pose of the moving platform, facilitating precise analysis, synthesis, kinematic calibration, and accurate motion simulation of the Stewart parallel mechanism.

The proposed algorithm treats the Stewart parallel mechanism as six branch chains that collectively support the platform. Each branch chain is regarded as a general 6-DOF serial robot with a single active kinematic pair driver. This approach introduces a novel and unified mathematical model for various parallel mechanisms, including the 6_6R structure, which was previously considered a distinct topological structure. The difference lies in the selection of active variables among the DH parameters of a specific branch chain, while the others remain as passive variables or constants. These constants can have nonzero or zero values, providing flexibility in the model representation.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This study was funded by the Tianjin Science and Technology Plan Project (21YFFCYS00080).

Open Research

Data Availability

Data can be obtained under application.

References

1 Lin W., Griffis M., and Duffy J., Forward displacement analyses of the 4-4 Stewart platforms, Journal of Mechanical Design. (1992) 114, no. 3, 444–450, https://doi.org/10.1115/1.2926572, 2-s2.0-0026914343.
10.1115/1.2926572
Web of Science® Google Scholar
2 Innocenti C., Direct kinematics in analytical form of the 6-4 fully-parallel mechanism, Journal of Mechanical Design. (1995) 117, no. 1, 89–95, https://doi.org/10.1115/1.2826122, 2-s2.0-0029274822.
10.1115/1.2826122
Web of Science® Google Scholar
3 Zhang Y., Liao Q., Su H., and Wei S., A new closed-form solution to the forward displacement analysis of a 5-5 in- parallel platform, Mechanism and Machine Theory. (2012) 52, 47–58, https://doi.org/10.1016/j.mechmachtheory.2012.01.003, 2-s2.0-84859598286.
10.1016/j.mechmachtheory.2012.01.003
Web of Science® Google Scholar
4 Gutman I., Geometric approach to degree–based topological indices: Sombor indices, MATCH Communications in Mathematical and in Computer Chemistry. (2021) 86, no. 1, 11–16.
Web of Science® Google Scholar
5 Zhuang H., Self-calibration of parallel mechanisms with a case study on Stewart platforms, IEEE Transactions on Robotics and Automation. (1997) 13, no. 3, 387–397, https://doi.org/10.1109/70.585901, 2-s2.0-0031169306.
10.1109/70.585901
Web of Science® Google Scholar
6 Praveen Kumar M. and Denis Ashok S., Artificial neural network based geometric error correction model for enhancing positioning accuracy of a robotic sewing manipulator, Procedia Computer Science. (2018) 133, 1048–1055, https://doi.org/10.1016/j.procs.2018.07.069, 2-s2.0-85051326344.
10.1016/j.procs.2018.07.069
Google Scholar
7 Bai Y., Luo M., and Pang F., An algorithm for solving robot inverse kinematics based on FOA optimized BP neural network, Applied Sciences. (2021) 11, no. 15, https://doi.org/10.3390/app11157129.
10.3390/app11157129
Google Scholar
8 Aginaga J., Zabalza I., Altuzarra O., and Nájera J., Improving static stiffness of the 6-R̲US parallel manipulator using inverse singularities, Robotics and Computer-Integrated Manufacturing. (2012) 28, no. 4, 458–471, https://doi.org/10.1016/j.rcim.2012.02.003, 2-s2.0-84857610491.
10.1016/j.rcim.2012.02.003
Web of Science® Google Scholar
9 Dai Y., Xiang C., Zhang Y., Jiang Y., Qu W., and Zhang Q., A review of spatial robotic arm trajectory planning, Aerospace. (2022) 9, no. 7, https://doi.org/10.3390/aerospace9070361.
10.3390/aerospace9070361
Web of Science® Google Scholar
10 Yang X., Wu H., and Yao Li B. C., A dual quaternion solution to the forward kinematics of a class of six-DOF parallel robots with full or reductant actuation, Mechanism and Machine Theory. (2017) 107, 27–36, https://doi.org/10.1016/j.mechmachtheory.2016.08.003, 2-s2.0-84988557282.
10.1016/j.mechmachtheory.2016.08.003
Web of Science® Google Scholar
11 Adrian O. D., Serban O. A., and Niculae M. C., Some proper methods for optimization in robotics, International Journal of Modeling and Optimization. (2017) 7, no. 4, 188–193, https://doi.org/10.7763/IJMO.2017.V7.582.
10.7763/IJMO.2017.V7.582
Google Scholar
12 Nabavi S. N., Akbarzadeh A., and Enferadi J., A study on kinematics and workspace determination of a general 6-P US robot, Journal of Intelligent & Robotic Systems. (2018) 91, no. 3-4, 351–362, https://doi.org/10.1007/s10846-017-0704-5, 2-s2.0-85030843609.
10.1007/s10846-017-0704-5
Web of Science® Google Scholar
13 Park J.-k., Inverse kinematics based on fuzzy logic and neural networks for the WAM-Titan II teleoperation system, 2007.
Google Scholar
14 Garziera R., Hajiyev E. T., and Riva R., Kinematic analysis of multi-loop spatial mechanisms: The five-loop case, Meccanica. (1991) 26, 101–110.
10.1007/BF00429875
Google Scholar
15 Jin Y., Chen I. M., and Yang G., Kinematic design of a 6-DOF parallel manipulator with decoupled translation and rotation, IEEE Transactions on Robotics. (2006) 22, no. 3, 545–551, https://doi.org/10.1109/TRO.2006.870648, 2-s2.0-33745137412.
10.1109/TRO.2006.870648
Web of Science® Google Scholar

All articles

A Forward Solution Algorithm of 6RUS Parallel Mechanism Based on Dual Quaternion Method

Abstract