Hepatitis B is one of the leading causes of morbidity and mortality, affecting hundreds of millions of people worldwide. Thus, this paper focuses on three control measures as the best way to intervene against the hepatitis B viral infection. These measures are condom use, testing and treatment, and vaccination to stop the disease from spreading over a community. The model comprises seven (7) compartments that include susceptible individuals, latent individuals, acute-infected individuals, chronic-infected individuals, infected by carrier individuals, recovered individuals from the disease, and the vaccinated population. We mathematically established a nonlinear differential equation to study the dynamics of the model. The disease-free equilibrium (DFE) and endemic equilibrium (EE) are reached. The basic reproduction numbers, , , and , determine the transmission of the disease and thus are gotten. We perform sensitivity analysis on the reproduction numbers to identify the factors that affect the reproduction numbers. The results of the sensitivity analysis paved a way for introducing a controlled system which was solved using Pontryagin’s maximum principle (PMP) and the optimality system got. The optimality system was then solved numerically using the forward and backward sweep approach, and graphs were generated, establishing the conditions for local and global stability of the disease-free equilibrium using the Routh-Hurwitz criterion and Castillo-Chavez approach, respectively. We also used Pontryagin’s maximum principle to determine the optimality system. The result of the analysis of the stability of the disease-free equilibrium states that hepatitis B virus can be completely wiped out if the rate of infection is kept at a number less than unity. A numerical simulation of the model was carried out and showed that hepatitis B virus transmission can best be controlled when condom use, testing and treatment, and vaccination are implemented.

1. Introduction

A viral infection called hepatitis B can cause both acute and chronic diseases and attack the liver. It is the most severe form of viral hepatitis and a significant global health issue. Around 780,000 individuals are expected to die each year because of the effects of hepatitis B, which include liver cancer and cirrhosis. The virus is extremely infectious and is spread by contact with an infected person’s blood or other body fluids. Hepatitis B virus has an average lifespan of seven days outside the body and is a significant occupational hazard for health workers [1]. Hepatitis means liver inflammation. A vital organ that processes nutrients, cleans the blood, and battles infections is the liver. When the liver is inflamed or impaired, its functions may be affected. Typically, a viral infection causes hepatitis, although other potential causes of hepatitis can exist, such as heavy use of alcohol, chemicals, certain drugs, and certain medical conditions. Acute hepatitis B usually takes 75 days to incubate, although it can range from approximately 30 to 180 days.

The host’s immune response controls liver damage when infected with HBV [1]. Results of HBV infection depend on host characteristics, such as age, gender, genetic background, coinfections, other coexisting diseases, and concomitant medicines, based on viral elements, such as the HBV genotype and viral DNA concentrations. Recent infections with HBV are characterized by the existence of HBsAg and immunoglobulin M (IgM) versus HBcAg in the blood. Patients are extremely HBeAgg-positive throughout the earliest stages of the infection’s replication phase. The initial infection may be symptomatic or asymptomatic, present as, with or without, acute (clinical) hepatitis jaundice, or it may contribute to hepatitis. Approximately 1 percent of acute hepatitis B, characterized by acute inflammation and hepatocellular necrosis, occurs 10 percent of infections in early childhood, perinatal infections (in kids 1-5 years of age), and 30 percent of late infections (in people > 5 years of age). The fulminant disorder progresses rarely in babies and teenagers, but 0.5 percent-1 percent exists. Acute hepatitis B cases in adults have a case-fatality rate of 20 percent to 33 percent. The rate of growth of chronic infection with HBV is inversely associated with age. About 80 percent to 90 percent of infants with perinatal infection develop the infection, 30-50 percent of children who are infected before 6 years of age, and <5 percent of otherwise occurring infections in adults that are well [2]. According to WHO [1], the two principal ways that hepatitis B is spread are horizontally(infected blood) or during pregnancy and childbirth (perinatal transmission), especially during the first 5 years of life from an infected child to an uninfected child. Infants who are infected by their mothers or who are under the age of five frequently get persistent infections. Contaminated bodily fluids like saliva, menstrual, vaginal, and seminal secretions can spread hepatitis B through needle stick damage, tattooing, piercing, and exposure. Hepatitis B can be sexually transmitted, especially in heterosexuals who have several partners and unvaccinated men who have sex with other men or who have sexual intercourse with sex workers.

When newly infected, most individuals do not experience any symptoms. Some individuals, however, have an acute disease with symptoms that extend for several weeks. These symptoms include skin and eye yellowing (jaundice), dark urine, extreme fatigue, nausea, and vomiting. Acute liver failure, which may lead to death, can occur in a small subset of individuals with acute hepatitis. Some patients who have the hepatitis B virus may also develop a persistent liver infection, which can later turn into cirrhosis (liver scarring) or liver cancer. The risk of developing a chronic infection varies with infection age and is highest in infants and young children. 90 percent of newborns and 25 to 50 percent of kids between the ages of 1 and 5 will continue to have chronic HBV infections. In contrast, about 95 percent of individuals fully recover from HBV infection and do not develop a chronic infection. Getting vaccinated is the greatest method to avoid hepatitis B [1]. It is possible to treat hepatitis B virus infection. Typically, therapy is permanent, but acute hepatitis B disease does not have any clear treatment. Providing adequate nutrition and replacing fluids lost from vomiting and diarrhea supports therapy and symptom alleviation, which are the foundation of clinical management [3]. Antiviral treatment for chronic infection with HBV should decrease morbidity and mortality because of progressive liver disease. To prevent the negative effects of drug resistance, the WHO advises using antiviral medications with a high barrier to resistance (either tenofovir or entecavir) as the preferred first-line treatment [4]. Chronic HBV infection can be treated, although it is not curative [5]. It can prevent or postpone the development of cirrhosis, lower the risk of developing hepatocellular carcinoma (HCC), and increase survival through long-term viral suppression. Although tenofovir is commonly available as part of fixed drug formulation antiretroviral regimens at a cheap cost, therapy for HBV infection is not always easily accessible in resource-constrained situations. Evidence suggests that antiviral therapy administered during the third trimester of pregnancy can reduce maternal viral loads and the risk of perinatal transmission of HBV from mothers with very high viral loads [6, 7]. However, evidence suggests that antiviral therapy administered during the third trimester of pregnancy can reduce maternal viral loads and the risk of perinatal transmission of HBV from mothers with very high viral loads [4].

According to WHO in 2015, statistically, about 325 million people worldwide were affected by viral hepatitis, with 257 million people living with hepatitis B and 71 million people living with hepatitis C being the two major killers of the five types of hepatitis. In 2015, 1.34 million deaths were because of viral hepatitis. To inspire further action toward the health targets in the 2030 Sustainable Development Goals, World Hepatitis Day 2017 will be observed under the theme “Eliminate Hepatitis.” In 2016, The World Health Assembly approved WHO’s initial global health sector strategy on viral hepatitis to aid nations in stepping up their responses. According to recent WHO data, over 86 percent of the countries under review have established national goals for the eradication of hepatitis, and over 70 percent have developed national hepatitis policies that include access to quality services for prevention, diagnosis, treatment, and care. In addition, nearly half of the countries surveyed are targeting elimination by ensuring equal access to care for hepatitis. But the WHO is worried that change needs to be sped up. In Africa, a hidden epidemic that affects over 70 million people is hepatitis B. Nine out of ten infected individuals have never undergone testing because of a lack of knowledge and inadequate access to testing and treatment. To meet the worldwide eradication goals by 2030, it is imperative to close the most critical gap in testing and treatment coverage. Viral hepatitis B and C should be promptly diagnosed and treated to prevent death. Considering the aforementioned findings, we suggest the best preventative measures for hepatitis B infections with saturation incidence. Many researchers have established mathematical models to describe the dynamics of the spread of hepatitis B virus infection.

For instance, [8] developed a hepatitis B virus transmission model. Acute infectious and chronic infectious stages are the two categories used to categorize the infectious compartments. As a result, the overall population is split into four groups: susceptible, acutely infected with hepatitis B, chronically infected with hepatitis B, and recovered individuals. Following the model’s formulation, they determine the basic reproduction rate and the disease-free and endemic equilibrium. They also proved that, under certain conditions, the model is both locally and globally stable. To construct a control strategy, three time-dependent control variables are used, such as isolation, treatment, and vaccination. This control technique is aimed at increasing the number of recovered individuals while reducing the number of infected people. To describe numerical simulations and validate all the analytical findings, they finally adopted a numerical approach.

A fractional derivative analysis of hepatitis B disease is developed by the authors [9, 10] by studying a new system of equations in the sense of the Atangana-Baleanu Caputo fractional order derivative (ABC). The proposed method has five distinct compartments, such as the susceptible population, acute infections, chronic infections, the immunized population, and the vaccinated population. Using some well-known results from the fixed point theory, these authors found the Ulam-Hyers type stability and qualitative analysis of the candidate solution. They also established the deterministic stability of the proposed system. These authors analyzed a noninteger order model for hepatitis B (HBV) based on a fractional order derivative of the Caputo singular type. Thus, they could analyze the proposed system to get an approximate or semianalytical solution using the Laplace transform. Similarly, Adomian polynomial decomposition techniques of the nonlinear terms and some homotopy perturbation techniques (HPM) are also studied by these authors.

[11, 12] proposed a model of the hepatitis B epidemic that describes the dynamic features of both acute and chronic HBV. Based on a few characteristics of how the virus spreads, they developed a mathematical model for the dynamics of HBV. The host population is identified by being separated into five groups, namely, susceptible persons, infected individuals, acutely infected individuals, chronic HBV-positive individuals, and individuals who have recovered from infection and have lifetime immunity. The model was examined for potential stable states, and the threshold number was calculated. The model yielded two equilibrium points, namely, disease-free equilibrium and endemic equilibrium. It was established that both of the model equilibrium points are globally stable under specific circumstances. The Lyapunov function theory method was used to determine the global stability of DFE, whereas the geometrical method was employed to determine the global stability of the EE. It is shown that the model displays a backward bifurcation. Two-time dependent controls, such as vaccination and treatment, were adopted to combat the virus. Pontryagin’s approach was used to successfully reduce both acute and chronic HB infections as part of the plan. Finally, some simulations that show the effectiveness of the controls were shown. It was determined that hepatitis B could be eliminated from any population by using such a long-term management plan.

In the “Methods” section, we have established and described the mathematical model. In the “Analysis of the model” section, we assumed constant control for the control parameters. The positivity of solution was proven to be positive, and the system of nonlinear differential equations was well-posed epidemiologically and mathematically. We could determine the fundamental reproduction number by using the next-generation method. The balance between the endemic and disease states was established. The disease-free is locally asymptotically stable when and unstable if . The global stability of the disease-free is proved globally asymptotically stable when the associated reproduction number . While the disease will completely disappear into a stable equilibrium, it will persist and spread endemic in an unstable equilibrium. Using Pontryagin’s maximum principle, we looked into the ideal threshold needed to stop the spread of the hepatitis B viral infection in a community. “Results” based on numerical findings, the combination of condom use for prevention, testing, treatment, and vaccine is the most effective method for controlling the disease. Finally, we conclude this research work in the “Conclusion” section.

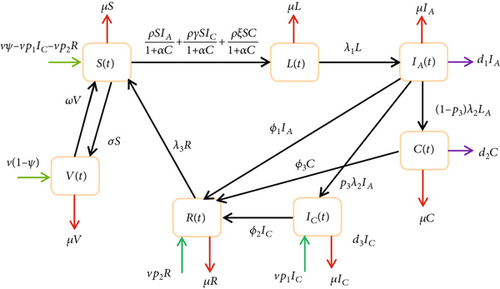
2. Formulation of Hepatitis B Model

In this work, we show the hepatitis B virus transmission dynamics together with three control strategies. We divided the entire population into seven compartmental classes, including susceptible individuals at time t, denoted by S(t), the latent class L(t), acutely infected individuals I_A(t), chronically infected individuals I_C(t), carriers C(t), recovered with permanent immunity R(t) and vaccinated individuals V(t).

(1)

The susceptible individual compartment increases because of recruitment at the birth of newborns that are not vaccinated νψ − νp₁I_C − νp₂R because of vaccination σS, where σ is the vaccination rate and a rate of loss of immunity among those who have recovered λ₃. The susceptible class reduces by a function (ρI_A + ργI_C + ρξC)S/1 + αC. Where ρ is the transmission rate of hepatitis B, γ is the modification parameter that accounts for higher infectiousness of I_C compared to I_A and C, ξ is the modification parameter that accounts for the infectiousness level of the carrier individuals, and α is the saturated parameter. The susceptible class also decreases due to natural death at the rate μ.

(2)

The population of latently infected individuals increases because of new infection at a rate (ρI_A + ργI_C + ρξC)S/1 + αC. The population decrease because of the progression of latently infected individuals to acutely infected individuals at a rate λ₁ and natural death occurs frequently at μ. The population of acutely infected individuals increases because of progression from latent class. The population decrease because of progression into the chronically infected class at a rate p₃λ₂, where p₃ is the proportion that becomes chronically infected, and λ₂ is the progression rate, progression into carrier class at a rate (1 − p₃)λ₂ and treatment of acutely infected individuals at a rate ϕ₁. The population of chronically infected individuals increases because of the proportion of acutely infected individuals I_A becoming chronically infected I_C, where p₃ is the progression rate, and it increases by a fraction of newborns that are chronically infected. The chronically infected class decreased because of treatment, and mortality rates were because of disease and natural causes. The carrier individuals increase from the acutely infected class because of the proportion of acutely infected at rate (1 − p₃)λ₃ and also reduce because of disease-induced death, natural death, and treatment rate. The recovery class increases because of treatment from acutely infected, chronically infected, and carrier individuals’ class, and it is increased by a fraction of newborns at the rate vp₃. It is reduced by the loss of immunity at the rate λ₃R and natural death rate.

We, therefore, present the equations for the model with constant controls.

(3)

with the initial conditions

(4)

The corresponding classes are combined together to provide the dynamics of the system’s overall population (3) that yields

(5)

2.1. Basic Properties

Theorem 1. Let the initial solution set S(0), L(0), I_A(0), I_C(0), C(0), R(0), (0), V(0) > 0 be a nonnegative initial condition, and then, system (2) has a nonnegative solution S(t), L(t), I_A(t), I_C(t), C(t), R(t), V(t) > 0 for all t > 0. Moreover, limsup_t⟶∞N(t) ≤ ν/μ. In addition, if N(0) ≤ ν/μ, then N(t) ≤ ν/μ if the feasible region for system (3)

(6)

is attractive and positively invariant with regard to the system (3).

Proof. From the first equation of system (3), we have the following

(7)

From time t = 0 to t = t, we are integrating (+ve of sp) to get

(8)

This means that

(9)

We used a similar approach to prove that L(t), I_A(t), I_C(t), R(t), V(t), V(t) > 0 remain nonnegative for all t > 0. The second portion of the theorem, which states that model system (3) is positively invariant, is proved using Equation (5) so that N(t) ≤ ν/μ + (N(0) − ν/μ)exp^−μt. It follows that as t⟶∞N(t) ≤ ν/μ. Furthermore, if N(0) ≤ ν/μ, then N(t) ≤ ν/μ. This establishes that Ω is the manifold on which the population has nonzero size.

Thus, it proves the boundedness of the solutions inside Ω. Hence, the solutions to the system (3) are attractive in a region and positively invariant Ω. We notice that system (3) is feasible biologically and mathematically well-posed in Ω from Theorem 1.

3. The Hepatitis B Model Analysis

This section establishes the hepatitis B-free equilibrium state and hepatitis B present equilibrium state, and the basic reproduction number is obtained and carried out stability analysis.

3.1. Equilibrium Points

The system (3) equilibrium points are established by the setting of the system (3) to zero to get

(10)

In the absence of hepatitis B virus infection, the system (3) has a steady state, and this steady state is termed hepatitis B-free equilibrium. We calculated and evaluated the Jacobian of the system (3) at the hepatitis B-free equilibrium to determine the type of stability of the hepatitis B-free equilibrium. The signs of the Jacobian’s eigenvalues are used to determine the local stability of the hepatitis B-free equilibrium. The system’s hepatitis B-free equilibrium (3) is

(11)

This only shows that the susceptible individuals’ recruitment and mortality rates change proportionally in the absence of hepatitis B disease.

For the second equilibrium point, we let

be the hepatitis B present equilibrium of the model (2). At the equilibrium state, we let

be the forces of infection and

, solving system (3) at steady state yields

(12)

where

(13)

3.2. Basic Reproduction Number

The term “basic reproduction number” refers to the typical number of secondary infections induced by one infectious person when the entire population is susceptible,

. The hepatitis B virus epidemiological threshold is represented by the symbol

, and ρ denotes the dominant eigenvalue. To determine the basic reproduction number of the system (3), we implemented the strategies in [13] to get

(14)

New infection terms and transition terms are, respectively, contained in the matrices F and V in the system (3). At hepatitis B-free equilibrium, the Jacobian matrices of F and V are evaluated, producing the following results.

(15)

Therefore, system (3) has a basic reproduction number provided by

(16)

where

(17)

3.3. Local Stability of the Hepatitis B Disease-Free Equilibrium

Theorem 2. The hepatitis B disease-free equilibrium of system (3) is locally asymptotically stable if and unstable if otherwise.

Proof. The Jacobian matrix of the system (3) at hepatitis B-free equilibrium J(E⁰) is be given by

(18)

where

(19)

The characteristics polynomial J(E⁰) for (18) is hereby defined as follows:

(20)

where the coefficients of (18) are given as

(21)

Using the Routh-Hurwitz criterion, which stipulates that all polynomial (Equation (20)) roots have a negative real component if and only if the coefficients are positive and the determinant of the matrices H_i > 1 for i = 1, ⋯7. It is clear that D₁ > 0. Therefore, if D_j > 0 for j = 2 ⋯ 7 and since the hepatitis B free equilibrium is locally asymptotically stable, the Routh-Hurwitz conditions for the 7th-order characteristics polynomial in (20) are satisfied, and we conclude the hepatitis B free equilibrium is locally asymptotically stable (LAS).

3.4. Global Asymptotic Stability for Hepatitis B

The strategy used in [14] is to examine the global asymptotic stability (GAS) of the hepatitis B-free equilibrium for the model (3).

Lemma 3. Let system (3) be in the form

(22)

where X = (S, V, R) and Z = (L, I_A, I_C, C) and components of X ∈ ℝ³ represent the population that are not infected and components of Z ∈ ℝ⁴ represent the population that are infected [14]. Considering the hepatitis B-free equilibrium E⁰ = (X⁰, 0), where

(23)

The following requirements must be satisfied to provide global asymptotic stability: H₁ : dX/dt = F(X⁰, 0), X⁰ is (GAS).

for (X, Z) ∈ Ω, where P = D_zG(X⁰, 0) is an M-matrix and Ω is the biologically feasible region. Hence, E⁰ is (GAS) if .

Theorem 4. The hepatitis B-free equilibrium of system (3) is (GAS) if and unstable if otherwise.

Proof. We have to establish that the conditions (H₁) and (H₂) hold when . For the uninfected population, we have

(24)

and X ∈ ℝ³ denotes the infected compartments in the model (3), and we have

(25)

where

(26)

Thus,

(27)

Therefore, Since S/1 + αC ≤ S⁰, we have . The global stability of X⁰ = (ν(σω + μω + μ²ψ + σμψ − σψω)/μ(μ + ω)(σ + μ + ω), 0, 0, 0, 0, 0, ν(σ + μ)(1 − ψ)/μ(μ + σ + ω)) of the system dX/dt = F(X⁰, 0) is easy to verify. Therefore, X⁰ is globally asymptotically stable if . This completes the proof.

3.5. Hepatitis B Model Sensitivity Analysis

In order to determine how these parameters affect the spread of hepatitis B, this subsection investigates on how the system (3) parameters affect the basic reproduction number . The sensitivity index was got by partially differentiating regarding the model (3) parameters. For example, we develop a formula to get the sensitivity index of all the basic parameters in this work, which is defined as ψ that is . The same applies to all model (3) parameters. The result is presented in Table 1.

Table 1. Sensitivity indices for the hepatitis B model

Parameter	Baseline values	Sensitivity index	Sensitivity index	Sensitivity index
ν	0.0121	1	1	1
σ	0.9	-0.9816	-0.9816	-0.9816
ω	0.01	0.9557	0.9557	0.9557
ψ	0.05	0.0335	0.0335	0.0335
p₁	0.11	—	1	—
p₂	0.1	—	—	—
p₃	0.33	—	1	-0.4925
ρ	0.8-20.49	1	1
γ	0.01	—	1	—
ξ	0.1	—	—	1
ϕ₁	0.05	-0.0122	-0.0122	-0.0122
ϕ₁	0.6	—	-0.8897	—
ϕ₃	0.98	—	—	-0.9923
d₁	0.04	-0.0098	-0.0098	-0.0098
d₂	0.0007	—	—	0.0007
d₃	0.00054	—	-0.0080	—
λ₁	6 per year	0.0012	0.0012	0.0012
λ₂	4 per year	-0.9764	—	0.0237
λ₃	0.03-0.06	—	—	—
α	0.75	—	—	—

We observe that the parameters ν, ω, ψ, p₁, p₃, ρ, γ, ξ, and λ₁ have positive sensitive indices; this means that as the parameter is increased, the basic reproduction numbers , , and rise. The remaining parameters, σ, ϕ₁, ϕ₃, d₁, d₂, and λ₁, have negative values which implies that , , and decrease for higher values of the parameters.

4. Optimal Control of the Hepatitis B Model

We must determine the best amount of effort that will be required to control the spread of the disease if the eradication of hepatitis B virus infection is not workable owing to economic or social and environmental factors. From Figure 1, we injected the controls, and we come up with a changed model as illustrated in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram for the model with constant controls.

We added control interventions to the system (3) in order to get

(28)

We present the objective functional J for the model with three (4) control strategies. The controls included are, namely, vaccination, prevention through condom use, testing, and treatment. Thus, we will examine the optimal level of effort needed to control the transmission of the hepatitis B virus at a minimal cost. This is done by maximizing the objective function, which is formulated in line with the derivation of [20].

(29)

Given the objective function, where t_f is the final time, the coefficients A₁, A₂, A₃, B₁, B₂, and B₃ are the positive weights to balance the factors. Our goal in controlling the transmission of the hepatitis B virus is to minimize the numbers of acutely infected individuals I_A(t) and chronically infected individuals I_C(t) and carry C(t), while minimizing the cost of control of implementing and I_A(t) representing vaccination, prevention through condoms use, testing, and treatment, respectively. Thus, we look for the best possible control

such that

where U represents the set of measurable functions defined from [0, t_f] onto [0, 1]. The necessary conditions that an optimal control must satisfy were derived from Pontryagin’s maximum principle [21], and the following set of differential equations are satisfied by the existence result for optimal control from the adjoint variable of the state variables. This principle converts the system (28) into a problem of minimizing point-wise a Hamiltonian H, regarding (u₁, u₂, u₃). The Hamiltonian is

(30)

where

, and λ_V are the costate or adjoint variables satisfactory.

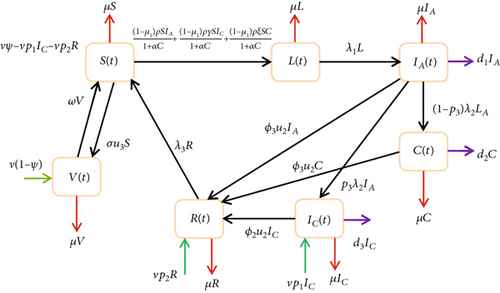
Theorem 5. Let , , and be optimal controls and S, L, I_A, I_C, C, R, and V be the solutions of the optimal control problem ((28) and (29)) that minimize J(u₁, u₂, u₃) over U, and then, there are adjoint variables λ_S, λ_L, , , λ_C, λ_R, and λ_V satisfying

(31)

where S, L, I_A, I_C, C, R, and V are the adjoint variables, and the controls

, and

obey the optimality conditions.

(32)

Proof. To get the differentiable equations governing the adjoint variables, we evaluated the differentiated Hamiltonian functional at the optimal control to prove the above-stated theorem. Hence

(33)

With requirements for transversality

(34)

Additionally, the optimal functions , , and satisfy

(35)

Therefore,

(36)

Under [22], we conclude that the a priori boundedness of the state system, the adjoint system, is how we could establish the uniqueness of the optimality system based on standard control arguments including the bound on the controls (33) and (34). The length of the time [0, t_f] is constrained in order to ensure the uniqueness of the optimality system [5].

5. Numerical Simulations

The effects of interventions on the spread of hepatitis B in a population are examined in this section. The forward and backward Runge-Kutta scheme is used in [5] to solve the numerically for the optimal control problems (28) and (29). To reduce the number of acute, chronic, and carrier hepatitis B virus infections, we apply the variables and parameter values in Tables 2 and 3. The initial values of the variables are given in Table 4. We set the time scale for fifty years. The results are shown in Figures 3–6 using the following techniques:

(I)
Strategy A. Use of condoms only as a control strategy in the infected population in latent stages of hepatitis B virus infection
(II)
Strategy B. Use of testing and treatment only for infected individuals in acutely, chronically, and carrier infection
(III)
Strategy C. Use of vaccination only as a control strategy in susceptible populace and newborn infants
(IV)
Strategy D. Use of condoms and testing and treatment only as a control strategy in infective individuals in latent, acute, chronic, and carriers of hepatitis B virus infection
(IV)
Strategy E. Use of condoms and vaccination only in susceptible, latent, and vaccinated populations of hepatitis B virus infection
(IV)
Strategy F. Use of a combination of testing, treatment, and vaccination in susceptible populations and treatment only in an infected population with acutely, chronically, and carriers of Hepatitis B virus infection
(IV)
Strategy G. Use of condoms, testing and treatment, and vaccination in susceptible individuals and treatment in an infected population with acutely, chronically, and carriers of hepatitis B virus infection

Table 2. Hepatitis B model variables.

Variable	Description
S(t)	Susceptible individuals at time t
L(t)	Latent individuals at time t
I_A(t)	Acute infection individuals at time t
I_C(t)	Chronic infection individuals at time t
C(t)	Carrier infection individuals at time t
R(t)	Recovered individuals from hepatitis B virus infection at time t
V(t)	Vaccinated individuals at time t

Table 3. Parameter values and notation for the hepatitis B model.

Parameters	Description	Values	Source
ν	Birth rate	0.0121	[15]
μ	Natural death rate	0.0069	[15]
σ	Vaccination rate	0.9	[16]
ω	Vaccination wine rate	0.01	[16]
ϕ	Proportional of unvaccinated infant	0.05	[16]
p₁	A fraction of new born from recovered	0.11	[17]
p₂	A fraction of new born from recovered	0.1	[17]
p₃	Progression of acute infected that progresses to chronic infected	0.33	[16]
ρ	Transmission rate of hepatitis B virus	0.8-20.49	[18]
γ	Modification parameter depicting infectiousness of chronic HB virus	0.01	Assumed
ξ	Modification parameter depicting infectiousness of chronic HB virus	0.1	Assumed
ϕ₁	Testing and treatment rate of acute infection	0.05	[8]
ϕ₂	Testing and treatment rate of chronic infection	0.06	[8]
ϕ₃	Testing and treatment rate of carrier infection	0.98	Assumed
d₁	Disease-induced death in acute infection	0.04	[8]
d₂	Disease-induced death in chronic infection	0.0007	Assumed
d₃	Disease-induced death in carrier infection	0.00054	[8]
λ₁	Rate of moving from latent to acute infection	6 per year	[19]
λ₂	Rate at which individual acute infection class	4 per year	[19]
λ₃	Loss of recovery rate	0.3-0.6	[19]
α	Saturated incidence	0.75	Assumed
A₁	Weight factor for acute infection	0.01	[1]
A₂	Weight factor for chronic infection	0.05	[1]
A₃	Weight factor for carrier infection	0.05	[8]
B₁	Weight factor for the control u₁	2.0	Assumed
B₂	Weight factor for the control u₂	1.5	[8]
B₃	Weight factor for the control u₃	2.7	[8]

Table 4. Initial values for the variables.

Initial variables	Value	Source
S(0)	0.493	[23]
L(0)	0.0035	[23]
I_A(0)	0.0035	[23]
I_C(0)	0.007	[23]
C(0)	0.11	[24]
R(0)	0.001	Assumed
V(0)	0.352	Assumed

5.1. Strategy A: Use of Condom Only

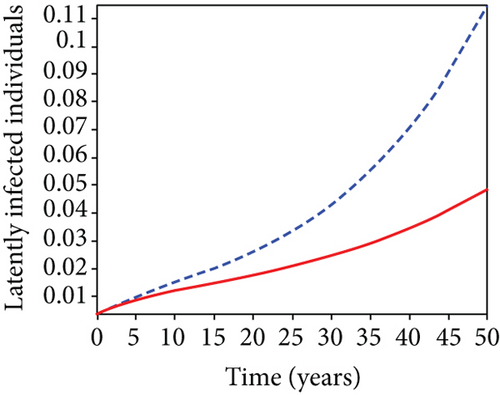
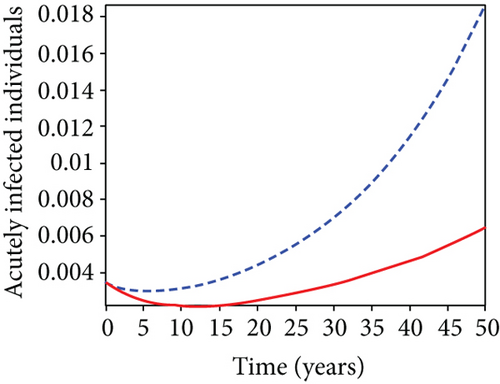
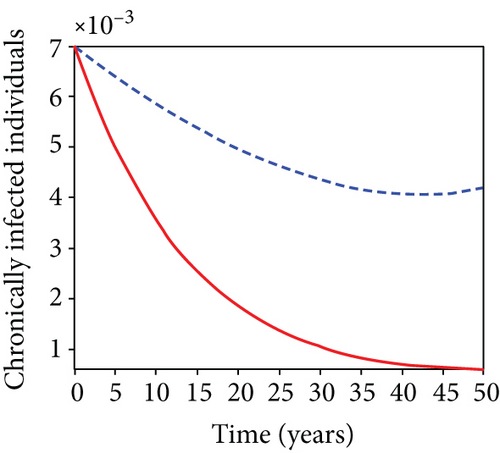
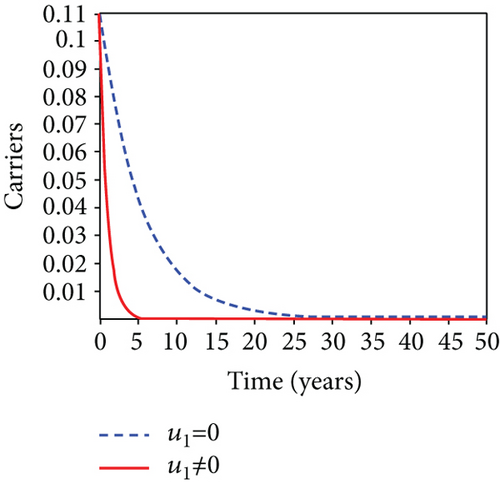
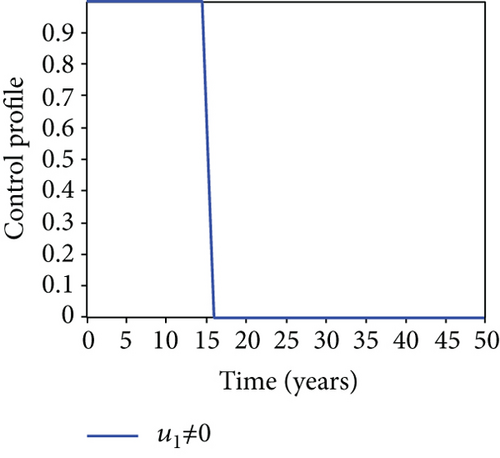
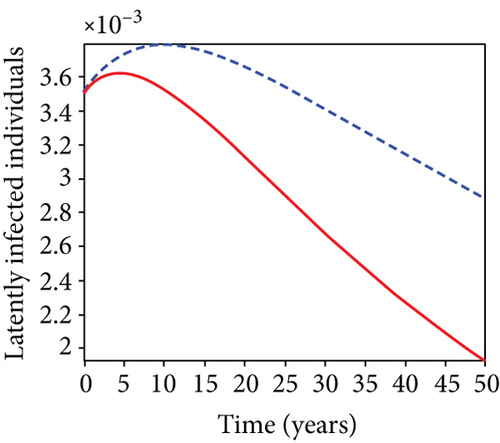
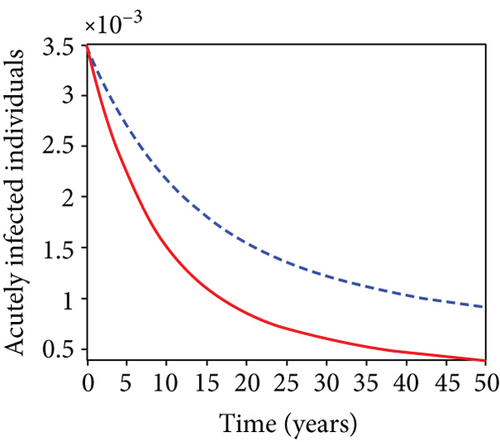
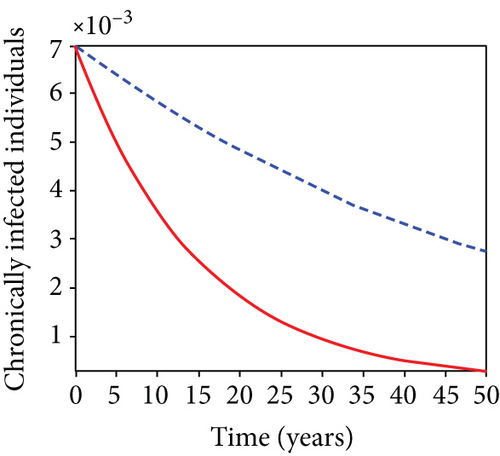
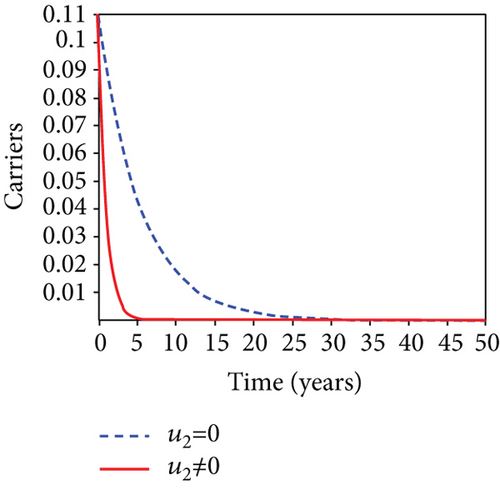
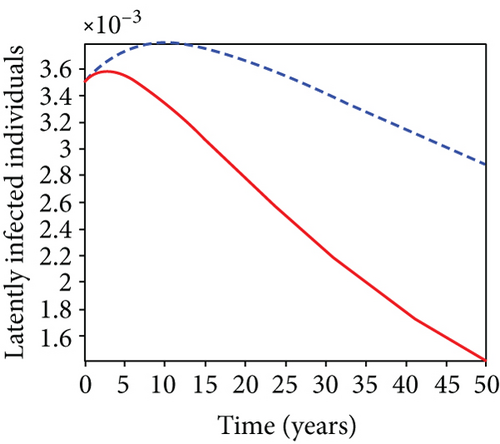
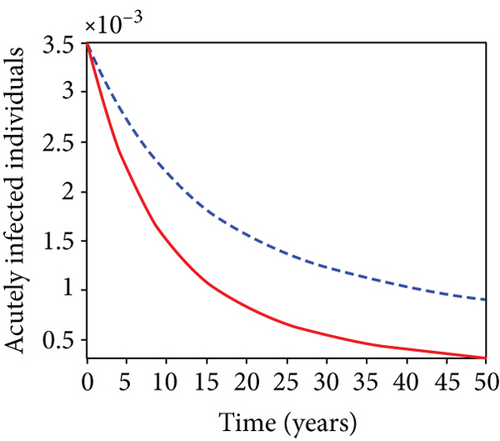
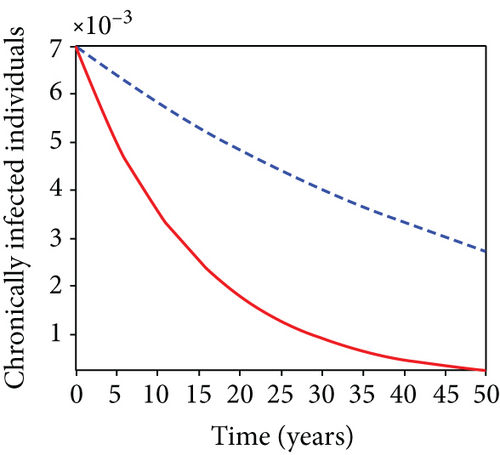
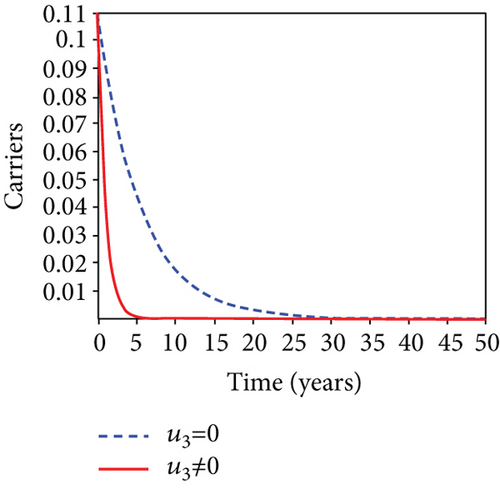
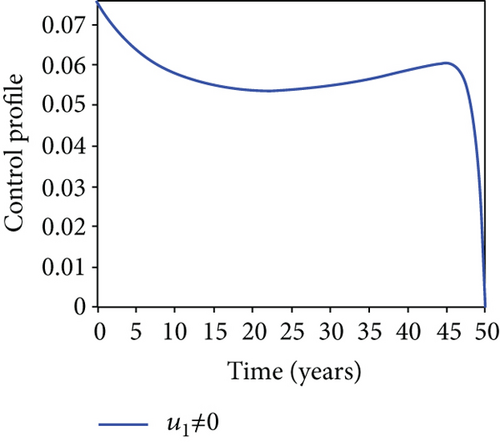
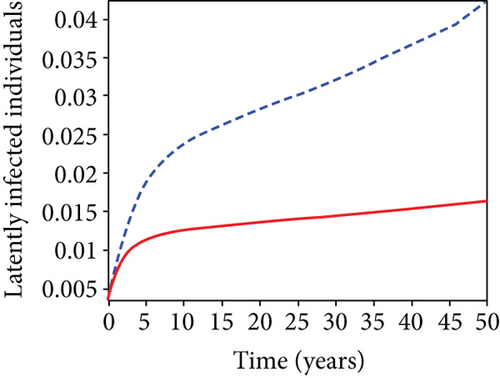
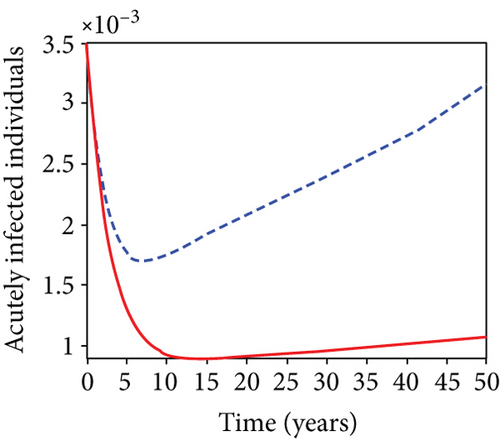
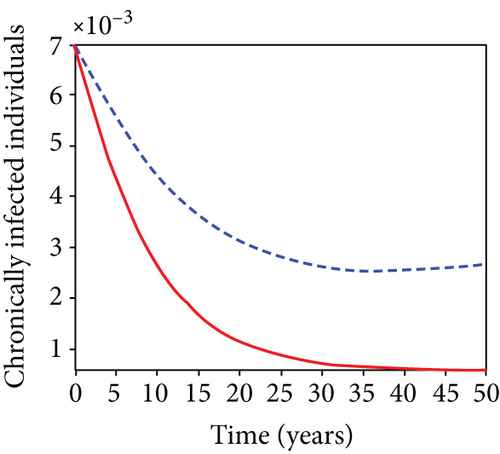
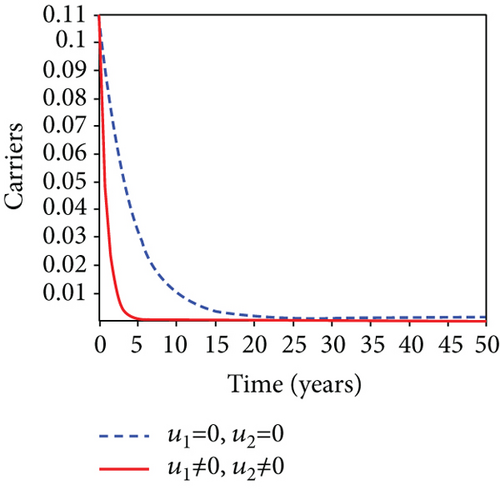
When condoms are used (u₁) as an individual defense against hepatitis B virus infection in the population, we describe the simulation of an optimum control system (28) for strategy A to maximize the objective functional J, while we set (u₂) and (u₃) to zero. Figures 3(a)–3(e) show a significant difference in the population at various infection levels, with optimal strategy (u₁ ≠ 0) when compared to the population without optimal strategy control (u₁ = 0). We observed in Figure 3(a) that because of the control strategy, the number of latently L infected individuals with HBV decreases, while the population increases when there is no control. Similarly, Figure 3(b) shows a decrease in the presence of control strategy for acutely I_A infected individuals with HBV in the population, but the uncontrolled population in Figure 3(b) resulted in increased endemic foci of the disease. In Figure 3(c), we see that the population of chronically I_C infected individuals with HBV also reduced due to control while the population increases in the absence of control. In Figure 3(d), the population of carrier individuals decreases because of the practice of condom use as a control strategy, while the population continued to grow in the absence of control. The control profile in Figure 3(e) revealed that using a condom only as a strategy for preventing HBV infection is at the upper bound of t_f = 50 years before it gradually dropped to the lower bound. The infection stage of HBV in both the population of latently, acutely, and chronically infected and carriers yielding the strategy is not the best result when the condom is only used as a control strategy.

5.2. Strategy B: Use of Testing and Treatment Only

This strategy shows the simulation of optimal control system (28) for testing and treatment (u₂); as the only control strategy in the infected population was used to optimize objective functional J, we set the other controls; u₁ is the use of condom and vaccination u₃ to zero. This simply means that only the infected population was considered for testing and treatment. In Figure 4(a), the findings reveal a substantial difference in acutely infected, chronically, and carrier individuals with optimal strategy compared to the infected population with HBV without control. This strategy shows that effective testing and treatment have a significant impact in reducing the disease among infected individuals in the population. Figure 4(b) demonstrates that in the presence of testing and treatment u₂ as a control strategy, the number of infected individuals in acutely, chronically, and carriers decreases, and it increases compared to when there is no control. In Figure 4(c), we noticed that there is a significant difference in the population of infected HBV when testing and treatment u₂ are used as control strategy compared to without optimal control. Similarly, in Figure 4(d), the results revealed that the population of infected carriers (C) reduced because of testing and treatment and eventually increase when there is no testing and treatment. This proves that there is a close connection between the three infectious people in the population. In the control profile in Figure 4(e), we observe that the most effective testing and treatment control u₂ rise and stabilize at the upper bound for t_f = 50 years before progressively declining to the lowest bound.

5.3. Strategy C: Use of Vaccination Only

In strategy C, we consider vaccination u₃ in the population of vaccinated as the only control strategy to optimize the objective functional J, and we set condom use u₁ and testing and treatment u₂ of infected individuals to zero. Figure 5(a) shows that when there is control, the number of HBV-infected people decreases to the minimal level as compared with the number of infected individuals when control is absent. The number of acutely I_A infected individuals with HBV in Figure 5(b) reduces because of vaccination of the infected population, and the population increases in the absence of control strategy. In Figure 5(c), the number of chronically I_C infected individuals with HBV decreases because of optimal strategy in the population, while the number increases in the absence of optimal control strategy. The population of carriers infected with HBV in Figure 5(d) decreases with optimal strategy while it increases in the absence of a control strategy. The control profile in Figure 5(e) rises at an upper bound of t_f = 50 years’ time before gradually dropping to the lower bound.

5.4. Strategy D: Use of Condom + Testing and Treatment Only

Condom use is presented in strategy D as (u₁) and testing and treatment (u₂) in infected population to optimize the objective functional J while setting the vaccination u₃ in susceptible population to zero. We observed in Figures 6(a)–6(c) that, because of the control strategies, the number of latently (L), acutely (I_A), and chronically (I_C) infected individuals with HBV decreases as against the increase in the uncontrolled case. Similar decrease in Figure 6(d) is observed for the carrier-infected population with HBV in the control strategy, while an increased number is observed when there is no control. In Figure 6(e), the control profile, on the control, is at the upper bound for a maximum time t_f = 10 years and drops gradually until it reaches the lower bound, while control on testing and treatment u₂ started from the lower bound, reaches the maximum (upper bound), and remain there for t_f = 16 years before it drops gradually falling to the lower bound.

5.5. Strategy E: Use of Condom + Vaccination Only

Strategy E presents the use of condom as the control (u₁) and vaccination (u₃) on the infected population to improve the functional objectives J, while setting the testing and treatment (u₂) of the infected population to zero. In Figures 7(a)–7(c), the population of infected individuals with HBV also decreases in the presence of control u₁ and u₃ whereas the number of infected individuals increases when there is no optimal strategy. Figure 7(d) describes a scenario where the population of infected individuals decreases because of the presence of control (u₁, u₃), and it increases when the control strategy is totally absent. In contrast to the control profile in Figure 7(e), it shows that the control (u₁) is reached at the upper bound t_f = 16 years before dropping to lower bound, while the vaccination (u₃) is at lower bound t_f = 1.7 years moved to the upper bound before coming back to lower bound again (in a graph which line is a vaccinated).

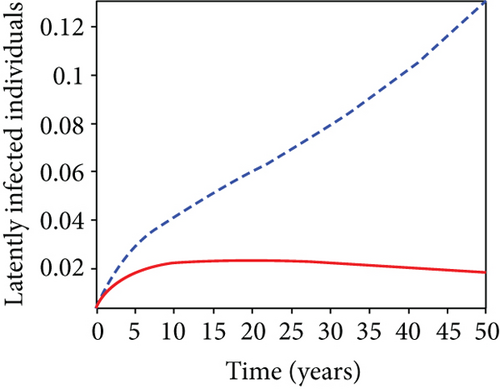
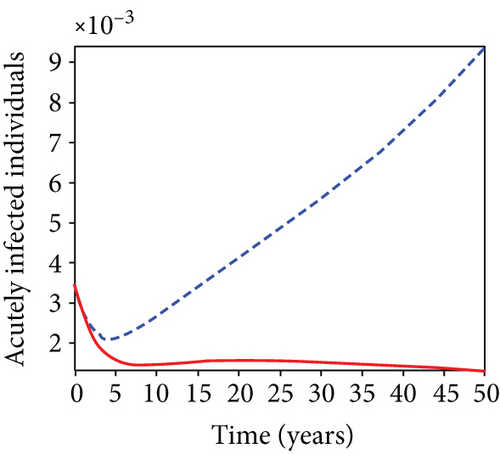
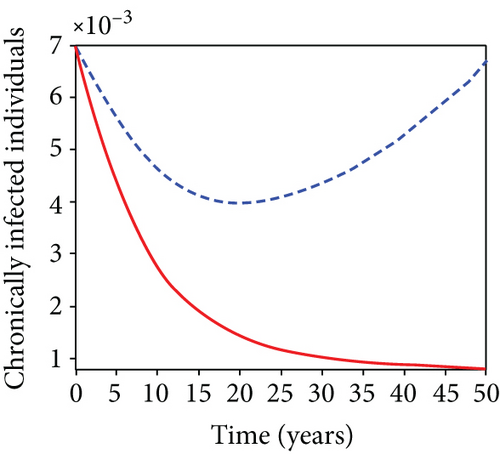
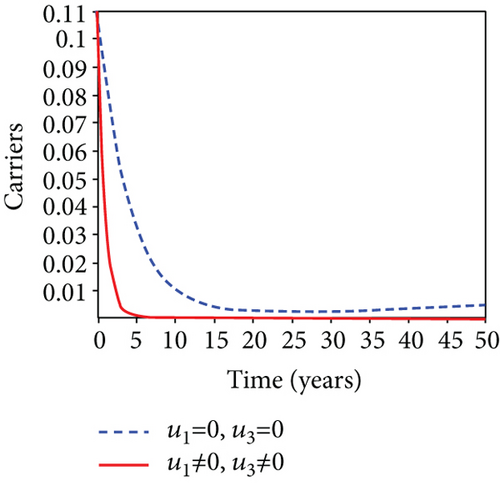
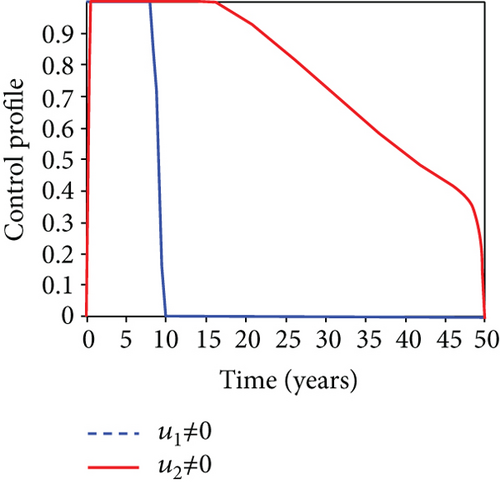
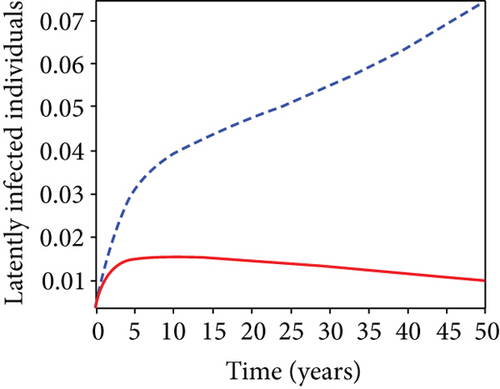
5.6. Strategy F: Testing and Treatment + Vaccination Only

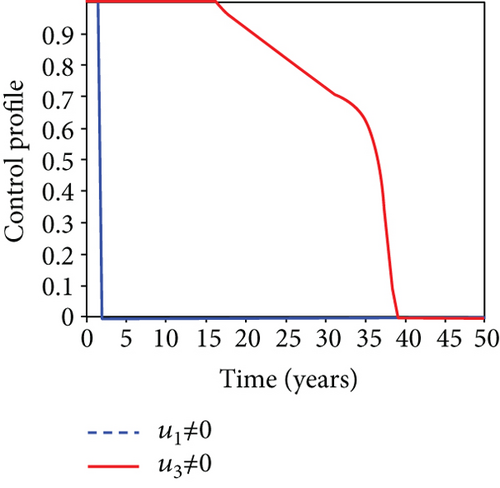
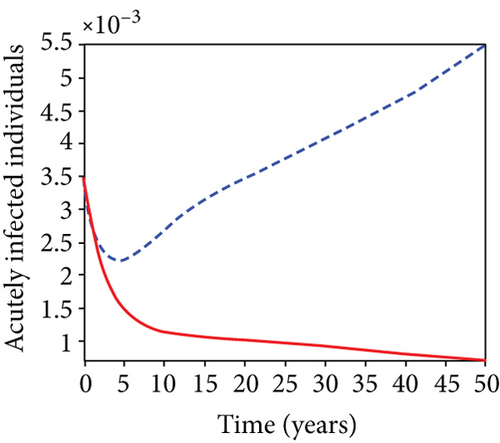
In this strategy, the testing and treatment of infected individuals u₂ and vaccination of susceptible individuals u₃ and the objective functional J are optimized through controls, while setting the control u₁ to zero. Figures 8(a)–8(c) demonstrate a substantial difference in the infected population with latently L, acutely I_A, and chronically I_C hepatitis B virus with optimal control strategy compared to the number of infected individuals when there is no control. Figure 8(d) shows that the control measures resulted in a drop in the number of infected individuals, but the number of infected persons increased in the absence of control. The control profile in Figure 8(e) shows that the optimal control on testing and treatment u₂ is at the upper bound t_f = 12.5 years before it drops to the lower bound, whereas control u₃ rises to the higher bound before it gradually fall to lower bound t_f = 5 years.

5.7. Strategy G: Use of Condom + Testing and Treatment + Vaccination

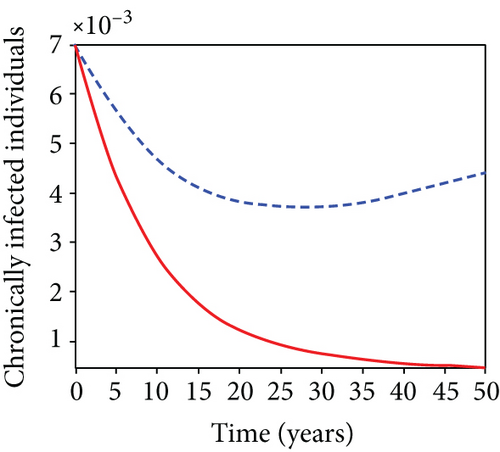
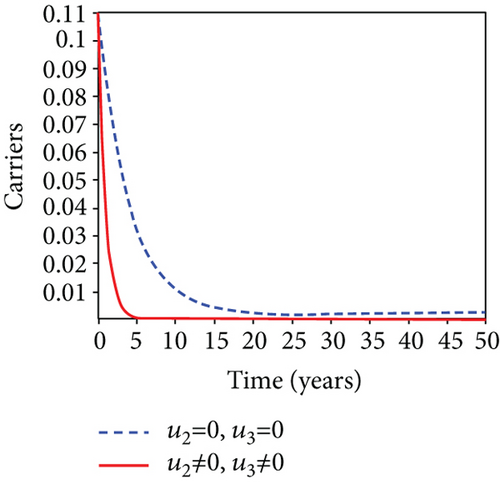
In strategy G, we present the use of condoms, testing and treatment of infected individuals, and vaccination; we considered all three (4) controls (u₁, u₂, u₃) in optimizing the objective functional J. Compared to the situation without control, the number of people infected with the hepatitis B virus significantly decreased because of the control techniques, as shown in Figures 9(a)–9(c). We discovered that, in contrast to the infected population without an optimal strategy, Figure 9(d) demonstrates that the number of infected populations with carriers (C) falls due to control (u₁, u₂, u₃).

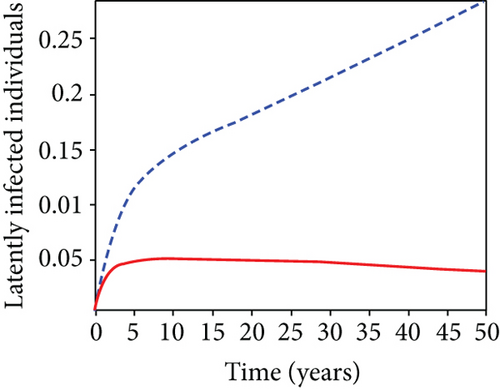
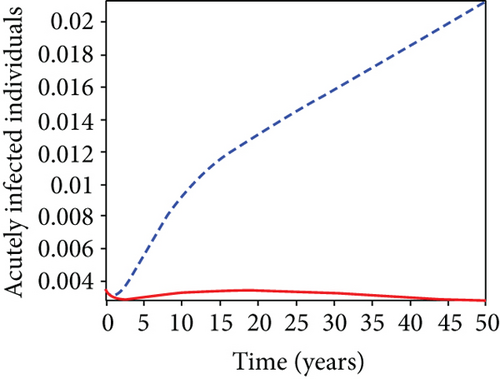
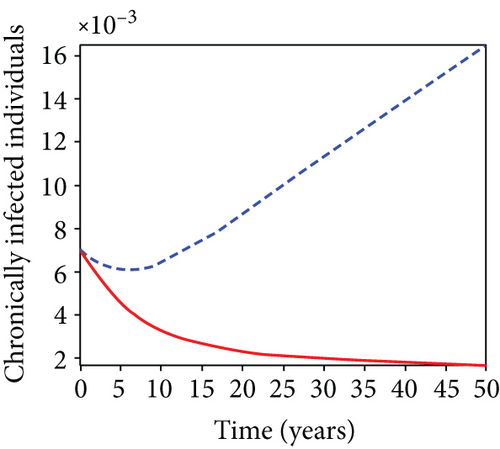
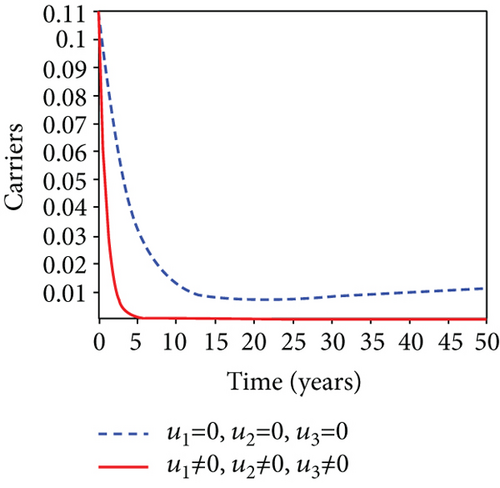
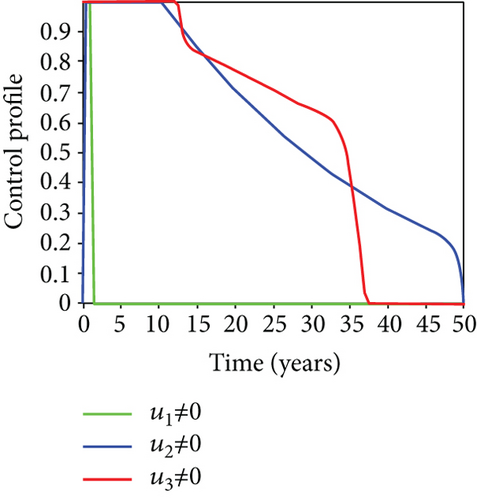
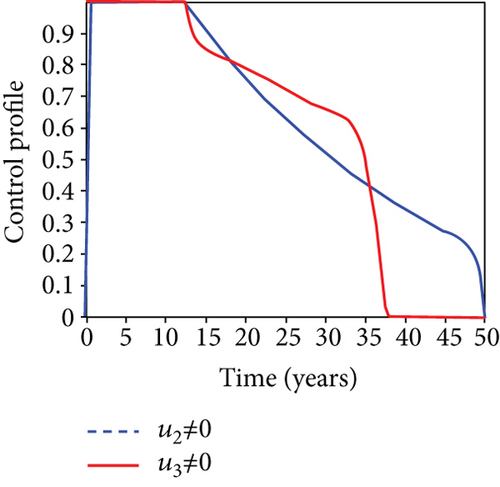
We observed in Figures 9(a)–9(c) that the number of people with hepatitis B virus infection significantly decreased because of the control techniques, in contrast to a situation where there is no control. We also noticed that Figure 9(d) demonstrates that the prevalence of infected people who are also carriers (C) decreases due to control (u₁, u₂, u₃) as compared to the infected population without an optimal strategy. The control profile in Figure 9(e) on control u₁ rises to the upper bound t_f = 0.1 year before it gradually drops to the lower bound t_f = 2 years’ time, and the control u₂ began from the lower bound and escalated to the upper bound in t_f = 10.5 years while the control u₃ is at the upper bound before it gradually drop to the lower bound. It simply depicts how the transmission of HBV might be decreased or eliminated in the shortest workable time if an ideal method was used on the population of infected classes. Using a condom, testing and treatment, and vaccination strategy appeared to be the most effective strategy, as was observed from the graphs.

6. Conclusion

In this research, we proposed an S − L − I_A − I_C − C − R − V model with three control intervention strategies, which is a changed version of the work of Vahindian, Akbari, and Heydari (2014). In the analytical solution, we considered the control parameters to be constant. The positivity of the solution was proven to be positive, and both mathematically and epidemiologically, the system of nonlinear differential equations was well-posed. Using the next-generation method, we could get the basic reproduction number. The disease-free and endemic equilibrium was established. The disease-free is locally asymptotically stable when and unstable if . The global stability of the disease-free is proved globally asymptotically stable when the associated reproduction number . In a stable equilibrium, the disease will entirely die out, whereas in an unstable equilibrium, it will persist and become endemic. We investigated the optimal level required to put down the spread of the hepatitis B virus infection in a population using Pontryagin’s maximum principle. Numerical results show the best strategy for control of the combination of the use of a condom for prevention and testing and treatment and vaccination.

As future work, we have broadened the number of compartments that make up our field of study of the hepatitis B virus disease (HBV). Thus, we plan to consider the economic aspect to understand this disease.

Conflicts of Interest

No competing interest is hereby declared by the authors.

Authors’ Contributions

The development and simulation of the model were done by Abdulfatai, Atte Momoh. Model analysis, discussion of results, and typesetting were implemented by Audu Abubakar. All authors approved the final manuscript.

Acknowledgments

The authors acknowledged the facilities provided by Modibbo Adama University, Yola, Nigeria, and Tertiary Education Trust Fund.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 WHO, Hepatitis B, 2020, July 2020, https://www.who.int/news-room/fact-sheets/detail/hepatitis-b.
Google Scholar
2 Gerlich W. H., Medical virology of hepatitis B: how it began and where we are now, Virology Journal. (2013) 10, no. 1, https://doi.org/10.1186/1743-422X-10-239, 2-s2.0-84880334408, 23870415.
10.1186/1743-422X-10-239
PubMed Web of Science® Google Scholar
3 Van Damme P. et al., S. A. Plotkin and W. A. Orenstein, Hepatitis B vaccines, In Vaccines, 2017, 6th edition, Elsevier Sanders.
Google Scholar
4 WHO, WHO, Hepatitis B Fact Sheet No. 204, 2017, The World Health Organisation, Geneva, Switzerland, 2000, http://www.who.int/mediacentre/factsheets/fs204/en/.
Google Scholar
5 Momoh A. A., Bala Y., Washachi D. J., and Déthié D., Mathematical analysis and optimal control interventions for sex structured syphilis model with three stages of infection and loss of immunity, Advances in Difference Equations. (2021) 2021, no. 1, https://doi.org/10.1186/s13662-021-03432-7.
10.1186/s13662-021-03432-7
PubMed Web of Science® Google Scholar
6 Garfein R. S., Vlahov D., Galai N., Doherty M. C., and Nelson K. E., Viral infections in short-term injection drug users: the prevalence of the hepatitis C, hepatitis B, human immunodeficiency, and human T-lymphotropic viruses, American Journal of Public Health. (1996) 86, no. 5, 655–661, https://doi.org/10.2105/ajph.86.5.655, 2-s2.0-0029867968, 8629715.
10.2105/AJPH.86.5.655
CAS PubMed Web of Science® Google Scholar
7 Levine O. S., Vlahov D., and Nelson K. E., Epidemiology of hepatitis B virus infections among injecting drug users: seroprevalence, risk factors, and viral interactions, Epidemiologic Reviews. (1994) 16, no. 2, 418–436, https://doi.org/10.1093/oxfordjournals.epirev.a036161, 7713187.
10.1093/oxfordjournals.epirev.a036161
CAS PubMed Web of Science® Google Scholar
8 Khan T., Zaman G., and Chohan M. I., The transmission dynamic and optimal control of acute and chronic hepatitis B, Journal of Biological Dynamics. (2017) 11, no. 1, 172–189, https://doi.org/10.1080/17513758.2016.1256441, 2-s2.0-84995910784, 27852159.
10.1080/17513758.2016.1256441
PubMed Web of Science® Google Scholar
9 Din A., Li Y., Khan F. M., Khan Z. U., and Liu P., On analysis of fractional order mathematical model of hepatitis B using Atangana–Baleanu Caputo (ABC) derivative, Fractals. (2022) 30, no. 1, article 2240017, https://doi.org/10.1142/S0218348X22400175.
10.1142/S0218348X22400175
Web of Science® Google Scholar
10 Din A., Li Y., Yusuf A., and Ali A. I., Caputo type fractional operator applied to Hepatitis B system, Fractals. (2022) 30, no. 1, https://doi.org/10.1142/S0218348X22400230.
10.1142/S0218348X22400230
Web of Science® Google Scholar
11 Din A., Li Y., and Liu Q., Viral dynamics and control of hepatitis B virus (HBV) using an epidemic model, Alexandria Engineering Journal. (2020) 59, no. 2, 667–679, https://doi.org/10.1016/j.aej.2020.01.034.
10.1016/j.aej.2020.01.034
Web of Science® Google Scholar
12 Din A. and Li Y., Stationary distribution extinction and optimal control for the stochastic hepatitis B epidemic model with partial immunity, Physica Scripta. (2021) 96, no. 7, article 074005, https://doi.org/10.1088/1402-4896/abfacc.
10.1088/1402-4896/abfacc
Web of Science® Google Scholar
13 Van den Driessche P. and Watmough J., Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences. (2002) 180, no. 1-2, 29–48, https://doi.org/10.1016/S0025-5564(02)00108-6, 2-s2.0-0036845274, 12387915.
10.1016/S0025-5564(02)00108-6
CAS PubMed Web of Science® Google Scholar
14 Castillo-Chavez C., Feng Z., and Huang W., On the computation of R0 and its role on global stability, 2002, Institute for mathematics and its applications.
Google Scholar
15 Zhang J. and Zhang S., Application and optimal control for an HBV model with vaccination and treatment, Discrete Dynamics in Nature and Society. (2018) 2018, 13, https://doi.org/10.1155/2018/2076983, 2-s2.0-85053688074, 2076983.
10.1155/2018/2076983
Web of Science® Google Scholar
16 Khan T. and Zaman G., Classification of different hepatitis B infected individuals with saturated incidence rate, Springerplus. (2016) 5, no. 1, https://doi.org/10.1186/s40064-016-2706-3, 2-s2.0-84978696195, 27468382.
10.1186/s40064-016-2706-3
PubMed Google Scholar
17 Bhattacharyya S. and Ghosh S., Optimal control of vertically transmitted disease: an integrated approach, Computational and Mathematical Methods in Medicine. (2010) 11, no. 4, 369–387, https://doi.org/10.1155/2010/520830, 21058080.
10.1155/2010/520830
PubMed Web of Science® Google Scholar
18 Pang J., Cui J.-A., and Zhou X., Dynamical behavior of a hepatitis B virus transmission model with vaccination, Journal of Theoretical Biology. (2010) 265, no. 4, 572–578, https://doi.org/10.1016/j.jtbi.2010.05.038, 2-s2.0-77954530183, 20553944.
10.1016/j.jtbi.2010.05.038
PubMed Web of Science® Google Scholar
19 Zou L., Zhang W., and Ruan S., Modeling the transmission dynamics and control of hepatitis B virus in China, Journal of Theoretical Biology. (2010) 262, no. 2, 330–338, https://doi.org/10.1016/j.jtbi.2009.09.035, 2-s2.0-70450227305, 19822154.
10.1016/j.jtbi.2009.09.035
PubMed Web of Science® Google Scholar
20 Lenhart S. M. and Workman J. T., Optimal Control Applied to Biological Model, 2007, CRC Press, New York, https://doi.org/10.1201/9781420011418.
10.1201/9781420011418
Google Scholar
21 Pontryaggin L. S., Boltryanskii V. G., Gamkrelidze R. V., and Mishchenco E. F., Mathematical Theory of Optimal Process, 1986, 4, Gordon and Breach Science, New York.
Google Scholar
22 Michael M., Libin M., and Weimin H., Convergence of the forward-backward sweep method in optimal control, Computational Optimization and Applications. (2012) 53, no. 1, 207–226.
10.1007/s10589-011-9454-7
Web of Science® Google Scholar
23 Medley G. F., Lindop N. A., Edmunds W. J., and Nokes D. J., Hepatitis-B virus endemicity: heterogeneity, catastrophic dynamics and control, Nature Medicine. (2001) 7, no. 5, 619–624, https://doi.org/10.1038/87953, 2-s2.0-0035041293, 11329065.
10.1038/87953
CAS PubMed Web of Science® Google Scholar
24 Zhang S. and Zhou Y., The analysis and application of an HBV model, Applied Mathematical Modelling. (2012) 36, no. 3, 1302–1312, https://doi.org/10.1016/j.apm.2011.07.087, 2-s2.0-83655163849.
10.1016/j.apm.2011.07.087
Web of Science® Google Scholar

All articles

On the Optimal Control of Intervention Strategies for Hepatitis B Model

Abstract

1. Introduction

2. Formulation of Hepatitis B Model

2.1. Basic Properties

3. The Hepatitis B Model Analysis

3.1. Equilibrium Points

3.2. Basic Reproduction Number

3.3. Local Stability of the Hepatitis B Disease-Free Equilibrium

3.4. Global Asymptotic Stability for Hepatitis B

3.5. Hepatitis B Model Sensitivity Analysis

4. Optimal Control of the Hepatitis B Model

5. Numerical Simulations

5.1. Strategy A: Use of Condom Only

5.2. Strategy B: Use of Testing and Treatment Only

5.3. Strategy C: Use of Vaccination Only

5.4. Strategy D: Use of Condom + Testing and Treatment Only

5.5. Strategy E: Use of Condom + Vaccination Only

5.6. Strategy F: Testing and Treatment + Vaccination Only

5.7. Strategy G: Use of Condom + Testing and Treatment + Vaccination

6. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the Optimal Control of Intervention Strategies for Hepatitis B Model

Abstract

1. Introduction

2. Formulation of Hepatitis B Model

2.1. Basic Properties

3. The Hepatitis B Model Analysis

3.1. Equilibrium Points

3.2. Basic Reproduction Number

3.3. Local Stability of the Hepatitis B Disease-Free Equilibrium

3.4. Global Asymptotic Stability for Hepatitis B

3.5. Hepatitis B Model Sensitivity Analysis

4. Optimal Control of the Hepatitis B Model

5. Numerical Simulations

5.1. Strategy A: Use of Condom Only

5.2. Strategy B: Use of Testing and Treatment Only

5.3. Strategy C: Use of Vaccination Only

5.4. Strategy D: Use of Condom + Testing and Treatment Only

5.5. Strategy E: Use of Condom + Vaccination Only

5.6. Strategy F: Testing and Treatment + Vaccination Only

5.7. Strategy G: Use of Condom + Testing and Treatment + Vaccination

6. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information