International Journal of Aerospace Engineering

Volume 2023, Issue 1 6906266

Research Article

Open Access

A New Unsteady Flow Control Technology of Centrifugal Compressor Based on Negative Circulation Concept

Shuli Hong,

Corresponding Author

Shuli Hong

[email protected]

orcid.org/0000-0003-1646-5606

College of Mechanical and Automotive Engineering, Ningbo University of Technology, Ningbo 315336, China nbut.cn

Search for more papers by this author

Yuxuan Yang,

Yuxuan Yang

College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China nuaa.edu.cn

Search for more papers by this author

Weiyu Lu,

Weiyu Lu

School of Physical and Mathematical Sciences, Nanjing Tech University, Nanjing 211816, China njtech.edu.cn

Search for more papers by this author

Xin Xiang,

Xin Xiang

School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China nchu.edu.cn

Search for more papers by this author

Shuli Hong,

Corresponding Author

Shuli Hong

[email protected]

orcid.org/0000-0003-1646-5606

College of Mechanical and Automotive Engineering, Ningbo University of Technology, Ningbo 315336, China nbut.cn

Search for more papers by this author

Yuxuan Yang,

Yuxuan Yang

College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China nuaa.edu.cn

Search for more papers by this author

Weiyu Lu,

Weiyu Lu

School of Physical and Mathematical Sciences, Nanjing Tech University, Nanjing 211816, China njtech.edu.cn

Search for more papers by this author

Xin Xiang,

Xin Xiang

School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China nchu.edu.cn

Search for more papers by this author

First published: 09 October 2023

https://doi.org/10.1155/2023/6906266

Academic Editor: Rongchun Zhang

Share a link

Email
Wechat
Bluesky

Abstract

The tip leakage vortex (TLV) induced by the tip clearance flow has a significant impact on the performance of centrifugal compressors, causing impeller flow losses and reducing the stall margin. To solve this problem, an unsteady flow control technology called the NCFC method is proposed based on the concept of negative circulation control, realized by a vortex generator placed in a tube connected with the shroud through a hole. The approach is derived from a theoretical study of the compressor TLV by introducing a two-dimensional vortex model. A numerical simulation is then performed to verify the effectiveness of the NCFC method. The result shows that the NCFC method can greatly stabilize the flow field at the blade tip and improve the stall margin and efficiency of the compressor without reducing the total pressure ratio of the compressor, which has the characteristics of both unsteadiness and negative circulation effect. In addition, a HC method with only unsteady excitation effect is also studied for comparison, which only slightly stabilizes the blade tip flow and increases the stall margin of the compressor, suggesting that the NCFC is more effective than the HC. Finally, it is highly recommended to improve the efficiency of any unsteady jet/suction and separation flow interaction.

1. Introduction

Since the invention of the centrifugal compressor, it has been widely used in military and civil fields, such as auxiliary power unit for aircraft [1], propulsion system for unmanned aerial vehicle or missile [2, 3], turbocharger for vehicle [4], and fuel cell for automobile [5, 6]. With the development of modern industrial system and the improvement of technical requirements, people’s demand for compressor performance is gradually increasing. At present, centrifugal compressors are developing towards high advanced pressure ratio, high efficiency, and high stability. The design technique of compressor has already evolved from the one-dimensional empirical formula to the full three-dimensional flow field analysis [7–9]. In addition, some blade optimization measures are also widely used, such as leading edge sweep blade [10, 11], split blade [12, 13], tandem blade [14, 15], and back-swept blade [16]. In recent years, artificial intelligence has further optimized the compressor structure and blade profile. Ma et al. [17] used NSGA-III algorithms to optimize a centrifugal compressor in a fuel cell system, significantly improving the pressure ratio and efficiency of the compressor. Based on blade profile optimization, flow control technology is beginning to attract people’s attention to further improve the performance of the compressor.

Most of the flow control techniques currently applied to centrifugal compressors at present are concentrated in the tip region, mainly for two reasons: one is that some devices installed in the blade or wheel hub are usually limited by space due to the compact structure of centrifugal compressors; the other is that the flow field structure of the centrifugal compressor tip is extremely complex due to the effects of meridian curvature and centrifugal force, and it has a great influence on the compressor performance [18–23]. It is precisely for these two reasons that our subsequent research and application of flow control will also be established at the blade tip. At present, the applications applied to the tip area of centrifugal compressor are various, among which the most widely used is casing treatment, including self-recirculation casing treatment (SRCT) [24], circumferential grooves [25], bleed slots [26], axial groove [27], nonaxisymmetric casing treatment [28], and ported shroud [29]. Except for casing treatment, the application of some other control methods, such as air injection [30], suction [31], and blade tip winglet [32], is relatively less. Although the compressor performance can be improved to some extent by these flow control techniques, the results obtained when applying these techniques are often inconsistent. Taking SRCT as an example, Wang et al. [33] can improve the operating efficiency of 1.5% while increasing the stable operating range of the compressor by 20% by applying SRCT. However, in Jung and Pelton’s research [34], he used SRCT to increase the stable working area of the compressor by 25%, but the efficiency decreased by 0.4%. Taking the circumferential grooves as an example, Bareiß et al. [25] found that the circumferential groove method would not affect the compressor efficiency while improving the compressor pressure ratio under any circumstances after applying this flow control technology to a centrifugal compressor. The circumferential groove method is also used by Park et al. [35], whose research found that this technology can increase the stall margin of the compressor, but the efficiency will decrease. Similar conclusions can be drawn from the review article [36]. Therefore, when these flow control technologies are applied in practice, many questions will arise, such as which control method is the most suitable? What is the essential difference between different control methods? Will the effect of the same flow control method change when applied to different compressors? How should the control parameters of the same flow control method applied to different compressors be optimized?

The basic reason for the above questions is the lack of sufficient understanding of the flow theory and flow control mechanism of the centrifugal compressor. To solve this problem, some researchers have carried out modeling research on the compressor based on the mathematical model and theoretical analysis [37–43]. Although these theories have made some achievements, the following problems still exist: (1) Some theories take the compressor as an integral unit, which lacks the details of the flow field and the complicated physical phenomena; (2) many models are based on cascade research, which may not be applicable to centrifugal compressors; (3) these one-dimensional models lack further support in describing complex flow structures; (4) part of the theories only predict the simple actions of vortices and cannot describe their complex motions; (5) the most important point is how to guide the flow control technology based on these models.

Due to the complex internal flow structure of the compressor, it is difficult to give a detailed and complete theoretical description, so we focus on the flow structure that plays a key role in the performance of the compressor. As mentioned above, the flow field in the tip region of the impeller is particularly important in the centrifugal compressor. In particular, the TLV (tip leakage vortex) often has a decisive influence on the performance of the centrifugal compressor [21–23, 44]. Tomita et al. [45] found that the blockage of the TLV breakdown is a major cause of compressor stall which may occur even at low flow rates. Schleer et al. [46] believe that a large TLV will cause the compressor stall and affect the performance of the compressor throughout the operating range. Cao et al. [22] found a Kelvin–Helmholtz-type instability of the shear layer formed between the mainstream flow and the tip leakage flow, which will form TLV with strong unsteadiness and pressure fluctuations causing the reduction of the blade loading. Kaneko and Tsujita [47] found that TLVs formed by the main blade and split blade reduce the blade loading and compressor efficiency. Therefore, considering the important influences of TLV on the performance of centrifugal compressors, our research focus is based on TLV. Our approach is to optimize the flow at the compressor blade tip by suppressing the TLV, thereby improving the compressor performance. The specific steps are as follows: First, in order to obtain regular and generalised conclusions, we conducted theoretical research on TLV by introducing a two-dimensional vortex model. Secondly, we investigated the behaviour of the TLV vortex model under some external factors to provide a reference for our subsequent flow control technology. Then, following the theoretical research results, we proposed a flow control technology applicable to centrifugal compressors, which we call the negative circulation flow control (NCFC) method. Finally, we used unsteady numerical simulation to compare the performance of the centrifugal compressor with and without flow control.

2. Introduction of a Two-Dimensional TLV Model

Through many numerical simulations and experimental studies, it is found that the cross-sectional profile of the compressor TLV has an obvious elliptical structure [48–50], so we use an elliptical vortex model to describe the TLV rather than a circular model often adopted by many researchers. The region where vorticity is concentrated in a two-dimensional inviscid flow field is called the vortex patch. For example, the vortex core of a Rankine vortex is the simplest circular vortex patch often used by researchers to analyze vortex structures. In general, the boundary shape of a vortex patch of any shape should change continuously as the vortex patch moves. There is a special case: an elliptical vortex patch with uniform vorticity will rotate on itself at a constant angular velocity and remain unchanged; this type of vortex is called a Kirchhoff elliptical vortex, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of the Kirchhoff elliptical vortex model.

The constant angular velocity is expressed by the following formula:

(1)

where a is the major semiaxis and b is the minor semiaxis. Based on the elliptical vortex model, we can divide the flow field inside the centrifugal compressor into the following two parts: inside the elliptical vortex, the vorticity is known, and the velocity field can be determined; the outside of the ellipse is equivalent to an elliptical column affected by the compressor passage flow. Finally, the two parts are combined to give the total velocity field. We applied this method previously in our research of a blade-divergent passage, resulting in favourable outcomes [51].

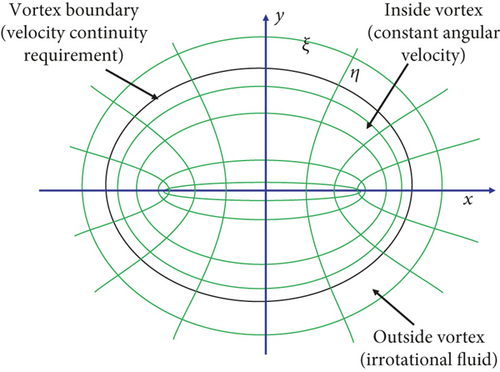
2.1. Outside the Elliptical Vortex

The governing equation for the stream function outside the elliptical vortex is

(2)

In the Cartesian coordinates (x, y), the ellipse boundary is

(3)

whose unit outer normal vector can be written by

(4)

where s is the surface arc length measured in a counterclockwise direction. When the elliptical vortex rotates counterclockwise, a point velocity at the vortex boundary is

(5)

Thus, the normal velocity can be given by

(6)

where r² = x² + y². On the other hand, the normal velocity can be also expressed with stream function:

(7)

According to Equations (6) and (7), we can obtain

(8)

By integrating the above equation, we can derive the boundary flow function:

(9)

Then, elliptic coordinates are used for the convenience of derivation, which has the form of

(10)

where the elliptic focus c² = a² − b² and on the ellipse border ξ = ξ₀. According to the CFD results [48–50], it can be observed that the velocity at the vortex boundary is very close to the blade tip velocity due to the influence of the viscous force and the relative motion of the shroud. Therefore, we assume

(11)

where U is approximately equal to the blade tip velocity. Then, we substitute a = ccoshξ₀ and b = csinhξ₀ into Equation (11) to get

(12)

Since the rotational direction of the vortex is opposite to that of the blade, a minus sign should be added in front of U. Combining Equations (9) and (12), we can obtain the boundary stream function expression:

(13)

Furthermore, the external flow function should simultaneously satisfy the governing Equation (2), the boundary condition of Equation (13), and the condition that the velocity at infinity is 0, so its solution should be of the form

(14)

Comparing Equation (13) with (14), we can obtain the constant:

(15)

Then, the external flow function becomes

(16)

Considering that the elliptical vortex has a circulation Γ = πabω, that is, the vortex flux passing through the cross-sectional area of the ellipse, the external stream function can be expressed as

(17)

where superscript “o” in the formula means external and ω is vorticity.

2.2. Inside the Elliptical Vortex

The governing equation of the stream function inside the elliptical vortex is

(18)

The solution of the stream function has a form of

(19)

where superscript “i” in the formula means internal. By plugging it into Equation (18), we get

(20)

The above undetermined constants can be derived from the continuity of the normal and tangential velocity components on the vortex boundary. The normal velocity component is

(21)

So, one related equation can be determined by the continuity according to Equations (3), (8), and (21), that is

(22)

From the continuity of tangential velocity

(23)

which holds true for any value of η, so we can get another relation:

(24)

Combining Equations (20), (22), and (24), we get the undetermined constants

(25)

Finally, we can get the internal stream function

(26)

3. Modeling Analysis of TLV under Imposed Strain

The flow field structures inside the compressor are complex, even a certain simple dynamic behaviour of the TLV may be the result of some combined effects of many different factors. Therefore, our approach is to use a theoretical expression to describe the overall performance of the TLV. Although a particular state of motion may also be a combination of many factors, the theory used to describe this phenomenon should be concise and clear. Our specific approach is to employ some typical external loads, which can be expressed by mathematical models, to the above TLV model. In addition, the specific performance of the model with external loads applied is also discussed. We expect that this approach will help us to understand the effect of the TLV and to find out what factors affect the TLV behaviour, such as other flow field structures or the configuration of the compressor itself, thereby guiding us to take appropriate flow control measures to improve the performance of the compressor.

Four external strain effects are considered in this paper. They are the “Flow Passage Constriction Effect,” “Passage Vortex Squeeze Effect,” “Leakage Flow Translation Effect,” and “Additional Circulation Effect.” As we have given detailed introductions to the first three in our previous research [48], this paper only briefly describes them and mainly introduces the “Additional Circulation Effect.”

3.1. Flow Passage Constriction Effect

To describe the “Flow Passage Constriction Effect,” we use the following flow function:

(27)

where e is a strain rate strength that is determined here by the geometry of the flow passage. After applying it to the TLV model, we can get

(28)

where ε = a/b is the axis ratio of the ellipse. The negative sign in the formula only reflects the rotational direction of the vortex, so the absolute value of the result can better reflect the intensity ratio of the external factor and the vortex. Further analysis of the above formula shows that the minimum value of the ratio of external factors to vortex intensity is 1/(ε + 1/ε + 2), depending on the axis ratio of the elliptical TLV, and there is no maximum value. This means that even the flow passage with small meridional curvature could potentially have a significant constricting effect on the TLV.

3.2. Passage Vortex Squeeze Effect

The “Passage Vortex Squeeze Effect” can be described by a flow function as

(29)

where e is determined here by the strength of the passage flow. Similar to the previous treatment, after applying it to the TLV model, we can get

(30)

whose value range is from −1/2(ε + 1) to −1/2(1/ε + 1). The negative sign indicates that the effect of the passage vortex on the TLV is opposite to our setting, meaning that the passage vortex actually produces a suction effect rather than a squeeze effect on TLV. Therefore, we believe that the passage vortex inside the compressor can increase the effective area of the TLV, thus accelerating the deterioration of the flow field.

3.3. Leakage Flow Translation Effect

For expressing the “Leakage Flow Translation Effect,” we employed a simplified linear flow function

(31)

where e is a constant determined by the strength of the leakage flow. When it acts on the TLV model, the ratio of leakage flow intensity to TLV can be obtained

(32)

The above formula also only gives the minimum value of ab/2(2b + a). As the leakage flow is a necessary condition for producing the TLV, it is easy to understand that the ratio of its strength to the TLV strength is only the minimum value.

3.4. Additional Circulation Effect

As mentioned above, the behaviour of the TLV may be a combination of several factors, including the additional circulation effect. Figure 2 illustrates the generation mechanism of the “Additional Circulation Effect.” As shown in the figure, the direction of the leakage flow and the viscosity effect caused by the passage vortex are the same as the direction of rotation of the TLV. Therefore, the leakage flow and passage vortex will strengthen the TLV, as if an additional circulation is imposed around the TLV, so we call it the “Additional Circulation Effect.”

If we set the coordinate origin at the center of the ellipse vortex, a point vortex model can be used for additional circulation. The corresponding stream function is

(33)

where the subscript “ace” means “Additional Circulation Effect” and Γ₀ is the intensity of the additional circulation determined by leakage flow and passage vortex. According to the continuity condition and TLV model, we can get

(34)

(35)

We can multiply Equation (34) by 2 and add it to Equation (35) to eliminate the second term to get

(36)

By analyzing the above equation, we can get the maximum and minimum values of Γ_o/ω:

(37)

(38)

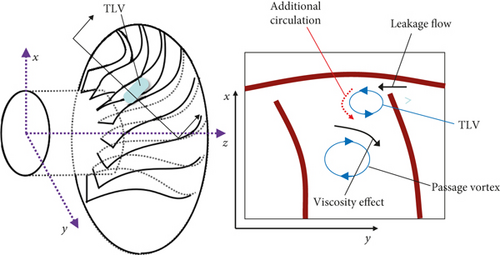
The above expression gives the range of Γ₀/ω. It can be seen that the “Additional Circulation Effect” depends on the long and short axis of the elliptical vortex. By analyzing the minimum value of Γ₀/ω, we can find that the minimum value of Γ₀/ω is always greater than 1 as long as b/a is not extremely small (corresponding to an extremely elongated ellipse). We can therefore conclude that in most cases, the value of Γ₀/ω is greater than 1. This means that in most cases, when the “Additional Circulation Effect” acts on the TLV, its influence will even exceed that of the TLV itself. As for the extremely narrow elliptical vortex, it can be generated at a very small tip clearance. Of course, in this case, the leakage flow generated by the small gap will also be small, and the corresponding “Additional Circulation Effect” may also be weakened at the same time. For most centrifugal compressors, the clearance may not reach this situation, so we will not discuss this extreme case.

4. A Negative Circulation Flow Control (NCFC) Method

From Equations (28) and (32), it can be seen that the intensity ratio of the “Flow Passage Constriction Effect” to the TLV and the ratio of the “Leakage Flow Translation Effect” to the TLV have only minimum values, which means that the two effects are the necessary conditions to affect the TLV. Therefore, from a flow control point of view, we are not willing to spend much energy on controlling these two effects. For the “Passage Vortex Squeeze Effect,” if we take a conventional ellipse with axis ratio ε = 2, the maximum intensity ratio of the “Passage Vortex Squeeze Effect” to TLV can be gotten from Equation (30) as 1/3. Comparing this value with the minimum value of Γ₀/ω (Equation (38)), which is greater than 1 in most cases, we can conclude that the effect of the “Additional Circulation Effect” on the TLV will be much greater than that of “Passage Vortex Squeeze Effect” on the TLV. Therefore, a proper flow control method that we adopt should be to weaken or better inhibit the “Additional Circulation Effect.” This is why we propose the negative circulation flow control (NCFC) method. Its essence is to create an effect opposite to the “Additional Circulation Effect” to weaken the TLV.

Figure 3 shows an NCFC device mounted on the shroud. A vortex generator to create negative circulation in the opposite direction to the TLV is located in a tube that connects to the hole near the starting position of the TLV on the shroud. A certain number of such devices can be placed around the circumference of the casing, depending on the structure of the compressor.

Due to the relative motion between the NCFC devices and the blades, the NCFC method can achieve unsteady flow control as the impeller rotates. Thus, the NCFC method has two characteristics of unsteadiness and negative circulation. Its unsteady control frequency is

(39)

where ω_r is the rotational speed (RPM) and N_c is the number of NCFC devices. Similarly, the blade passing frequency (BPF) is

(40)

where N_b is the number of blades. From references [52–55], it can be seen that the unsteady fluctuation frequency of TLV (f_T) is approximately between 40% and 100% BPF (f_T ≈ 0.4 ~ 1.0 f_BPF). On the other hand, researchers found that the unsteady flow control performs well when the frequency of unsteady flow control is close to the frequency of the controlled object [56–58]. Therefore, we can get

(41)

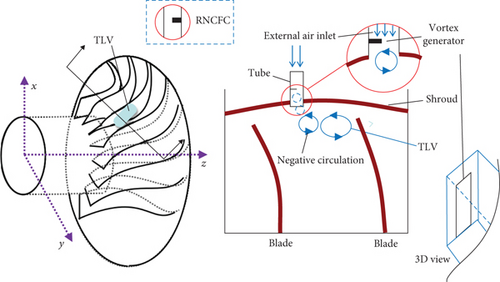
Because this article mainly focuses on the feasibility of the NCFC method, we choose f_c ≈ f_BPF here for simplification, which means N_c = N_b. In the similar way, other frequencies can also be studied.

5. The Numerical Simulation Methods

The investigated microcentrifugal compressor is used in a 30 kW distribution power generation system. The impeller consists of 10 pairs of main and split back-swept blades (N_b = 10). The meridional channel shape is determined by a cubic Bezier curve. Table 1 shows the main geometric and aerodynamic parameters of the compressor.

Table 1. Main parameters of the microcentrifugal compressor in this study.

	Parameter	Value
Overall performance	Mass flow rate	0.36 kg/s
	Rotation speed	80,000 RPM
	Total pressure ratio	3.2

Impeller inlet	Inlet tip diameter	59.5 mm
	Outlet tip diameter	19.5 mm
	Relative Mach’s number of inlet blade tip	0.87
	Relative flow angle of inlet blade tip	30.6°
	Relative flow angle of inlet blade root	59.3°

Impeller outlet	Outlet diameter	98.5 mm
	Outlet blade width	4.08 mm
	Outlet absolute airflow angle	30.0
	Outlet relative airflow angle	71.7

To simulate the effect of the relative positioning of the NCFC devices and the blades changing due to the rotation of the impeller, two very thin transition layers (layer 1 and layer 2 in Figure 4) are added between the NCFC device computational domain and the shroud. Figure 4 shows the computational grid of the compressor and the data exchange settings between the different computational domains. The total thickness of the additional layer is 0.075 mm, which is 1/8 of the tip clearance height of 0.3 mm. A full nonmatching (FNM) connection is used between the shroud and layer 1. The calculation domain of the impeller and layer 1 is performed in the rotating coordinate system. This is because FNM requires the coordinate system solved on both sides to be consistent but does not need to consider mesh matching. FNM is also set for data exchange between the NCFC device and layer 2, and the two domains are calculated in the static coordinate system. Therefore, a rotor-stator (R-S) interaction is used to link layer 1 and layer 2.

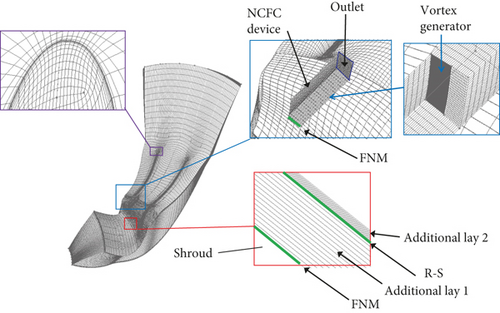
Considering the relative motion between the NCFC device and the impeller, we adopt an unsteady numerical simulation to study a single blade passage with Numeca/Fine. Since we use the same unsteady control frequency as BPF, the number of NCFC devices is the same as the number of blades N_b, so one blade passage corresponds to one NCFC device. The total number of grids in the compressor calculation domain without flow control is approximately 900,000. The total number of additional meshes for layer 1, layer 2, and NCFC devices for the controlled compressor calculation is approximately 30,000. The thickness of the first layer of mesh near the wall surface is set to 0.001 mm. The Reynolds number is approximately 3.1 × 10⁵, and the dimensionless wall distance y⁺ varies from 1 − 3.

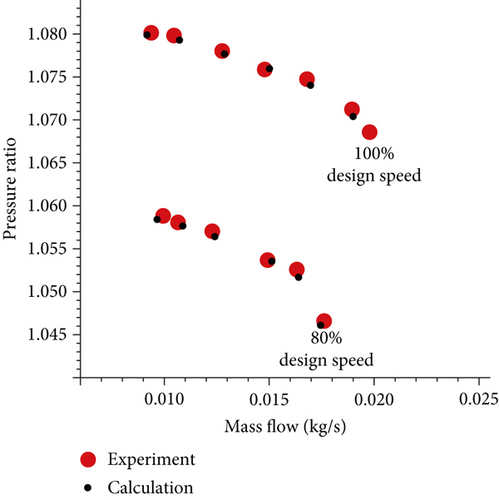
The time step is determined by the number of angular positions, which is set to be 30 points. Therefore, according to the rotational speed, the time step is 2.5 × 10⁻⁶ s with 30 inner iterations. The domain scaling method is used for rotor/stator interface. The impeller inlet is set to at a rotational speed of 80,000 RPM, a total pressure of 101,325 Pa, and a total temperature of 293 K. The given static pressure at the outlet of the NCFC device is 101,325 Pa. The solid wall is set to adiabatic no-slip condition. The Spalart-Allmaras (S-A) model is employed for the turbulent model. If the compressor performance parameters change periodically, we assume that the calculation is convergent. By continuously increasing the static pressure at the impeller outlet, the calculation becomes divergent. A state before divergence is defined as a near-stall condition. We have validated the effectiveness of the numerical simulation method on a low-speed commercial centrifugal compressor as shown in Figure 5. Figure 6 shows the comparison of experimental and calculated results of the centrifugal compressor at 100% and 80% design speed (the red circle corresponding to the experimental point is large, reflecting the error band). From the characteristic diagram, it can be seen that the numerical calculation results are in good agreement with the experimental results. Therefore, it is believed that the numerical simulation method used in this article has a certain degree of credibility. More detailed experimental information can be found in references [53, 57].

6. Compressor Performance with and without NCFC Devices

6.1. Overall Performance

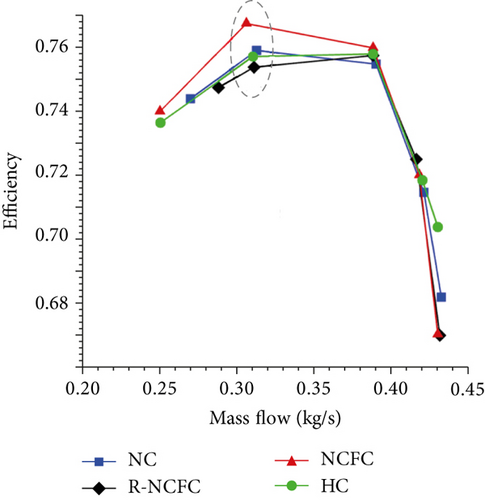
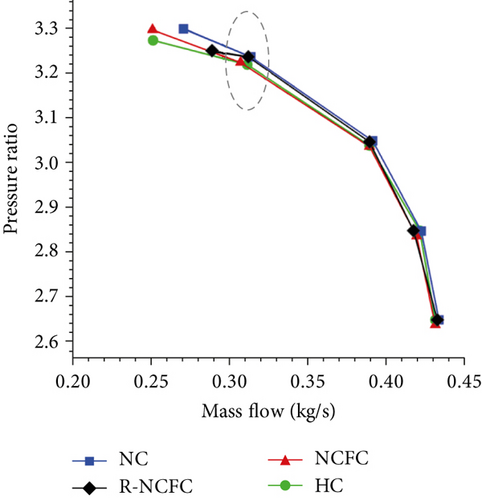
In order to have a comparative analysis, we have simulated the cases of the compressor with noncontrolled (NC), hole control (HC, holes are placed on the shroud with the same size and number with NCFC devices), NCFC, and reverse NCFC (R-NCFC, generating vortex opposite with NCFC as shown in Figure 4). The flow field in one blade passage period after calculation convergence is selected for analysis. The performance of the time-averaged flow field of the compressor in this period is shown in Figure 7. The figure shows that for high flow conditions, these control methods have little effect on compressor efficiency. For conditions spanning a wide range of flow rates, including the design point (the mass flow is 0.36 kg/s), these control methods have a significant impact on compressor efficiency. In particular, the NCFC method can significantly improve the efficiency of the compressor among these flow control technologies, with a maximum efficiency increase of 0.95%. Compared to the uncontrolled compressor, the efficiency of the compressor with the HC method hardly changes. However, the R-NCFC method reduces the efficiency of the compressor by about 0.05%. Therefore, it is obvious that the NCFC method is optimal among these methods. As mentioned above, the NCFC method has the advantages of both unsteadiness and negative circulation effect. The HC method has only the unsteadiness characteristic.

We can therefore conclude that the negative circulation effect is beneficial for flow control. A reverse negative circulation effect (with the R-NCFC method) actually reduces the efficiency of the compressor, which can further illustrate this conclusion. Further observation of the compressor pressure characteristics shows that after applying these flow controls, the pressure ratio of the compressor does not change much, and the pressure ratio of the controlled compressor decreases slightly, with a maximum decrease of about 0.05. The relative stall margin is defined as

(42)

where π_cs and

are the total pressure ratio and mass flow rate of the compressor near stall condition with control and π_ocs and

are the total pressure ratio and mass flow rate of the compressor near stall condition without control. The SM_rel is 6.9%, 5.2%, and -7.3% corresponding to the compressor with NCFC, HC, and R-NCFC, respectively. From Figure 7, it can also be seen that the operating ranges of the compressor under NCFC and HC conditions are larger than those under NC and R-NCFC conditions.

6.2. Flow Field Analysis of the Centrifugal Compressor

For the analysis, we use the same flow field data in one blade passing period as above. Figures 8–11 show the pressure distribution at 95% of the blade height of the compressor under no control and three other different controls. These cases are selected from the calculation point before the stall point, as shown by the dotted line in Figure 7. The mass flow and total pressure ratio of these cases are almost the same, so we consider this comparison to be credible. In addition, in order to present a good comparison effect, we recorded the range of blade tip high-pressure zone as T0 at its minimum and T3 at its maximum under different operating conditions. Moreover, in order to eliminate the differences of the compressor under different working conditions and to have better comparability, the dimensionless static pressure coefficient is selected here, which has the following form:

(43)

where p(t) is the transient static pressure value and p_inlet is the average static pressure at the inlet.

From Figure 8, it can be seen that the blade tip flow field of the uncontrolled compressor appears to have pressure fluctuations. The high pressure zone reaches its maximum value at T3 and then gradually decreases until T5, showing a relatively regular periodicity. From references [50, 53, 54], it can be seen that the formation and fluctuation of the high-pressure zone are mainly caused by the TLV. When the NCFC method is applied (as shown in Figure 9), the high-pressure zone at the blade tip is significantly reduced. From T0 to T5, there is almost no high-pressure zone compared with NC, which means that the flow passage blockage effect at the blade tip is weakened. Figure 12 shows the variation of the static pressure coefficient at two points of the blade tip during a blade passing period. It is clear from the figure that the curve of the NCFC is smoother than that of the other schemes, which is an indication that its pressure change has better continuity. For a better quantitative understanding of pressure fluctuations, a static pressure coefficient variance of one point is defined as

(44)

where CP_i is the instantaneous static pressure coefficient and

is the average static pressure coefficient. Table 2 shows the variance of the static pressure coefficients at points A and B in Figure 12 under different schemes. From the combination of the curves in Figure 12 and the data in Table 2, it can be concluded that the use of the NCFC scheme has great advantages for pressure stabilisation.

Table 2. The variance of the static pressure coefficients under different schemes.

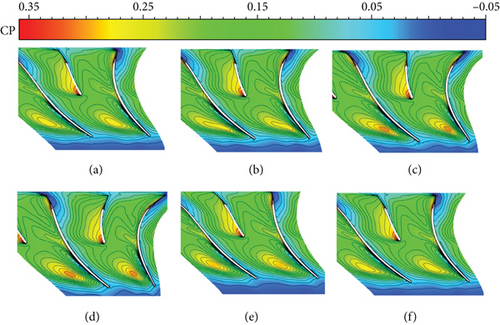
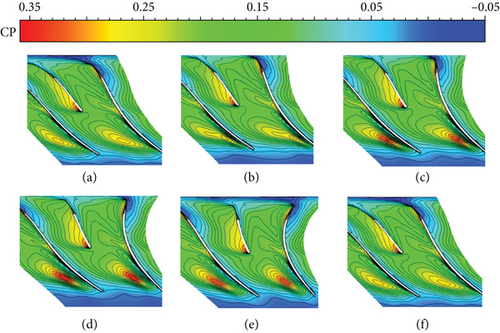
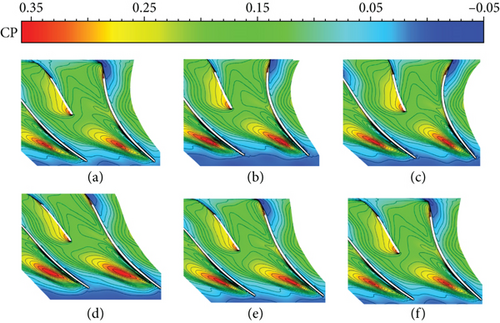
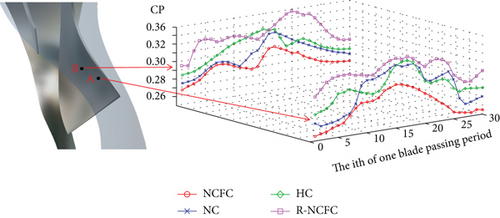
Location	NC	NCFC	HC	R-NCFC
A	0.0277	0.0275	0.0421	0.0232
B	0.0247	0.0182	0.0238	0.0249

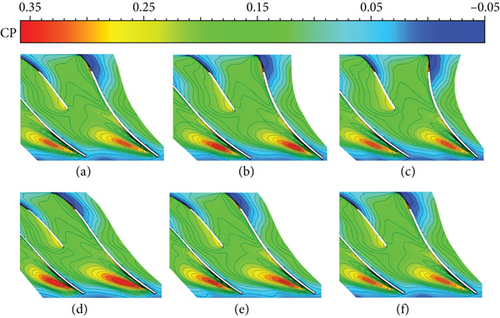
Figure 10 shows the case of the compressor using the HC method. It can be seen that only a small area of the high-pressure zone appears at T2-T4. In addition, a comparison of the HC method with the NCFC and NC methods shows that the HC method is less stable to pressure fluctuations. The use of the R-NCFC method gives the worst flow field (Figure 11). In this operation, the overall characteristics of the flow field are similar to those of the NC case, but the area of the high-pressure zone is larger than that of the NC, which means that the clogging effect will increase.

Based on the above results, we can see that the NCFC method can effectively stabilize the blade tip flow field of the compressor, thus improving the stable operating range and efficiency of the compressor, without affecting the total pressure ratio. The HC method can also give good results, which is very useful for increasing the stall margin of the compressor. However, the excitation that is opposite to the mode of action of the NCFC, namely, R-NCFC, will deteriorate the flow field at the compressor blade tip and will cause the performance of the compressor to decrease.

The HC method uses the unsteady effect created by the relative motion of the impeller and hole to realize periodic excitation. However, the efficiency of each excitation is not taken into account. The NCFC method not only takes advantage of the same unsteady property as HC but also considers the efficiency of each excitation. Here, we use the concept of negative circulation to force the momentum to exchange in the original flow field. Therefore, from the perspective of flow control, we propose to strengthen the efficiency of each unsteady incentive, which is very beneficial to improve the overall effect of unsteady control.

7. Conclusions

In order to improve the performance of the centrifugal compressor, we carried out a theoretical study on the compressor TLV and proposed a two-dimensional vortex model. Through the analysis of this model, we put forward a view based on the concept of negative circulation control and conducted numerical simulation verification. The conclusions are as follows:

(1)
The Kirchhoff elliptical vortex is introduced to represent the compressor TLV. A point vortex model is drawn into the two-dimensional model to reveal an additional circulation effect caused by leakage flow and passage vortex viscous effect. The result shows that the additional circulation effect will exceed the TLV itself in most cases, which is also larger than the passage vortex squeeze effect
(2)
A negative circulation flow control device is designed and verified by numerical simulation. It is found that the NCFC method can greatly stabilize the flow field at the blade tip and improve the stall margin and efficiency of the compressor without affecting the total pressure ratio of the compressor
(3)
The effect of NCFC is better than that of the HC. The former utilizes both unsteady excitation and injection of negative circulation to improve momentum exchange. The latter only uses the unsteady effect. Therefore, it is highly recommended to improve the efficiency of each unsteady jet/suction and separation flow interaction

Nomenclature

A:: Undetermined constant
a:: Long axis
B:: Undetermined constant
b:: Short axis
C:: Undetermined constant
CP:: Dimensionless static pressure coefficient
:: Average static pressure coefficient
CP_i:: Instantaneous static pressure coefficient
c:: Elliptic focus
e:: Strain rate strength
e_x:: Unit vector in the x direction
e_y:: Unit vector in the y direction
e_z:: Unit vector in the z direction
F:: Genetic function
f_BPF:: Blade passing frequency
f_c:: Unsteady control frequency
f_T:: Unsteady fluctuation frequency of the TLV
:: Mass flow rate of the compressor near stall condition with control
:: Mass flow rate of the compressor near stall condition without control
N_b:: The number of blades
N_c:: The number of NCFC devices
n:: Unit outer normal vector
n_x:: X component of the unit outer normal vector
n_y:: Y component of the unit outer normal vector
p(t):: Transient static pressure
p_inlet:: Average static pressure at inlet
r:: Vector distance from origin
r:: Distance from origin
SM_rel:: Relative stall margin
s:: Surface arc length
U:: Main flow velocity
V:: Strain rate matrix
V_b:: Velocity of a point on the vortex border
x:: x coordinate
y:: y coordinate
Γ:: Circulation of the ellipse vortex
Γ_o:: Circulation of the point vortex
ε:: Axis ratio of the ellipse
η:: Elliptic coordinate in η direction
ξ:: Elliptic coordinate in ξ direction
ξ₀:: Elliptic coordinate on the ellipse border
π_cs:: Total pressure ratio of the compressor near stall condition with control
π_ocs:: Total pressure ratio of the compressor near stall condition without control
σ_cp:: Static pressure coefficient variance
Ψ:: Stream function
Ψ_b:: Stream function on the ellipse border
Ψ⁽ⁱ⁾:: Internal flow function
Ψ^(o):: External flow function
:: External flow function with additional circulation effect
Ω:: Angular velocity
ω:: Vorticity
ω_r:: Impeller rotational speed.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This research was funded by the Zhejiang Provincial Natural Science Foundation of China under grant number LQ20E060004. This research was also supported by the Fundamental Research Funds for the Ningbo University of Technology. We are also grateful to Fuxin (NUAA) and Huang Guoping (NUAA) for the technical aspects.

Open Research

Data Availability

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

References

1 Bai C., Xuan H., He Z., Zou Y., Tang G., and Tang J., Research on centrifugal compressor disk containment of auxiliary power unit, Aerospace Science and Technology. (2017) 68, 37–45, https://doi.org/10.1016/j.ast.2017.05.002, 2-s2.0-85019461791.
10.1016/j.ast.2017.05.002
Web of Science® Google Scholar
2 Turan O., Exergetic effects of some design parameters on the small turbojet engine for unmanned air vehicle applications, Energy. (2012) 46, no. 1, 51–61, https://doi.org/10.1016/j.energy.2012.03.030, 2-s2.0-84867233470.
10.1016/j.energy.2012.03.030
Web of Science® Google Scholar
3 Colin R., Airturbojet or turbojet for small tactical missile propulsion, AIAA 34th Aerospace Sciences Meeting and Exhibit, January 1996, Reno, NV, USA, https://doi.org/10.2514/6.1996-378.
10.2514/6.1996-378
Google Scholar
4 Tamaki H., Unno M., Kawakubo T., and Hirata Y., Aerodynamic design to increase pressure ratio of centrifugal compressors for turbochargers, Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, June 2009, Florida, USA, https://doi.org/10.1115/GT2009-59160, 2-s2.0-77953206811.
10.1115/GT2009-59160
Google Scholar
5 Li W. and Feng G., Design and experimental study of centrifugal compressor in fuel cell vehicle, Mechanics. (2021) 27, no. 1, 52–61, https://doi.org/10.5755/j02.mech.28301.
10.5755/j02.mech.28301
Google Scholar
6 Liu Z., Liu Z., Jiao K., Yang Z., Zhou X., and Du Q., Numerical investigation of ejector transient characteristics for a 130-kW PEMFC system, International Journal of Energy Research. (2020) 44, no. 5, 3710, https://doi.org/10.1002/er.5156.
10.1002/er.5156
PubMed Web of Science® Google Scholar
7 Dehner R. and Selamet A., Three-dimensional computational fluid dynamics prediction of turbocharger centrifugal compression system instabilities, Journal of Turbomachinery. (2019) 141, no. 8, article 081004, https://doi.org/10.1115/1.4042728, 2-s2.0-85062594589.
10.1115/1.4042728
Web of Science® Google Scholar
8 Laveau A., Kapat J. S., Chow L. C., Enikov E., and Sundaram K. B., Design, analysis and fabrication of a meso-scale centrifugal compressor, Proceedings of the ASME 2000 International Mechanical Engineering Congress and Exposition, November 2000, Orlando, FL, USA, https://doi.org/10.1115/IMECE2000-1305.
10.1115/IMECE2000-1305
Google Scholar
9 Lüdtke K. H., Process Centrifugal Compressors: Basics, Function, Operation, Design, Application, 2004, Springer-Verlag, Berlin, Germany, https://doi.org/10.1007/978-3-662-09449-5.
10.1007/978-3-662-09449-5
Google Scholar
10 Denton J. D. and Xu L., The exploitation of three-dimensional flow in turbomachinery design, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (1998) 213, no. 2, 125–137, https://doi.org/10.1243/0954406991522220.
10.1243/0954406991522220
Web of Science® Google Scholar
11 Vad J., Aerodynamic effects of blade sweep and skew in low-speed axial flow rotors at the design flow rate: an overview, Proceedings of the Institution of Mechanical Engineers: Part A Journal of Power and Energy. (2008) 222, no. 1, 69–85, https://doi.org/10.1243/09576509JPE471, 2-s2.0-41949099243.
10.1243/09576509JPE471
Web of Science® Google Scholar
12 Omidi M., Liu Y., Mohtaram S., and Li S., Investigating on performance parameters and flow field of centrifugal compressor based on the splitter blade leading edge’s location effect, Journal of Mechanical Science and Technology. (2022) 36, no. 8, 4015–4020, https://doi.org/10.1007/s12206-022-0722-5.
10.1007/s12206-022-0722-5
Web of Science® Google Scholar
13 Malik A. and Zheng Q., Effect of double splitter blades position in a centrifugal compressor impeller, Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy. (2019) 233, no. 6, 689–701, https://doi.org/10.1177/0957650918792462, 2-s2.0-85052553543.
10.1177/0957650918792462
CAS Web of Science® Google Scholar
14 Li Z., Han G., Lu X., Huang E., and Zhao S., Improving the operating range using a centrifugal compressor with a tandem impeller, Aerospace Science and Technology. (2020) 96, article 105548, https://doi.org/10.1016/j.ast.2019.105548.
10.1016/j.ast.2019.105548
Web of Science® Google Scholar
15 Oh J., Buckley C. W., and Agrawal G. L., Numerical investigation of low solidity vaned diffuser performance in a high-pressure centrifugal compressor—part iii: tandem vanes, Journal of Turbomachinery. (2012) 134, no. 6, article 061025, https://doi.org/10.1115/1.4006300, 2-s2.0-84865790021.
10.1115/1.4006300
Web of Science® Google Scholar
16 Farge T. Z. and Johnson M. W., The effect of backswept blading on the flow in a centrifugal compressor impeller, Proceedings of the ASME 1990 International Gas Turbine and Aeroengine Congress and Exposition, June 1990, Brussels, Belgium, https://doi.org/10.1115/90-GT-231, 2-s2.0-85011568229.
10.1115/90-GT-231
Google Scholar
17 Ma C., Yang Z., Jiao K., Liu Z., and Du Q., Multi-objective optimization of the centrifugal compressor impeller in 130 kW PEMFC through coupling SVM with NSGA -III algorithms, International Journal of Green Energy. (2021) 18, no. 13, 1383–1395, https://doi.org/10.1080/15435075.2021.1904942.
10.1080/15435075.2021.1904942
CAS Web of Science® Google Scholar
18 Ishida M. and Senoo Y., On the pressure losses due to the tip clearance of centrifugal blowers, Journal of Engineering for Gas Turbines and Power. (1981) 103, no. 2, 271–278, https://doi.org/10.1115/1.3230717, 2-s2.0-0019557881.
10.1115/1.3230717
Google Scholar
19 Senoo Y. and Ishida M., Pressure loss due to the tip clearance of impeller blades in centrifugal and axial blowers, Journal of Engineering for Gas Turbines and Power. (1986) 108, no. 1, 32–37, https://doi.org/10.1115/1.3239882, 2-s2.0-0022497563.
10.1115/1.3239882
Web of Science® Google Scholar
20 Harada H., Performance characteristics of shrouded and unshrouded impellers of a centrifugal compressor, Journal of Engineering for Gas Turbines and Power. (1985) 107, no. 2, 528–533, https://doi.org/10.1115/1.3239765, 2-s2.0-0022045545.
10.1115/1.3239765
Web of Science® Google Scholar
21 Chen H., Zhuge W., Zhang Y., Ma X., and Tao L., Performance improvement of a centrifugal compressor for the fuel cell vehicle by tip leakage vortex control, Journal of Thermal Science. (2021) 30, no. 6, 2099–2111, https://doi.org/10.1007/s11630-021-1430-7.
10.1007/s11630-021-1430-7
Web of Science® Google Scholar
22 Cao T., Kanzaka T., Xu L., and Brandvik T., Tip leakage flow instability in a centrifugal compressor, Journal of Engineering for Gas Turbines and Power. (2021) 143, no. 4, article 041012, https://doi.org/10.1115/1.4049821.
10.1115/1.4049821
Web of Science® Google Scholar
23 Tomita I. and Furukawa M., Design concept with tip leakage vortex control for centrifugal compressor flow stabilization, Journal of Physics Conference Series. (1909) 2021, article 012020, https://doi.org/10.1088/1742-6596/1909/1/012020.
10.1088/1742-6596/1909/1/012020
Google Scholar
24 Zhang H., Jing F., Li Q., Wang H., and Chu W., Mechanism affecting the performance and stability of a centrifugal impeller by changing bleeding positions of self-recirculating casing treatment, Aerospace. (2023) 10, no. 2, https://doi.org/10.3390/aerospace10020104.
10.3390/aerospace10020104
Web of Science® Google Scholar
25 Bareiß S., Vogt D. M., and Chebli E., Investigation on the impact of circumferential grooves on aerodynamic centrifugal compressor performance, Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, June 2015, Montreal, Quebec, Canada, https://doi.org/10.1115/GT2015-42211, 2-s2.0-84954160351.
10.1115/GT2015-42211
Google Scholar
26 Gancedo M., Guillou E., and Gutmark E., Effect of bleed slots on turbocharger centrifugal compressor stability, International Journal of Heat and Fluid Flow. (2018) 70, 206–215, https://doi.org/10.1016/j.ijheatfluidflow.2017.12.007, 2-s2.0-85042867976.
10.1016/j.ijheatfluidflow.2017.12.007
Web of Science® Google Scholar
27 Harley P. X. L., Starke A., Bamba T., and Filsinger D., Axial groove casing treatment in an automotive turbocharger centrifugal compressor, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2018) 232, no. 24, 4472–4484, https://doi.org/10.1177/0954406216688495, 2-s2.0-85045020081.
10.1177/0954406216688495
Web of Science® Google Scholar
28 Zheng X., Zhang Y., Yang M., Bamba T., and Tamaki H., Stability improvement of high-pressure-ratio turbocharger centrifugal compressor by asymmetric flow control: part ii—non-axisymmetric self recirculation casing treatment, Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, June 2010, Glasgow, UK, https://doi.org/10.1115/GT2010-22582, 2-s2.0-82055200515.
10.1115/GT2010-22582
Google Scholar
29 Christou G. A., Tan C. S., Sirakov B. T., Lei V.-M., and Alescio G., Characterizing flow effects of ported shroud casing treatment on centrifugal compressor performance, Journal of Turbomachinery. (2017) 139, no. 8, article 081005, https://doi.org/10.1115/1.4035664, 2-s2.0-85016441769.
10.1115/1.4035664
Web of Science® Google Scholar
30 Hirano T., Takano M., and Tsujita H., Effect of double air injection on performance characteristics of centrifugal compressor, Journal of Thermal Science. (2015) 24, no. 1, 10–16, https://doi.org/10.1007/s11630-015-0749-3, 2-s2.0-84920798091.
10.1007/s11630-015-0749-3
CAS Web of Science® Google Scholar
31 Ak S. E. and Cadirci S., Investigation of suction flow control on centrifugal compressor with vaned diffuser, Energies. (2022) 15, no. 2, https://doi.org/10.3390/en15020583.
10.3390/en15020583
Web of Science® Google Scholar
32 Zhong J., Wu W., and Han S., Research progress of tip winglet technology in compressor, Journal of Thermal Science. (2021) 30, no. 1, 18–31, https://doi.org/10.1007/s11630-020-1402-3.
10.1007/s11630-020-1402-3
Web of Science® Google Scholar
33 Wang T., Xu W., Gu C., and Xiao J., A new type of self-adaptive casing treatment for a centrifugal compressor, Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, June 2010, Glasgow, UK, https://doi.org/10.1115/GT2010-23457, 2-s2.0-82055184003.
10.1115/GT2010-23457
Google Scholar
34 Jung S. and Pelton R., Numerically derived design guidelines of self recirculation casing treatment for industrial centrifugal compressors, Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, June 2016, Seoul, South Korea, https://doi.org/10.1115/GT2016-56672, 2-s2.0-84991678539.
10.1115/GT2016-56672
Google Scholar
35 Park C.-Y., Choi Y.-S., Lee K.-Y., and Yoon J.-Y., Numerical study on the range enhancement of a centrifugal compressor with a ring groove system, Journal of Mechanical Science and Technology. (2012) 26, no. 5, 1371–1378, https://doi.org/10.1007/s12206-012-0320-z, 2-s2.0-84861785613.
10.1007/s12206-012-0320-z
Web of Science® Google Scholar
36 Jonna T., Grönman A., Jaatinen-Värri A., and Backman J., Flow control methods and their applicability in low-Reynolds-number centrifugal compressors—a review, International Journal of Turbomachinery, Propulsion and Power. (2018) 3, no. 1, https://doi.org/10.3390/ijtpp3010002.
10.3390/ijtpp3010002
Google Scholar
37 Seymour L., Schwenk F. C., and Broderick R. L., Diffusion Factor for Estimating Losses and Limiting Blade Loadings in Axial-Flow-Compressor Blade Elements, 1953, National Advisory Committee For Aeronautics Cleveland OH Lewis Flight Propulsion Lab.
Google Scholar
38 Dunham J., A new endwall model for axial compressor throughflow calculations, Proceedings of the ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition, June 1994, The Hague, Netherlands, https://doi.org/10.1115/94-GT-075, 2-s2.0-84926322722.
10.1115/94-GT-075
Google Scholar
39 Emmons H. W., Pearson C. E., and Grant H. P., Compressor surge and stall propagation, Journal of Fluids Engineering. (1955) 77, no. 4, 455–467, https://doi.org/10.1115/1.4014389.
10.1115/1.4014389
Google Scholar
40 Stenning A. H., Kriebel A. R., and Montgomery S. R., Stall Propagation in Axial-Flow Compressors, 1956, No. NACA-TN-3580.
Google Scholar
41 Greitzer E. M., Surge and rotating stall in axial flow compressors—part I: theoretical compression system model, Journal of Engineering for Power. (1976) 98, no. 2, 190–198, https://doi.org/10.1115/1.3446138, 2-s2.0-85020055849.
10.1115/1.3446138
Web of Science® Google Scholar
42 Jiang W., Khan J., and Dougal R. A., Dynamic centrifugal compressor model for system simulation, Journal of Power Sources. (2006) 158, no. 2, 1333–1343, https://doi.org/10.1016/j.jpowsour.2005.10.093, 2-s2.0-33748095661.
10.1016/j.jpowsour.2005.10.093
CAS Web of Science® Google Scholar
43 Hong S., Huang G., and Lu W., Study on a subsonic micro-centrifugal compressor stall mechanism, Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, June 2017, North Carolina, USA, https://doi.org/10.1115/GT2017-63758, 2-s2.0-85029003150.
10.1115/GT2017-63758
Google Scholar
44 Semlitsch B. and Mihăescu M., Flow phenomena leading to surge in a centrifugal compressor, Energy. (2016) 103, no. 15, 572–587, https://doi.org/10.1016/j.energy.2016.03.032, 2-s2.0-84961644406.
10.1016/j.energy.2016.03.032
Web of Science® Google Scholar
45 Tomita I., Ibaraki S., Furukawa M., and Yamada K., The effect of tip leakage vortex for operating range enhancement of centrifugal compressor, Journal of Turbomachinery. (2013) 135, no. 5, article 051020, https://doi.org/10.1115/1.4007894, 2-s2.0-84888032030.
10.1115/1.4007894
Web of Science® Google Scholar
46 Schleer M., Song S. J., and Abhari R. S., Clearance effects on the onset of instability in a centrifugal compressor, Journal of Turbomachinery. (2008) 130, no. 3, article 031002, https://doi.org/10.1115/1.2776956, 2-s2.0-49049118948.
10.1115/1.2776956
Web of Science® Google Scholar
47 Kaneko M. and Tsujita H., Influences of tip leakage flows discharged from main and splitter blades on flow field in transonic centrifugal compressor stage, Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, June 2018, Oslo, Norway, https://doi.org/10.1115/GT2018-75345, 2-s2.0-85054087223.
10.1115/GT2018-75345
Google Scholar
48 Hong S., Chi J., Xiang X., and Lu W., Theoretical model and numerical analysis of the tip leakage vortex variations of a centrifugal compressor, Aerospace. (2022) 9, no. 12, https://doi.org/10.3390/aerospace9120830.
10.3390/aerospace9120830
Web of Science® Google Scholar
49 Kaneko M. and Tsujita H., Numerical investigation of influence of tip leakage flow on secondary flow in transonic centrifugal compressor at design condition, Journal of Thermal Science. (2015) 24, no. 2, 117–122, https://doi.org/10.1007/s11630-015-0763-5, 2-s2.0-84924762655.
10.1007/s11630-015-0763-5
Web of Science® Google Scholar
50 Yamada K., Furukawa M., Fukushima H., Ibaraki S., and Tomita I., The role of tip leakage vortex breakdown in flow fields and aerodynamic characteristics of transonic centrifugal compressor impellers, Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, June 2011, Vancouver, British Columbia, Canada, https://doi.org/10.1115/GT2011-46253, 2-s2.0-84865524561.
10.1115/GT2011-46253
Google Scholar
51 Hong S., Lu W., Xiang X., and Qiu L., An unsteady flow control technique based on negative circulation conception and its application to a blade-divergent passage, Frontiers in Energy Research. (2023) 11, article 1184687, https://doi.org/10.3389/fenrg.2023.1184687.
10.3389/fenrg.2023.1184687
Web of Science® Google Scholar
52 Wang H., Studies of Unsteady Tip Flow and Rotating Instability in Axial Compressor, 2016, Ph. D. Thesis, Shanghai Jiao Tong University, Shanghai, China.
Google Scholar
53 Huang G., Yang Y., Hong S., Liu Z., and Du S., A new unsteady casing treatment for micro centrifugal compressors to enlarge stall margin, Aerospace Science and Technology. (2020) 106, article 106176, https://doi.org/10.1016/j.ast.2020.106176.
10.1016/j.ast.2020.106176
Web of Science® Google Scholar
54 Hah C., Voges M., Mueller M., and Schiffer H., Characteristics of tip clearance flow instability in a transonic compressor, Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, June 2010, Glasgow, UK, https://doi.org/10.1115/GT2010-22101, 2-s2.0-82055184799.
10.1115/GT2010-22101
Google Scholar
55 Du J., Lin F., Zhang H., and Chen J., Numerical investigation on the self-induced unsteadiness in tip leakage flow for a transonic fan rotor, Journal of Turbomachinery. (2010) 132, no. 2, article 021017, https://doi.org/10.1115/1.3145103, 2-s2.0-77955283816.
10.1115/1.3145103
Web of Science® Google Scholar
56 Lu W., Huang G., Wang J., and Yang Y., Interpretation of four unique phenomena and the mechanism in unsteady flow separation controls, Energies. (2019) 12, no. 4, https://doi.org/10.3390/en12040587, 2-s2.0-85061994336.
10.3390/en12040587
Web of Science® Google Scholar
57 Hong S., Research on Centrifugal Compressor Technology in Micro Miniature High Efficiency Brayton Cycle, 2018, Ph. D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China.
Google Scholar
58 Zheng X., Zhou X., and Zhou S., Investigation on a type of flow control to weaken unsteady separated flows by unsteady excitation in axial flow compressors, Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, June 2004, Vienna, Austria, https://doi.org/10.1115/GT2004-53167.
10.1115/GT2004-53167
Google Scholar

All articles

A New Unsteady Flow Control Technology of Centrifugal Compressor Based on Negative Circulation Concept

Abstract

1. Introduction