International Journal of Aerospace Engineering

Volume 2023, Issue 1 6651286

Research Article

Open Access

Cascaded Control System Design for Quadrotor UAV through Relay with Embedded Integrator-Based Automatic Tuning Approach

Ayaz Ahmed Hoshu,

Corresponding Author

Ayaz Ahmed Hoshu

[email protected]

orcid.org/0000-0003-2882-7483

School of Engineering, RMIT University, Melbourne, VIC 3000, Australia rmit.edu.au

Department of Electronic Engineering, Quaid-e-Awam University of Engineering, Science and Technology, Campus Larkana 77150, Pakistan quest.edu.pk

Search for more papers by this author

Ghulam E Mustafa Abro,

Ghulam E Mustafa Abro

orcid.org/0000-0003-1874-1889

Electrical and Electronic Engineering, Universiti Teknologi PETRONAS, Seri Iskandar, 32610 Perak, Malaysia utp.edu.my

Search for more papers by this author

Musaed Alhussein,

Musaed Alhussein

orcid.org/0000-0002-5538-6778

Department of Computer Engineering, College of Computer and Information Sciences, King Saud University, P.O. Box 51178, Riyadh 11543, Saudi Arabia ksu.edu.sa

Search for more papers by this author

Irfan Ali Tunio,

Irfan Ali Tunio

orcid.org/0000-0003-0299-7572

Department of Electronic Engineering, Quaid-e-Awam University of Engineering, Science and Technology, Campus Larkana 77150, Pakistan quest.edu.pk

Search for more papers by this author

Khursheed Aurangzeb,

Khursheed Aurangzeb

orcid.org/0000-0003-3647-8578

Department of Computer Engineering, College of Computer and Information Sciences, King Saud University, P.O. Box 51178, Riyadh 11543, Saudi Arabia ksu.edu.sa

Search for more papers by this author

Anwar Ali,

Anwar Ali

Department of Electronic and Electrical Engineering, Faculty of Science and Engineering, Swansea University Bay Campus Swansea, UK

Search for more papers by this author

Ayaz Ahmed Hoshu,

Corresponding Author

Ayaz Ahmed Hoshu

[email protected]

orcid.org/0000-0003-2882-7483

School of Engineering, RMIT University, Melbourne, VIC 3000, Australia rmit.edu.au

Department of Electronic Engineering, Quaid-e-Awam University of Engineering, Science and Technology, Campus Larkana 77150, Pakistan quest.edu.pk

Search for more papers by this author

Ghulam E Mustafa Abro,

Ghulam E Mustafa Abro

orcid.org/0000-0003-1874-1889

Electrical and Electronic Engineering, Universiti Teknologi PETRONAS, Seri Iskandar, 32610 Perak, Malaysia utp.edu.my

Search for more papers by this author

Musaed Alhussein,

Musaed Alhussein

orcid.org/0000-0002-5538-6778

Department of Computer Engineering, College of Computer and Information Sciences, King Saud University, P.O. Box 51178, Riyadh 11543, Saudi Arabia ksu.edu.sa

Search for more papers by this author

Irfan Ali Tunio,

Irfan Ali Tunio

orcid.org/0000-0003-0299-7572

Department of Electronic Engineering, Quaid-e-Awam University of Engineering, Science and Technology, Campus Larkana 77150, Pakistan quest.edu.pk

Search for more papers by this author

Khursheed Aurangzeb,

Khursheed Aurangzeb

orcid.org/0000-0003-3647-8578

Department of Computer Engineering, College of Computer and Information Sciences, King Saud University, P.O. Box 51178, Riyadh 11543, Saudi Arabia ksu.edu.sa

Search for more papers by this author

Anwar Ali,

Anwar Ali

Department of Electronic and Electrical Engineering, Faculty of Science and Engineering, Swansea University Bay Campus Swansea, UK

Search for more papers by this author

First published: 10 October 2023

https://doi.org/10.1155/2023/6651286

Academic Editor: Shaoming He

Share a link

Email
Wechat
Bluesky

Abstract

Due to their enormous characteristics and applicability, quadrotor unmanned aerial vehicles (UAVs) have enjoyed much popularity lately. However, designing a stable control strategy for quadrotors still remains one of the major concerns mainly due to the requirement of an accurate system model. They are naturally underactuated systems, with complex and nonlinear dynamics as well as interaxes couplings. Considering the dynamical complexities of these vehicles, one of the efficient methods is to utilize the relay feedback experiments and automatic tuning approach to tackle these issues. This paper investigates the employment of the relay with embedded integrator approach, wherein the quadrotor dynamics are estimated effectively with minimal parameters as compared to previously utilized relay with hysteresis technique. Frequency sampling filter (FSF) is further utilized for the extraction of the needful data through the signals obtained using the relay experiments, followed by the estimation of the plant dynamics. PID controllers have then been developed using the approximated quadrotor models. Which are used in the proposed cascade control structure for the quadrotor. The demonstrated results and analysis present the efficacy of designed control system technique for the quadrotor UAV.

1. Introduction

Multirotor UAVs are regarded as one of the most revolutionary inventions in the present era [1, 2]. They have enjoyed a great attention and applicability in a vast variety of applications lately [3, 4], as they offer numerous characteristics such as controllability, maneuverability, simple design, economy, and vertical take-off and landing (VTOL) capability [5, 6]. Quadrotor UAVs have turned out to be the most popular out of all the available multirotor configurations [7]. Consequently, quadrotor UAVs are extensively explored over the past three decades in order to advance them mainly in terms of configuration, modelling, and control [8–11]. Quadrotor UAVs are considered as an underactuated system as they offer four control inputs to control the six degrees of freedom [12]. The complex nonlinearities and interchannel couplings are also the issues that require attention when designing the control system for these rotorcrafts [5, 13]. Additionally, when operated outdoor, quadrotors are susceptible to atmospheric turbulences [14, 15]. As well, during the indoor operation, the airflow of the propellers reflected from the shelters and walls also causes the external disturbance [16]. Furthermore, when multiple multircopters operate in the closer proximity to one another, the downwash from one another also causes an impact over the flight performance. Therefore, considering these attributes of the quadrotors, design of the stable and robust control system has been considered as the most challenging task.

The cascade control structure technique is proposed in this paper to realize the control system solutions for the quadrotor UAV, wherein PID controllers have been used in the cascaded control loop. Several control strategies have been designed for the multirotor UAVs over the years, such as [17–21]. PID controllers are supposed to be the most vastly utilized controllers in the quadrotor control system because of their simplified structure and ease of practical implementation [22, 23]. Due to these reasons, presently the majority of the mainstream commercial autopilot flight controllers are using PID controllers as their main control algorithm, i.e., micropilot [24], ardupilot [25], paparazzi autopilot [26], AfroFlight Naze32, and Multiwii SE V2.0. During the design of the control algorithm for the quadrotor, appropriate tuning of the parameters of respective controllers has been one of the most challenging tasks. The quadrotor dynamics are defined through a set of nonlinear equation [27]. It would be a very complex to design the controller for quadrotor through conventional methods that utilize dynamic model of the plant. Furthermore, these physical parameters of the quadrotor are usually determined with the help of certain experimentation, which in turn is supposed to be difficult and time-consuming. Also, these parameters may vary as per operating conditions [28]. Additionally, in the quadrotor’s physical model, dynamics for the sensor and actuator are often neglected. Also, the quadrotor model is mostly linearized to simplify the designing process of the controller that is performed at the cost of loss of few dynamical details [29]. Hence, taking into account, all the aforementioned hitches, the PID controllers designed through model-based design approach do not necessarily ensure the desired quadrotor control performance.

An alternate method has been proposed in this paper in which the dynamics of UAVs are estimated using response data obtained experimentally from the multirotor through relay feedback system. Relay with hysteresis mechanism is used previously for this purpose in [30, 31], wherein two parameters are required to execute the required mechanism such as hysteresis and relay amplitude. The hysteresis parameter is mainly required for the filtration of noisy signal. The relay with an embedded integrator method has been proposed in this paper. One of the major features of the relay with an integrator approach is the simplification of the identification of the dynamics that otherwise need the information of the complex and higher-order models [32]. The major theme of opting for the relay with embedded integrator approach is to make sure that the determined information of the plant is encompassed within medium and lower range of frequencies. Moreover, the effect of high-frequency measurement noise is minimized due to the presence of the embedded integrator, and the need to use a hysteresis for the noise is reduced.

FSF is used to estimate the system dynamics through the system responses obtained through the relay feedback system. Then, on the basis of the estimated system model, PID controllers have been tuned automatically through the well-established set of tuning rules proposed in [32]. The contributions of this paper are summarized as follows:

(1)
Robust and stable control solution has been featured for the quadrotor UAV through the automatically tuned cascade control algorithm
(2)
PID controllers have been designed through the automatic tuning approach that is based on the relay with the embedded integrator technique and system identification. Which incorporates all of the actual quadrotor dynamics that include actuators, sensor dynamics, and gyroscopics

2. Dynamic Model of Quadrotor and Control Architecture

Body-fixed and earth-fixed frames are the couple of frames referred to as references that are employed to study the quadrotor dynamics. In the earth-fixed frame, Euler angles described as roll, pitch, and yaw are denoted as η = [ϕ θ ψ]^T. Here, roll angle (ϕ) is the rotation around the x-axis, and similarly, pitch angle (θ) and yaw angle (ψ) are the rotations around the y-axis and z-axis. Then, in the body-fixed frame, the quadrotor’s angular velocity can be described as Ω = [p q r]^T. Here, p, q, and r are the angular velocities of the quadrotor in the body-fixed frame for three attitude axes (roll, pitch, and yaw). Figure 1 illustrates the configuration of the quadrotor. Subsequently, the acceleration of rotation for the quadrotor’s attitude axes in the body-fixed frame can be defined by equations of motion as follows [33]:

(1)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Quadrotor UAV model.

I_xx, I_yy, and I_zz denote the moments of inertia for each x-, y- and z-axes. J_r and ω account for the inertia and velocity of the rotor, respectively, while J_rqω and J_rpω express the propellers’ gyro effect. Moreover, the equations above express the angular velocities of the quadrotor in the body-fixed frame, which are subsequently converted into the earth-fixed frame through

(2)

In this equation, N expresses the transformation matrix and is defined as

(3)

Moreover, thrust and drag torques of each rotor can be expressed as

(4)

where Q_i and T_i are the drag and thrust of each rotor. k_d and Q_i account for the coefficient for thrust and drag, respectively. ω_i represents the speed of rotation for each rotor. The moments for the attitude axes (roll, pitch, and yaw) are produced through the control of the thrust difference produced individually by each of the four rotors. Which are represented as τ_x, τ_y, and τ_z for roll, pitch, and yaw, whereas the total thrust as T. These are expressed as

(5)

The dynamics of the motor would also have an impact over the quadrotor’s, especially under turbulences. Therefore, they have also been employed in the quadrotor model and are subsequently estimated using a transfer function of first order as [32]

(6)

In this equation, ε_m and r_wv denote the motor’s constant for time and steady-state gain, respectively.

2.1. Control System Structure

Quadrotor is termed as an underactuated system that additionally offers coupled dynamics and nonlinearities. Also, the strong coupling among multiple input-output channels is supposed to be challenging when designing the control system for the quadrotors. The controlled variables in the quadrotor system are three torques to provide angular position control, whereas the altitude control is performed through force (f). The stable and robust tracing of the desired signals such as ϕ^∗, θ^∗, and ψ^∗ is used to be the main objective of the quadrotor control system as well as to tackle any unwanted disturbances.

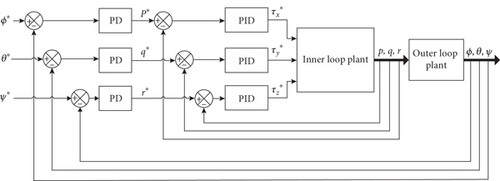
Cascaded control system using PID controllers has been proposed in this paper to feature the control solution to the aforementioned problems associated with the quadrotor. In the cascaded control structure, the multirotor system dynamics are decomposed in the several simpler and smaller subsystems. For which, a separate PID controller is tuned for each of the decomposed subsystem totally based upon the concerned subsystem dynamics. Which in turn provides the effective resolution towards the control issues of the systems, which exhibit complexity in the dynamics [34]. The attitude control system is supposed to be the heart of the quadrotor control structure as it is responsible to maintain the desired 3D orientation of the unmanned vehicle [35]. For the quadrotor cascaded control design, dynamics of the attitude system are broken down as inner loop that deals with angular rate and outer loop that deals with angular position. The proposed structure of the quadrotor cascaded attitude control system is depicted in Figure 2. In the inner loop control system, PID controllers attain the angular rate control. While in the outer loop, PD controllers are utilized to provide the control algorithm for the angular position of the quadrotor. Due to the existence of an integrator already in the system dynamics of the outer loop, as presented in Equation (2), the integral term from the PID has not been employed in the outer loop control system. Consequently, the addition of an integral controller in the control system of outer loop would lead to the oscillatory response.

3. Estimation of the System Dynamics and Controller Design

3.1. Relay with Embedded Integrator

The setup of the relay feedback experiment with the embedded integrator is presented in Figure 3.

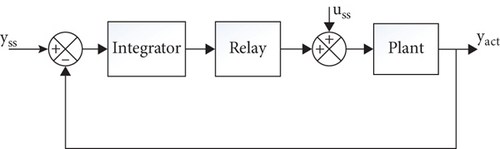
The incorporation of the integrator into the relay process is actually from the perspective of the identification of the system fundamental frequency (ω₁). This type of relay feedback system provides fundamental frequency that intersects the imaginary axis when observing the frequency response at the Nyquist plot. The relay embedded with an integrator leads to the fundamental frequency that exhibits larger time period. This helps the user to negate the hectic process of selecting the appropriate hysteresis parameter in the relay with hysteresis experiments. Also, the system’s frequency response is held into the lower and medium range of frequencies that subsequently prevent the signal from high-frequency noises.

From Figure 3, let us assume that y_ss and u_ss are the output and steady-state signals of the unknown system. The integral error is then determined as

(7)

The first-order approximation of this equation, at the t_i time interval, would be

(8)

Subsequently, the integral error e(t_i) can now be determined as

(9)

Consider the steady-state gain to be positive. The relay with embedded integrator mechanism can be defined as follows:

(10)

where a and ε are the amplitude of the relay and hysteresis, respectively. The relay feedback experiments are performed over the quadrotor model through the mechanism presented in Figure 3. The obtained response for the roll attitude axis has been presented in Figure 4, where the amplitude of the relay is set as 20°/sec, whereas the hysteresis is kept at the lowest possible value of 0.01. The proposed quadrotor configuration is symmetric across the roll and pitch axes. Consequently, the dynamics for both axes would be identical. Therefore, the relay feedback experiments are not repeated for the pitch axis. The estimated model obtained from the roll axis experiments would be used for the pitch attitude axis as well. The yaw axis response for the relay system is depicted in Figure 5. The relay parameters for the yaw axis are set as similar to the roll axis experiments.

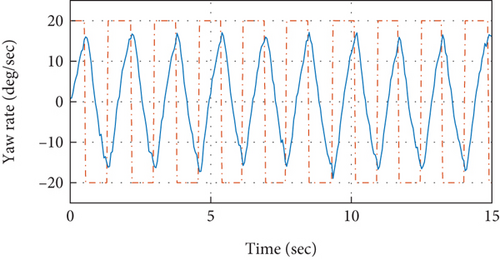
3.2. Frequency Response Analysis

The objective of frequency response analysis is to analyze the data obtained through relay feedback experiments and to extract the information from that data. Which leads to estimation of the dynamics of the related model. Both input and output signals acquired through the relay experiments are analyzed as periodic in nature. Therefore, FSF would be effective to use for the extraction of the useful data from the set of both periodic input and periodic output signals [36, 37].

The periodic input signal represented as (u(k)) and the periodic output signal represented as (y(k)) that are successfully obtained using relay feedback experiments possess the fundamental discrete frequency as ω_d = 2π/N. The N in this expression represents the period indicated as number of samples. Accordingly, output is expressed utilizing frequency sampling filter model, relating to the input signal as

(11)

Here, l = 1, 2, 3..⋯N, while G(0) and

account for the frequency response points of the system. v(k) is measurement noise at output, which is considered the Gaussian distributed possessing variance (σ²) and zero mean. Furthermore, f^l(k) is output vector of the frequency sampling filter, while f⁰(k) is the frequency sampling filter output at a frequency of zero. These are formulated as

(12)

q⁻¹ in this expressions represents back shift operator that is formulated as q⁻¹x(k) = x(k − 1).

When dealing with perfect periodic signals such as u(k) that have period N, Fourier analysis [38] indicates that it will only be possessing the odd frequencies in number and magnitude would be decaying as the number increases. Because of the noise effects and nonlinearities, it has not been practically often for the u(k) signal to be realized as perfectly periodic. Accordingly, by neglecting the higher frequency terms, the output signal is defined as

(13)

Moreover, the vector possessing complex parameters and the correlating regressor vector are also defined as

(14)

The ^∗ in this expression indicates the transpose of complex conjugate. The recursive least square (RLS) algorithm has been employed for the calculation of the vector having estimated frequency parameters that are represented as

and formulated as

(15)

Subsequently, the frequency response of the plant

is obtained via the relation of the closed-loop system’s frequency response and the information of K_T.

(16)

Hence, the open loop system’s frequency response is then determined as follows:

(17)

Supposedly, the system is being operated under the faster sampling environment; the discrete time frequency response

would then be closely approximating to the continuous time frequency response G_p(jω₁). Where ω₁ is the fundamental frequency and is defined as ω₁ = ω_d/ΔT. Hence, it can be expressed as

(18)

A single frequency from the frequency response would be enough for the calculation of the gain (K_p) and time delay required to estimate the integrating time delay model for the plant. That is supposed to be as

(19)

The time delay element in this model is utilized for the estimation of the time constants related to system mainly from the actuator and sensor. Let us assume that the integrating time delay model’s frequency response has been equivalent to the approximated G_p(jω₁) that leads to

(20)

Through the (20), K_p is determined as

(21)

Here,

. Time delay approximation is obtained through the comparison of the phase angle over both sides of (20). Which is expressed as,

(22)

Initially, the FSF is used for the extraction of useful information from the relay experiment response obtained from the roll axis system. The frequency response of the inner closed-loop system can now be estimated as follows:

(23)

Accordingly, the inner loop plant frequency response is then approximated as follows:

(24)

The frequency sampling filter also provides the fundamental frequency that is determined as ω₁ = 3.67 radians. K_p and d are then obtained through (21) and (22). Accordingly, with the help of inner loop frequency response and fundamental frequency information, these are calculated as K_p = 0.669 and d = 0.134. Which results into the formation of the estimated integrator plus delay model of the inner plant as

(25)

Subsequently, the similar procedure is repeated for the yaw axis identification, where the frequency responses have been estimated as

(26)

For the yaw inner loop, the fundamental frequency is calculated as ω₁ = 2.98 radians. Moreover, integrator plus time delay model for the yaw attitude axis plant is identified as

(27)

Hence, the overall estimated model for the attitude system of the quadrotor is presented as

(28)

where G_p(s), G_q(s), and G_r(s) are the estimated transfer functions for the roll, pitch, and yaw axes of the quadrotor, respectively. It can be noted that the estimated transfer function of the roll axis has also been assigned to pitch axis. The proposed quadrotor configuration is symmetric across the roll and pitch axes. Consequently, the dynamics for both axes would be identical. Hence, the identified roll axis transfer function would be used to design the control system for the pitch axis as well.

3.3. PID Controller Design

After obtaining the integrating time delay models, the PID controllers have been tuned on the basis of the estimated attitude models. The controller parameters were acquired through the set of well-established, simple, and robust tuning rules presented in [39, 40]. For these tuning rules, the values of the PID controllers are determined utilizing normalized parameters as presented below.

(29)

Assuming that the damping coefficient (ξ) is 1, the normalized parameters are then formulated as [32]

(30)

(31)

(32)

where β represents the scale factor, which has been chosen according to the requirement of the closed-loop time constant that is described as τ_cl = βd.

The inner loop plant of the quadrotor exhibits the dynamics that are faster. Hence, to achieve the quicker closed-loop response, a comparatively low-performance factor would be required. Hence, it is chosen to be β = 2. Accordingly, the PID parameters for the inner loop (roll rate) control system have been determined through (30)–(32) as K_c = 1.566, τ_I = 2.0281, and τ_D = 0.1018, whereas, for the yaw rate control, the PID controller values are determined as K_c = 8.170, τ_I = 1.031, and τ_D = 0.051.

After designing the inner loop PIDs, the controller parameters for the outer loop PIDs are tuned utilizing an approach that is illustrated in Figure 6. Since the dynamics of the plant in the outer loop are already known that are consisting of the integrator, such that, they achieve the angle position with the help of angular rate as illustrated in the given figure. Additionally, the inner loop systems have already been estimated. The approximated model depicting the plant in the outer plant can be obtained using the integrator plus delay system as [32]

(33)

where τ_cl denotes the closed-loop time constant and the d accounts for the inner loop time delay. While the integrating term in the above equation has been through the plant of outer loop, the delay time is practically through the approximation of the closed-loop inner subsystem. Therefore, for the controlled closed-loop inner, K_p is opted as 1.

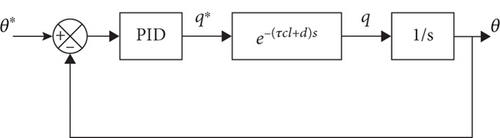
For the cascade control algorithm, to achieve closed-loop stability and robustness, it is required for the outer loops to possess the response time much slower than the subsequent inner loops for the robust and stable cascade control system [32]. Therefore, the outer loop time constant is chosen to be twice of the delay time, and β is opted as 4. In this way, the PID controller’s outer loop parameters are calculated as K_c = 1.566, τ_I = 2.028, and τ_D = 0.101 for the roll attitude axis. Similarly, values for the PID controllers to be used for the yaw attitude axis are obtained as K_c = 1.028, τ_I = 3.089, and τ_D = 0.155.

4. Validation

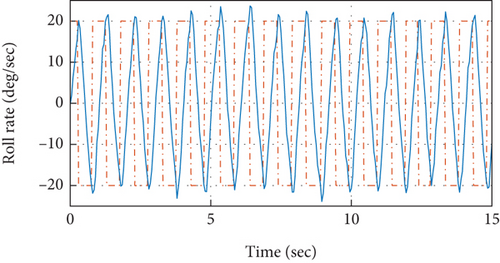
To validate the proposed idea, the PID controllers tuned and designed based on the relay with integrator mechanism are implemented over the quadrotor model under simulation environment. The model specifications of the quadrotor are presented in Table 1. The control system is implemented in the cascaded structure as presented in Figure 2. Atmospheric turbulences that are modeled based on the Dryden turbulence model [41] are injected into the model of the system as well that are demonstrated in [34, 42]. The attitude control performance to track desired roll axis is presented in Figure 7. It is observed from the measured roll angular response that the reference command for the roll axis has been traced efficiently without exhibiting any steady-state error. While the stable response of the quadrotor for the roll angular rate to achieve the required roll angle has been presented in Figure 8, it can further be observed that the control signals produced by outer control loops serve as reference signal for the related inner loop, as also depicted in Figure 8. Therefore, the set point command for roll angular rate in Figure 8 depicts the response of control system from the outer loop. In the similar approach, the efficacy of the designed and implemented control system for the remaining attitude axes such as pitch and yaw has also been analyzed in Figures 9-11–12.

Table 1. Quadrotor UAV model parameters.

Parameter	Value
I_xx	3.4 × 10⁻⁴ kgm²
I_yy	3.4 × 10⁻⁴ kgm²
I_zz	4.5 × 10⁻⁴ kgm²
α	9.5 × 10⁻⁷
k_d	2.4 × 10⁻⁹
r	0.3 m
ε_ms	70 ms
r_wv	1
m	0.7 kg
g	9.8 m/s²

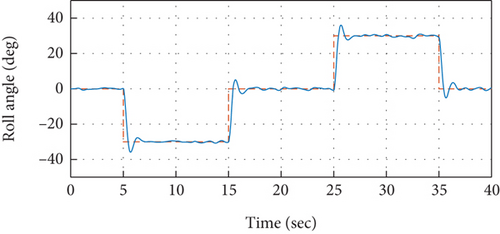
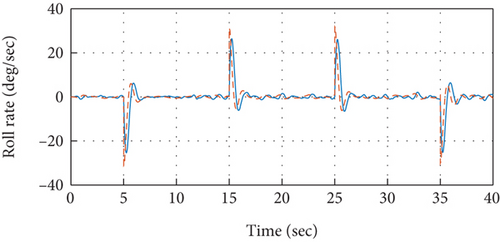
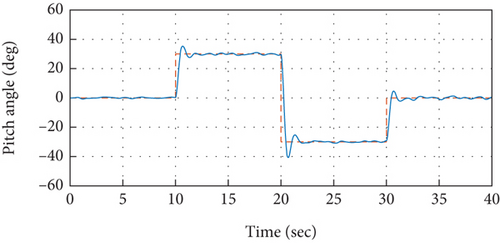
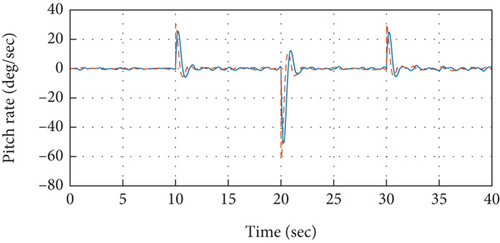
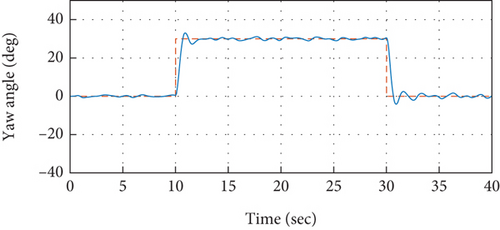
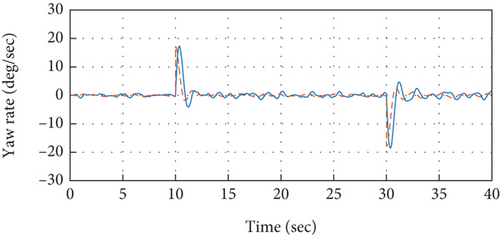
Moreover, comparison is performed in order to examine the superiority of the presented relay with embedded integrator-based automatic tuning approach over the conventional model-based PID controller design approach that is presented in [34]. The model-based PID controller is designed for the roll attitude system and is implemented over the quadrotor system. The comparison analysis is presented in Figure 13. It has been analyzed in the demonstrated results that the control performance of the relay-based autotuned control system provides superior attitude response compared to the model-based control system. An improved overall time response including both transient as well steady-state performance is experienced by the autotuned PID control system. Especially when implemented experimentally, the autotuned control system would prove to be even superior over its conventional counterpart control system. Due to the fact that it incorporates almost all of the actual dynamics of the quadrotor including sensors, actuators, and gyroscopics.

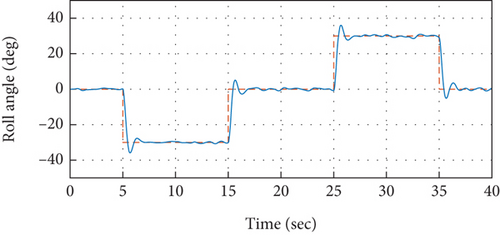
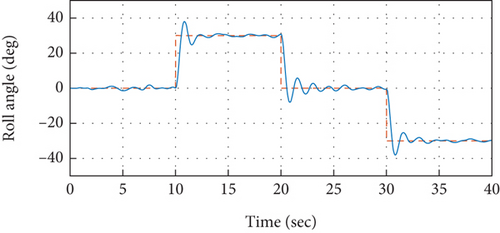
It is evident from the analysis of the demonstrated results that the proposed control system, based on cascaded PID control mechanism that has been tuned via the automatic tuning method based on the relay with integrator technique, is providing the required attitude performance with efficacy through keeping a better overall time response of the system including both transient and steady-state responses, since it exhibits minimal overshoots and is providing control operations at an improved rise and settling time.

5. Conclusions

A robust and stable control design approach for the quadrotor UAV has been presented. Cascaded control structure has been proposed to offer the control solutions to the dynamically complex underactuated quadrotor system. PID controllers for the each cascaded control structure stage are designed through the automatic tuning approach. Wherein the automatic tuning approach is based on the actual data acquired through the relay with an embedded integrator approach. The major theme of opting for the relay with embedded integrator approach is to make sure that the determined information of the plant is encompassed within the low and medium range of frequencies. Moreover, the effect of the measurement noise associated with the high frequencies is minimized due to the presence of the embedded integrator, and the need to use a hysteresis for the noise is reduced. The proposed cascaded PID control system designed through relay with an integrator-based automatic tuning approach is implemented over the actual quadrotor model. The results and observations demonstrated in this paper suggest that the designed control strategy is able to achieve the robust and stable attitude performance with an improved transient and steady state response.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research is funded by the Researchers Supporting Project Number (RSPD2023R947), King Saud University, Riyadh, Saudi Arabia.

Open Research

Data Availability

Data used to support the findings of this study are included within the article.

References

1 Floreano D. and Wood R. J., Science, technology and the future of small autonomous drones, Nature. (2015) 521, no. 7553, 460–466, https://doi.org/10.1038/nature14542, 2-s2.0-84930680445, 26017445.
10.1038/nature14542
CAS PubMed Web of Science® Google Scholar
2 Bassolillo S. R., D’Amato E., Notaro I., Ariante G., del Core G., and Mattei M., Enhanced attitude and altitude estimation for indoor autonomous UAVs, Drones. (2022) 6, no. 1, https://doi.org/10.3390/drones6010018.
10.3390/drones6010018
Google Scholar
3 Hua H., Fang Y., Zhang X., and Biao L., A novel robust observer-based nonlinear trajectory tracking control strategy for quadrotors, IEEE Transactions on Control Systems Technology. (2021) 29, no. 5, 1952–1963, https://doi.org/10.1109/TCST.2020.3024805.
10.1109/TCST.2020.3024805
Web of Science® Google Scholar
4 Kunovjanek M. and Wankmuller C., Containing the COVID-19 pandemic with drones-feasibility of a drone enabled back-up transport system, Transport Policy. (2021) 106, 141–152, https://doi.org/10.1016/j.tranpol.2021.03.015, 33846672.
10.1016/j.tranpol.2021.03.015
PubMed Web of Science® Google Scholar
5 Idrissi M., Salami M., and Annaz F., A review of quadrotor unmanned aerial vehicles: applications, architectural design and control algorithms, Journal of Intelligent & Robotic Systems. (2022) 104, no. 2, 1–33, https://doi.org/10.1007/s10846-021-01527-7.
10.1007/s10846-021-01527-7
Web of Science® Google Scholar
6 Nex F., Armenakis C., Cramer M., Cucci D. A., Gerke M., Honkavaara E., Kukko A., Persello C., and Skaloud J., UAV in the advent of the twenties: where we stand and what is next, ISPRS Journal of Photogrammetry and Remote Sensing. (2022) 184, 215–242, https://doi.org/10.1016/j.isprsjprs.2021.12.006.
10.1016/j.isprsjprs.2021.12.006
Web of Science® Google Scholar
7 Lu Q., Ren B., and Parameswaran S., Uncertainty and disturbance estimator-based global trajectory tracking control for a quadrotor, IEEE/ASME Transactions on Mechatronics. (2020) 25, no. 3, 1519–1530, https://doi.org/10.1109/TMECH.2020.2978529.
10.1109/TMECH.2020.2978529
Web of Science® Google Scholar
8 Wang H., Cui G., and Li H., Fixed-time adaptive tracking control for a quadrotor unmanned aerial vehicle with input saturation, Actuators. (2023) 12, no. 3, https://doi.org/10.3390/act12030130.
10.3390/act12030130
PubMed Web of Science® Google Scholar
9 Li Y., Yonezawa K., and Liu H., Effect of ducted multi-propeller configuration on aerodynamic performance in quadrotor drone, Drones. (2021) 5, no. 3, https://doi.org/10.3390/drones5030101.
10.3390/drones5030101
Google Scholar
10 He X., Kou G., Calaf M., and Leang K. K., In-ground-effect modeling and nonlinear-disturbance observer for multirotor unmanned aerial vehicle control, Journal of Dynamic Systems, Measurement, and Control. (2019) 141, no. 7, https://doi.org/10.1115/1.4043221, 2-s2.0-85065234057.
10.1115/1.4043221
Web of Science® Google Scholar
11 Hoshu A. A., Fisher A., and Wang L., Cascaded attitude control for heterogeneous multirotor UAS for enhanced disturbance rejection, 2019 Australian and New Zealand control conference (ANZCC), 2019, Auckland, New Zealand, 110–115, https://doi.org/10.1109/anzcc47194.2019.8945696.
10.1109/anzcc47194.2019.8945696
Google Scholar
12 Emran B. J. and Najjaran H., A review of quadrotor: an underactuated mechanical system, Annual Reviews in Control. (2018) 46, 165–180, https://doi.org/10.1016/j.arcontrol.2018.10.009, 2-s2.0-85055019601.
10.1016/j.arcontrol.2018.10.009
Web of Science® Google Scholar
13 Yang P., Wang Z., Zhang Z., and Hu X., Sliding mode fault tolerant control for a quadrotor with varying load and actuator fault, Actuators. (2021) 10, no. 12, https://doi.org/10.3390/act10120323.
10.3390/act10120323
Web of Science® Google Scholar
14 Sattar A., Wang L., Ansari S., Hoshu A. A., and Khan S. K., Disturbance rejection enhancement using predictive control for the fixed-wing uav with multiple ailerons, International Journal of Adaptive Control and Signal Processing. (2023) 37, no. 5, 1072–1101, https://doi.org/10.1002/acs.3561.
10.1002/acs.3561
Web of Science® Google Scholar
15 Zhao K., Zhang J., Ma D., and Xia Y., Composite disturbance rejection attitude control for quadrotor with unknown disturbance, IEEE Transactions on Industrial Electronics. (2020) 67, no. 8, 6894–6903, https://doi.org/10.1109/TIE.2019.2937065.
10.1109/TIE.2019.2937065
Web of Science® Google Scholar
16 Wang H. and Chen M., Trajectory tracking control for an indoor quadrotor uav based on the disturbance observer, Transactions of the Institute of Measurement and Control. (2016) 38, no. 6, 675–692, https://doi.org/10.1177/0142331215597057, 2-s2.0-84976395902.
10.1177/0142331215597057
Web of Science® Google Scholar
17 Zheng L. and Zhang Z., Convergence and robustness analysis of novel adaptive multilayer neural dynamics-based controllers of multirotor UAVs, IEEE Transactions on Cybernetics. (2021) 51, no. 7, 3710–3723, https://doi.org/10.1109/TCYB.2019.2923642, 31295138.
10.1109/TCYB.2019.2923642
PubMed Web of Science® Google Scholar
18 Zheng L., Deng F., Yu Z., Luo Y., and Zhang Z., Multilayer neural dynamics-based adaptive control of multirotor UAVs for tracking time-varying tasks, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2022) 52, no. 9, 5889–5900, https://doi.org/10.1109/TSMC.2021.3130748.
10.1109/TSMC.2021.3130748
Web of Science® Google Scholar
19 Zhang Z., Zhou B., Zheng L., Zhang Z., Song C., and Pei H., A varying-parameter adaptive multi-layer neural dynamic method for designing controllers and application to unmanned aerial vehicles, IEEE Transactions on Intelligent Transportation Systems. (2021) 22, no. 8, 4876–4888, https://doi.org/10.1109/TITS.2020.2983522.
10.1109/TITS.2020.2983522
Web of Science® Google Scholar
20 Zuo Z. and Mallikarjunan S., adaptive backstepping for robust trajectory tracking of UAVs, IEEE Transactions on Industrial Electronics. (2017) 64, no. 4, 2944–2954, https://doi.org/10.1109/TIE.2016.2632682, 2-s2.0-85015336738.
10.1109/TIE.2016.2632682
Web of Science® Google Scholar
21 Abbaspour A., Yen K. K., Forouzannezhad P., and Sargolzaei A., A neural adaptive approach for active fault-tolerant control design in UAV, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2020) 50, no. 9, 3401–3411, https://doi.org/10.1109/TSMC.2018.2850701, 2-s2.0-85050245079.
10.1109/TSMC.2018.2850701
Web of Science® Google Scholar
22 Kang C., Park B., and Choi J., Scheduling PID attitude and position control frequencies for time-optimal quadrotor waypoint tracking under unknown external disturbances, Sensors. (2022) 22, no. 1.
Web of Science® Google Scholar
23 Mystkowski A., Robust control of the micro UAV dynamics with an autopilot, Journal of Theoretical and Applied Mechanics. (2013) 51, no. 3, 751–761.
Web of Science® Google Scholar
24 Micropilot, Micropilot autopilots, https://www.micropilot.com/index.htm.
Google Scholar
25 Pixhawk-Ardupilot, Px4 autopilot, https://docs.px4.io/master/en/flight_stack/controller_diagrams.html.
Google Scholar
26 Paparrazzi, Paparazzi UAV flight controllers, https://wiki.paparazziuav.org.
Google Scholar
27 Zhang R., Quan Q., and Cai K.-Y., Attitude control of a quadrotor aircraft subject to a class of time-varying disturbances, IET Control Theory and Applications. (2011) 5, no. 9, 1140–1146, https://doi.org/10.1049/iet-cta.2010.0273, 2-s2.0-79960599728.
10.1049/iet-cta.2010.0273
Web of Science® Google Scholar
28 Hoffer N. V., Coopmans C., Jensen A. M., and Chen Y. Q., A survey and categorization of small low-cost unmanned aerial vehicle system identification, Journal of Intelligent & Robotic Systems. (2014) 74, no. 1-2, 129–145, https://doi.org/10.1007/s10846-013-9931-6, 2-s2.0-84892832486.
10.1007/s10846-013-9931-6
Web of Science® Google Scholar
29 Liang X., Fang Y., Sun N., and He L., Nonlinear hierarchical control for unmanned quadrotor transportation systems, IEEE Transactions on Industrial Electronics. (2018) 65, no. 4, 3395–3405, https://doi.org/10.1109/TIE.2017.2752139, 2-s2.0-85030790526.
10.1109/TIE.2017.2752139
Web of Science® Google Scholar
30 Hoshu A. A., Wang L., Sattar A., and Fisher A., Auto-tuning of attitude control system for heterogeneous multirotor uas, Remote Sensing. (2022) 14, no. 7, https://doi.org/10.3390/rs14071540.
10.3390/rs14071540
Web of Science® Google Scholar
31 Chen X. and Wang L., Quadrotor cascade PID controller automatic tuning, 2016 Australian control conference (AuCC), 2016, Newcastle, NSW, Australia, 311–316, https://doi.org/10.1109/aucc.2016.7868208, 2-s2.0-85016972190.
10.1109/aucc.2016.7868208
Google Scholar
32 Wang L., PID Control System Design and Automatic Tuning Using MATLAB/Simulink, 2020, John Wiley and Sons, https://doi.org/10.1002/9781119469414.
10.1002/9781119469414
Google Scholar
33 Bouabdallah S., Murrieri P., and Siegwart R., Design and control of an indoor micro quadrotor, IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA ′04. 2004, 2004, New Orleans, LA, USA, 4393–4398, https://doi.org/10.1109/robot.2004.1302409.
10.1109/robot.2004.1302409
Google Scholar
34 Hoshu A. A., Wang L., Fisher A., and Sattar A., Cascade control for heterogeneous multirotor UAS, International Journal of Intelligent Unmanned Systems. (2022) 10, no. 4, 363–384, https://doi.org/10.1108/IJIUS-02-2021-0008.
10.1108/IJIUS-02-2021-0008
Web of Science® Google Scholar
35 Huo X., Huo M., and Karimi H. R., Attitude stabilization control of a quadrotor UAV by using backstepping approach, Mathematical Problems in Engineering. (2014) 2014, 9, https://doi.org/10.1155/2014/749803, 2-s2.0-84896138008, 749803.
10.1155/2014/749803
Web of Science® Google Scholar
36 Hoshu A. A., Wang L., Ansari S., Sattar A., and Bilal M. H. A., System identification of heterogeneous multirotor unmanned aerial vehicle, Drones. (2022) 6, no. 10, https://doi.org/10.3390/drones6100309.
10.3390/drones6100309
Google Scholar
37 Sattar A., Wang L., Hoshu A. A., Ansari S., Karar H.-e., and Mohamed A., Automatic tuning and turbulence mitigation for fixed-wing UAV with segmented control surfaces, Drones. (2022) 6, no. 10, https://doi.org/10.3390/drones6100302.
10.3390/drones6100302
Google Scholar
38 Kreyszig E., Advanced Engineering Mathematics, 2010, John Wiley and Sons.
Google Scholar
39 Wang L. and Cluett W. R., Tuning PID controllers for integrating processes, IEE Proceedings-Control Theory and Applications. (1997) 144, no. 5, 385–392, https://doi.org/10.1049/ip-cta:19971435, 2-s2.0-0031223920.
10.1049/ip-cta:19971435
Web of Science® Google Scholar
40 Wang L., From Plant Data to Process Control: Ideas for Process Identification and PID Design, 2000, CRC Press, https://doi.org/10.1201/9781482273007, 2-s2.0-85054397474.
10.1201/9781482273007
Google Scholar
41 US Military Handbook MIL-HDBK, Flying Qualities of Piloted Aircraft, 1997, Department of Defence.
Google Scholar
42 Abichandani P., Lobo D., Ford G., Bucci D., and Kam M., Wind measurement and simulation techniques in multi-rotor small unmanned aerial vehicles, IEEE Access. (2020) 8, 54910–54927, https://doi.org/10.1109/ACCESS.2020.2977693.
10.1109/ACCESS.2020.2977693
Web of Science® Google Scholar

All articles

Cascaded Control System Design for Quadrotor UAV through Relay with Embedded Integrator-Based Automatic Tuning Approach

Abstract

1. Introduction