Volume 2023, Issue 1 6506144

Research Article

Open Access

Maximum Power Extraction in Photovoltaic Systems Using High-Performance Adaptive Control Approach

Ahmed Ouaret

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Hocine Lehouche,

Hocine Lehouche

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Adel Oubelaid,

Adel Oubelaid

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Arvind Yadav,

Arvind Yadav

Department of Electrical Engineering, GLA University, Mathura, India gla.ac.in

Search for more papers by this author

Boubekeur Mendil,

Boubekeur Mendil

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Ievgen Zaitsev,

Corresponding Author

Ievgen Zaitsev

[email protected]

orcid.org/0000-0003-3303-471X

Department of Theoretical Electrical Engineering and Diagnostics of Electrical Equipment, Institute of Electrodynamics, National Academy of Sciences of Ukraine, Peremogy, 56, Kyiv-57 03680, Ukraine nas.gov.ua

Search for more papers by this author

Ahmed Ouaret,

Ahmed Ouaret

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Hocine Lehouche,

Hocine Lehouche

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Adel Oubelaid,

Adel Oubelaid

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Arvind Yadav,

Arvind Yadav

Department of Electrical Engineering, GLA University, Mathura, India gla.ac.in

Search for more papers by this author

Boubekeur Mendil,

Boubekeur Mendil

Laboratoire de Technologie Industrielle et de l’Information, Faculté de Technologie, Université de Bejaia, 06000 Bejaia, Algeria univ-bejaia.dz

Search for more papers by this author

Ievgen Zaitsev,

Corresponding Author

Ievgen Zaitsev

[email protected]

orcid.org/0000-0003-3303-471X

Search for more papers by this author

First published: 19 December 2023

https://doi.org/10.1155/2023/6506144

Academic Editor: Daniel T. Cotfas

Share a link

Email
Wechat
Bluesky

Abstract

The nonlinearities present in photovoltaic (PV) generator models can significantly impact the performance of PV systems, leading to decreased system efficiency and reduced profitability. This paper is aimed at addressing these challenges by developing a novel control algorithm based on a high-performance adaptive control method for photovoltaic systems. The proposed algorithm is designed to effectively track set points and optimize power extraction even in the presence of disturbances. The key contribution of this work lies in the application of this control strategy specifically to PV systems to achieve optimal performance. When compared to traditional control methods, the proposed approach demonstrates significant improvements, notably in terms of power extraction efficiency and system loss reduction. Moreover, the control algorithm effectively ensures accurate tracking of set points. These outcomes underscore the notable performance enhancements facilitated by the proposed algorithm. In conclusion, the developed control algorithm offers superior performance in optimizing power extraction and maintaining precise set point tracking for PV systems, leading to improved system efficiency and increased profitability.

1. Introduction

In the pursuit of sustainable and low-carbon energy solutions, the imperative to mitigate carbon emissions has fueled extensive research into renewable energy systems [1]. Solar renewable energy systems create significantly fewer harmful environmental effects than conventional energy sources, such as air pollution and greenhouse gas emissions [2]. Renewable energy sources are extensively used in several sectors, such as energy production [3, 4], transportation [5, 6], and agriculture [7, 8]. The effectiveness of renewable energy systems in energy production depends greatly on external (environmental) factors. Due to changing effects and circumstances, solar renewable energy does not have a fixed voltage or current source [9].

Maximum power point tracking (MPPT) is a technique used in solar renewable energy systems (SRES) to automatically track photovoltaic arrays’ maximum power point (MPP) [10, 11]. The rapid and abrupt changes in the environment have a substantial impact on both the MPP and the output I-V curve of PV arrays [12, 13]. Therefore, when developing and putting into practice MPPT algorithms, the environment parameter fluctuation should be considered. The literature on SRES has thoroughly covered a number of significant research subjects, including rapid changes in solar irradiance, changes in PV array temperature, and partial shadowing conditions (PSC) [14, 15]. A variety of high-accuracy MPPT methods have been provided by researchers to control the internal and exterior effects of SRES. Additionally, as stated in [16, 17], researchers have created a variety of analytical and numerical MPPT methods for application in SRES. The terminal voltage (V) and current of the detected PV array have mostly been tuned (I). To harvest the maximum PV power possible, further research projects have employed the measured λ and T.

MPPT algorithms are classified into three categories (Figure 1) based on the type of optimization algorithm used [18]. The first group represents the conventional MPPT methods, which are classified into two categories: the direct (online) and indirect (offline) approach [9, 19]. Perturb and observe and incremental conductance algorithms, derived from hill climbing local search family optimization algorithms, have been presented as direct MPPT methods [20]. Fractional open circuit voltage and fractional short circuit current are the commonly used indirect MPPT methods, where V and I are computed based on a ratio of the open circuit voltage (V_oc) or the short circuit current (I_sc) in the offline state [21]. The second group represents the novel MPPT methods, which were used to obtain the global MPP in SRES. Novel optimization algorithms, including artificial intelligence and biologically inspired, have been used to obtain the global MPP [9, 22, 23]. In this article, the novel MPPT approaches are classified according to their interaction with λ and T. The third group represents the hybrid methods, which are a combination between conventional MPPT algorithms and novel MPPT techniques [14]. Various hybrid techniques have been used in the SRES. However, only a few hybrid MPPT methods based on linear or nonlinear control systems are found in the literature [24].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A flowchart of the existing MPPT technique.

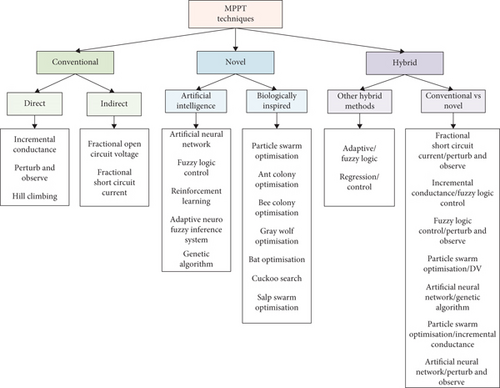
The aim of this paper is the development of a new algorithm inspired from an indirect adaptive control method applied to the photovoltaic system to ensure optimum power point tracking. The superiority of this control technique compared with others appears in its ability to adapt to different functional circumstances and its speed, accuracy, and robustness against the presence of various disturbances.

This paper is structured as follows: Section 2 presents the solar PV cell model. Section 3 is devoted to the presentation of indirect adaptive control. Section 4 addresses the use of the proposed control algorithm in the PV system. The robustness study is presented in Section 4. In the final section, conclusions and perspectives are drawn.

2. PV Cell Modeling

Generally, the choice of a model is related to the targeted utility. Since a PV cell forms the cornerstone of a module, it is preferable to provide a broad description of a PV cell before moving on to the study of the model with five parameters. The inputs and outputs of a solar PV cell are highlighted in Figure 2, where E, T, V, and I represent, respectively, irradiation, environment temperature, voltage, and current.

Several mathematical models are used to describe the behavior and operation of PV. Two methods are presented below: the single-diode model and the dual-diode model.

2.1. Modeling of a Single-Diode PV Cell

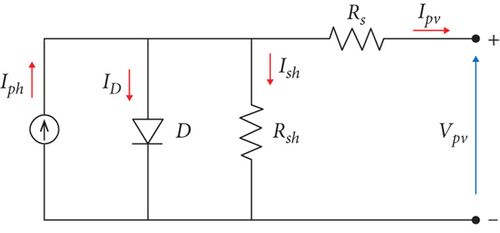
The equivalent electric circuit of the PV cell is given in Figure 3. The diode in the equivalent circuit below emulates some phenomena that occur at the panel cell level. A shunt resistor R_sh is used to model the losses caused by contaminants surrounding the junction and on the cell’s corners, while a series resistor R_S is used to model the ohmic losses [25, 26].

The PV current obtained from the equivalent circuit shown in Figure 3 is given by equation (1) [25] in which I_ph represents the photocurrent, which is related to the illumination E and the temperature T as shown in Figure 3, and E_ref represents the illumination and temperature under STC conditions. T_j, T_jref in the last-mentioned equation are, respectively, the junction and reference temperature, respectively (°K). P₁, P₂, P₃ are fixed parameters. Current I_ph is given by equation (2) [25].

()

The junction temperature T_j is provided by equation (3) shown below in which N_oct represents the nominal solar cell operating temperature or model T_a is the ambient temperature [25].

()

2.1.1. The Diode Current (I_D)

The diode current is given by the equation (4) [26], as shown below where R_s, q, k, A, N_s, and I_s stand, respectively, for series resistance (Ohm), elementary charge (1.6 × 10⁻¹⁹ C), constant of Boltzmann (1.38 × 10⁻²³ (SI)), the ideality coefficient of a cell, the number of cells linked in series and/or parallel, and the saturation current (A).

()

The detailed expression of the peak current mentioned in equation (4) is given by equation (5) [26], where P4 is a constant and E_g is the gap energy (1.76 × 10⁻¹⁹).

()

2.1.2. Saturation Current (I_sh)

Equation (6) [26] below gives the shunt saturation current:

()

By inserting equations (2), (4), and (6) into equation (1), we obtain the overall PV current as indicated by the following equation:

()

2.2. Modeling of a Dual-Diode PV Cell

In this model, the photovoltaic cell is represented by the electrical circuit illustrated in Figure 4 which consists of a current source modeling the luminous flux, two diodes for the polarization of the cell, a shunt resistance, and a series resistance.

The current generated by the PV cell is given by equation (8) [27–29], shown below:

()

The current of the diode is given by [28].

()

With I₀₁ and I₀₂ being the diode saturation currents,

()

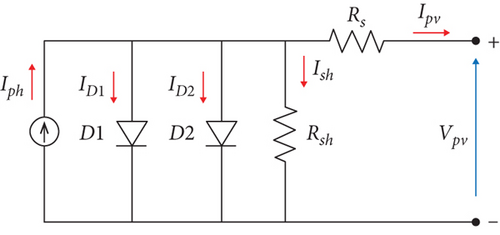
The method used in our work is that of single-diode because it is the most commonly used method for modeling the behavior of a photovoltaic (PV) cell due to its simplicity, sufficient accuracy, intuitive understanding, availability, and standardization. As mentioned earlier, the single-diode model requires only a few parameters to characterize the performance of the PV cell, making it easily accessible even to beginners. Additionally, the single-diode model is based on a representation of the PV cell in terms of a single-diode element, which makes it easier to understand intuitively. Furthermore, the one-diode model has been standardized by the International Electrotechnical Commission (IEC) and is widely used in the PV industry for the characterization and certification of PV cells.

In this paper, a PV cell of type SIEMENS SM 110-24 is used. Table 1 shown below provides the technical information of the last-mentioned PV cell type.

Table 1. Used PV cell parameters [30, 31].

Symbol	Description	Values	Unit
P_pv	PV power	110	W
I_mpp	Maximum current at PPM	3.15	A
V_mpp	The maximum voltage at PPM	35	V
I_cc	Short circuit current	3.45	A
V_co	Open circuit voltage	43.5	V
a_oc	Temperature coefficient of short circuit current	1.4	mA/°C
B_oc	Voltage coefficient	-152	mV/°C
P_mpp	Maximum power	110	W

3. Indirect Adaptative Control

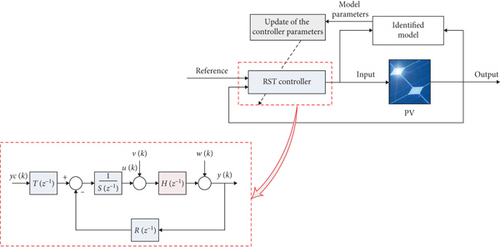
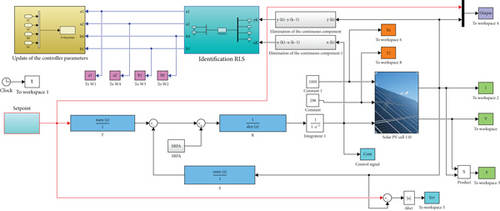
The basic philosophy of indirect adaptive control is to use input-output data to estimate the parameters of an unknown system. The estimated parameters are then used to alter the controller settings so that the controlled system’s transfer function matches that of the model [32, 33]. The indirect adaptive control has been applied on many applications, among them [30–32]. The block diagram of the indirect adaptive control is shown in Figure 5. One can notice how controller parameters are continuously adapted by the designed model.

Equation (11), which is shown below, describes the transfer function of the model depicted in Figure 5 when a monovariable discrete linear invariant model is taken into account. A(z⁻¹) and B(z⁻¹) are two discrete polynomials of n^th and m^th order as stated by equations (12) and (13). It is worth noticing that variables u and y in equation (11) represent, respectively, system input and output. v is a random external disturbance, and d is the difference in order between the discrete polynomials A and B.

()

The polynomial coefficients A(z⁻¹) and B(z⁻¹) given by equations (12) and (13) are identified using the recursive least square method, as it will be discussed in the subsection below.

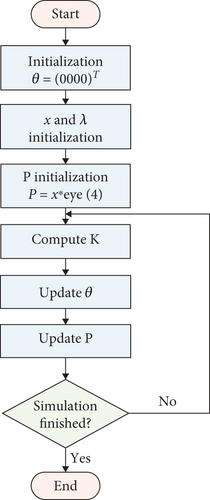
3.1. Algorithm of Recursive Least Squares

The purpose is to minimize the quadratic criterion—a discrepancy in the actual PV system output—at each sample period and to minimize, at each sampling time, the quadratic criterion formed by the difference between the output of the actual PV system. This is expressed mathematically using equation (14), shown below, where λ is the forgetting factor limited between 0 and 1.

()

where θ is a vector that contains the coefficients of the two polynomials A and B as highlighted by equation (15). φ^T(k) is a vector that includes the identified PV system inputs and outputs.

()

The overall form of the recursive least square method is given by equations (17), (18), and (19), as shown below.

()

The estimated output of the PV system is then calculated using equations (20) and (21), as shown below.

()

The flowchart shown in Figure 6 describes the main steps of the used least square method.

3.2. RST Control Approach

By using an algebraic approach of pole positioning, the RST controller is created. The aim is to simulate in closed loop the system behavior that may be represented as a rational fraction z⁻¹ using a transfer function model z⁻¹. This function is typically of the second order and is defined using the following types of criteria: static gain, damping, and overshoot [33, 34]. The model’s denominator A_m(z⁻¹) is often determined using these criteria. On the other hand, B_m(z⁻¹) cannot be entirely forced as an option. These limits will not have a significant impact on the behavior of the system since the influence of the transfer function’s zeros is less than that of its poles [35, 36].

The internal structure of the RST controller used in this paper is highlighted in Figure 5, where R, S, and T are discrete polynomials [37, 38].

The general form of the control law is given by equation (22), where Y and Y_c represent the system output and the setpoint, respectively.

()

The input U(z) can be written as indicated in the following equation:

()

The PV system’s closed-loop output is provided by equation (24) below.

()

where v(k) and w(k) are random external disturbances. Multiplying (22) and (24) by A(z⁻¹) and R(z⁻¹) successively, then replacing (23) in (25), we get equation (26), as shown below.

()

Multiplying equation (26) by B(z⁻¹) and equation (23) by S(z⁻¹) yields equation (28), as shown below.

()

3.2.1. Algebraic Synthesis of the RST Control Law

For V = W = 0, the transfer function of the PV system shown in Figure 5 is given in the following equation:

()

The polynomials R(z⁻¹), S(z⁻¹), S(z⁻¹), and T(z⁻¹) of the RST controller will be dimensioned in order that this closed loop transfer function will be equal to the transfer function of the model. This is expressed mathematically using equation (31), as shown below.

()

It can be noted that the term z^−d or d denotes the integer number of sample periods in the pure delay [39, 40]. Poles are chosen so that p(z⁻¹) will be stable and will express the desired natural frequency and damping ratio. This is done by separating the polynomial p(z⁻¹) into two parts as expressed by equation (32), as shown below.

()

(i)
P_d(z⁻¹) consists of the system’s dominant poles
(ii)
P_a(z⁻¹) consists of the system’s auxiliary poles

For the calculation of P_d(z⁻¹), the part of P_d(z⁻¹) contains two dominant complex poles, which are characterized by the proper pulsation w_n and the damping coefficient ξ. The polynomial P_d is then rewritten as indicated by equation (33), as shown below [41, 42].

()

With , , 0.25 ≤ w_nT_e ≤ 1.5, and 0.7 ≤ ζ ≤ 1. For P_a(z⁻¹), the auxiliary poles are introduced for robustness, and they are chosen faster than the dominant poles [43, 44].

4. Simulation and Results

Table 2 lists the different PV panel parameters. The control method consists of an identifier based on the least mean squares algorithm with a forgetting factor, an adaptive controller, a system, and RST polynomials [45, 46]. The recursive method with a fixed forgetting factor was used to estimate the system parameters in real time and to update the coefficients of the RST controller polynomials at each instant t. The developed Simulink simulation model is illustrated in Figure 7.

Table 2. Lists of different PV panel parameters.

Experimental parameters	Value
E_s	1000 W/m²
T_a	25°C
P₁	0.00345
P₂	0.58 × 10⁻⁵
P₃	−0.336 × 10⁻⁴
P₄	381.2367
R_s	0.6 Ω
R_p	150 Ω
N_s	72

The recursive least squares method implementation presented above is used to evaluate the system using the equation’s second-order model.

()

After several simulations were performed using the different parameter values obtained using the identification algorithm, we obtained the best plant parameters in terms of error and convergence. These parameters are summarized in Table 3 [47, 48].

Table 3. Parameter identification results.

1. Initialization
(i) A(z⁻¹) = 1 + 0.5z⁻¹ + 0.5z⁻².
(ii)B(z⁻¹) = 0.5z⁻¹ + 0.5z⁻².
2. Parameter identification
(i) λ = 0.956, F(0) = 10^6∗I_4X4..
(ii) Sampling period T_e = 0.1sec.
3. The simulation time is 24 s
4. The coefficients of the model after simulation
(i) A(z⁻¹) = 1 + 0.0007561z⁻¹ − 0.00177z⁻².
(ii) B(z⁻¹) = 0.00323z⁻¹ + 0.0007561z⁻².
The model’s transfer function is as follows:
H(z⁻¹) = 0.00323z⁻¹ + 0.0007561z⁻²/1 + 0.0007561z⁻¹ − 0.00177z⁻².

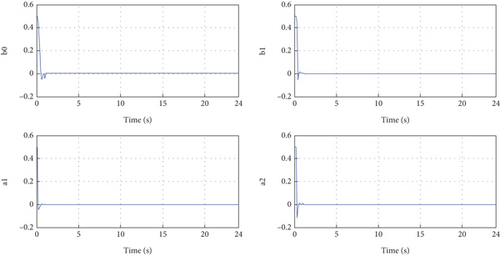
Figure 8 presents a significant observation regarding the evolution of the determined model parameters. The plotted data clearly demonstrates the convergence of all coefficients of the identified model to constant values. This convergence implies that the identification model successfully captures the dynamics and behavior of the actual system. Consequently, the identification approach used in this study is validated, as it effectively estimates the parameters of the system based on available data. The confirmed accuracy of the identification model establishes its reliability in representing the actual system, reinforcing the validity of the employed methodology [49, 50]. Therefore, the findings from Figure 8 provide strong evidence supporting the successful validation of the identification approach and its ability to accurately represent the behavior of the studied system.

The obtained RST controller parameters are given in Table 4.

Table 4. Results and parameters of the RST controller.

1. Initialization
(i) S(z⁻¹) = 1 + z⁻¹ + z⁻².
(ii) R(z⁻¹) = 1 + z⁻¹ + z⁻².
(iii) T(z⁻¹) = 1 + z⁻¹ + z⁻² + z⁻³.
2. The controller algorithm parameters
(i) α = 10⁶, λ = 0.956, T_e = 0.1sec and d = 0.
3. The simulation period is 24 s.
4. RST polynomials after simulation
(i) R(z⁻¹) = [1 − 0.33672446714 − 4.14600796735e − 005.]
(ii) S(z⁻¹) = [98.3401255755 − 1.54654023733 0.836989869629]
(iii) T(z⁻¹) = [85.2367329234 − 1.53426119262 ⋯ 0.00920556715572 1.84111343114e − 005]

To maximize power extraction and restore the reference signal that served as our control, we simulated the panel in an open loop with 1000 W/m² of irradiation and 25°C of temperature, and the simulation results are shown in Figure 9.

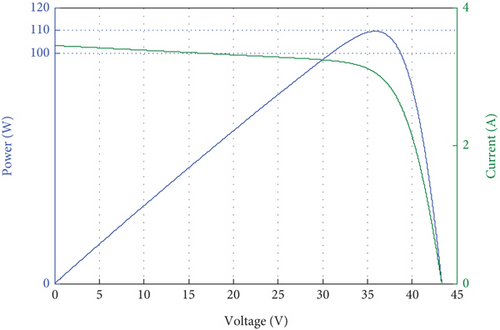
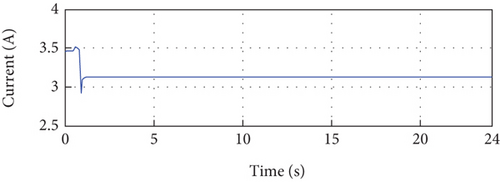
From Figure 9, one can notice that the maximum power, voltage, and current at the maximum power point are, respectively, as follows: P_mpp = 109.2092W, V_mpp = 34.9980V, and I_mpp = 3.1204A.

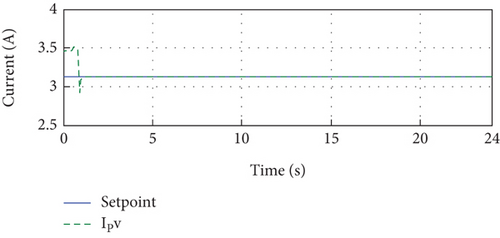
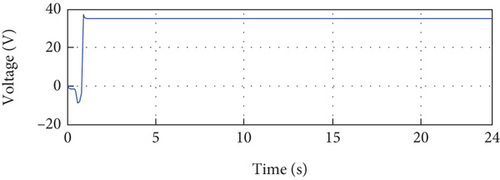
Figure 10 presents the simulation results conducted under specific conditions of a temperature of 25°C and an irradiance of 1000 W/m². In Figure 10(a), it is evident that the PV current closely tracks its reference value with a tolerable error, indicating a successful current control. Moving to Figure 10(c), the behavior of the PV voltage is depicted. After an initial transition period of 1 second, the PV voltage converges to the desired reference voltage of 35 volts, demonstrating effective voltage control.

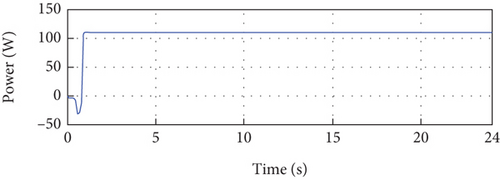
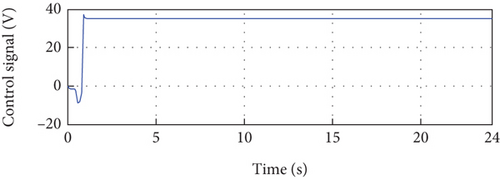
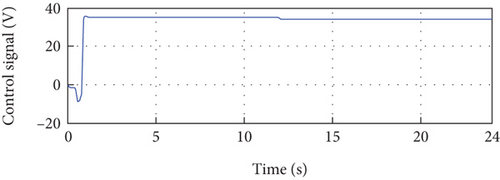
Examining Figure 10(e), we observe the developed PV power, which is the product of the PV current and voltage. This figure showcases the power output of the PV system, reflecting the combined effect of the controlled current and voltage. Figure 10(f) presents the control signal, which exhibits initial oscillations at the beginning of the simulation due to parameter adaptation. However, it stabilizes over time and reaches a steady-state value, indicating a successful control response.

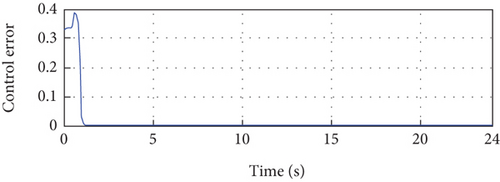
Lastly, Figure 10(b) illustrates the error between the control signal and the reference signal. Initially, this error experiences transient behavior due to parameter adaptation, but it gradually converges to almost zero, indicating the effectiveness of the control algorithm in minimizing deviations from the desired reference.

Overall, the simulation results presented in Figure 10 provide detailed insights into the behavior and performance of the PV system under the given conditions. The close tracking of the PV current and voltage to their respective references, the development of PV power, and the convergence of the control signal and error demonstrate the successful implementation of the control strategy and its ability to regulate the PV system’s performance simulation due to parameter adaptation. After that, it stabilizes at its steady-state value. Figure 10(b) depicts the error between the error control signal, which converges to almost zero after transient parameter adaptation.

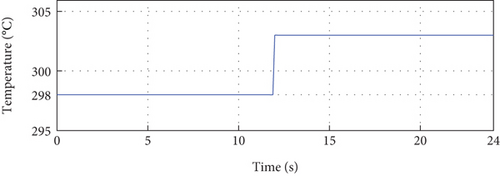
To verify the effectiveness and robustness of the proposed control technique, three scenarios are considered. In the first scenario, the irradiance is varied, as shown in Figure 11(a), with a temperature fixed at a value of 25°C. The second scenario corresponds to the variation of the temperature, as shown in Figure 11(b), with irradiance set at a value of 1000 W/m².

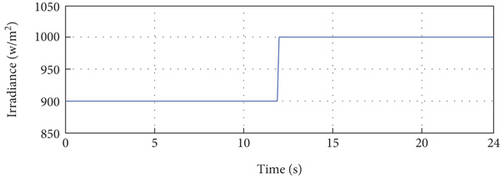
In the third scenario, we consider the variation of irradiance and temperature simultaneously, as shown in Figure 12.

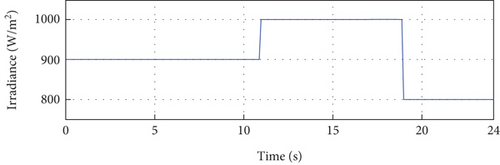
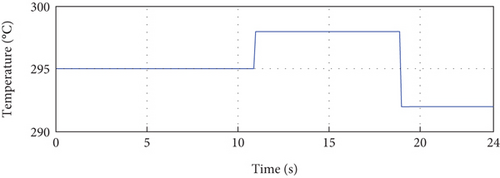
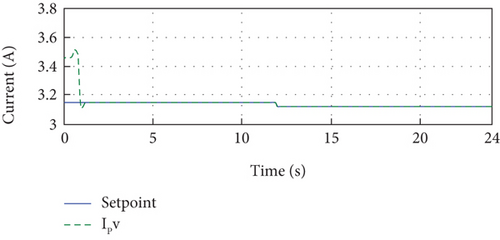
Figure 13(a) shows the PV output current and its reference. From Figure 13(a), we notice that the current I_PV follows its reference perfectly despite the variation of the irradiance. This confirms that the control technique is efficient and robust against the variation of irradiance. The error between the PV-developed current and its reference is very small during the whole simulation period. The deviation at the beginning of the simulation period is due to the variation in the parameters of the identified model. In other words, as soon as we obtain the PV model parameters, the error between the PV current and its reference will vanish.

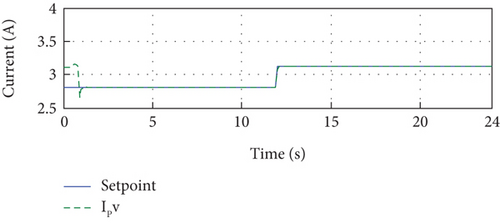
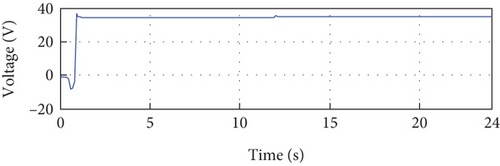
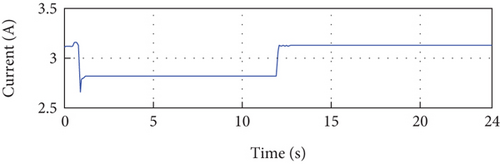
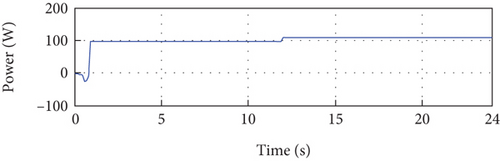
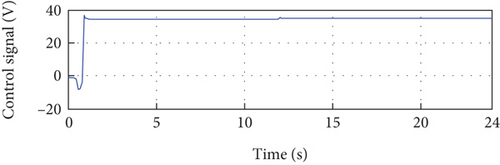
Figure 13(a) presents the comparison between the PV output current and its reference. It is evident from this figure that the current I_PV consistently tracks its reference, demonstrating the effectiveness and robustness of the control technique against irradiance variations. The small error observed between the PV-developed current and its reference throughout the entire simulation period further confirms the accuracy of the control approach. The initial deviation in the error can be attributed to the variation in the identified model’s parameters. However, as soon as the PV model parameters are obtained, the error between the PV current and its reference diminishes.

Figure 13(b) displays the error between the reference and the output PV current over the entire simulation time. This error is consistently small, validating the precise tracking of the current with respect to the reference.

Additionally, Figures 13(c) and 13(e) illustrate the corresponding voltage and power, respectively, for the current depicted in Figure 13(a). These figures demonstrate that both the voltage and current closely follow their respective references, indicating accurate control of these parameters.

Furthermore, Figure 13(f) exhibits the control signal, which remains stable throughout the simulation without any oscillations. This stability of the control signal affirms the reliability and effectiveness of the proposed control method.

In conclusion, the simulation results depicted in Figure 13 provide detailed insights into the performance of the control technique. The close tracking of the PV output current to its reference, the small error between them, and the precise control of voltage and power signify the efficiency and stability of the proposed control method, even in the presence of irradiance variations.

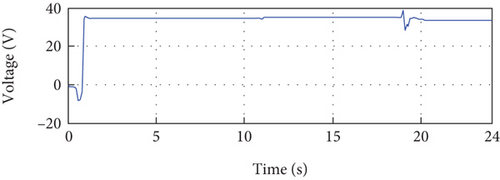
Figure 14(a) depicts the comparison between the output of the PV system and its reference. Notably, it is evident that the PV current I_PV precisely follows its reference, even in the presence of temperature variations. This observation demonstrates the robustness and efficiency of our control approach. Throughout the entire simulation period, the error between the output of the PV system and its reference remains remarkably low, approaching zero. The initial deviation observed can be attributed to variations in the parameters of the identified model. However, once the model corresponding to the real system is obtained, the control becomes perfect.

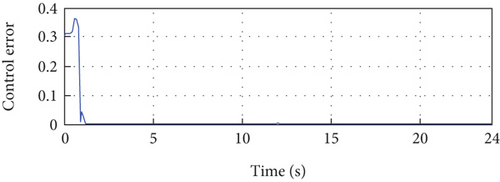
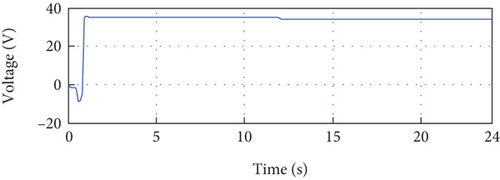
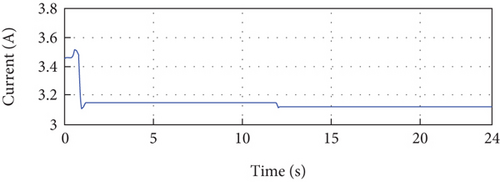
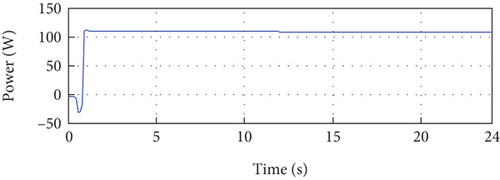
The error between the reference and the output PV current over the entire simulation period is illustrated in Figure 14(b), revealing consistently small error magnitudes. Figures 14(c) and 14(e) showcase the output voltage and power of the PV system, respectively. These figures are obtained from the control signal depicted in Figure 14(f).

In summary, the simulation results presented in Figure 14 provide detailed insights into the performance of the control approach. The precise tracking of the PV current to its reference, the minimal error observed, and the accurate control of voltage and power collectively demonstrate the robustness and effectiveness of the proposed control method, even in the face of temperature variations.

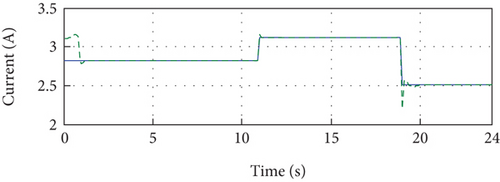
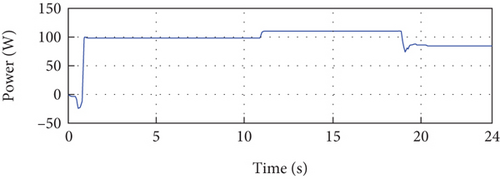
Figure 15(a) demonstrates the remarkable performance of the proposed method as the output of the PV system closely aligns with the reference, despite simultaneous variations in irradiance and temperature. This impressive tracking capability confirms the high performance of the proposed method. Furthermore, Figure 15(b) illustrates the error between the reference and the PV current output throughout the simulation period, showing consistently small error magnitudes. Figure 15(e) presents the output power of the PV system, which showcases the effectiveness of the proposed method in maintaining the desired power output.

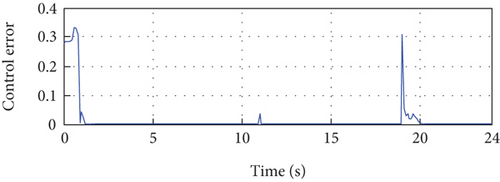
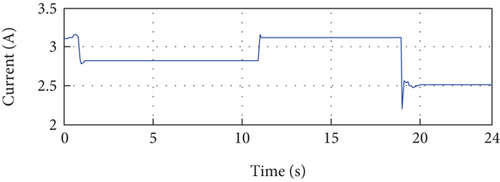
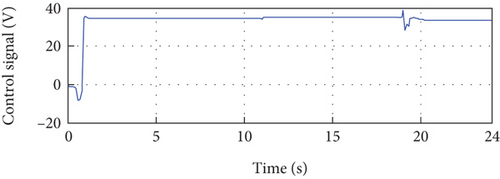
The analysis of the control signal (Figure 15(f)) reveals several important observations. Initially, oscillations are observed at the beginning of the simulation, which can be attributed to changes in the identified model parameters (a1, a2, b1, and b2). These oscillations may also be caused by initial disturbances. However, these oscillations quickly attenuate, and the control signal stabilizes. Two small oscillations are observed at instants 11 s and 19 s, which are due to changes in irradiance and temperature. Despite these disturbances, the control signal stabilizes after these two instants. This observation demonstrates the ability of the control to maintain system stability despite changes in irradiance and temperature. Overall, the analysis confirms the stability of the proposed control approach, despite the initial oscillations and variations in model parameters, irradiance, and temperature. This stability is crucial for ensuring consistent and predictable performance of the regulated system.

The simulation results obtained from the third scenario highlight the efficiency and robustness of the proposed method in handling simultaneous variations in temperature and irradiance. This observation allows us to conclude that the method presented in this paper exhibits strong resilience and performance in real-world conditions.

Overall, the simulation results presented in Figure 15 provide detailed evidence of the effectiveness and robustness of the proposed method. The accurate tracking of the PV system output, the minimal error between the output and reference, and the successful management of temperature and irradiance variations collectively emphasize the efficiency and reliability of the proposed method in practical applications.

4.1. Numerical Evaluation

Table 5 represents the obtained numerical results of the proposed method in terms of response time and current error.

Table 5. Numerical results.

Scenarios/performance	Response time	Current error
Scenario 1: the irradiance is varied and the temperature is fixed at a value of 25°C	0.8 s	2.7736e − 007 A
Scenario 2: the temperature is varied and the irradiance is fixed at 1000 W/m²	0.8 s	4.9307e − 007 A
Scenario 3: variation of irradiation and temperature simultaneously	0.8 s	1.4754e − 007 A

From the results presented in Table 5, one can see that the accuracy values are very low, meaning that the error between the setpoint and the output of the system converges to zero, which means that the desired power is achieved. On the other hand, the system transient response is very satisfying because, at the beginning of the simulation period, the proposed method requires the identification of the real system, and once the system is identified, we notice the good follow-up of the maximum power.

5. Conclusion and Future Perspectives

In conclusion, this research introduces a novel and adaptive control strategy tailored for optimizing the performance of photovoltaic (PV) systems. By integrating indirect adaptive control, recursive least squares, and the RST controller, our approach effectively addresses the challenges posed by nonlinearities in PV models. The outcomes of our simulations demonstrate substantial advancements over conventional control methods, showcasing significant enhancements in power extraction efficiency, reduction of system losses, and accurate set point tracking. The incorporation of MPPT algorithms for automatic tracking of the maximum power point, coupled with a comprehensive mathematical modeling of PV cells through single-diode and dual-diode models, establishes a robust theoretical foundation for our study. The simulations conducted under varying environmental conditions, including fluctuations in irradiance and temperature, consistently validate the adaptability and effectiveness of the proposed control algorithm. Numerical results, characterized by low current errors and swift response times, underscore the precision and efficiency of our control strategy. These findings position our work as a valuable contribution to the field of renewable energy systems, offering insights into the intricacies of PV system optimization.

Looking ahead, future research endeavors will focus on broadening the scope of our control methodology. The incorporation of additional components such as converters, loads, and energy storage systems will enable a more comprehensive evaluation of our approach in diverse energy scenarios. Exploring the synergy with various renewable energy sources will further contribute to the versatility of the proposed control strategy. Moreover, ongoing efforts will be directed towards real-world implementation and validation of the developed control algorithm, paving the way for practical applications and industry integration. Continuous refinement and adaptation of the control strategy will be pursued to ensure its effectiveness in dynamic and evolving energy landscapes. In summary, this research not only advances the optimization of PV systems but also lays the groundwork for future investigations into the integration of renewable energy sources and the practical deployment of sophisticated control algorithms in real-world settings.

Nomenclature

I:: Current
I_PV:: PV current
I_ph:: Photocurrent
I_sh:: Saturation current
I_D, I_D1, I_D2:: Current of the diodes
I₀₁, I₀₂:: Diode saturation currents
I_s:: Saturation current
I_cc:: Short circuit current
I_mpp:: Maximum current at PPM
E:: Irradiation
T:: Temperature
V:: Voltage
V_pv:: PV voltage
V_mpp:: The maximum voltage at PPM
V_co:: Open circuit voltage
P_pv:: PV power
P_mpp:: Maximum power
D, D₁, D₂:: Diodes
R_sh:: Shunt resistor
R_s:: Series resistor
T_j:: Junction temperature
T_jref:: Reference temperature
T_a:: Ambiante temperature
E, E_s:: Illumination
E_ref, E_sref:: Illumination under STC conditions
E_g:: Gap energy
P₁, P₂, P₃:: Fixed parameters
P₄:: Constant
E_sref:: Reference illumination
N_oct:: Nominal solar cell operating temperature or mode
T_e:: Simpling period
u(z):: Input
y(z), y(k):: Output
y_c(z):: Setpoint
v(k), w(k):: Random external disturbances
z^−d, d:: Delay
P(z⁻¹):: Polynomial
P_a(z⁻¹):: System’s auxiliary poles
P_d(z⁻¹):: System’s dominant poles
A(z⁻¹), B(z⁻¹):: Discrete polynomials
ξ:: Damping coefficient
w_n:: Proper pulsation
λ:: Forgetting factor
φ:: Vector that includes the identified PV system inputs and outputs.
:: Vector that contains the coefficients
q:: Elementary charge (1.6 × 10⁻¹⁹ C)
k:: Constant of Boltzmann
A:: The ideality coefficient of a cell
N_s:: Number of cells linked in series and/or parallel
a_oc:: Temperature coefficient of short circuit current
B_oc:: Voltage coefficient.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

Data is available on request.

References

1 Bendib B., Belmili H., and Krim F., A survey of the most used MPPT methods: Conventional and advanced algorithms applied for photovoltaic systems, Renewable and Sustainable Energy Reviews. (2015) 45, 637–648, https://doi.org/10.1016/j.rser.2015.02.009, 2-s2.0-84923775819.
10.1016/j.rser.2015.02.009
Web of Science® Google Scholar
2 Khan Z. A., Khan L., Ahmad S., Mumtaz S., Jafar M., and Khan Q., RBF neural network based backstepping terminal sliding mode MPPT control technique for PV system, PLoS One. (2021) 16, no. 4, article e0249705, https://doi.org/10.1371/journal.pone.0249705.
10.1371/journal.pone.0249705
Google Scholar
3 Rezk H., Al-Oran M., Gomaa M. R., Tolba M. A., Fathy A., Abdelkareem M. A., Olabi A. G., and El-Sayed A. H. M., A novel statistical performance evaluation of most modern optimization-based global MPPT techniques for partially shaded PV system, Renewable and Sustainable Energy Reviews. (2019) 115, article 109372, https://doi.org/10.1016/j.rser.2019.109372, 2-s2.0-85072053658.
10.1016/j.rser.2019.109372
Web of Science® Google Scholar
4 Yahiaoui F., Chabour F., Guenounou O., Bajaj M., Bukhari S. S. H., Nazir M. S., Pushkarna M., and Wapet D. E. M., An experimental testing of optimized fuzzy logic-based MPPT for a standalone PV system using genetic algorithms, Mathematical Problems in Engineering. (2023) 2023, 12, 4176997, https://doi.org/10.1155/2023/4176997.
10.1155/2023/4176997
Google Scholar
5 Mohapatra B., Sahu B. K., Pati S., Bajaj M., Blazek V., Prokop L., Misak S., and Alharthi M., Real-time validation of a novel IAOA technique-based offset hysteresis band current controller for grid-tied photovoltaic system, Energies. (2022) 15, no. 23, https://doi.org/10.3390/en15238790.
10.3390/en15238790
Google Scholar
6 Podder A. K., Roy N. K., and Pota H. R., MPPT methods for solar PV systems: a critical review based on tracking nature, IET Renewable Power Generation. (2019) 13, no. 10, 1615–1632, https://doi.org/10.1049/iet-rpg.2018.5946, 2-s2.0-85068657035.
10.1049/iet-rpg.2018.5946
Web of Science® Google Scholar
7 Khosravi N., Abdolvand A., Oubelaid A., Khan Y. A., Bajaj M., and Govender S., Improvement of power quality parameters using modulated-unified power quality conditioner and switched-inductor boost converter by the optimization techniques for a hybrid AC/DC microgrid, Scientific Reports. (2022) 12, no. 1, https://doi.org/10.1038/s41598-022-26001-8, 36522398.
10.1038/s41598-022-26001-8
PubMed Web of Science® Google Scholar
8 Arsalan M., Iftikhar R., Ahmad I., Hasan A., Sabahat K., and Javeria A., MPPT for photovoltaic system using nonlinear backstepping controller with integral action, Solenergy Systems. (2018) 170, 192–200, https://doi.org/10.1016/j.solener.2018.04.061, 2-s2.0-85047603893.
10.1016/j.solener.2018.04.061
Google Scholar
9 Belkhier Y., Abdelyazid A., Oubelaid A., Khosravi N., Bajaj M., Vishnuram P., and Zaitsev I., Experimental analysis of passivity-based control theory for permanent magnet synchronous motor drive fed by grid power, IET Control Theory and Applications. (2023) 1–16, https://doi.org/10.1049/cth2.12574.
10.1049/cth2.12574
Web of Science® Google Scholar
10 Khosravi N., Baghbanzadeh R., Oubelaid A., Tostado-Véliz M., Bajaj M., Hekss Z., Echalih S., Belkhier Y., Abou Houran M., and Aboras K. M., A novel control approach to improve the stability of hybrid AC/DC microgrids, Applied Energy. (2023) 344, article 121261, https://doi.org/10.1016/j.apenergy.2023.121261.
10.1016/j.apenergy.2023.121261
Web of Science® Google Scholar
11 Lu C., Zhou H., Li L., Yang A., Xu C., Zhengyu O., Wang J., Wang X., and Tian F., Split-core magnetoelectric current sensor and wireless current measurement application, Measurement: Journal of the International Measurement Confederation. (2022) 188, article 110527, https://doi.org/10.1016/j.measurement.2021.110527.
10.1016/j.measurement.2021.110527
Web of Science® Google Scholar
12 Huang S., Huang M., and Lyu Y., Seismic performance analysis of a wind turbine with a monopile foundation affected by sea ice based on a simple numerical method, Engineering Applications of Computational Fluid Mechanics. (2021) 15, no. 1, 1113–1133, https://doi.org/10.1080/19942060.2021.1939790.
10.1080/19942060.2021.1939790
Web of Science® Google Scholar
13 Huang N., Chen Q., Cai G., Xu D., Liang Z., and Zhao W., Fault diagnosis of bearing in wind turbine gearbox under actual operating conditions driven by limited data with noise labels, IEEE Transactions on Instrumentation and Measurement. (2021) 70, 1–10, https://doi.org/10.1109/TIM.2020.3025396.
10.1109/TIM.2020.3025396
PubMed Web of Science® Google Scholar
14 Liu S. and Liu C., Virtual-vector-based robust predictive current control for dual three-phase PMSM, IEEE Transactions on Industrial Electronics. (2021) 68, no. 3, 2048–2058, https://doi.org/10.1109/TIE.2020.2973905.
10.1109/TIE.2020.2973905
Web of Science® Google Scholar
15 Hu W., Wang T., and Chu F., Novel Ramanujan digital twin for motor periodic fault monitoring and detection, IEEE Transactions on Industrial Informatics.(2023) 19, no. 12, 11564–11572, https://doi.org/10.1109/TII.2023.3248110.
10.1109/TII.2023.3248110
Google Scholar
16 Zhu X., Xu Z., Liu Z., Liu M., Yin Z., Yin L., and Zheng W., Impact of dam construction on precipitation: a regional perspective, Marine and Freshwater Research, 2023, CSIRO Publishing, https://doi.org/10.1071/MF22135.
Google Scholar
17 Song J., Mingotti A., Zhang J., Peretto L., and Wen H., Fast iterative-interpolated DFT phasor estimator considering out-of-band interference, IEEE Transactions on Instrumentation and Measurement. (2022) 71, https://doi.org/10.1109/TIM.2022.3203459.
10.1109/TIM.2022.3203459
Web of Science® Google Scholar
18 Zhu L., Li Z., and Hou K., Effect of radical scavenger on electrical tree in cross-linked polyethylene with large harmonic superimposed DC voltage, High Voltage. (2023) 8, no. 4, 739–748, https://doi.org/10.1049/hve2.12302.
10.1049/hve2.12302
Google Scholar
19 Lu L., Wu W., Gao Y., Pan C., Yu X., Zhang C., and Jin Z., Study on current discrepancy and redistribution of HTS non-insulation closed-loop coils during charging/discharging and subsequent transient process toward steady-state operation, Superconductor Science and Technology. (2022) 35, no. 9, article 95001, https://doi.org/10.1088/1361-6668/ac7dfe.
10.1088/1361-6668/ac7dfe
PubMed Google Scholar
20 Ding Z., Wu X., Chen C., and Yuan X., Magnetic field analysis of surface-mounted permanent magnet motors based on an improved conformal mapping method, IEEE Transactions on Industry Applications. (2023) 59, no. 2, 1689–1698, https://doi.org/10.1109/TIA.2022.3228509.
10.1109/TIA.2022.3228509
Web of Science® Google Scholar
21 Yang M., Wang Y., Cheng W., Liang Y., Yang S., Wang L., and Wang S., Digital twin-driven industrialization development of underwater gliders, IEEE Transactions on Industrial Informatics.(2023) 19, no. 9, 9680–9690, https://doi.org/10.1109/TII.2023.3233972.
10.1109/TII.2023.3233972
Web of Science® Google Scholar
22 Zhang X., Wang Z., and Lu Z., Multi-objective load dispatch for microgrid with electric vehicles using modified gravitational search and particle swarm optimization algorithm, Applied Energy. (2022) 306, article 118018, https://doi.org/10.1016/j.apenergy.2021.118018.
10.1016/j.apenergy.2021.118018
Google Scholar
23 Liu Z., Xu J., Liu M., Yin Z., Liu X., Yin L., and Zheng W., Remote sensing and geostatistics in urban water-resource monitoring: a review, Marine and Freshwater Research. (2023) 74, no. 10, 747–765, https://doi.org/10.1071/MF22167.
10.1071/MF22167
Web of Science® Google Scholar
24 Wu Z., Lin B., Fan J., Zhao J., Zhang Q., and Li L., Effect of dielectric relaxation of epoxy resin on dielectric loss of medium-frequency transformer, IEEE Transactions on Dielectrics and Electrical Insulation. (2022) 29, no. 5, 1651–1658, https://doi.org/10.1109/TDEI.2022.3193652.
10.1109/TDEI.2022.3193652
Web of Science® Google Scholar
25 Yin L., Wang L., Li J., Lu S., Tian J., Yin Z., Liu S., and Zheng W., YOLOV4_CSPBi: enhanced land target detection model, Land. (2023) 12, no. 9, https://doi.org/10.3390/land12091813.
10.3390/land12091813
PubMed Google Scholar
26 Zheng X., Cai G., Guo J., Gao W., Huang Y., and Tong X., Combustion characteristics and thermal decomposition mechanism of the flame-retardant cable in urban utility tunnel, Case Studies in Thermal Engineering. (2023) 44, article 102887, https://doi.org/10.1016/j.csite.2023.102887.
10.1016/j.csite.2023.102887
Web of Science® Google Scholar
27 Xiao T., Lin Z., Liu C., Liu L., and Li Q., Integration of desalination and energy conversion in a thermo-osmotic system using low-grade heat: performance analysis and techno-economic evaluation, Applied Thermal Engineering. (2023) 223, article 120039, https://doi.org/10.1016/j.applthermaleng.2023.120039.
10.1016/j.applthermaleng.2023.120039
Web of Science® Google Scholar
28 Duan Y., Zhao Y., and Hu J., An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: modeling, optimization and analysis, Sustainable Energy, Grids and Networks. (2023) 34, article 101004, https://doi.org/10.1016/j.segan.2023.101004.
10.1016/j.segan.2023.101004
Web of Science® Google Scholar
29 Shi Y., Hu J., Wu Y., and Ghosh B. K., Intermittent output tracking control of heterogeneous multi-agent systems over wide-area clustered communication networks, Nonlinear Analysis: Hybrid Systems. (2023) 50, article 101387, https://doi.org/10.1016/j.nahs.2023.101387.
10.1016/j.nahs.2023.101387
Web of Science® Google Scholar
30 Lu Y., Tan C., Ge W., Zhao Y., and Wang G., Adaptive disturbance observer-based improved super-twisting sliding mode control for electromagnetic direct-drive pump, Smart Materials and Structures. (2023) 32, no. 1, article 17001, https://doi.org/10.1088/1361-665X/aca84e.
10.1088/1361-665X/aca84e
Google Scholar
31 Deng W., Zhang Y., Tang Y., Li Q., and Yi Y., A neural network-based adaptive power-sharing strategy for hybrid frame inverters in a microgrid, Frontiers in Energy Research. (2023) 10, https://doi.org/10.3389/fenrg.2022.1082948.
10.3389/fenrg.2022.1082948
Web of Science® Google Scholar
32 Xu B., Wang X., Zhang J., Guo Y., and Razzaqi A. A., A novel adaptive filtering for cooperative localization under compass failure and non-gaussian noise, IEEE Transactions on Vehicular Technology. (2022) 71, no. 4, 3737–3749, https://doi.org/10.1109/TVT.2022.3145095.
10.1109/TVT.2022.3145095
Web of Science® Google Scholar
33 Liu K., Sheng W., Li Z., Liu F., Liu Q., Huang Y., and Li Y., An energy optimal schedule method for distribution network considering the access of distributed generation and energy storage, IET Generation, Transmission & Distribution. (2023) 17, no. 13, 2996–3015, https://doi.org/10.1049/gtd2.12855.
10.1049/gtd2.12855
Google Scholar
34 Xiao S., Wang Z., Wu G., Guo Y., Gao G., Zhang X., Cao Y., Zhang Y., Yu J., Liu P., and Li P., The impact analysis of operational overvoltage on traction transformers for high-speed trains based on the improved capacitor network methodology, IEEE Transactions on Transportation Electrification.(2023) https://doi.org/10.1109/TTE.2023.3283668.
10.1109/TTE.2023.3283668
Google Scholar
35 Liang J., Kato B., and Wang Y., Constructing simplified models for dynamic analysis of monopile-supported offshore wind turbines, Ocean Engineering. (2023) 271, article 113785, https://doi.org/10.1016/j.oceaneng.2023.113785.
10.1016/j.oceaneng.2023.113785
Web of Science® Google Scholar
36 Zhang W., Zheng Z., and Liu H., Droop control method to achieve maximum power output of photovoltaic for parallel inverter system, CSEE Journal of Power and Energy Systems. (2022) 8, no. 6, 1636–1645, https://doi.org/10.17775/CSEEJPES.2020.05070.
10.17775/CSEEJPES.2020.05070
Web of Science® Google Scholar
37 Wang H., Wu X., Zheng X., and Yuan X., Model predictive current control of nine-phase open-end winding PMSMs with an online virtual vector synthesis strategy, IEEE Transactions on Industrial Electronics. (2023) 1, https://doi.org/10.1109/TIE.2022.3174241.
10.1109/TIE.2022.3174241
Google Scholar
38 Liu S. and Liu C., Direct harmonic current control scheme for dual three-phase PMSM drive system, IEEE Transactions on Power Electronics. (2021) 36, no. 10, 11647–11657, https://doi.org/10.1109/TPEL.2021.3069862.
10.1109/TPEL.2021.3069862
Web of Science® Google Scholar
39 Li M., Yang M., Yu Y., and Lee W., A wind speed correction method based on modified hidden Markov model for enhancing wind power forecast, IEEE Transactions on Industry Applications. (2022) 58, no. 1, 656–666, https://doi.org/10.1109/TIA.2021.3127145.
10.1109/TIA.2021.3127145
Google Scholar
40 Gao Y., Doppelbauer M., Ou J., and Qu R., Design of a double-side flux modulation permanent magnet machine for servo application, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2022) 10, no. 2, 1671–1682, https://doi.org/10.1109/JESTPE.2021.3105557.
10.1109/JESTPE.2021.3105557
Web of Science® Google Scholar
41 Su Y., Liu L., Gao X., Yu W., Hong Y., and Liu C., A high-efficient and salt-rejecting 2D film for photothermal evaporation, iScience. (2023) 26, no. 8, https://doi.org/10.1016/j.isci.2023.107347, 37554456.
10.1016/j.isci.2023.107347
PubMed Google Scholar
42 Ma X., Liao Z., Wang Y., and Zhao J., Fast dynamic phasor estimation algorithm considering DC offset for PMU applications, IEEE Transactions on Power Delivery.(2023) 38, no. 5, 3582–3593, https://doi.org/10.1109/TPWRD.2023.3285949.
10.1109/TPWRD.2023.3285949
Web of Science® Google Scholar
43 Yuan C., Liu D.-D., Zhu Y.-J., Tan Z., Jiang B.-X., Tang C.-X., Zhou Y., He J.-L., and Li Q., Effect of charge transport on electrical degradation in polypropylene/organic molecular semiconductor composites for HVDC cable insulation, Applied Physics Letters. (2023) 122, no. 11, https://doi.org/10.1063/5.0133417.
10.1063/5.0133417
Web of Science® Google Scholar
44 Taghieh A., Mohammadzadeh A., Zhang C., Kausar N., and Castillo O., A type-3 fuzzy control for current sharing and voltage balancing in microgrids, Applied Soft Computing. (2022) 129, article 109636, https://doi.org/10.1016/j.asoc.2022.109636.
10.1016/j.asoc.2022.109636
Web of Science® Google Scholar
45 Lin L., Zhang J., Gao X., Shi J., Chen C., and Huang N., Power fingerprint identification based on the improved V-I trajectory with color encoding and transferred CBAM-ResNet, PLoS One. (2023) 18, no. 2, article e0281482, https://doi.org/10.1371/journal.pone.0281482, 36757938.
10.1371/journal.pone.0281482
PubMed Google Scholar
46 Chen H., Wu H., Kan T., Zhang J., and Li H., Low-carbon economic dispatch of integrated energy system containing electric hydrogen production based on VMD-GRU short-term wind power prediction, International Journal of Electrical Power & Energy Systems. (2023) 154, article 109420, https://doi.org/10.1016/j.ijepes.2023.109420.
10.1016/j.ijepes.2023.109420
Google Scholar
47 Zhu D., Guo X., Tang B., Hu J., Zou X., and Kang Y., Feedforward frequency deviation control in PLL for fast inertial response of DFIG-based wind turbines, IEEE Transactions on Power Electronics. (2024) 39, no. 1, 664–676, https://doi.org/10.1109/TPEL.2023.3319134.
10.1109/TPEL.2023.3319134
Google Scholar
48 Liao K., Lu D., Wang M., and Yang J., A low-pass virtual filter for output power smoothing of wind energy conversion systems, IEEE Transactions on Industrial Electronics. (2022) 69, no. 12, 12874–12885, https://doi.org/10.1109/TIE.2021.3139177.
10.1109/TIE.2021.3139177
Web of Science® Google Scholar
49 Song J., Mingotti A., Zhang J., Peretto L., and Wen H., Accurate damping factor and frequency estimation for damped real-valued sinusoidal signals, IEEE Transactions on Instrumentation and Measurement. (2022) 71, https://doi.org/10.1109/TIM.2022.3220300.
10.1109/TIM.2022.3220300
Google Scholar
50 Li D., Ge S. S., and Lee T. H., Fixed-time-synchronized consensus control of multiagent systems, IEEE Transactions on Control of Network Systems. (2021) 8, no. 1, 89–98, https://doi.org/10.1109/TCNS.2020.3034523.
10.1109/TCNS.2020.3034523
Web of Science® Google Scholar

All articles

Maximum Power Extraction in Photovoltaic Systems Using High-Performance Adaptive Control Approach

Abstract

1. Introduction