This paper is aimed at constructing and analyzing a fitted approach for singularly perturbed time delay parabolic problems with two small parameters. The proposed computational scheme comprises the implicit Euler and especially finite difference method for the time and space variable discretization, respectively, on uniform step size. The stability and convergence analysis of the method is provided and is first-order parameter uniform convergent. Further, the numerical results depict that the present method is more convergent than some methods available in the literature.

1. Introduction

Consider one-dimensional unsteady singularly perturbed time delay parabolic problems with two parameters on the domain ∇ = ∇_s × ∇_t = (0, 1) × (0, T] of the form:

()

where ε(0 < ε ≪ 1) and μ(0 ≤ μ ≪ 1) are two small perturbation parameters and λ > 0 is the delay parameter. For the existence and uniqueness of the solution, the functions a(s, t), δ(s, t), c(s, t), f(s, t), χ₀(t), χ₁(t), and φ(s, t) are sufficiently smooth and bounded with a(s, t) ≥ α > 0 and δ(s, t) ≥ β > 0. Under sufficiently smoothness and compatibility conditions on the functions χ₀(t), χ₁(t), and φ(s, t), the IBVP (1) has a unique solution w(s, t) [1, 2].

The nature of Equation (1) changes based on the values of perturbations ε and μ. If μ = 0, then the problem is reaction-diffusion type [3] and boundary layers exhibit near s = 0 and s = 1 of width . If μ = 1, then the problem is convection-diffusion type [4, 5] and boundary layers exhibit near s = 0 of width O(ε). These problems have several fascinating phenomena in lubrication theory [6] and chemical flow reactor theory [7, 8]. When 0 ≤ μ ≤ 1, problem (1) is modelling different phenomena in applied sciences and engineering, for instance, problems found in control theory [9], mechanical systems, population dynamics in the biosciences [10], and heat and mass transfer in chemical engineering [11].

Various parameter uniform numerical methods for singularly perturbed parabolic problems with two parameters without time lag are suggested by several scholars. For instance, the authors in [12] developed robust nonstandard finite difference method based on Micken’s type discretization rule for spatial discretization and the implicit finite difference method for temporal discretization for singularly perturbed parabolic problems with two parameters. The researchers in [13, 14] suggested parameter uniform numerical methods using finite difference schemes with fitted techniques to solve singularly perturbed two parametric parabolic problems. In article [15], the authors developed a fitted mesh cubic spline in tension for singularly perturbed problems with two parameters. [16] suggested a uniformly convergent computational scheme which consists of the Crank-Nicholson method to discretize the time variable and the central difference approximation on the nonstandard methodology of Mickens for the space variable for Equation (58). Quadratic B-spline collocation method on exponentially graded mesh for two-parameter singularly perturbed problem is presented by [17]. An implicit computational method on a predefined Shishkin mesh is presented for solving two-parameter parabolic singularly perturbed boundary value problems with nonsmooth data by [18]. [19] suggested parameter uniform finite element method for two-parameter singularly perturbed parabolic reaction-diffusion problems. [20] developed nonstandard finite difference method on uniform mesh for two-parameter singular perturbation problem.

The authors in papers [21, 22] developed uniform numerical methods for a singularly perturbed reaction-convection-diffusion equation in one dimension with a discontinuous source term. In articles [23–25], the authors have developed robust numerical methods for singularly perturbed time delay parabolic problems with two parameters based on adaptive layer mesh methods. However, exponentially fitted difference (EFD) schemes have gained popularity as a powerful technique to solve boundary value problems. For instance, the authors in [26–28] suggested different EFD schemes for singularly perturbed two-point boundary value problems.

Nevertheless, the solution methodologies for singularly perturbed time delay parabolic problems with two parameters are at a primarily stage and need a lot of investigation. Therefore, to diminish the gap observed, we proposed a novel parameter uniform numerical approach formulated based on uniform mesh implicit Euler approximation for time variable and especially finite difference method for the spatial variable. The novelty of the presented method, unlike the Shishkin and Bakhvalov mesh types, does not require a priori information about the location and width of the boundary layer.

2. Properties of Continuous Solution

Lemma 1 (minimum principle). Suppose w|_∂∇ ≥ 0 and , then .

Proof (see [24].)An immediate consequence of minimum principle above for the solution of Equation (1) provides the next Lemma 2.

Lemma 2 (uniform stability estimate). Let w(s, t) be the solution of problem (1); then, we have

()

Proof. By defining barrier functions

()

and using Lemma 1, we get the desired bound.

3. Construction of the Numerical Scheme

3.1. Temporal Semidiscretization

On applying the implicit Euler method to approximate the t-direction of Equation (1) with the uniform mesh,

and

, where M is number of mesh points in t-direction in the interval [0, T] and θ is the number of mesh points in [−λ, 0]. The step size Δt satisfies θΔt = λ, where θ is a natural number and t_j = jΔt, j ≥ −θ; we obtain

()

where

, v(s, t_j+1) = −Δtc(s, t_j+1)W(s, t_j−λ+1) + Δtf(s, t_j+1) − W(s, t_j).

Clearly, the operator achieves the maximum principle, which confirms the stability of the semidiscrete (4).

The local truncation error (LTE) devoted in the semidiscrete scheme is the difference between the analytical solution w(s, t_j+1) and the estimate solution W(s, t_j+1) of Equation (4), i.e., (LTE)_j+1 = w(s, t_j+1) − W(s, t_j+1), and the global error E_j+1 is the contribution of the local error up to the (j + 1)th time level. The bound of error for the semidiscrete scheme is estimated as follows.

Lemma 3 (LTE). If , then the LTE in the temporal direction gratifies

()

where C is a positive constant independent of ε and Δt.

Proof. Using Taylor’s series expansion for w(s, t_j−1), we have

()

This implies

()

Substituting Equation (1) into Equation (7), we have

()

Subtracting Equation (4) from Equation (8), the local truncation error (LTE)_j+1 = w(s, t_j+1) − W(s, t_j+1) at (j + 1)th is the solution of a boundary problem

()

where W(s, t_j) is the solution of the boundary value problem (4).

Hence, using the maximum principle on the operator provides

()

Lemma 4 (global error estimate (GEE)). Under the hypothesis of Lemma 3, the GEE in the temporal direction is given by

()

Proof. Using Lemma 3 at (j + 1)th time step, we have

()

where c₁ and C are the positive constants independent of ε and Δt.

Rewrite Equation (4) as

()

where

()

3.2. Spatial Semidiscretization

For right boundary layer problem from the theory of singular perturbation in [29], the asymptotic solution of the zero-order approximation of Equation (13) is written as

()

where

is the solution of reduced problem

()

Taking Taylor’s series expansion for a(s) about the point “1” and restricting to their first terms, Equation (15) becomes

()

Let us subdivide the domain [0, 1] into N uniform meshes Δs = 1/N as

, and the mesh can be written as s_i = iΔs, i = 0, 1, 2, ⋯, N. By considering problem (17) at s_i = iΔs as Δs⟶0, we have

()

where ρ = Δs/ε.

Assume that W^j+1(s) is a smooth function in the domain

. Then, by employing Taylor’s series, we obtain

()

Adding Equation (19) and Equation (20), we get

()

Plugging

from Equation (22) into Equation (21), we get

()

where

Equation (13) at s_i,i±1 can be written as

()

where we approximate

, and

using nonsymmetric finite differences [30]:

()

Taking Equation (25) into Equation (24), we get

()

Substitute Equation (26) into Equation (23) and rearrange the result as

()

To handle the effect of the perturbation parameter, exponential fitting factor σ(ρ) is multiplied (Equation (27)) on the term containing the perturbation parameter as

()

Multiplying (28) by ℓ and taking the limit as Δs⟶0, we get

()

Using Equation (18), we have

()

Substituting Equation (30) in Equation (29), we obtain

()

Simplifying Equation (31), we get

()

which is the required value of the fitting factor σ(ρ). Finally, from Equation (28) and Equation (32), we obtain

()

where

()

For small mesh sizes, the above matrix is (i.e., the matrix is diagonally dominant) and nonsingular. Hence, by [31], the matrix ϑ is M-matrix and the system of equations can be solved by matrix inverse with the given boundary conditions.

4. Convergence Analysis

Lemma 5. The matrix associated with the discrete scheme (33) is M-matrix.

Proof. By assuming that a(s) = A and q(s) = B are constant functions in [0, 1], where A and B are arbitrary constants, one can easily see that the inequalities , , , , and are satisfied under the assumptions that (a(s) = A) > 0, (q(s) = B) > 0, and (A/2Δs + B/30) < σ(ρ)ε/Δs². Therefore, the matrix associated with the discrete scheme (33) is M-matrix.

Lemma 6 (discrete maximum principle). Assume that the discrete function gratifies on i = 0, N. Then, on implies that at each point of .

Lemma 7. The solution of the discrete scheme in (33) on gratifies the following estimate:

()

where q(s_i) ≥ q^∗ > 0.

Hence, Lemma 7 depicts that the scheme in Equation (33) is stable in supremum norm.

Lemma 8. If W ∈ C³(I), then the LTE in space discretization is written as

()

Proof. By definition

()

Using the relation (33) with W = (μa(0)/2)coth(μa(1)ρ/2) we get,

()

Thus, the desired result is obtained.

Lemma 9. Let W(s_i, t_j+1) be the solution of problem (13) and be the solution of the discrete problem (33). Then, the following estimate is obtained:

()

Proof. Rewrite Equation (33) in matrix vector form as

()

where Y = (ϑ_i,j), 0 ≤ j ≤ M − 1, 1 ≤ i ≤ N − 1 is a tridiagonal matrix with

()

and

is a column vector with

for i = 1, 2, ⋯, N − 1, with local truncation error e_i:

()

We also have

()

where

and

denote the actual solution and the local truncation error, respectively.

From Equations (40) and (43), we get

()

Thus, the error equation is

()

where

. Let S be the sum of elements of the ith row of Y; then, we have

()

where

Since 0 < ε ≪ 1, for sufficiently small Δs, the matrix W is irreducible and monotone. Then, it follows that Y⁻¹ exists, and its elements are nonnegative [32]. Hence, from Equation (45), we obtain

()

Let be the (ki)th elements of Y⁻¹. Since by the definition of multiplication of matrices with its inverses, we have

()

Therefore, it follows that

()

for some i0 between 1 and N − 1, and B_i0 = Ω_i From Equations (40), (48), and (50), we obtain

()

which implies

()

Therefore,

()

Theorem 10. Let w(s, t) be the solution of the problem (1) and be the numerical solution obtained by the proposed scheme (33). Then, for sufficiently small Δs, the error estimate for the totally discrete scheme is given by

()

Proof. By combining the result of Lemma 4 and Lemma 9, the required bound is obtained.

5. Numerical Examples, Results, and Discussions

Some numerical examples are presented to show the applicability of the proposed numerical scheme. Since the analytical solutions of the considered problems are not available, we used double mesh principle to compute the maximum principle given in [33]

()

where W^N,M(s_i) are computed numerical solutions obtained on the mesh

with N and M mesh intervals in the spatial and temporal directions, respectively, whereas W^2N,2M(s_i, t_j+1) are computed numerical solutions on the mesh

by adding the midpoint s_i+1/2 = (s_i+1 + s_i)/2 and t_j+1/2 = (t_j+1 + t_j)/2 into the mesh points. The corresponding rate of convergence for the proposed scheme is determined by

()

The parameter uniform maximum absolute error (E^N,M) and uniform order of convergence (r^N,M) are calculated using

()

respectively.

Example 1 (see [24].)Consider

()

Example 2 (see [24].)Consider

()

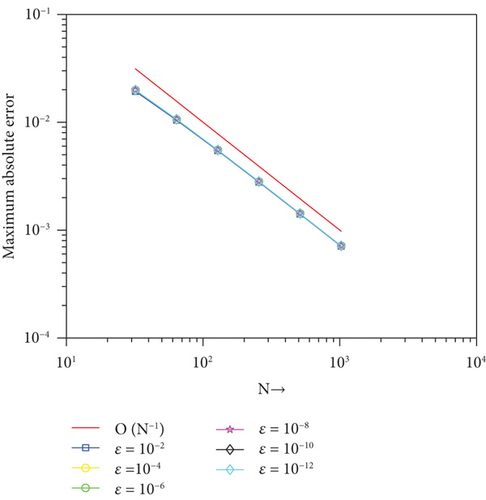
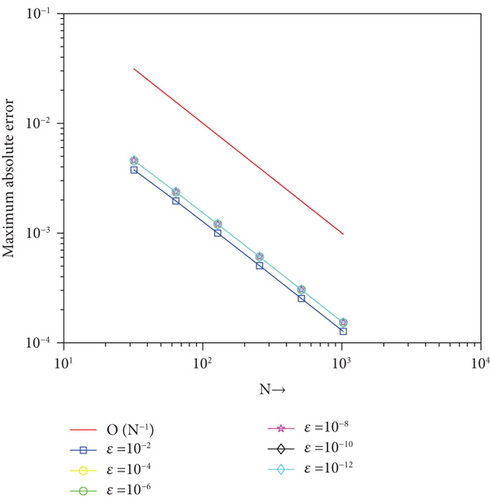
The validation of the theoretical findings is carried out by considering two examples whose , , E^N,M, and r^N,M are plotted in Tables 1 and 2. From these tables, one can see that as ε⟶0 and μ = 10⁻³, the error goes constant. Moreover, as the mesh size decreases, the order of convergence goes to one, and the maximum absolute error decreases. These reveal that the solution of the proposed method converges parameter uniformly with the order of convergence in good agreement with the theoretical findings.

Table 1.

, E^N,M, and r^N,M for Example 1 with μ = 10⁻³.

εN⟶	2⁵	2⁶	2⁷	2⁸	2⁹	2¹⁰
↓M⟶	2³	2⁴	2⁵	2⁶	2⁷	2⁸
Proposed scheme
10^-0	7.3516e-03	5.7683e-03	3.6428e-03	2.1296e-03	1.1630e-03	6.0953e-04
10^-0	3.4991e-01	6.6310e-01	7.7447e-01	8.7273e-01	9.3208e-01
10^-2	1.9343e-02	1.0465e-02	5.4599e-03	2.7902e-03	1.4107e-03	7.0935e-04
10^-2	8.8624e-01	9.3863e-01	9.6851e-01	9.8396e-01	9.9184e-01
10^-4	1.9854e-02	1.0658e-02	5.5313e-03	2.8189e-03	1.4231e-03	7.1502e-04
10^-4	8.9749e-01	9.4625e-01	9.7249e-01	9.8610e-01	9.9298e-01
10^-6	1.9860e-02	1.0660e-02	5.5318e-03	2.8190e-03	1.4231e-03	7.1503e-04
10^-6	8.9766e-01	9.4639e-01	9.7257e-01	9.8615e-01	9.9296e-01
10^-8	1.9861e-02	1.0661e-02	5.5327e-03	2.8195e-03	1.4234e-03	7.1518e-04
10^-8	8.9760e-01	9.4629e-01	9.7254e-01	9.8610e-01	9.9296e-01
10^-10	1.9861e-02	1.0661e-02	5.5327e-03	2.8195e-03	1.4234e-03	7.1518e-04
10^-10	8.9760e-01	9.4629e-01	9.7254e-01	9.8610e-01	9.9296e-01
10^-12	1.9861e-02	1.0661e-02	5.5327e-03	2.8195e-03	1.4234e-03	7.1518e-04
10^-12	8.9760e-01	9.4629e-01	9.7254e-01	9.8610e-01	9.9296e-01
E^N,M	1.9861e-02	1.0661e-02	5.5327e-03	2.8195e-03	1.4234e-03	7.1518e-04
r^N,M	8.9760e-01	9.4629e-01	9.7254e-01	9.8610e-01	9.9296e-01
Results in [24]
E^N,M	4.3705e-2	1.6704e-2	7.3802e-3	3.7406e-3	1.8967e-3	9.5511e-4
r^N,M	1.3876	1.1785	9.803e-01	9.797e-01	9.898e-01

Table 2.

, E^N,M, and r^N,M for Example 2 with μ = 10⁻³.

εN⟶	2⁵	2⁶	2⁷	2⁸	2⁹	2¹⁰
↓M⟶	2³	2⁴	2⁵	2⁶	2⁷	2⁸
Proposed scheme
10^-0	3.9899e-04	2.0538e-04	1.0431e-04	5.2577e-05	2.6397e-05	1.3226e-05
10^-0	9.5806e-01	9.7742e-01	9.8837e-01	9.9406e-01	9.9700e-01
10^-2	3.7603e-03	1.9594e-03	9.9849e-04	5.0406e-04	2.5324e-04	1.2692e-04
10^-2	9.4044e-01	9.7259e-01	9.8615e-01	9.9309e-01	9.9659e-01
10^-4	4.5642e-03	2.3635e-03	1.2012e-03	6.0550e-04	3.0394e-04	1.5227e-04
10^-4	9.4944e-01	9.7645e-01	9.8828e-01	9.9434e-01	9.9715e-01
10^-6	4.5778e-03	2.3685e-03	1.2040e-03	6.0687e-04	3.0463e-04	1.5261e-04
10^-6	9.5068e-01	9.7614e-01	9.8838e-01	9.9433e-01	9.9721e-01
10^-8	4.5773e-03	2.3682e-03	1.2038e-03	6.0679e-04	3.0458e-04	1.5259e-04
10^-8	9.5071e-01	9.7620e-01	9.8833e-01	9.9438e-01	9.9716e-01
10^-10	4.5773e-03	2.3682e-03	1.2038e-03	6.0679e-04	3.0458e-04	1.5259e-04
10^-10	9.5071e-01	9.7620e-01	9.8833e-01	9.9438e-01	9.9716e-01
10^-12	4.5773e-03	2.3682e-03	1.2038e-03	6.0679e-04	3.0458e-04	1.5259e-04
10^-12	9.5071e-01	9.7620e-01	9.8833e-01	9.9438e-01	9.9716e-01
E^N,M	4.5778e-03	2.3685e-03	1.2040e-03	6.0687e-04	3.0463e-04	1.5261e-04
r^N,M	9.5068e-01	9.7614e-01	9.8838e-01	9.9433e-01	9.9721e-01
Results in [24]
E^N,M	1.1161e-2	5.1087e-3	2.4749e-3	1.2214e-3	6.0706e-4	3.0264e-4
r^N,M	1.1274	1.0455	1.0188	1.0086	1.0042

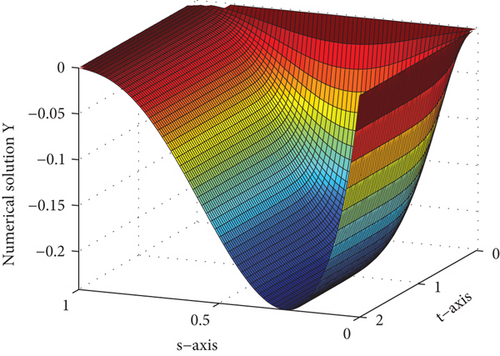
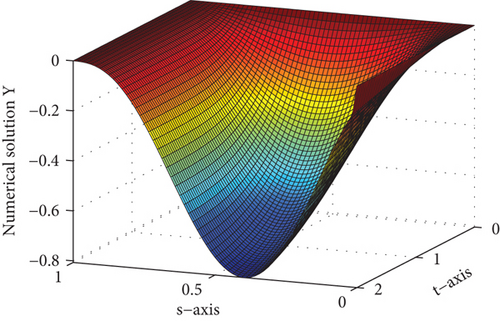
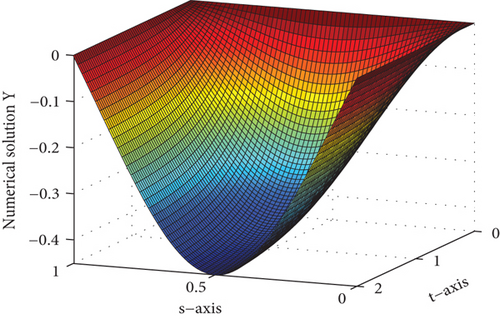
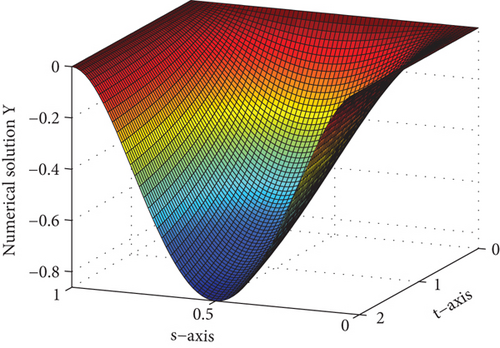
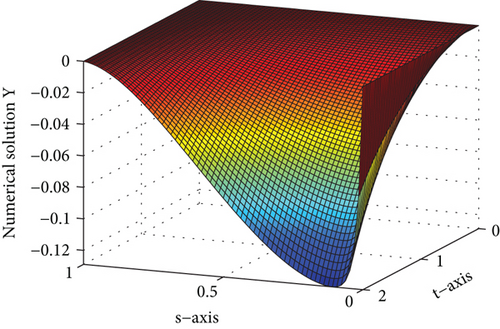
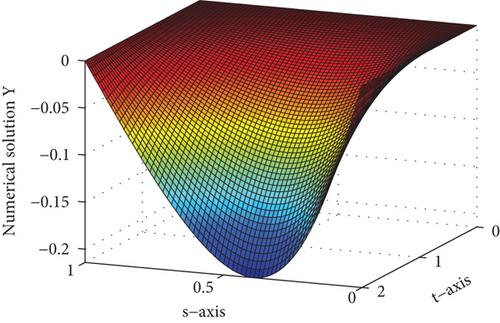
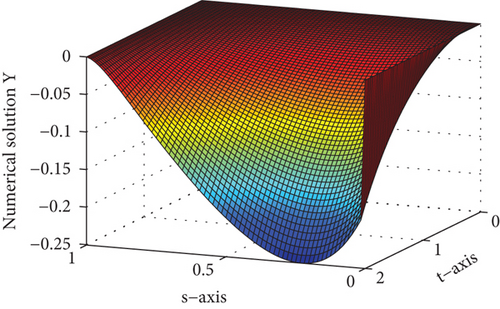
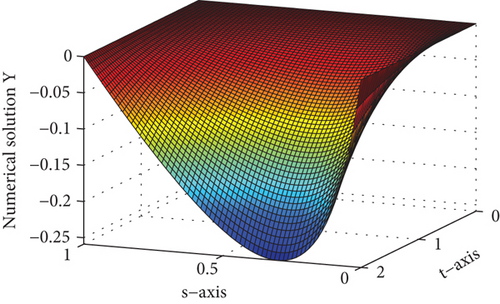
For several values of ε and μ, the numerical solutions for Examples 1 and 2 are plotted in Figures 1 and 2, respectively. These figures depict that the solution to the problem under consideration exhibits a parabolic type boundary layer. To show the relationship between the space variable and the solution, we have used the log-log plot in Figure 3 which is a straight line. This shows that the solution changes as a power of the space variable and confirms the first-order uniform convergence of the proposed method.

Details are in the caption following the image — **Figure 1 (a) ε = 10−1, μ = 100**
Open in figure viewer PowerPoint

Numerical solution of Example 1 for N = M = 64.

6. Conclusion

A parameter uniform convergent numerical scheme for singularly perturbed two parametric parabolic problem with time lag is presented. The proposed numerical scheme comprises the implicit Euler method and novel finite difference method in the time and space directions, respectively. Parameter uniform convergence analysis of the scheme is investigated theoretically as well as numerically. The obtained results show that the presented scheme gives better accuracy than the existing schemes. The presented scheme is accurate and convergent with the order of convergence O(Δt + Δs²).

Conflicts of Interest

The authors declared no potential conflicts of interest concerning the research, authorship, and publication of this article.

Open Research

Data Availability

No data were used to support this study.

References

1 Ladyzenskaja O. A., Solonnikov V. A., and Uralceva N. N., Linear and quasilinear equations of parabolic type, Translations of Mathematical Monographs. (1968) 23, https://doi.org/10.1090/mmono/023.
10.1090/mmono/023
Google Scholar
2 Mishra V., Some Problems on Approximations of Functions in Banach Spaces, 2007, Ph.D. thesis, Indian Institute of Technology, Roorkee, Uttarakhand, India.
Google Scholar
3 Miller J. J. H., O’Riordan E., Shishkin G. I., and Shishkina L. P., Fitted mesh methods for problems with parabolic boundary layers, Mathematical Proceedings of the Royal Irish Academy. (1998) 98A, 173–190.
Google Scholar
4 Kopteva N., Uniform pointwise convergence of difference schemes for convection-diffusion problems on layer-adapted meshes, Computing. (2001) 66, no. 2, 179–197, https://doi.org/10.1007/s006070170034, 2-s2.0-0034953680.
10.1007/s006070170034
Web of Science® Google Scholar
5 Yüzbaşı Ş. and Şahin N., Numerical solutions of singularly perturbed one-dimensional parabolic convection-diffusion problems by the Bessel collocation method, Applied Mathematics and Computation. (2013) 220, 305–315, https://doi.org/10.1016/j.amc.2013.06.027, 2-s2.0-84880064322.
10.1016/j.amc.2013.06.027
Web of Science® Google Scholar
6 DiPrima R. C., Asymptotic methods for an infinitely long slider squeeze-film bearing, Transactions of the American Society of Mechanical Engineers Series Film, Journal of Lubrication Technology. (1968) 90, no. 1, 173–183, https://doi.org/10.1115/1.3601534, 2-s2.0-85024556835.
10.1115/1.3601534
Google Scholar
7 Chen J. and O’Malley R., On the asymptotic solution of a twoparameter boundary value problem of chemical reactor theory, SIAM Journal on Applied Mathematics. (1974) 26, no. 4, 717–729, https://doi.org/10.1137/0126064.
10.1137/0126064
Web of Science® Google Scholar
8 Schlichting H., Boundary Layer Theory, 1979, 7th edition, McGraw-Hill, New York.
Google Scholar
9 Van Harten A. and Schumacher J. M., On a class of partial functional differential equations arising in feed-back control theory, North-Holland Mathematics Studies. (1978) 31, 161–179, https://doi.org/10.1016/S0304-0208(08)70556-5, 2-s2.0-85023536055.
10.1016/S0304-0208(08)70556-5
Google Scholar
10 Kuang Y., Delay Differential Equations: With Applications in Population Dynamics, 1993, Academic press.
Google Scholar
11 Samarskii A. A. and Vabishchevich P. N., Computational Heat Transfer, 1995, John Wiley.
Google Scholar
12 Bullo T. A., Duressa G. F., and Degla G. A., Robust finite difference method for singularly perturbed two-parameter parabolic convection-diffusion problems, International Journal of Computational Methods. (2021) 18, no. 2, article 2050034, https://doi.org/10.1142/S0219876220500346.
10.1142/S0219876220500346
Web of Science® Google Scholar
13 Bullo T. A., Duressa G. F., and Degla G. A., Parameter-uniform finite difference method for singularly perturbed parabolic problem with two small parameters, International Journal for Computational Methods in Engineering Science and Mechanics. (2022) 23, no. 3, 210–218, https://doi.org/10.1080/15502287.2021.1948148.
10.1080/15502287.2021.1948148
Web of Science® Google Scholar
14 Bullo T. A., Duressa G. F., and Degla G. A., Accelerated fitted operator finite difference method for singularly perturbed parabolic reaction-diffusion problems, Computational Methods for Differential Equations. (2021) 93, 886–898, https://doi.org/10.22034/CMDE.2020.39685.1737.
10.22034/CMDE.2020.39685.1737
Google Scholar
15 Mekonnen T. B. and Duressa G. F., A fitted mesh cubic spline in tension method for singularly perturbed problems with two parameters, International Journal of Mathematics and Mathematical Sciences. (2022) 2022, 11, https://doi.org/10.1155/2022/5410754, 5410754.
10.1155/2022/5410754
Google Scholar
16 Mekonnen T. B. and Duressa G. F., Computational method for singularly perturbed two-parameter parabolic convection-diffusion problems, Cogent Mathematics & Statistics. (2020) 7, no. 1, article 1829277, https://doi.org/10.1080/25742558.2020.1829277.
10.1080/25742558.2020.1829277
Web of Science® Google Scholar
17 Shivhare M., Chakravarthy P. P., and Kumar D., QuadraticB-spline collocation method for two-parameter singularly perturbed problem on exponentially graded mesh, International Journal of Computer Mathematics. (2021) 98, no. 12, 2461–2481, https://doi.org/10.1080/00207160.2021.1901277.
10.1080/00207160.2021.1901277
Web of Science® Google Scholar
18 Kumar D. and Kumari P., Uniformly convergent scheme for two-parameter singularly perturbed problems with non-smooth data, Numerical Methods for Partial Differential Equations. (2021) 37, no. 1, 796–817, https://doi.org/10.1002/num.22553.
10.1002/num.22553
Web of Science® Google Scholar
19 Kadalbajoo M. K. and Yadaw A. S., Parameter-uniform finite element method for two-parameter singularly perturbed parabolic reaction-diffusion problems, International Journal of Computational Methods. (2012) 9, no. 4, article 1250047, https://doi.org/10.1142/S0219876212500478, 2-s2.0-84872314328.
10.1142/S0219876212500478
Web of Science® Google Scholar
20 Patidar K. C., A robust fitted operator finite difference method for a two-parameter singular perturbation problem1, Journal of Difference Equations and Applications. (2008) 14, no. 12, 1197–1214, https://doi.org/10.1080/10236190701817383, 2-s2.0-54349114974.
10.1080/10236190701817383
Web of Science® Google Scholar
21 Prabha T., Chandru M., Shanthi V., and Ramos H., Discrete approximation for a two-parameter singularly perturbed boundary value problem having discontinuity in convection coefficient and source term, Journal of Computational and Applied Mathematics. (2019) 359, 102–118, https://doi.org/10.1016/j.cam.2019.03.040, 2-s2.0-85064271152.
10.1016/j.cam.2019.03.040
Web of Science® Google Scholar
22 Chandru M., Prabha T., and Shanthi V., A parameter robust higher order numerical method for singularly perturbed two parameter problems with non-smooth data, Journal of Computational and Applied Mathematics. (2017) 309, 11–27, https://doi.org/10.1016/j.cam.2016.06.009, 2-s2.0-84978077096.
10.1016/j.cam.2016.06.009
Web of Science® Google Scholar
23 Govindarao L., Sahu S. R., and Mohapatra J., Uniformly convergent numerical method for singularly perturbed two parameter time delay parabolic problem, International Journal of Applied and Computational Mathematics. (2019) 5, no. 3, 1–9, https://doi.org/10.1007/s40819-019-0672-5.
10.1007/s40819-019-0672-5
Google Scholar
24 Sumit, Kumar S., Kuldeep, and Kumar M., A robust numerical method for a two-parameter singularly perturbed time delay parabolic problem, Computational and Applied Mathematics. (2020) 39, no. 3, 1–25, https://doi.org/10.1007/s40314-020-01236-1.
10.1007/s40314-020-01236-1
Web of Science® Google Scholar
25 Govindarao L., Sahu S. R., and Mohapatra J., Uniformly convergent numerical method for singularly perturbed time delay parabolic problem with two small parameters, Iranian Journal of Science and Technology, Transactions A: Science. (2019) 43, no. 5, 2373–2383, https://doi.org/10.1007/s40995-019-00697-2, 2-s2.0-85073226551.
10.1007/s40995-019-00697-2
Web of Science® Google Scholar
26 Vigo-Aguiar J. and Natesan S., An efficient numerical method for singular perturbation problems, Journal of Computational and Applied Mathematics. (2006) 192, no. 1, 132–141, https://doi.org/10.1016/j.cam.2005.04.042, 2-s2.0-33646088987.
10.1016/j.cam.2005.04.042
Web of Science® Google Scholar
27 Natesan S., Vico-Acuiar J., and Ramanujam N., A numerical algorithm for singular perturbation problems exhibiting weak boundary layers, Computers and Mathematics with Applications. (2003) 45, no. 1-3, 469–479, https://doi.org/10.1016/S0898-1221(03)80031-7, 2-s2.0-0037284594.
10.1016/S0898-1221(03)80031-7
Web of Science® Google Scholar
28 Vico-Acuiar J. and Natesan S., A parallel boundary value technique for singularly perturbed two-point boundary value problems, The Journal of Supercomputing. (2004) 27, no. 2, 195–206, https://doi.org/10.1023/B:SUPE.0000009322.23950.53, 2-s2.0-0742307481.
10.1023/B:SUPE.0000009322.23950.53
Web of Science® Google Scholar
29 O’malley R. E., Singular perturbation methods for ordinary differential equations, Applied Mathematical Sciences. (1991) 89, https://doi.org/10.1007/978-1-4612-0977-5.
10.1007/978-1-4612-0977-5
Google Scholar
30 Ranjan R. and Prasad H. S., A novel approach for the numerical approximation to the solution of singularly perturbed differential-difference equations with small shifts, Journal of Applied Mathematics and Computing. (2021) 65, no. 1-2, 403–427, https://doi.org/10.1007/s12190-020-01397-6.
10.1007/s12190-020-01397-6
Web of Science® Google Scholar
31 Nichols N. K., On the numerical integration of a class of singular perturbation problems, Journal of Optimization Theory and Applications. (1989) 60, no. 3, 439–452, https://doi.org/10.1007/BF00940347, 2-s2.0-1542277366.
10.1007/BF00940347
Web of Science® Google Scholar
32 File G. and Reddy Y. N., Terminal boundary-value technique for solving singularly perturbed delay differential equations, Journal of Taibah University for Science. (2014) 8, no. 3, 289–300, https://doi.org/10.1016/j.jtusci.2014.01.006.
10.1016/j.jtusci.2014.01.006
Google Scholar
33 Daba I. T. and Duressa G. F., Fitted numerical method for singularly perturbed Burger–Huxley equation, Computational and Applied Mathematics. (2022) 2022, no. 1, https://doi.org/10.1186/s13661-022-01681-3.
10.1186/s13661-022-01681-3
Google Scholar

All articles

A Fitted Numerical Approach for Singularly Perturbed Two-Parameter Parabolic Problem with Time Delay

Abstract

1. Introduction

2. Properties of Continuous Solution

3. Construction of the Numerical Scheme

3.1. Temporal Semidiscretization

3.2. Spatial Semidiscretization

4. Convergence Analysis

5. Numerical Examples, Results, and Discussions

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Fitted Numerical Approach for Singularly Perturbed Two-Parameter Parabolic Problem with Time Delay

Abstract

1. Introduction

2. Properties of Continuous Solution

3. Construction of the Numerical Scheme

3.1. Temporal Semidiscretization

3.2. Spatial Semidiscretization

4. Convergence Analysis

5. Numerical Examples, Results, and Discussions

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Related

Information