Volume 2023, Issue 1 5845263

Research Article

Open Access

A Novel Collocation Method for Numerical Solution of Hypersingular Integral Equation with Singular Right-Hand Function

M. R. Elahi,

M. R. Elahi

Department of Mathematics, Tabriz Branch, Islamic Azad University, Tabriz, Iran azad.ac.ir

Search for more papers by this author

Y. Mahmoudi,

Corresponding Author

Y. Mahmoudi

[email protected]

orcid.org/0000-0001-9979-0951

Department of Mathematics, Tabriz Branch, Islamic Azad University, Tabriz, Iran azad.ac.ir

Search for more papers by this author

A. Salimi Shamloo,

A. Salimi Shamloo

orcid.org/0000-0001-9563-9832

Department of Mathematics, Shabestar Branch, Islamic Azad University, Shabestar, Iran azad.ac.ir

Search for more papers by this author

M. Jahangiri Rad,

M. Jahangiri Rad

orcid.org/0000-0002-6033-0357

Department of Mathematics, Tabriz Branch, Islamic Azad University, Tabriz, Iran azad.ac.ir

Search for more papers by this author

M. R. Elahi,

M. R. Elahi

Department of Mathematics, Tabriz Branch, Islamic Azad University, Tabriz, Iran azad.ac.ir

Search for more papers by this author

Y. Mahmoudi,

Corresponding Author

Y. Mahmoudi

[email protected]

orcid.org/0000-0001-9979-0951

Department of Mathematics, Tabriz Branch, Islamic Azad University, Tabriz, Iran azad.ac.ir

Search for more papers by this author

A. Salimi Shamloo,

A. Salimi Shamloo

orcid.org/0000-0001-9563-9832

Department of Mathematics, Shabestar Branch, Islamic Azad University, Shabestar, Iran azad.ac.ir

Search for more papers by this author

M. Jahangiri Rad,

M. Jahangiri Rad

orcid.org/0000-0002-6033-0357

Department of Mathematics, Tabriz Branch, Islamic Azad University, Tabriz, Iran azad.ac.ir

Search for more papers by this author

First published: 20 March 2023

https://doi.org/10.1155/2023/5845263

Citations: 2

Academic Editor: Eugen Radu

Share a link

Email
Wechat
Bluesky

Abstract

In this study, the Fredholm hypersingular integral equation of the first kind with a singular right-hand function on the interval [−1, 1] is solved. The discontinuous solution on the domain [−1, 1] is approximated by a piecewise polynomial, and a collocation method is introduced to evaluate the unknown coefficients. This method, which can be applied to both linear and nonlinear integral equations, is very simple and straightforward. The presented illustrations relate that the results are very accurate compared to the other methods in the literature.

1. Introduction

Hypersingular integral equations (HSIEs) are widely presented in different fields of physics and engineering such as crack problems in fracture mechanics [1], radiation problems involving thin-submerged plates [2–4], antenna theory [5], aerodynamics [6, 7], elliptic wing case in Prandtl’s equation [8, 9], electrodynamics, and quantum physics [6].

Many two-dimensional boundary value problems in mathematical physics can be formulated as HSIEs. It is investigated that how the problems such as two-dimensional flow post a rigid plate in an infinite fluid, acoustic scattering by a hard plate, water wave interaction with thin impermeable barriers, stress fields around cracks, certain specific problems involving cracks in an elastic medium and scattering of surface water waves by obstacles in the form of thin barriers, and some other issues give rise to HSIEs (see [7]). There are two strategies to solve these problems. The direct methods in which the problem is solved using the method of solving differential equations are finite difference methods [10] and Runge-Kutta-embedded methods [11]. Another robust tool is indirect methods in which the differential equation is transformed into an equivalent equation such as a HSIE. The numerical solutions for the second category is often less complicated.

In certain cases, there exist some analytical methods for solving HSIEs, but in general, there is no known analytical method. Thus, different numerical methods are introduced and developed for solving HSIEs [8, 9, 12–26].

The following first kind HSIE

(1)

with various justifications on the boundaries x = ±1 was studied in [21] by using different types of Chebyshev polynomials. In Equation (1), the right-hand function f(x) is considered a smooth function, and the hypersingular integral is understood as Hadamard finite part as follows:

(2)

Recently, a special class of Equation (1) was introduced under the assumption that the right-hand function f(x) possesses singularities at some points c₁ < c₂ < ⋯<c_m−1 of the interval (−1, 1) [5, 6, 27]. In this case, the solution is not smooth in the integration domain. It was shown in [21] that if the right-hand function f(x) in Equation (1) belongs to a Hölder class, then, under some additional conditions on the boundaries, the solution can be represented as or u(x) = ((1 + x)/(1 − x))^±1/2ϕ(x), where ϕ(x) is a smooth function. While, for the singular right-hand function f(x), the class of solutions for Equation (1) is not determined yet.

Authors in [28, 29] introduced a variant of the generalized Euler-Maclaurin summation formula for the product integration rule and applied it for approximating weakly singular integrals. Also, with the expansion of the theory of fractional calculus in recent years, many attempts have been made to use fractional calculus to solve singular integral equations. These methods are suitable for solving weakly singular integral equations, but they cannot be used for a stronger singular integral equations such as HSIEs.

Recently, an iterative projection method is presented for solving linear and nonlinear HSIEs with non-Riemann integrable functions on the right-hand side [25]. They applied the continuous method and presented the convergence of the proposed method based on the Lyapunov stability theory. Not many papers have been published to solve the Equation (1) with singular right-hand function yet. To avoid the complexity of the method presented in [25] in the present study, we consider a simple collocation method for the numerical solution of HSIE (Equation (1)) with the singular right-hand function. The most important advantage of our method is its simplicity and adaptability to different states of the right-hand function. The rest of this paper is organized as follows: in Section 2, the piecewise polynomial collocation method is introduced and applied to the proposed linear and nonlinear hypersingular integral equation. The numerical illustrations are presented in Section 3, and finally, a brief conclusion appeared in Section 4.

2. Method of Solution

In this section, we consider a new collocation method for solving the following linear and nonlinear HSIE of the first kind:

(3)

where the right-hand function f(x) = f₁(x) + f₂(x) + f₃(x) + ⋯ has different types of singularities at the points c₁ < c₂ < ⋯<c_m−1 of the interval (−1, 1). The singularities of f(x) may have the following structure:

(4)

or any other singular type. In Equation (4), g(x) and g_i(x), i = 1, 2, ⋯, m − 1 are considered smooth functions. To introduce the new method, we need the following definitions.

Definition 1. We define the Cauchy and Hadamard integrals, respectively, as follows

(5)

(6)

Theorem 2. The Cauchy and Hadamard integrals defined in Equations (5) and (6) are calculated as follows:

(7)

(8)

Proof. By the definition of Cauchy integral (Equation (5)), we have

(9)

Also, by the definition of Hadamard integral (Equation (6)), we have

(10)

Now, we intend to solve Equation (3) by representing the solution as a piecewise continuous polynomial. To do this, we set c₀ = −1 and c_m = 1, and then, we seek a solution for Equation (3) on the interval [−1, 1]. According to the structure of the function on the right hand, the solution may be discontinuous at the points c_i, i = 1, 2, ⋯, m − 1. Therefore, we consider the solution in the following form:

(11)

where N is a given integer.

2.1. Application to Linear HSIE

Consider Equation (3) with p = 1. We rewrite Equation (3) as follows:

(12)

Substituting Equation (11) in Equation (3), we get

(13)

which gives

(14)

We select N + 1 distinct points x_r0 < x_r1 < ⋯<x_rN on the jth subinterval (c_r−1, c_r), r = 1, 2, ⋯m.

Now, we collocate (14) as follows:

(15)

Equation (15) represents a system of m(N + 1) linear equations of m(N + 1) unknowns a_ji, j = 1, 2, ⋯, m, i = 0, 1, ⋯, N, which can be converted to matrix format as

(16)

where

(17)

and A is a m(N + 1) square matrix. The elements of A are as follows:

(18)

Remark 3. Due to Definition 1, the Hadamard integrals H_i(x, t), i = 0, 1, ⋯N are linearly independent functions. Also, the points are distinct and x_rs ≠ c_j. Then, from Haar property for independent functions, we conclude that |A| ≠ 0. This means that the linear system (Equation (16)) has a unique solution.

2.2. Application to Nonlinear HSIE

Let us consider Equation (3) with p > 1. For solving the nonlinear HSIE (Equation (3)), we rewrite it as follows:

(19)

Substituting Equation (11) in Equation (19), we get

(20)

after some simplification we get

(21)

which gives

(22)

We note that A_jn in Equation (21) is the corresponding coefficient of tⁿ in the expansion of

, which is calculated using Adomian polynomials as follows:

(23)

If we collocate Equation (22) at the points x_rs, r = 1, 2, ⋯, m, s = 0, 1, ⋯, N, we get the following nonlinear system of equations:

(24)

3. Numerical Illustrations

In this section, we present the effectiveness of the proposed method by solving some HSIEs. All the simulations have been done using Maple software with an accuracy of 20 digits. The first few H_i(x, t) are as follows (see Equation (8)).

(25)

Example 4. Suppose the following linear HSIE of the first kind [25],

(26)

where

(27)

Here, we set c₀ = −1, c₁ = 0, and c₂ = 1, where f(x) has singularity. Then, we apply the proposed method with N = 3 and get

(28)

which gives the exact solution. In Figure 1, we plotted the graph of exact and approximate solutions for N = 2, 4 and 6.

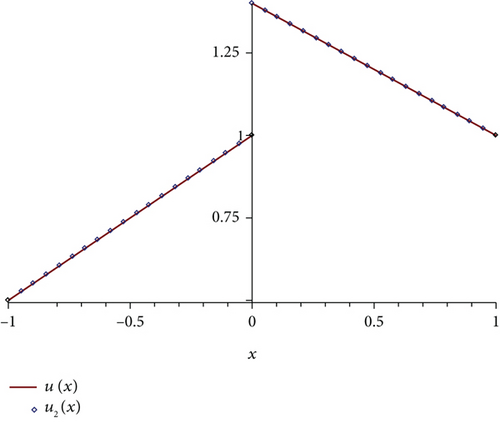
Example 5. Consider the following linear HSIE of the first kind,

(29)

where

(30)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The graph of exact solution u(x) and approximate solutions u₂(x), u₄(x), u₆(x) for Example 4.

Here, we set c₀ = −1, c₁ = −0.5, c₂ = 0.5, and c₃ = 1. Then, we apply the proposed method with N = 3 and get

(31)

which is the exact solution to the problem. The graph for the exact and approximate solution for N = 3 and 5 is plotted in Figure 2.

Example 6. Suppose the following nonlinear HSIE of the first kind [25],

(32)

where

(33)

The right-hand function f(x) is singular at three points c₀ = −1, c₁ = 0, and c₂ = 1. Then, we apply the proposed method with N = 3, and we get

(34)

which is the exact solution to the problem. The corresponding graphs for the exact and approximate solution are plotted in Figure 3.

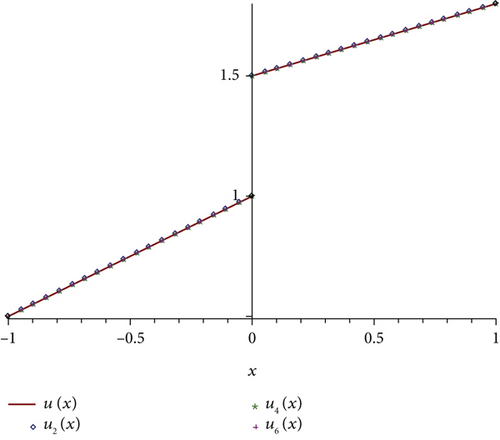
Example 7. For the next example, we suppose the following nonlinear HSIE of the first kind,

(35)

where

(36)

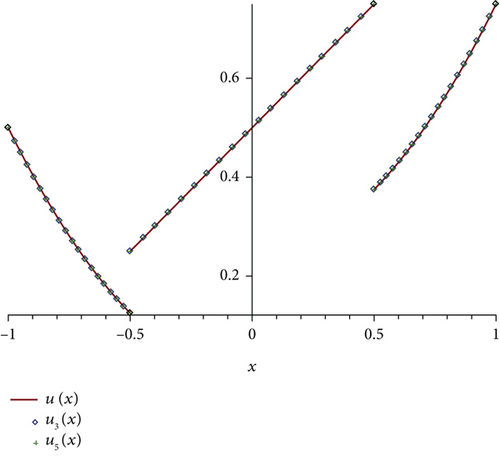
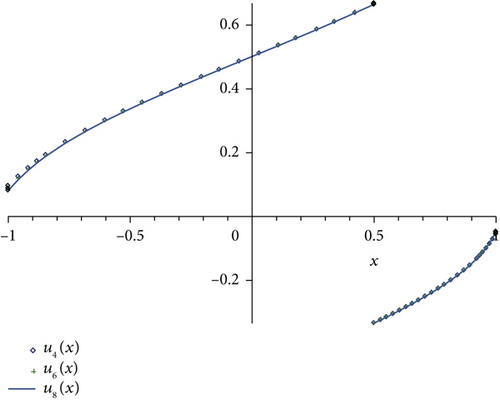
The right-hand function f(x) is singular at three points c₀ = −1, c₁ = 0, and c₂ = 1, while the exact solution is not known. The graph for approximate solutions for different values of N is plotted in Figure 4.

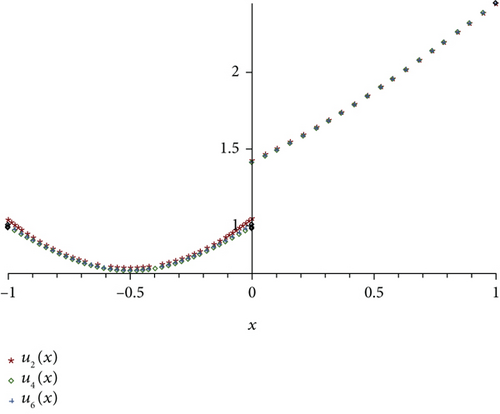
Example 8. Suppose the following nonlinear HSIE of the first kind,

(37)

where the right-hand function f(x) is singular at c₁ = 0.5. We solved this problem with different values of N. The graphs for approximate solutions are plotted in Figure 5. Note that the exact solution is not known here.

Remark 9. According to the illustrated examples, we can see that when the solution of the HSIE is polynomial, the present method produces the exact solution of the problem. In case the exact solution is not available, the numerical approximations converge to each other by increasing N (see Examples 7 and 8). Comparison of numerical results with the results of [25] show that the present method is very efficient.

4. Conclusion

In this study, we have developed a novel collocation method for solving the first kind of hypersingular integral equations of the first kind with a singular right-hand function. The solution is considered as a piecewise polynomial on the integration domain, and the unknown coefficients are determined by solving an algebraic system of equations. The new method applies to both linear and nonlinear integral equations. This method covers a wide range of singular integral equations with different types of singularities on the right-hand function. It can also be applied for supersingular integral equations with singular right-hand function.

For further research in this field, it is suggested that the class of the solution space of the equation be analyzed analytically based on the type of singularity of the right-hand function.

Conflicts of Interest

The authors declare that they have no conflict of interest.

Open Research

Data Availability

No underlying data was collected or produced in this study.

References

1 Chan Y., Fannjiang A. C., and Paulino G. H., Integral equations with hypersingular kernels--theory and applications to fracture mechanics, International Journal of Engineering Science. (2003) 41, no. 7, 683–720, https://doi.org/10.1016/S0020-7225(02)00134-9, 2-s2.0-0037397139.
10.1016/S0020-7225(02)00134-9
Web of Science® Google Scholar
2 Abbasbandy S., Application of He′s homotopy perturbation method to functional integral equations, Chaos Solitons and Fractals. (2007) 31, no. 5, 1243–1247, https://doi.org/10.1016/j.chaos.2005.10.069, 2-s2.0-33748421926.
10.1016/j.chaos.2005.10.069
Web of Science® Google Scholar
3 Abbasbandy S., Numerical solutions of the integral equations: homotopy perturbation method and Adomian′s decomposition method, Applied Mathematics and Computation. (2006) 173, no. 1, 493–500, https://doi.org/10.1016/j.amc.2005.04.077, 2-s2.0-32144434395.
10.1016/j.amc.2005.04.077
Web of Science® Google Scholar
4 Bellman R., Perturbation Techniques in Mathematics Physics and Engineering, 1964, Holt, Rinehart and Winston, Inc..
Google Scholar
5 Lifanov I. K. and Nenashev A. S., Hypersingular integral equations and the theory of wire antennas, Differential Equations. (2005) 41, no. 1, 126–145, https://doi.org/10.1007/s10625-005-0142-1, 2-s2.0-17444411935.
10.1007/s10625-005-0142-1
Web of Science® Google Scholar
6 Lifanov I. K., Poltavskii L. N., and Vainikko G. M., Hypersingular integral equations and their applications, 2004, Chapman and Hall/CRC.
Google Scholar
7 Mandal B. N. and Chakrabarti A., Applied Singular Integral Equation, 2011, CRC press.
Google Scholar
8 Mandal B. N. and Bera G. H., Approximate solution for a class of hypersingular integral equations, Applied Mathematics Letters. (2006) 19, no. 11, 1286–1290, https://doi.org/10.1016/j.aml.2006.01.013, 2-s2.0-33745644447.
10.1016/j.aml.2006.01.013
Web of Science® Google Scholar
9 Mandal B. N. and Bera G. H., Approximate solution of a class of singular integral equations of second kind, Journal of Computational and Applied Mathematics. (2007) 206, no. 1, 189–195, https://doi.org/10.1016/j.cam.2006.06.011, 2-s2.0-34249338721.
10.1016/j.cam.2006.06.011
Web of Science® Google Scholar
10 Dehghan M., A finite difference method for a non-local boundary value problem for two-dimensional heat equation, Applied Mathematics and Computation. (2000) 112, no. 1, 133–142, https://doi.org/10.1016/S0096-3003(99)00055-7, 2-s2.0-0033744321.
10.1016/S0096-3003(99)00055-7
Web of Science® Google Scholar
11 Kovalnogov V. N., Fedorov R. V., Karpukhina T. V., Simos T. E., and Tsitouras C., Runge--Kutta embedded methods of orders 8(7) for use in quadruple precision computations, Mathematics. (2022) 10, no. 18, https://doi.org/10.3390/math10183247.
10.3390/math10183247
Web of Science® Google Scholar
12 Golberg M. A., The convergence of several algorithms for solving integral equations with finite-part integrals, II, The Journal of Integral Equations and Applications. (1985) 9, no. 3, 267–275.
Web of Science® Google Scholar
13 Chen Z. and Zhou Y. F., A new method for solving hypersingular integral equations of the first kind, Applied Mathematics Letters. (2011) 24, no. 5, 636–641, https://doi.org/10.1016/j.aml.2010.11.028, 2-s2.0-79551490164.
10.1016/j.aml.2010.11.028
Web of Science® Google Scholar
14 Boykov I. V., Ventsel E. S., and Boykova A. I., An approximate solution of hypersingular integral equations, Applied Numerical Mathematics. (2010) 60, no. 6, 607–628, https://doi.org/10.1016/j.apnum.2010.03.003, 2-s2.0-77953132260.
10.1016/j.apnum.2010.03.003
Web of Science® Google Scholar
15 Boykov I. V., Ventsel E. S., and Boykova A. I., Accuracy optimal methods for evaluating hypersingular integrals, Applied Numerical Mathematics. (2009) 59, no. 6, 1366–1385, https://doi.org/10.1016/j.apnum.2008.08.004, 2-s2.0-62549117808.
10.1016/j.apnum.2008.08.004
Web of Science® Google Scholar
16 Gulsu M. and Ozturk Y., Numerical approach for the solution of hypersingular integro-differential equations, Applied Mathematics and Computation. (2014) 230, 701–710, https://doi.org/10.1016/j.amc.2013.12.163, 2-s2.0-84893061429.
10.1016/j.amc.2013.12.163
Web of Science® Google Scholar
17 Abdulkawi M., Nik Long N. M. A., and Eshkuvatov Z. K., Numerical solution of hypersingular integral equations, International Journal of Pure and Applied Mathematics. (2011) 69, no. 3, 265–274.
Google Scholar
18 Novin R., Fariborzi Araghi M. A., and Mahmoudi Y., A novel fast modification of the Adomian decomposition method to solve integral equations of the first kind with hypersingular kernels, Journal of Computational and Applied Mathematics. (2018) 343, 619–634, https://doi.org/10.1016/j.cam.2018.04.055, 2-s2.0-85047630418.
10.1016/j.cam.2018.04.055
Web of Science® Google Scholar
19 Mahmoudi Y., A new modified Adomian decomposition method for solving a class of hypersingular integral equations of second kind, Journal of Computational and Applied Mathematics. (2014) 255, 737–742, https://doi.org/10.1016/j.cam.2013.06.026, 2-s2.0-84880360633.
10.1016/j.cam.2013.06.026
Web of Science® Google Scholar
20 Novin R. and Fariborzi Araghi M. A., Hypersingular integral equations of the first kind: a modified homotopy perturbation method and its application to vibration and active control, Control. (2019) 38, no. 2, 706–727, https://doi.org/10.1177/1461348419827378, 2-s2.0-85061721263.
10.1177/1461348419827378
Google Scholar
21 Ahdiaghdam S., Solving singular integral equations by using orthogonal polynomials, Computational Methods for Differential Equations. (2018) 6, no. 4, 411–425.
Google Scholar
22 Eshkuvatov Z. K. and Narzullaev A., Projection method for bounded and unbounded solution of hypersingular integral equations of the first kind, Indian Journal of Industrial and Applied Mathematics, Indian Journal of Industrial and Applied Mathematics. (2019) 10, no. 1, 11–37, https://doi.org/10.5958/1945-919X.2019.00002.1.
10.5958/1945-919X.2019.00002.1
Google Scholar
23 Eshkuvatov Z., Kommuji M., Aloev R., Long N. M. A. N., and Khudoyberganov M., Semi bounded solution of hypersingular integral equations of the first kind on the rectangle, Mathematics and Statistics. (2020) 8, no. 2, 106–120, https://doi.org/10.13189/ms.2020.080206.
10.13189/ms.2020.080206
Google Scholar
24 Khubezhty S. S., Onnumerical solution of hypersingular integral equations of the first kind, Vladikavkaz Mathematical Journal. (2020) 22, no. 1, 85–92.
Google Scholar
25 Boykov I., Roudnev V. M., and Boykova A., Approximate methods for solving linear and nonlinear hypersingular integral equations, Axioms. (2020) 9, no. 3, https://doi.org/10.3390/axioms9030074.
10.3390/axioms9030074
Web of Science® Google Scholar
26 Aghigh K., Masjed-Jamei M., and Dehghan M., A survey on third and fourth kind of Chebyshev polynomials and their applications, Applied Mathematics and Computation. (2008) 199, no. 1, 2–12, https://doi.org/10.1016/j.amc.2007.09.018, 2-s2.0-41949118011.
10.1016/j.amc.2007.09.018
Web of Science® Google Scholar
27 Lifanov I. K. and Nenashev A. S., Analysis of some computational schemes for a hypersingular integral equation on an interval, Differential Equations. (2005) 41, no. 9, 1343–1348, https://doi.org/10.1007/s10625-005-0283-2, 2-s2.0-27844485306.
10.1007/s10625-005-0283-2
Google Scholar
28 Rzadkowski G. and Tohidi E., A fourth order product integration rule by using the generalized Euler- Maclaurin summation formula, Journal of Computational and Applied Mathematics. (2018) 335, 334–348, https://doi.org/10.1016/j.cam.2017.12.017, 2-s2.0-85040037949.
10.1016/j.cam.2017.12.017
Web of Science® Google Scholar
29 Rzadkowski G. and Tohidi E., Convergence analysis of the generalized Euler-Maclaurin quadrature rule for solving weakly singular integral equations, Univerzitet u Nišu. (2019) 33, no. 6, 1801–1815, https://doi.org/10.2298/FIL1906801R.
10.2298/FIL1906801R
Google Scholar

Citing Literature

All articles

A Novel Collocation Method for Numerical Solution of Hypersingular Integral Equation with Singular Right-Hand Function

Abstract

1. Introduction

2. Method of Solution

2.1. Application to Linear HSIE

2.2. Application to Nonlinear HSIE

3. Numerical Illustrations

4. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Novel Collocation Method for Numerical Solution of Hypersingular Integral Equation with Singular Right-Hand Function

Abstract

1. Introduction

2. Method of Solution

2.1. Application to Linear HSIE

2.2. Application to Nonlinear HSIE

3. Numerical Illustrations

4. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information