International Journal of Geophysics
Volume 2023, Issue 1 4405266
Research Article
Open Access

New Analysis of the Seasonal Variation of the Critical Frequencies foF2 by a Proposed Formula of the Power of Solar Radiation

Segda Abdoul-kader, 

Segda Abdoul-kader

Laboratory of Analytical Chemistry of Space and Energy Physics (LACAPSE) UFR-ST, Université Norbert ZONGO, BP 376 Koudougou, Burkina Faso unz.bf

Search for more papers by this author
Gnabahou Doua Allain, 

Corresponding Author

Gnabahou Doua Allain

Laboratory of Analytical Chemistry of Space and Energy Physics (LACAPSE) UFR-ST, Université Norbert ZONGO, BP 376 Koudougou, Burkina Faso unz.bf

Search for more papers by this author
Gyebre Aristide, 

Gyebre Aristide

Laboratory of Analytical Chemistry of Space and Energy Physics (LACAPSE) UFR-ST, Université Norbert ZONGO, BP 376 Koudougou, Burkina Faso unz.bf

Search for more papers by this author
First published: 20 November 2023
https://doi.org/10.1155/2023/4405266
Citations: 1
Academic Editor: Stelios M. Potirakis

Abstract

The present article is a new analysis of the seasonal variation of the critical frequencies foF2 by establishing a formula as a tool. Thus, from the formula of the power of solar radiation proposed, by its two components, one the power linked to the angles of attack of the solar rays and the other the power imparted to the Earth-Sun distance, we will understand the asymmetries foF2 peaks at the equinoxes and the various winter and semiannual anomalies. By the power component imparted to the contribution of sunspots, we will understand the reversal of the maximum peak during the growth and waning phase of the solar cycle. Finally, by the power component linked to the transport mechanism and the reinforcement by the solar wind of the ionization, we will understand the why of the noninversion of the maximum of the peaks.

1. Introduction

This paper is an approach that takes into account results from in situ measurements of the solar cycle 21 of the Ouagadougou and Dakar stations and the solar cycle 20 of the Djibouti station. The long-term objective is to find a formula for the temporal variation of the solar radiation power PS(t) and the critical frequencies foF2(t) which on the one hand would reproduce as well as possible the variations of the critical frequencies given by in situ measurements and on the other hand would be able to explain the main characteristics [1, 2]. To do this, this article will first present the curves of the in situ measurements of the stations of Ouagadoudou, Dakar, and Djibouti and the curves resulting from the proposed formula of PS(t). The second step in the discussion will be to show the process of elaboration of the solar radiation power PS(t) and by ricochet foF2(t).

2. Data

The data used are from the station of Ouagadougou (latitude 12.5° N, longitude 358.5° E) and Dakar (latitude 14.8° N, longitude 342.6° E) of solar cycle 21 during the period from 1975 to 1984 [3] and the Djibouti station (latitude 11.5° N, longitude 42.8° E) of solar cycle 20 during the period from 1964 to 1974 [3]. If for Djibouti we have considered the solar cycle 20, it is because all the data of the solar cycle 21 of this station are not available.

3. Materials and Methods

The Excel 2010 software is the “hardware” used to build the different curves. The method consists of using the data of the in situ measurements to build the graphs and in a second time to establish the formula of the power of the solar radiation and also to obtain graphs. After that observed profiles, we proceed to comments or explanations to justify the validity of the formula for the variations in the power of solar radiation that we have proposed.

4. Discussion

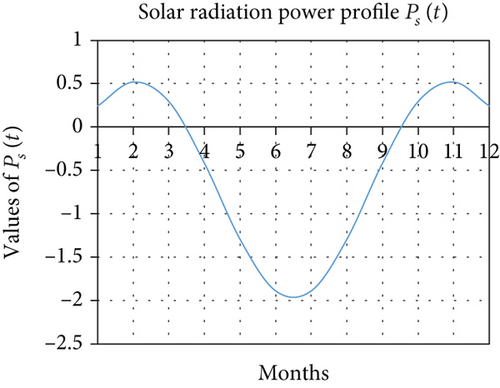
The proposed formula of PS(t) would be based on the observation (Figure 1) of variations in the powers of solar radiation Pα(t),  Pd(t), and Pa(t) (Figure 1). These different powers have been used in our previous articles [4, 5] to explain the different characteristics observed in the seasonal variation of foF2. Thus, as a brief reminder in order to be better understood, Pα(t) is the part of the power induced by the variation of the angles,  Pd(t) induced by the variation of the distance of the Earth from the Sun, and finally Pa(t) the part of the power which represents the contribution of sunspots.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Variation curves of the solar radiation powers.
The decor or context being planted or clarified the proposed formula of the power of solar radiation which reproduces the main characteristics given by the curves of the in situ measurements of the monthly average variability of the critical frequencies foF2 or seasonal is
(1)
where Pα0 and fα would represent the amplitude and the frequency of the variation of Pα(t), respectively. These parameters represent amplitude and frequency, respectively. The alpha index designates that of the solar power imparted to the angles of incidence on the ionosphere. The formula proposed for this purpose which reproduces this variation observed during the year is of the following form:
(2)
where Tα is the period of Pα(t) which would be eight (08) months because an alternation is counted as half a period. If we add to this power of the solar radiation Pα(t), the power of the solar radiation related to the distance Earth-Sun present only one negative alternation is thus of the form:
(3)
By considering Pα0 is equal to Pd0, we arrive at the formula for PS(t) given by equation (1) whose graphic representation is given in Figure 1. For this purpose of simulation representation, Pα0 is taken as 1 because any other value assigned to them will not modify the pace or the profile of the variation PS(t). We will obtain an enlarged or reduced form of PS(t) just like an image that we can enlarge or reduce. This established power PS(t) would oscillate around an almost constant average value PS(φ, Ф) linked to the geographical position of the station such as its latitude φ and its longitude Ф. Thus, the profile of solar radiation linked to latitude φ at longitude Ф of the station and at time t is given by the following formula:
(4)

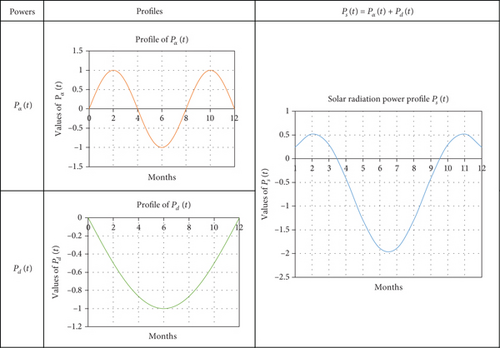
It is thus the effect of this power PS(φ, Ф) linked to the station if it is not zero that allows on the one hand to keep the profile given by PS(t) and on the other hand to no longer observe the negative values that would be given by the only representation of PS(t) that would rather mean that PS(t) would oscillate around an average value PS(φ, Ф) = 0. For example, if we consider the Ouagadougou station and then oscillate PS(t)  around this average value given by the set of values, we obtain the following graph (Figure 2).

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Profile of the in situ measurements of the Ouagadougou station and profile of the solar radiation power.

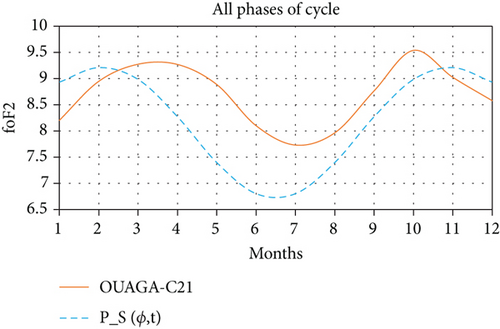
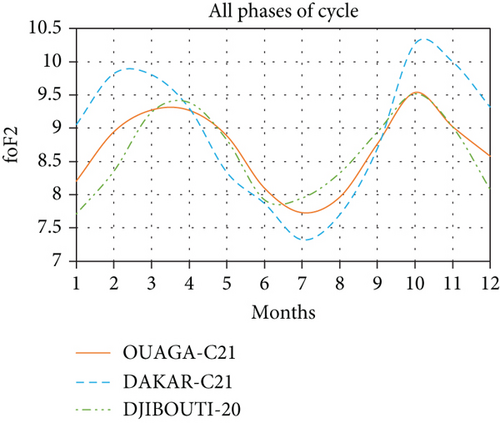
Thus, we see a near agreement in the variation of the two curves. Indeed, while the peaks reflecting the equinoctial asymmetry are observed for the in situ measurements in the months of March and October of 9.27 MHz and 9.53 MHz, respectively, those given by the simulation of PS(φ, Ф, t) are observed in the months of February and November of 9.21 and 9.22, respectively. Also, the lowest minimum is observed in the month of July both for in situ measurements of critical frequencies at 7.73 MHz and that given by the power of solar radiation at 6.80. The concordances observed with the Ouagadougou station are also observed if we consider the Dakar or Djibouti stations as shown in Figures 3(a) and 3(d). Thus, if the proposed formula reproduces the main characteristics as possible, would it also be able to reproduce the effects of sunspots on the variation of critical frequencies? Or, taking into account the very good correlation cycle of the sunspots and variation of the critical frequencies [6], one observes the strong tendency to the inversion of the maximum of peak during the phases of growth and decrease of the cycle of the sunspots.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Graphical comparison of in situ measurements and solar radiation profile.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Graphical comparison of in situ measurements and solar radiation profile.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Graphical comparison of in situ measurements and solar radiation profile.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
Graphical comparison of in situ measurements and solar radiation profile.
Details are in the caption following the image
Figure 3 (e)
Open in figure viewerPowerPoint
Graphical comparison of in situ measurements and solar radiation profile.
Details are in the caption following the image
Figure 3 (f)
Open in figure viewerPowerPoint
Graphical comparison of in situ measurements and solar radiation profile.
Indeed, this problem was solved by starting from the fact that the sunspots would bring a supplement or an addition of power Pa(t) to that PS(t) (1.1) which we named for this purpose clean power P0(t). Thus, the temporal variation of the power of the solar radiation is given by the following expression:
(5)
Also, to mark for the same year the increasing contribution by the sunspots from January to December during the phase of growth of the solar cycle of a solar power supplement, the proposed formula whose pace is given in Figure 4:
(6)
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Effect of sunspots.
And also, to mark for the same year the decreasing contribution by the sunspots from January to December during the phase of decrease of the solar cycle of a solar power supplement, the proposed formula whose pace is given to Figure 4:
(7)

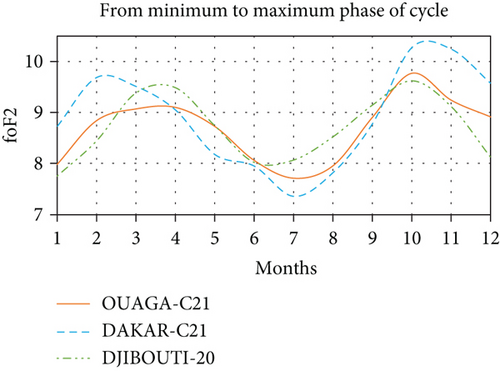
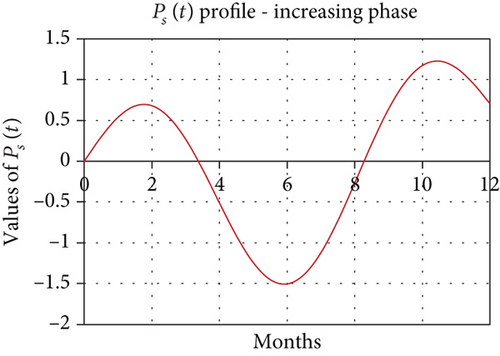
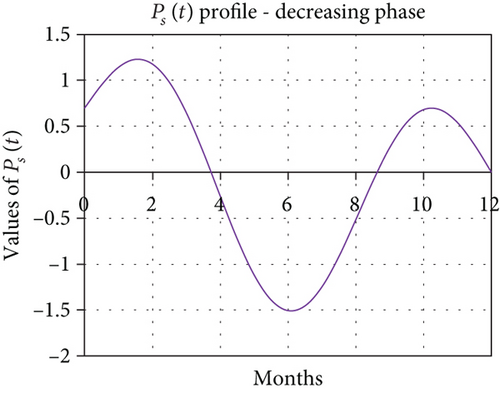
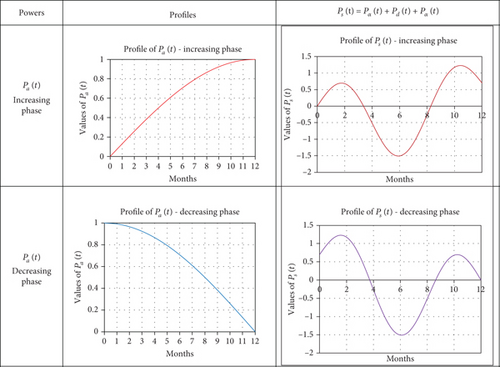
where Pa0 and Ta are counted as half an alternation, respectively, the amplitude and period of the additional power. The expected effects follow. Indeed and for example, if we consider the station of Dakar during the phase of growth of the minimum to the maximum of phase we obtain by also making oscillate Ps(t) around the average value considered as PS(φ, Ф) given by the set of values, we obtain the following graph (Figure 5).

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Profile of the in situ measurements of the Dakar station and profile of the solar radiation power.

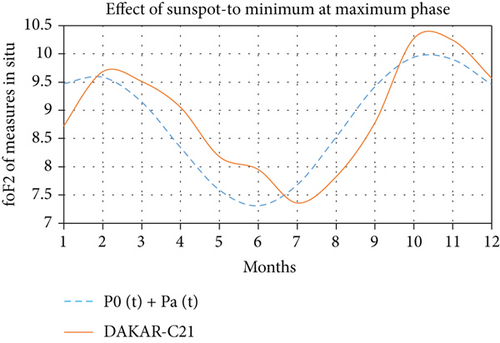
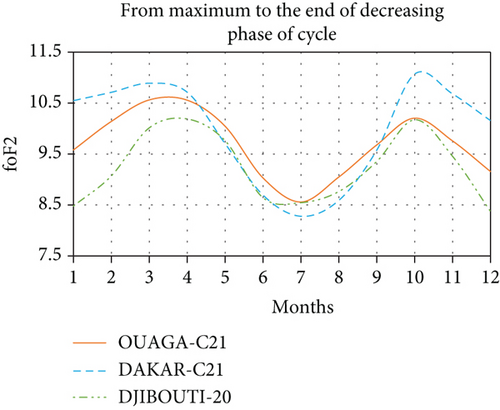
We also notice a quasiconcordant reproduction of the curve of variation of critical frequencies of the in situ measurements of the Dakar station to that given by the simulation of PS(φ, Ф, t). The equinox peaks are observed at the same period in February and October but at even higher amplitudes of 9.68 MHz and 10.27 MHz, respectively, for the in situ measurements and 9.59 and 9.94, respectively, for those given by the simulation of PS(φ, Ф, t). However, the lowest minimum is observed in July for the in situ measurements of critical frequencies at 7.36 MHz while that given by the simulation of the power of solar radiation at 7.31 in June. The concordances observed with the station of Dakar are also observed if we consider the stations of Ouagadougou or Djibouti as shown in Figures 3(b) and 3(e). For the decrease relating to the periods of the maximum of phase until the end of the phase of decrease, one notices by taking, for example, the station of Ouagadougou on the one hand a quasiconcordance from the point of view profile with the power of the solar radiation and on the other hand the effects of sunspots during this phase of decay as the following graph (Figure 6).

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Profile of the in situ measurements of the Ouagadougou station and profile of the solar radiation power during the decay phase.

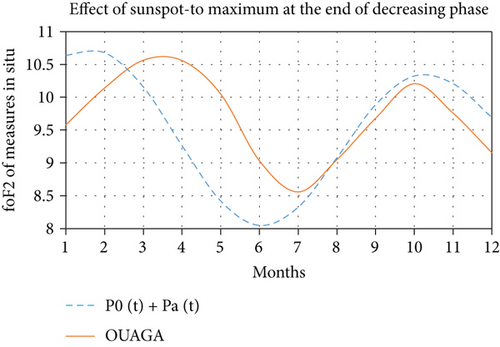
The amplitudes are large, and we note an inversion of the period of the peak maximum. Indeed, during the phase of growth of the minimum to the maximum of phase, the peaks of the equinoxes were observed in April at 9.10 MHz and in October at 9.77 MHz, whereas during the phase of decline, the peaks of the equinoxes are recorded in March at 10.56 MHz and 10.20 MHz in October. It is the same with the simulation of the solar radiation power where we note an inversion of the period of the maximum of peak. The month of February recorded the highest peak during the decay phase while it was recorded in November during the growth phase. However, we consider the Djibouti station, where Ps(t) has also been oscillated around the average value considered as PS(φ, Ф) given by all the values in the figures of the following graph (Figure 7).

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Profile of the in situ measurements of the Djibouti station and profile of the solar radiation power.

We note to this effect a quasiconcordance even if it is not very pronounced given the fact that the peaks observed during the equinoxes for the in situ measurements of the station of Djibouti are almost identical to 10.19 MHz in April against 10.17 in October while it is not the case with the simulation of the power of solar radiation or the difference is much more noticeable. It could be observed for the Dakar station (Figures 3(c) and 3(f)) that even if there was no inversion of the period of the maximum peak, the gap between the two peaks is strongly reduced showing this strong propensity to peak inversion. It is therefore appropriate to recognize that the inversions announced by the sunspots of the maximum peak in favor of the autumn peak during the growth phase and in favor of the spring peak during the waning phase of the solar cycle are not always effective.

If so, how can we justify the noninversion of the peaks observed both at the Dakar station and at the Djibouti station during the phase of the decrease in the solar cycle?

This noninversion observed despite the contribution by the sunspots of a supplement of power in the solar radiation could be attributed to multiple combinations of factors. In particular the strong preponderance in this period of the transport to another location of a part of the ions produced electrons, and even neutrals. Everything then happens as if the power of solar radiation Ps(t) mainly responsible for production was amputated or reduced by part of its power which we will name for this purpose Ptp(t) linked to this phenomenon. The formula for the power of solar radiation Ps(t) becomes
(8)
We could also justify this noninversion to a reinforcement at the peak of the autumn equinox by the solar wind or solar flares of ionization by an additional power Pvt(t) linked to the winds or flares which prevails on Ptp(t); hence, (Pvt(t) − Ptp(t) > 0). This was not the case at the peak of the vernal equinox, where the power Ptp(t) prevails over the power Pvt(t); hence, (Pvt(t) − Ptp(t) < 0). The formula for the power of solar radiation Ps(t) becomes
(9)

Thus, justify why at this phase of decline the inversion was not effective as expected. The same analysis could be carried out in the growth phase. In such a case, the power Pvt(t) prevails over Ptp(t) at the peak of the spring equinox and Ptp(t) prevails over the power Pvt(t) at the peak of the autumn equinox.

Finally, the formula proposed on the power of solar radiation strongly responds to it both in terms of the profile, therefore of the main characteristics, and the effects of sunspots, the transport mechanism, and the reinforcement by solar winds. The proposed formula is therefore a powerful tool for analyzing. Taking into account good solar irradiant correlation and variation of the critical frequencies foF2 [6], we deduce that the formula of the temporal variation of the critical frequencies is as follows:
(10)

5. Conclusion

At the end of this study, the formula proposed on the power of solar radiation inducing the variation of critical frequencies, to really say simple, is adapted. This formula is not only mathematical because it takes into account physical realities such as the Earth-Sun distance, the effects of sunspots, the transport mechanism, and the winds and solar flares and geographical position. Finally, the formula could strongly contribute to bringing a rational explanation both to the problem of the diurnal profiles of the critical frequencies foF2 and to that of the geomagnetic anomaly or equatorial anomaly.

Disclosure

The research was carried out within the framework of our scientific productions such as articles.

Conflicts of Interest

We declare that there is no conflict of interest regarding the publication of this article.

Data Availability

The data of the in situ measurements were made available to us by the National School of Telecommunications of Brittany.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.