In this article, a singularly perturbed convection-diffusion problem with a small time lag is examined. Because of the appearance of a small perturbation parameter, a boundary layer is observed in the solution of the problem. A hybrid scheme has been constructed, which is a combination of the cubic spline method in the boundary layer region and the midpoint upwind scheme in the outer layer region on a piecewise Shishkin mesh in the spatial direction. For the discretization of the time derivative, the Crank-Nicolson method is used. Error analysis of the proposed method has been performed. We found that the proposed scheme is second-order convergent. Numerical examples are given, and the numerical results are in agreement with the theoretical results. Comparisons are made, and the results of the proposed scheme give more accurate solutions and a higher rate of convergence as compared to some previous findings available in the literature.

1. Introduction

The delay differential equations are versatile in mathematical modeling of processes where they provide a realistic simulation of the real-world phenomena. The real-world operations/interactions that take time to complete can be utilized to simulate the time lag experience such as gestation time, incubation period, and transportation delays. In the model, if a small parameter multiplies the highest order derivative term, involving at least one shift term in the temporal variable, we call it singularly perturbed time delay differential equations (SPTDDE). These problems arise in the varied area of science and engineering models, for instance, in population dynamics, in epidemiology, in respiratory system, and in tumor growth [1–6]. For more additional models, one can refer [7, 8]. Due to the appearance of the boundary layer in the solution of a singularly perturbed differential equation, classical numerical methods on equidistant grids are inadequate and fail to provide a reliable approximation, when the perturbation parameter tends to zero, unless otherwise, if one uses an unacceptably large number of grid points. Several articles have been written on the solution method for singularly perturbed delay differential equations, to cite a few [9–13]. Among the recently conducted studies on SPTDDE of the convection-diffusion type, having a right end boundary layer, in [14], the authors used an implicit-trapezoidal scheme on uniform mesh for temporal discretization, and for spatial discretization, a hybrid scheme, which is a combination of the midpoint upwind scheme and the central difference scheme on Shishkin type meshes, is applied. In [8], the scheme is constructed using the Crank-Nicolson method for temporal discretization, and a midpoint upwind finite difference scheme on a fitted piecewise-uniform mesh in spatial discretization is applied. In [15], the scheme is devised using backward Euler’s scheme on uniform mesh for temporal discretization and a new stable finite difference scheme on Shishkin mesh for spatial discretization. In [16], the problem is solved using the Crank-Nicolson method in temporal discretization, and in the spatial discretization, an exponentially fitted operator finite difference method on uniform mesh is used. All these developed schemes can work for both small and large time delays. However, except [14], the results of the above studies are first-order convergent, and there are some exceptional properties which work only for a small time delay (δ < ε) that cannot be assessed by these authors.

So, when we come to a singularly perturbed convection-diffusion problem of small time lag, the following researchers address the case which works only for small time lag. In [17], the authors used the backward Euler scheme for temporal discretization and a central difference scheme with an adaptive mesh selection strategy for spatial discretization. In [18], the authors used the Euler method to discretize the time derivative and a B-spline collocation scheme for the spatial discretization on a uniform mesh. In this paper, both small and large time delays are considered, and the developed scheme is first-order convergent. In [19], the scheme is developed using the backward Euler method in the discretization of the time derivative, and a higher-order finite difference method is employed for the approximation of the spatial derivative. In this scheme, an exponential fitting factor is introduced, and the resulting scheme is first-order convergent.

From these, we are motivated to construct and analyze a higher order ε-uniform numerical scheme, for the problem considered in [17]. The proposed hybrid scheme is a combination of the cubic spline method and the midpoint upwind scheme on piecewise Shishkin mesh in the spatial direction and the Crank-Nicolson method in the temporal direction. The advantage of the present method over the other methods in [17–19] is that it is a second-order accurate in both time and space variables, as well as its accuracy. In addition, in the paper [17–19], Taylor’s series expansion is applied at the beginning without any restriction on the domain. In such a case, the advantage of the interval condition for the delay term in the approximation is meaningless. So we incorporate the condition where Taylor’s series expansion is applied without losing the interval condition.

Notations: all through this paper, C and its subscripts denote generic positive constants independent of the perturbation parameter ε and mesh sizes. Also, ‖∙‖ denotes the standard supremum norm, defined as for a function f defined on some domain .

2. Problem Formulation

Consider the following singularly perturbed delay parabolic problem [17, 19]:

()

subject to

()

where 0 < ε < <1 is the perturbation parameter, δ > 0 is the delay parameter, δ < ε, D = Ω_x × Ω_t, Ω_x = (0, 1), Ω_t = (0, T], and

; the functions α(x, t), β(x, t), γ(x, t), and f(x, t) on

and ψ_l(t), ψ_r(t), ψ_b(x, t) on Γ are assumed to be smooth and bounded functions that satisfy the conditions α(x, t) ≤ α₀ < 0, and β(x, t) + γ(x, t) ≥ 0 on

Under the above assumption, problem (1) exhibits a boundary layer along x = 0. The existence and uniqueness of the solution for problem (1) can be guaranteed by the sufficient smoothness of ψ_l(t), ψ_r(t), and ψ_b(x, t), along with the following compatibility conditions:

()

The problem (1) has a unique solution with the above conditions and assumptions [20]. Let us use the notation

()

3. Bounds on the Solution and Its Derivatives

Lemma 1. Suppose . Assume that ξ(0, t) ≥ 0, ξ(1, t) ≥ 0, and L_εξ(x, t) ≥ 0, ∀(x, t) ∈ D. Then, .

Proof. Suppose such that and ξ(x^⋆, t^⋆) < 0. It is visible that (x^⋆, t^⋆) ∉ Γ and (x^⋆, t^⋆) ∈ D. At the point (x^⋆, t^⋆), ξ_x = 0, ξ_t = 0 and ξ_xx ≥ 0. Then, L_ε(x^⋆, t^⋆) < 0, which contradicts L_ε(x, t) ≥ 0, ∀(x, t) ∈ D. Therefore,

Lemma 2. The solution u(x, t) of problem (1) is bounded and satisfies the following estimate:

()

Proof. Please refer [21].

Lemma 3. The solution to the problem (1) satisfies the following bound:

()

Proof. Please refer [22].

Lemma 4. The solution u(x, t) of (1) satisfies the bound

()

Proof. Let us take |u(x, t)| = |u(x, t) − ψ_b(x, t) + ψ_b(x, t)| ≤ |u(x, t) − ψ_b(x, t)| + |ψ_b(x, t)|. Using Lemma 3, |u(x, t)| ≤ Ct + |ψ_b(x, t)| and the fact that ψ_b(x, t) is bounded and t ∈ (0, 2]. Hence, we get the required result.

Lemma 5. Let u be the solution of problem (1), then

()

where r and y are nonnegative integers.

Proof. The reader can follow the procedure in [21, 23, 24].

4. Numerical Scheme

The problem defined in (1) can be rewritten as

()

where

()

with initial and boundary conditions, D₁ = (0, 1) × (0, δ) and D₂ = (0, 1) × (δ, T]. Since the delay parameter (δ) is smaller than the singular perturbation parameter (ε), it is possible to apply Taylor’s series expansion as follows:

()

Substituting (11) into (9), we obtain

()

where

()

4.1. Temporal Discretization

This section is devoted to the discretization of the temporal variable. So on the time domain [0, T], we use uniform mesh

, where M is the number of mesh intervals and Δt is the time step. On

, problem (12) is discretized by using the Crank-Nicolson method as follows:

()

After some rearrangement, (14) is written in the form

()

where

()

and U^j+1(x) = U(x, t_j+1) is the semidiscrete approximation to the exact solution u(x, t) of (1) at the (j + 1)^th time level.

Lemma 6. Suppose that . The local truncation error associated to scheme (15) satisfies

()

Proof. Using Taylor’s series expansion, expanding U(x, t_j+1) and U(x, t_j) centered at t_j+1/2, we get

()

Substituting (18) in to (1), we obtain

()

where

()

From (19), the local truncation error is the solution of the following BVP:

Theorem 7 (global error estimate). The global error estimate in the time direction at (j + 1)^th time level is given by

()

Proof. Using the local error estimate in Lemma 6, we obtain

()

Lemma 8 (discrete maximum principle). Suppose . Assume that ξ^j+1(0) ≥ 0, ξ^j+1(1) ≥ 0, and . Then, ξ^j+1(x) ≥ 0, ∀(x) ∈ Ω.

Proof. Suppose such that ; let ξ(x^⋆, t_j+1) < 0. This gives (x^⋆, t_j+1) ∉ {(0, t_j+1), (1, t_j+1)}, which implies that the point (x^⋆, t_j+1) ∈ Ω_x. Also, we have and .

()

which is a contradiction. Hence, the minimum of ξ^j+1(x) is nonnegative.

To prove that the approach is ε-uniform, more specific information on the behavior of the exact solution is required. This is done by decomposing the solution u(x, t) into a smooth component v_ε and a singular component w_ε as follows: u = v_ε + w_ε; for more detail on the decomposition, one can refer [25].

Lemma 9. The regular and the singular components of the solution of the discrete scheme (15) satisfy the following bounds:

()

Proof. Follow the approach given in [21, 23, 24].

4.2. Discretization in the Spatial Direction

4.2.1. Shishkin Mesh

The piecewise-uniform mesh having N ≥ 4 mesh intervals on [0, 1] is generated by dividing the interval [0, 1] into two subintervals as [0, τ] and [1 − τ, 1], where the transition parameter τ separates the coarse and fine region and is given by

()

where τ₀ is a constant satisfying τ₀ ≥ 1/|α₀|. Hence, the piecewise-uniform mesh is given by

()

where

()

4.3. Cubic Spline Difference Scheme

In this subsection, we derive the cubic spline scheme on the meshes, Ω^N = {0 = x₀, x₁, ⋯, x_N = 1} and h_i = x_i − x_i−1. Assume Q^j+1(x) is an interpolating cubic spline function corresponding to the values U^j+1(x_i) of a function U^j+1(x₀), U^j+1(x₁), …, U^j+1(x_N) of a function U^j+1(x) at the nodal points x₀, x₁, ⋯, x_N, satisfying the following properties:

(i)
Q^j+1(x) coincides with a polynomial of degree three on each subintervals [x_i−1, x_i], i = 1, ⋯, N
(ii)
(iii)
Q(x_i) = U(x_i), i = 0, 1, ⋯, N

Then, the cubic spline function can be written as

()

where M_i = d²Q^j+1(x_i)/dx², i = 1, 2, ⋯, N.

From the properties of spline [26],

()

For the approximation of dU^j+1(x)/dx and d²U^j+1(x)/dx², we use the Taylor series approximations as follows:

()

Multiplying (31) by

and then subtracting the resulting equation from (30), we get

()

In the same fashion multiplying (30) by

and then adding the resulting equation into (31), we get

()

Using (32) and (33), in

()

we obtain the following approximation:

()

Then, express (14) at x = x_k in the form

()

Insert (32), (35), and (36) at (j + 1)^th and j^th time level into (37), and substitute the resulting equation into (29). After some simplification, we obtain

()

where

()

4.4. Midpoint Upwind Scheme

For any mesh function

, let us define the backward

, forward

, and central difference

operators as follows:

()

Using the midpoint upwind scheme, (15) can be discretized as

()

where

()

After some simplification, we obtain the following three-term recurrence relation:

()

where

()

4.4.1. Hybrid Scheme

The upwind scheme is stable and produces a first-order accurate solution [27–29]. The cubic spline method satisfies the discrete maximum norm only in the fine mesh region, whereas in the coarse mesh region, the solution is unstable [28, 29]. The benefit of constructing a hybrid scheme is that it gives higher-order parameter uniform convergent schemes that are oscillation-free across the region. So, using a piecewise-uniform Shishkin mesh, we develop a second-order parameter uniform convergent scheme that combines the cubic spline approach in the fine mesh region and the midpoint upwind scheme in the coarse mesh region. Thus, the discrete problem of (1) is given by

()

Therefore, we have the following totally discrete scheme:

()

where the coefficients

, and

are described in (39); also,

, and

are described in (44).

5. Stability and Error Analysis

In this section, we study the stability and ε-uniform convergence of the proposed scheme. For the analysis, we follow the approach given in [23, 25]. The numerical solution U^N,M on D is decomposed as U = V + W, where V and W are the numerical solutions of the regular and singular components, respectively; for detail on the decomposition, please refer [25].

Lemma 10. Assume that N ≥ N₀, where N₀ is the smallest positive integer satisfying

()

Then, we have

()

Proof. Divide the interval into two cases.

Case 1. For 1 ≤ i ≤ N/2, since the mesh is piecewise uniform, so that it is possible to fix the mesh size in the inner layer region by h_i = h = 2τ₀εlnN/lnN and substitute (47) into (39) and simply, we get

()

since |α₀| < ‖α‖, h < 1/N and (48).

Similarly, s⁺ < 0, and from (39), it is clear that

()

Case 2. For N/2 < i < N, the mesh size in the outer layer region is h_i = (2(1 − τ₀εlogN)/N) < 2/N. Next, using (47) and (48) into (44), it is easy to see that s⁻ < 0 and s⁺ < 0. Simple mathematical calculation gives

()

Hence, the proof is completed.

Note: Lemma 10 confirms that under the hypotheses given in (47) and (48), the tridiagonal matrix corresponding to the operator defined in (46) is an M-matrix. This implies that the operator satisfies the next discrete maximum principle.

Lemma 11. Let ζ^N,M be any mesh function defined on . Assume that . Then, implies that .

Proof. Assume that there exists a mesh point (i^∗, j + 1) for i^∗ ∈ {1, ⋯, N − 1} such that , and assume that , so it is clear that i^∗ ∉ {0, N}. Then, for i^∗ ∈ {1, 2, ⋯, N − 1}; this contradicts with the assumption . Hence, the result follows.

The uniform stability estimate of the discrete solution is provided by the subsequent lemma.

Lemma 12. Let U_i,j+1 be the solution of the discrete problem (48). Then,

()

Proof. Let us construct the barrier function as follows:

()

and using Lemma 11, we can obtain the required bound.

5.1. Truncation Error

()

Case 1. Truncation error in the inner layer region using (15) at in (46) is given by

()

where

and

. Substituting Taylor’s series expansion in the spatial variable of

, and

into (56)

()

where

()

It can be easily seen that T_0,j+1 = T_0,j = T_1,j+1 = T_1,j = T_2,j+1 = T_2,j = 0, . Thus, we get

()

where ℏ = max(h_i), for i = 1, 2.., N.

Case 2. In the outer layer region, applying a similar procedure like the inner layer region, we obtain , which is

()

Theorem 13. Let u(x_i, t_j+1) and U_i,j+1 be the solution of problems (1) and (45), respectively; then, the proposed scheme satisfies the following error estimate in the spatial direction:

()

Proof. The proof is divided into two cases as a singular part and a regular part.

Case 1. The bound for the regular component of the solution U_i,j of (1).

From the truncation error of the spatial direction (60), we have

()

Since ℏ ≤ 2/N, for i = 1, 2, ⋯, N − 1, using Lemma 9, we obtain

()

Now, construct the barrier function for each interval; let us take i = (N/2) + 1, (N/2) + 2, ⋯, N − 1,

()

It is easy to see , and . As a result, by applying Lemma 11, it is possible to obtain the required estimate, which is

()

Apply a similar procedure for i = 1, 2, ⋯, N/2; then, we can get

()

Case 2. The bound for the singular component of the solution U_i,j of (1). The proof is done separately in [0, τ] and [τ, 1].

(i)
On [0, τ]

()

In this region, ℏ = 2τ/N = 2τ₀εlnN/N, and Lemma 9 gives

()

Now, construct the barrier function for i = 1, 2, ⋯, N/2,

()

It is easy to see , and , for i = 1, 2, ⋯, N − 1. As a result, by applying Lemma 11, we obtain the estimate

()

(ii)
on [τ, 1]

()

In this region, ℏ ≤ 2/N, and Lemma 9 gives

()

and following the procedure like [0, τ], we get

()

Therefore, combining (66) and (73), we can obtain the desired result.

Theorem 14. Let u(x_i, t_j) and U_i,j be the solution of problems (1) and (45), respectively; then, the proposed scheme satisfies the following bound:

()

Proof. Combining Theorems 7 and 13 gives the required result.

6. Numerical Illustration

In this section, the performance of the proposed scheme is tested through numerical examples. The exact solution of the following examples is not known, so to compute the maximum point-wise errors, we use the double mesh principle given by the following formula:

()

where U^N,M(x_i, t_j) denote the numerical solution. The corresponding rate of convergence is computed by using the following formula:

()

In addition, the ε-uniform maximum point-wise error E^N,M is computed as

()

and the corresponding ε-uniform rate of convergence R^N,M is given by

()

Example 1. Consider the following problem [19]:

()

Example 2. Consider the following problem [17]:

()

7. Conclusion

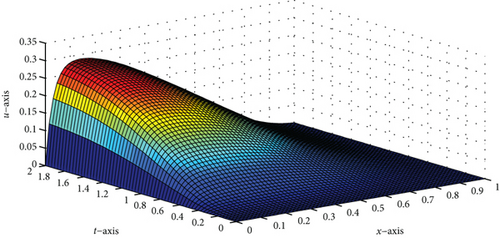
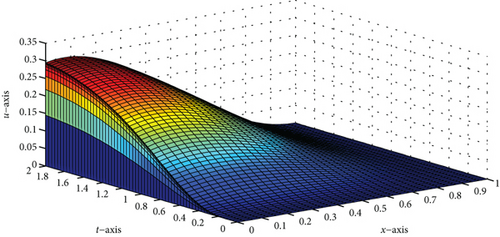
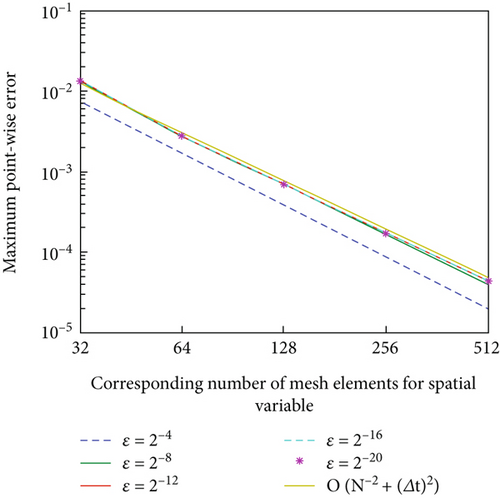
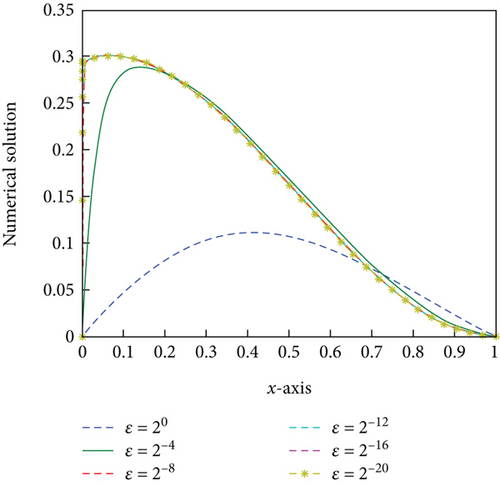
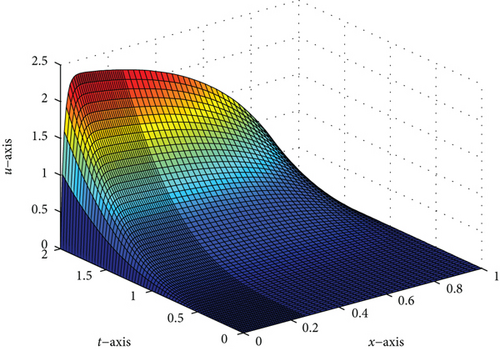
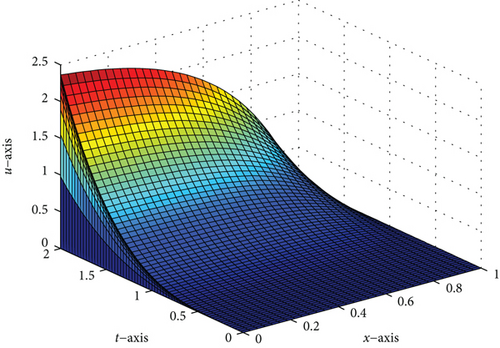
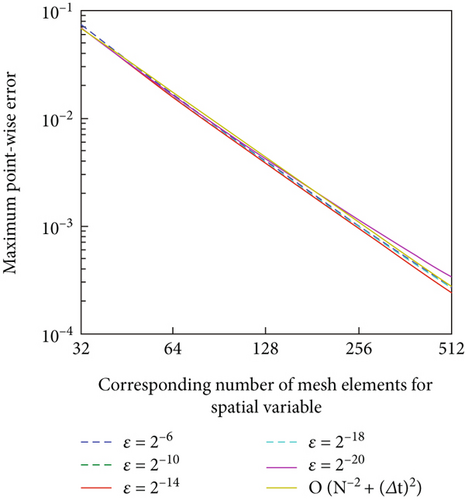
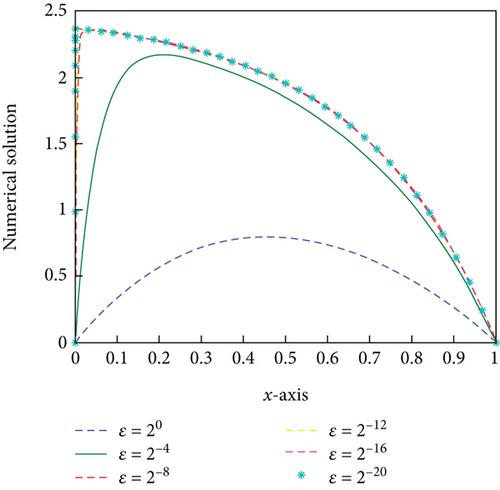
A singularly perturbed convection-diffusion problem of small time lag is treated, via a hybrid fitted mesh scheme for the space discretization and the Crank–Nicolson method on a uniform mesh for time derivative. Due to the presence of a small perturbation parameter, the problem exhibits the left side boundary layer at x = 0. Figures 1, 2(b), 3, and 4(b) of the surface plot and one-dimensional plot for the numerical solution of the problems in Example 1 and Example 2 clearly demonstrate the behavior of the boundary layer as ε⟶0. The maximum point-wise error of Example 1 and Example 2 is plotted in Figures 2(a) and 4(a), respectively, in the log-log plot. The error analysis of the proposed scheme is proved, and the proposed scheme is second order ε-uniform convergent. The numerical results in Tables 1 and 2 of Example 1 and Example 2, respectively, confirm that the tabulated numerical results are in agreement with the theoretical error estimates. In addition, we observed that the proposed scheme is more accurate and gives a higher rate of convergence as compared to some studies available in the literature. Since the approach is mesh dependent, when the number of mesh points increases, the effectiveness of the proposed scheme also increases. Due to the time limitations, we only discuss small time delays; however, with some slight adjustments, the scheme can also work for large time delays.

Details are in the caption following the image — **Figure 1 (a) ε = 2−4**
Open in figure viewer PowerPoint

Surface plot of numerical solution of Example 1 at N = M = 64.

Table 1. Computed

, E^N,M, and R^N,M for Example 1 at M = N, δ = 0.5ε.

Method	ε↓	N→32	64	128	256	512
Present	2⁻⁴	7.4172e-03	1.6104e-03	3.7310e-04	8.4234e-05	1.9588e-05
		2.2034	2.1098	2.1471	2.1044
	2⁻⁶	1.3309e-02	2.7086e-03	6.6643e-04	1.5562e-04	3.4549e-05
		2.2968	2.0230	2.0984	2.1714
	2⁻⁸	1.3254e-02	2.7249e-03	6.8167e-04	1.6529e-04	3.9616e-05
		2.2822	1.9991	2.0440	2.0609
	2⁻¹⁰	1.3244e-02	2.7338e-03	6.8823e-04	1.6927e-04	4.1768e-05
		2.2763e	1.9899	2.0236	2.0189
	2⁻¹²	1.3241e-02	2.7364e-03	6.9006e-04	1.7037e-04	4.2365e-05
		2.2747	1.9875	2.0180	2.0077
	2⁻¹⁴	1.3241e-02	2.7370e-03	6.9055e-04	1.7066e-04	4.2522e-05
		2.2743	1.9868	2.0166	2.0048
	2⁻¹⁶	1.3240e-02	2.7373e-03	6.9073e-04	1.7077e-04	4.2578e-05
		2.2741	1.9865	2.0161	2.0039
	2⁻¹⁸	1.3240e-02	2.7375e-03	6.9101e-04	1.7092e-04	4.2656e-05
		2.2739	1.9861	2.0154	2.0025
	2⁻²⁰	1.3237e-02	2.7385e-03	6.9201e-04	1.7148e-04	4.2932e-05
		2.2731	1.9845	2.0128	1.9979
	E^N,M	1.3309e-02	2.7385e-03	6.9201e-04	1.7148e-04	4.2932e-05
	R^N,M	2.2968	1.9845e	2.0128	1.9979

[19]	E^N,M	2.9454e-03	1.6032e-03	8.4467e-04	4.3881e-04	—
[19]	R^N,M	0.8775	0.9245	0.9448	—

Table 2. Computed

, E^N,M, and R^N,M for Example 2 at M = N, δ = 0.5ε.

Method	ε↓	N→32	64	128	256	512
Present	2⁻⁶	7.3197e-02	1.6164e-02	3.9632e-03	1.0028e-03	2.5984e-04
		2.1790	2.0280	1.9827	1.9483
	2⁻⁸	7.0418e-02	1.5592e-02	3.8049e-03	9.5202e-04	2.4123e-04
		2.1752	2.0348	1.9988	1.9806
	2⁻¹⁰	6.9688e-02	1.5431e-02	3.7564e-03	9.3481e-04	2.3431e-04
		2.1751	2.0384	2.0066	1.9962
	2⁻¹²	6.9502e-02	1.5391e-02	3.7448e-03	9.3075e-04	2.3270e-04
		2.1750	2.0392	2.0084	1.9999
	2⁻¹⁴	6.9452e-02	1.5387e-02	3.7460e-03	9.3186e-04	2.3336e-04
		2.1743	2.0383	2.0072	1.9975
	2⁻¹⁶	6.9425e-02	1.5411e-02	3.7629e-03	9.4068e-04	2.3775e-04
		2.1715	2.0340	2.0001	1.9843
	2⁻¹⁸	6.9360e-02	1.5513e-02	3.8335e-03	9.7707e-04	2.5572e-04
		2.1606	2.0168	1.9721	1.9339
	2⁻²⁰	6.9112e-02	1.5927e-02	4.1170e-03	1.1253e-03	3.3204e-04
		2.1174	1.9519	1.8712	1.7609
	E^N,M	7.3197e-02	1.6164e-02	4.1170e-03	1.1253e-03	3.3204e-04
	R^N,M	2.1790	2.0280	1.8712	1.7609

[18]	E^N,M	4.9224e-02	2.6666e-02	1.3880e-02	7.0816e-03	—
[18]	R^N,M	0.88436	0.94199	0.97086	—

[19]	E^N,M	2.1953e-02	1.1908e-02	6.1994e-03	3.1627e-03	—
[19]	R^N,M	0.88249	0.94173	0.97097	—

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

To support the finding of this study, no data were used.

References

1 Arino J. and Van Den Driessche P., Time delays in epidemic models, Delay differential equations and applications, 2006, Springer, 539–578.
10.1007/1-4020-3647-7_13
Google Scholar
2 Bejan A., Convection Heat Transfer, 2013, Wiley, New York.
10.1002/9781118671627
Google Scholar
3 Cooke K., Van den Driessche P., and Zou X., Interaction of maturation delay and nonlinear birth in population and epidemic models, Journal of Mathematical Biology. (1999) 39, no. 4, 332–352, https://doi.org/10.1007/s002850050194, 2-s2.0-0033209987, 10550577.
10.1007/s002850050194
CAS PubMed Web of Science® Google Scholar
4 Murray J. D., Mathematical Biology: I. An introduction, 2002, Springer, https://doi.org/10.1007/b98868.
10.1007/b98868
Google Scholar
5 Vielle B. and Chauvet G., Delay equation analysis of human respiratory stability, Mathematical Biosciences. (1998) 152, no. 2, 105–122, https://doi.org/10.1016/S0025-5564(98)10028-7, 2-s2.0-0032169353, 9780610.
10.1016/S0025-5564(98)10028-7
CAS PubMed Web of Science® Google Scholar
6 Villasana M. and Radunskaya A., A delay differential equation model for tumor growth, Journal of Mathematical Biology. (2003) 47, no. 3, 270–294, https://doi.org/10.1007/s00285-003-0211-0, 2-s2.0-1442290947.
10.1007/s00285-003-0211-0
PubMed Web of Science® Google Scholar
7 Das A. and Natesan S., Uniformly convergent hybrid numerical scheme for singularly perturbed delay parabolic convection-diffusion problems on Shishkin mesh, Applied Mathematics and Computation. (2015) 271, 168–186, https://doi.org/10.1016/j.amc.2015.08.137, 2-s2.0-84942508971.
10.1016/j.amc.2015.08.137
Web of Science® Google Scholar
8 Kumar D. and Kumari P., A parameter-uniform numerical scheme for the parabolic singularly perturbed initial boundary value problems with large time delay, Journal of Applied Mathematics and Computing. (2019) 59, no. 1-2, 179–206, https://doi.org/10.1007/s12190-018-1174-z, 2-s2.0-85041893391.
10.1007/s12190-018-1174-z
Web of Science® Google Scholar
9 Cimen E., Numerical solution of a boundary value problem including both delay and boundary layer, Mathematical Modelling and Analysis. (2018) 23, no. 4, 568–581, https://doi.org/10.3846/mma.2018.034, 2-s2.0-85055260895.
10.3846/mma.2018.034
Google Scholar
10 Cimen E. and Amiraliyev G. M., Uniform convergence method for a delay differential problem with layer behaviour, Mediterranean Journal of Mathematics. (2019) 16, no. 3, https://doi.org/10.1007/s00009-019-1335-9, 2-s2.0-85064275780.
10.1007/s00009-019-1335-9
Google Scholar
11 Gebeyaw W., Andargie A., and Adamu G., Solving second order singularly perturbed delay differential equations with layer behavior via initial value method, Journal of Applied Mathematics & Informatics. (2018) 36, no. 34, 331–348.
Google Scholar
12 Melesse W. G., Tiruneh A. A., and Derese G. A., Solving linear second-order singularly perturbed differential difference equations via initial value method, International Journal of Differential Equations. (2019) 2019, 10, 5259130, https://doi.org/10.1155/2019/5259130.
10.1155/2019/5259130
Web of Science® Google Scholar
13 Woldaregay M. M., Solving singularly perturbed delay differential equations via fitted mesh and exact difference method, Research in Mathematics. (2022) 9, no. 1, article 2109301, https://doi.org/10.1080/27684830.2022.2109301.
10.1080/27684830.2022.2109301
Google Scholar
14 Govindarao L. and Mohapatra J., A second order numerical method for singularly perturbed delay parabolic partial differential equation, Engineering Computations. (2019) 36, no. 2, 420–444, https://doi.org/10.1108/EC-08-2018-0337, 2-s2.0-85058347474.
10.1108/EC-08-2018-0337
Google Scholar
15 Podila P. C. and Kumar K., A new stable finite difference scheme and its convergence for time-delayed singularly perturbed parabolic pdes, Computational and Applied Mathematics. (2020) 39, no. 3.
10.1007/s40314-020-01170-2
Google Scholar
16 Woldaregay M. M., Aniley W. T., and Duressa G. F., Novel numerical scheme for singularly perturbed time delay convection- diffusion equation, Advances in Mathematical Physics. (2021) 2021, 13, https://doi.org/10.1155/2021/6641236, 6641236.
10.1155/2021/6641236
Google Scholar
17 Kumar K., Gupta T., Pramod Chakravarthy P., and Nageshwar Rao R., An adaptive mesh selection strategy for solving singularly perturbed parabolic partial differential equations with a small delay, Applied Mathematics and Scientific Computing, 2019, Springer, 67–76, https://doi.org/10.1007/978-3-030-01123-9_8, 2-s2.0-85061330678.
10.1007/978-3-030-01123-9_8
Google Scholar
18 Negero N. T. and Duressa G. F., Uniform convergent solution of singularly perturbed parabolic differential equations with general temporal-lag, Iranian Journal of Science and Technology, Transactions A: Science. (2022) 46, no. 2, 507–524, https://doi.org/10.1007/s40995-021-01258-2.
10.1007/s40995-021-01258-2
Google Scholar
19 Tesfaye S. K., Woldaregay M. M., Dinka T. G., and Duressa G. F., Fitted computational method for solving singularly perturbed small time lag problem, BMC Research Notes. (2022) 15, no. 1, https://doi.org/10.1186/s13104-022-06202-0, 36221103.
10.1186/s13104-022-06202-0
PubMed Google Scholar
20 Salama A. and Al-Amery D., A higher order uniformly convergent method for singularly perturbed delay parabolic partial differential equations, International Journal of Computer Mathematics. (2017) 94, no. 12, 2520–2546, https://doi.org/10.1080/00207160.2017.1284317, 2-s2.0-85012297089.
10.1080/00207160.2017.1284317
Web of Science® Google Scholar
21 Kadalbajoo M. and Sharma K., Numerical treatment of a mathematical model arising from a model of neuronal variability, Journal of Mathematical Analysis and Applications. (2005) 307, no. 2, 606–627, https://doi.org/10.1016/j.jmaa.2005.02.014, 2-s2.0-18944375881.
10.1016/j.jmaa.2005.02.014
Web of Science® Google Scholar
22 Govindarao L. and Mohapatra J., Numerical analysis and simulation of delay parabolic partial differential equation involving a small parameter, Engineering Computations. (2019) 37, no. 1, 289–312, https://doi.org/10.1108/EC-03-2019-0115, 2-s2.0-85071654741.
10.1108/EC-03-2019-0115
Google Scholar
23 Mushahary P., Sahu S. R., and Mohapatra J., Spline approximation method for singularly perturbed differential-difference equation on nonuniform grids, International Journal of Modeling, Simulation, and Scientific Computing. (2021) 12, no. 1, article 2150005, https://doi.org/10.1142/S1793962321500057.
10.1142/S1793962321500057
Google Scholar
24 Majumdar A. and Natesan S., Anϵ-uniform hybrid numerical scheme for a singularly perturbed degenerate parabolic convection–diffusion problem, International Journal of Computer Mathematics. (2019) 96, no. 7, 1313–1334, https://doi.org/10.1080/00207160.2018.1485896, 2-s2.0-85048881271.
10.1080/00207160.2018.1485896
Web of Science® Google Scholar
25 Miller J., O’Riordan E., and Shishkin G., Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions, 2012, World Scientific, https://doi.org/10.1142/8410, 2-s2.0-84995514150.
10.1142/8410
Google Scholar
26 Priyadharshini R. M., Ramanujam N., and Valanarasu T., Hybrid difference schemes for singularly perturbed problem of mixed type with discontinuous source term, Journal of Applied Mathematics & Informatics. (2010) 28, no. 56, 1035–1054.
Google Scholar
27 Stynes M. and Roos H.-G., The midpoint upwind scheme, Applied Numerical Mathematics. (1997) 23, no. 3, 361–374, https://doi.org/10.1016/S0168-9274(96)00071-2, 2-s2.0-0031141256.
10.1016/S0168-9274(96)00071-2
Web of Science® Google Scholar
28 Mushahary P., Sahu S., and Mohapatra J., A parameter uniform numerical scheme for singularly perturbed differential-difference equations with mixed shifts, Journal of Applied and Computational Mechanics. (2020) 6, no. 2, 344–356.
Web of Science® Google Scholar
29 Bawa R. K. and Natesan S., An efficient hybrid numerical scheme for convection-dominated boundary-value problems, International Journal of Computer Mathematics. (2009) 86, no. 2, 261–273, https://doi.org/10.1080/00207160801955678, 2-s2.0-57349174596.
10.1080/00207160801955678
Web of Science® Google Scholar

Citing Literature

All articles

Hybrid Fitted Numerical Scheme for Singularly Perturbed Convection-Diffusion Problem with a Small Time Lag

Abstract

1. Introduction

2. Problem Formulation

3. Bounds on the Solution and Its Derivatives

4. Numerical Scheme

4.1. Temporal Discretization

4.2. Discretization in the Spatial Direction

4.2.1. Shishkin Mesh

4.3. Cubic Spline Difference Scheme

4.4. Midpoint Upwind Scheme

4.4.1. Hybrid Scheme

5. Stability and Error Analysis

5.1. Truncation Error

6. Numerical Illustration

7. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Hybrid Fitted Numerical Scheme for Singularly Perturbed Convection-Diffusion Problem with a Small Time Lag

Abstract

1. Introduction

2. Problem Formulation

3. Bounds on the Solution and Its Derivatives

4. Numerical Scheme

4.1. Temporal Discretization

4.2. Discretization in the Spatial Direction

4.2.1. Shishkin Mesh

4.3. Cubic Spline Difference Scheme

4.4. Midpoint Upwind Scheme

4.4.1. Hybrid Scheme

5. Stability and Error Analysis

5.1. Truncation Error

6. Numerical Illustration

7. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information