In the present work, a new approximated method for solving the nonlinear Duffing-Van der Pol (D-VdP) oscillator equation is suggested. The approximate solution of this equation is introduced with two separate techniques. First, we convert nonlinear D-VdP equation to a nonlinear Volterra integral equation of the second kind (VIESK) using integration, and then, we approximate it with the hybrid Legendre polynomials and block-pulse function (HLBPFs). The next technique is to convert this equation into a system of ordinary differential equation of the first order (SODE) and solve it according to the proposed approximate method. The main goal of the presented technique is to transform these problems into a nonlinear system of algebraic equations using the operational matrix obtained from the integration, which can be solved by a proper numerical method; thus, the solution procedures are either reduced or simplified accordingly. The benefit of the hybrid functions is that they can be adjusted for different values of n and m, in addition to being capable of yield greater correct numerical answers than the piecewise constant orthogonal function, for the results of integral equations. Resolved governance equation using the Runge-Kutta fourth order algorithm with the stepping time 0.01 s via numerical solution. The approximate results obtained from the proposed method show that this method is effective. The evaluation has been proven that the proposed technique is in good agreement with the numerical results of other methods.

1. Introduction

The nonlinear differential equations become the most important topic in various scientific problems that arise in the field of engineering and physics that can be represented by nonlinear ordinary differential equation such as oscillator equations. Oscillators are found in most of the electronic systems, which provide an important limiting cycle of the mathematical model. For example, phenomena arise in all fields of the natural and engineering sciences [1, 2] and in many physical problems [3, 4]. In recent studies, extensive studies have focused on the concept capable of damping harmful vibrations in environmental energy, which are generated or induced by mechanical machinery, vehicles, wind, and so on. These vibrations can be harvested and turned to useful electrical energy like [5–7]. Numerous studies have been dedicated to the exploitation of various vibratory energy harvesting systems, for instance, He et al. [8] have shown vibration alleviation and energy harvesting in a dynamical system of a spring pendulum, Tien and Dsouza [9] investigated a theoretical model of a piecewise-linear nonlinear vibration harvester, Shorakaei et al. [10] studied the nonlinear vibration energy harvesting from a magneto-electro-elastic plate. Based on the aim of this article, we consider the mathematical of unforced D-VdP oscillator equation as follows:

(1)

where dots denote time derivative; α and γ are two positive coefficients. Usually, getting exact solutions by the analytical methods for these systems, even if the exact solutions exist, seems to be difficult. Hence, it needs of numerical techniques for approximate solutions. Some of these numerical methods applied by various researchers include the following: Haar wavelet [11], Adomian decomposition method [12], successive linearisation method [13], iterative method [14], restarted Adomian decomposition method [15], variational iteration method [16], parameter expansion method [17], the chaotic motions [18], and block multistep method [19]. Numerical integration is a particularly effective and multipurpose technique in solving the solution to arbitrary nonlinear differential equations. We will solve Equation (1) in two ways using the HLBPF method. In the first way, we convert Equation (1) to a VIESK using integration and then approximate it with the proposed technique. In the next way, we transform Equation (1) into a SODE and then solve it with the proposed method. The main feature of this method is to convert this problem to a system of algebraic equations which, using the operational matrix obtained from the integration, simplifies complex calculations. When the integration operation is eliminated using the resulting operational matrix, there are several methods of approximation, such as the block-pulse function [20], modified block-pulse function [21], HLBPF method [22], Bernoulli polynomials [23], and many other methods. In this article, since the D-VdP equations do not have an exact solution, we first solved all the examples with the Runge-Kutta of the fourth order method (RK4), which uses 0.01 s time step, and consider the answers obtained from the RK4 as the exact solution, and then, we do a comparative study between methods such as Adomian’s decomposition method (ADM), homotopy perturbation method (HPM) [24], and the presented method in this article. Now, we get the absolute error of method’s ADM and HPM as well as the proposed technique with the RK4 method, which in some cases, these are more efficient than the presented method.

The present article is divided into the following sections: in Section 2, the D-VdP oscillator equation will be described. In Section 3, HLBPFs and operational matrix are reviewed. Our proposed method for solving D-VdP is studied in Section 4. In Section 5, the HPM is described for solving this equation. In Section 6, an error analysis for the suggested methods is presented. Then, Section 7 presents numerical results. Finally, conclusion is described in Section 8.

2. The Duffing-Van der Pol Oscillator Equation

In this section, we describe the D-VdP oscillator equation. This equation is a self-maintained electrical circuit. Consider the general hybrid Rayleigh-Duffing-Van der Pol oscillator equation as follows [25].

(2)

where a₁, a₂, a₃, a₄, λ, and γ are constants. Equation (2) contains several well-known oscillator equations. For a₂ = a₃ = γ = 0, Equation (2) becomes the Rayleigh oscillator [26]. Whena₂ = γ = 0, this equation reduces to the Rayleigh-Van der Pol oscillator, and whena₁ = a₂ = 0, it transforms into the famous Duffing-Van der Pol oscillator equation. An interesting feature of the hybrid oscillator is that depending on the relation among the values, it assumes comparable behavior to the Van der Pol oscillator or Duffing oscillator. Suppose an oscillator of mass m and stiffness coefficient k is moving under the influence of damping force, and b is the damping coefficient, which is usually considered a constant number, all of which are connected in series as indicated (Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Damping mechanical oscillator.

We consider the damping force on the oscillator as a function of the oscillator velocity. In this case, the equation of motion of the oscillator will be as follows:

(3)

where k is the linear stiffness term and k₃ is the nonlinear stiffness term. If we consider the damping coefficient as a function of the oscillator place as b(1 − y²), in other words, as the oscillator moves, damping force on the oscillator changes, and then, the oscillator motion equation will be as follows:

(4)

where

and

. By substituting τ = ω₀t, we can get that

(5)

Now, we will substitute by using the move equation:

(6)

Therefore, we get to a D-VdP oscillator equation

(7)

where α = b/mω₀ and

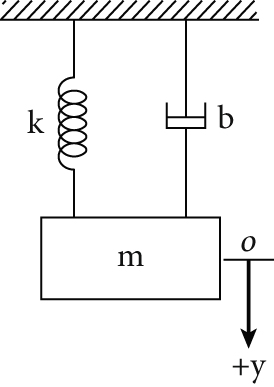
3. Some Properties of Hybrid Functions

In this section, some properties of hybrid functions are recalled.

3.1. Hybrid Legendre Polynomials and Block-Pulse Function

Hybrid functions, b_ij(t), i = 1, ⋯, n and j = 0, ⋯, m − 1, possess three arguments; i and j denote the order of BPFs and Legendre polynomials, respectively, and t is cited to the normalized time that is defined on [0, T_f) as [27].

(8)

where P_j(t) denotes the Legendre polynomials of order j that is satisfied in the following relation:

(9)

And on the interval [0, 1), a set of BPFs b_i(t), i = 1, ⋯n is given as the following [20].

(10)

The BPFs on [0, 1) interval are disjoint; that is, for i, j = 1, ⋯, n, we have b_i(t)b_j(t) = δ_ijb_i(t). Furthermore, one of the properties of these functions on interval [0, 1) is orthogonality. The set of hybrid functions b_ij(t) is taken as a complete orthogonal system in L²[0, 1), since b_ij(t) are a combination of BPFs and Legendre polynomials; each of them is orthogonal and complete.

3.2. Approximating a Function

The expansion of function f, that is square integrable over the interval [0, 1), can be given as the following [28]:

(11)

where

(12)

(13)

where

(14)

In Equation (11), the hybrid coefficients are given by c_ij = <f(t), b_ij(t) > /<b_ij(t), b_ij(t) > , i = 1, ⋯, n, j = 0, ⋯, m − 1, and <..> denotes an inner product. In addition, the function k(s, t) ∈ L²([0, 1) × [0, 1)) can be approximated as

(15)

where K = (k_ij) is an mn × mn matrix

(16)

3.3. The Operational Matrix of Integration

The integration of the vector B(t) given by Equation (13) can be approximated using the following equation:

(17)

where P is the mn × mn operational matrix used for integration, which is shown as follows [28].

(18)

where E and S are m × m matrices as the following:

(19)

3.4. The Product Operational Matrix of the HLBPFs

Additionally, the property of a couple of hybrid function vectors will be used, which is presented as the following [29]. Let us consider

(20)

where C and B(t) are given in Equations (12) and (13), respectively. Also,

is a m × m product operational matrix as

(21)

In Equation (21), 0 denotes a m × m-dimensional zero matrix, and

are m × m matrices that are influenced by m. We consider that n = 2 and m = 8, and then,

in Equation (20) can be determined by

(22)

where

are an array of 8 × 8 matrices as the following

(23)

4. The HLBPFs for Solving Duffing-Van der Pol

4.1. Converting Duffing-Van der Pol Equation to a Volterra Integral Equation of the Second Kind

of second order

(24)

where y(t₀) and y^′(t₀) are known. For this present, we converted Equation (24) into nonlinear VIESK, and now that Equation (24) based on t from t₀ to t is integrated, we have

(25)

Again, Equation (25) would be integrated based on t from t₀ to t so that

(26)

and then, we have

(27)

Finally, we obtain the VIE2 as follows:

(28)

so that

(29)

where g_γ(s, t) ∈ L²([0, 1) × [0, 1)) and q, y ∈ L²([0, 1)). y(t) is an unknown function, and q(t), g_γ(s, t) are known functions that can be expanded into hybrid functions as follows [30].

(30)

where Y is an unknown nm-vector, Q is a known nm-vector, and G_γ is a known nm × nm-dimensional matrix. We consider computing Y_γ in terms of Y, which is Y_γ is the nm-vectors whose elements are nonlinear combination of the elements of the vector Y. Now, substituting Equation (30) into Equation (27), we have

(31)

By using Equations (17) and (20), we get

(32)

For making approximations for y(t), by collocating the system of Equation (32) at the point t_i = (2i − 1)/2nm, i = 1, 2, ⋯, nm and using Equation (14), we obtain

(33)

and by solving the obtained nonlinear system of algebraic equations by numerical method for example Newton’s method, obviously, the unknown vector Y can be obtained by solving Equation (33).

4.1.1. Evaluating Y_γ

We need to evaluate Y_γ so that each element is a nonlinear combination of the components of vector Y. From Equation (20) and y(t)≅Y^TB(t), we have [31]

(34)

where

is a nm-row vector. Then, for (y(s))³, we get

(35)

As a result, through this approach, we can approximate (y(s))^γ for arbitrary γ. Suppose that this technique holds for γ − 1 where (y(t))^γ−1 = Y_γ−1B(t), we can get it for γ as shown in the following:

(36)

So, the component of Y_γ can be calculated in terms of the component of the unknown vector Y.

4.2. Converting Duffing-Van der Pol Equation to a System of Ordinary Differential Equation of the First Order

In this section, considering Equation (24), we convert this equation into a SODE, and we put w₁ = y(t), w₂ = y^′(t), and w′₂ = y^′′(t). Substituting w₁, w₂, and w′₂ into Equation (23), this leads

(37)

with the initial conditions

(38)

In order to solve Equation (37) with HLBPFs, by expanding w₂(0), in terms of hybrid functions, it gives

(39)

Let

(40)

where C can be obtained similar to Equation (12). Integrating of Equation (40) from 0 to t and using Equation (39), we have

(41)

(42)

where H^T = A^TP and P are the operational matrix of integration given in Equation (17). By substituting Equations (40)–(42) in Equation (37), we obtain

(43)

and using Equation (20) gives

(44)

(45)

where Equation (45) is a nonlinear system of algebraic equation which can be solved by Newton’s method.

5. Homotopy Perturbation Method

In this section, the HPM is described for the solution of nonlinear differential equations, and this method can be extensively used to solve different nonlinear problems [32–34]. To that end, assume

(46)

where N is a general differential operator. A homotopy H(y(t), p) can be defined as

(47)

where F(y(t)) is the functional operator with known solution y₀ that can be easily achieved, and L(y(t)) = N(y(t)). Usually, a convex homotopy is selected by

(48)

and continuously trace an implicitly defined curve from a starting point H(y₀(t), 0) to a solution function H(Y(t), 1), where Y is a solution of Equation (46). The embedding parameter p is applied as the classical perturbation technique, and it can be assumed that the solution of Equation (46) can be given through a power series in p,

(49)

and setting p = 1 gives in the approximate solution of Equation (46) as

(50)

5.1. The HPM for Solving Duffing-Van der Pol

In this part, we look at the D-VdP equation and use HPM to solve it. For this purpose, as a result (Equation (24)), we put d²/dt² by κ and κ⁻¹ as the two integral from 0 to t. Therefore, we have

(51)

which is converted to the following equation after applying κ⁻¹:

(52)

where p is the constant of integration and satisfies Lp = 0. As a possible solution, we consider the convex homotopy

(53)

(54)

By substituting Equations (53) and (54) into Equation (48), we get

(55)

Rewriting Equation (55) as

(56)

And using the initial condition y(t₀) = β₀, y^′(t₀) = β₁ in Equation (24), we have

(57)

By substituting Equation (49) into Equation (57) and by assimilating terms with equal powers of p, we obtain

(58)

Lastly, the approximate solution of Equation (24) is computed as

(59)

6. Error Analysis

In this section, we calculate the error bound of the presented method for the approximate solution D-VdP equation in Section 4. When we convert the D-VdP equation to a SODE, we refer the readers to the error bound that is calculated in [22], and we get an error bound for the approximate solutions of nonlinear VIESK which implies the convergence of the present method in Section 4, and we have the following theorems. Suppose that Ω = ⋃_1≤i≤nΩ_i where Ω_i = [(i − 1)/n, i/n).

Theorem 1. Suppose that y ∈ C^m[0, 1] is an m times continuous function and |y^(m)(t)| ≤ λ, such that , where y_i is the restriction of to Ω_i and E_i = span{b_i0(t), b_i1(t), ⋯, b_{i(m − 1)}(t)}, i = 1, 2, ⋯, n. If is the best approximation of y_i(t) from E_i, where , then approximates y(t) with the following error bound

(60)

Proof. Let . Assume that P_{(m − 1)i} for i = 1, 2, ⋯, n, are the interpolating polynomials to y_i at points t_j, j = 0, 1, ⋯, m − 1 that implies the zeros of m-degree-shifted Chebyshev polynomials in the interval [(i − 1)/n, i/n). Then, we have [35]

(61)

The following equation is obtained by considering the estimates for Chebyshev interpolation nodes [36]. Therefore, we obtain

(62)

Since is the best approximation of y_i from E_i and P_{(m − 1)i} ∈ E_i, we obtain

(63)

Now,

(64)

The following equation is obtained by calculating the square root of both sides and through replacing C^TB by ,

(65)

Theorem 2. Assume that is the hybrid expansion of function k with the real value expressed by Equation (15) and k is adequately smooth on every single subdomain [(i − 1)/n, i/n) × [(j − 1)/n, j/n), i, j = 1, 2, ⋯, n, and then, there is a positive constant γ as shown in the following

(66)

Proof. Suppose that , where k_ij is the restriction of k to [(i − 1)/n, i/n) × [(j − 1)/n, j/n). For i, j = 1, 2, ⋯, n assume that P_{(m − 1)ij} is the interpolating polynomial to k_ij at points (s_r, t_l), where s_r, t_l, r, l = 0, 1, 2, ⋯, m − 1 implies the zeros of m-degree-shifted Chebyshev polynomials in [(i − 1)/n, i/n), [(j − 1)/n, j/n) intervals, respectively, and then, we have [35]

(67)

Now, suppose that γ = max{γ₁, γ₂, γ₃}, in which

(68)

Then, the equation mentioned in the following is obtained by considering the estimates for Chebyshev interpolation nodes [36].

(69)

Since is the best unique approximation of k_ij from E_i × E_j, we obtain

(70)

Now,

(71)

The following equation is obtained by calculating the square roots and replacing B^TKB, by . Then, we have

(72)

Lemma 3 (Gronwall Inequality). Let e(t), a(t), and b(t) be real continuous functions defined on Ω, for fixed t₀ ∈ Ω. If

(73)

then

(74)

where

Proof. In [37].

The following discrete Gronwall lemma can be found in [38].

Lemma 4. Assume that {k_j}, j ≥ 0 is a given nonnegative sequence, and the sequence {ε_n} satisfies ε₀ ≤ ρ₀ and

(75)

with ρ₀ ≥ 0, q_j ≥ 0(j ≥ 0). Then

(76)

Now, consider the nonlinear integral equation (Equation (27)) or under the following assumptions:

(1)
q and g satisfy the hypotheses of Theorems 1 and 2, respectively, and ,
(2)
C₁ = sup|H(s)| < ∞
(3)
C₂ = sup|H_ς(s)| < ∞
(4)
C₃ = sup|g(s, t)| < ∞

Theorem 5. Suppose y and are, respectively, the exact and approximate solutions of Equation (27) obtained by Section 4. Suppose also that the assumption (1-4) is fulfilled. Then, there exist positive constants ζ and ϱ such that

(77)

Proof. From Equation (28), we have

(78)

The above equation can be rewritten in the following form:

(79)

By using the mean value theorem, the following result is concluded

(80)

where

. Suppose that

(81)

Since 0 ≤ t < 1, by taking L²-norm in Equation (66) and applying the error bounds obtained in Theorems 1 and 2, we get

(82)

where ζ = λ + C₁3γ. Now let

(83)

considering the above equation, together with Equations (80) and (81), we have

(84)

where ϱ = C₂C₃. Now, let fix the values n and m, and then, for 1 ≤ i < n, we can define

(85)

From Equation (84), we have that for any t ∈ Ω_i = [(i − 1)/n, i/n),

(86)

The above equation can be rewritten as

(87)

Let t ∈ Ω₁ = [0, 1/n), and then, the inequality (Equation (87)) reduces to

(88)

It follows from Gronwall Inequality in Lemma 3 that

(89)

Therefore, we get

(90)

where ϑ = 1 + ϱ/nexp(ϱ/n). Let us assume that t ∈ Ω_i, and then, the inequality (Equation (87)) can be rewritten as

(91)

where

(92)

By using the Gronwall inequality for t ∈ Ω, we obtain

(93)

Therefore, . Now, taking L²-norm in Equation (92), we obtain

(94)

which results

(95)

Now, a suitable application of Lemma 4 to Equation (95) yields

(96)

Since, , regarding the disjointness of e_i for i = 1, 2, ⋯, n, we obtain

(97)

By taking the square root of both sides, we get

(98)

Finally, considering the error bound of ‖I‖₂ obtained in Equation (82) and substituting ϑ with ϑ = 1 + (ϱ/n)exp(ϱ/n), we get

(99)

It is obvious that error bound tends to zero as n and m tend to infinity.

7. Numerical Examples

In this section, the HLBPFs are applied with n = 2, m = 8, and T_f = 1.00001 for all examples. As a result, the methodology suggested in Section 4 is used to find the approximate solution directly. In these examples, the approximate results given by presented method, HPM, and ADM are compared to the numerical solution obtained from RK4. In all cases, the results are presented in Tables 1–3. Based on these results, we see that the results of the HLBPFs are closer to the numerical solutions obtained using RK4. All experiments are implemented using MATLAB.

Example 7.1. Take the following unforced Van der Pol equation into consideration [39, 40].

(100)

The approximate analytical solution of Equation (100) is obtained by method’s RK4, HPM, and ADM.

Table 1. Numerical result for Example 7.1.

t	Approximate solution (RK4)	Absolute error
t	Approximate solution (RK4)	\|RK4-ADM\|	\|RK4-HPM\|	\|RK4-VIESK\|	\|RK4-SODE\|
0	0.200000	0	0	2.88 × 10⁻¹⁰	1.13×10^-11
0.1	0.198569	1.36 × 10⁻¹²	3.98 × 10⁻⁹	1.42 × 10⁻⁸	3.92 × 10^-12
0.2	0.194322	1.90 × 10⁻¹²	7.68 × 10⁻⁸	3.61 × 10⁻⁸	2.99 × 10^-12
0.3	0.187362	1.33 × 10⁻¹⁰	4.63 × 10⁻⁷	3.18 × 10⁻⁷	6.64 × 10^-12
0.4	0.177826	1.53 × 10⁻⁹	1.67 × 10⁻⁶	1.22 × 10⁶	1.24 × 10^-11
0.5	0.165889	1.06 × 10⁻⁸	4.51 × 10⁻⁶	3.41 × 10⁻⁶	1.93 × 10^-11
0.6	0.151756	5.34 × 10⁻⁸	1.00 × 10⁻⁵	7.76 × 10⁻⁶	1.99 × 10^-11
0.7	0.135662	2.15 × 10⁻⁷	1.94 × 10⁻⁵	1.53 × 10⁻⁵	2.42 × 10^-11
0.8	0.117866	7.33 × 10⁻⁷	3.37 × 10⁻⁵	2.68 × 10⁻⁵	2.90 × 10(-11)
0.9	0.098649	2.19 × 10⁻⁶	5.35 × 10⁻⁵	4.32 × 10⁵	3.44 × 10⁻¹¹
1.0	0.078307	5.90 × 10⁻⁶	7.86 × 10⁻⁵	6.45 × 10⁻⁵	3.84 × 10⁻¹¹

Table 2. Numerical result for Example 7.2.

t	Approximate solution (RK4)	Absolute error
t	Approximate solution (RK4)	\|RK4-ADM\|	\|RK4-HPM\|	\|RK4-VIESK\|	\|RK4-SODE\|
0	-0.288680	0	0	2.63 × 10⁻¹⁰	1.13 × 10⁻¹¹
0.1	-0.277018	1.13 × 10⁻⁷	3.05 × 10⁻⁵	3.99 × 10⁻⁶	3.04 × 10⁻¹²
0.2	-0.265993	8.40 × 10⁻⁶	4.87 × 10⁻⁵	2.76 × 10⁻⁵	8.79 × 10⁻¹³
0.3	-0.255551	1.11 × 10⁻⁴	1.11 × 10⁻⁴	8.37 × 10⁻⁵	1.21 × 10⁻¹²
0.4	-0.245646	7.23 × 10⁻⁴	6.97 × 10⁻⁴	1.80 × 10⁻⁴	4.04 × 10⁻¹²
0.5	-0.236235	3.20 × 10⁻³	2.06 × 10⁻³	3.19 × 10⁻⁴	6.73 × 10⁻¹²
0.6	-0.227283	1.11 × 10⁻²	4.67 × 10⁻³	5.03 × 10⁻⁴	2.81 × 10⁻¹²
0.7	-0.218756	3.25 × 10⁻²	9.16 × 10⁻³	7.30 × 10⁻⁴	1.99 × 10⁻¹²
0.8	-0.210624	8.41 × 10⁻²	1.64 × 10⁻²	9.96 × 10⁻⁴	2.25 × 10⁻¹²
0.9	-0.202863	1.98 × 10⁻¹	2.74 × 10⁻²	1.30 × 10⁻³	2.54 × 10⁻¹²
1.0	-0.195446	4.32 × 10⁻¹	4.37 × 10⁻²	1.63 × 10⁻³	2.19 × 10⁻¹²

Table 3. Numerical result for Example 7.3.

t	Approximate solution (RK4)	Absolute error
t	Approximate solution (RK4)	\|RK4-ADM\|	\|RK4-HPM\|	\|RK4-VIESK\|	\|RK4-SODE\|
0	0.000000	0	0	1.18 × 10⁻¹⁰	8.80 × 10⁻¹²
0.1	0.050042	4.18 × 10⁻¹²	1.54 × 10⁻⁹	6.04 × 10⁻⁷	6.04 × 10⁻¹²
0.2	0.099832	8.39 × 10⁻¹²	5.37 × 10⁻⁸	2.66 × 10⁻⁶	8.03 × 10⁻¹²
0.3	0.148870	1.25 × 10⁻¹¹	4.36 × 10⁻⁷	9.80 × 10⁻⁶	1.22 × 10⁻¹¹
0.4	0.196656	1.64 × 10⁻¹¹	1.94 × 10⁻⁶	2.76 × 10⁻⁵	1.80 × 10⁻¹¹
0.5	0.242704	1.99 × 10⁻¹¹	6.15 × 10⁻⁶	6.38 × 10⁻⁵	2.35 × 10⁻¹¹
0.6	0.286537	2.26 × 10⁻¹¹	1.57 × 10⁻⁵	1.26 × 10⁻⁴	2.07 × 10⁻¹¹
0.7	0.327703	1.90 × 10⁻¹¹	3.42 × 10⁻⁵	2.22 × 10⁻⁴	2.64 × 10⁻¹¹
0.8	0.365772	3.88 × 10⁻¹¹	6.63 × 10⁻⁵	3.58 × 10⁻⁴	2.64 × 10⁻¹¹
0.9	0.400343	4.51 × 10⁻¹⁰	1.17 × 10⁻⁴	5.39 × 10⁻⁴	2.72 × 10⁻¹¹
1.0	0.431051	2.67 × 10⁻⁹	1.90 × 10⁻⁴	7.68 × 10⁻⁴	2.80 × 10^-11

Now, we converted Equation (100) into nonlinear VIESK, by integrating of this equation in order to have

(101)

We solve above-mentioned equation using the present method, as well as we converted Equation (100) into a SODE that gives

(102)

where w₁ = y and w₂ = y^′. Again, we solve Equation (102) with the present method. Now, according to Subsection 5.1, we solve Equation (100) with HPM, and we have

(103)

Based on Equation (59), the approximate answer is obtained as follows:

(104)

Table 1 can be used to compare the results of the absolute errors of methods with RK4. Figure 2 shows the approximate answers obtained by HLBPFs for Equations (101) and (102) with RK4.

Example 7.2. In this example, the famous Duffing-Van der Pol equation is included like the following [41, 42].

(105)

where α = −0.28868 and β = 0.12. The approximate analytical solution of Equation (105) is obtained by method’s RK4, HPM, and ADM.

Now, we converted Equation (105) into nonlinear VIESK, by integrating the both sides in order to have

(106)

We solve above-mentioned equation using the present method, as well as we converted Equation (105) into a SODE that gives

(107)

where w₁ = y and w₂ = y^′. Again, we solve Equation (107) with the present method. According to Subsection 5.1, we solve Equation (105) with HPM that gives

(108)

according to Equation (59), the approximate answer is obtained as follows:

(109)

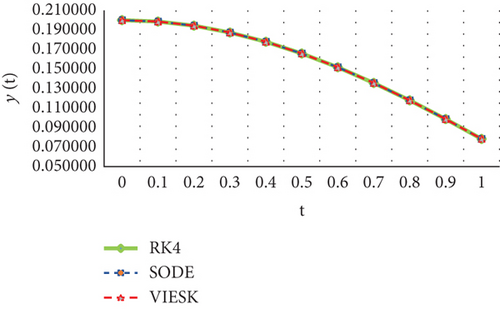
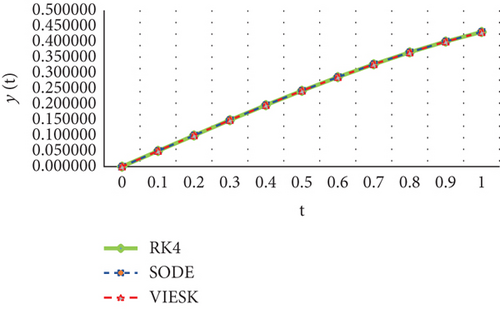
Table 2 can be used to compare the results of the absolute errors of methods with RK4. Figure 3 shows the approximate answers obtained by HLBPFs for Equations (106) and (107) with RK4.

Example 7.3. Let us solve the following oscillator equation [11, 43–45].

(110)

The approximate analytical solution of Equation (110) is obtained by method’s RK4, HPM, and ADM.

Now, we converted Equation (110) into nonlinear VIESK, by integrating of this equation in order to have

(111)

We solve above-mentioned equation using the present method, as well as we converted Equation (110) into a SODE that gives

(112)

where w₁ = y and w₂ = y^′. Again, we solve Equation (112) with the present method. According to Subsection 5.1, we solve Equation (110) with HPM, and we have

(113)

According to Equation (59), the approximate answer is obtained as follows:

(114)

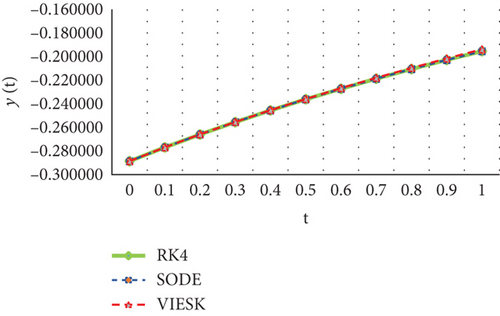
Table 3 can be used to compare the results of the absolute errors of methods with RK4. Figure 4 shows the approximate answers obtained by HLBPFs for Equations (111) and (112) with RK4.

8. Conclusions

In this work, we solved the D-VdP problem by transformation into a Volterra integral equation of the second kind and a system of ordinary differential equation of the first order. It was found that the numerical solution of these equations is using the expansion based on HLBPFs and their integration operational matrix. In this technique, integration is not needed because examples are solved quickly, and calculation time is minimized by employing the matrices P and . The advantage of our proposed method is its high accuracy when the D-VdP equation converted to a SODE.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

All authors contributed to the study’s conception.

Open Research

Data Availability

No data were used to support this study.

References

1 Mickens R. E., Oscillations in Planar Dynamics System, 1996, World Scientific, Singapor, https://doi.org/10.1142/2778.
10.1142/2778
Google Scholar
2 Mickens R. E. and Gumel A. B., Numerical study of a non-standard finite-difference scheme for the van der pol equation, Journal of Sound and Vibration. (2002) 250, no. 5, 955–963, https://doi.org/10.1006/jsvi.2001.3783, 2-s2.0-0037035145.
10.1006/jsvi.2001.3783
Web of Science® Google Scholar
3 Hale J., Ordinary Differential Equations, 1969, Wiley Inter Science, New York.
Google Scholar
4 Guckenheimer J. and Holmes P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 1983, Springer-verlag, New York, https://doi.org/10.1007/978-1-4612-1140-2.
10.1007/978-1-4612-1140-2
Google Scholar
5 Sodano H., Inman D. J., and Park G., Generation and storage of electricity from power harvesting devices, Journal of Intelligent Material Systems and Structures. (2005) 16, no. 1, 67–75, https://doi.org/10.1177/1045389X05047210, 2-s2.0-12844259559.
10.1177/1045389X05047210
Web of Science® Google Scholar
6 Beeby S. and White N. M., Energy Harvesting for Autonomous Systems, 2010, Artech House, USA.
Google Scholar
7 Priya S. and Inman D., Energy Harvesting Technologies, 2009, Springer US, New York.
10.1007/978-0-387-76464-1
Web of Science® Google Scholar
8 He C. H., Amer T. S., Tian D., Abolila A. F., and Galal A. A., Controlling the kinematics of a spring-pendulum system using an energy harvesting device, Journal of Low Frequency Noise, Vibration and Active Control. (2022) 41, no. 3, 1234–1257, https://doi.org/10.1177/14613484221077474.
10.1177/14613484221077474
Web of Science® Google Scholar
9 Tien M. H. and Dsouza K., Method for controlling vibration by exploiting piecewise-linear nonlinearity in energy harvesters, Proceedings of the Royal Society A. (2020) 476, no. 2233, article 20190491, https://doi.org/10.1098/rspa.2019.0491, 32082056.
10.1098/rspa.2019.0491
PubMed Google Scholar
10 Shorakaei H., Shooshtari A. R., and Karami H. R., Analytical solution and optimization for energy harvesting from nonlinear vibration of magneto-electro-elastic plate, AUT Journal of Mechanical Engineering. (2019) 3, no. 1, 63–76.
Google Scholar
11 Kaur H., Mittal R. C., and Mishra V., Haar wavelet solutions of nonlinear oscillator equations, Applied Mathematical Modelling. (2014) 38, no. 21-22, 4958–4971, https://doi.org/10.1016/j.apm.2014.03.019, 2-s2.0-84908551301.
10.1016/j.apm.2014.03.019
Web of Science® Google Scholar
12 Asadi Cordshooli G. and Vahidi A. R., Solutions of Duffing-van der pol equation using decomposition method, Advanced Studies in Theoretical Physics. (2011) 5, no. 1, 121–129.
Google Scholar
13 Motsa S. S. and Sibanda P., A note on the solutions of the Van der Pol and duffing equations using a linearisation method, Mathematical Problems in Engineering. (2012) 2012, 10, 693453, https://doi.org/10.1155/2012/693453, 2-s2.0-84877296535.
10.1155/2012/693453
Web of Science® Google Scholar
14 Al-Jawary M. A. and Al-Razaq S. G., A semi analytical iterative technique for solving Duffing equations, International Journal of pure and applied Mathematics. (2016) 108, no. 4, 871–885, https://doi.org/10.12732/ijpam.v108i4.13, 2-s2.0-84982295366.
10.12732/ijpam.v108i4.13
Google Scholar
15 Vahidi A. R., Azimzadeh Z., and Mohammadifar S., Restarted Adomian decomposition method for solving Duffing-Van der Pol equation, Applied Mathematical Sciences. (2012) 6, no. 11, 499–507.
Google Scholar
16 Al-Sawoor A. J. and Samarchi M. A., An application of He’s variational iteration method for solving Duffing - Van der pol equation, AL-Rafidain Journal of Computer Sciences and Mathematics. (2013) 10, no. 2, 153–163, https://doi.org/10.33899/csmj.2013.163482.
10.33899/csmj.2013.163482
Google Scholar
17 Molaei H. and Kheybari S. A., A numerical solution of classical Van der Pol-Duffing oscillator by He′s parameter-expansion method, International Journal of Contemporary Mathematical Sciences. (2013) 8, no. 15, 709–714, https://doi.org/10.12988/ijcms.2013.3554.
10.12988/ijcms.2013.3554
Google Scholar
18 Zhou L. and Chen F., Chaotic motions of the Duffing-Van der Pol oscillator with external and parametric excitations, Shock and Vibration. (2014) 2014, 5, 131637, https://doi.org/10.1155/2014/131637, 2-s2.0-84934955912.
10.1155/2014/131637
Web of Science® Google Scholar
19 Rasedee A. F. N., Abdul Sathar M. H., Ishak N., Kamarudin N. S., Nazri M. A., Ramli N. A., Ismail I., and Sahrim M., Solution for nonlinear Duffing oscillator using variable order variable stepsize block method, Mathematica. (2017) 33, no. 2, 165–175, https://doi.org/10.11113/matematika.v33.n2.1015.
10.11113/matematika.v33.n2.1015
Google Scholar
20 Jiang Z. H. and Schaufelberger W., Block-Pulse Functions and their Applications in Control Systems, 1992, Springer-Verlag, Berlin, https://doi.org/10.1007/BFb0009162.
10.1007/BFb0009162
Google Scholar
21 He J. H., Taha M. H., Ramadan M. A., and Moatimid G. M., Improved block-pulse functions for numerical solution of mixed Volterra-Fredholm integral equations, Axioms. (2021) 10, no. 3, 200–224, https://doi.org/10.3390/axioms10030200.
10.3390/axioms10030200
Web of Science® Google Scholar
22 Doostdar M. R., Vahidi A. R., Damercheli T., and Babolian E., A hybrid functions method for solving linear and nonlinear systems of ordinary differential equations, Mathematical Communications. (2021) 26, no. 2, 197–213.
Web of Science® Google Scholar
23 Bazm S., Bernoulli polynomials for the numerical solution of some classes of linear and nonlinear integral equations, Journal of Computational and Applied Mathematics. (2015) 275, 44–60, https://doi.org/10.1016/j.cam.2014.07.018, 2-s2.0-84906664129.
10.1016/j.cam.2014.07.018
Web of Science® Google Scholar
24 He C. H. and El-Dib Y. O., A heuristic review on the homotopy perturbation method for non-conservative oscillators, Journal of Low Frequency Noise, Vibration and Active Control. (2022) 41, no. 2, 572–603, https://doi.org/10.1177/14613484211059264.
10.1177/14613484211059264
Web of Science® Google Scholar
25 He C. H., Tian D., Moatimid G. M., Salman H. F., and Zekry M. H., Hybrid Rayleigh-Van der Pol-Duffing oscillator: stability analysis and controller, Journal of Low Frequency Noise, Vibration and Active Control. (2022) 41, no. 1, 244–268, https://doi.org/10.1177/14613484211026407.
10.1177/14613484211026407
Web of Science® Google Scholar
26 Jordan D. W. and Smith P., Nonlinear Ordinary Differential Equations: Problems and Solutions, 2007, Oxford University Press, New York.
10.1093/oso/9780199208241.001.0001
Google Scholar
27 Hesameddini E. and Riahi M., Hybrid Legendre block-pulse functions method for solving partial differential equations with nonlocal integral boundary conditions, Journal of Information & Optimization Sciences. (2019) 40, no. 7, 1391–1403, https://doi.org/10.1080/02522667.2018.1501921.
10.1080/02522667.2018.1501921
Web of Science® Google Scholar
28 Marzban H. R. and Razzagi M., Hybrid functions approach for linearly constrained quadratic optimal control problems, Applied Mathematical Modelling. (2003) 27, no. 6, 471–485, https://doi.org/10.1016/S0307-904X(03)00050-7, 2-s2.0-0038476405.
10.1016/S0307-904X(03)00050-7
Web of Science® Google Scholar
29 Maleknejad K., Basirat B., and Hashemizadeh E., Hybrid Legendre polynomials and block-pulse functions approach for nonlinear Volterra-Fredholm integro-differential equations, Computers & Mathematcs with Applications. (2011) 61, no. 9, 2821–2828, https://doi.org/10.1016/j.camwa.2011.03.055, 2-s2.0-79955473251.
10.1016/j.camwa.2011.03.055
Web of Science® Google Scholar
30 Sohrabi S., Study on convergence of hybrid functions method for solution of nonlinear integral equations, Applicable Analysis. (2013) 92, no. 4, 690–702, https://doi.org/10.1080/00036811.2011.632769, 2-s2.0-84874624613.
10.1080/00036811.2011.632769
Web of Science® Google Scholar
31 Hashemizadeh E., Maleknejad K., and Basirat B., Hybrid functions approach for the nonlinear Volterra-Fredholm integral equations, Procedia Computer Science. (2011) 3, 1189–1194, https://doi.org/10.1016/j.procs.2010.12.192, 2-s2.0-79952531451.
10.1016/j.procs.2010.12.192
Google Scholar
32 He J. H., Jiao M. L., and He C. H., Homotopy perturbation method for fractal Duffing oscillator with arbitrary conditions, Fractals. (2022) 30, no. 9, 1–10, https://doi.org/10.1142/S0218348X22501651.
10.1142/S0218348X22501651
Web of Science® Google Scholar
33 He J. H., Moatimid G. M., and Zekry M. H., Forced nonlinear oscillator in a fractal space, Mechanical Engineering. (2022) 20, no. 1, 001–020, https://doi.org/10.22190/FUME220118004H.
10.22190/FUME220118004H
Web of Science® Google Scholar
34 He J. H., Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering. (1999) 178, no. 3-4, 257–262, https://doi.org/10.1016/S0045-7825(99)00018-3, 2-s2.0-0032672778.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
35 Gasca M. and Sauer T., On the history of multivariate polynomial interpolation, Journal of Computational and Applied Mathematics. (2000) 122, no. 1-2, 23–35, https://doi.org/10.1016/S0377-0427(00)00353-8, 2-s2.0-0034289836.
10.1016/S0377-0427(00)00353-8
Web of Science® Google Scholar
36 Nemati S., Lima P. M., and Ordokhani Y., Numerical solution of a class of two-dimensional nonlinear Volterra integral equations using Legendre polynomials, Journal of Computational and Applied Mathematics. (2013) 242, 53–69, https://doi.org/10.1016/j.cam.2012.10.021, 2-s2.0-84868705456.
10.1016/j.cam.2012.10.021
Web of Science® Google Scholar
37 Holte J. M., Discrete Gronwall Lemma and Applications, 2009, North Dakota, Maa north centeral section meeting.
Google Scholar
38 Brunner H., Collocation Methods for Volterra Integral and Related Functional Differential Equations, 2004, Cambridge University Press.
10.1017/CBO9780511543234
Google Scholar
39 Sadeghi S. A. M., Ebrahimpour B., Bakhshinezhad N., and Sadeghi S. M. N. M. M., Analytical solution of nonlinear Van der Pol oscillator using a hybrid intelligent analytical inverse method, Turkish Journal of Computer and Mathematics Education (TURCOMAT). (2021) 12, no. 13, 5614–5625.
Google Scholar
40 Rani D. and Mishra V., Numerical inverse Laplace transform based on Bernoulli polynomials operational matrix for solving nonlinear differential equations, Results in Physics. (2020) 16, article 102836, https://doi.org/10.1016/j.rinp.2019.102836.
10.1016/j.rinp.2019.102836
Web of Science® Google Scholar
41 Khan N. A., Jamil M., Anwar S. A., and Khan N. A., On efficient method for system of fractional differential equations, Advances in Difference Equations. (2011) 2011, 15, 303472, https://doi.org/10.1155/2011/303472, 2-s2.0-79959278529.
10.1155/2011/303472
Google Scholar
42 Mukherjee S., Roy B., and Dutta S., Solution of the Duffing-Van der Pol oscillator equation by a differential transform method, Physica Scripta. (2011) 83, no. 1, article 015006, https://doi.org/10.1088/0031-8949/83/01/015006, 2-s2.0-78751549017.
10.1088/0031-8949/83/01/015006
Web of Science® Google Scholar
43 Ozturk Y. and Gulsu M., The approximate solution of high-order nonlinear ordinary differential equations by improved collocation method with terms of shifted Chebyshev polynomials, International Journal of Applied and Computational Mathematics. (2016) 2, no. 4, 519–531, https://doi.org/10.1007/s40819-015-0075-1, 2-s2.0-85065259903.
10.1007/s40819-015-0075-1
Google Scholar
44 Akyuz Dascloglu A. and Cerdik Yaslan H., The solution of high-order nonlinear ordinary differential equations by Chebyshev series, Applied Mathematics and Computation. (2011) 217, no. 12, 5658–5666, https://doi.org/10.1016/j.amc.2010.12.044, 2-s2.0-79551645703.
10.1016/j.amc.2010.12.044
Google Scholar
45 Bota C., The approximation of solutions for second order nonlinear oscillators using the polynomial least square method, Journal of Nonlinear Sciences and Applications. (2017) 10, no. 1, 234–242, https://doi.org/10.22436/jnsa.010.01.23.
10.22436/jnsa.010.01.23
Google Scholar

Citing Literature

All articles

Numerical Solutions of Duffing Van der Pol Equations on the Basis of Hybrid Functions

Abstract

1. Introduction

2. The Duffing-Van der Pol Oscillator Equation

3. Some Properties of Hybrid Functions

3.1. Hybrid Legendre Polynomials and Block-Pulse Function

3.2. Approximating a Function

3.3. The Operational Matrix of Integration

3.4. The Product Operational Matrix of the HLBPFs

4. The HLBPFs for Solving Duffing-Van der Pol

4.1. Converting Duffing-Van der Pol Equation to a Volterra Integral Equation of the Second Kind

4.1.1. Evaluating Y_γ

4.2. Converting Duffing-Van der Pol Equation to a System of Ordinary Differential Equation of the First Order

5. Homotopy Perturbation Method

5.1. The HPM for Solving Duffing-Van der Pol

6. Error Analysis

7. Numerical Examples

8. Conclusions

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical Solutions of Duffing Van der Pol Equations on the Basis of Hybrid Functions

Abstract

1. Introduction

2. The Duffing-Van der Pol Oscillator Equation

3. Some Properties of Hybrid Functions

3.1. Hybrid Legendre Polynomials and Block-Pulse Function

3.2. Approximating a Function

3.3. The Operational Matrix of Integration

3.4. The Product Operational Matrix of the HLBPFs

4. The HLBPFs for Solving Duffing-Van der Pol

4.1. Converting Duffing-Van der Pol Equation to a Volterra Integral Equation of the Second Kind

4.1.1. Evaluating Yγ

4.2. Converting Duffing-Van der Pol Equation to a System of Ordinary Differential Equation of the First Order

5. Homotopy Perturbation Method

5.1. The HPM for Solving Duffing-Van der Pol

6. Error Analysis

7. Numerical Examples

8. Conclusions

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

4.1.1. Evaluating Y_γ