In this manuscript, we focus on the application of recently developed analytical scheme, namely, the rational sine-Gordon expansion method (SGEM). Some new exact solutions of Riemann wave system and the nonlinear Gross−Pitaevskii equation (GPE) by using this method are extracted. This method is based on the general properties of the SGEM which uses the fundamental properties of trigonometric functions. Many novel analytical solutions such as dark, bright, mixed dark–bright, hyperbolic, and periodic wave solutions are successfully extracted. Physical meanings of solutions are simulated by the various figures in 2D and 3D along with the contour graphs. Strain conditions of the existence are also reported in detail. Finally, modulation instability analysis of the nonlinear GPE is studied in detail.

1. Introduction

In modern century, the real-world problems arising in various fields of daily life, particularly, engineering such as computer viruses, cyber security, artificial intelligence, magnetism, physics, oceanography, and so on have been symbolized via mathematical norms. Scientists have investigated their connections among multidisciplinary properties. For the last several decades, newly developed mathematical properties have been used to explain many physical problems [1–5]. In [6], scientists have applied the Hopf Bifurcation theorem on the models arising in the group competitive martial arts. In [7], the modified double Laplace transform method is handled to extract some results of the pseudo-hyperbolic telegraph model. The relativistic wave equation associated with the Schrödinger equation was studied in terms of traveling wave distribution in [8]. Wazwaz [9, 10] introduced the several optical solitons for (2 + 1)-dimensional Schrödinger (NLS) equation. In [11], modified exponential function method have been applied to the nonlinear Gerdjikov–Ivanov equation with the M-fractional. Hu et al. [12] focused on the rational and semirational properties of B-type Kadomtsev Petviashvili Boussinesq model. Kudryashov [13] presented the Lax pair and the first integrals for some mathematical properties. Ghanbari et al. [14] observed the rational function solutions for the extended Zakharov Kuzetsov equation. M-type dark soliton facts in optical fibers have been investigated by Yao et al. [15]. Hybrid method has been applied into Rosenau–Hyman equation [16]. Real quadratic fields have been focused on the Handy method in [17]. Generalized (3 + 1) Shallow Water-Like (SWL) equation was observed by Dusunceli [18]. The perturbed Schrödinger and the Heisenberg ferromagnetic spin chain have been investigated in [19, 20]. Park et al. [21] have observed the fifth-order Korteweg-de Vries equations. The multiple exp-function method has been applied on some mathematical models [22]. Chebyshev series have been used to investigate numerically the integro-differential equations in [23]. Duffing and diffusion reaction models have been investigated in the M-derivative operator in [24]. W-shape properties of the (3 + 1)-dimensional nonlinear evolution equations have been reported in [25]. The general and wide-spectral explicit properties of the complex coupled Maccari system have been introduced in [26]. The superconductivity models have been studied in [27]. The Benjamin–Bona–Mahony–Peregrine equation with power law nonlinearity has been studied in [28]. The finite element method have been used to observe a surface plasmon resonance (SPR) sensor in [29]. A current decoupling control strategy was considered on combining a fast terminal sliding mode control and an adaptive extended state observer [30]. A Robust Hammerstein–Wiener Model identification method was applied in [31]. A robust model predictive current control scheme was proposed in [32]. Liu and Liu [32] have studied on the photoacoustic microfluidic pumps [33]. A linear AC unit commitment formulation have been presented in [34]. Moreover, seismic-wave attenuation, shear-wave attenuations, and waves with a wide range of frequencies in digital core have been introduced [35–38]. Some control problems and optimization application have been presented [39–45]. In [46], bipolar cubic fuzzy graphs have been studied. The shallow ocean-waves and rogue waves with translational coordination have been observed in [47, 48]. The influence of Woods–Saxon potential was presented in [49]. Soliton, numerical, and closed solutions of nonlinear models have been investigated by using various schemes [49–56]. To represent the wave’s amplitude, simplest equation algorithms have been used by Inc et al. [57]. Az-Zo’bi et al. [58] studied and used to observe the pulses propagation with power nonlinearity via conformable. Some novel liquid crystals models have been investigated by using some analytical schemes in [59]. Ur Rahman et al. [60] extracted the deeper properties of the fractional regularized long-wave Burgers problem by using two different fractional operators, Beta and M-truncated. In [61], the fractional Huxley equation with Beta and M-truncated derivatives have been considered for reporting nonlinear coherent structures arising in a variety of environments, like spectrum energy, applied mathematics, mechanics, control theory, biology, seismology, and many more.

One of such models belongs to the Riemann wave systems (RWS) defined by the following:

(1)

being α, β, and γ are constants. RWS studied in this paper are used to explain the tidal and tsunami waves in ocean [62]. The nonlinear terms of first equation in Equation (1) give the stationary wave propagation properties in the frame of physical sense. Kundu et al. [63] investigated the parametric analysis via sine-Gordon expansion method (SGEM). Gurevich et al. [64] has used the slow modulation method. They have applied the generalized hodograph method to find some analytical solutions.

Another important model is considered as follows:

(2)

in which λ ≪ 1, N is a constant value and a_s is the axial and transverse harmonic oscillator frequencies. This equation is used to describe the rogue wave in the evolution of the macroscopic wave function of Bose–Einstein condensates (BECs) and also to investigate the deeper properties at the mean-field level [65], via

(3)

in which equation

, the nonlinear Gross−Pitaevskii equation (GPE) can be rewritten as follows [66, 67]:

(4)

in which

is conformable derivative order in 0 < θ < 1. Equation (4) arises in the magnetic field theory observed by magnetically tuning the interatomic interaction.

The paper is organized as follows. In Section 2, the rational sine-Gordon expansion method (RSGEM) is given in detail. In Section 3, RSGEM is applied to extract the stationary optical solitons, mixed dark, and bright solitons to the Equations (1) and (4). Additionally, stability properties of the complex mixed dark–bright soliton solutions are also reported. Finally, the paper is completed by presenting the important novelties of this paper in Section 4.

2. General Properties of RSGEM

This part introduces the general properties of RSGEM, First, let us consider the following sine-Gordon equation [68–70].

(5)

Here, m is a real constant with nonzero. Taking the traveling wave transformation as u(x, t) = U(ξ), ξ = μ(x − ct) into Equation (5) produces

(6)

where U = U(ξ),

and c, μ are also real constants with nonzero. With some calculations, it may be obtained as follows:

(7)

where k is an integral constant. For simplicity, by considering as

and

Equation (7) reads as follows:

(8)

in which w = w(ξ). Gaining a = 1 in Equation (8), we obtain the following two interesting and important relationship

(9)

(10)

Let us take into account the general mathematical model as follows:

(11)

Taking into account as Ψ = Ψ(x, t) = U(ξ), ξ = μ(x − ct), it is converted as follows:

(12)

Here

. In Equation (12), the trial equation for solution function may be considered as follows:

(13)

Equation (13) may be rewritten with the help of Equations (9) and (10) as following:

(14)

in which the values of n, m will be determined later via balance principle. After putting the necessary derivations of Equation (14) into Equation (12), we obtain an equation of sinⁱ(ω)cos^j(ω). Taking all these terms to zero yields a system of equations. Solving this system by using some computational programs, gives the values of A_i, B_i, c_i, d_i, μ, and c. Via these values of parameters A_i, B_i, c_i, d_i, μ, and c in Equation (13), we obtain the new traveling wave solutions to Equation (11).

3. Applications of Projected Scheme

In this part of the paper, the stationary soliton and new analytical solutions to the Riemann wave system and conformable GPE is studied by using RSGEM.

3.1. RSGEM to the Riemann Wave System of Equations

First of all, we apply RSGEM to the Riemann wave system of equations for reporting new stationary soliton solutions. Applying the traveling wave transformation defined by

(15)

into Equation (1) results in the following NODE:

(16)

where

(17)

After taking n = m especially in this paper, via the balance rule in Equation (16) gives n = m = 2. Getting n = m = 2 in Equation (14), one can write the trial equation of solution function given as follows:

(18)

Substituting Equation (18) and its second derivative into Equation (16), we obtain an equation of sinⁱ(w)cosⁱ(w). Getting all coefficients of these terms to zero, we gain a system of equations. Solving this system produces the values of parameters A_i, B_i, c₁, d₁, μ, ω, and δ which results in many entirely new traveling wave solutions to the Equation (1).

Case-1: when

into Equation (13) with n = 2, it yields the following entirely complex mixed dark–bright soliton solution to the RWE as follows

(19)

(20)

(21)

where

. Selecting several parameters values from the physical meanings of the RWE, we can observe the simulations of Equation (19) via Figure 1 in 3D, Figure 2 contour sense, and Figure 3 in 2D according to the specific time scala. From these simulations, one can see that this solution has singular properties.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The 3D simulations of V₁.

Case-2: choosing as

; for Equation (13) with n = 2, it produces entirely new complex mixed dark–bright soliton solution given by

(22)

(23)

(24)

where

. More strict simulations of Equations (22)–(26) are also seen by Figure 4 in three-dimensional, Figure 5 contour sense, and Figure 6 in two-dimensional in a specific time. From the Figures 4 to –6, it may be observed that this solution has dark–bright properties.

Case-3: once it is selected as

for Equation (13) with n = 2, and inserting these values into Equation (13) along with n = 2, we obtain dark–bright soliton solution as following:

(25)

(26)

(27)

where κ = αδμ², f(x, y, t) = δy + μx + κt. Moreover, −1 < B₁ < 1 for strain condition. The intersection points of Equations (25)–(27) are also observed by Figure 7 in three- and two-dimensional in a specific time and Figure 8 in the low region. From the Figures 7 and 8, it may be also seen that Equations (25)–(27) have singular property.

Case-4: if it is chosen as

, mixed-dark soliton solution to the Equation (1) is obtained as following

(28)

(29)

(30)

where κ = αδμ², f(x, y, t) = δy + μx + κt, and also δ, μ, α, B₁ are real constants and nonzero. The periodic wave behaviors of Equations (28)–(30) may be also presented by Figure 9. Figure 9 has stable wave propagation.

Case-5: when

results in the another entirely new exact solution as follows:

(31)

(32)

(33)

where

, and also δ, μ, A₂, d₁ are real constants and nonzero. Smooth wave distribution of Equations(31)–(33) are also plotted by Figure 10 in three-dimensional, Figure 11 contour sense, and Figure 12 in two-dimensional in a specific time. From the Figures 10–12, these solution have the dark–bright properties.

Case-6: using

produces combined dark–bright stationary soliton solution as follows:

(34)

(35)

(36)

where

and δ, μ, A₂ are real constants and nonzero. Intercrossing wave distribution of Equations (34)–(36) are also introduced by Figures 13 and 14. Such sketches is estimated that soliton wavelength is closely related to the gravitational potential. Thus, it may be said that the gravitational potential affect the wavelength and its power. From the Figures 13 and 14, it is estimated that they may be used to explain the gravitational potential energy properties.

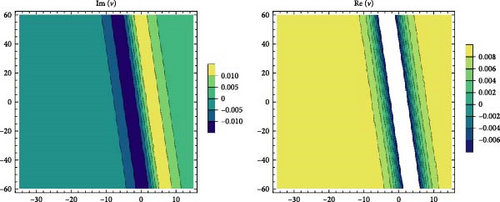
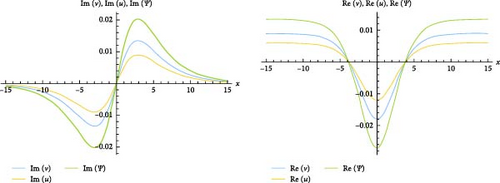
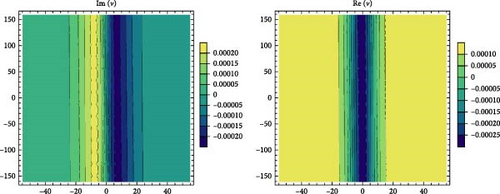
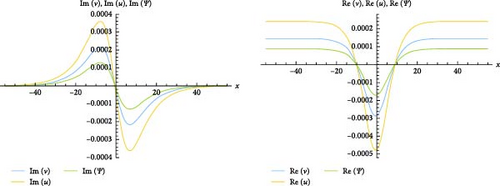
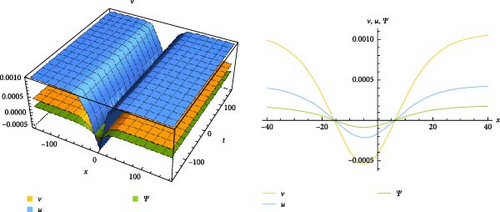
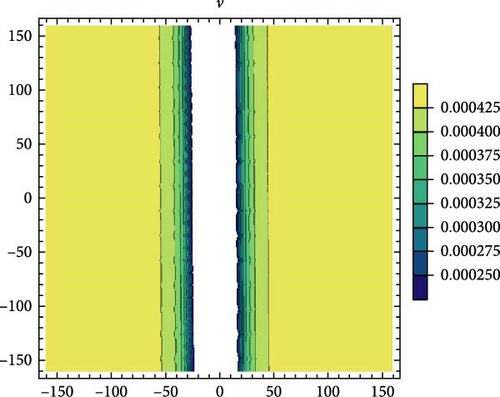
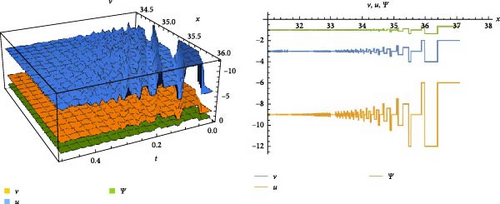
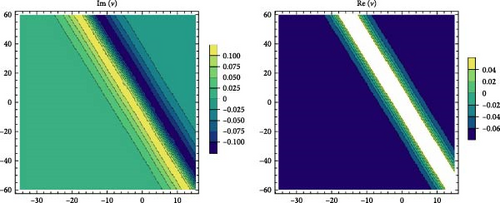
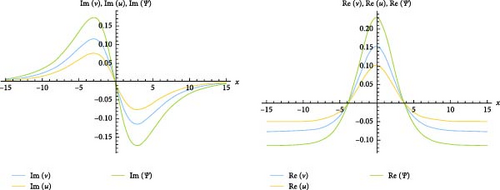
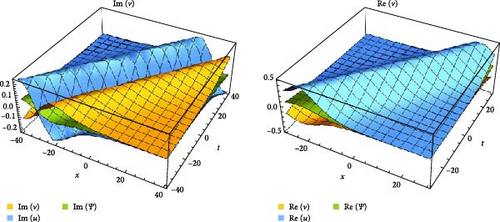
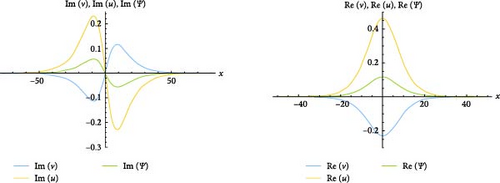
3.2. RSGEM for the Nonlinear GPE in Conformable Operator

This subsection of the manuscript extracts the stationary soliton, mixed dark–bright and complex traveling wave solutions to the conformable GPE by using RSGEM. Applying wave transform given as follows:

(37)

in which α, β, κ are nonzero and also 0 < θ < 1 into Equation (4) converts

(38)

Here Υ is a real constant. Considering balance properties in Equation (38), we find n = 1 for Equations (13) and (14). Using n = 1 Equation (14) reaches the following trial solution function given as:

(39)

where B₁, d₁ are each nonzero constants. Putting Equation (39) and its second derivation in Equation (38) gives various terms containing sin^s⁡(w)cos^s⁡(w). This produces a system of algebraic equations. Solving this system, we find the desired analytical solutions as follows to the conformable GPE.

Case-1: using

produces mixed dark–bright stationary soliton solution as follows:

(40)

where α, A₀, A₁, p, d₁, 0 < θ < 1 are real constants and nonzero. Selecting suitable to the physical properties of conformable GPE, we plot various wave distributions Figure 15. From the Figure 15, it is estimated that it has mixed dark–bright stationary.

3.3. Stability Properties of q₁(X, T)

In this subsection of this paper, Hamiltonian system is considered and applied on the mixed dark–bright stationary soliton solution to investigate its stability on a general range. This system is introduced in detail [71, 72] as following

(41)

in which Π symbolizes the momentum function and also w is used to express the wave speed and Ψ(ζ) is the projected analytical solution. Sandstede et al. [72] observed some important models by using various spaces properties such as Banach and so on. The sufficient condition for the stability is as follows:

(42)

If we take into account Equations (41), and (42) on Equation (40), we obtain

(43)

Thus, the Equation (40) solution is unconditionally stable.

Case-2: when

reaches the mixed dark–bright stationary soliton solution as follows:

(44)

where p, α, A₀, A₁, d₁, κ, 0 < θ < 1 are real constants and nonzero. With the suitable values related to the physical properties for governing model, various wave distributions may be observed Figure 16. From the Figure 16, it is estimated that it has some important wave propagations.

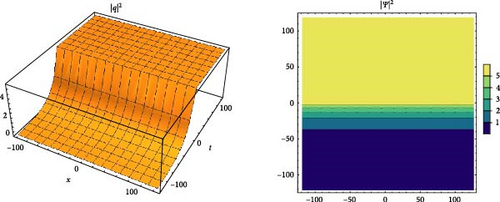
3.4. Stability Properties of q₂(X, T)

Here, if we reconsider the momentum function as follows:

(45)

and the sufficient condition for the stability condition by

(46)

on Equation (44), we obtain

(47)

which is the mixed dark–bright stationary soliton solution given as Equation (44) is unconditionally stable.

4. Modulation Instability Analysis of the Nonlinear GPE

In this section of the article, we discuss the modulation instability (MI) analysis for the stationary solutions of Equation (4) by assuming the following stationary solutions

(48)

where Ω represents the incident power. We investigate the evolution of the perturbation Ξ(X, T) using the concept of linear stability analysis. Substituting Equation (48) into Equation (4) and linearizing the result in Ξ(X, T), we acquire

(49)

supposing solutions of Equation (49) are in the following

(50)

where β is the wave number, and α is the frequency. Putting Equation (50) in Equation (49) gives a set of two homogenous equations as follows:

(51)

(52)

From the Equations (51) and (52), one can easily obtain the following coefficients matrix of ζ and ξ as follows:

(53)

The coefficient matrix in Equation (53) has a nontrivial solution if the determinant equal to zero. By expanding the determinant, we obtain the following

(54)

Equation (54) has the following solutions

(55)

and

(56)

The stability of the steady state is determined by Equations (55) and (56). If the wave number has an imaginary part, the steady-state solution is unstable since the perturbation grows exponentially. But if the wave number is real, the steady state is stable against small perturbation. Thus, the condition is necessary for the existence of MI to occur from Equations (55) and (56) is when either

(57)

(58)

Now for investigating instability modulation gain spectrum it should be noticed that

(59)

We have the following cases

Case 1: when

(60)

We have the following subcases

Case 1.1: for these values

, of constants in Equation (59) we have

(61)

Case 1.2: when it is considered as

, of constants in Equation (59) we have

(62)

Case 1.3: taking as

, of constants in Equation (59) we have

(63)

Case 1.4: once they are considered as

of constants in Equation (59) we have

(64)

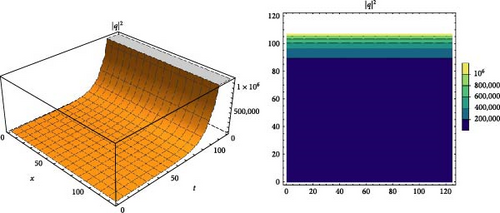
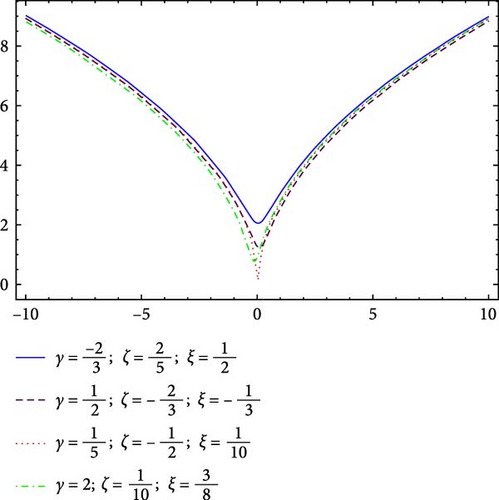
These subcases can be expressed in Figure 17 between −10 < α < 10.

5. Conclusions

In this work, we introduced a recently developed scheme being RSGEM. RSGEM has been handled to the Riemann wave system and nonlinear GPE in conformable frame. Main novelty of this paper is the solutions such as complex, mixed dark–bright, and hyperbolic in conformable operator were extracted. Via graphical illustrations, the dynamical behaviors of solutions found have been reported. The stability properties of the obtained solutions have been introduced, as well. Moreover, the strain conditions of solutions for valid have been also given.

It is estimated that these dark solitons may be closely related to the gravitational dynamical potential [73]. MI analysis of the nonlinear Gross–Pitaevskii equation has been studied, as well. Its various wave simulations have been also plotted in Figure 17. From these results, it may be suggested that the RSGEM is a power tool to solve such nonlinear partial models arising in applied and engineering sciences. Therefore, it may be also applied to investigate deeper properties of some real-world problems [74–77].

As the future direction of this topic, it is envisaged and suggested that some important analytical schemes will be developed by the experts studying in these areas of nonlinear sciences to solve more complex PDEs. This comes from the properties of real-world problems.

Conflicts of Interest

The authors declare that they have no known conflicts of interest.

Authors’ Contributions

W. Gao majorly contributed and H.M. Baskonus contributed on typing collection and formal analyzing.

Open Research

Data Availability

The data that support the findings of this study are available within the article.

References

1 Yamgoué S. B., Deffo G. R., and Pelap F. B., A new rational sine-Gordon expansion methodand its application to nonlinear wave equations arising in mathematical physics, The European Physical Journal Plus. (2019) 134, https://doi.org/10.1140/epjp/i2019-12733-8, 380.
10.1140/epjp/i2019-12733-8
Web of Science® Google Scholar
2 Zhao Z. and He L., Multiple lump solutions of the (3 + 1)-dimensional potential Yu–Toda–Sasa–Fukuyama equation, Applied Mathematics Letters. (2019) 95, 114–121, https://doi.org/10.1016/j.aml.2019.03.031, 2-s2.0-85063931558.
10.1016/j.aml.2019.03.031
Web of Science® Google Scholar
3 Xu Z.-W., Yu G.-F., and Zhu Z.-N., Bright–dark soliton solutions of the multi-component AB system, Wave Motion. (2018) 83, 134–147, https://doi.org/10.1016/j.wavemoti.2018.09.005, 2-s2.0-85053759242.
10.1016/j.wavemoti.2018.09.005
Web of Science® Google Scholar
4 Tariq K. U.-H. and Seadawy A. R., Bistable bright–dark solitary wave solutions of the (3 + 1)-dimensional breaking soliton, Boussinesq equation with dual dispersion and modified Korteweg–de Vries–Kadomtsev–Petviashvili equations and their applications, Results in Physics. (2017) 7, 1143–1149, https://doi.org/10.1016/j.rinp.2017.03.001, 2-s2.0-85015359073.
10.1016/j.rinp.2017.03.001
Web of Science® Google Scholar
5 Cao Y., He J., and Mihalache D., Families of exact solutions of a new extended (2 + 1)-dimensional Boussinesq equation, Nonlinear Dynamics. (2018) 91, no. 4, 2593–2605, https://doi.org/10.1007/s11071-017-4033-9, 2-s2.0-85040322924.
10.1007/s11071-017-4033-9
Web of Science® Google Scholar
6 Chen S. and Ren Y., Small amplitude periodic solution of Hopf Bifurcation Theorem for fractional differential equations of balance point in group competitive martial arts, Applied Mathematics and Nonlinear Sciences. (2022) 7, no. 1, 207–214, https://doi.org/10.2478/amns.2021.2.00152.
10.2478/amns.2021.2.00152
Google Scholar
7 Abdulazeez S. T. and Modanli M., Analytic solution of fractional order pseudo-hyperbolic telegraph equation using modified double laplace transform method, International Journal of Mathematics and Computer in Engineering. (2023) 1, no. 1, 105–114, https://doi.org/10.2478/ijmce-2023-0008.
10.2478/ijmce-2023-0008
Google Scholar
8 Yokuş A., Construction of different types of traveling wave solutions of the relativistic wave equation associated with the Schrödinger equation, Mathematical Modelling and Numerical Simulation with Applications. (2021) 1, no. 1, 24–31, https://doi.org/10.53391/mmnsa.2021.01.003.
10.53391/mmnsa.2021.01.003
Google Scholar
9 Wazwaz A.-M., Bright and dark optical solitons for (2 + 1)-dimensional Schrödinger (NLS) equations in the anomalous dispersion regimes and the normal dispersive regimes, Optik. (2019) 192, https://doi.org/10.1016/j.ijleo.2019.162948, 2-s2.0-85067430128, 162948.
10.1016/j.ijleo.2019.162948
Web of Science® Google Scholar
10 Wazwaz A.-M., Multiple complex and multiple real soliton solutions for the integrable sine–Gordon equation, Optik. (2018) 172, 622–627, https://doi.org/10.1016/j.ijleo.2018.07.080, 2-s2.0-85050496658.
10.1016/j.ijleo.2018.07.080
Web of Science® Google Scholar
11 Ismael H. F., Baskonus H. M., Bulut H., and Gao W., Instability modulation and novel optical soliton solutions to the Gerdjikov–Ivanov equation with M-fractional, Optical and Quantum Electronics. (2023) 55, 1–15, https://doi.org/10.1007/s11082-023-04581-7, 303.
10.1007/s11082-023-04581-7
Web of Science® Google Scholar
12 Hu C. C., Deng Y. S., Tian B., Sun Y., and Zhang C. R., Rational and semi-rational solutions for the (3 + 1)-dimensional B-type Kadomtsev Petviashvili Boussinesq equation, Modern Physics Letters B. (2019) 1950296, 1–10.
Google Scholar
13 Kudryashov N. A., Traveling wave reduction of the modified KdV hierarchy: the lax pair and the first integrals, Communications in Nonlinear Science and Numerical Simulation. (2019) 73, 472–480, https://doi.org/10.1016/j.cnsns.2019.03.007, 2-s2.0-85062637223.
10.1016/j.cnsns.2019.03.007
Web of Science® Google Scholar
14 Ghanbari B., Osman M. S., and Baleanu D., Generalized exponential rational function method for extended Zakharov–Kuzetsov equation with conformable derivative, Modern Physics Letters A. (2019) 34, no. 20, https://doi.org/10.1142/S0217732319501554, 2-s2.0-85065056640, 1950155.
10.1142/S0217732319501554
Web of Science® Google Scholar
15 Yao Y., Ma G., Zhang X., and Liu W., M-typed dark soliton generation in optical fibers, Optik. (2019) 193, https://doi.org/10.1016/j.ijleo.2019.162997, 2-s2.0-85068226268, 162997.
10.1016/j.ijleo.2019.162997
Web of Science® Google Scholar
16 Arslan D., The comparison study of hybrid method with RDTM for solving Rosenau–Hyman equation, Applied Mathematics and Nonlinear Sciences. (2020) 5, no. 1, 267–274, https://doi.org/10.2478/amns.2020.1.00024.
10.2478/amns.2020.1.00024
Google Scholar
17 Özer Ö., A handy technique for fundamental unit in specific type of real quadratic fields, Applied Mathematics and Nonlinear Sciences. (2020) 5, no. 1, 495–498, https://doi.org/10.2478/amns.2019.2.00033.
10.2478/amns.2019.2.00033
Google Scholar
18 Dusunceli F., New exact solutions for generalized (3 + 1) shallow water-like (SWL) equation, Applied Mathematics and Nonlinear Sciences. (2019) 4, no. 2, 365–370, https://doi.org/10.2478/AMNS.2019.2.00031.
10.2478/AMNS.2019.2.00031
Google Scholar
19 Akbar M. A., Mahmud F., Wazwaz A.-M., Roy R., Baleanu D., Barman H. K., Mahmoud W., Sharif M. A. A., and Osman M. S., Dynamical behavior of solitons of the perturbed nonlinear Schrödinger equation and microtubules through the generalized Kudryashov scheme, Results in Physics. (2022) 43, https://doi.org/10.1016/j.rinp.2022.106079, 106079.
10.1016/j.rinp.2022.106079
Google Scholar
20 Osman M. S., Tariq K. U., Bekir A., Elmoasry A., Elazab N. S., Younis M., and Abdel-Aty M., Investigation of soliton solutions with different wave structures to the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation, Communications in Theoretical Physics. (2020) 72, no. 3, https://doi.org/10.1088/1572-9494/ab6181, 035002.
10.1088/1572-9494/ab6181
Web of Science® Google Scholar
21 Park C., Nuruddeen R. I., Ali K. K., Muhammad L., Osman M. S., and Baleanu D., Novel hyperbolic and exponential ansatz methods to the fractional fifth-order Korteweg–de Vries equations, Advances in Difference Equations. (2020) 2020, no. 1, https://doi.org/10.1186/s13662-020-03087-w, 627.
10.1186/s13662-020-03087-w
Web of Science® Google Scholar
22 Nisar K. S., Ilhan O. A., Abdulazeez S. T., Manafian J., Mohammed S. A., and Osman M. S., Novel multiple soliton solutions for some nonlinear PDEs via multiple exp-function method, Results in Physics. (2021) 21, https://doi.org/10.1016/j.rinp.2020.103769, 103769.
10.1016/j.rinp.2020.103769
Web of Science® Google Scholar
23 Ali K. K., Abd El Salam M. A., Mohamed E. M. H., Samet B., Kumar S., and Osman M. S., Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series, Advances in Difference Equations. (2020) 2020, no. 1, https://doi.org/10.1186/s13662-020-02951-z, 494.
10.1186/s13662-020-02951-z
Web of Science® Google Scholar
24 Siddique I., Jaradat M. M. M., Zafar A., Bukht Mehdi K., and Osman M. S., Exact traveling wave solutions for two prolific conformable M-fractional differential equations via three diverse approaches, Results in Physics. (2021) 28, https://doi.org/10.1016/j.rinp.2021.104557, 104557.
10.1016/j.rinp.2021.104557
Web of Science® Google Scholar
25 Saliou Y., Abbagari S., Houwe A., Osman M. S., Yamigno D. S., Crépin K. T., and Inc M., W-shape bright and several other solutions to the (3 + 1)-dimensional nonlinear evolution equations, Modern Physics Letters B. (2021) 35, no. 30, https://doi.org/10.1142/S0217984921504686, 2150468.
10.1142/S0217984921504686
CAS Google Scholar
26 Yiasir Arafat S. M., Fatema K., Rayhanul Islam S. M., Islam M. E., Ali Akbar M., and Osman M. S., The mathematical and wave profile analysis of the Maccari system in nonlinear physical phenomena, Optical and Quantum Electronics. (2023) 55, no. 2, https://doi.org/10.1007/s11082-022-04391-3, 136.
10.1007/s11082-022-04391-3
Web of Science® Google Scholar
27 Akbar M. A., Abdullah F. A., Islam M. T., Sharif M. A. A., and Osman M. S., New solutions of the soliton type of shallow water waves and superconductivity models, Results in Physics. (2023) 44, https://doi.org/10.1016/j.rinp.2022.106180, 106180.
10.1016/j.rinp.2022.106180
Web of Science® Google Scholar
28 Osman M. S., Rezazadeh H., Eslami M., Neirameh A., and Mirzazadeh M., Analytical study of solitons to Benjamin–Bona–Mahony–Peregrine equation with power law nonlinearity by using three methods, UPB Scientific Bulletin, Series A: Applied Mathematics and Physics. (2018) 80, no. 4, 267–278.
Google Scholar
29 Zhao Q., Liu J., Yang H., Liu H., Zeng G., and Huang B., High birefringence d-shaped germanium-doped photonic crystal fiber sensor, Micromachines. (2022) 13, no. 6, https://doi.org/10.3390/mi13060826, 826.
10.3390/mi13060826
PubMed Web of Science® Google Scholar
30 Xu W., Qu S., and Zhang C., Fast terminal sliding mode current control with adaptive extended state disturbance observer for PMSM system, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2023) 11, no. 1, 418–431, https://doi.org/10.1109/JESTPE.2022.3185777.
10.1109/JESTPE.2022.3185777
Web of Science® Google Scholar
31 Sun L., Hou J., Xing C., and Fang Z., A robust Hammerstein–Wiener model identification method for highly nonlinear systems, Processes. (2022) 10, no. 12, https://doi.org/10.3390/pr10122664, 2664.
10.3390/pr10122664
Web of Science® Google Scholar
32 Liu S. and Liu C., Virtual-vector-based robust predictive current control for dual three-phase PMSM, IEEE Transactions on Industrial Electronics. (2021) 68, no. 3, 2048–2058, https://doi.org/10.1109/TIE.2020.2973905.
10.1109/TIE.2020.2973905
Web of Science® Google Scholar
33 Liu J., MAO S., Song S., Huang L., Belfiore L. A., and Tang J., Towards applicable photoacoustic micro-fluidic pumps: tunable excitation wavelength and improved stability by fabrication of Ag–Au alloying nanoparticles, Journal of Alloys and Compounds. (2021) 884, https://doi.org/10.1016/j.jallcom.2021.161091, 161091.
10.1016/j.jallcom.2021.161091
CAS Web of Science® Google Scholar
34 Shao Z., Zhai Q., Han Z., and Guan X., A linear AC unit commitment formulation: an application of data-driven linear power flow model, International Journal of Electrical Power & Energy Systems. (2023) 145, https://doi.org/10.1016/j.ijepes.2022.108673, 108673.
10.1016/j.ijepes.2022.108673
Web of Science® Google Scholar
35 Bouchaala F., Ali M. Y., Matsushima J., Bouzidi Y., Jouini M. S., Takougang E. M., and Mohamed A. A., Estimation of seismic wave attenuation from 3d seismic data: a case study of OBC data acquired in an offshore oilfield, Energies. (2022) 15, no. 2, https://doi.org/10.3390/en15020534, 534.
10.3390/en15020534
Web of Science® Google Scholar
36 Bouchaala F., Ali M. Y., and Matsushima J., Compressional and shear wave attenuations from walkway VSP and sonic data in an offshore Abu Dhabi oilfield, Comptes Rendus. Géoscience. (2021) 353, no. 1, 337–354, https://doi.org/10.5802/crgeos.83.
10.5802/crgeos.83
Web of Science® Google Scholar
37 Matsushima J., Ali M. Y., and Bouchaala F., Propagation of waves with a wide range of frequencies in digital core samples and dynamic strain anomaly detection: carbonate rock as a case study, Geophysical Journal International. (2021) 224, no. 1, 340–354, https://doi.org/10.1093/gji/ggaa467.
10.1093/gji/ggaa467
CAS Web of Science® Google Scholar
38 Bouchaala F., Ali M. Y., Matsushima J., Bouzidi Y., Takam Takougang E. M., Mohamed A. A. I., and Sultan A., Azimuthal investigation of compressional seismic-wave attenuation in a fractured reservoir, GEOPHYSICS. (2019) 84, no. 6, B437–B446, https://doi.org/10.1190/geo2019-0079.1.
10.1190/geo2019-0079.1
Web of Science® Google Scholar
39 Srinivasareddy S., Narayana Y. V., and Krishna D., Sector beam synthesis in linear antenna arrays using social group optimization algorithm, National Journal of Antennas And Propagation. (2021) 3, no. 2, 6–9, https://doi.org/10.31838/NJAP/03.02.02.
10.31838/NJAP/03.02.02
Google Scholar
40 Liu S. and Liu C., Direct harmonic current control scheme for dual three-phase PMSM drive system, IEEE Transactions on Power Electronics. (2021) 36, no. 10, 11647–11657, https://doi.org/10.1109/TPEL.2021.3069862.
10.1109/TPEL.2021.3069862
Web of Science® Google Scholar
41 Liu S., Liu C., Zhao H., Liu Y., and Dong Z., Improved flux weakening control strategy for five-phase PMSM considering harmonic voltage vectors, IEEE Transactions on Power Electronics. (2022) 37, no. 9, 10967–10980, https://doi.org/10.1109/TPEL.2022.3164047.
10.1109/TPEL.2022.3164047
Web of Science® Google Scholar
42 Liu F., Zhang T., Alghazzawi D. M., and Soltan M. A. A., Optimisation of modelling of finite element differential equations with modern art design theory, Applied Mathematics and Nonlinear Sciences. (2022) 7, no. 2, 277–284, https://doi.org/10.2478/amns.2021.2.00089.
10.2478/amns.2021.2.00089
Google Scholar
43 Bilal M., Haris H., Waheed A., and Faheem M., The analysis of exact solitons solutions in monomode optical fibers to the generalizednonlinear Schrödinger system by the compatible techniques, International Journal of Mathematics and Computer in Engineering. (2023) 1, no. 2, 149–170, https://doi.org/10.2478/ijmce-2023-0012.
10.2478/ijmce-2023-0012
Google Scholar
44 Johnson V. C., Bali J. S., Kolanur C. B., and Tanwashi S., Industry 4.0: intelligent quality control and surface defect detection, 3C Empresa. Investigación y Pensamiento Crítico. (2022) 11, no. 2, 186–192.
Google Scholar
45 Choudhari S. A., Kumbhalkar M. A., Bhise D. V., and Sardeshmukh M. M., Optimal reservoir operation policy determination for uncertainty conditions, 3C Empresa. Investigación y Pensamiento Crítico. (2022) 11, no. 2, 277–295, https://doi.org/10.17993/3cemp.2022.110250.277-295.
10.17993/3cemp.2022.110250.277-295
Google Scholar
46 Lu J., Zhu L., and Gao W., Remarks on bipolar cubic fuzzy graphs and its chemical applications, International Journal of Mathematics and Computer in Engineering. (2023) 1, no. 1, 1–10, https://doi.org/10.2478/ijmce-2023-0001.
10.2478/ijmce-2023-0001
Google Scholar
47 Xu B., Zhang Y., and Zhang S., Line soliton interactions for shallow ocean-waves and novel solutions with peakon, ring, conical, columnar and lump structures based on fractional KP equation, Advances in Mathematical Physics. (2021) 2021, 15, https://doi.org/10.1155/2021/6664039, 6664039.
10.1155/2021/6664039
Web of Science® Google Scholar
48 Xu B., Zhang Y., and Zhang S., Fractional rogue waves with translational coordination, steep crest and modified asymmetry, Complexity. (2021) 2021, 14, https://doi.org/10.1155/2021/6669087, 6669087.
10.1155/2021/6669087
Web of Science® Google Scholar
49 Gu Y., Chen B., Ye F., and Aminakbari N., Soliton solutions of nonlinear Schrödinger equation with the variable coefficients under the influence of Woods–Saxon potential, Results in Physics. (2022) 42, https://doi.org/10.1016/j.rinp.2022.105979, 105979.
10.1016/j.rinp.2022.105979
Web of Science® Google Scholar
50 Gu Y. and Liao L., Closed form solutions of Gerdjikov–Ivanov equation in nonlinear fiber optics involving the beta derivatives, International Journal of Modern Physics B. (2022) 36, no. 19, https://doi.org/10.1142/S0217979222501168, 2250116.
10.1142/S0217979222501168
Web of Science® Google Scholar
51 Gu Y., Yuan W., Aminakbari N., and Lin J., Meromorphic solutions of some algebraic differential equations related Painlevé equation IV and its applications, Mathematical Methods in the Applied Sciences. (2018) 41, no. 10, 3832–3840, https://doi.org/10.1002/mma.4869, 2-s2.0-85048866473.
10.1002/mma.4869
Web of Science® Google Scholar
52 Wang Y., Veeresha P., G. Prakasha D., Mehmet Baskonus H., and Gao W., Regarding deeper properties of the fractional order Kundu–Eckhaus equation and massive thirring model, Computer Modeling in Engineering & Sciences. (2022) 133, no. 3, 697–717, https://doi.org/10.32604/cmes.2022.021865.
10.32604/cmes.2022.021865
Web of Science® Google Scholar
53 Gu Y. and Aminakbari N., Bernoulli (G′/G) -expansion method for nonlinear Schrödinger equation with third-order dispersion, Modern Physics Letters B. (2022) 36, no. 11, https://doi.org/10.1142/S0217984922500282, 2250028.
10.1142/S0217984922500282
CAS Web of Science® Google Scholar
54 Yan L., Sabir Z., Ilhan E., Asif Zahoor Raja M., Gao W., and Mehmet Baskonus H., Design of a computational heuristic to solve the nonlinear liénard differential model, Computer Modeling in Engineering & Sciences. (2023) 136, no. 1, 201–221, https://doi.org/10.32604/cmes.2023.025094.
10.32604/cmes.2023.025094
Web of Science® Google Scholar
55 Raut S., Saha S., Das A. N., and Talukder P., Complete discrimination system method for finding exact solutions, dynamical properties of combined Zakharsov–Kuznetsov-modified Zakarsov–Kuznetsov equation, Alexandria Engineering Journal. (2023) 76, 247–257, https://doi.org/10.1016/j.aej.2023.06.020.
10.1016/j.aej.2023.06.020
Web of Science® Google Scholar
56 Gu Y. and Yuan W., Closed form solutions of nonlinear space-time fractional Drinfel’d–Sokolov–Wilson equation via reliable methods, Mathematical Methods in the Applied Sciences. (2021) 1–17, https://doi.org/10.1002/mma.7868.
10.1002/mma.7868
Google Scholar
57 Inc M., Az-Zo’bi E. A., Jhangeer A., Rezazadeh H., Nasir Ali M., and Kaabar M. K. A., New soliton solutions for the higher-dimensional non-local ito equation, Nonlinear Engineering. (2021) 10, no. 1, 374–384, https://doi.org/10.1515/nleng-2021-0029.
10.1515/nleng-2021-0029
Google Scholar
58 Az-Zo’bi E., Akinyemi L., and Alleddawi A. O., Construction of optical solitons for conformable generalized model in nonlinear media, Modern Physics Letters B. (2021) 35, no. 24, https://doi.org/10.1142/S0217984921504091, 2150409.
10.1142/S0217984921504091
Web of Science® Google Scholar
59 Altawallbeh Z., Az-Zo’bi E., Alleddawi A. O., Şenol M., and Akinyemi L., Novel liquid crystals model and its nematicons, Optical and Quantum Electronics. (2022) 54, no. 12, https://doi.org/10.1007/s11082-022-04279-2, 861.
10.1007/s11082-022-04279-2
CAS Web of Science® Google Scholar
60 Ur Rahman R., Faridi W. A., El-Rahman M. A., Taishiyeva A., Myrzakulov R., and Az-Zo’bi E. A., The sensitive visualization and generalized fractiona solitons’ construction fo regularized long-wave governing model, Fractal and Fractional. (2023) 7, no. 2, https://doi.org/10.3390/fractalfract7020136, 136.
10.3390/fractalfract7020136
Web of Science® Google Scholar
61 Rahman R. U., Al-Maaitah A. F., Qousini M., Az-Zo’bi E. A., Eldin S. M., and Abuzar M., New soliton solutions and modulation instability analysis of fractional Huxley equation, Results in Physics. (2023) 44, https://doi.org/10.1016/j.rinp.2022.106163, 106163.
10.1016/j.rinp.2022.106163
Web of Science® Google Scholar
62 Barman H. K., Seadawy A. R., Akbar M. A., and Baleanu D., Competent closed form soliton solutions to the Riemann wave equation and the Novikov–Veselov equation, Results in Physics. (2020) 17, https://doi.org/10.1016/j.rinp.2020.103131, 103131.
10.1016/j.rinp.2020.103131
Web of Science® Google Scholar
63 Kundu P. R., Fahim M. R. A., Islam M. E., and Akbar M. A., The sine-Gordon expansion method for higher-dimensional NLEEs and parametric analysis, Heliyon. (2021) 7, no. 3, https://doi.org/10.1016/j.heliyon.2021.e06459, e06459.
10.1016/j.heliyon.2021.e06459
PubMed Web of Science® Google Scholar
64 Gurevich A. V., Krylov A. L., and El G. A., Evolution of a Riemann wave in dispersive hydrodynamics, Soviet Physics - JETP. (1992) 74, no. 6, 957–962.
Google Scholar
65 Li Q.-Y., Li Z.-D., Li L., and Fu G.-S., Nonautonomous bright and dark solitons of Bose–Einstein condensates with feshbach-managed time-dependent scattering length, Optics Communications. (2010) 283, no. 17, 3361–3366, https://doi.org/10.1016/j.optcom.2010.04.039, 2-s2.0-77956296636.
10.1016/j.optcom.2010.04.039
CAS Web of Science® Google Scholar
66 Liang Z. X., Zhang Z. D., and Liu W. M., Dynamics of a bright soliton in Bose–Einstein condensates with time-dependent atomic scattering length in an expulsive parabolic potential, Physical Review Letters. (2005) 94, no. 5, https://doi.org/10.1103/PhysRevLett.94.050402, 2-s2.0-18144402005, 050402.
10.1103/PhysRevLett.94.050402
CAS PubMed Web of Science® Google Scholar
67 Pérez-García V. M., Konotop V. V., and Brazhnyi V. A., Feshbach resonance induced shock waves in Bose–Einstein condensates, Physical Review Letters. (2004) 92, no. 22, https://doi.org/10.1103/PhysRevLett.92.220403, 2-s2.0-3042795863, 220403.
10.1103/PhysRevLett.92.220403
PubMed Web of Science® Google Scholar
68 Gao W., Yel G., Baskonus H. M., and Cattani C., Complex solitons in the conformable (2 + 1)-dimensional Ablowitz–Kaup–Newell–Segur equation, AIMS Mathematics. (2020) 5, no. 1, 507–521, https://doi.org/10.3934/math.2020034.
10.3934/math.2020034
Web of Science® Google Scholar
69 Kumar A., Ilhan E., Ciancio A., Yel G., and Baskonus H. M., Extractions of some new travelling wave solutions to the conformable DateJimbo–Kashiwara–Miwa equation, AIMS Mathematics. (2021) 6, no. 5, 4238–4264, https://doi.org/10.3934/math.2021251.
10.3934/math.2021251
Web of Science® Google Scholar
70 Guirao J. L. G., Baskonus H. M., and Kumar A., Regarding new wave patterns of the newly extended nonlinear (2 + 1)-dimensional Boussinesq equation with fourth order, Mathematics. (2020) 8, no. 3, https://doi.org/10.3390/math8030341, 341.
10.3390/math8030341
Web of Science® Google Scholar
71 Chandrasekhar S., Hydrodynamic and Hydromagnetic Stability, 1981, Dover Publications Inc., New York, United States.
Google Scholar
72 Sandstede B., Chapter 18: stability of travelling waves, Handbook of Dynamical Systems. (2002) 2, 983–1055, https://doi.org/10.1016/S1874-575X(02)80039-X, 2-s2.0-67649363651.
10.1016/S1874-575X(02)80039-X
Google Scholar
73 Weisstein E. W., Concise Encyclopedia of Mathematics, 2002, 2nd edition, CRC, New York.
10.1201/9781420035223
Google Scholar
74 Pan J., Rahman M. U., and Rafiullah, Breather-like, singular, periodic, interaction of singular and periodic solitons, and a-periodic solitons of third-order nonlinear Schrödinger equation with an efficient algorithm, The European Physical Journal Plus. (2023) 138, https://doi.org/10.1140/epjp/s13360-023-04530-z, 912.
10.1140/epjp/s13360-023-04530-z
Web of Science® Google Scholar
75 Manafian J. and Lakestani M., N-lump and interaction solutions of localized waves to the (2+1)-dimensional variable-coefficient Caudrey–Dodd–Gibbon–Kotera–Sawada equation, Journal of Geometry and Physics. (2020) 150, https://doi.org/10.1016/j.geomphys.2020.103598, 103598.
10.1016/j.geomphys.2020.103598
Web of Science® Google Scholar
76 Mathanaranjan T., Optical solitons and stability analysis for the new (3 + 1)-dimensional nonlinear Schrödinger equation, Journal of Nonlinear Optical Physics & Materials. (2023) 32, no. 2, https://doi.org/10.1142/S0218863523500169, 2350016.
10.1142/S0218863523500169
Web of Science® Google Scholar
77 Kumar S. and Niwas M., Exploring lump soliton solutions and wave interactions using new inverse G′/G-expansion approach: applications to the (2 + 1)-dimensional nonlinear Heisenberg ferromagnetic spin chain equation, Nonlinear Dynamics. (2023) 111, 20257–20273, https://doi.org/10.1007/s11071-023-08937-2.
10.1007/s11071-023-08937-2
Web of Science® Google Scholar

Citing Literature

All articles

The Modulation Instability Analysis and Analytical Solutions of the Nonlinear Gross−Pitaevskii Model with Conformable Operator and Riemann Wave Equations via Recently Developed Scheme

Abstract

1. Introduction

2. General Properties of RSGEM

3. Applications of Projected Scheme

3.1. RSGEM to the Riemann Wave System of Equations

3.2. RSGEM for the Nonlinear GPE in Conformable Operator

3.3. Stability Properties of q₁(X, T)

3.4. Stability Properties of q₂(X, T)

4. Modulation Instability Analysis of the Nonlinear GPE

5. Conclusions

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Modulation Instability Analysis and Analytical Solutions of the Nonlinear Gross−Pitaevskii Model with Conformable Operator and Riemann Wave Equations via Recently Developed Scheme

Abstract

1. Introduction

2. General Properties of RSGEM

3. Applications of Projected Scheme

3.1. RSGEM to the Riemann Wave System of Equations

3.2. RSGEM for the Nonlinear GPE in Conformable Operator

3.3. Stability Properties of q1(X, T)

3.4. Stability Properties of q2(X, T)

4. Modulation Instability Analysis of the Nonlinear GPE

5. Conclusions

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

3.3. Stability Properties of q₁(X, T)

3.4. Stability Properties of q₂(X, T)