Everybody wants to maintain solitariness to some extent or entirely in his dealings with other people during different modes of communication. To retain privacy, researchers materialized distinct image encryption algorithms using chaotic maps. Due to their extraordinary features, most researchers employed multidimensional chaotic maps to barricade clandestine information or digital images from potential invaders. Still, multidimensional chaotic maps have many impediments conferred in the literature review. In this paper, we developed a cryptosystem utilizing multiple chaotic maps to mitigate the shortcoming of multidimensional chaotic maps. A distinctive approach is adopted to sire a key stream using a combination of chaotic maps and create a sequence of random integers linked with the pixels of the plain image to shatter the association between neighboring pixels of a plain image. Finally, diffusion is accomplished using the previously diffused pixels at a decimal level. Security and statistical analysis demonstrate that the presented encryption algorithm is robust against well-known attacks. An ample key space indicates that it is best suited for secure communication.

1. Introduction

The importance of image encryption is increased to transmit confidential data (images, videos, audios, and agreements) via the internet because digital images are frequently used to communicate and share sensitive information, whether in the military, banking, or personal moments. Many image encryption techniques [1] have been constructed based on a variety of chaotic [2, 3] to protect the plain images from prying eyes or unlawful access. Traditional security encryption schemes like AES [4], DES [5], and IDEA [6] are inadequate to maintain acceptable standards for the safety of digital images because of the strong association among neighboring pixels, enormous storage capacities, and significant redundancy.

Chaotic systems are deemed to be appropriate for image encryption schemes due to their features like ergodicity, pseudorandomness, ambiguity, high sensitivity to initial conditions, and controlled parameters. Most researchers designed cryptosystems [7, 8] either by modifying existing chaotic systems [9, 10] or developing new chaotic systems [11, 12], keeping in mind the usefulness of chaotic systems due to their characteristics, as mentioned earlier. The authors of [13] proposed a 2D-LSM chaotic system and ascertained that it is more chaotic than some lately developed two-dimensional chaotic maps using a bifurcation diagram, LE, phase plane trajectory, and sample entropy. Furthermore, it materializes a color image encryption algorithm (CIEA) using orthogonal Latin square and 2D-LSM. Hua et al. [14] conferred a new 2D-PPCS (two-dimensional parametric polynomial chaotic system) to mitigate the flaws of existing chaotic systems, and theoretical analysis exhibits the chaotic behavior of the 2D PPCS. The study of [15] modifies the chaotic behavior of a 1-dimensional chaotic map, further analyzed the chaotic behavior through phase diagram and Lyapunov exponent spectrum, and constructs a novel image encryption scheme. There are two types of chaotic systems: (i) one or 2− dimensional chaotic maps and (ii) multidimensional chaotic maps. Most recent image encryption techniques are based on multidimensional chaotic maps [16, 17], which are more sensitive than 1-dimensional chaotic maps. It contains many initial values and controlled parameters that help enlarge the length of key space to resist brute force attacks. In [18], Malik et al. developed a cryptosystem for a color image using two multidimensional chaotic maps and used the idea of histogram equalization to equalize histogram of chaotic sequences of Lorenz system. Hua et al. [19] suggested an image encryption scheme using S-box, yielded using a complete Latin square. Experimental consequences divulge that the presented cryptosystem can defy all well-known security and statistical seizures from potential invaders. The authors of [20] designed an image encryption scheme utilizing parallel compressing sensing with adaptive thresholding sparsification. In [21], to get the random sequences of a 5-dimensional hyperchaotic map, first generate the initial values that depend on pixels of a plain image. A unique key is generated after rearranging the random sequences and constructed an image encryption algorithm. Multidimensional chaotic maps take more time during the execution process due to their intricate structure and method to find the solutions of a multidimensional chaotic map. Alternatively, one or 2− dimensional chaotic maps are simple in structure and execute efficiently in the available MATLAB versions, not taking more time during the computational process. Therefore, we use a combination of chaotic maps rather than the multidimensional chaotic system in this paper. The logistic map, piecewise linear chaotic map, tent map, and Henon map are used to propose an encryption algorithm. Two unique keys are generated using the aforementioned chaotic maps to diffuse the pixels of the plain image at the decimal level. To break the connection among nearby pixels in a plain image, generate a random sequence of integers using any chaotic map, relate it with the diffused pixels, and further use it to scramble the diffused pixels. Finally, the presented encryption algorithm is evaluated on various images, including Lena, Baboon, Pepper, Cameraman, and House. The experimental results demonstrate the effectiveness of our presented image encryption algorithm.

The remaining sections of the paper are organized as follows. The basic features of distinct chaotic maps are described in Section 2. Each step of the proposed encryption method is discussed in detail in Section 3. Various security and statistical tests are performed in Section 4 to assess the performance of the constructed cryptosystem. Conclusions are discussed in Section 5.

2. Chaotic Map

In this section, we will discuss some chaotic maps which are further utilized in an image encryption scheme.

2.1. Logistic Map

Logistic map is a 1-dimensional chaotic map with excellent chaotic features and its numerical expression is described as follows:

()

where u₁ is a controlled parameter and its range is [0, 4], but the bifurcation diagram of a logistic map shows chaotic behavior only when u₁ ∈ [3.567,4] can be seen in Figure 1(a). This map highly sensitive to initial condition x_(i) and the range of initial condition is (0, 1).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Bifurcation diagrams of logistic map, piecewise linear chaotic map, tent map, and Henon map.

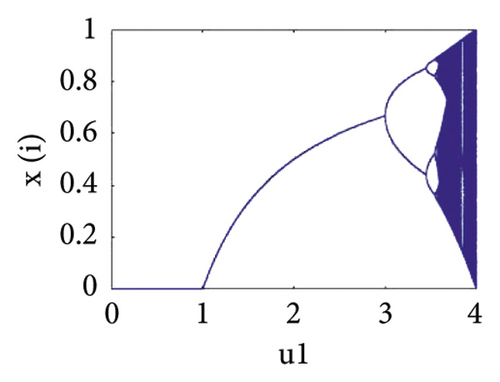
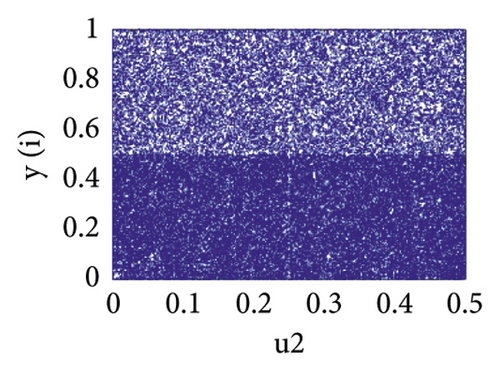
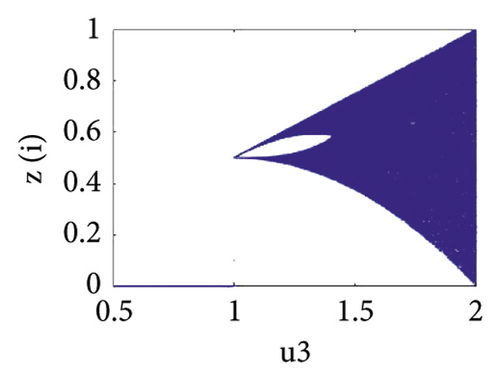
2.2. Piecewise Linear Chaotic Map

Piecewise linear chaotic map [22] is a one dimensional map that generates the random sequence necessary for image encryption scheme during the process of confusion and diffusion. Mathematical formula of piecewise linear chaotic map is given as follows:

()

where u₂ ∈ (0,0.5) is a parameter and its initial value range is (0,1). The bifurcation diagram of piecewise linear chaotic is in Figure 1(b) that shows the chaotic behavior of piecewise linear chaotic map.

2.3. Tent Map

Numerical formula of tent map is described as follows:

()

where u₃ ∈ (0.5,2) is a parameter and its initial value range is (0,1). Chaotic behavior of tent map can be seen in Figure 1(c).

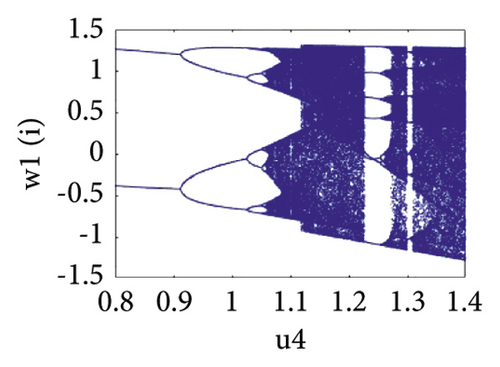
2.4. Hénon Map

Hénon map [23] is a 2-dimensional chaotic map and its mathematical equation is described as follows:

()

The Hénon map depends on two control parameters u₄ and u₅, and highly sensitive to initial conditions which belongs (0, 1). The chaotic behavior of the Hénon map can be seen in bifurcation diagram against the parameter u₄ ∈ [0.8,1.4] in Figure 1(d).

3. Proposed Image Encryption Scheme

This section will discuss all the necessary things of an encryption process in detail, like key generation, block scrambling, and pixels scrambling process, and decimal level diffusion process.

Step 1. Transformation
Let I be a grayscale image of size M × N, where M and N indicate rows and columns, respectively. Now, we transform image I into a 1− dimensional array P₁ of size L = M × N.
Step 2. Key Stream Generation
(i)
Let x₀, y₀, z₀, w₁₀, w₂₀, u₁, u₂, u₃, u₄, and u₅ be the initial conditions and control parameters that are used to iterate the equations from (1) to (5).
(ii)
After iteration the pseudorandom generated sequences , , , , and .
(iii)
To remove the transient effect, discard the first n₀ iterations from each sequence , {y_L}, {z_L}, , and {x_L} and obtained new sequences x₁, x₂, x₃, x₄, and x₅, respectively, of length L.
(iv)
Choose the one sequence from the sequences x₁, x₂, x₃, x₄, and x₅ and after selecting the sequence, store them in A , in ascending order.
(v)
Now generate sequence T of random integers by storing the position of each member of A in the selected sequence.
(vi)
Divide the sequence T into four subsequences T₁, T₂, T₃, and T₄, the length of each subsequence is L/4;
()
(vii)
Now, select the state of variables from the remaining four sequence named as Y₁, Y₂, Y₃, and Y₄ and get the subsequences S₁, S₂, S₃, and S₄, respectively of length L/4 using the expression described as follows:
()
where n means number of encryption rounds and for each n, i = 1,2,3,4 and j = 0,1,2,3. if (n + j) > 4 then (n + j) = (n + j) mod 4.
(viii)
The subsequences S₁, S₂, S₃, and S₄ are used to form a sequence of length L.
(ix)
We have 4! ways to form a sequence of length L by using the subsequences S₁, S₂, S₃, and S₄.
(x)
Now obtained two sequences B₁ and B₂ of length L using two different arrangements of S₁, S₂, S₃, and S₄.
B₁ = arrangement of sequences {S₂, S₁, S₃, S₄}.
B₂ = arrangement of sequences {S₃, S₂, S₄, S₁}.
(xi)
Compute the key streams D₁ and D₂ using the mathematical formula described as follows:
()
where i = 1 to L.
Step 3. Decimal Diffusion Level 1
The following analytical equation is used to diffuse the pixels of P₁ using D₁ and previously diffused pixels;
()
where d₁ is a seed value used to diffuse the first pixel of P₁.
Step 4. Block Scrambling Process
(i)
First, divide I₁ into blocks, and the size of each block is M₁ × N₁; then, the number of blocks is h, where h = M × N/M₁ × N₁.
(ii)
Now, obtain a subsequence Q₁ of length h from the sequence, which is selected from the sequences w_1,y, z, w₂x and generate the sequence Q₂ of random integers using the same procedure on Q₁, described in Step 2 (iv, v).
(iii)
Q₂ is used to scramble the blocks of I₁ for n₁ times where n₁ indicates the number of scrambling rounds; after block scrambling of I_1, transform the I₁ into a 1-dimensional array I₂.
Step 5. Decimal Diffusion Level 2
The pixels of I₂ is diffused using the sum of previously diffused pixels and D₂, with mathematical expression described as follows:
()
where d₂ is the seed value used to diffuse the first pixel of I₂.
Step 6. Pixels Scrambling Process
(i)
Let T be a random integers sequence of length L, described in Step 2. (v).
(ii)
T is used to scramble the pixels of I₃ for n₂ times where n₂ indicates the number of pixels scrambling rounds.
Step 7. Cipher Image
Transform the I₃ into matrix C of size M × N. Figure 2 illustrates the encryption process.
Decryption is performed in the opposite direction as encryption.

4. Performance Evaluation

The performance of a presented cryptosystem is tested utilizing statistical and security analysis on distinct images such as Lena, Baboon, Pepper, Cameraman, and House. The parameters of the secret key are x₀ = 0.23, y₀ = 0.25, z₀ = 0.25, w₁₀ = 0.2, w₂₀ = 0.01, u₁ = 3.8956, u₂ = 0.25678900, u₃ = 1.5, u₄ = 1.4, u₅ = 0.3, d₁ = 234, d₂ = 234, n₀ = 700, n = 1, n₁ = 1, and n₂ = 1, and all experimental results are computed in MATLAB 2018b on a compatible computer with Windows 10, 8.00 GB RAM, and an Intel(R) Core(TM) i5-6300U CPU @ 2.5 GHz. Figure 3 demonstrates the encryption effect of our presented cryptosystem, and all experimental data are documented in tables, demonstrating that our cryptosystem’s performance is outstanding against any security and statistical threats.

4.1. Key Space Analysis

The key space analysis helps us to decide whether or not our cryptosystem can withstand brute force attacks. The length of a key space is crucial to withstand a brute force assault because a prospective intruder would try every possible combination of key space to crack the cryptosystem. It is believed that if a cryptosystem’s key space is larger than 2¹⁰⁰, it is robust. Let x₀, y₀, z₀, w₁₀, w₂₀, u₁, u₂, u₃, u₄, and u₅ be the secret key parameters, and each has a computational accuracy of 10⁻¹⁵, and d₁, d₂, and d₃ are the positive integers used at diffusion level, and n₀ is the number of discarding iterations where 100 ≤ n₀ ≤ 1000. Consequently, the length of the key size 9 × 10¹⁵⁹ which is higher than 2¹⁰⁰, demonstrating that our presented encryption technique is resistant to brute force attacks. Table 1 shows the key space comparison to some existing encryption cryptosystems.

Table 1. Key space comparison.

Schemes	Key space
Proposed	9 × 10¹⁵⁹
Reference [24]	10⁸⁸
Reference [25]	10⁶⁰
Reference [26]	2.4 × 10¹¹²
Reference [27]	2.9645 × 10¹⁴⁹
Reference [28]	1.6777 × 10⁶⁴
Reference [29]	10⁷⁰

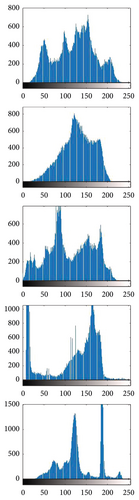
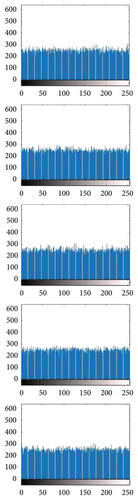
4.2. Histogram Analysis

Histogram analysis is the simplest and pictorial way to see the frequency distribution in plain and encrypted images. If the frequency distribution is uniform, then it is considered that the proposed encryption scheme is suitable for the secure transmission of data through the internet in daily use applications. In 8− bit grayscale image, the range of pixels value is 0 to 255. Histogram of plain and encrypted images (Lena, Baboon, Pepper, Cameraman, and House) can be seen in column (b, d) of Figure 3, and column (b) shows that the frequency distribution of pixels is not uniform. Still, on the other side, column (d) shows that the frequency distribution of pixels is uniform. The uniform distribution of pixels demonstrates that our proposed image encryption scheme can resist any statistical attack. A potential invader does not get any reliable information from the histogram of encrypted images.

4.3. Entropy

It is deemed that entropy is used to compute the uncertainty present in the source of information (digital image); if m is a source of information, the entropy of m can be computed described as follows:

()

where p(m_i) is a frequency of the symbol m_i, the entropy of a source of information m is 8 according to entropy formula, if the frequency of symbol m_i is uniformly distributed. The entropy of different encrypted images (Lena, Baboon, Pepper, Cameraman, and House) is nearly equal to 8, as shown in Table 2.

Table 2. Entropy, local entropy and Chi-square score of encrypted image of Lena, Baboon, Pepper, Cameraman, and House.

Images	Size	Entropy	Local entropy	Chi-square score
Lena	256 × 256	7.9969	7.9091	286.4766
Baboon	256 × 256	7.9976	7.9065	219.5625
Pepper	256 × 256	7.9976	7.9066	214.7813
Cameraman	256 × 256	7.9968	7.9069	291.6484
House	256 × 256	7.9972	7.9076	253.4357

Sometimes global Shannon entropy does not measure the true randomness in the encrypted image; we estimate the local Shannon entropy [30] to overcome this drawback. In local Shannon entropy, the encrypted image divided into randomly selected K nonoverlapping blocks with T_B pixels in each block. Compute the entropy of each block using (11). Finally, compute the mean of all the block’s entropy. The mathematical formula to calculate the local Shannon entropy is described as follows:

()

The benchmark of local Shannon entropy is 7.90. It is evident from the Table 2 that our proposed encryption scheme can produce adequate randomness in an encrypted image that a potential invader cannot get any reliable information about the plain image.

4.4. Chi-Square Analysis

Chi-square is a quantitative method of assessing pixel uniformity. Chi-square is a statistical technique that is described mathematically as follows:

()

where C_i indicates the actual frequency of i^th pixel, the range of pixels value is 0 to 255 because we are working on the 8-bit grayscale image. The numerical value

for the level of significance 0.05. The distribution of pixels in encrypted images is highly uniform if the Chi-square score of the encrypted image is lower than 293.2478 as much as possible. The Chi-square score of distinct encrypted images (Lena, Baboon, Pepper, Cameraman, and House) is listed in Table 2, which proved that our proposed encryption scheme uniformly distribute the pixels value 0 to 255 in different rounds of encryption.

4.5. Majority Logic Criteria (Texture Analysis of the Image)

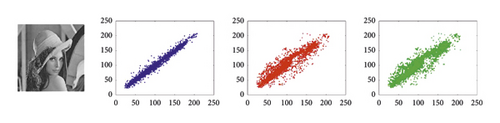
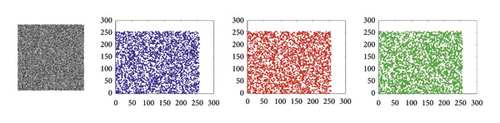
To evaluate the presented encryption scheme’s efficiency on digital images, the MLC [31, 32] tool is utilized, which is a collection of five statistical tests such as correlation, contrast, entropy, energy, and homogeneity.

4.5.1. Contrast

The brightness deterioration of plain images throughout the encryption process is calculated using contrast analysis. The better the encryption technology, the higher the contrast value. The numerical equation is as follows:

()

where p(i, j) indicates the grayscale co-occurrences matrix.

4.5.2. Correlation

The range of correlation values is [1, −1]. In plain images, the correlation value of a pixel to its neighboring pixels is one or nearly equal to 1. The correlation value one or almost equal to 1 shows that the correlation of a pixel to its neighboring pixels is very strong. On the other hand, the correlation value 0 or negative shows that the correlation of a pixel to its neighboring pixels is weak. The purpose of any encryption scheme is to break the correlation of a pixel to its adjacent pixels. Mathematical equation which is used to measure correlation is described as follows:

()

where p(i, j) indicates the grayscale co-occurrences matrix, we also find the correlation of a pixel to its adjacent pixels in the horizontal, vertical, and diagonal direction. The correlation of a pixel to its adjacent pixels is listed in Table 3 and the correlation of a pixel to its neighboring pixel in a horizontal, vertical, and diagonal direction of plain and encrypted images (Lena, Baboon, Pepper, Cameraman, and House) listed in Table 4. Figure 4 shows the correlation of plain and encrypted images of Lena in a horizontal, vertical, and diagonal direction. The experimented results of correlation demonstrate that the performance of the proposed encryption scheme is excellent and able to resist any attack.

Table 3. MLC score of the proposed cryptosystem for standard images.

Images	P/E	Contrast	Correlation	Energy	Homogeneity
Lena	Plain	0.5047	0.8918	0.1094	0.8525
Lena	Encrypted	10.4180	0.0036	0.0156	0.3893

Baboon	Plain	0.4318	0.8495	0.1120	0.8193
Baboon	Encrypted	10.4939	−0.0004	0.0156	0.3906

Pepper	Plain	0.4868	0.9614	0.1061	0.8802
Pepper	Encrypted	10.4459	0.0036	0.0156	0.3915

Cameraman	Plain	0.5872	0.9227	0.1805	0.8953
Cameraman	Encrypted	10.4980	0.0002	0.0156	0.3893

House	Plain	0.1863	0.9497	0.2029	0.9251
House	Encrypted	10.5117	−0.0004	0.0156	0.3887

Average	Plain	0.4394	0.9150	0.1422	0.8745
Average	Encrypted	10.4735	0.0013	0.0156	0.3899

Table 4. Correlation coefficient results of plain and encrypted images of Lena, Baboon, Pepper, Cameraman, and House in the horizontal, vertical, and diagonal direction, respectively.

Images	Direction	Correlation
Images	Direction	Plain image	Encrypted image
Lena	Horizontal	0.9907	0.0222
	Vertical	0.9380	0.0354
	Diagonal	0.9377	0.0006

Baboon	Horizontal	0.8341	0.0346
	Vertical	0.8989	0.0205
	Diagonal	0.8270	−0.0049

Pepper	Horizontal	0.9830	0.0017
	Vertical	0.9667	0.0222
	Diagonal	0.9511	0.0076

Cameraman	Horizontal	0.8842	0.0149
	Vertical	0.9201	0.0162
	Diagonal	0.8425	−0.0168

House	Horizontal	0.9218	−0.0312
	Vertical	0.9959	−0.0031
	Diagonal	0.9134	−0.0294

4.5.3. Energy

To execute the energy analysis, we use a gray-level co-occurrence matrix. The numerical expression of energy is given as follows:

()

where p(i, j) indicates the grayscale co-occurrences matrices.

4.5.4. Homogeneity

Homogeneity analysis is used to compute the closeness of the grayscale level of co-occurrence matrices in (GLCM). The encryption method is deemed to be excellent if the homogeneity value is lower as much as possible. The mathematical expression of homogeneity is described as follows:

()

where p(i, j) indicates the grayscale co-occurrences matrices.

The experimental MLC score of plain and encrypted images is listed in Table 3. MLC scores indicate that the encryption technique is excellent for digital images for secure transmission through the internet.

4.6. MSE/MAD/PSNR/SSIM Analysis

A cryptosystem’s encryption quality may be assessed using mean square error (MSE) and mean absolute difference (MAD) tests. MSE and MAD are mathematically expressed as follows:

()

where M and N indicate the dimensions of plain image P and encrypted image C, the cryptosystem is deemed efficient and secure if MSE and MAD values are higher.

The peak signal to noise ratio (PSNR) is inversely proportional to the square root of MSE, as seen in equation (19). The PSNR value should be as low as feasible for the best encryption quality. The PSNR is calculated using the following mathematical formula:

()

The structural similarity index measurement (SSIM) evaluates how much an encrypted image deteriorates throughout the encryption process. The SSIM mathematical equation is as follows:

()

where μ_P and μ_E are the average pixel values and σ_P, and σ_E are the variance of corresponding images P and E. Also, σ_PE represents the covariance between P and E, and α and β are two predetermined constants used to ensure stability. The MSE, MAD, PSNR, and SSIM experimental findings are presented in Table 5, and the experimental results show that the proposed cryptosystem can withstand any statistical attack.

Table 5. MAD, MSE, SSIM, and PSNR scores of the proposed encryption algorithm.

Images	MAD	MSE	SSIM	PSNR
Lena	73.0485	7782	−0.0012	9.2198
Baboon	73.2823	7833	−0.0015	9.1916
Pepper	73.1300	7780	0.0013	9.2210
Cameraman	73.1966	7796	0.000828	9.2118
House	73.0063	7792	−0.0015	9.2145
Average	73.1327	7797	0.0011	9.2117

4.7. Data Loss Attack Analysis

A data loss attack means a potential invader artificially dethrones the pixels of a particular area of an encrypted image or loses some portion of the image during transmission through the internet. A cryptosystem is immaculate if it convalesces the critical information from the encrypted image, which loses the data. It is clear from Figure 5 that our proposed cryptosystem can retrieve helpful information from the encrypted images which lose data during communication. In Figure 5, a₁ to a₅ the figures which lose a block of data size 32 × 32 to demonstrate the data loss attack and a₆ lose data from all sides, and b₁ to b₆ represent the figures after performing the decryption process on the figures which lose data respectively.

4.8. Noise Attack Analysis

Normally, images possess information, but during the transmission, the image is polluted with some noise. The appearance of noise will annihilate the original information from the image. The pepper and salt noise effect on our encryption algorithm is examined in this paper on Lena’s image, and different salt and pepper noise ratios represent the attack intensity. In Figure 6, we use the pepper and salt noise ratios 0.01, 0.03, 0.05 on the figure a₁, a₂, and a₃, respectively. The decryption process are employed on the a₁, a₂, and a₃ and as a result get figures b₁, b₂, and b₃, respectively. Figure 6 demonstrates that our proposed system is flawless for dealing with polluted images and retrieving important information as much as possible.

4.9. Differential Attacks

The two main criteria for evaluating the robustness [33] of a cryptosystem against a slight change in any pixel or secret key parameter are NPCR (number of pixel changing rate) and UACI (unified averaged changed intensity). The mathematical equations for NPCR and UACI are as follows:

()

where M and N are the dimensions of an image, also E₁ and E₂ are two encrypted images corresponding to plain images differ by single pixel. Benchmark values of the NPCR and UACI for different sizes of images are listed in Table 6.

Table 6. Benchmark values of NPCR and UACI.

Test/size of images	256 × 256	512 × 512	1024 × 1024
NPCR	99.5954	99.5893	99.5954
UACI	[33.2824, 33.6447]	[33.3730, 33.5541]	[33.4183, 33.5088]

4.10. Plaintext Sensitivity Analysis

A cryptosystem is plaintext sensitive if a slight change in randomly selected pixel of plain image will produce a different encrypted image; that encrypted image does not provide any important clue about plain image. Method to test the plaintext sensitivity, let P₁ and P₂ be two plain images; all the pixels of P₁ and P₂ are the same except one randomly selected pixel. The original key is used to encrypt the plain images P₁ and P₂, get two encrypted images E₁ and E₂, respectively. NPCR and UACI between two encrypted images E₁ and E₂, are computed using equations (21) and (22). A cryptosystem is sensitive to plaintext if the value of NPCR > 99% and UACI is greater or closer to 33%. The procedure, as mentioned earlier of plaintext sensitivity employed on the image (Lena, Baboon, Pepper, Cameraman, and House) and compute the NPCR and UACI score, is listed in Table 7. The plaintext sensitivity score of different images demonstrates that our cryptosystem can resist any differential attack.

Table 7. Results of and after a slight change in randomly selected pixel P(x, y) of Lena, Baboon, Pepper, Cameraman, and House.

Images	Size	NPCR(%)	UACI(%)	Randomly selected pixel
Lena	256 × 256	99.6460	33.4271	P_(1,1)
Baboon	256 × 256	99.6426	33.4309	P_(256,256)
Pepper	256 × 256	99.6475	33.4078	P_(167,233)
Cameraman	256 × 256	99.6521	33.4538	P_(217,17)
House	256 × 256	99.6353	33.3731	P_(128,128)

4.11. Key Sensitivity Analysis

The cryptosystem is regarded as extremely key sensitive; if the encrypted image acquired after a subtle change in any of the secret key parameters provided in Table 8 is distinctive from the encrypted image generated without any change in secret key parameters. To test the key sensitivity, first, encrypt plain image P using the original secret key parameters listed in Table 8, then encrypt the same plain image using a minor modification of 10⁻¹⁵ in any secret key parameter, yielding two encrypted images E₁ and E₂. NPCR and UACI are computed between to encrypted images E₁ and E₂ using the equations (21) and (22). We performed a key sensitivity analysis on the Lena image by making minor changes to each secret key parameter one at a time. The resulting NPCR and UACI scores are shown in Table 8, indicating that our proposed cryptosystem is extremely key sensitive and resistant to differential attacks.

Table 8. Results of NPCR and UACI after a minor change in any parameter of secret key.

Parameters	Change in parameter	NPCR(%)	UACI(%)
x₀	x₀ + 10⁻¹⁵	99.6048	33.4169
y₀	y₀ + 10⁻¹⁵	99.6124	33.3899
z₀	z_o + 10⁻¹⁵	99.6613	33.3942
w₁₀	w₁₀ + 10⁻¹⁵	99.5941	33.3327
w₂₀	w₂₀ + 10⁻¹⁵	99.5911	33.5274
u₁	u₁ + 10⁻¹⁵	99.5834	33.2567
u₂	u₂ + 10⁻¹⁵	99.5728	33.3396
u₃	u₃ + 10⁻¹⁵	99.6155	33.6749
u₄	u₄ + 10⁻¹⁵	99.6094	33.6089
u₅	u₅ + 10⁻¹⁵	99.5911	33.5005
n₀	100 ≤ n₀ ≤ 1000	99.5956	33.3028

4.12. Randomness Test for Cipher

Our proposed cryptosystem creates enough randomness in the pixel of encrypted images; a potential invader can never acquire reliable information about the plain image. The Nist test in [34] is used to check the randomness present in the pixels of encrypted images. The Table 9 exhibits the two Nist test results, which confirm that the security of our proposed cryptosystem is excellent to resist any attack.

Table 9. Nist test analysis for distinct encrypted images.

Images/tests	Frequency	Runs	Rank
P_value for Lena	0.8265	0.3085	0.0852
P_value for Baboon	0.9761	0.4672	0.0852
P_value for Pepper	0.8420	0.1909	0.0852
P_value for Cameraman	0.2991	0.2048	0.0852
P_value for House	0.6390	0.4285	0.0852

4.13. Speed Analysis

The speed and security of any encryption scheme are the key characteristics in the application of real life. The analysis, as mentioned earlier, exhibits that the security of our proposed encryption scheme is immaculate. We test the speed of our encryption scheme in MATLAB 2018b on a compatible computer with Windows 10, 8.00 GB RAM, and an Intel(R) Core(TM) i5-6300U CPU @ 2.5 GHz. Table 10 shows the speed analysis of our proposed scheme with other encryption schemes developed using multidimensional chaotic maps. The speed analysis confirmed that our encryption scheme is unassailable and efficient. Also, the statistical test results of the baboon image are compared in Table 11 with the existing encryption scheme.

Table 10. Speed of distinct encryption schemes in seconds.

Images	Size	Proposed	[3]
Lena	256 × 256	3.222	3.350
Baboon	256 × 256	3.259	3.504
Pepper	256 × 256	3.316	3.079
Cameraman	256 × 256	3.319	3.371
House	256 × 256	3.284	3.624

Table 11. Comparison of statistical test of baboon image.

Comparison	Entropy	Chi-square	NPCR	UACI
Proposed	7.9976	219.5625	99.6426	33.4309
[16]	7.9969	229.73	99.6048	33.5547
[29]	7.9974	247.98	−	−

5. Conclusion

The novelty of this paper is to generate a unique key stream and scrambling process (blocks of plain image and pixels of plain images) using different chaotic maps, which is further utilized to propose a cryptosystem for the security of digital images during transmission from a potential invader. The aforementioned cryptosystem is employed on the standard grayscale images to see its effectiveness. The simulations and results of the experimental analysis demonstrate that the presented cryptosystem is exceptional in preserving high security and privacy requirements. We can confidently assert that the presented scheme is ideally suited to multimedia communications and online systems.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The data used to support the study are included in the paper.

References

1 Yavuz E., A novel chaotic image encryption algorithm based on content-sensitive dynamic function switching scheme, Optics & Laser Technology. (2019) 114, 224–239, https://doi.org/10.1016/j.optlastec.2019.01.043, 2-s2.0-85061245544.
10.1016/j.optlastec.2019.01.043
Web of Science® Google Scholar
2 Bashir Z., Rashid T., and Zafar S., Hyperchaotic dynamical system based image encryption scheme with time-varying delays, Pacific Science Review A:Natural Science and Engineering. (2016) 18, no. 3, 254–260, https://doi.org/10.1016/j.psra.2016.11.003.
10.1016/j.psra.2016.11.003
Google Scholar
3 Bashir Z., Wątróbski J., Rashid T., Zafar S., and Sałabun W., Chaotic dynamical state variables selection procedure based image encryption scheme, Symmetry. (2017) 9, no. 12, https://doi.org/10.3390/sym9120312, 2-s2.0-85040057738.
10.3390/sym9120312
PubMed Web of Science® Google Scholar
4 Tromer E., Osvik D. A., and Shamir A., Efficient cache attacks on AES, and countermeasures, Journal of Cryptology. (2010) 23, no. 1, 37–71, https://doi.org/10.1007/s00145-009-9049-y, 2-s2.0-74349098073.
10.1007/s00145-009-9049-y
Web of Science® Google Scholar
5 Toughi S., Fathi M. H., and Sekhavat Y. A., An image encryption scheme based on elliptic curve pseudo random and advanced encryption system, Signal Processing. (2017) 141, 217–227, https://doi.org/10.1016/j.sigpro.2017.06.010, 2-s2.0-85020844411.
10.1016/j.sigpro.2017.06.010
Web of Science® Google Scholar
6 Zhang L. Y., Liu Y., Pareschi F., Zhang Y., Wong K. W., Rovatti R., and Setti G., On the security of a class of diffusion mechanisms for image encryption, IEEE Transactions on Cybernetics. (2018) 48, no. 4, 1163–1175, https://doi.org/10.1109/tcyb.2017.2682561.
10.1109/TCYB.2017.2682561
PubMed Web of Science® Google Scholar
7 Amina S. and Mohamed F. K., An efficient and secure chaotic cipher algorithm for image content preservation, Communications in Nonlinear Science and Numerical Simulation. (2018) 60, 12–32, https://doi.org/10.1016/j.cnsns.2017.12.017, 2-s2.0-85040104442.
10.1016/j.cnsns.2017.12.017
Web of Science® Google Scholar
8 Yavuz E., A new parallel processing architecture for accelerating image encryption based on chaos, Journal of Information Security and Applications. (2021) 63, 103056, https://doi.org/10.1016/j.jisa.2021.103056.
10.1016/j.jisa.2021.103056
Web of Science® Google Scholar
9 Elmanfaloty R. A. and Abou-Bakr E., An image encryption scheme using a 1D chaotic double section skew tent map, Complexity. (2020) 2020, 18, 7647421, https://doi.org/10.1155/2020/7647421.
10.1155/2020/7647421
Web of Science® Google Scholar
10 Moysis L., Volos C., Jafari S., Munoz-Pacheco J. M., Kengne J., Rajagopal K., and Stouboulos I., Modification of the logistic map using fuzzy numbers with application to pseudorandom number generation and image encryption, Entropy. (2020) 22, no. 4, https://doi.org/10.3390/e22040474.
10.3390/e22040474
PubMed Web of Science® Google Scholar
11 Hua Z., Jin F., Xu B., and Huang H., 2D Logistic-Sine-coupling map for image encryption, Signal Processing. (2018) 149, 148–161, https://doi.org/10.1016/j.sigpro.2018.03.010, 2-s2.0-85044464984.
10.1016/j.sigpro.2018.03.010
Web of Science® Google Scholar
12 Zhu S. and Zhu C., Secure image encryption algorithm based on hyperchaos and dynamic DNA coding, Entropy. (2020) 22, no. 7, https://doi.org/10.3390/e22070772.
10.3390/e22070772
Web of Science® Google Scholar
13 Hua Z., Zhu Z., Chen Y., and Li Y., Color image encryption using orthogonal Latin squares and a new 2D chaotic system, Nonlinear Dynamics. (2021) 104, no. 4, 4505–4522, https://doi.org/10.1007/s11071-021-06472-6.
10.1007/s11071-021-06472-6
Web of Science® Google Scholar
14 Hua Z., Chen Y., Bao H., and Zhou Y., Two-dimensional parametric polynomial chaotic system, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2022) 52, no. 7, 4402–4414, https://doi.org/10.1109/tsmc.2021.3096967.
10.1109/TSMC.2021.3096967
Web of Science® Google Scholar
15 He P., Sun K., and Zhu C., A novel image encryption algorithm based on the delayed maps and permutation-confusion-diffusion architecture, Security and Communication Networks. (2021) .
10.1155/2021/6679288
Web of Science® Google Scholar
16 Idrees B., Zafar S., Rashid T., and Gao W., Image encryption algorithm using S-box and dynamic Henon bit level permutation, Multimedia Tools and Applications. (2020) 79, no. 9-10, 6135–6162, https://doi.org/10.1007/s11042-019-08282-w.
10.1007/s11042-019-08282-w
Web of Science® Google Scholar
17 Malik M. G. A., Bashir Z., Iqbal N., and Imtiaz M. A., Color image encryption algorithm based on hyper-chaos and DNA computing, IEEE Access. (2020) 8, 88093, https://doi.org/10.1109/access.2020.2990170.
10.1109/ACCESS.2020.2990170
Google Scholar
18 Malik D. S. and Shah T., Color multiple image encryption scheme based on 3Dchaotic maps, Mathematics and Computers in Simulation. (2020) 178, 646–666, https://doi.org/10.1016/j.matcom.2020.07.007.
10.1016/j.matcom.2020.07.007
Web of Science® Google Scholar
19 Hua Z., Li J., Chen Y., and Yi S., Design and application of an S-box using complete Latin square, Nonlinear Dynamics. (2021) 104, no. 1, 807–825, https://doi.org/10.1007/s11071-021-06308-3.
10.1007/s11071-021-06308-3
Web of Science® Google Scholar
20 Hua Z., Zhang K., Li Y., and Zhou Y., Visually secure image encryption using adaptive-thresholding sparsification and parallel compressive sensing, Signal Processing. (2021) 183, 107998, https://doi.org/10.1016/j.sigpro.2021.107998.
10.1016/j.sigpro.2021.107998
Web of Science® Google Scholar
21 Fang D. and Sun S., A new secure image encryption algorithm based on a 5D hyperchaotic map, PLoS One. (2020) 15, no. 11, e0242110, https://doi.org/10.1371/journal.pone.0242110.
10.1371/journal.pone.0242110
CAS PubMed Web of Science® Google Scholar
22 Wang X. and Jin C., Image encryption using game of life permutation and PWLCM chaotic system, Optics Communications. (2012) 285, no. 4, 412–417, https://doi.org/10.1016/j.optcom.2011.10.010, 2-s2.0-81355146372.
10.1016/j.optcom.2011.10.010
CAS Web of Science® Google Scholar
23 Hénon M., A two-dimensional mapping with a strange attractor, The Theory of Chaotic Attractors, 1976, 50, Springer, New York, NY, USA, 69–77.
10.1007/978-0-387-21830-4_8
Google Scholar
24 Wu X., Wang K., Wang X., Kan H., and Kurths J., Color image DNA encryption using NCA map-based CML and one-time keys, Signal Processing. (2018) 148, 272–287, https://doi.org/10.1016/j.sigpro.2018.02.028, 2-s2.0-85042721226.
10.1016/j.sigpro.2018.02.028
Web of Science® Google Scholar
25 Chen J., Zhu Z. L., Zhang L. B., Zhang Y., and Yang B. Q., Exploiting self-adaptive permutation–diffusion and DNA random encoding for secure and efficient image encryption, Signal Processing. (2018) 142, 340–353, https://doi.org/10.1016/j.sigpro.2017.07.034, 2-s2.0-85026675226.
10.1016/j.sigpro.2017.07.034
Web of Science® Google Scholar
26 Liao X., Liao X., Hahsmi M. A., and Haider R., An efficient mixed inter-intra pixels substitution at 2bits-level for image encryption technique using DNA and chaos, Optik-International Journal for Light and Electron Optics. (2018) 153, 117–134, https://doi.org/10.1016/j.ijleo.2017.09.099, 2-s2.0-85030657787.
10.1016/j.ijleo.2017.09.099
Google Scholar
27 Wang X., Wang Y., Zhu X., and Luo C., A novel chaotic algorithm for image encryption utilizing one-time pad based on pixel level and DNA level, Optics and Lasers in Engineering. (2020) 125, 105851, https://doi.org/10.1016/j.optlaseng.2019.105851.
10.1016/j.optlaseng.2019.105851
Web of Science® Google Scholar
28 Mohamed H. G., ElKamchouchi D. H., and Moussa K. H., A novel color image encryption algorithm based on hyperchaotic maps and mitochondrial DNA sequences, Entropy. (2020) 22, no. 2, https://doi.org/10.3390/e22020158.
10.3390/e22020158
Web of Science® Google Scholar
29 Niu Y., Zhou Z., and Zhang X., An image encryption approach based on chaotic maps and genetic operations, Multimedia Tools and Applications. (2020) 79, no. 35-36, 25613, https://doi.org/10.1007/s11042-020-09237-2.
10.1007/s11042-020-09237-2
Web of Science® Google Scholar
30 Wu Y., Zhou Y., Saveriades G., Agaian S., Noonan J. P., and Natarajan P., Local Shannon entropy measure with statistical tests for image randomness, Information Sciences. (2013) 222, 323–342, https://doi.org/10.1016/j.ins.2012.07.049, 2-s2.0-84870053104.
10.1016/j.ins.2012.07.049
Web of Science® Google Scholar
31 Bibi N., Farwa S., Muhammad N., Jahngir A., and Usman M., Correction: a novel encryption scheme for high-contrast image data in the Fresnelet domain, PLoS One. (2018) 13, no. 11, e0208305, https://doi.org/10.1371/journal.pone.0208305, 2-s2.0-85057180917.
10.1371/journal.pone.0208305
PubMed Web of Science® Google Scholar
32 Farwa S., Bibi N., and Muhammad N., An efficient image encryption scheme using Fresnelet transform and elliptic curve based scrambling, Multimedia Tools and Applications. (2020) 79, no. 37-38, 28225, https://doi.org/10.1007/s11042-020-09324-4.
10.1007/s11042-020-09324-4
Web of Science® Google Scholar
33 Wu Y., Noonan J. P., and Agaian S., NPCR and UACI randomness tests for image encryption, Cyber journals: multidisciplinary journals in science and technology, Journal of Selected Areas in Telecommunications (JSAT). (2011) 1, no. 2, 31–38.
Google Scholar
34 Zaman J. K. M. S. and Ghosh R., Review on fifteen statistical tests proposed by NIST, Journal of Theoretical Physics and Cryptography. (2012) 1, 18–31.
Google Scholar

Citing Literature

All articles

A Chaos-Based Image Encryption Scheme Is Proposed Using Multiple Chaotic Maps

Abstract

1. Introduction