Ion Acoustic Solitary Wave Solutions to mKdV-ZK Model in Homogeneous Magnetized Plasma
Abstract
In this exploration, we reflect on the wave transmission of three-dimensional (3D) nonlinear electron–positron magnetized plasma, counting both hot as well as cold ion. Treated equation acquiesces to nonlinear-modified KdV-Zakharov–Kuznetsov (mKdV-ZK) dynamical 3D form. The model is integrated by the φ6-model expansion scheme and invented few families of ion acoustic solitonic propagation results in term of Jacobi elliptic functions. Various shock waves, bullet like bright soliton, dark soliton, singular soliton, as well as periodic signal solutions, are formed from the Jacobi elliptic solution for different parametric constraints. Some of the solutions are illustrated graphically and analyzed width and height due to change of exist parameters in the solutions. Figures are provided to explain the wave natures and effects of nonlinear and fractional parameters are presented in the same two-dimensional (2D) plots.
1. Introduction
2. Sketch of the φ6-Model Expansion Method
-
Step 1: Let us reflect on the following general NLEE in the form given as follows:
-
Step 2: Assembling wave adaptation relation is given as follows:
-
Step 3: Assume a trial solution of Equation (4) subsists and can be written in a series as follows:
-
Step 4: An answer to Equation (6) is in the following form:
-
Step 5: According to Zayed et al. [29], it is recognized that the Jacobi elliptic function solution of Equation (8) exhibits for 0 < m < 1, otherwise it will be sinusoidal or hyperbolic function solutions for m → 0 < or m → 1. Determination of solutions of Equation (2) will be completed taking advantages of Equations (7) and (8) into Equation (5).
3. Implementation of the φ6-Model Expansion Scheme
Making use of balance principle between U″ with U3 gives N = 1. Inserting N = 1 into Equation (5)
-
Set 1:
-
Set 2:
- 1.
If ℓ0 = 1, ℓ2 = −(1 + m2), ℓ4 = m2, 0 < m < 1, then U(τ) = sn(τ, m) or U(τ) = cd(τ, m), therefore, solution is:
- 2.
If ℓ0 = 1 − m2, ℓ2 = 2m2 − 1, ℓ4 = −m2, m ∈ (0, 1), afterward U(τ) = cn(τ, m) and solution yields:
- 3.
If, ℓ0 = m2 − 1, ℓ2 = 2 − m2, ℓ4 = −1, 0 < m < 1, then U(τ) = dn(τ, m) and solution yields:
- 4.
If, ℓ0 = m2, ℓ2 = −(1 + m2), ℓ4 = 1, m ∈ (0, 1), then U(τ) = ns(τ, m) or U(τ) = dc(τ, m) and solution yields:
- 5.
If ℓ0 = −m2, ℓ2 = 2m2 − 1, ℓ4 = 1 − m2, 0 < m < 1, then U(τ) = nc(τ, m); therefore, solution is:
- 6.
If ℓ0 = −1, ℓ2 = 2 − m2, ℓ4 = −(1 − m2), m ∈ (0, 1), then U(τ) = nd(τ, m); therefore, result is:
- 7.
If, ℓ0 = 1, ℓ2 = 2 − m2, ℓ4 = 1 − m2, m ∈ (0, 1), afterward U(τ) = sc(τ, m); therefore, result is:
- 8.
If ℓ0 = 1, ℓ2 = 2m2 − 1, ℓ4 = −m2(1 − m2), m ∈ (0, 1), afterward U(τ) = sd(τ, m); therefore, solution is:
- 9.
If ℓ0 = 1 − m2, ℓ2 = 2 − m2, ℓ4 = 1, m ∈ (0, 1), afterward U(τ) = cs(τ, m); therefore, result is:
- 10.
If ℓ0 = −m2(1 − m2), ℓ2 = 2m2 − 1, ℓ4 = 1, m ∈ (0, 1), afterward U(τ) = ds(τ, m); therefore, solution is:
- 11.
If ℓ0 = 1 − m2/4, ℓ2 = 1 + m2/2, ℓ4 = 1 − m2/4, m ∈ (0, 1), afterward U(τ) = nc(τ, m) ± sc(τ, m)
- 12.
If afterward U(τ) = m cn(τ, m) ± dn(τ, m); therefore, solution is given as follows:
- 13.
If ℓ0 = 1/4, ℓ2 = 1 − 2m2/2, ℓ4 = 1/4, 0 < m < 1, then U(τ) = sn(τ, m)/1 ± cn(τ, m); therefore, solution is given as follows:
-
14. If afterward U(τ) = sn(τ, m)/cn(τ, m) ± dn(τ, m);
- 1.
If ℓ0 = 1, ℓ2 = −(1 + m2), ℓ4 = m2, m ∈ (0, 1), afterward U(τ) = sn(τ, m) or U(τ) = cd(τ, m) leads solution as:
- 2.
If, ℓ0 = 1 − m2, ℓ2 = 2m2 − 1, ℓ4 = −m2, m ∈ (0, 1) after that U(τ) = cn(τ, m), thus solution is given as follows:
- 3.
If, ℓ0 = m2 − 1, ℓ2 = 2 − m2, ℓ4 = −1, m ∈ (0, 1), after that U(τ) = dn(τ, m), leads to solution as follows:
- 4.
If, ℓ0 = m2, ℓ2 = −(1 + m2), ℓ4 = 1, m ∈ (0, 1), after that U(τ) = ns(τ, m) or U(τ) = dc(τ, m) gives:
- 5.
If, ℓ0 = −m2, ℓ2 = 2m2 − 1, ℓ4 = 1 − m2, m ∈ (0, 1), next U(τ) = nc(τ, m), leads to solution as follows:
- 6.
If ℓ0 = −1, ℓ2 = 2 − m2, ℓ4 = −(1 − m2), m ∈ (0, 1), afterward U(τ) = nd(τ, m); therefore, result is given as follows:
- 7.
If, ℓ0 = 1, ℓ2 = 2 − m2, ℓ4 = 1 − m2, m ∈ (0, 1), in that case U(τ) = sc(τ, m) leads to:
- 8.
If, ℓ0 = 1, ℓ2 = 2m2 − 1, ℓ4 = −m2(1 − m2), m ∈ (0, 1), next, U(τ) = sd(τ, m) leads to:
- 9.
If, ℓ0 = 1 − m2, ℓ2 = 2 − m2, ℓ4 = 1, m ∈ (0, 1), after that U(τ) = cs(τ, m); therefore, solution is given as follows:
- 10.
If, ℓ0 = −m2(1 − m2), ℓ2 = 2m2 − 1, ℓ4 = 1, m ∈ (0, 1), afterward U(τ) = ds(τ, m), leads to:
- 11.
If, ℓ0 = 1 − m2/4, ℓ2 = 1 + m2/2, ℓ4 = 1 − m2/4, m ∈ (0, 1), afterward U(τ) = nc(τ, m) ± sc(τ, m) or, U(τ) = cn(τ, m)/1 ± sn(τ, m), thus solution is given as follows:
- 12.
If, afterward U(τ) = m cn(τ, m) ± dn(τ, m), thus solution is given as follows:
- 13.
If, ℓ0 = 1/4, ℓ2 = 1 − 2m2/2, ℓ4 = 1/4, m ∈ (0, 1), afterward U(τ) = sn(τ, m)/1 ± cn(τ, m), thus solution is given as follows:
- 14.
If, afterward U(τ) = sn(τ, m)/cn(τ, m) ± dn(τ, m) then solution takes the form given as follows:
4. Results, Discussions, and Numerical Illustration
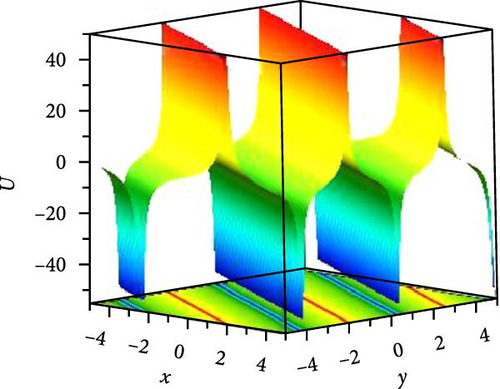
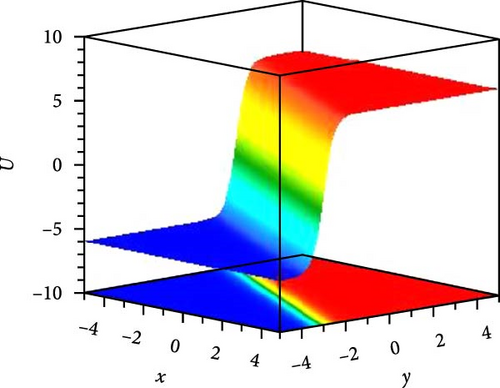
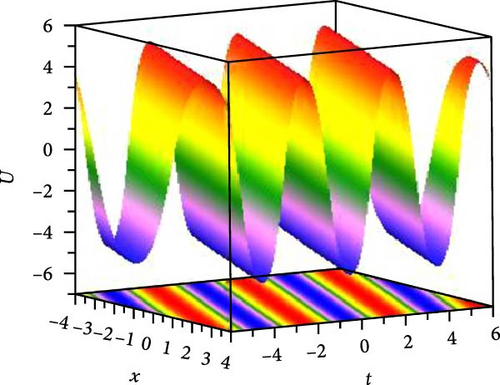
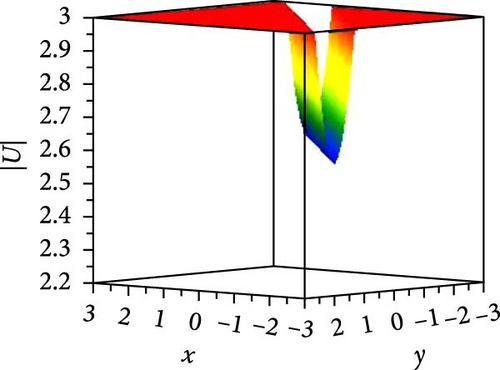
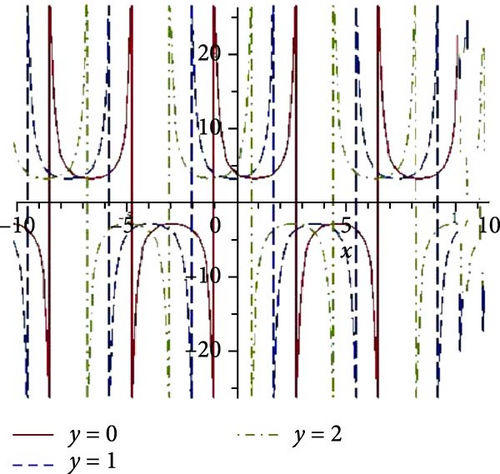
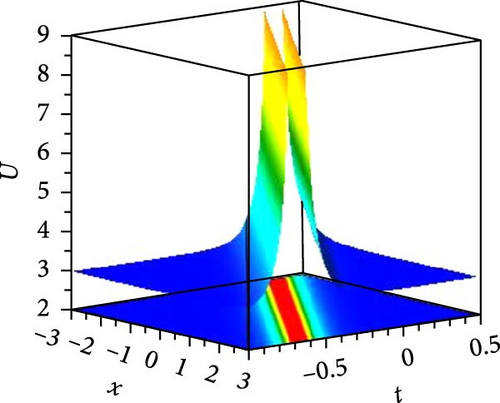
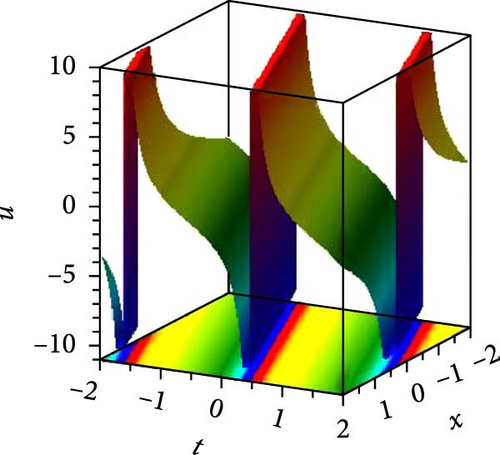
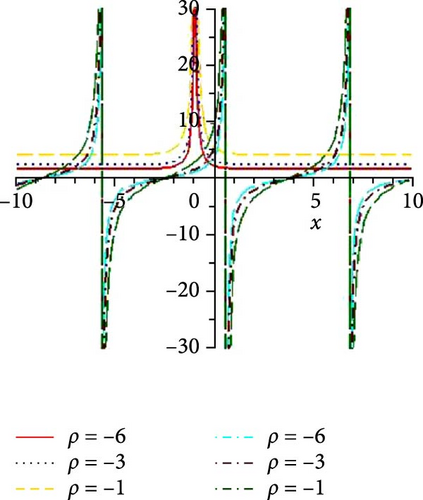
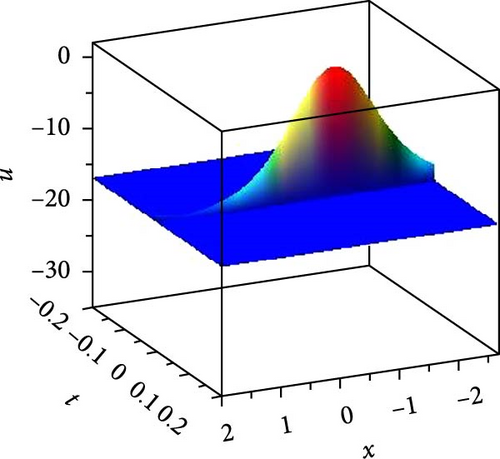
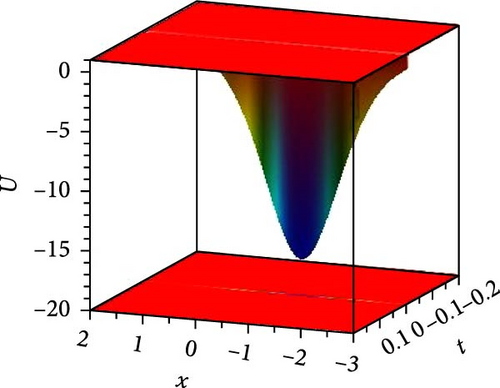
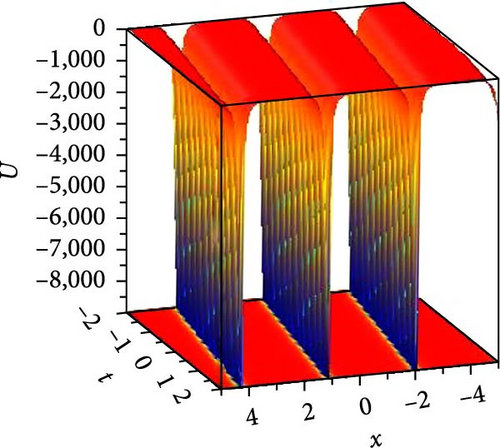
We foremost explored the influence of nonlinearity constant on soliton states and changing energy states. Such nonlinearity intensities have a noteworthy influence on the amplitude, width, and stability of solitons, even on dipole and tripole solitons. We investigated the stability of bright and dark solitons by linear stability analysis. Jacobi elliptic wave solution reduces to periodic wave and solitary wave for different parametric states. Few of the solutions are numerically illustrated as superperiodic wave by Equation (19), as shown in Figure 1(a), with g1 = 2, ρ = −1, δ1 = δ3 = 1, δ2 = 2, t = 0, z = 1 as m = 0.9, r2 = 1.19, it exhibits shock wave, as shown in Figure 1(b), due to change of m = 1, r2 = −2 and except unity of m (with m = 0.8, r2 = −1.64) the solution expressed periodic wave, as shown in Figure 1(c). The periodic wave with m = 0.7, r2 = 1.51, g1 = 2, ρ = −2, δ1 = δ3 = δ2 = 1, t = 0, z = 1 of the solution, as shown in Equation (27), depicted in 3D, as shown in Figure 2(a), and different changing of nonlinear intensity, as shown in Figure 2(c). A single dark soliton is achieved from the same Equation (27) just taking m = 1 retaining the rest parametric values are same, as shown in Figure 2(b). Singular bright peak soliton comes via Equation (31) as m = 1, r2 = ρ = −2, g1 = δ2 = 2, δ1 = δ3 = 1, y = 0, z = 1, as shown in Figure 3(a). Singular periodic wave solutions are visualized via Equation (44) for r2 = 0.5, ρ = −2, g1 = δ2 = 2, δ1 = δ3 = 1, y = 0, z = 1, as shown in Figure 3(b) and its 2D plots for varying nonlinearity are presented in Figure 3(c). Bright soliton visualized in Figure 4(a) via Equation (52) with r2 = −2, ρ = δ2 = r0 = 2, r4 = 3g0 = δ1 = δ3 = 1, y = 0, z = 1; dark soliton visualized in Figure 4(b) via Equation (55) with r2 = −2, ρ = δ2 = r0 = 2, r4 = 3g0 = δ1 = δ3 = 1, y = 0, z = 1, and beside this periodic wave visualized in Equation (64) with r2 = −2, δ2 = r0 = 2, ρ = r4 = g0 = δ1 = δ3 = 1, y = 0, z = 1. Rest of the other solutions are similar to the illustrated solutions, with and without singularities are explained in this research.

5. Conclusions
This paper had achieved ion-acoustic soliton solutions to mKdV-ZK model in homogeneous magnetized plasma media via the φ6-model expansion scheme. We successfully utilized and invented novel families of ion-acoustic solitons propagation due to Jacobi elliptic forms. Various shock waves, bullet type bright, dark, bright-dark solitons, as well as periodic wave solutions are formed starting the Jacobi elliptic results on different parametric constraints. Some obtained results are numerically illustrated in Figures 1–4 and analyzed the effect of nonlinearity on the change of height and weight of the wave form in 2D, 3D plots. The activities and the transmission of such solutions are discussed in a rating index waveguide for selecting suitable parameters. To best our knowledge, the achieved dynamical natures, in contrast with other’s results in literature, are innovative in dissimilar structures. Such critical behaviors can be crucial to recognize attribute of the mKdV-ZK model those are used to explain various phenomena in nonlinear sciences.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
Investigation, methodology, and writing draft, M.R. Pervin; conceptualization, software, and valdation, H.O. Roshid; modifications, corrections, and simulation, P. Dey; supervision and finalization, S. S. Shanta; supervision, idea maker, modification, and checking draft, S. Kumer. All authors have read and agreed to the published version of the manuscript.
Open Research
Data Availability
Supported data are included inside this article.




