In this paper, an improved force characteristic curve fitting memetic algorithm of urban rail vehicles is proposed for establishing precise train operation models. In order to improve the memetic algorithm global convergence, three strategies are adopted. In the improved memetic algorithm framework, an improved moth-flame optimization is used in global search; an improved simulated annealing is applied in local search; a new learning mechanism incorporated into reverse learning is adopted. Experimental simulation results under real-time data monitoring system show that the improved memetic algorithm proposed in this paper can increase the optimization performance effectively so more perfect force characteristic curve fitting effort can be obtained, and the calculated average force error and max running distance error can be reduced effectively. Moreover, the above relative results indicate that the train energy consumption model using the improved force characteristic curve fitting algorithm can obtain more precise energy consumption. Obviously, the improved force characteristic curve fitting algorithm can effectively improve the curve fitting precision.

1. Introduction

The accuracy of force characteristic curve fitting has a great influence on the force characteristic analysis, the train operation models establishment, and the train operation process simulation result [1].

The train operation models are extremely important for the train operation process, in the safety, comfort, and economy of the urban rail transit operation. Various improved methods and algorithms have been proposed in recent works about the train key parameters identification and calculation and the train operation model establishment. In the field of modern urban rail transit, operation quality and cost are two key factors, which are closely related to the accuracy of the vehicle operation models. A method for calculating traction characteristics of traction motor is proposed [2]. The inrush current identification system is established, the inrush current identification algorithm is realized, and it is applied to the digital signal processing of the traction transformer [3]. A new method to identify the train key design variables against the running performance indicators based on the sensitivity analysis is proposed, which is in turn based itself on simulation-oriented surrogate models [4]. A new system for moving train loads and parameter identification is proposed. In this system, time history displacements of measurement stations on the bridge are simultaneously measured by using a displacement image monitoring system when the model train moves across the bridge [5]. A new numerical method for moving train parameters identification is proposed. This method is adopted to simulate the experimental system and to investigate the effect of the system on the identification of the moving train parameters [6]. Aiming at estimating the vehicle suspension parameters, the estimation of the parameter values is performed by minimizing a misfit function describing the distance between the measured and the simulated vehicle response, and an optimization algorithm is applied in order to find the best parameter estimation [7]. It is obvious that studies about train parameters calculation and train operation model establishment can be found in the existing literatures. However, the research on force characteristic curve fitting for urban rail vehicles is absent.

Because there are many uncertain factors and complex relationships in rail transit vehicles, it is easy to fall into local convergence only using traditional optimization algorithms (genetic algorithm, particle swarm optimization algorithm, fruit fly algorithm, etc.). Aiming at the problem that the traditional automatic optimization algorithm is easy to fall into local convergence, many literatures have proposed various improved traditional optimization algorithms. A new hybrid annual power load-forecasting model based on the least-square support vector machine (LSSVM) and moth-flame optimization (MFO) algorithm was proposed in [8]. A moth-flame optimization (MFO) technique was investigated for obtaining an accurate simulation of the nonuniform electric field represented by needle-to-plane gap configuration in [9]. A multiobjective decomposition-based moth-flame optimization (MOMFO/D) algorithm was proposed in [10] that decomposes the objectives into multiple single objectives which are optimized simultaneously. The ability of two nature-inspired algorithms namely the whale optimization algorithm (WOA) and moth-flame optimization (MFO) was examined in [11] to determine the optimal multilevel thresholding for image segmentation. An improved quantum evolutionary algorithm (QEA) based on the niche coevolution strategy and enhanced particle swarm optimization (PSO), namely IPOQEA, was designed [12]. A novel learning scheme for the kernel extreme learning machine (KELM) based on the chaotic moth-flame optimization (CMFO) strategy was proposed in [13]. A hybrid moth-flame optimization algorithm (HMFO) was proposed in [14], and the convergence ability of the HMFO algorithm was analyzed on the basis of test functions. To improve the diversity of flames and the searching ability of moths, an improved moth-flame optimization (IMFO) algorithm was proposed in [15]. A novel memetic algorithm (MA) based on the integer-coded genetic algorithm and local search was proposed in [16]. A hybrid learning algorithm combining genetic algorithm (GA) with gradient descent (GD), called HGAGD, was proposed in [17]. A novel memetic algorithm was proposed in [18], which is explorative particle swarm optimization (ePSO), combined with mesh adaptive direct search, and it was applied to the design of a permanent magnet synchronous machine (PMSM). A memetic algorithm was proposed in [19] for solving the traveling salesman problem, which is based on the combination of an evolutionary algorithm and local search (2-opt). The above research can improve the optimization performance of traditional optimization algorithms. However, force characteristic curve fitting optimization of urban rail vehicles based on improved memetic algorithm has not been considered.

In order to improve the force characteristic curve fitting accuracy of the urban rail vehicle force characteristics, so as to establish reasonably accurate train operation models, based on the urban rail vehicle running force characteristic curve optimization model and the actual collected operational data, an improved memetic algorithm is proposed for force characteristic curve fitting in this paper. In order to verify the effectiveness of the proposed algorithm, this paper uses real-time data monitoring device to collect the actual data (real-time instantaneous velocity and force) of the Lanzhou Line No.1 subway vehicle. Several different optimization algorithms are used in the test platform for comparative testing. The results show that the proposed memetic algorithm has excellent optimization performance.

The main novelty and contributions of this paper are as follows:

(1)
The improvement of the memetic algorithm: to solve the problem of falling into local convergence easily of traditional algorithms, this paper proposes a novel improved memetic algorithm with powerful optimization ability. The reconstructed optimal frame can effectively improve the optimization capability, an improved moth-flame optimization is incorporated into the global search; an improved simulated annealing is applied in the local search; and an improved learning mechanism incorporated into reverse learning is adopted for increasing evolution efficiency. The experimental simulation results show that compared with the traditional algorithms, the improved memetic algorithm can effectively improve the optimization performance
(2)
The improvement of force characteristic curve fitting and train operation model establishment: aiming at the problems that the force characteristic curve fitting and train operation model establishing are not precise enough; this paper proposes to use improved force characteristic curve fitting algorithm for obtaining more appropriate force characteristic curve. The experimental simulation results show that compared with the traditional force characteristic curve fitting algorithms, the precision for force characteristic curve fitting and train operation model establishment could be improved to a certain extent

The paper is organized as follows. Section 2 introduces the mathematical model for force characteristic curve fitting. Section 3 illustrates the improved memetic algorithm. Section 4 provides the experimental simulation results to illustrate the proposed method. Section 5 concludes this article.

2. Mathematical Model of Force Characteristic Curve Fitting

2.1. Force Characteristic of Urban Rail Vehicles

The operation process of urban rail vehicles is affected by its own force and environmental resistance in real time. In general, the force characteristic curves of the train are divided into four design regions: braking start-up (0 ≤ v < V_BS), constant torque (0 ≤ v < V_TC, V_BS ≤ v < V_BC), constant power (V_TC ≤ v < V_TR, V_BC ≤ v < V_BR), and power reduction (V_TR ≤ v < V_max, V_BR ≤ v < V_max). Due to the difference in factory motor design, with the increase of train running time increases, the aging degree of the traction motor and the wear degree of the wheel and track, the actual traction and braking force characteristics, and design values are somewhat different.

(1)

(2)

where F^Ta(v) and F^Ba(v) represent the actual force (traction and braking) of the instantaneous velocity v, F^Ta(v) ≈ F^Ts(v), F^Ba(v) ≈ F^Bs(v); F^Ts(v) and F^Bs(v) represent the designed force (traction and braking) of the instantaneous velocity v;

and

represent the designed force (traction or braking) maximum value;

and

represent the designed power and (traction or braking) maximum value; V_BS, V_TC, V_BC, V_TR, and V_BR, respectively, represent the corresponding inflexion velocities of these four design regions; and V_max represents the maximum train velocity.

2.2. Optimization Models for Force Characteristic Curve Fitting

Combining with the train operation process, the optimization model for force curve characteristic fitting of urban rail vehicles is described as follows:

(3)

where F^′ represents the actual tractive force, F_r represents the corresponding value of the force characteristic fitting curve, F represents the designed tractive force, j represents the discrete value of the instantaneous velocity v, which is the integer of v, n = fit(V_max), F_Ferr indicates the average error between force characteristic fitting curve and actual force characteristic curve, s represents the actual running position, t represents the actual running time, w_s(v) represents the basic resistance of the vehicle on the straight track, which is determined by the instantaneous speed and the position, F_s indicates the cumulative running distance of the whole process of running on the straight track, and F_Serr represents cumulative running distance error between the force characteristic fitting curve and actual force characteristic curve.

The above optimization model can be solved by the conventional systematic identification methods such as the le4ast square method, but the solution accuracy is not ideal. For the optimization model which is not easy to be solved by conventional systematic identification methods, it is easy to obtain more satisfying optimization results by using intelligent algorithms such as the genetic algorithm (GA), particle swarm optimization (PSO), and ant colony optimization (ACO). Still, these intelligent optimization algorithms have poor global searchability in the last stage of iteration, which makes the improvement of the optimization solution accuracy lower than expected [20].

3. Improved Memetic Algorithm for Force Characteristic Curve Fitting

3.1. Synopsis of Memetic Algorithm

The memetic algorithm that evolved from the simulation of memetic evolution is proposed by Pablo Moscato in 1989. It is a hybrid optimization algorithm based on global search and local heuristic search. The memetic algorithm is an algorithmic framework similar to GA [21].

3.2. Segmented Fitting Function of Force Characteristic Curve

The actual force characteristic curve is relatively smooth, and tendencies in different regions are relatively fixed. Therefore, the univariate equation of the n-degree is used in this paper for segment fitting. The independent variable is velocity v, and the dependent variable is the corresponding value of the force characteristic fitting curve F_r. The specific segmented fitting function is as follows:

(4)

where V^k represents the kth characteristic region,

is the polynomial coefficient of an univariate equation with n-degree,

is the inflexion point velocity of the kth characteristic region, and

and

are decision variables.

This fitting method is easy to obtain a force characteristic fitting curve close to the actual curve. Meanwhile, there are no exponential function, logarithmic function, and other complex functions.

3.3. Improved MFO for Global Search

The moth-flame optimization (MFO) is a new group intelligent optimization algorithm proposed by Mirjalili in 2015. It is a bionic intelligent optimization algorithm used to simulate the motion behavior of moths flying on a near-flame spiral curve [22]. Although MFO has perfect optimized performance, since the MFO always makes all moths rotate around the flame, this single optimization model tends to fall into local convergence easily. So, an improved MFO algorithm is proposed in this paper, which is a hybrid optimization algorithm incorporated into the particle swarm optimization. The calculation steps of the specific hybrid algorithm are as follows:

Step 1: initialize artificial moth population M_n×D, which is a matrix of n rows and D columns, n represents the number of artificial moths, and D represents the dimension of artificial moths. The specific matrix is as follows:

(5)

Step 2: obtain the individual extremum of each moth and the global extremum of the current moth population

Step 3: the updating rules of particle swarm optimization (PSO) are used to update all moths in the population. The specific updating formula is as follows:

(6)

(7)

where w is the inertia weight coefficient, which is used to balance the degree of global search and local search, c₁ and c₂ are learning factors, which are used to balance the degree of particles learned from self-historical experience and population optimization achievement, rand is the random number of [0, 1],

and

represent the velocity and position updated of the imth particle, dth dimension, and lth iteration,

and

represent the velocity and position original of the imth particle, dth dimension, and lth iteration,

represents the optimal position of the imth particle and dth dimension, and gbest^d represents the global optimal position of the dth dimension

Step 4: the current flame matrix F_{f_n×D} is obtained from the historical and current states of the artificial moth population M_n×D, and F is a matrix of f_D rows and D columns. The specific matrix F is as follows:

(8)

Step 5: the artificial moth moves in the search space. Because of its own phototaxis, it will perceive the flame F_j that is closest to itself in the flame group and move toward to F_j following the logarithmic spiral. This bionic behavior simulation is called capture flame. The specific updating formula is as follows:

(9)

(10)

where M′_im represents the moth state of the imth particle after capturing flame simulation, M_im represents the original moth state of the imth, F_jm represents the jmth flame which is closest to moth M_im, D_im represents the distance between M_im and F_jm, b is a constant relating to the logarithmic spiral morphology (the value is 1), and t is a random number, t ∈ [−1, 1]; the closer t is to 1, and the closer M_im is to F_jm

Step 6: in the iteration process, the useless flame will be thrown away. The number of flames f_D will gradually decrease to 1. The specific formula of discarding the flames is as follows:

(11)

where f_n_max represents the maximum number of flames, T represents the maximum number of iterations, round(X) represents the rounded value of the number X, and l represents the index of the current iteration

Step 7: if the index of the current iteration l is equal to the maximum number of iterations T, the iteration is over; otherwise, Steps 2–7 are executed repeatedly.

3.4. Improved SA for Local Search

Simulated annealing (SA) was first applied to the field of combinatorial optimization by Kirk-Patrick et al. The principle of the simulated annealing algorithm is based on the cooling process of the metal. During this cooling simulation process, new solutions are continuously generated and accepted according to the Metrolips standard, and a number of some better optimal solutions can be obtained. SA is a greedy algorithm with strong local searchability that is often used in the local search [23]. In order to increase the speed for generating new solutions, this paper gives the following improved strategy using the univariate equation of the n-degree. The steps of improved simulated annealing for local searching are as follows:

Step 1: initialize initial temperature T₀, termination temperature T_end, and cooling coefficient α. Make the current temperature T_c = T₀ and the current iteration index isa = 1

Step 2: the current optimal moth individual obtained by IMFO is selected as the initial solution X₀

Step 3: partial parameters in the decision variables and of X_isa−1 remained, and the other parameters that are not retained in the decision variables are replaced by a slightly different value. This newly generated solution is called the pending solution (recorded as X_p)

Step 4: according to the above segmented fitting function, ((9)) used the univariate equation of the n-degree, substituting multiple sets of actual speed and force values into the left and right sides of the equation. If it can be guaranteed to accept the difference (less than the threshold given), execute from Step 5; otherwise, execute from Step 6.

Step 5: determine whether to accept the solution X_p according to the Metrolips guidelines. According to the above mathematical model described in formula (3), the fitness function value fit(X_p) of the solution X_p is calculated. If the following formula is satisfied, the latter is replaced by the former X_isa−1 = X_p.

(12)

where exp(X) represents an exponential function based on natural constant e ≈ 2.718

Step 6: make T_isa = T_isa−1, T_c = T_c × α, and isa = isa + 1. If the current temperature T_c < T_end, the iteration is over; otherwise, Steps 2–6 are executed repeatedly.

3.5. Improvement of the Learning Mechanism for Memetic Algorithm

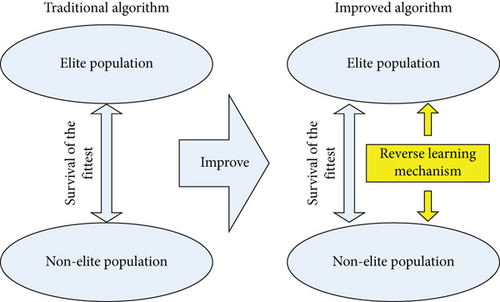
The memetic algorithm is an optimization algorithm based on the “competition mechanism” and memetic evolution. In the long-term evolution process, the elite group has accumulated its own advantages, and a certain degree of domination is formed. At the end of the iteration, due to the limitations of the evolutionary environment and initial population, it is difficult to evolve continually. The reason is that it is difficult for nonelite individuals to enter the elite group, and it is difficult for the elite groups to evolve further. This limitation makes the memetic algorithm easy to fall into local convergence. In order to improve the optimization performance, a new learning mechanism incorporated into reverse learning is proposed for the memetic algorithm in this paper, and the improved memetic algorithm is denoted as IMFO. The specific schematic diagram and flow chart are shown in Figures 1 and 2.

Details are in the caption following the image — Open in figure viewer PowerPoint

The reverse learning mechanism is capable of generating a certain number of solutions that are far from the local optimum. If the memetic algorithm falls into the local convergence, these solutions can make the population move away from the local region and expand the search scope to promote global convergence performance. In the calculation process of iteration, when the individual update process ends, IMA will generate a random number P_r. If P_r < P_l (P_l represents the probability of reverse learning), then the individual will be learned in reverse. The specific reverse learning formula is as follows:

(13)

where a_id and b_id represent the minimum and maximum values on the boundary of the idth dimension, β ∈ [0, 1] is the generalization coefficient, which can avoid the individual to excessive escape, and

and x_id represent the reverse learning and original solutions of the idth dimension.

4. The Experimental Simulation

4.1. Real-Time Data Monitoring Device

The real-time data monitoring device is an indispensable crucial component of ATO control systems, which is composed of speed sensors, torque meter, displacement pickup, slide and slip detection installation, and speed analyzer. The schematic diagram of the real-time data monitoring device is shown in Figure 3.

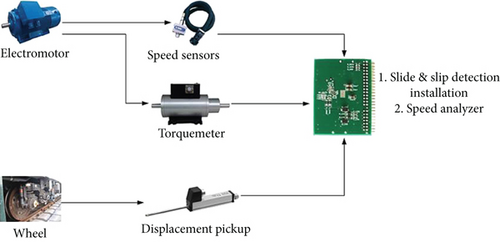
In Figure 3, the speed sensors, torquemeter, and displacement pickup are data acquisition devices for collecting real-time motor speed, motor torque, and physical displacement; wheels and motors are monitored objects; slide and slip detection installation is the computing equipment for calculating the severity degree of train idling and taxiing; speed analyzer is the core equipment used to obtain the precision instantaneous velocity based on analyzing and processing the acquired real-time data.

To obtain real-time velocity accurately, a new type of networked intelligent digital torque sensor (model No. JN338) is adopted. The specific physical diagram of networked intelligent digital torque sensor is shown in Figure 4.

In Figure 4, the acquisition equipment is a torque sensor of model No. JN338, which contains the actual functions of the two main components (speed sensors and torquemeter) in Figure 4; the fixed bracket is made of iron and has two functions of fixing and preventing jitter; the power source supplies electricity to torque sensor of model No. JN338; the communication module transmits the real-time value of motor speed and torque using the 485 communication protocol.

4.2. Force Characteristic Curve Fitting Experiment Simulation

The urban rail vehicle velocity monitoring device is used for collecting relative data sets that fit the experiment simulation required in AW3 load of the Lanzhou rail transit line number 1, including the force characteristic curves and its tracking control running distance curves on the straight track. The specific characteristics curves are shown in Figures 5 and 6.

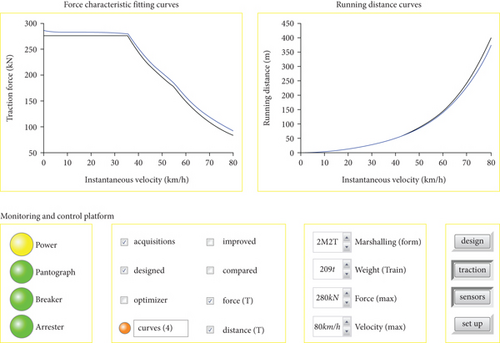
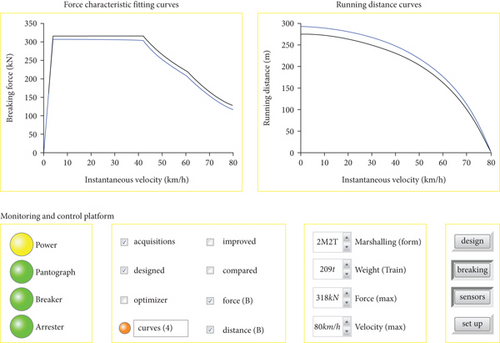
As can be seen from Figures 5 and 6, the urban rail vehicle velocity monitoring device is in a normal working state, and some significant parameters are displayed at the “Monitoring and Control Platform”; 8 curves about force characteristics and its tracking control running distance on the straight track are displayed at the display area. Among the above data sets, the traction force characteristic curves have changed from static to maximum velocity, and the braking force characteristics are the opposite. Since the actual force characteristic curves are different from their expected design, the running distance results also have corresponding differences. The actual force characteristic curves are collected by dozens of times of actual sampled and complex postprocessing (massive data analysis and error data filtering), to avoid the imprecision caused by random sampling. Some facts can be seen in Figures 5 and 6. The actual traction capacity of the above train is slightly higher than the initial design standard, because it is hoped that the traction performance of the train has a certain margin in special circumstances (e.g., in rainy weather; ATO is easy to tend to slip.). The traction motors with slightly stronger traction ability for ensuring that the train has sufficient traction in any conditions were manufactured by traction motor manufacturer. Due to long running time, the actual braking capacity of the above train is slightly lower than the initial design criteria. The abrasiveness of the wheel rim is slightly more serious and affects the braking performance.

The least-square method (LSM) [24], genetic algorithm (GA) [25], traditional memetic algorithm (MA) [26], and improved memetic algorithm proposed in this paper (IMA) are used to obtain the force characteristic fitting curves and related results based on above collected actual data sets. The global search algorithm of the traditional memetic genetic algorithm is a genetic algorithm, and the simulated annealing algorithm is used in the local search. The essential parameters of SA are set as follows: the initial temperature is 400°C, the cooling coefficient is 0.8, and the termination temperature is °C; the essential parameters of GA are set as follows: the number of individuals is 20, the cross-over probability is 85%, the mutation probability is 4%, and the maximum number of iterations is 300; the essential parameters of reverse learning are set as follows: the reverse learning rate is 20%; the essential parameters of MFO are set as follows: moth number is 20, the number of flames is 10, the constant of logarithmic spiral morphology is 1, and the maximum number of iterations is 300; the essential parameters of PSO are set as follows: the inertia weight coefficient is 0.9, and the learning factors are 0.1.

The fitting experiment simulation is based on the real-time data monitoring device. The DSP programming environment is adopted, and the core chip of the system is “TMS320F28335,” the monitoring software revision is “VS2015,” the monitoring computer processor is “Core i7-7700K @ 4.2 GHZ,” and the core chip programming software revision is “CCS5.5.” The specific corresponding simulation results of the force characteristic curve fitting are as follows. The specific characteristics curves fitted by various algorithms are shown in Figures 7 and 8.

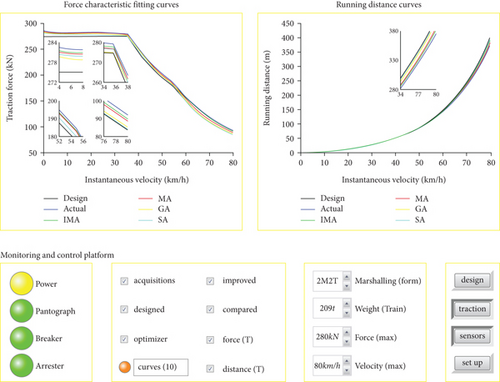
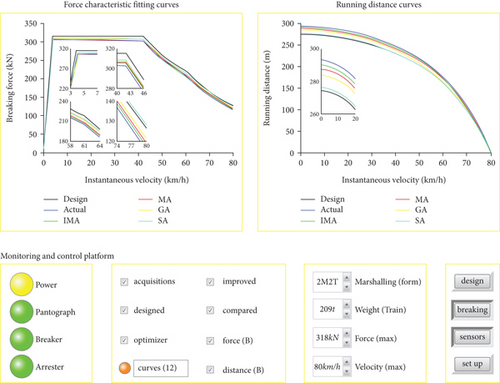
As can be seen from Figures 7 and 8, both the urban rail vehicle velocity monitoring device and the force characteristic curve fitting (FCF) optimizer are in a normal working state concurrently. IMA and the other three comparison algorithms are used in fitting experiment simulation, and the 24 curves about force characteristic and its tracking control running distance on the straight track fitted by various algorithms are displayed at the display area. As can be seen from the curves fitted in Figures 7 and 8, the fitting curves obtained by IMA are closer to the actual than other fitting optimization algorithms used for comparison. This indicates that the IMA has a more powerful optimization ability in force characteristic curve fitting.

In this paper, the force characteristic fitting curves are segmented by the univariate equation of the 4-degree. The average force error and max running distance error calculated by using various algorithms are shown in Table 1. The univariate equation coefficients of the 4-degree of the traction and braking force characteristic fitting curves are shown in Tables 2 and 3.

1. The average force error and max running distance error calculated by various algorithms.

Algorithm	Traction force error (kN)	Traction distance error (m)	Braking force error (kN)	Braking distance error (m)
LSM	3.485	38.171	3.144	16.730
GA	2.872	29.510	2.747	9.255
MA	1.970	13.176	1.507	5.493
IMA	0.928	7.857	0.856	3.235

2. The coefficients

of the traction subsection fitting polynomials calculated by various algorithms.

Algorithm	V¹ = {0, V_TC}	V² = {V_TC, V_TR}	V³ = {V_TR, V_max}
LSM	3.5271 × 10⁻⁵ −3.0253 × 10⁻³ 0.0817 -0.8229 282.4155	5.5697 × 10⁻⁵ -0.0122 1.0612 -46.3520 1.0422 × 10³	7.9669 × 10⁻⁶ −3.2640 × 10⁻³ 0.5183 -38.7073 1.2116 × 10³
GA	4.3785 × 10⁻⁵ −3.7556 × 10⁻³ 0.1014 -1.0215 282.8744	7.4036 × 10⁻⁵ -0.0157 1.3108 -54.1595 1.1321 × 10³	1.0935 × 10⁻⁵ −4.2540 × 10⁻³ 0.6408 -45.3699 1.3442 × 10³
MA	4.8650 × 10⁻⁵ −4.1729 × 10⁻³ 0.1126 -1.1350 280.2977	1.0030 × 10⁻⁴ -0.0205 1.6312 -63.1913 1.2189 × 10³	1.6398 × 10⁻⁵ −6.1137 × 10⁻³ 0.8762 -58.4875 1.6107 × 10³
IMA	3.6488 × 10⁻⁵ −3.1297 × 10⁻³ 0.0845 -0.8513 279.4334	1.3356 × 10⁻⁴ -0.0277 2.2089 -84.2509 1.5057 × 10³	1.5110 × 10⁻⁵ −5.6741 × 10⁻³ 0.8204 -55.3683 1.5436 × 10³

3. The coefficients

of the braking subsection fitting polynomials calculated by various algorithms.

Algorithm	V² = {V_BS, V_BC}	V³ = {V_BC, V_BR}	V⁴ = {V_TR, V_max}
LSM	3.6488 × 10⁻⁵ −3.1297 × 10⁻³ 0.0845 0.8513 313.8288	3.0204 × 10⁻⁵ −8.1126 × 10⁻³ 0.8666 -46.0670 1.2225 × 10³	−2.5448 × 10⁻⁶ −3.7391 × 10⁻³ 0.0635 -15.3210 860.0670
GA	2.1893 × 10⁻⁵ −1.8779 × 10⁻³ 0.0507 0.5108 310.0579	3.1061 × 10⁻⁵ −8.2181 × 10⁻³ 0.8642 -45.5030 1.2058 × 10³	7.8287 × 10⁻⁶ −3.4193 × 10⁻³ 0.5798 -46.3179 1.5458 × 10³
MA	2.0676 × 10⁻⁵ −1.7735 × 10⁻³ 0.0479 0. 4824 308.9764	2.3087 × 10⁻⁶ −6.6897 × 10⁻³ 0.7669 -43.4305 1.2012 × 10³	−3.9005 × 10⁻⁶ −1.9995 × 10⁻³ 0.3890 -35.0118 1.2948 × 10³
IMA	2.3109 × 10⁻⁵ −1.9821 × 10⁻³ 0.0535 0.5391 308.6534	2.0429 × 10⁻⁶ −6.1801 × 10⁻³ 0.7344 -42.7397 1.1994 × 10³	−3.7057 × 10⁻⁶ −1.9293 × 10⁻³ 0.3796 -34.4598 1.2814 × 10³

As can be seen from Table 1, compared with other algorithms, the switching velocity and its corresponding force and running distance obtained by IMA are closer to the actual situation. The improvement effect of the error between fitting curves and actual curves is more significant by IMA. The average force error and max running distance error are smaller than 1 kN and 10 m, respectively. It can indicate that IMA has better fitting performance than traditional improved algorithms. In Tables 2 and 3, the coefficients of the subsection fitting polynomials obtained by a certain algorithm are given in corresponding cells sequentially. A specific example is explained as follows. The first cell of Table 1 shows the fitting relationship between the traction force and velocity in the constant torque region, and the specific fitting polynomial is F_r(v) = 3.5271 × 10⁻⁵ × v⁴ − 3.0253 × 10⁻³ × v³ + 0.0817 × v² − 0.8229 × v + 282.4155.

4.3. Train Energy Consumption Calculation of Experiment Simulation

Compared with the improving fitting effort of force characteristic curve fitting algorithm, improving the precision of the actual calculation effect for the train operation model is more practical. The train energy consumption is a vital performance index for the train operation process. To further verify the effectiveness of the proposed algorithm, the train energy consumption calculation of the experiment simulation is chosen.

The train energy consumption is expressed as the energy consumed by overcoming resistance during the whole process, and the specific calculation formula is as follows.

(14)

where K_E is the energy consumption, a_i is the acceleration of the ith condition, s_i is the position of the ith condition, and R_i is the resistance of the ith condition.

Combined with Newton’s second law, the specific acceleration calculation formula of the ith condition based on the force analysis for train operation process is as follows:

(15)

where v_i is the velocity of the ith condition, R(v(i), s(i)) is resistance calculation function about velocity and position, M is the train mass, M = (1 + r_m)M_T, r_m is the rotating mass factor, and M_T is the weight of the train.

The practical train energy consumption calculation of the experiment simulation example which has an inquiry value should be chosen. The station area between Dongfanghong Square and Lanzhou University of Lanzhou Line No.1 subway is chosen as the experiment simulation object. Lanzhou rail transit line number 1 is a significant urban rail transit line extending from Chen Guanying to Donggang Station, which has 20 stations, which started the official operation on June 23, 2019. The running distance of the above station area between two stations is 1.63 km, with a long downhill near Lanzhou University, which has the characteristics of a great stream of people in daily operation, moderate running distance, and a certain extent of complexity.

The train operation process scenario in the night period (20:00-23:00) is chosen for the experiment simulation object. The slope and velocity limit of all position points for the running line were known, and the target velocity curve has been optimized by the optimization algorithm of the automatic train operation (ATO) optimizer. The one-time whole running tracking control velocity and force data in nighttime were collected by a real-time data monitoring device. The specific velocity and slope curves for the station area between Dongfanghong Square and Lanzhou University in the night period can be drawn and are shown in Figure 9. The main parameters of the above train operation process scenario for the train energy consumption calculation of the experiment simulation are shown in Table 4.

4. The main parameters of the train operation process scenario for the train energy consumption calculation of the experiment simulation.

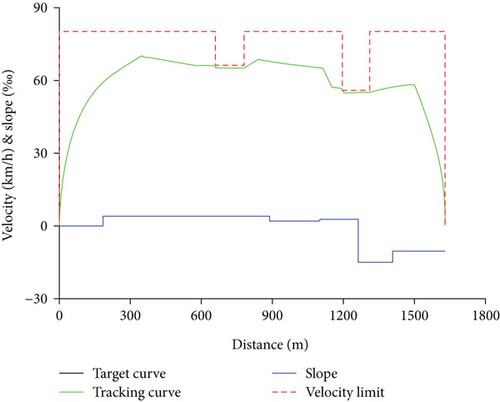
Maximum running speed (km/h)	Prospective running time (s)	Maximum allowable parking error (m)	Maximum allowable punctual error (s)
80	110	±0.2	±0.4

The train energy consumption for prospective and practical tracking control are 65331 and 68470 kJ, respectively. The train energy consumption model using LSM [25], GA [26], MA [27], and IMA is used to calculate the train energy consumption for the whole train operation process, respectively. The specific train energy consumption calculation of the experiment simulation result obtained by each algorithm is shown in Table 5.

5. The train energy consumption calculation of the experiment simulation result by various algorithms.

Algorithm	Prospective energy consumption (kJ)	Practical energy consumption (kJ)	Prospective error rate	Practical error rate
LSM	65257	68338	1.135 × 10⁻³	1.924 × 10⁻³
GA	65275	68365	8.590 × 10⁻⁴	1.537 × 10⁻³
MA	65312	68433	2.976 × 10⁻⁴	5.359 × 10⁻⁴
IMA	65328	68464	4.462 × 10⁻⁵	8.140 × 10⁻⁵

As can be seen from Table 1, compared with other algorithms for contrast, the train energy consumption obtained by the train energy consumption model using IMA is closer to the actual situation; the improvement effect of calculation error for the train energy consumption model is more significant by IMA. The calculation error rates are smaller than 10⁻⁴, respectively.

5. Conclusions

Based on the force characteristics of urban rail vehicles and other related conditions, an improved force characteristic curve fitting algorithm is proposed. Aiming at the problem of falling into local convergence easily of traditional algorithms, an improved memetic algorithm with powerful global optimization performance is utilized using three strategies. Firstly, combining moth-flame optimization and particle swarm optimization, it established a hybrid algorithm to facilitate global search. In order to improve the performance of the local search optimization algorithm, an improved simulated annealing is applied in local search. Meanwhile, an improved learning mechanism incorporated into reverse learning is adopted for overcoming the shortcoming of evolution difficulty.

To verify the effectiveness of the proposed improved force characteristic curve fitting algorithm, experimental simulations based on a real-time data monitoring system were carried out. The results indicate that, compared with the algorithms contrasted, the proposed algorithm has better performance and the relative fitting curves are closest to the actual curves. In addition, the train energy consumption model using the proposed algorithm can be further improved to achieve more accurate results. In summary, the proposed algorithm can greatly improve inaccurate defects of calculation results.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work is supported by the National Nature Science Foundation of China (60574018), National Science Fund cultivation project of the Inner Mongolia University for Nationalities (NMDGP17101), and Inner Mongolia University for Nationalities doctoral research initiation Fund Project (BS416).

Open Research

Data Availability

No data were used to support this study.

References

1 Huang Y., Yang L., Tang T., Cao F., and Gao Z., Saving energy and improving service quality: bicriteria train scheduling in urban rail transit systems, IEEE Transactions on Intelligent Transportation Systems. (2016) 17, no. 12, 3364–3379, https://doi.org/10.1109/TITS.2016.2549282, 2-s2.0-84966377328.
10.1109/TITS.2016.2549282
Web of Science® Google Scholar
2 Fu Q., Zhu J., Mao Z., Zhang G., and Chen T., Online condition monitoring of onboard traction transformer core based on core-loss calculation model, IEEE Transactions on Industrial Electronics. (2018) 65, no. 4, 3499–3508, https://doi.org/10.1109/TIE.2017.2758721, 2-s2.0-85030791361.
10.1109/TIE.2017.2758721
Web of Science® Google Scholar
3 Yu W., Liu X., Zhang Y., Cao Y., Ma W., Hei X., Huang Z., and Jiang D., A design of inrush current identification system for high-speed train’s traction transformer, 2014 International Power Electronics Conference (IPEC-Hiroshima 2014 - ECCE ASIA), 2014, Hiroshima, Japan, 647–650, https://doi.org/10.1109/IPEC.2014.6869655, 2-s2.0-84906659146.
10.1109/IPEC.2014.6869655
Google Scholar
4 Zhang J., Ding G., Zhou Y., Jiang J., Ying X., and Qin S. F., Identification of key design parameters of high-speed train for optimal design, The International Journal of Advanced Manufacturing Technology. (2014) 73, no. 1-4, 251–265, https://doi.org/10.1007/s00170-014-5822-7, 2-s2.0-84903315861.
10.1007/s00170-014-5822-7
Web of Science® Google Scholar
5 Wang Y., Qu W., and Xiao C., Moving train loads and parameters identification on a steel truss girder model, International Journal of Steel Structures. (2015) 15, no. 1, 165–173, https://doi.org/10.1007/s13296-015-3012-6, 2-s2.0-84928236461.
10.1007/s13296-015-3012-6
Google Scholar
6 Wang Y. and Qu W., Numerical study on moving train parameter identification system through a simply supported bridge, Journal of Mechanical Science & Technology. (2012) 26, no. 9, 2641–2648, https://doi.org/10.1007/s12206-012-0720-0, 2-s2.0-84866440518.
10.1007/s12206-012-0720-0
Google Scholar
7 Kraft S., Puel G., Aubry D., and Funfschilling C., Improved calibration of simulation models in railway dynamics: application of a parameter identification process to the multi-body model of a TGV train, Vehicle System Dynamics. (2013) 51, no. 12, 1938–1960, https://doi.org/10.1080/00423114.2013.847467, 2-s2.0-84889882941.
10.1080/00423114.2013.847467
Google Scholar
8 Li C., Li S., and Liu Y., A least squares support vector machine model optimized by moth-flame optimization algorithm for annual power load forecasting, Applied Intelligence. (2016) 45, no. 4, 1166–1178, https://doi.org/10.1007/s10489-016-0810-2, 2-s2.0-84978171046.
10.1007/s10489-016-0810-2
Web of Science® Google Scholar
9 Talaat M., Alsayyari A., Farahat M., and Said T., Moth-flame algorithm for accurate simulation of a non-uniform electric field in the presence of dielectric barrier, IEEE Access. (2018) 7, no. 99, 3836–3847, https://doi.org/10.1109/ACCESS.2018.2889155, 2-s2.0-85059268176.
10.1109/ACCESS.2018.2889155
Web of Science® Google Scholar
10 Sapre S. and Mini S., Moth flame optimization algorithm based on decomposition for placement of relay nodes in WSNs, Wireless Networks. (2020) 26, no. 2, 1473–1492, https://doi.org/10.1007/s11276-019-02213-1.
10.1007/s11276-019-02213-1
Web of Science® Google Scholar
11 El Aziz M. A., Ewees A. A., and Hassanien A. E., Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation, Expert Systems with Applications. (2017) 83, 242–256, https://doi.org/10.1016/j.eswa.2017.04.023, 2-s2.0-85018397343.
10.1016/j.eswa.2017.04.023
Web of Science® Google Scholar
12 Deng W., Xu J., Zhao H., and Song Y., A novel gate resource allocation method using improved PSO-based QEA, IEEE Transactions on Intelligent Transportation Systems. (2022) 23, no. 3, 1737–1745, https://doi.org/10.1109/TITS.2020.3025796.
10.1109/TITS.2020.3025796
Web of Science® Google Scholar
13 Wang M., Chen H., Yang B., Zhao X., Hu L., Cai Z. N., Huang H., and Tong C., Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses, Neurocomputing. (2017) 267, 69–84, https://doi.org/10.1016/j.neucom.2017.04.060, 2-s2.0-85019950299.
10.1016/j.neucom.2017.04.060
Web of Science® Google Scholar
14 Zhang B., Tan R., and Lin C., Forecasting of e-commerce transaction volume using a hybrid of extreme learning machine and improved moth-flame optimization algorithm, Applied Intelligence. (2021) 51, no. 2, 952–965, https://doi.org/10.1007/s10489-020-01840-y.
10.1007/s10489-020-01840-y
Web of Science® Google Scholar
15 Zhao X., Fang Y., Liu L., Li J., and Xu M., An improved moth-flame optimization algorithm with orthogonal opposition-based learning and modified position updating mechanism of moths for global optimization problems, Applied Intelligence. (2020) 50, no. 12, 4434–4458, https://doi.org/10.1007/s10489-020-01793-2.
10.1007/s10489-020-01793-2
Google Scholar
16 Liao C. and Ting C., A novel integer-coded memetic algorithm for the set k-cover problem in wireless sensor networks, IEEE Transactions on Cybernetics. (2018) 48, no. 8, 2245–2258, https://doi.org/10.1109/TCYB.2017.2731598, 2-s2.0-85028467111.
10.1109/TCYB.2017.2731598
Google Scholar
17 Ganjefar S. and Tofighi M., Optimization of quantum-inspired neural network using memetic algorithm for function approximation and chaotic time series prediction, Neurocomputing. (2018) 291, 175–186, https://doi.org/10.1016/j.neucom.2018.02.074, 2-s2.0-85042849954.
10.1016/j.neucom.2018.02.074
Web of Science® Google Scholar
18 Lee J. H., Kim J. W., Song J. Y., Kim Y. J., and Jung S. Y., A novel memetic algorithm using modified particle swarm optimization and mesh adaptive direct search for PMSM design, IEEE Transactions on Magnetics. (2016) 52, no. 3, article 7001604, https://doi.org/10.1109/TMAG.2015.2482975, 2-s2.0-84962178526.
10.1109/TMAG.2015.2482975
Google Scholar
19 Serna A., a memetic algorithm for the traveling salesman problem, IEEE Latin America Transactions. (2015) 13, no. 8, 2674–2679, https://doi.org/10.1109/TLA.2015.7332148, 2-s2.0-84959454902.
10.1109/TLA.2015.7332148
Google Scholar
20 Lin J. and Chen Y., Analysis on the collaboration between global search and local search in memetic computation, IEEE Transactions on Evolutionary Computation. (2011) 15, no. 5, 608–623, https://doi.org/10.1109/TEVC.2011.2150754, 2-s2.0-80054693896.
10.1109/TEVC.2011.2150754
Web of Science® Google Scholar
21 Gong X., Liu Y., Lohse N., de Pessemier T., Martens L., and Joseph W., Energy and labor aware production scheduling for industrial demand response using adaptive multi-objective memetic algorithm, IEEE Transactions on Industrial Informatics. (2019) 15, no. 2, 942–953.
10.1109/TII.2018.2839645
Web of Science® Google Scholar
22 Kaur N., Rattan M., and Gill S. S., Performance optimization of Broadwell-Y shaped transistor using artificial neural network and moth-flame optimization technique, Majlesi Journal of Electrical Engineering.(2018) 12, no. 1, 61–69.
Google Scholar
23 Lyden S. and Haque M., A simulated annealing global maximum power point tracking approach for PV modules under partial shading conditions, IEEE Transactions on Power Electronics. (2016) 31, no. 6, 4171–4181, https://doi.org/10.1109/TPEL.2015.2468592, 2-s2.0-84962428187.
10.1109/TPEL.2015.2468592
Web of Science® Google Scholar
24 Hong M., Söderström T., and Zheng W., A simplified form of the bias-eliminating least squares method for errors-in-variables identification, IEEE Transactions on Automatic Control. (2007) 52, no. 9, 1754–1756, https://doi.org/10.1109/TAC.2007.904322, 2-s2.0-34648831807.
10.1109/TAC.2007.904322
Web of Science® Google Scholar
25 Hojjati S., Ebrahimzadeh A., Najimi M., and Reihanian A., Sensor selection for cooperative spectrum sensing in multiantenna sensor networks based on convex optimization and genetic algorithm, IEEE Sensors Journal. (2016) 16, no. 10, 3486–3487, https://doi.org/10.1109/JSEN.2016.2535862, 2-s2.0-84963860100.
10.1109/JSEN.2016.2535862
Web of Science® Google Scholar
26 Gong M., Fu B., Jiao L., and du H., Memetic algorithm for community detection in networks, Physical Review E. (2011) 84, no. 5, article 056101, https://doi.org/10.1103/PhysRevE.84.056101, 2-s2.0-81555214724, 22181467.
10.1103/PhysRevE.84.056101
PubMed Google Scholar

Citing Literature

All articles

An Improved Force Characteristic Curve Fitting Algorithm of Urban Rail Vehicles

Abstract

1. Introduction

2. Mathematical Model of Force Characteristic Curve Fitting

2.1. Force Characteristic of Urban Rail Vehicles

2.2. Optimization Models for Force Characteristic Curve Fitting