1. Introduction

Electrolyte solutions widely exist in salt lake, marine, underground water, oil/gas-field water, and the engineering of inorganic chemistry and hydrometallurgy [1]. The mean activity coefficients of the electrolytes are essential for the design development of processes such as salt chemical industry and desalination. In China, cesium levels in many salt lake brine range from 10 to 20 mg/L [2]. Therefore, it is of great significance to determine the activity coefficients of the solution of cesium salts.

A series of ion-interaction models of electrolytes have been proposed to predict the activity coefficients of solute and osmotic coefficients of the aqueous systems. Pitzer’s ion-interaction model is one of the most commonly used models [3, 4]. The research methods of the thermodynamic properties of aqueous electrolytes involve the isopiestic vapor pressure [5–7], electromotive force method [8–10], volume properties method [11], hygrometric method, and calorimetric method [12, 13]. Compared with other methods, the electromotive force (EMF) method has the advantages of good selectivity, rapid response, and easy to achieve continuous assay.

The mixed ion-interaction parameter of the ternary system provides basic thermodynamic data for the separation and extraction of pure salts from salt lake brines. The thermodynamic properties of aqueous mixed-electrolyte solutions have received considerable attention. Using EMF method in Hu’s research group [14–18], the mean ionic activity coefficients in the following ternary systems (CsCl + Cs₂SO₄+H₂O), (CsF + Cs₂SO₄ + H₂O), (CsF + CsBr + H₂O), (CsF + CsNO₃+H₂O), (CsCl + CaCl₂ + H₂O), and (CsCl + MgCl₂ + H₂O) have been reported systematically, but the activity coefficients of (NaNO₃+CsNO₃+H₂O) system at 298.15 K have not been reported in the literature till now. Therefore, the electromotive forces of the ternary system at 298.15 K were measured by EMF, and the mean activity coefficients of NaNO₃ and the mixing ion-interaction parameters θ_Na,Cs and ψNa, Cs, NO₃ are obtained for the first time.

2. Experimental

All of the instructions of the chemical reagents used in this work are shown in Table 1, and they were used without further purification. The deionized distilled water (DDW) produced by ULUP-II-10T (Chongqing Jiuyang Co. Lt., China), whose conductivity is less than 1.0 × 10⁻⁴ S·m⁻¹ and pH =6.60 at 298.15 K, was used during the whole experiment.

The Na-ISE and NO₃-ISE were purchased from Shanghai Miriam Electric Science Instruments Co., Ltd. Before use, the Na-ISE and NO₃-ISE were activated at least 2 h in a sodium nitrate with a concentration of 0.001 mol/L and purified with deionized water to a blank potential. Both electrodes were calibrated before use, and they had an excellent Nernst response and selectivity. The ion analyzer was PHSJ-4F with an uncertainty of ±0.1 mV.

The double-walled glass bottle was held at a constant temperature at (298.15 ± 0.02) K by water circulation from a thermostat.

Above galvanic cells contain no liquid junction. Here, m_A0 and m_B0 are the molalities of NaNO₃ and CsNO₃ as single salt in water, m_A and m_B are the molalities of NaNO₃ and CsNO₃ in the ternary system, respectively.

Each concentration of the above solutions was prepared by directly weighing the materials using a Sartorius electronic balance whose accuracy was 0.1 mg. Voltage readings were taken as final when they were constant within 0.2 mV for at least 5 min.

The electromotive force of the above three cells was measured at 298.15 K. First, the electromotive force of the cell (a) was measured to determine whether the electrode pair of Na-ISE and NO₃-ISE had a satisfactory Nernst response, which could judge its suitability for this experiment. Cell (b) was used to measure the electromotive force of CsNO₃ solution at different concentrations, and the selectivity coefficient K^pot of electrode Na-ISE to Cs⁺ can be calculated by equation (2). The purpose was to determine the effect of the presence of Cs⁺ on the response of Na-ISE. Finally, the EMF of cell (c) was measured under different ionic strength fractions (y_B) of CsNO₃ in the solutions.

3. Results and Discussion

3.1. The Calibration of Electrode Pair of Na-ISE and NO₃-ISE

For cell (a), 13 measurements of m_A0 from 0.01 to 4.5 mol·kg^-1 were selected to determine each corresponding potential (E_a). The Nernst equation for cell (a) can be expressed as:

$$ (1)

E⁰ is the standard potential of cell (a), k = RT/F represents the theoretical Nernst slope. The R, F, and T are the gas constant, Faraday constant, and absolute temperature, respectively. The γ_±A0 is the mean activity coefficient of pure NaNO₃ in water, whose values were taken and calculated from the literature [19] and listed in Table 2.

2. Values of the Pitzer parameters for CsNO₃ and NaNO₃ at 298.15 K.

Electrolyte	β(0)	β(1)	CΦ	Imax	σ	Ref
CsNO3	-0.13004	0.08169	0.03018	1.500	0.00057	[19]
NaNO3	0.00388	0.21151	-0.00006	10.830	0.00073	[19]

To check their linear relationship, E_a was plotted against ln(m_A0γ_±A) and shown in Figure 1. By way of this line, E⁰, k, and the linear correlation coefficient (r) can be evaluated using a linear regression method, and they are 120.3, 25.96 mV, and 0.9995, respectively. The obtained value of k gets quite close to the theoretical one (25.69 mV) of the Nernst slope. Those results mean that the electrode pair used in this work have a satisfactory Nernst response and are well suitable for our measurements.

3.3. Measurements of the Mean Activity Coefficients of NaNO₃ in the Ternary System

The cell (c) was employed to determine the EMF values E_m of the ternary system (NaNO₃ + CsNO₃ + H₂O) at different ionic strengths I and mole fractions y_B (y_B = I_B/I = m_B/(m_A + m_B)). The mean activity coefficients of NaNO₃ in the ternary system can be derived from the following Nernst equation and shown in Table 3.

$$ (3)

where γ_±A and γ_±B are the mean activity coefficients of NaNO₃ and CsNO₃, respectively. Because K^pot can be neglected [20] without leading to an appreciable error, we get the simplified form the following equation:

$$ (4)

$$ (5)

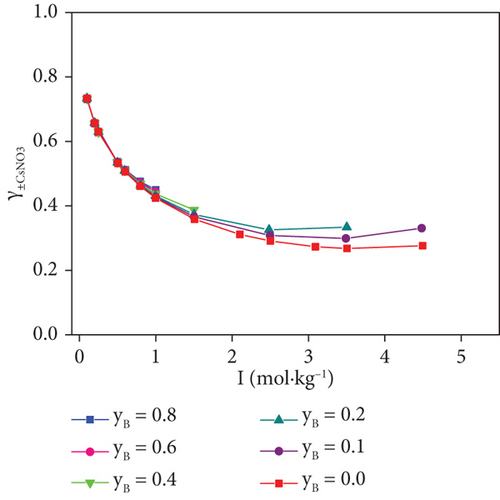
The mean activity coefficients of NaNO₃ in the aqueous ternary system can be calculated with equation (5). The related results of cell (c) are collected in Table 4 and shown in Figure 2. It can be seen from Figure 2 that when the mole fractions remain constant substantially, the mean activity coefficient of NaNO₃ decreases with the increase of ionic strength.

3.5. Pitzer Model

In this paper, the Pitzer and its extended Harvie-Weare model was used to fit the experimental data [23]. The mixed ion-interaction parameter can be obtained by substituting the binary interaction parameters and the mean activity coefficient of the aqueous electrolyte into equation (9). For the ternary system studied, the mean activity coefficients and the osmotic coefficients can be given as in the following equations:

$$ (7)

$$ (8)

$$ (9)

$$ (10)

$$ (11)

$$ (12)

$$ (13)

$$ (14)

$$ (15)

$$ (16)

$$ (17)

where M, a, and a^’ are anions. X, c, and c^’ are cations. γ_M, Z_M, and m_c are the activity coefficient, valence number, and molar concentration of the cation, respectively. γ_X, Z_X, and m_a are the activity coefficient, valence number, and molar concentration of the anion, respectively. A_ϕ is called the Debye−Hückel constant. Ψ is the ionic interaction parameters. B is the coefficient in the second dimension. For type 1-1 electrolytes, α₁ = 2.0 mol·kg^-1, α₂ = 0.

Pitzer’s mixing ion-interaction parameters are evaluated through equation (10) by using multiple linear regression techniques, and the result is shown in Table 6.

5. The parameter values of Harned equation^a.

I/mol·kg-1	lnγ±A0	αAB	βAB	103·RMSD
0.01	-0.1053	-0.1526	0.0518	0.9004
0.02	-0.1396	-0.1453	0.0362	0.0075
0.04	-0.1871	-0.0637	0.0126	0.8753
0.05	-0.2095	-0.0732	0.0219	5.2820
0.10	-0.2733	-0.0437	0.0030	1.9200
0.20	-0.3516	-0.0574	0.0223	1.8110
0.25	-0.3789	-0.0629	0.0185	1.0150
0.50	-0.4790	-0.0327	0.0040	1.2240
0.60	-0.5058	-0.0144	0.0078	0.6157
0.80	-0.5530	0.0018	0.0012	3.5060
1.00	-0.5929	-0.0437	0.0058	1.1530
1.50	-0.6719	-0.0212	0.0192	0.2707
2.50	-0.7793	0.0050	-0.0368	0.0000
3.50	-0.8561	-0.4656	0.7928	0.0000

• ^aStandard uncertainties u are u(T) =0.02 K, u($$) =0.0007 mol·kg^-1, u($$) =0.0003 mol·kg^-1, u(E) =0.1 mV.

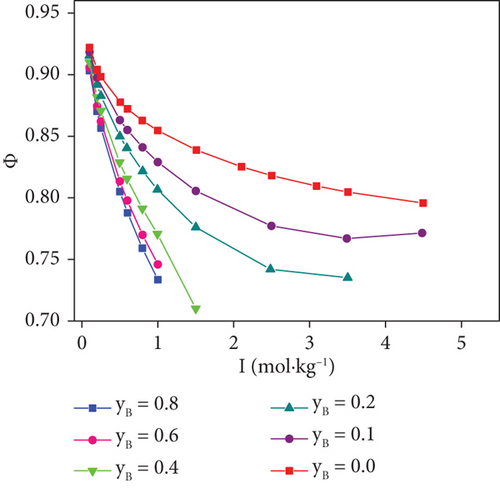
The mean activity coefficients of CsNO₃ and the osmotic coefficients for the ternary system at different ionic strengths are calculated by Pitzer and its extended Harvie-Weare model. These results are given in Table 6 and Figures 3 and 4. From Figure 3, we can see that for the ternary system studied, the mean activity coefficients of CsNO₃ decrease with an increase of total ionic strengths. It can be seen from Figure 4 that when the ionic strengths are constant, the osmotic coefficient of the ternary system is reduced by increasing the mole fractions of CsNO₃ in the system.

6. Values of the mixing ion-interaction parameters of the Pitzer equation at 298.15 K^a.

I/mol·kg-1	θNa,Cs	ψNa,Cs,NO3	RMSE	Ref
0.1-4.5	-0.1750	0.02561	0.02	This work

• ^aStandard uncertainties u are u(T) =0.02 K, u($$) =0.0007 mol·kg^-1, u($$) =0.0003 mol·kg^-1, u(E) =0.1 mV.

7. The mean activity coefficients of CsNO₃, osmotic coefficients, water activities, and excess free energies in the ternary system^a.

I/mol·kg-1	yB	$$	Φ	aw	GE/KJ·mol-1
0.10	0.0	0.7337	0.9219	0.9967	-0.0968
	0.1	0.7330	0.9182	0.9967	-0.09512
	0.2	0.7335	0.9154	0.9967	-0.0927
	0.4	0.7324	0.9098	0.9967	-0.0929
	0.6	0.7315	0.9058	0.9967	-0.0957
	0.8	0.7307	0.9031	0.9967	-0.1002
0.20	0.0	0.6571	0.9041	0.9935	-0.2541
	0.1	0.6571	0.8975	0.9936	-0.2515
	0.2	0.6574	0.8917	0.9936	-0.2452
	0.4	0.6564	0.8817	0.9937	-0.2458
	0.6	0.6553	0.8743	0.9937	-0.2560
	0.8	0.6554	0.8702	0.9938	-0.2675
0.25	0.0	0.6303	0.8982	0.9920	-0.3416
	0.2	0.6292	0.8827	0.9921	-0.3330
	0.4	0.6286	0.8706	0.9922	-0.3342
	0.6	0.6279	0.8619	0.9923	-0.3472
	0.8	0.6272	0.8565	0.9923	-0.3687
0.50	0.0	0.5318	0.8776	0.9841	-0.8922
	0.1	0.5337	0.8630	0.9845	-0.8837
	0.2	0.5344	0.8499	0.9848	-0.8700
	0.4	0.5358	0.8287	0.9852	-0.8842
	0.6	0.5359	0.8134	0.9854	-0.9206
	0.8	0.5369	0.8050	0.9856	-0.9734
0.60	0.0	0.5056	0.8721	0.9813	-1.1240
	0.1	0.5068	0.8550	0.9817	-1.1184
	0.2	0.5092	0.8403	0.9822	-1.1070
	0.4	0.5103	0.8155	0.9827	-1.1350
	0.6	0.5111	0.7978	0.9829	-1.1877
	0.8	0.5120	0.7878	0.9830	-1.2609
0.80	0.0	0.4611	0.8627	0.9755	-1.6372
	0.1	0.4622	0.8409	0.9760	-1.6430
	0.2	0.4640	0.8217	0.9765	-1.6541
	0.4	0.4685	0.7912	0.9775	-1.6799
	0.6	0.4718	0.7699	0.9780	-1.7371
	0.8	0.4758	0.7591	0.9784	-1.8246
1.00	0.0	0.4243	0.8546	0.9697	-2.2148
	0.1	0.4272	0.8289	0.9705	-2.2120
	0.2	0.4312	0.8067	0.9714	-2.1785
	0.4	0.4375	0.7707	0.9727	-2.2025
	0.6	0.4431	0.7459	0.9734	-2.2907
	0.8	0.4492	0.7335	0.9738	-2.4112
1.50	0.0	0.3586	0.8387	0.9553	-3.8197
	0.1	0.3663	0.8055	0.9573	-3.7860
	0.2	0.3733	0.7761	0.9588	-3.7815
	0.4	0.3876	0.7100	0.9623	-3.6367
2.5	0.0	0.2911	0.8180	0.9288	-7.4100
	0.1	0.3080	0.7772	0.9323	-7.3837
	0.2	0.3257	0.7420	0.9356	-7.2564
3.5	0.0	0.2680	0.8046	0.9032	-11.4829
	0.1	0.2992	0.7669	0.9079	-10.7852
	0.2	0.3339	0.7351	0.9112	-10.2471
4.5	0.0	0.2764	0.7957	0.8788	-15.8282
	0.1	0.3308	0.7714	0.8826	-14.8822

• ^aStandard uncertainties u are u(T) =0.02 K, u(m_A) =0.0007 mol·kg^-1, u(m_B) =0.0003 mol·kg^-1, u(E) =0.1 mV, A = NaNO₃, B = CsNO₃.

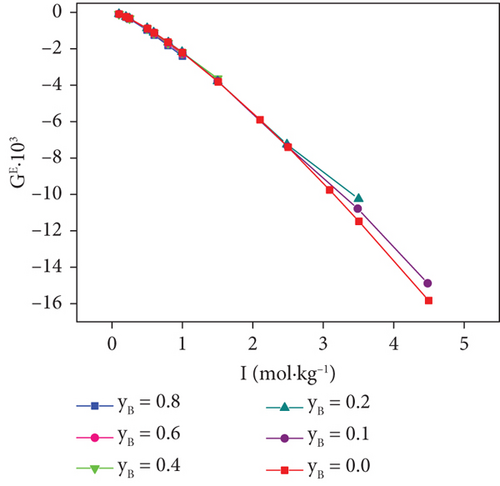
3.6. Excess Gibbs Free Energies and Water Activities of the Ternary System

The excess Gibbs free energies and water activities of the ternary system have been calculated by using the following relation [22]:

$$ (18)

The calculated results are given in Table 7 and Figures 5 and 6. It can be seen that water activities and the excess Gibbs free energies decrease with an increase of total ionic strengths for all of the investigated ternary systems, respectively.

4. Conclusions

In this work, the electromotive force method was used to study the mean activity coefficients of NaNO₃ in the ternary system (NaNO₃ + CsNO₃ + H₂O) at 298.15 K. The electromotive force method plays an essential role in the study of the thermodynamic properties of dilute electrolyte solutions because of its advantages such as simple device and operation, fast determination speed, and no change in the interaction between ions in solution. Using multiple linear regression fitted the Pitzer mixing ion-interaction parameters of the system. This study could provide the basic thermodynamic data to establish the thermodynamic model of the complex salt lake brine system containing cesium. In addition, the mixed salt parameters of NaNO₃ and CsNO₃ are helpful to establish the predictive phase diagram of the ternary system (NaNO₃+CsNO₃+H₂O) to separate the mixtures of sodium and cesium nitrates.

Conflicts of Interest

The authors declare that they have no conflicts of interest.