1. Introduction

The rock bulk modulus reflects the ability of a rock to resist deformation under external loads, using which one can characterize the mechanical characteristics of rocks. The bulk modulus is a comprehensive response of the rock mineral composition, fluid, pore, and structure under the action of the original internal environment, such as the formation pressure and temperature [1]. These unique characteristics make the bulk modulus an important parameter to study.

The joints in a rock fundamentally affect its bulk modulus. For instance, parallel joints can exist in sedimentary rocks, thereby significantly affecting the bulk modulus [2]. At the same time, the number of parallel joint spacings (PJS) in the rock causes a difference in the bulk modulus. For instance, Zhao et al. [3] have used the finite element method to study the bulk modulus of rock. Moreover, some scholars have studied the effects of different factors on bulk modulus. For instance, Blake and Faulkner [4] have conducted seepage tests on granite to examine the effect of bulk modulus on fracturing permeability. Furthermore, Davarpanah et al. [5] studied the relationship between the modulus ratio and bulk modulus. Liu and Zhang [6] conducted an indoor triaxial creep test and found that the absolute value of the bulk modulus decreases with an increase in creep stress. Scholars have also addressed the calculation methods for bulk modulus. For instance, Shen et al. [7] studied the relationship between the tensile failure strain of rock and the initial fracture density spacing. They ultimately established a calculation method for the rock bulk modulus under tensile conditions. Zhao et al. [8] studied the failure and cracking characteristics of a broken rock mass cut using joints. Li et al. [9] obtained the volumetric fracture and crack propagation law of rocks through a dynamic load test. Overall, research literature extensively examined bulk modulus, but only a few studies have considered the size and PJS, while the relationship between bulk modulus and PJS is poorly understood.

The rock has a side effect, and the change in rock size also affects the rock bulk modulus. For instance, the change in the size of some sedimentary rocks rich in joints fundamentally affects the change in the rock bulk modulus [10]. In this regard, Pang et al. [11] demonstrated that the bulk modulus of coal increases with a decrease in particle size. Jiang [12] reported that the size of the rock particles affects the rock pore structure, thereby triggering changes in the rock bulk modulus. Zhang and Yang [13] quantified the bulk modulus of montmorillonite by measuring changes in the length and density of the sample. Some other scholars have studied the effect of irregular particles on the bulk modulus. For instance, Kerimov et al. [14] have elucidated the effects of irregularly shaped particles and particle size on the porosity, permeability, and bulk modulus of granular porous media. Researchers also examined the effect of size on bulk modulus, but the elements of PJS, as well as the relationship between bulk modulus and size, are both poorly understood.

The mechanical parameters of rocks fundamentally vary with the size of the jointed rock and eventually tend toward a stable value, which is defined as the representative essential volume (REV). Some researchers have previously proposed various methods to evaluate the REV, whereas Hu and Ma [15] used a realistic failure process analysis (RFPA) to study the characteristic size. Ying et al. [16] established a method based on volume rupture strength (P32) and a statistical test method to estimate rock mass REV. Wu et al. [17] studied the effect of size on bulk modulus, while taking into account the effect of the model location, and reported that the REV size was 18 m. Liu et al. [18] elucidated the size effect of the defective rock mass strength through uniaxial and confining pressure tests and obtained a REV size of 5 m × 10 m. Hu et al. [19] obtained the relationship between the characteristic size of the rock elastic modulus and the PJS. Overall, although the bulk modulus has been extensively studied, only a few researchers investigated the relationship between the characteristic size of the bulk modulus (CSBM) and PJS and established a model of the CSBM and PJS.

This study established 12 numerical models to investigate the influence of the PJS and rock size on rock K. Within this research aim, (1) the corresponding stress-strain curves were analyzed, (2) the relationship between K and PJS, as well as the relationship between K and size were both established. Finally, (3) a model of the CSBM and PJS and a model of the rock characteristic bulk modulus (CBM) and PJS were established.

2. Numerical Simulation Plans

This study primarily focuses on two aspects: (1) elucidating the influence of PJS on rock K, with PJS of 10, 20, 30, 40, and 50 mm and (2) elucidating the effect of rock size with PJS on rock K, with the rock sizes of 100, 200, 400, 600, 800, 1,000, and 1,200 mm. Table 1 summarizes the research plans of this study based on [15].

This study uses RFPA as the simulation software. The boundary conditions and rock mechanical parameters used in the numerical simulation are summarized in referred to [15].

The roughness coefficient of the joint applied for the numerical simulations was 3, its elastic modulus was 1.5 MPa, its compressive strength was 2 MPa, its Poisson’s ratio was 0.3, and its internal friction angle was 30°.

3. Numerical Results and Analysis

3.1. Stress-Strain Curve Analysis

The research analysis included plotting of the stress-strain curves in the plans 1 to 7 (Figure 1). Furthermore, the stress-strain curves in plans 8 to 12 were plotted as well (Figure 2).

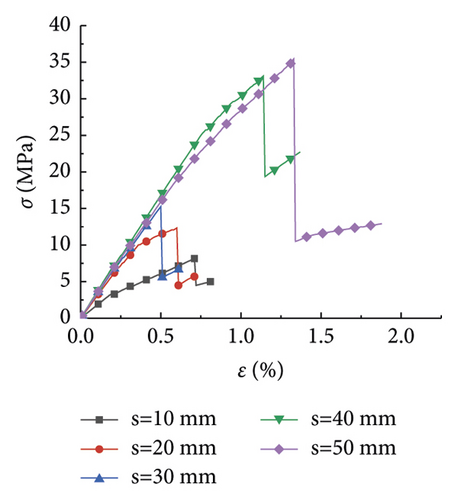
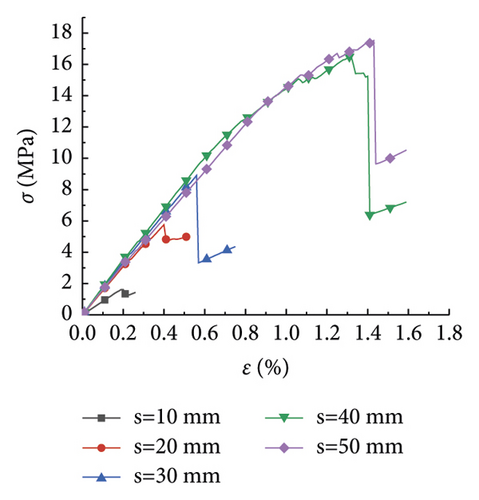
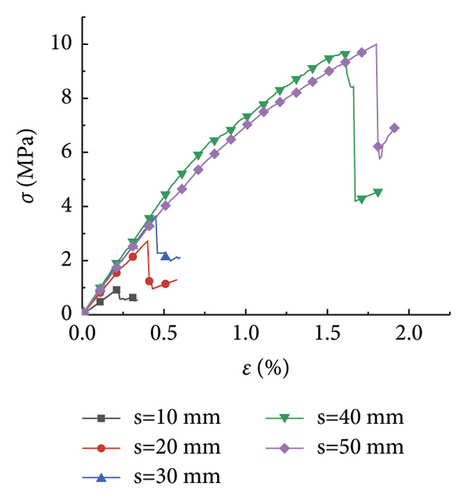
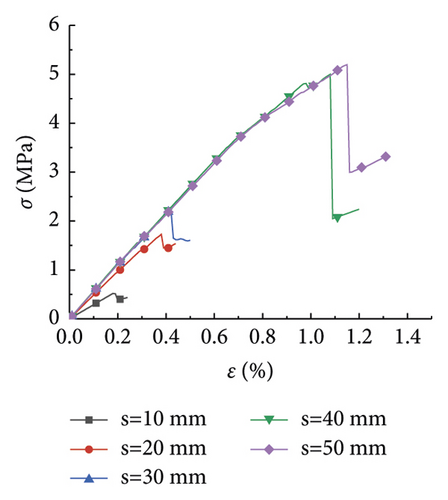
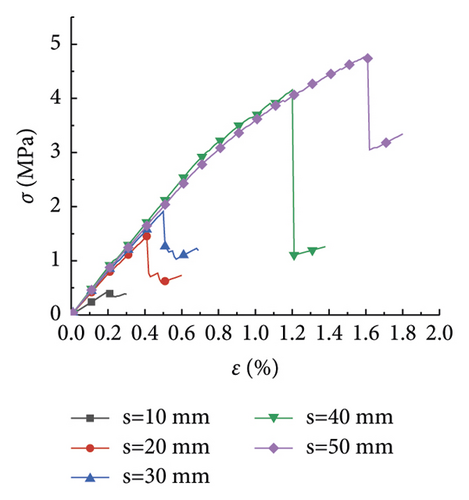
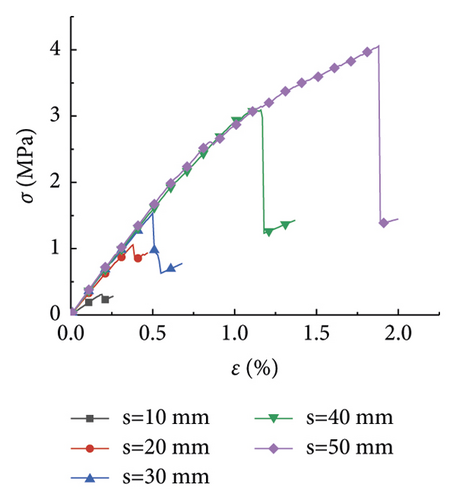
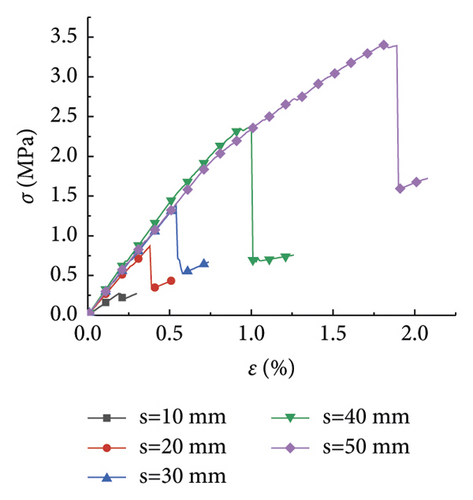
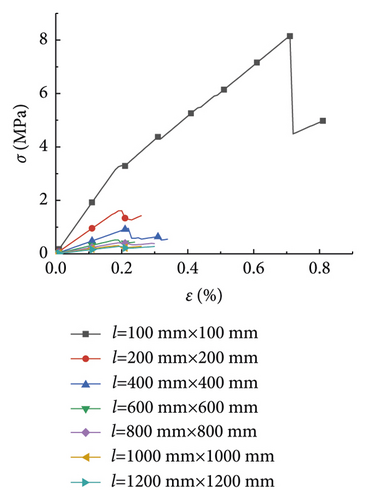
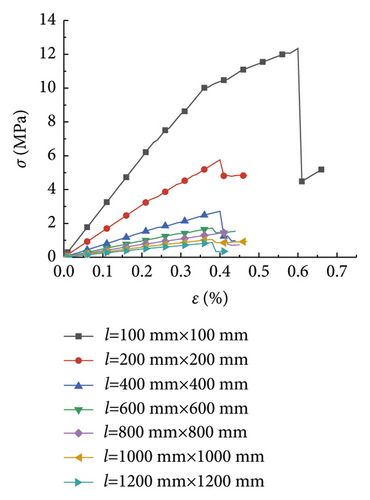
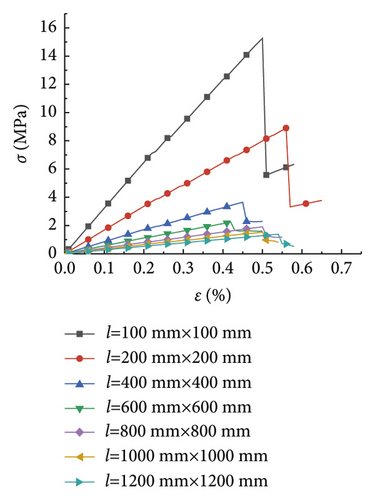
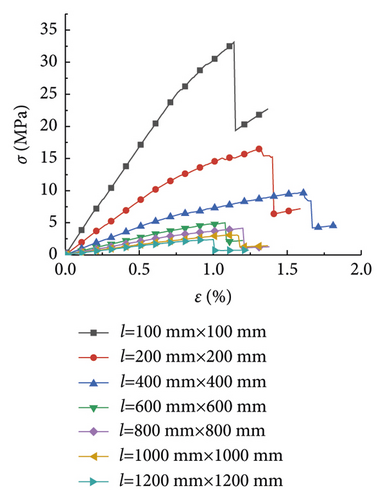
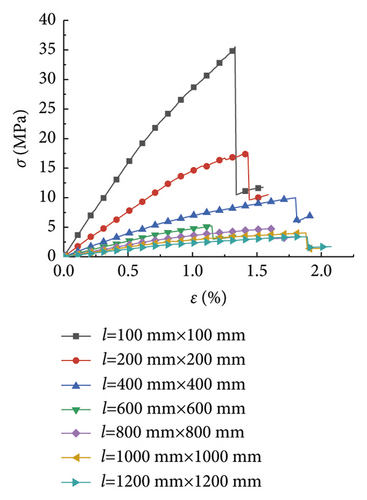
Figure 1 illustrates the effect of the PJS on the compressive strength of rocks with different rock sizes. As seen in Figures 1(a)–1(g), the laws of the stress-strain curves were similar as the rock size increased from 100 to 1,200 mm. The strain of the rock gradually increased with the increase of the stress under the pressure effect. Moreover, it exhibited a linear elastic failure, which was further exacerbated by a plastic failure. Figure 1(a) is shown as an example, where the rock size is 100 mm. As seen, the compressive strength of the rock gradually increased, as the PJS increased from 10 to 50 mm.

Figure 2 displays the effect of the rock size on the compressive strength of the rock at different PJS. As seen from Figures 2(a)–2(e), when the PJS increased from 10 to 50 mm, the laws of rock stress-strain curves were also similar. Like in Figure 2, the rock was also destroyed by the elastic deformation first, which was further exacerbated by plastic deformation. Figure 2(e) is shown as an example with a PJS of 50 mm. As seen, the compressive strength of the rock gradually decreased with the increase of the rock size from 100 mm to 1,200 mm, thereby somewhat manifesting the size effect. Notably, the law of the curve is consistent with the law from [15], thereby indicating that the size effect of the rock was the same when the parameters of the joints changed.

The elastic modulus fundamentally reflects the proportional relationship between the stress and strain of a material during the elastic deformation stage. Figures 1 and 2 shows the obtained values of the elastic modulus and Poisson’s ratio for each working condition, as summarized in Tables 2 and 3.

2. Values of elastic modulus.

Numerical plans	Rock size (mm)	Elastic modulus (GPa)
		Plan 8	Plan 9	Plan 10	Plan 11	Plan 12
		s = 10 mm	s = 20 mm	s = 30 mm	s = 40 mm	s = 50 mm
Plan 1	l = 100	1.750	2.957	3.236	3.519	3.338
Plan 2	l = 200	0.864	1.542	1.681	1.769	1.607
Plan 3	l = 400	0.438	0.734	0.859	0.911	0.834
Plan 4	l = 600	0.290	0.488	0.563	0.570	0.557
Plan 5	l = 800	0.218	0.380	0.406	0.439	0.418
Plan 6	l = 1000	0.172	0.298	0.327	0.333	0.344
Plan 7	l = 1200	0.145	0.243	0.272	0.297	0.273

3. Values of Poisson’s ratio.

Numerical plans	Rock size (mm)	Poisson’s ratio
		Plan 8	Plan 9	Plan 10	Plan 11	Plan 12
		s = 10	s = 20	s = 30	s = 40	s = 50
Plan 1	100	0.3000	0.2049	0.2200	0.2369	0.2930
Plan 2	200	0.2326	0.1667	0.1429	0.1654	0.2396
Plan 3	400	0.1523	0.2000	0.2111	0.2754	0.2861
Plan 4	600	0.1754	0.1875	0.1867	0.2118	0.2486
Plan 5	800	0.1875	0.1964	0.2097	0.2177	0.2638
Plan 6	1000	0.1053	0.1750	0.2340	0.2689	0.2673
Plan 7	1200	0.1586	0.1667	0.1607	0.1944	0.3013

Bulk modulus is a relatively stable material constant. Fundamentally, there is a relationship between bulk modulus K, elastic modulus E, and Poisson’s ratio ν: K = (E/3) × (1 − 2ν). Furthermore, the bulk modulus K of each working condition was solved according to this equation and the values from Tables 2 and 3, as shown in Table 4.

4. Values of bulk modulus.

Numerical plans	Rock size (mm)	Bulk modulus (GPa)
		Plan 8	Plan 9	Plan 10	Plan 11	Plan 12
		s = 10	s = 20	s = 30	s = 40	s = 50
Plan 1	100	1.458	1.670	1.926	2.229	2.687
Plan 2	200	0.538	0.771	0.784	0.881	1.028
Plan 3	400	0.210	0.408	0.495	0.676	0.650
Plan 4	600	0.149	0.260	0.299	0.330	0.369
Plan 5	800	0.117	0.209	0.233	0.259	0.295
Plan 6	1000	0.073	0.153	0.205	0.240	0.246
Plan 7	1200	0.071	0.122	0.134	0.162	0.229

3.2. Influence of PJS on K

Table 3 summarizes the statistical data, which revealed no clear relationship between Poisson’s ratio, rock size, and PJS, and the data obtained are relatively discrete.

The statistical data, shown in Table 4, demonstrate that K gradually increased as the PJS increased. A data point plot of K and PJS for each size was drawn, and the corresponding curve was fitted, as shown in Figure 3.

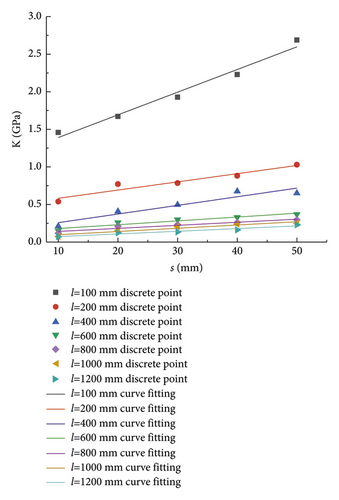
As seen in Figure 3, when the rock size was fixed and unchanged, K was affected by the PJS and increased with the increasing PJS. This pattern of variation remained the same even when the rock size varied. When the PJS was fixed and unchanged, K was affected by the rock size and decreased with an increase in the rock size. This finding indicates that K of the rock with parallel joints exhibited a positive correlation with the PJS and a negative correlation with the rock size. To illustrate this relationship in detail, see the formulae for the regression curves in Table 5.

5. Fitting relationships between K and PJS.

Rock size (mm)	Fitting formula	Fitting coefficient (R2)
100	K(s) = 0.027s + 1.089	0.976
200	K(s) = 0.013s + 0.473	0.927
400	K(s) = 0.012s + 0.143	0.907
600	K(s) = 0.005s + 0.128	0.917
800	K(s) = 0.004s + 0.100	0.916
1000	K(s) = 0.004s + 0.053	0.907
1200	K(s) = 0.004s + 0.036	0.942

The fitting formula from Table 5 was further used. The relationship indicated that K and PJS exhibited a linear relationship, and the mathematical model for K and PJS was formalized as

$$ (1)

where K(s) is K when PJS is s (GPa) and s is PJS (mm); a and b are the parameters.

The values of the parameters a and b from Table 5 are listed in Table 6 according to (1). The values from Table 6 were used to draw the fitting curves of the rock size and the parameters a and b (see Figure 4).

6. Values of a and b under different rock sizes.

Parameter	Values
	l = 100 mm	l = 200 mm	l = 400 mm	l = 600 mm	l = 800 mm	l = 1000 mm	l = 1200 mm
A	0.027	0.013	0.012	0.005	0.004	0.004	0.004
B	1.089	0.473	0.143	0.128	0.100	0.053	0.036

Figure 4 shows that the parameters a and b exhibited a power function relationship to s. Thus, we established the following formulae:

$$ (2)

$$ (3)

From equations (1)–(3), we obtained a special relational formula for K and PJS:

$$ (4)

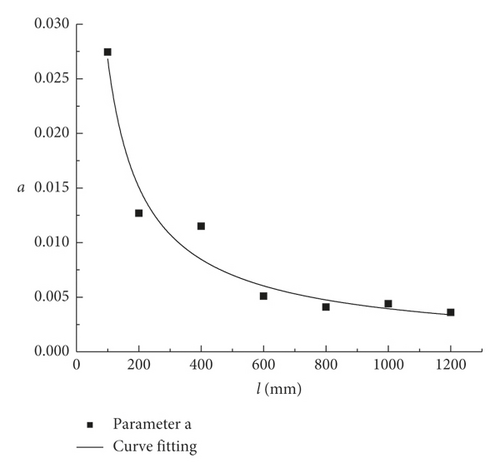
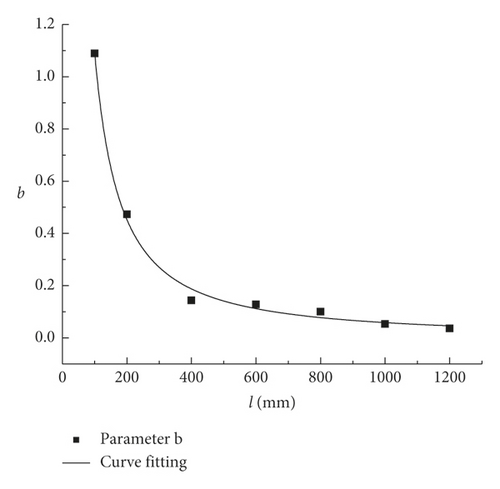
(3) was used to quantify K, thereby providing a special relationship between K and PJS. Overall, it is applicable for solving K on a two-dimensional plane. In particular, for a known rock size, K can be obtained when the PJS was determined.

3.3. Influence of the Size Effect of K

A data point plot of K and the rock size under each PJS was drawn according to the values from Table 4. The corresponding curve was fitted, as shown in Figure 5.

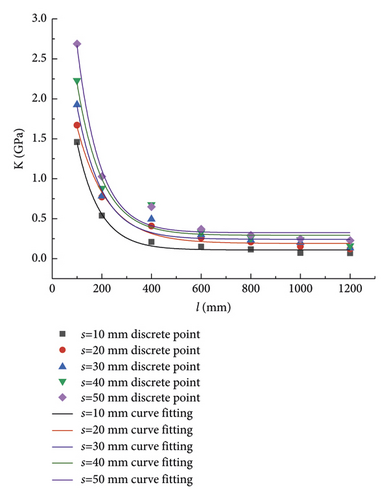
Figure 5 shows that when the PJS was fixed and unchanged, K was affected by the rock size and decreased with the increase in size. This pattern of variation remained the same even if PJS differed. Furthermore, when the rock size was fixed and unchanged, K was affected by rock size and increased accordingly. This phenomenon suggests that, for a rock with parallel joints, its K would have a positive correlation with the PJS, but a negative correlation with the rock size. For details of this relationship, see the formula of the regression curves summarized in Table 7.

7. Fitting relationships between K and rock size.

PJS (mm)	Fitting formula	Fitting coefficient (R2)
10	K(l) = 0.110 + 3.254e−0.0093l	0.995
20	K(l) = 0.191 + 3.321e−0.0094l	0.988
30	K(l) = 0.243 + 4.517e−0.0111l	0.979
40	K(l) = 0.293 + 5.132e−0.0126l	0.963
50	K(l) = 0.326 + 6.507e−0.0129l	0.983

The fitting formula in Table 7 was used to infer an exponential relationship between K and the rock size. The mathematical model for K and rock size was proposed:

$$ (5)

where K(l) is K at the size l and the unit is GPa; d, f, and g are parameters.

The values of the parameters d, f, and g in Table 7 are listed in Table 8 according to (5). Furthermore, the values from Table 8 were used to draw the fitting curves of the rock size (d, f, and g are drawn), as shown in Figure 6.

8. Values of d, f, and g.

Parameters	Values
	s = 10 mm	s = 20 mm	s = 30 mm	s = 40 mm	s = 50 mm
d	0.1096	0.1905	0.2431	0.2927	0.3255
f	3.2541	3.3206	4.5174	5.1317	6.5067
g	0.0093	0.0094	0.0111	0.0126	0.0129

Figure 6 shows that the parameters d, f, and g all were linearly associated to s, thereby laying the foundation for the following formulae:

$$ (6)

$$ (7)

$$ (8)

Furthermore, equations (5)–(8) were used to obtain a special relational formula for K and the rock size:

$$ (9)

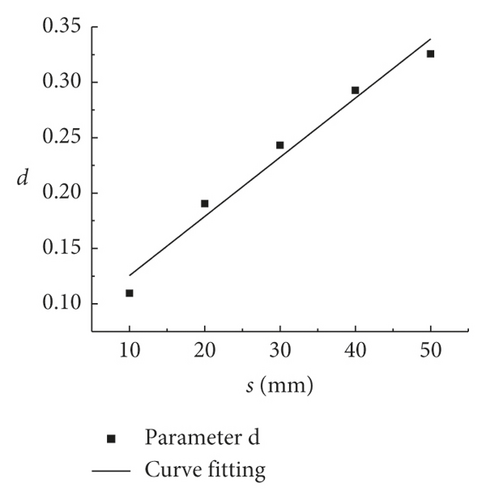
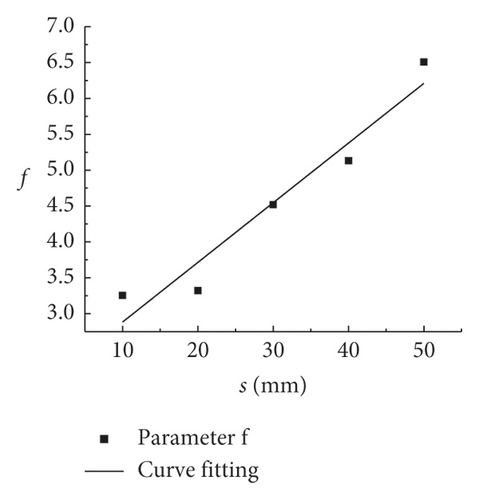
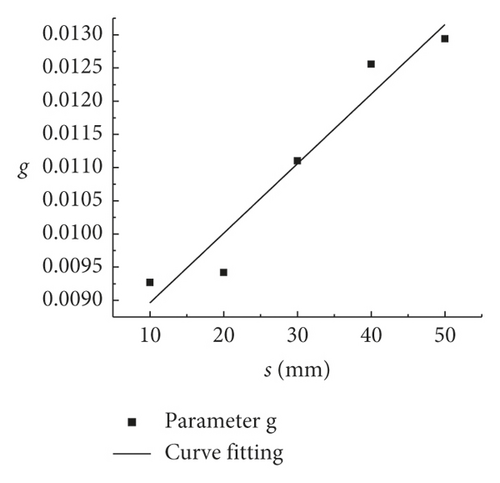
(9) quantifies K, while also providing a special relationship between K and the rock size. Moreover, it can be used for solving K on a two-dimensional plane. Thus, K can be obtained when PJS is known and when the rock size is determined.

3.4. Relationships of CSBM, CBM, and PJS

3.4.1. Derived Formula of CSBM

The size effect of K can be characterized by the characteristic size of the bulk modulus (CSBM). In particular, Liang et al. [20] previously provided the method for quantifying the characteristic size; one can solve the CSBM by

$$ (10)

where γ is the acceptable absolute value of the inclination.

3.4.2. Relationship of CSBM and PJS

The CSBM was solved, as summarized in Table 9, when the PJS was 10, 20, 30, 40, and 50 mm. The regression curves for the CSBM and PJS are shown in Figure 7.

9. Relationship between CSBM and PJS.

PJS (mm)	10	20	30	40	50
Characteristic size of bulk modulus (mm)	690.66	683.52	622.58	570.2	574.1

Figure 7 shows that, as the PJS increased from 10 to 50 mm, the CSBM decreased from 690.66 mm to 574.1 mm. Moreover, a linear relationship between CSBM and PJS was discerned, where the slope of the curve was found to be negative. Thus, according to the fitting curve, the following specific relationship was formalized:

$$ (11)

where B(s) is the characteristic size of bulk modulus (unit: mm).

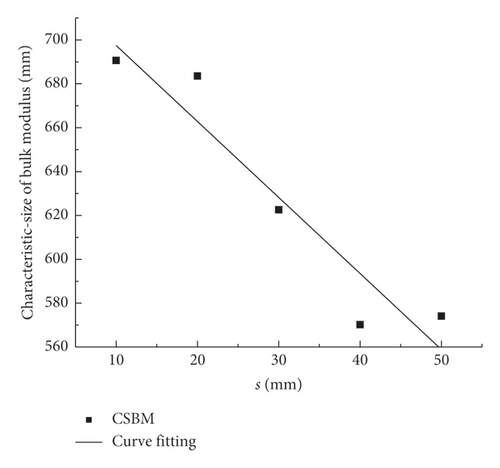
(11) quantifies the CSBM, thereby providing a special relationship between the CSBM and PJS, which can be used for solving the CSBM in a two-dimensional plane. Note that, in field applications, the CSBM can be generally obtained when the PJS is measured.

3.4.3. Relationship of CBM and PJS

The value of CSBM was substituted into (5), and the characteristic bulk modulus (CBM) of rocks with different PJS values is described in Table 10.

10. Relationship between CBM and PJS.

PJS (mm)	10	20	30	40	50
Characteristic bulk modulus (GPa)	0.115	0.196	0.248	0.297	0.329

Figure 8 shows that the CBM increases gradually with the increase of the PJS, thereby exhibiting a linear relationship. On this basis, the special relation was obtained:

$$ (12)

where K_w(s) is the CBM (unit: GPa).

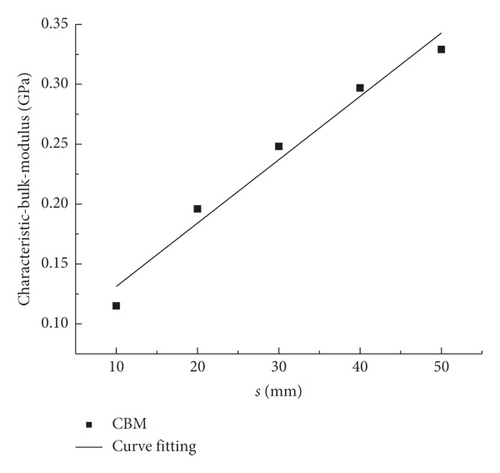
(12) quantifies the CBM and provides a special relationship between the CBM and PJS. It can be used for solving the CBM on a two-dimensional plane. In field applications, the CBM can be obtained when the PJS is measured.

3.5. Verification Analysis

To evaluate the accuracy of our results, we analyzed the applicability of (5). The verification was conducted using the data of elastic moduli for different rock sizes from Figure 3.11 (page 44) in reference [21], as shown in Table 11. From these elastic modulus, the corresponding bulk modulus were calculated and summarized in Table 11. According to Table 11, we obtained a scatter plot and relationship curve of the bulk modulus and rock size (see Figure 9).

11. Elastic modulus and bulk modulus with different rock sizes.

Rock size	2 m	4 m	8 m	12 m	16 m
Elastic modulus (GPa)	11.38	8.06	7.66	7.39	7.29
Bulk modulus (GPa)	2.0484	1.4508	1.3788	1.3302	1.3122

The relationship between the bulk modulus and different sizes is shown in Figure 9 and was formalized as follows:

$$ (13)

where K(l) (GPa) is K of the rock when the rock size is l and l (m) is the rock size.

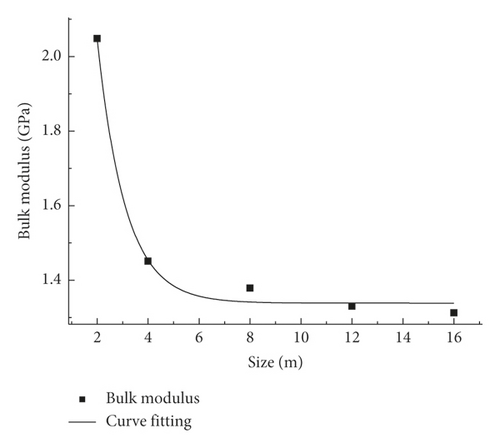
The function type of (13) generally conformed to the mathematical model, introduced in (5). It can be therefore concluded that the numerical simulation and experimental conclusions were consistent. Moreover, the evaluation analysis indicates that the mathematical model, proposed in (5), is applicable for the solution of the bulk modulus with respect to the size.

4. Discussion

The K values of rocks of different sizes varied with the PJS. Importantly, this study established the following four relationships: (1) K and PJS; (2) K and rock size; (3) CSBM and PJS; as well as (4) CBM and PJS. Only a few previous studies considered the size effect of rocks with PJS on K. Moreover, the effect of rock size changes on the K of rocks with PJS, and the effect of the changes in PJS on the size effect of K; both remained understudied.

In this study, the K values of rocks with different sizes were obtained using the data from [21], and (15) was obtained, which confirmed the accuracy of (5). Moreover, it proved that the formula, proposed in the study, stands out with certain universality, thereby also confirming the high accuracy of the research results. However, some differences between the numerical and experimental results were discerned. In addition, the two-dimensional model is limited in simulating three-dimensional samples. Both these challenges can be alleviated in future studies.

Overall, the specific relationships of rock K were obtained in this study. The information about the rock size effect and the PJS is essential as input for the setting of mechanical parameters such as K in rock engineering, which can prevent rock engineering disasters. When the PJS and rock size are available, rock K, CSBM, and CBM can be quickly obtained for a selected engineering site, thereby providing valuable data-driven guidelines for engineering purposes.

5. Conclusions

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Authors’ Contributions

G Hu contributed to conceptualization, software, and funding acquisition. T Zhao contributed to methodology, data curation, investigation, writing, and original draft preparation. T Wang contributed to data curation and formal analysis. H Zhang was responsible for funding acquisition and formal analysis.