For the case of ultralow surface separation, in a hydrodynamic wedge-platform thrust slider bearing, the outlet zone and a portion of the inlet zone are in boundary lubrication, while most of the inlet zone is in the multiscale lubrication contributed by both the adsorbed boundary layer and the intermediate continuum fluid film. The present paper first presents the mathematical derivations for the generated pressure and carried load of this bearing based on the governing equation for boundary lubrication and the multiscale flow equation. Then, the full numerical calculation is carried out to verify the analytical derivations. It was found that the mathematical derivations normally have considerable errors when calculating the hydrodynamic pressure distribution in the bearing, owing to introducing the equivalent parameter λ_bf,e which is constant in the inlet zone; however they can be used to calculate the carried load of the bearing when the surface separation in the outlet zone is sufficiently high. The study suggests the necessity of the numerical calculation of the hydrodynamic pressure and even the carried load of this bearing. It is also shown that owing to the fluid-bearing surface interaction, the pressure and carried load of this bearing are significantly greater than those calculated from the classical hydrodynamic theory.

1. Introduction

There is an intrinsic very thin boundary layer (normally with the thickness no more than 10 nm) physically adsorbed to the solid surfaces in a hydrodynamic slider bearing [1, 2]. When the bearing surface separation is on the 1μm scale or greater, the adsorbed boundary layer effect is negligible, and the classical hydrodynamic theory [3] may be applied. It was found that only when the minimum bearing surface separation is lower than one hundred times of the thickness of the boundary layer, the boundary layer effect should be considered [4]. With the increases of the load, sliding speed, and/or the fluid film temperature, the bearing will work with the surface clearance on the same scale with the thickness of the boundary layer. For this case, the classical hydrodynamic theory fails, and new hydrodynamic theory needs to be developed by incorporating the boundary layer effect.

For the fluids with long-chain molecules, the boundary layer may be only monolayer with a considerable thickness, and it can be taken as a solid layer [5–9]. For this case, the analysis is simple just by adding the boundary layer thicknesses. We can apparently notice the effect of the residual boundary film for the low bearing surface clearance. For the fluids with short-chain molecules or simple fluids such as water, alcohol, and methane, the boundary layer on a sold surface may consist of several molecule layers in the range of the fluid-solid interaction, and its rheological properties including the local density and local viscosity are varied across the boundary layer thickness according to molecular dynamics simulation results [10–14]; this boundary layer should essentially be considered as a flowing layer under the entrainment of the moving surfaces. By equivalently treating the boundary layer as orientated normal to the solid surface, Zhang [15] developed the flow equations, respectively, for the two adsorbed boundary layers and the intermediate continuum fluid in the two-dimensional multiscale flow when the distance between the two solid surfaces is comparable to the boundary layer thickness.

Shao et al. [16] analyzed the multiscale hydrodynamic wedge-platform thrust slider bearing by using Zhang’s multiscale flow equations when the two bearing surfaces approached to one another, but there was still a continuum fluid film existing in the whole contact intervening the two boundary layers. Their analysis is obviously more advanced than the classical hydrodynamic analysis [3], which only considered the continuum fluid. It is applied for the condition of heavy loads and/or low sliding speeds. They found that when the minimum bearing surface separation is below 100 nm, the boundary layer effect significantly increases the hydrodynamic pressure and carried load of the bearing for the medium and strong fluid-bearing surface interactions.

When the bearing surface clearance is further reduced so that in the outlet zone the intermediate continuum fluid film vanishes and there is only the physically adsorbed boundary layer, the analysis by Shao et al. [16] will fail, and new mathematical analysis should be developed for this special model of the bearing. In this bearing with ultralow surface separation, the boundary layer in the outlet zone should follow the nanoscale flow equation; in the inlet zone area adjacent to the outlet zone, there is also only the boundary layer existing which should be described by the nanoscale flow equation; and in the other area of the inlet zone, there is still the multiscale flow incorporating both the boundary layer flows and the intermediate continuum fluid flow. The present paper attempts to address this bearing by developing the full mathematical derivation, though Zhang [17] has analyzed this specific mode of hydrodynamics in a line contact. Numerical calculation is also made to verify the accuracy of the derived mathematical equations for the pressure and carried load of the bearing. Important conclusions are drawn concerning the analysis and performance of this particular bearing.

2. Model of the Studied Bearing

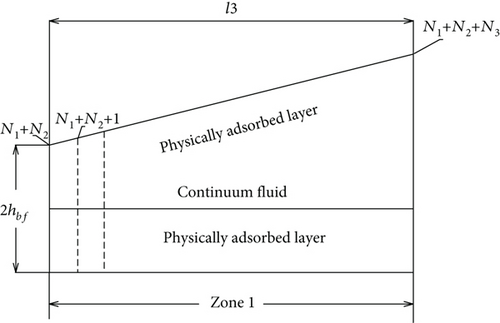
Figure 1 shows the hydrodynamic wedge-platform thrust slider bearing with ultralow surface separation studied in this paper. In this bearing, the surface separation in the outlet zone is so low (normally on the 1 nm scale) that only the physically adsorbed boundary layer exists (i.e., the intermediate continuum fluid film disappears) in the outlet zone; in the inlet zone area adjacent to the outlet zone, there is also only the physically adsorbed boundary layer because of the very low surface separation, but in the remaining area of the inlet zone occurs the multiscale hydrodynamics consisting of both the adsorbed boundary layer flows and the intermediate continuum fluid flow. This bearing model is new and deserves a proper study, as the classical (continuum) hydrodynamics fail for it.

Details are in the caption following the image — Open in figure viewer PowerPoint

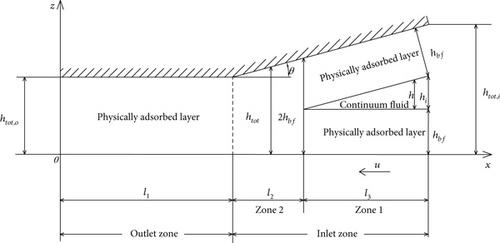
Molecular dynamics simulation (MDS) [18–21] may be used to model the flow of the confined fluid in the nanoscale surface separation in the outlet zone, and it may also be used to model the flow of the adsorbed boundary layer in the multiscale hydrodynamic area in the inlet zone. This should be feasible if the bearing width is on the 1 nm or 10 nm scales. However, when the bearing width is on the micrometer or millimeter scales, MDS should be given up for modeling the molecular scale flow in the bearing owing to costing too long computational time and too large computer storage. This is often true so that the conventional multiscale scheme by using MDS [18–21] is not applicable for the present bearing model.

Fortunately, Zhang [15] derived the closed-form explicit flow equations, respectively, for the adsorbed boundary layer flows and the intermediate continuum fluid flow in the two-dimensional multiscale flow. These equations can be directly implemented for the multiscale hydrodynamic area in the inlet zone of the bearing. The nanoscale flow equation [22] can be implemented for the other area of the bearing, where only the boundary layer exists. These construct the frame of the present mathematical analysis for the studied bearing.

3. Theoretical Analysis

The analysis is based on the following assumptions for the simplification:

(1) The fluid is isoviscous and incompressible; (2) the two bearing surfaces are identical and perfectly smooth; (3) the fluid film thermal effect is negligible; (4) the side leakage of the bearing is negligible; and (5) no interfacial slippage occurs on any interface. Assumptions (1), (3), and (5) are correct for the case of very low sliding speeds and very light loads such as for microslider bearings. When the bearing clearance is ultralow, even the nanometer-scale surface roughness is comparable, and the surface roughness effect should be considered. This subject will be addressed in the following research. For the other factors deviating from the above assumptions such as the side leakage, the film viscous heating, or the wall slippage in a macrosize bearing, the correction factors can be introduced to modify the present results for the practical application.

3.1. Mathematical Derivations

3.1.1. For the Zone 1 of the Inlet Zone

In this subzone, the total mass flow rate through the bearing consists of the boundary layer flows and the intermediate continuum fluid flow, which are, respectively, nanoscale noncontinuum and macroscale. According to Zhang’s multiscale flow equations [15, 23], this total mass flow rate per unit contact length is:

()

where λ_bf = h_bf/h; h_bf is the thickness of the adsorbed boundary layer; h is the intermediate continuum fluid film thickness; ρ is the hydrodynamic pressure; x is the coordinate shown in Figure 1; u is the sliding speed and here is positive; ρ and η are, respectively, the bulk density and the bulk viscosity of the fluid;

and

are, respectively, the average density and the effective viscosity of the physically adsorbed boundary layer in the inlet zone; D and Δx are, respectively, the fluid molecule diameter and the separation between the neighboring fluid molecules in the x coordinate direction in the adsorbed layer; q₀ = Δ_j+1/Δ_j (Δ_j is the separation between the (j + 1)^th and j^th fluid molecules across the layer thickness) and q₀ is constant; n is the equivalent number of the fluid molecules across the layer thickness; and Δ_n−2 is the separation between the neighboring fluid molecules across the layer thickness just on the adsorbed layer-fluid interface,

, and

. Here,

, and

,where η_line,j−1 is the local viscosity between the j^th and (j − 1)^th fluid molecules across the layer thickness and

Equation (1) is highly nonlinear. For the feasible integration of Equation (1), the parameter λ_bf in Equation (1) is taken as the equivalent constant value λ_bf,e = 2h_bf/(kh_i), where k is constant and ranges between 0 and 2. This treatment should surely introduce some calculation errors. The direct numerical solution to Equation (1) afterwards is also obtained to verify the accuracy of the mathematical derivation based on this equivalent treatment.

Substituting dx = dh/tanθ into Equation (1) and rearranging gives that:

()

where θ is the wedge angle of the bearing,

()

Integrating Equation (2) by substituting h(x) = (x − l₁ − l₂)tanθ gives that:

()

where ζ_x = (c/b)^1/3(x − l₁ − l₂)tanθ and y₁ is an integral constant.

By using the boundary condition

, it is solved from Equation (4) that:

()

where ζ = (c/b)^1/3l₃tanθ.

The pressure in the zone 1 is thus formulated as:

()

where

()

The pressure on the boundary between the zone 1 and the zone 2 as shown in Figure 1 is:

()

3.1.2. For the Zone 2 of the Inlet Zone

In this subzone, the surface separation is so low that the intermediate continuum fluid film disappears, and only the adsorbed boundary layer exists; the flow is molecular-scale and noncontinuum. According to the nanoscale flow equation [22], the total mass flow rate per unit contact length through this subzone is:

()

where

and

are, respectively, the average density and the effective viscosity of the confined fluid, and S the parameter describing the noncontinuum effect of the confined fluid across the surface separation.

Substituting dx = dh_tot/tanθ into Equation (9) and rearranging gives that:

()

where

and

Integrating Equation (10) gives that:

()

where y₂ is an integral constant.

Substituting h_tot = h_tot,o + (x − l₁)tanθ into Equation (11) gives that:

()

Based on the pressure continuity condition

, it is solved from Equation (12) that:

()

The pressure in this subzone is thus:

()

where

()

According to Equation (14), the pressure on the boundary between this subzone and the outlet zone is:

()

3.1.3. For the Outlet Zone

In the outlet zone, the surface separation is smaller than the total thickness of the two adsorbed boundary layers on the bearing surfaces so that there is only the adsorbed boundary layer. According to the nanoscale flow equation [22], the total mass flow rate per unit contact length through the outlet zone is:

()

where

and

are, respectively, the average density and the effective viscosity of the adsorbed boundary layer across the surface separation in the outlet zone, and S is the parameter describing the noncontinuum effect of the boundary layer in the outlet zone.

Integrating Equation (17) gives that:

()

where

, and y₃ is an integral constant.

Based on the boundary condition p|_x=0 = 0, it is solved from Equation (18) that y₃ = 0. The pressure in the outlet zone is thus:

()

where

and

According to Equation (19), the pressure on the boundary between the inlet zone and the outlet zone is:

()

3.1.4. Mass Flow Rate and Carried Load of the Bearing

Solving the coupled Equations (16) and (20) gives the mass flow rate per unit contact length through the bearing as:

()

The load per unit contact length carried by the bearing is:

()

where

()

where k₁ = c^2/3tan²θ, k₂ = −2c^2/3(l₁ + l₂)tan²θ − (bc)^1/3tanθ,

, and

3.2. Numerical Solution

For examining the accuracy of the derived equations in Section 3.1 based on the assumed equivalent value λ_bf,e, direct numerical calculations were also carried out based on Equations (1) and (17). This section describes the detailed numerical procedure.

In Figure 2, the discretized points are, respectively, evenly distributed in the outlet zone, in the zone 2 and in the zone 1 with the total numbers (N₁ + 1), (N₂ + 1), and (N₃ + 1).

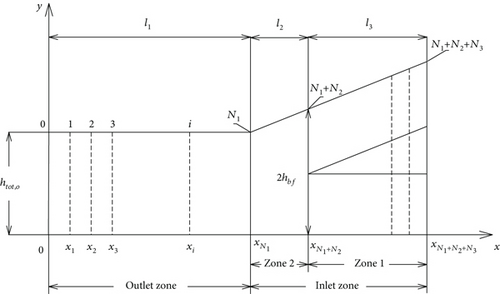
3.2.1. Numerical Analysis for the Outlet Zone

By backward difference, the pressure on the i^th discretized point in the outlet zone as shown in Figure 3 is expressed as:

()

where p_i and p_i−1 are, respectively, the pressures on the i^th and (i − 1)^th discretized points of the outlet zone, and δ_x,1 = l₁/N₁.

The pressure on the i^th discretized point is:

()

According to Equations (17) and (24) and the boundary condition p₀ = 0, it is obtained from Equation (25) that:

()

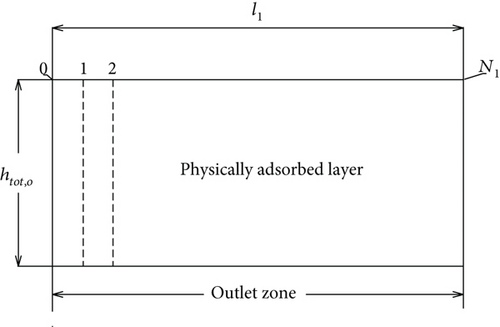
As shown above, the backward difference scheme can make the numerical results be easily obtained.

The pressure on the

discretized point is:

()

The load per unit contact length carried by the bearing outlet zone is:

()

3.2.2. Numerical Solution for the Zone 2 of the Inlet Zone

By backward difference, the pressure on the i^th discretized point in the zone 2 of the inlet zone as shown in Figure 4 is expressed as:

()

where p_i and p_i−1 are, respectively, the pressures on the i^th and (i − 1)^th discretized points in this subzone, and δ_x,2 = l₂/N₂.

The pressure on the i^th discretized point is:

()

By substituting Equations (9) and (29), it is obtained from Equation (30) that:

()

The pressure on the

discretized point is:

()

The force per unit contact length generated by the film in this subzone is:

()

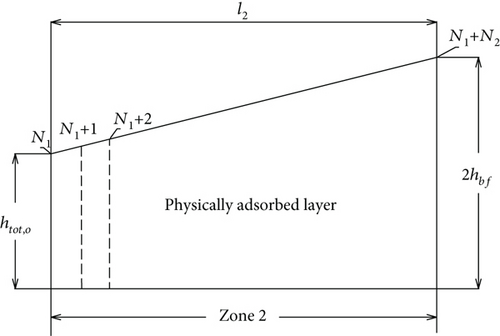
3.2.3. Numerical Solution for the Zone 1 of the Inlet Zone

By backward difference, the pressure on the i^th discretized point in the zone 1 of the inlet zone as shown in Figure 5 is expressed as:

()

where p_i and p_i−1 are, respectively, the pressures on the i^th and (i − 1)^th discretized points in this subzone, and δ_x,3 = l₃/N₃.

The pressure on the i^th discretized point is:

()

By substituting Equations (2) and (34), it is obtained from Equation (35) that:

()

The pressure on the

discretized point is:

()

The force per unit contact length generated by the film in this subzone is:

()

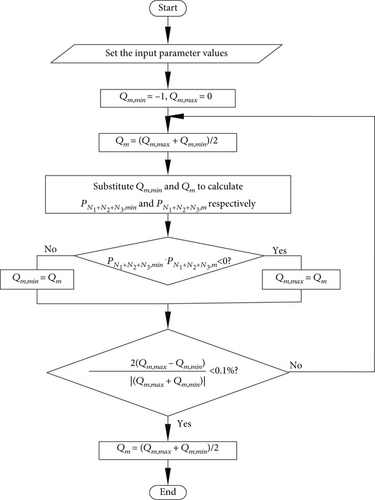
3.2.4. Numerical Solution Procedure

In the numerical calculation, the initial value of q_m is chosen as that calculated from the classical hydrodynamic theory [3]. Then, the pressures on all discretized points can be calculated from the equations shown above, by starting the calculation from the exit of the bearing. The value of q_m in the iteration will be changed until the following convergence criterion is satisfied: |2(Q_m,max − Q_m,min)/(Q_m,max + Q_m,min)| < 0.1%. Figure 6 shows the numerical solution procedure.

4. Calculation

Exemplary calculations were made for the following operational parameter values:

()

The parameters C_q1(H_bf,1) and C_q2(H_bf,2) are generally expressed as [24]:

()

where H_bf is H_bf,1 or H_bf,2;

;

; and m₀, m₁, m₂, and m₃ are, respectively, constant; H_bf,1 = h_bf/h_cr,bf,1; H_bf,2 = h_tot/h_cr,bf,2; and h_cr,bf,1 and h_cr,bf,2 are, respectively, the critical thicknesses for characterizing the rheological properties of the adsorbed boundary layer in the zone 1 of the inlet zone and those of the boundary layer confined in the whole surface separation in the zone 2 of the inlet zone and in the outlet zone. In the analytical derivation, the values of C_q2 in the zone 2 of the inlet zone as shown in Figure 1 are treated as an approximate and constant value to reduce the problem nonlinearity although they are actually varied and dependent on the surface separation in this subzone as shown by Equation (40). When calculating C_q2 from Equation (40) for the zone 2 of the inlet zone, it is taken that h_tot = (h_tot,o + 2h_bf)/2 to find the average and constant value of H_bf,2 in this subzone according to Figure 1.

The parameters C_y1(H_bf,1) and C_y2(H_bf,2) are generally expressed as [24]:

()

where

, and H_bf is same as in Eq.(40), and a₀, a₁, and a₂ are, respectively, constant.

The parameter S is expressed as [24]:

()

where H_bf,2 is same as in Equation (40), and n₀, n₁, n₂, and n₃ are, respectively, constant.

The regressed equations for F₁, F₂, and ε are repeated as follows [15]:

()

The thickness of the adsorbed boundary layer was calculated from the following equation:

()

The weak, medium, and strong fluid-bearing surface interactions were, respectively, considered. The input parameter values for these interactions are, respectively, shown in Tables 1–4.

1. Fluid viscosity data for different fluid-bearing surface interactions [24].

Interaction	Parameter
Interaction	a₀	a₁	a₂
Strong	1.8335	-1.4252	0.5917
Medium	1.0822	-0.1758	0.0936
Weak	0.9507	0.0492	1.6447E-4

2. Fluid density data for different fluid-bearing surface interactions [24].

Interaction	Parameter
Interaction	m₀	m₁	m₂	m₃
Strong	1.43	-1.723	2.641	-1.347
Medium	1.30	-1.065	1.336	-0.571
Weak	1.116	-0.328	0.253	-0.041

3. Fluid noncontinuum property data for different fluid-bearing surface interactions [24].

Interaction	Parameter
Interaction	n₀	n₁	n₂	n₃
Strong	0.4	-1.374	-0.534	0.035
Medium	-0.649	-0.343	-0.665	0.035
Weak	-0.1	-0.892	-0.084	0.1

4. The values of n, q₀, γ, h_cr,bf,1, and h_cr,bf,2 for different fluid-bearing surface interactions.

Interaction	Parameter
Interaction	n	q₀	γ	h_cr,bf,1(nm)	h_cr,bf,2(nm)
Strong	8	1.2	1.5	40	80
Medium	5	1.1	1	20	40
Weak	3	1.03	0.5	7	14

5. Results

5.1. Validation of the Numerical Calculation

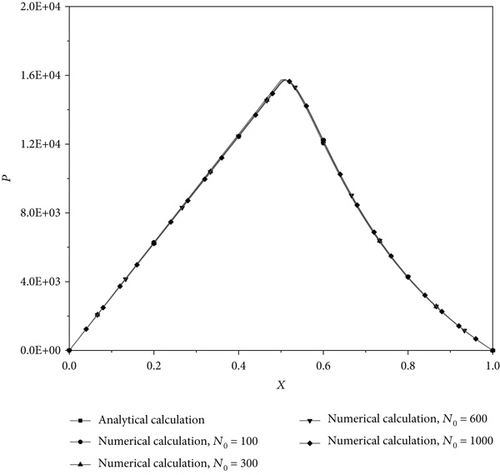
For validating the numerical calculation, the numerically solved pressures for different discretized points in the bearing are compared in Figure 7 with the classical hydrodynamic theory calculations [3] when the model of the bearing is assumed as classical (i.e., the fluid is Newtonian with the adsorbed boundary layer neglected). With the discretized points nearly evenly distributed in the bearing, it is shown that N₀ = N₁ + N₂ + N₃=1000 is sufficient for the numerical accuracy.

5.2. Validation of the Analytical Derivations for the Present Model of the Bearing

In the analytical derivations of the pressure and carried load of the present model of the bearing as shown above, it is critically important to assume the equivalently constant parameter λ_bf,e and to take h_tot = (h_tot,o + 2h_bf)/2 to calculate the approximate and constant values of C_q2, C_y2, and S in the zone 2 of the inlet zone. These treatments will unavoidably cause the calculation errors. For estimating the accuracy of the analytical derivations for the present bearing, the calculations of the pressure from Equations (6), (14), and (19) are compared with the full numerically calculated pressures. In the numerical calculation, N₀ = 1000.

Figure 8(a) compares the dimensionless pressure distributions in the present model of the bearing, respectively, analytically calculated and numerically solved for different fluid-bearing surface interactions for the same operating conditions. It is shown that for the weak and medium fluid-bearing surface interactions, there are only small differences between these two calculations; however, for the strong fluid-bearing surface interaction, there are significant differences between these two calculations. It is suspected that the analytical calculation errors should mainly be arising from the approximate calculations of C_q2, C_y2, and S (respectively, from Equations(40)–(42)) in the zone 2 of the inlet zone by putting h_tot = (h_tot,o + 2h_bf)/2. As shown in Figure 1, if h_tot,o is very close to 2h_bf, the surface separation in the zone 2 of the inlet zone is nearly constant, and it can be taken as h_tot = (h_tot,o + 2h_bf)/2. In such a case, the calculation errors of C_q2, C_y2, and S in the zone 2 of the inlet zone should be small enough so that the accuracy of the analytical calculation is good.

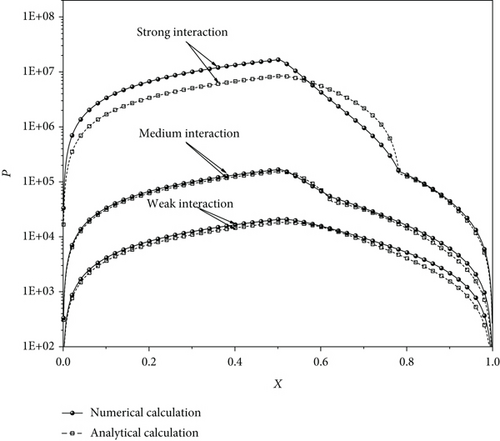
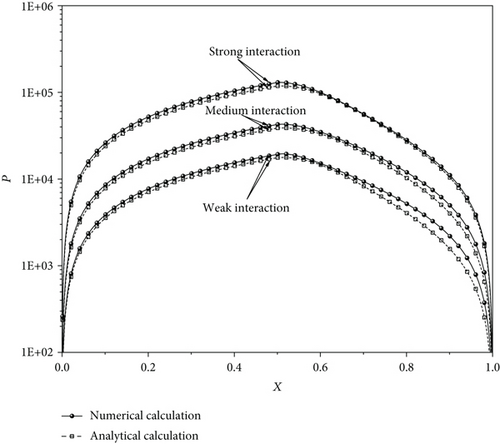
For justifying this suspect, we use h_tot,o = (2h_bf)0.99 to recalculate the analytical pressures and make the similar comparisons in Figure 8(b). This chosen value of h_tot,o is very close to 2h_bf, and it should substantially improve the accuracies of the analytical calculation. It is shown that for the strong interaction, the calculation error of the analytical equations is much reduced compared to those in Figure 8(a). Figure 8(b) verifies our conjecture.

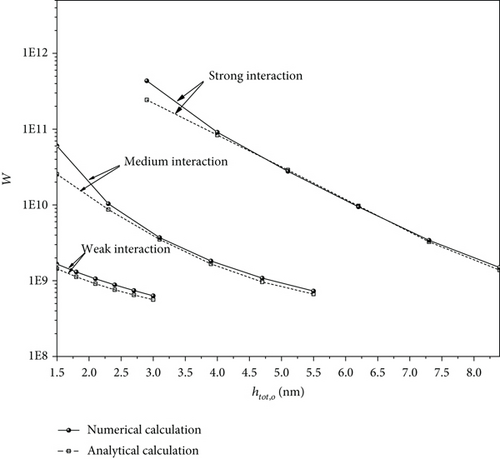
Figure 9 compares the analytically calculated dimensionless loads of the present model of the bearing (by Equation (22)) with those numerically calculated for different fluid-bearing surface interactions. It is shown that for the weak interaction, the accuracy of the analytical calculation is acceptable, and for the medium interaction, it is acceptable for h_tot,o ≥ 2.5nm, while for the strong interaction, it is acceptable for h_tot,o ≥ 4nm. The comparisons validate the value of the present analytical derivations.

5.3. Bearing Performances

This section presents the numerical calculation results for the hydrodynamic pressure and carried load of the present model of the bearing. In all these calculations, N₀ = 1000.

5.3.1. Pressure Distribution

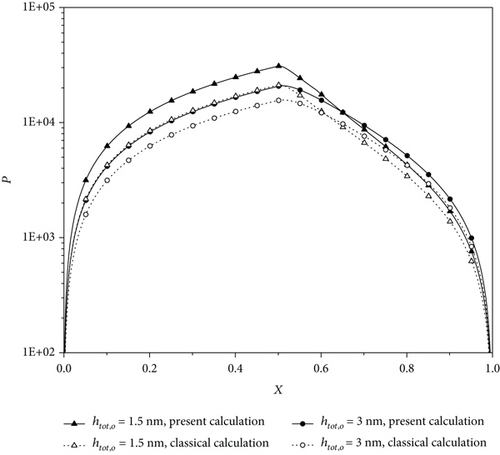
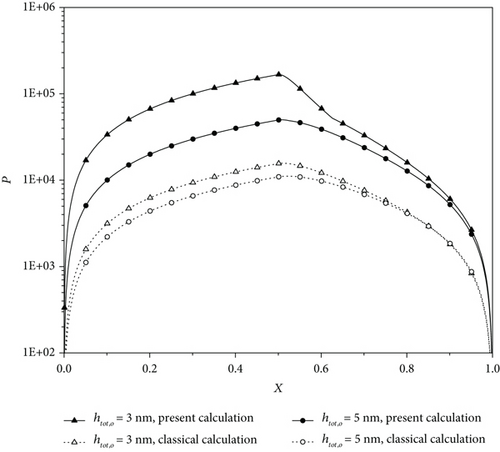
Figures 10(a)–10(c) show the dimensionless hydrodynamic pressure distributions in the present model of the bearing, respectively, for different fluid-bearing surface interactions and different bearing clearances. Compared to the classical hydrodynamic theory calculation, the present calculation shows that for the weak interaction and the outlet bearing clearances of 1.5 nm and 3 nm, the pressures in the bearing are very significantly increased due to the physically adsorbed boundary layers on the two bearing surfaces. For the medium and strong interactions, the pressure increases can, respectively, be 1 and 2 orders. These figures strongly indicate that the fluid-bearing surface interaction has a heavy influence on the pressures in the bearing.

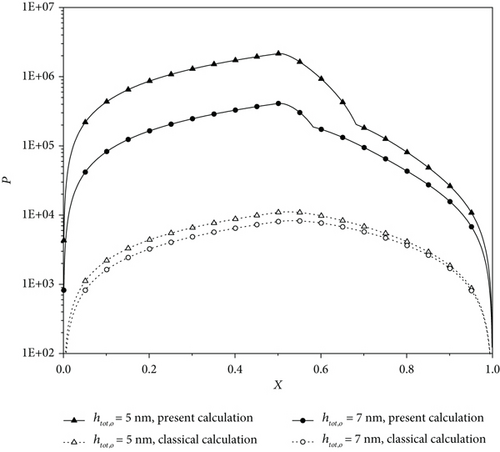
5.3.2. Carried Load of the Bearing

Figure 11 compares the calculated dimensionless carried loads of the present model of the bearing for different fluid-bearing surface interactions for the same operating conditions. For maintaining the model of the bearing for all these three interactions, the plotted range of h_tot,o is narrow. The weak interaction gives the load of the bearing a bit larger than that calculated from the classical hydrodynamic theory. The medium and strong interactions give the loads of the bearing, respectively, 1 and 3 orders larger than the classical hydrodynamic theory calculation. In the studied model of the bearing, owing to the ultralow surface separating and the resulting heavy influence of the physically adsorbed boundary layer on the bearing surface, the fluid-bearing surface interaction largely alters the bearing performance.

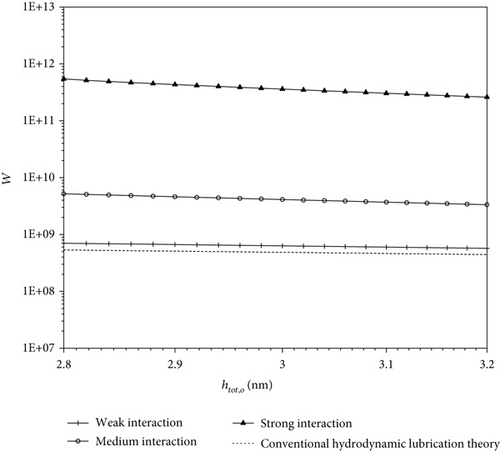
6. Conclusions

In a hydrodynamic thrust slider bearing, when the surface separation in the outlet zone is ultralow (e.g. on the 1 nm scale), in the outlet zone there is only the boundary layer physically adsorbed to the bearing surfaces, while in most of the inlet zone, there are the adsorbed boundary layers and the continuum fluid film. In this case, the bearing outlet zone is in the boundary lubrication, while most of the bearing inlet zone is in the multiscale lubrication. The classical analysis fails for this bearing owing to neglecting the adsorbed boundary layer.

The present study develops the mathematical analysis for the hydrodynamic wedge-platform thrust slider bearing with ultralow clearances by addressing this mode of lubrication. The nanoscale flow equation [22] describes the flow of the boundary layer in the outlet zone, and the multiscale flow equations [22] describes the flows of the adsorbed boundary layers and the intermediate continuum fluid film in the inlet zone.

The closed-form explicit equations have been derived, respectively, for calculating the hydrodynamic pressure and carried load of the studied bearing by making some simplifying assumptions, i.e., by introducing the equivalent parameter λ_bf,e for the multiscale hydrodynamic area and by using h_tot = (h_tot,o + 2h_bf)/2 to calculate the values of C_q2, C_y2, and S in the boundary lubrication area in the inlet zone. The numerical calculations were also carried out to verify the accuracies of the derived analytical equations. It was found that for the weak fluid-bearing surface interaction, the accuracies of the analytical equations are acceptable; for the medium interaction, they are acceptable for h_tot,o ≥ 2.5 nm (h_tot,o is the surface separation in the bearing outlet zone), while for the strong interaction, they are acceptable for h_tot,o ≥ 4 nm. It was found that the errors of the derived analytical equations are mainly caused by using h_tot = (h_tot,o + 2h_bf)/2 to calculate C_q2, C_y2, and S in the boundary lubrication area in the inlet zone.

The numerical calculations show that in the present model of the bearing with ultralow surface separations, even for the weak fluid-bearing surface interaction, the pressures are very significantly increased due to the physically adsorbed boundary layers on the two bearing surfaces; for the medium and strong interactions; the pressure increases can, respectively, be 1 and 2 orders; and the load-carrying capacity of the bearing is correspondingly increased by the fluid-bearing surface interaction.

Nomenclature

a₀, a₁, a₂:: Constant
C_y1:
C_q1:
C_y2:
C_q2:
D:: Fluid molecule diameter
F₁, F₂, ε:: Parameters accounting for the noncontinuum effect of the adsorbed boundary layer
h:: Continuum fluid film thickness
h_cr,bf,1:: Critical thickness for characterizing the rheological properties of the adsorbed boundary layer in the zone 1
h_cr,bf,2:: Critical thickness for characterizing the rheological properties of the adsorbed boundary layer in the zone 2 or in the outlet zone
h_bf:: Thickness of the adsorbed layer
h_i:: Continuum fluid film thicknesses on the entrance of the bearing
h_tot:: Surface separation
h_tot,i:: Surface separation on the entrance of the bearing
h_tot,o:: Surface separation on the exit of the bearing
H_bf,1:
H_bf,2:: h_bf/h_cr,bf,2
k:: Parameter for formulating λ_bf,e
l₁, l₂, l₃:: Widths of the outlet zone, the zone 2 and the zone 1, respectively
m₀, m₁, m₂, m₃:: Constant
n₀, n₁, n₂, n₃:: Constant
n:: Equivalent number of the fluid molecules across the adsorbed layer thickness
N₀:: N₁ + N₂ + N₃
N₁ + 1:: Number of the discretized points in the outlet zone
N₂ + 1:: Number of the discretized points in the zone 2
N₃ + 1:: Number of the discretized points in the zone 1
p:: Hydrodynamic pressure
P:: Dimensionless pressure, ph_tot,o/uη
q₀:: Δ_j+1/Δ_j
q_m:: Total mass flow rate per unit contact length through the bearing
Q_m:: Dimensionless total mass flow rate, q_m/(uh_tot,oρ)
S:: Parameter accounting for the noncontinuum effect across the surface separation
u:: Sliding speed of the bearing
w₁,w₂,w₃:: Load components, respectively, contributed by the outlet zone, the zone 2 and the zone 1
W:: Dimensionless load, w/uη
x:: Coordinate
X:: Dimensionless coordinate, x/(l₁ + l₂ + l₃)
y₁, y₂, y₃:: Integral constant, respectively
θ:: Wedge angle of the bearing
γ:: Exponent
ρ:: Fluid bulk density
:: Average density of the adsorbed boundary layer in the zone 1
:: Average density of the adsorbed boundary layer across the whole surface separation in the zone 2 or in the outlet zone
η:: Fluid bulk viscosity
:: Effective viscosity of the adsorbed boundary layer in the zone 1
:: Effective viscosity of the adsorbed boundary layer in the zone 2 or in the outlet zone
η_line,j−1:: Local viscosity between the j^th and (j − 1)^th fluid molecules across the layer thickness
λ_bf:: h_bf/h
λ_bf,e:: 2h_bf/(kh_i)
Δ_j:: Separation between the (j + 1)^th and j^th fluid molecules across the layer thickness
Δx:: Separation between the neighboring fluid molecules in the flow direction in the adsorbed boundary layer
Δ_n−2:: Separation between the neighboring fluid molecules across the layer thickness just on the boundary between the adsorbed boundary layer and the continuum fluid film
δ_x,1:: l₁/N₁
δ_x,2:: l₂/N₂
δ_x,3:: l₃/N₃
ζ:: (c/b)^1/3l₃tanθ
ζ_x:: (c/b)^1/3(x − l₁ − l₂)tanθ.

Conflicts of Interest

The authors declare that there is no conflict of interest with this research.

Open Research

Data Availability

The data reported in this paper will be available from the corresponding author with reasonable request.

References

1 Chauveteau G., Tirrell M., and Omari A., Concentration dependence of the effective viscosity of polymer solutions in small pores with repulsive or attractive walls, Journal of Colloid and Interface Science. (1984) 100, no. 1, 41–54, https://doi.org/10.1016/0021-9797(84)90410-7, 2-s2.0-0021458355.
10.1016/0021-9797(84)90410-7
CAS Web of Science® Google Scholar
2 Cheng S., Luan B., and Robbins M. O., Contact and friction of nanoasperities: effects of adsorbed monolayers, Physical Review E. (2010) 81, no. 1, article 016102, https://doi.org/10.1103/PhysRevE.81.016102, 2-s2.0-76649118801, 20365427.
10.1103/PhysRevE.81.016102
PubMed Web of Science® Google Scholar
3 Pinkus O., Sternlicht B., and Saibel E., Theory of hydrodynamic lubrication, Journal of Applied Mechanics. (1962) 29, no. 1, 221–222, https://doi.org/10.1115/1.3636485.
10.1115/1.3636485
Google Scholar
4 Gu K. C., Shao S. J., and Zhang Y. B., Multiscale analysis of hydrodynamic journal bearing considering the effect of the physically adsorbed boundary layer, International Journal of Non-Linear Mechanics. (2021) submitted.
PubMed Google Scholar
5 Findenegg G. H., The volumetric behavior of hydrocarbon liquids near the graphon surface, Journal of Colloid and Interface Science. (1971) 35, no. 2, 249–253, https://doi.org/10.1016/0021-9797(71)90117-2, 2-s2.0-0015020216.
10.1016/0021-9797(71)90117-2
CAS Web of Science® Google Scholar
6 Brown C. E., Everett D. H., Powell A. V., and Thome P. E., Adsorption and structuring phenomena at the solid/liquid interface, Faraday Discussions of the Chemical Society. (1975) 59, 97–108, https://doi.org/10.1039/dc9755900097, 2-s2.0-37049113910.
10.1039/dc9755900097
CAS Google Scholar
7 Grosse-Rhode M. and Findenegg G. H., Formation of ordered monolayers of n -alkanes at the cleavage face of nickel chloride, Journal of Colloid and Interface Science. (1978) 64, no. 2, 374–376, https://doi.org/10.1016/0021-9797(78)90375-2, 2-s2.0-0011749843.
10.1016/0021-9797(78)90375-2
CAS Web of Science® Google Scholar
8 Kern H., Rybinski W. V., and Findenegg G. H., Prefreezing of liquid n-alkanes near graphite surfaces, Journal of Colloid and Interface Science. (1977) 59, no. 2, 301–307, https://doi.org/10.1016/0021-9797(77)90012-1, 2-s2.0-0001128922.
10.1016/0021-9797(77)90012-1
CAS Web of Science® Google Scholar
9 Zhang Y. B., New explanation for the measured very low film thicknesses in lubricated concentrated contacts, Journal of the Balkan Tribological Association. (2021) 27, 439–444.
Google Scholar
10 Bitsanis I., Vanderlick T. K., Tirrell M., and Davis H. T., A tractable molecular theory of flow in strongly inhomogeneous fluids, The Journal of Chemical Physics. (1988) 89, no. 5, 3152–3162, https://doi.org/10.1063/1.454972, 2-s2.0-36549093806.
10.1063/1.454972
CAS Web of Science® Google Scholar
11 Somers S. A. and Davis H. T., Microscopic dynamics of fluids confined between smooth and atomically structured solid surfaces, The Journal of Chemical Physics. (1992) 96, no. 7, 5389–5407, https://doi.org/10.1063/1.462724, 2-s2.0-84953659603.
10.1063/1.462724
CAS Web of Science® Google Scholar
12 Takaba H., Onumata Y., and Nakao S., Molecular simulation of pressure-driven fluid flow in nanoporous membranes, The Journal of Chemical Physics. (2007) 127, no. 5, article 054703, https://doi.org/10.1063/1.2749236, 2-s2.0-34547661704, 17688353.
10.1063/1.2749236
PubMed Web of Science® Google Scholar
13 Jiang C., Ouyang J., Zhuang X., Wang L., and Li W., An efficient fully atomistic potential model for dense fluid methane, Journal of Molecular Structure. (2016) 1117, 192–200, https://doi.org/10.1016/j.molstruc.2016.03.093, 2-s2.0-84962019279.
10.1016/j.molstruc.2016.03.093
CAS Web of Science® Google Scholar
14 Jiang C., Wang X., Liu Q., and Ke C., Investigation of the relationship between nanochannel width and mass transfer characteristics for dense methane nanofluidics, International Communications in Heat and Mass Transfer. (2020) 118, article 104879, https://doi.org/10.1016/j.icheatmasstransfer.2020.104879.
10.1016/j.icheatmasstransfer.2020.104879
Web of Science® Google Scholar
15 Zhang Y. B., Modeling of flow in a very small surface separation, Applied Mathematical Modelling. (2020) 82, 573–586, https://doi.org/10.1016/j.apm.2020.01.069.
10.1016/j.apm.2020.01.069
Web of Science® Google Scholar
16 Shao X. Y., Zhang Y. B., Pang M. J., and Jiang X. D., Multiscale analysis of hydrodynamic wedge-platform thrust slider bearing, Multiscale Science Engineering. (2021) 3, no. 1, 95–107, https://doi.org/10.1007/s42493-021-00059-4.
10.1007/s42493-021-00059-4
Google Scholar
17 Zhang Y. B., Multiscale mixed hydrodynamics in line contacts, Continuum Mechanics and Thermodynamics. (2022) 34, 507–518, https://doi.org/10.1007/s00161-021-01076-2.
10.1007/s00161-021-01068-2
CAS Web of Science® Google Scholar
18 Atkas O. and Aluru N. R., A combined continuum/DSMC technique for multiscale analysis of microfluidic filters, Journal of Computational Physics. (2002) 178, no. 2, 342–372, https://doi.org/10.1006/jcph.2002.7030, 2-s2.0-0037141173.
10.1006/jcph.2002.7030
CAS Web of Science® Google Scholar
19 Liu J., Chen S., Nie X., and Robbins M. O., A continuum-atomistic simulation of heat transfer in micro- and nano-flows, Journal of Computational Physics. (2007) 227, no. 1, 279–291, https://doi.org/10.1016/j.jcp.2007.07.014, 2-s2.0-35348910160.
10.1016/j.jcp.2007.07.014
Web of Science® Google Scholar
20 Sun J., He Y., and Tao W. Q., Scale effect on flow and thermal boundaries in micro-/nano-channel flow using molecular dynamics-continuum hybrid simulation method, International Journal for Numerical Methods in Engineering. (2010) 81, no. 2, 207–228, https://doi.org/10.1002/nme.2683, 2-s2.0-73149120465.
10.1002/nme.2683
Web of Science® Google Scholar
21 Yen T. H., Soong C. Y., and Tzeng P. Y., Hybrid molecular dynamics-continuum simulation for nano/mesoscale channel flows, Microfluidics and Nanofluidics. (2007) 3, no. 6, 665–675, https://doi.org/10.1007/s10404-007-0154-7, 2-s2.0-35949000822.
10.1007/s10404-007-0154-7
CAS Web of Science® Google Scholar
22 Zhang Y. B., The flow equation for a nanoscale fluid flow, International Journal of Heat and Mass Transfer. (2016) 92, 1004–1008, https://doi.org/10.1016/j.ijheatmasstransfer.2015.09.008, 2-s2.0-84943548725.
10.1016/j.ijheatmasstransfer.2015.09.008
CAS Web of Science® Google Scholar
23 Zhang Y. B., Multiscale hydrodynamics in line contacts, Mechanics Research Communications. (2021) 111, article 103658, https://doi.org/10.1016/j.mechrescom.2021.103658.
10.1016/j.mechrescom.2021.103658
Web of Science® Google Scholar
24 Zhang Y. B., Lubrication analysis for a line contact covering from boundary lubrication to hydrodynamic lubrication: part I-micro contact results, Journal of Computational and Theoretical Nanoscience. (2014) 11, no. 1, 62–70, https://doi.org/10.1166/jctn.2014.3318, 2-s2.0-84889067575.
10.1166/jctn.2014.3318
Google Scholar

All articles

Analysis for Hydrodynamic Wedge-Platform Thrust Slider Bearing with Ultralow Surface Separation

Abstract

1. Introduction

2. Model of the Studied Bearing

3. Theoretical Analysis

3.1. Mathematical Derivations

3.1.1. For the Zone 1 of the Inlet Zone

3.1.2. For the Zone 2 of the Inlet Zone

3.1.3. For the Outlet Zone

3.1.4. Mass Flow Rate and Carried Load of the Bearing

3.2. Numerical Solution

3.2.1. Numerical Analysis for the Outlet Zone

3.2.2. Numerical Solution for the Zone 2 of the Inlet Zone

3.2.3. Numerical Solution for the Zone 1 of the Inlet Zone

3.2.4. Numerical Solution Procedure

4. Calculation

5. Results

5.1. Validation of the Numerical Calculation

5.2. Validation of the Analytical Derivations for the Present Model of the Bearing

5.3. Bearing Performances

5.3.1. Pressure Distribution

5.3.2. Carried Load of the Bearing

6. Conclusions

Nomenclature

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analysis for Hydrodynamic Wedge-Platform Thrust Slider Bearing with Ultralow Surface Separation

Abstract

1. Introduction

2. Model of the Studied Bearing

3. Theoretical Analysis

3.1. Mathematical Derivations

3.1.1. For the Zone 1 of the Inlet Zone

3.1.2. For the Zone 2 of the Inlet Zone

3.1.3. For the Outlet Zone

3.1.4. Mass Flow Rate and Carried Load of the Bearing

3.2. Numerical Solution

3.2.1. Numerical Analysis for the Outlet Zone

3.2.2. Numerical Solution for the Zone 2 of the Inlet Zone

3.2.3. Numerical Solution for the Zone 1 of the Inlet Zone

3.2.4. Numerical Solution Procedure

4. Calculation

5. Results

5.1. Validation of the Numerical Calculation

5.2. Validation of the Analytical Derivations for the Present Model of the Bearing

5.3. Bearing Performances

5.3.1. Pressure Distribution

5.3.2. Carried Load of the Bearing

6. Conclusions

Nomenclature

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Related

Information