Advances in Mathematical Physics
Volume 2022, Issue 1 7753879
Research Article
Open Access

New Results of Some of the Conformable Models Arising in Dynamical Systems

Md Nur Alam, 

Corresponding Author

Md Nur Alam

Department of Mathematics, Pabna University of Science and Technology, Pabna, 6600, Bangladesh pust.ac.bd

Search for more papers by this author
Onur Alp Ilhan, 

Onur Alp Ilhan

Department of Mathematics and Science Education, Faculty of Education, Erciyes University, Kayseri 38039, Turkey erciyes.edu.tr

Search for more papers by this author
Jalil Manafian, 

Jalil Manafian

Department of Applied Mathematics, Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran tabrizu.ac.ir

Natural Sciences Faculty, Lankaran State University, 50, H. Aslanov str., Lankaran, Azerbaijan lsu.edu.az

Search for more papers by this author
Muhammad Imran Asjad, 

Muhammad Imran Asjad

Department of Mathematics, University of Management and Technology, Lahore 54700, Pakistan umt.edu.pk

Search for more papers by this author
Hadi Rezazadeh, 

Hadi Rezazadeh

Faculty of Engineering Technology, Amol University of Special Modern Technologies, Amol, Iran shomal.ac.ir

Search for more papers by this author
Haci Mehmet Baskonus, 

Haci Mehmet Baskonus

Department of Mathematics and Science Education, Faculty of Education, Harran University, Sanliurfa, Turkey harran.edu.tr

Search for more papers by this author
First published: 20 September 2022
https://doi.org/10.1155/2022/7753879
Citations: 8
Academic Editor: Jorge E. Macias-Diaz

Abstract

This article investigates the new results of three nonlinear conformable models (NLCMs). To study such varieties of new soliton structures, we perform the generalized Kudryashov (GK) method. The obtained new results are defined in the styles of the exponential and rational functions. The derived new soliton structures are stable, serviceable, and fitting to embrace the conformable dynamics, chaotic vibrations, global bifurcations, optimal control problems, fluid mechanics, plasma physics, system identification, local bifurcations, control theory and resonances, and so many. The outcomes declare that the process is hugely valuable and accessible for investigating nonlinear conformable order models treated in theoretical physics.

1. Introduction

Conformable calculus is a part of an analytical investigation that scrutinizes the actual or complicated number order integral or differential supervisors. It is a presently debated problem with scientists since many multidimensional operations could be formed through conformable derivatives in numerous disciplines of implemented science which as solid-state physics, fractional dynamics, fluid mechanics, control theory, geochemistry, plasma physics, astrophysics, system identification, chemical physics, and many more. The various appeals of conformable derivatives show that there is an essential requirement for better numerical and analytical algorithms including real objects and methods. Consequently, the examination of the soliton solutions for nonlinear conformable models expresses a critical function for the research of nonlinear wave phenomena. Numerous mathematical procedures have been presented to get results of NLCMs, for example, homotopy perturbation method [1], residual power series method [2], Shifted Jacobi spectral collocation method [3], reproducing kernel Hilbert space method [4], modified generalized Taylor fractional series method [5], the improved fractional Riccati extension scheme [6], method of separation variables [7], generalized (G′/G)-extension scheme [8], Chebyshev collocation way [9], rational (G′/G)-extension scheme [10], the first integral way [11], modified exp-task way [12], variational iteration method [13], modified Khater method [14], and iterative reproducing kernel Hilbert space approach [15].

The paper applied the GK method [16] to derive the different types of solitary wave structures for the conformable Duffing equation (DE) [8], the conformable Riccati equation (RE) [8], and the conformable biological population model (BPM) [6, 10]; in [17], it is examined time-fractional biological population model and gained some new solitary wave structures through the modified (G′/G)-expansion method.

Firstly, the conformable RE [8] is as follows:
(1)
where
(2)
and β0, β1, and β2 are constants. If ϖ = 1, then the Eq. (1) decreases to the classical RE. The significance of the Eq. (1) normally occurs in optimal control difficulties. The result of the linear-quadratic optimal control depends on a RE, which has to be observed for the control rule’s all-time horizon. The present research on conformable RE leads to concentrate on accurate values for ϖ. ϖ = 1/2 is remarkably familiar. This is because, in classical conformable calculus, numerous of the models were improved applying these appropriate orders of derivatives. In current attention, many further usual values of the ϖ arrive in the models. Consequently, one requires to analyze mathematical processes to determine the RE of arbitrary order. Inserting appropriate values of β0 = 1, β1 = 0, and β2 = −1 in (1), the general conformable RE uses
(3)

Eq. (3) exposes numerous charming soliton structures that have not yet been confirmed. In the equations modeling wave phenomena, one of the key goals is the soliton structures, maintaining results of the constant form with a constant velocity. Soliton constructions, together with their result definitions, are in explicit or implicit ways and are pretty fantastic from the perspective of applications. Such a diversity of soliton constructions is instantly named because they do not exchange their sketches when propagation. Our attention in this investigation is to analyze the soliton constructions; the solitary waves enclosed through asymptotically zero at a substantial distance, traveling waves, the kink variety waves, and the periodic waves, which increase or run down from one asymptotic state to other states.

Secondly, the conformable DE [8] is as follows:
(4)
where ϖ is a conformable constant. In the model, the damping force is proportionate to the initial order derivative of the displacement. Numerous prosperous importance in manufacturing engineering have been informed by maintaining the integral form damping to a conformable form one because it can describe the compound frequency of damping materials. The display of fusion phenomena and the manifestation of fission aspects for solitons have been introduced theoretically and experimentally.
Finally, the conformable BPM [6, 10] is as follows:
(5)

Here W describes the population density, S1 and S2 are free parameters, and s1(W2 − s2) expresses the population supply owing to births and deaths. The solutions obtained exhausting the mentioned procedure can be expressed in the form of trigonometric, hyperbolic, and rational type functions. These arrangements of the solutions are reasonable for revising convinced real type physical phenomena. However, there are various types of models that are useful for computing different models, for instance, ranking extreme efficient decision?, new extended rational SGEEM for construction of optical solitons?, the time nonlinear fractional generalized equal width model arising in shallow water channel?, an efficient alternating direction explicit method?, the variable coefficients generalized shallow water wave equation?, M-fractional solitary wave solutions and convergence analysis for Boussinesq equations?, the solving the Volterra integral equations with a weakly singular kernel? and an analytical analysis to solve the fractional differential equations? In the literature, these nonlinear model of equations for natural models are well used. These nonlinear models can be used alone or in combination to model physical processes relevant to engineering, technology, and sciences.

2. Glimpse of the GK Method

Step 1. Suppose a conformable PDE for W(x, t) takes the form

(6)
where R represents a polynomial in W, and ∂ϖW/∂tϖ and ∂2ϖW/∂t2ϖ are conformable derivatives of W. (7).

To locate the transformation of Eq. (6),
(7)
From Eq. (6) and Eq. (7), we locate the following ODE:
(8)

Step 2. Compute M and N on Eq. (8).

Step 3. We examine the following:

(9)

Here, Ai and Bj are constants as well as AN, BM ≠ 0 and Φ:
(10)
Eq. (10) provides
(11)

Step 4. Compute N and M in Eq. (9) with the nonlinear term of W(ξ) in Eq. (6) or Eq. (8).

Step 5. From Eq. (9), Eq. (8), and Eq. (11), we could be solved to determine Φ(ξ) through MAPLE.

3. Solitons to the Conformable RDE

Using ξ = x + (ctϖ/ϖ), then Eq. ((1)) changes for Z(x, t) = Z(ξ):
(12)
From Eq. (12), (Z′(ξ) and Z2(ξ))⇒(2(N − M) = N − M + 1)⇒(N = M + 1). Setting M = 1, then N = 2. Therefore, we get
(13)

Through Eq. (13) and Eq. (12), we find the following:

The first set:
(14)
where B0 and B1 are constants. From the first set, Eq. (13) and Eq. (12), we have
(15)
The second set:
(16)

where B0 and B1 are constants.

Similarly, we get
(17)
The third set:
(18)
where B0 is constants. Similarly, we get
(19)
The fourth set:
(20)
where B0 is constants. Similarly, we get:
(21)

4. Solitons to the Conformable DE

Using ξ = x + (ctϖ/ϖ), then Eq. (4) changes for V(x, t) = V(ξ):
(22)
From Eq. (22), (V″(ξ) and V3(ξ))⇒(3(N − M) = N − M + 2)⇒(N = M + 1). Setting M = 1, then N = 2. Therefore, we get
(23)

Through Eq. (23) and Eq. (22), we have the following sets:

The first set:
(24)
From the first set, Eq. (13) and Eq. (12), we have
(25)
The second set:
(26)
Similarly, we get
(27)

5. Solitons to the Conformable BPM

Let us consider the Eq. (5).

Making W(x, y, t) = W(ξ), ξ = S3(x + iy) − S0tϖ/ϖ, and i2 = −1 into the Eq. (5), we derive
(28)
From Eq. (28), (V′′(ξ) and V3(ξ))⇒(3(N − M) = N − M + 2)⇒(N = M + 1). Setting M = 1, then N = 2. Therefore, we get
(29)

Through Eq. (29) and Eq. (28), we have the following sets:

The first set:
(30)
From the first set, Eq. (29) and Eq. (28), we have
(31)
The second set:
(32)
Similarly, we get
(33)
The third set:
(34)
Similarly, we get
(35)
The fourth set:
(36)
Similarly, we get
(37)

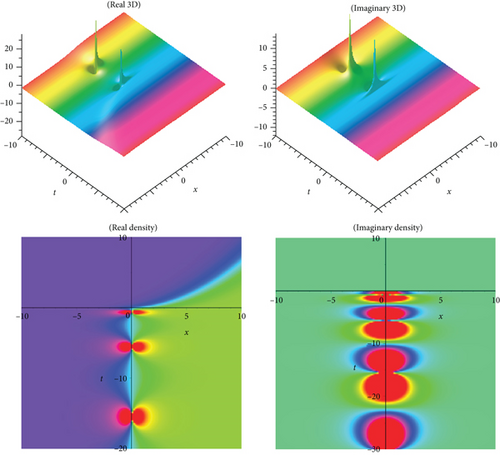
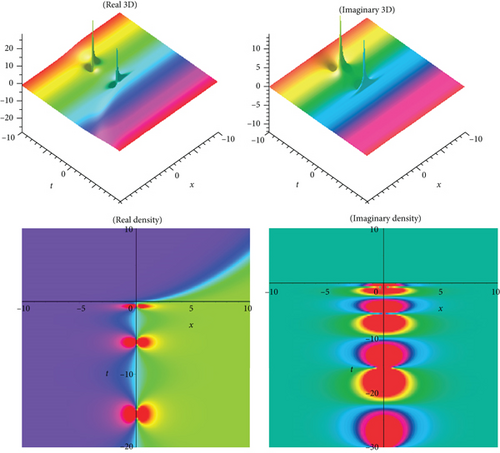
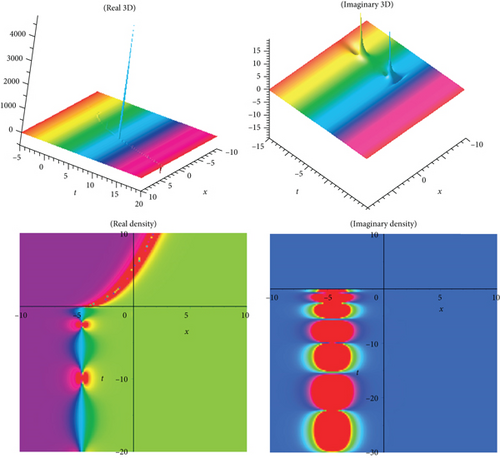
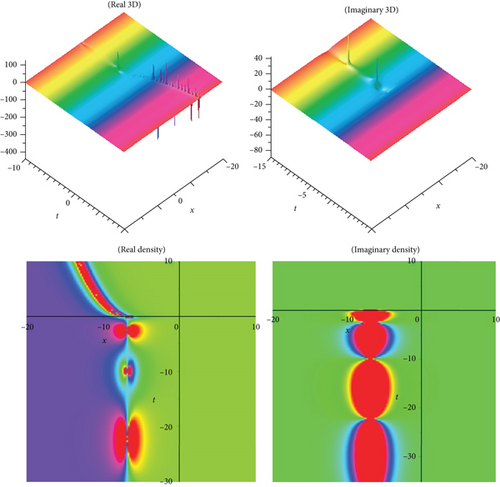
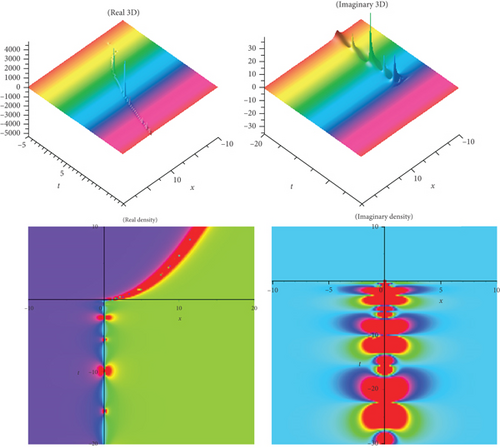
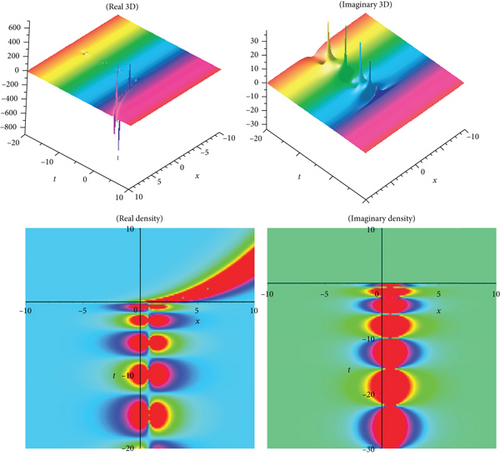
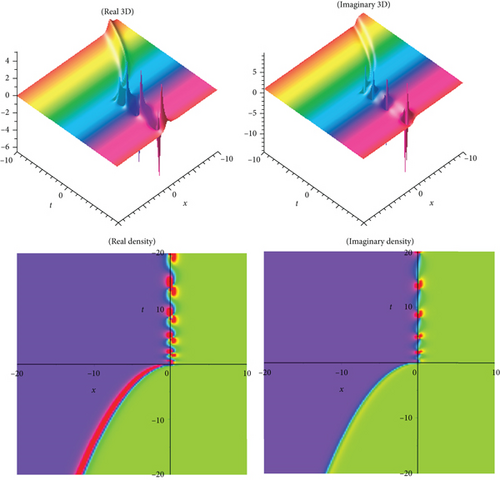
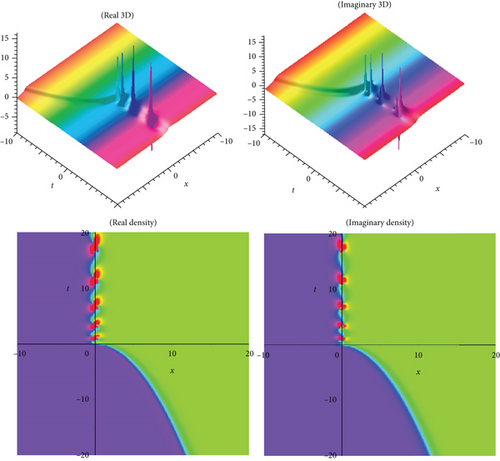
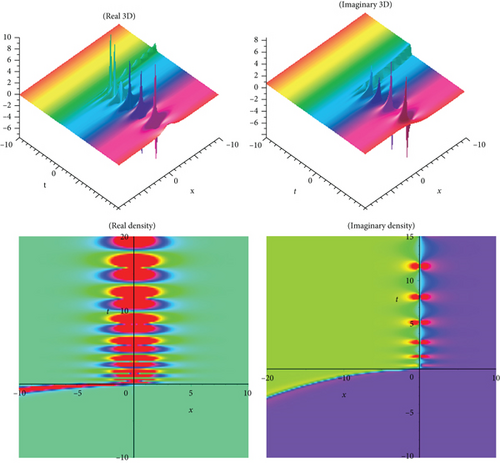
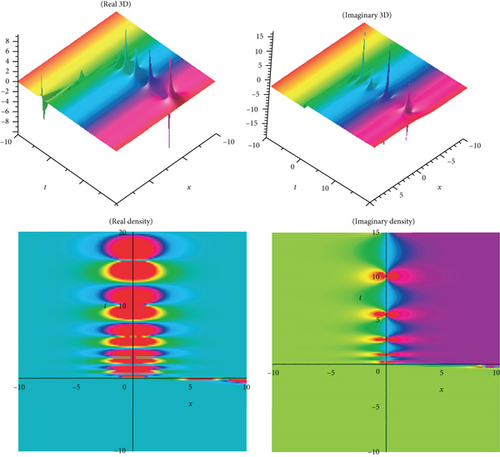
The physical meaning of solutions is as follows: this segment will examine the physical explanation of the time-fractional biological population model of the acknowledged exact influencing wave equation. The three-dimensional (3D) charts and density plots including real and imaginary parts of the newest fractional BPM equations’ travelling wave solutions are discussed in this subsection. A three-dimensional plot depicts the extent of divergence across time or relates many wave issues. Wave facts are arranged in a logical order with equally spaced disturbances and connected by a line to show the relationships between them. The diagram’s pictorial value is enhanced by the 3D style. The density plot and 3D plot are designed to show the low and high frequency and amplitude extremely clearly.

6. Conclusion

In the current work, we have secured the exact traveling wave answers in the novel method, for instance, kink variety traveling wave answers, double soliton, multiple solitons, periodic, and singular soliton of the Eqs. (1), (4), and (5). The two models’ established answers, as mentioned above, are applicable to search the fusion and fission aspects. This natural phenomenon happens for solitons, electromagnetic interactions, scalar electrodynamics, quantum relativistic one-particle theory, relativistic energy-momentum relation, etc. The magnitude of the Eq. (1) usually rises in determining the optimal control difficulties. In the echo region, the oscillation of vibration depends on the damping exponent in a nontrivial way. So, to reduce severe fluctuation is an introductory presentation of the Eq. (4). The picture is a crucial device for information and to express the answers to the difficulties lucidly. When performing the calculation in daily life, we need a fundamental knowledge of building graphs. Subsequently, the graphical displays of a few answers are illustrated in Figures 1–10, respectively. We displayed Figures 1–10, respectively, for a few of the derived answers to reveal more features for the prescribed model. The GK method’s performance is more accessible and reliable than the other approaches to define the exact answers derived in this research. The technique can be significant for further examining distinct conformable PDEs in high energy physics, mathematical physics, quantum gravity, and numerous nonlinear physics branches. It is obvious that the technique we suggest is successful, dependable, and easy to use, and that it provides enough well-matched answers for NLFPDEs that emerge in engineering, applied mathematics, and mathematical physics.

Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image
Details are in the caption following the image

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Data Availability

The data used to support the findings of this study are included within the article.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.