Let G be a simple connected graph. The second Gourava index of graph G is defined as GO₂(G) = ∑_θϑ∈E(G)(d(θ) + d(ϑ))d(θ)d(ϑ) where d(θ) denotes the degree of vertex θ. If removal of a vertex of G forms a tree, then G is called an apex tree. Let L ⊂ V(G) with ∣L | = q. If removal of L from V(G) forms a tree and any other subset of V(G) whose cardinality is less than ∣L∣ does not form a tree, then G is known as q-apex tree. In this paper, we have calculated upper bound for 2^nd Gourava index with respect to q-apex trees.

1. Introduction

Topological index is basic tool in chemical modeling. In molecular graph, atoms are considered as vertices and chemical bonds as edges. Short graph is a combination of vertices and edges. First topological index was Wiener index introduced by Wiener in 1947 to compare the boiling points of few alkane isomers. He observed that this index is highly correlated with the boiling point of alkanes. Later study on QSAR manifested that this index is also helpful to correlate with other quantities like density, critical point, and surface tension. The mathematical formula of this index is

(1)

where d_G(θ, ϑ) denotes the distance between the vertices θ and ϑ in G. The detailed study about this invariant is given in [1]. Among degree-based topological indices, the most studied indices are first Zagreb index and second Zagreb index [2]. The first Zagreb index is defined as the sum of square of degrees of all the vertices of a graph, where in second Zagreb index, we take the sum of product of degrees of all those vertices of graph which are linked by an edge. For more information about these chemical invariants, see [3]. The first and second Gourava indices were presented by Kulli in 2017 [4]. These indices are defined as

(2)

(3)

A topological index is a numerical number associated with a molecular graph which has significant applications in chemical graph theory, because it is used as a molecular descriptor to investigate physical as well as chemical properties of chemical structure. Therefore, it is a powerful technique in avoiding high cost and long-term laboratory experiments. There are more than 3,000 topological invariants registered till now. Most of these indices have their applications in chemical graph theory. In these molecular descriptors, Gourava and hyper-Gourava invariants are used to find out the physical and chemical properties (such as entropy, acentric factor, and DHAVP) of octane isomers. The first and second Gourava invariants are highly correlated with entropy and acentric factors, respectively.

All graphs considered in our study are simple and connected. Let G be a simple graph with vertex set V and edge set E. For a graph G, the degree of a vertex θ is defined as the number of edges attached to it. The smallest degree of a vertex in G is denoted by δ(G). The vertex in a graph whose degree is one is known as pendent vertex. The neighborhood of a vertex θ is the set containing all nodes attached with θ, denoted by N(θ). There are two types of neighborhood, open neighborhood and closed neighborhood. If N(θ) includes all the other nodes except θ, then it is called open neighborhood but if it includes the node θ, then it is called closed neighborhood. Closed neighborhood of θ is defined as N[θ] = N(θ) ∪ θ. If we remove one vertex (say) θ from G, then the resulting graph is denoted by G − θ. If we remove subset (say) X^′ ⊂ V of vertex set of graph G, then the obtained graph is denoted by G − X^′. In molecular graph theory, an acyclic connected graph having order λ is known as tree and is denoted by . A tree with order λ is said to be star if central node has degree λ − 1 while all other nodes are pendent. In other way, a complete bipartite graph κ_1,λ−1 is called a star of order λ. Let G₁ and G₂ be two vertex disjoint graphs then their join is denoted by G₁ + G₂ having vertex set as a union of their vertex sets, and the edge set contains all the edges of G₁ and G₂ and all those edges obtained by linking each node of G₁ with each node of G₂.

Ali et al. [5] investigated second and third modified Zagreb invariants for T-sum graph operation. Using the obtained results, they computed the second and third modified Zagreb of certain well-known chemical structures like alkanes. Cao et al. [6] give an exact formulas for the upper bounds of modified first Zagreb connection index and second Zagreb connection index for several binary graph operations like corona, Cartesian, and lexicographic product. Using the obtained closed formulas, they computed these invariants for several well-known graphs. In [7], the Gourava index for several graph operations is presented.

In molecular graph theory, apex graphs play a significant role, which can be elucidated as if removal of single vertex or subset of vertex set from a graph G yields a planar graph, then the graph G is known as apex graph [8]. Embedding of apex graphs having face width three are characterized in [9]. By using the same idea, one can explain the apex and q-apex trees. If we remove a vertex from G and the resulting graph is a tree, then that G is called an apex tree [10]. Similarly, if we remove a subset (say) X^′ of vertex set of cardinality q from G and it results in a tree, then G is known as q-apex tree, provided that the removal of any other subset of vertex set whose cardinality is less than q does not form a tree [10]. A tree is known as trivial apex tree or 0-apex tree.

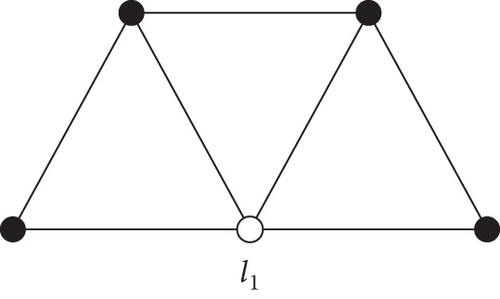
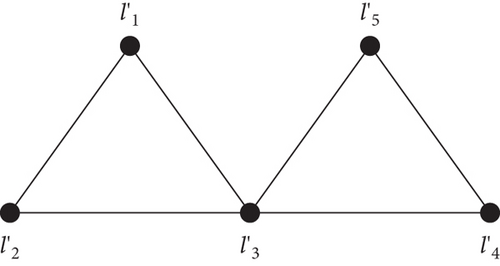
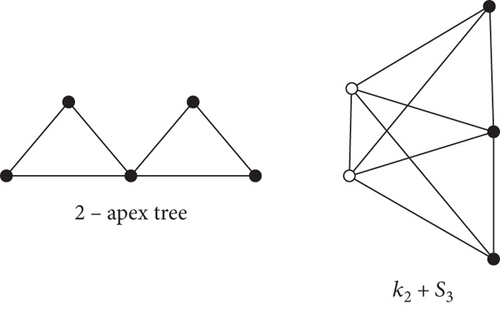
Therefore, a non-trivial apex tree is one which is not a tree itself but it can be converted into a tree by removing a single or number of vertices. In short, 1-apex tree is a graph which can be made a tree by removing single vertex as shown in Figure 1 (2-apex tree can be converted into a tree by removing 2 vertices as shown in Figure 2) and so on. In fact, apex trees are quasitrees which were introduced by Xu et al. [11]. Xu et al. [12] determined bounds on harary indices in case of apex trees. In 2018, Akhter et al. determined k-apex trees with extremal first reformulated Zagreb index [13].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

1-apex tree.

2. Upper Bound of GO₂ for q-Apex Trees

Let λ ≥ 3, q ≥ 1, and T^∗(λ), and denotes the set of all no-trivial apex trees and q-apex trees on λ vertices, respectively.

Lemma 1. Let T^∗ be a tree of order λ, and then

(4)

with equality holds if and only if T^∗ = S_λ.

Proof. Since T^∗ is a tree, it follows that for any edge θϑ ∈ E(T^∗), we have N(θ)∩N(ϑ) = ∅. Hence, . Now, using the value of in the definition of second Gourava index, we get

(5)

Example 2. Let BS (a, b) be bistar graph obtained by joining the apex vertices of two star graph K_1,a and K_1,b on different vertices with a, b ≥ 1, and S_λ,a be the graph obtained by joining a − 1 pendent edges to the end vertex of path P_λ−a+1. Figure 3 depicts the graphs of BS(4, 4) and , respectively. By definition of second Gourava index, we have . In Table 1, we have computed the second Gourava index of some classes of trees on 8 vertices. Observe that has the maximum value among all other trees.

Lemma 3. Let u^′, v^′ ∈ V(G) be two nonadjacent vertices of G, and then

(6)

Proof. By definition of GO₂(G), we have

(7)

Since d(u^′), d(v^′) > 0, it follows that GO₂(G + u^′v^′) > GO₂(G).

Lemma 4. Let G ∈ T^∗(λ) with maximum GO₂ value, and let x^′ ∈ V(G) be an apex vertex, and then

(8)

(9)

Proof.

(1)
Suppose δ(G) = 1 and y^′ is a leaf node in G, then x^′y^′ is not an edge in G and G + x^′y^′ ∈ T^∗(λ). Then, by Lemma 3, GO₂(G + x^′y^′) > GO₂(G) is a contradiction. Next, we prove that δ(G) > 2 is not possible. Suppose d(θ) ≥ 3 for all θ ∈ V(G), then for any θ ∈ V(G), the degree of all vertices in G − θ is greater or equal to two. This implies that G − θ is not a tree. Hence, δ(G) = 2.
(2)
Suppose d(x^′) < (λ − 1), then there exists a vertex y^′ ∈ V(G) with x^′y^′ ∉ EG. Now, G + x^′y^′ ∈ T^∗(λ) and GO₂(G + x^′y^′) > GO₂(G) are a contradiction. Hence, d(x^′) = (λ − 1).

Lemma 5. Let G₁ and G₂ be two graphs on disjoint vertex sets with ∣V(G₁) | = π₁, ∣V(G₂) | = π₂, ∣E(G₁) | = ϖ₁, and |E(G₂)| = ϖ₂. Then,

(10)

Proof. By definition of second Gourava index,

(11)

Now, using the definition of joint of two graphs having disjoint vertex sets, we get

(12)

Let

(13)

Now, using the fact the value of A₁ can be computed as

(14)

Similarly,

(15)

The value of C₁ can be calculated as

(16)

Now, using the values of A₁, B₁, and C₁ in Equation (2), we get

(17)

Theorem 6. Let G ∈ T^∗(λ) and λ ≥ 5, and then

(18)

with equality holds if G = κ₁ + S_λ−1.

Proof. Let G ∈ T^∗(λ) with maximum GO₂ value. By Lemma 4, we have . Let the cardinality of vertex sets of κ₁ and be ρ₁ and ρ₂ where cardinality of their edge sets is ς₁ and ς₂, respectively. Now by, using Lemma 1., we have

(19)

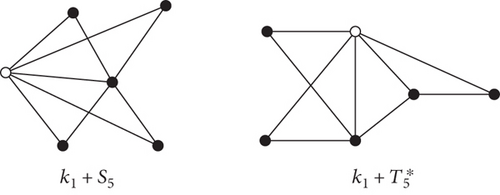
Example 7. Let G₁ = κ₁ + S₆₋₁, as depicted in Figure 4 and G₃ be 1 -apex tree of order 6 as shown in Figure 5. Then, the values of second Gourava index of these 1-apex trees are GO₂(G₁) = 810, GO₂(G₁) = 720, and GO₂(G₁) = 214. Table 2 depicts the values second Gourava index of some graphs in the class of 1-apex trees of order 8. Observe that GO₂ of κ₁ + S₇ is maximum among all other graphs.

Theorem 8. Let q ≥ 2, λ ≥ 5, and , and then

(20)

with equality holds if G = κ_q + S_λ−q

Proof. We prove it by induction the value of q. For q = 1, the result follows from Theorem 6. Suppose the result is true for q − 1 apex trees, let with maximum GO₂ and V_q ⊂ V(G) be the set of q-apex vertices. Since GO₂(G + u^′v^′) > GO₂(G) for any nonadjacent edges u^′, v^′ ∈ V(G), it follows that V_q is a clique in G. Hence, d(u^′) = λ − 1 for all u^′ ∈ V_q, and the number of edges m^′ of the graph G is

(21)

Let x^′ be an apex vertex and V_q−1 = V_q − x^′. Observe that d(x^′) = λ − 1 and G − x^′ are an (q − 1)-apex tree. Then,

(22)

(23)

Hence, we get

(24)

Since GO₂(G − x^′) = (q² − q)(λ − 1)³ + (λ − q − 1)(λ + q − 2)(q²λ − 2q) and for q ≥ 2,λ ≥ 5, we have

(25)

(26)

(27)

Using all the values in the above equation, we get

(28)

After simplification, we have

(29)

Example 9. Let G₁ and G₂ = κ₂ + S₅₋₂ be 2 -apex trees of order 5 as shown in Figure 6. Then, GO₂(G₁) = 224 and GO₂(G₂) = 888. Table 3 depicts the values of some 2 apex trees on 9 vertices. Observe that GO₂ value of κ₂ + S₇ is the maximum among all others.

Table 1. GO₂(T^∗) of certain trees T^∗ of order 8.

T^∗	GO₂(T^∗)
S₈	392
BS (5, 1)	312
BS (4, 2)	264
BS (3, 3)	248
S_8,5	212
S_8,4	146
S_8,3	108

Table 2. GO₂ value of some 1-apex trees of order 8.


κ₁ + S₇	2198
κ₁ + BS(4, 1)	1962
κ₁ + S_7,4	1758
κ₁ + S_7,3	1634
κ₁ + BS(3, 2)	1277

Table 3. GO₂ values of some 2-apex trees on 9 vertices.


κ₂ + S₇	7824
κ₂ + BS(4, 1)	7344
κ₂ + S_7,4	7108
κ₂ + S_7,3	6712
κ₂ + BS(3, 2)	6684

3. Conclusion

In our present discussion, we have determined the maximum value of second Gourava invariant for q-apex trees. In future, it would be interesting to find the same results for those chemical invariants which are not investigated till now.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 62172116) and the Guangzhou Academician and Expert Workstation (No. 20200115-9).

Open Research

Data Availability

No data is required to support the study.

References

1 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107, 20291038.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
2 Gutman I. and Das K. C., The first Zagreb index 30 years after, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 50, no. 1, 83–92.
CAS Google Scholar
3 Gutman I. and Trinajstić N., N. Graph theory and molecular orbitals. Total ϕ-electron energy of alternant hydrocarbons, Chemical physics letters. (1972) 17, no. 4, 535–538, https://doi.org/10.1016/0009-2614(72)85099-1, 2-s2.0-33845352210.
10.1016/0009-2614(72)85099-1
CAS Web of Science® Google Scholar
4 Kulli V. R., The Gourava indices and coindices of graphs, Annals of Pure and Applied Mathematics. (2017) 14, no. 1, 33–38.
10.22457/apam.v14n1a4
Google Scholar
5 Ali U., Javaid M., and Kashif A., Modified Zagreb connection indices of the T-sum graphs, Main Group Metal Chemistry. (2020) 43, no. 1, 43–55, https://doi.org/10.1515/mgmc-2020-0005.
10.1515/mgmc-2020-0005
CAS Web of Science® Google Scholar
6 Cao J., Ali U., Javaid M., and Huang C., Zagreb Connection Indices of Molecular Graphs Based on Operations, Complexity. (2020) 2020, 15, https://doi.org/10.1155/2020/7385682, 7385682.
10.1155/2020/7385682
Web of Science® Google Scholar
7 Kulli V. R., The Gourava index of four operations on graphs, Mathematical Combinatorics. (2018) 4, 65–67.
Google Scholar
8 Aigner-Horev E., Subdivisions in apex graphs, 2012, 82, no. 1, Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, https://doi.org/10.1007/s12188-012-0063-x, 2-s2.0-84861226664.
10.1007/s12188-012-0063-x
Google Scholar
9 Mohar B., Apex graphs with embeddings of face-width three, Discrete Mathematics. (1997) 176, no. 1-3, 203–210, https://doi.org/10.1016/S0012-365X(96)00363-9, 2-s2.0-0038980980.
10.1016/S0012-365X(96)00363-9
Web of Science® Google Scholar
10 Akhter N., Jamil M. K., and Tomescu I., Extremal First and Second Zagreb Indices of Apex Trees, 2016, 78, no. 4, Jangjeon Mathematical Society.
Google Scholar
11 Xu K., Wang J., and Liu H., The Harary index of ordinary and generalized quasi-tree graphs, Journal of Applied Mathematics and Computing. (2014) 45, no. 1-2, 365–374, https://doi.org/10.1007/s12190-013-0727-4, 2-s2.0-84900447177.
10.1007/s12190-013-0727-4
Google Scholar
12 Xu K., Wang J., Das K. C., and Klavžar S., Weighted Harary indices of apex trees and k-apex trees, Discrete Applied Mathematics. (2015) 189, 30–40, https://doi.org/10.1016/j.dam.2015.01.044, 2-s2.0-84929702778.
10.1016/j.dam.2015.01.044
Web of Science® Google Scholar
13 Akhter N., Naz S., and Jamil M. K., Extremal first reformulated Zagreb index ofk-apex trees, International journal of applied graph theory. (2018) 2, 29–41.
Google Scholar

Citing Literature

All articles

[Retracted] On Second Gourava Invariant for q-Apex Trees

Retraction(s) for this article

Retracted: On Second Gourava Invariant for q-Apex Trees

Abstract

1. Introduction

2. Upper Bound of GO₂ for q-Apex Trees

3. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] On Second Gourava Invariant for q-Apex Trees

Retraction(s) for this article

Retracted: On Second Gourava Invariant for q-Apex Trees

Abstract

1. Introduction

2. Upper Bound of GO2 for q-Apex Trees

3. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

2. Upper Bound of GO₂ for q-Apex Trees