In this work, we applied the fractional reduced differential transform method (FRDTM) to find the exact solutions of the three-dimensional fractional Helmholtz equation (FHE) and compared our outcomes with the tenth-order approximate solutions for diverse fractional orders. Different values of fractional derivatives are signified explicitly in three dimensions. Outcomes are denoted in the tables for nonfractional exact and approximate solutions and fractional approximate solutions for different fractional orders. Two examples are given to prove the proficiency of the suggested method, to resolve diverse categories of fractional partial differential equations.

1. Introduction

The Helmholtz equation is a second-order elliptic partial differential equation of potential theory that can be consequent from the wave equation. Typically we write it as

(1)

where ∇² is the Laplace operator and λ is the wavenumber. The Helmholtz equation is a generalization of Laplace’s equation, and when λ = 0, the Helmholtz equation is identical to Laplace’s equation.

In a 2D nonhomogeneous isotropic medium whose speed is c, the wave solution is ψ(x, y) corresponding to a harmonic source f(x, y) vibrating at a definite fixed frequency ω > 0 a suitable scalar Helmholtz equation on an assumed region W

(2)

where ψ(x, y) is a necessarily differentiable function on the boundary of W, and f(x, y) is a certain function, λ > 0 is a constant number, and

is the wavenumber, with wavelenght

[1].

If the Helmholtz equation models a physical reality, then it must have a unique solution. Helmholtz equation is essential for countless applications in real life. Some of them are as follows: it is used in seismology which is the scientific study of earthquakes and elastic waves, tsunamis, medical imaging, volcanic eruptions, and electromagnetism; in the science of optics, the Gibbs-Helmholtz equation is used in the calculation of changes in enthalpy using the change in Gibbs energy when the temperature is varied at constant pressure; and CHELS, a combined Helmholtz equation-least squares abbreviated as CHELS, this method is used for reconstructing acoustic radiation from an arbitrary object.

Abuasad et al. [2] established exact solutions for two-dimensional FHE using FRDTM. Ghaffar et al. [3] employed a higher-order compact difference (HOC) scheme with uniform mesh sizes in different coordinate directions to discretize a two- and three-dimensional Helmholtz equation. Gupta et al. [4] created the approximate analytical solutions of a multidimensional partial differential equation of Helmholtz equation with space fractional derivatives.

The three-dimensional Helmholtz equation has fascinated the attention of numerous researchers; for instance, Li [5] offered a fast singular boundary method (SBM) for the three-dimensional (3D) Helmholtz equation, Li et al. [6] presented a regularized approach for solving the near-boundary and boundary solutions for 3D Helmholtz equation with wideband wave numbers by the boundary collocation method, and Bespalov et al. [7] examined an adaptive boundary element method for the weakly singular and hypersingular integral equations for the 2D and 3D Helmholtz problem. Wang et al. [8] introduced a new finite difference scheme for solving the Helmholtz equation in polar and spherical coordinates. Qu et al. [9] presented a fast multipole accelerated singular boundary method (SBM) for the solution of the large-scale three-dimensional Helmholtz equation at low frequency.

Fractional derivative (FD) is a generalization of integer derivative, the FD generalizes the order of differentiation from integer to real or even to complex, and a series of phenomena can be defined by FD [10]. There is no doubt that fractional calculus has established an original mathematical method of solution for innumerable applications in diverse branches of sciences [11]. Fractional calculus has played an accurate central part in countless applications, e.g., mechanics, interaction, ecology, finances, and signal and image processing. The main subjects of fractional calculus contain anomalous diffusion, vibration, and control and continuous-time random walk [12]. Recently, several books [13–16] on fractional calculus were available, and in all of them, its history is addressed in one way or another. Podliubny [15] presented a review of several applications that have developed from fractional calculus; for instance, he indicated that the use of fractional derivatives for the mathematical modeling of viscoelastic materials is quite natural. Innumerable forms of fractional derivatives were considered: Riemann-Liouville, Caputo, Hadamard, Erdélyi-Kober, Grünwald-Letnikov, Marchaud, and Riesz are just samples. The greatest often used definitions for the common fractional differ-integral are the Grünwald-Letnikov definition, the Riemann-Liouville, and the Caputo definition. Various techniques were intended for explaining fractional differential equations, for instance, monotone iterative method [17], collocation method [18], auxiliary equation method [19], trapezoidal method [20], exponential rational function method [21], first integral method [22], homotopy analysis method [23], local fractional homotopy perturbation method [24], fractional variational iteration method [25], and modified Laplace decomposition method [26].

Vargas [27] presents a new meshless technique for solving a class of fractional differential equations based on moving least squares. Hashim et al. [28] study a class of second-order delay fractional differential equations with a variable-order Caputo derivative. Alesemi et al. [29] applied a new iterative transform technique and homotopy perturbation transform method to calculate the fractional-order Cauchy-reaction diffusion equation solution. Alesemi et al. [30] presented an HPTM and a VITM for studying the fractional-order nonlinear system of the unsteady flow of a polytropic gas. Iqbal et al. [31] investigated the numerical solution of the Fornberg-Whitham equations, involving fractional-order derivatives. Nonlaopon et al. [32] presented the Elzaki transform decomposition method to solve the time-fractional Swift–Hohenberg equations. Naeem et al. [33] used the new iterative transform method and the HPTM to solve fractional-order equal-width equations. Alshammari et al. [34] proposed residual power series (RPS) to find the numerical solution of a class of fractional Bagley--Torvik problems (FBTP) arising in a Newtonian fluid. Agarwal et al. [35] solved fractional-order parabolic equations using an innovative analytical technique.

In actual applications, due to inhomogeneity, nonlinearities, and general boundary conditions, exact solutions are remarkable in numerous divisions of solid mechanics, physics, motion, and fluid mechanics. Consequently, most scholars are satisfied with the approximate solutions to the problems facing them [36].

FRDTM was announced by Keskin and Oturanc [37] to generalize the reduced differential transform method (RDTM) from integer to fractional differential equations, which is a general method of differential transform method (DTM) to decrease the complexity and computations. FRDTM involves four core steps: first of all, we have to find the fractional reduced transformed function, then find the inverse of a fractional reduced transformed function, after that find the approximate solution, finally with the help of some special functions we try to find the exact solution. These four steps will be enlightened in detail in Section 3. Abuasad et al. [38] presented a novel modification called m-FRDTM to catch the solutions for MT-TFDEs.

Saravanan and Magesh [39] linked two analytical methods: FRDTM vs fractional variational iteration method (FVIM) to catch numerical solutions of the linear and nonlinear Fokker-Planck partial differential equations with space and time-fractional derivatives. Arshad et al. [40] presented a general form of FRDTM to solve wave-like problems, Zakharov–Kuznetsov equation, and couple BE. Abuasad et al. [41] obtained the exact and approximate solutions of higher-dimensional time-fractional diffusion equations using FRDTM.

The significance of this study is obtaining the exact solution for the 3D factional Helmholtz equation by a comparatively original technique and matching the exact solutions of non-FHE with the tenth-order approximate solutions for diverse values of the fractional derivatives. The different thing in this study is the description of FRDTM for three-dimensional FHE with modest and successive steps,; thus, this research can be used as a basic reference for researchers to understand this method and apply it in different applications to obtain exact and approximate solutions in very simple steps. This study is scheduled as providing simple definitions and properties of fractional calculus in Section 2. Section 3 presents the suggested method, while Section 4 offers the exact solutions of two examples of 3D FHE. We close the paper in Section 5 by main results.

2. Basic Definitions

2.1. Caputo Fractional Derivative

Assume that a ∈ ℝ and then the CFD

of order α ∈ ℝ⁺ is ([42])

(3)

for (n − 1 < α < n; x ≥ a), n ∈ ℕ. We represent the CFD as

3. FRDTM for 3 Variables

Now, let us give some basic properties of FRDTM [40, 43–45]. Consider a function of 3 variables f(x, y, z), such that

(4)

From the assets of DTM, and inspired by the components of the form

, we can describe the general solution function f(x, y, z) as an infinite linear combination of such components

(5)

where F(j, i₁, i₂) = m₁(j)m₁(i₁)m₂(i₂) is the spectrum of f(x, y, z).

Furthermore, the lowercase f(x, y, z) represents the original function, though its fractional reduced transformed function is denoted by the uppercase F_k(y, z), which is termed the T function. Let f(x, y, z) be analytical and continuously differentiable with respect to 3 variables x, y, and z in the domain of attention, and then, the FRDTM in 3 dimensions of f(x, y, z) is

(6)

where k = 0, 1, 2, ⋯.

The inverse FRDTM of F_k(y, z) is

(7)

From (6) and (7), we have

(8)

In particular, for x₀ = 0, the above equation becomes

(9)

The inverse transformation of the set of values

provides an approximate solution as

(10)

and n is the order of the approximate solution. Then, the exact solution is

(11)

Table 1 represents selected properties of FRDTM, the proofs of these properties can be found in [40, 46–48], wherever δ(a − b) is

(12)

where f = f(x, y, z), u = u(x, y, z), F_k = F_k(y, z), and U_k = U_k(y, z).

Table 1. Properties of FRDTM for 3 variables.

Original function	T-function
1. f = c₁u ± c₂v	F_αk = c₁U_αk ± c₂V_αk
2. f = uv
3.	F_αk = (Γ(α(k + m) + 1)/Γ(kα + 1))U_{α(k + m)}
4.	, i = 1, 2, ⋯, n
5.	, i = 1, 2, ⋯, n
6.	, i = 1, 2, ⋯, n

4. Computational Illustrations

To show the efficiency of this method, we consider two homogeneous fractional 3D-Helmholtz equations subject to appropriate initial conditions (I.C.). We can find the exact solutions with the help of some special functions. The exact and approximate solutions for fractional and nonfractional 3D-Helmholtz equations are represented numerically and graphically for different values of the fractional order (α) to show the importance and effectiveness of the proposed method.

4.1. First Application

Let us study this 3D FHE

(13)

and 1 < α ≤ 2, subject to the I.C.

(14)

By the rules from Table 1 to Eq. (13), we can find the recurrence relation:

(15)

where k = 0, 1, 2, ⋯.

By (15), we find the inverse transform coefficients of x^kα as

(16)

Similarly, the differential inverse transform of

gives the series solution

(17)

and in compact form, we write the series as

(18)

By the Mittag-Leffler function (M-L), we can catch the exact solution of Eq. (13) with respect to I.C. (14)

(19)

such that 1 < α ≤ 2, E_α(x) is the M-L function. If α = 2, then

(20)

Then, the exact solution of nonfractional differential equation for Eq. (13); (α = 2) with respect to the I.C. (14) is

(21)

The tenth-order approximate solution is given by:

(22)

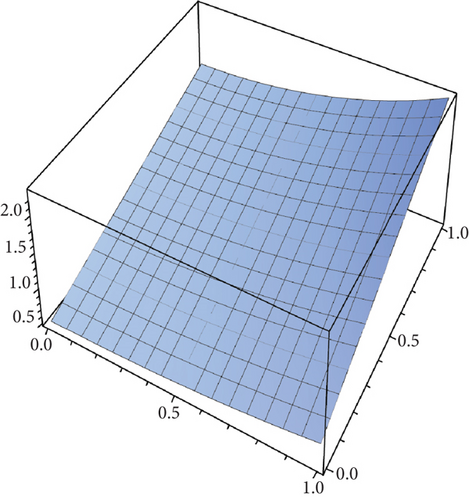
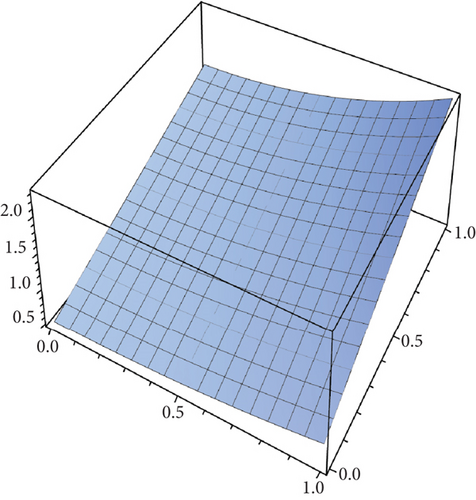
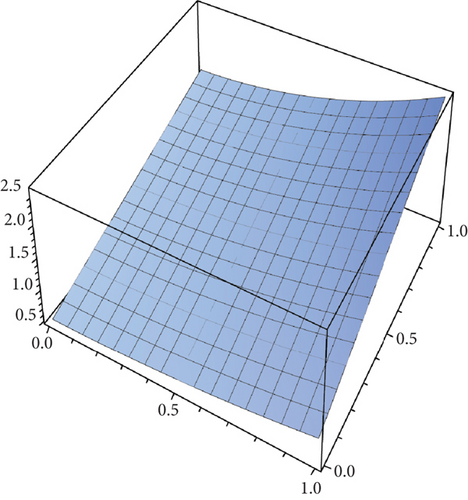
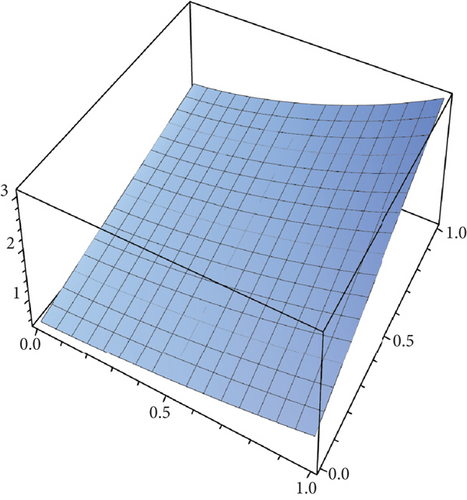
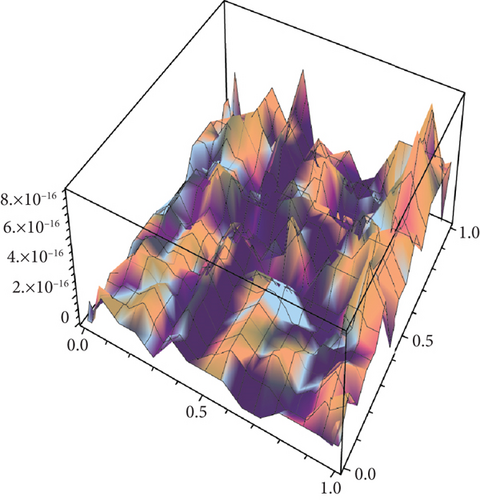
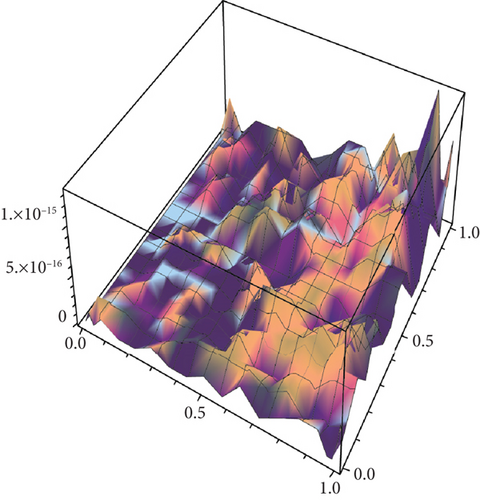
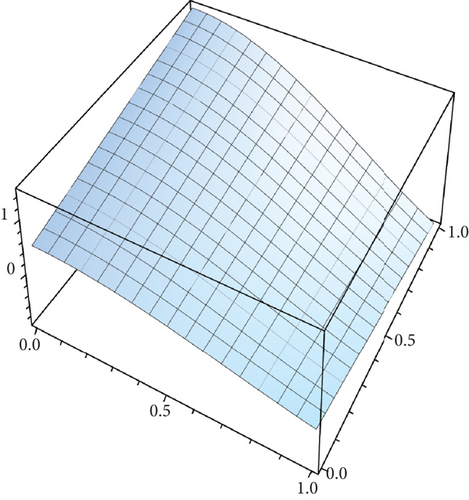
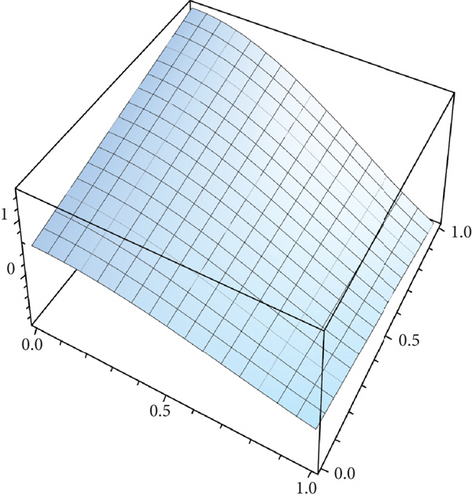
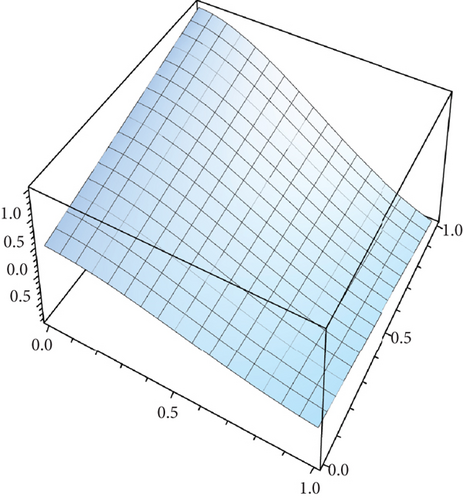
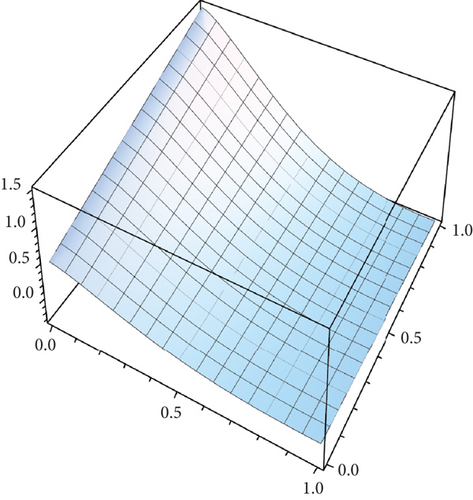
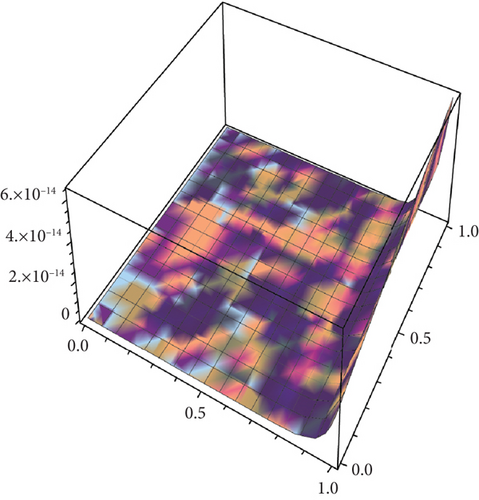
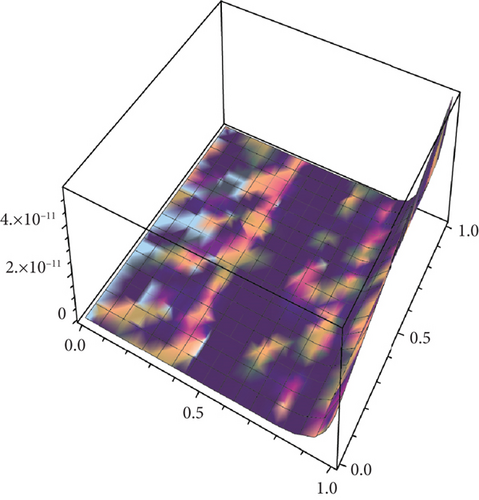
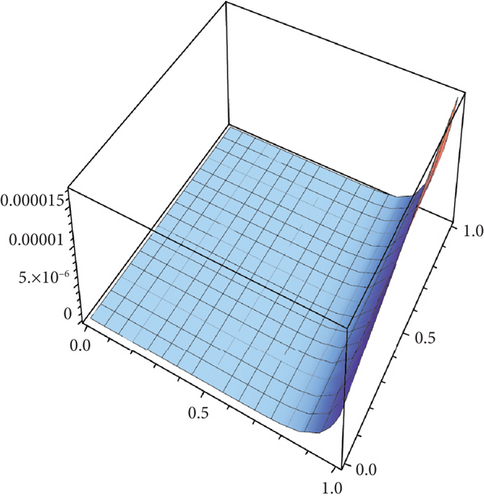
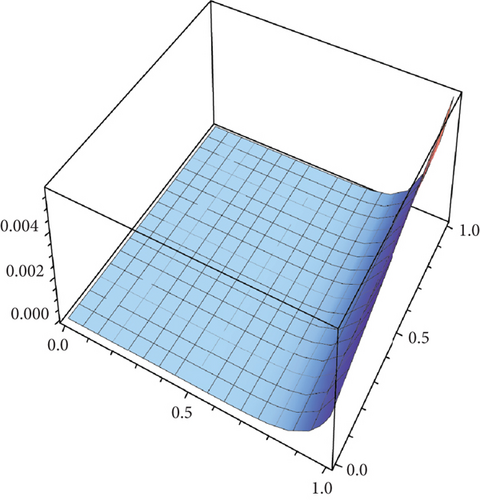
Table 2 presents the numerical solutions for u₁₀(x, y, z) by FRDTM at different values of α and a comparison of absolute errors at α = 2 for FRDTM between exact solution and tenth-order approximate solution. Figure 1 depicts the three-dimensional exact and the tenth-order approximate solution of FRDTM for nonfractional order (α = 2), while Figure 2 depicts the approximate solutions of FRDTM for α = 1.8 and α = 1.4. Figures 3 and 4 depict the absolute error between the exact solution and tenth-order approximate solutions for different values of α; we note that the absolute error between the tenth-order approximate solutions and the exact solution becomes small as alpha becomes large: approximately less than 4 × 10⁻⁸ when α = 1 and less than 8 × 10⁻¹⁶ when α = 2.

Table 2. Exact solution of nonfractional order and tenth-order approximate solutions of FRDTM.

x	Nonfractional order (α = 2)				Fractional order
x	z	u_Exact	u₁₀	\|u_Exact − u₁₀\|	α = 1.6	α = 1.4	α = 1.2
0.2	0.2	0.714047	0.714047	0	0.737811	0.760876	0.797191
	0.5	0.789338	0.789338	1.11022e − 16	0.87164	0.936162	1.02565
	0.8	0.936204	0.936204	1.11022e − 16	1.08973	1.20119	1.35002

0.5	0.2	1.02007	1.02007	0	1.05402	1.08697	1.13884
	0.5	1.12763	1.12763	0	1.2452	1.33737	1.46522
	0.8	1.33743	1.33743	0	1.55675	1.71599	1.9286

0.8	0.2	1.32609	1.32609	2.22045e − 16	1.37022	1.41306	1.4805
	0.5	1.46591	1.46591	0	1.61876	1.73859	1.90478
	0.8	1.73867	1.73867	2.22045e − 16	2.02378	2.23079	2.50718

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The FRDTM solutions u(x, y, z): (a) nonfractional exact α = 2 and (b) nonfractional tenth-order approximate α = 2.

4.2. Second Application

Let us study this 3D FHE, with x-space fractional derivative:

(23)

1 < α ≤ 2, subject to the I.C.

(24)

By using the rules from Table 1 to Eq. (23), we find the recurrence relation

(25)

where k = 0, 1, 2, ⋯.

From (25), we can find the inverse transform coefficients of x^kα as

(26)

In the similar way, the differential inverse transform of

gives the series solution

(27)

In compact form, we write the series as

(28)

The exact solution of Eq. (23) with respect to the I.C. (24):

(29)

1 < α ≤ 2. If α = 2,

(30)

Now, the exact solution of nonfractional differential equation (α = 2) for Eq. (23) subject to (24) is

(31)

The 10 − th order approximate solution is given by:

(32)

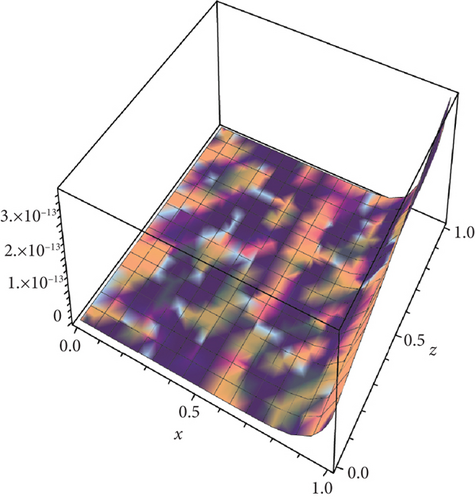
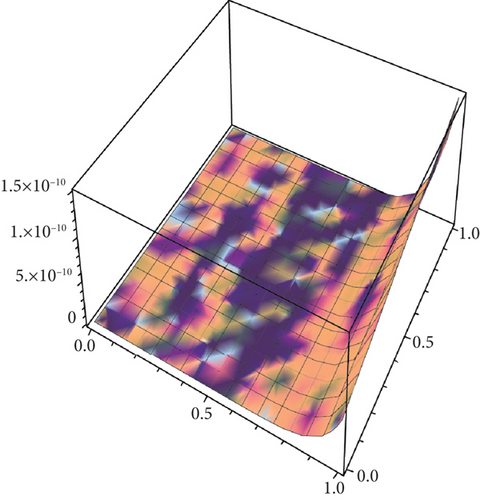
Table 3 shows the numerical solutions for u₁₀(x, y, z) by FRDTM at different values of α and a comparison of absolute errors at α = 2 for FRDTM between the exact solution and tenth-order approximate solution. Figure 5 depicts the three-dimensional exact and the tenth-order approximate solution of FRDTM for nonfractional order (α = 2). Figure 6 represents the approximate solutions of FRDTM for α = 1.8 and α = 1.4. Figures 7 and 8 depict the absolute error between the exact solution and tenth-order approximate solutions for different values of α; we note that the absolute error between the tenth-order approximate solutions and the exact solution becomes small as alpha becomes large: approximately less than 4 × 10⁻⁸ when α = 1 and less than 8 × 10⁻¹⁶ when α = 2.

Table 3. Exact solution of nonfractional order and tenth-order approximate solutions by FRDTM.

x	Nonfractional order (α = 2)				Fractional order
x	z	u_Exact	u₁₀	\|u_Exact − u₁₀\|	α = 1.8	α = 1.4	α = 1.2
0.2	0.2	0.631159	0.631159	0	0.588705	0.442158	0.345033
	0.5	0.306216	0.306216	5.55112e − 17	0.200098	0.0445607	0.0345265
	0.8	-0.151434	-0.151434	2.77556e − 16	-0.209474	-0.130004	-0.0476061

0.5	0.2	0.901656	0.901656	0	0.841007	0.631655	0.492904
	0.5	0.437451	0.437451	5.55112e − 17	0.285854	0.0636582	0.0493236
	0.8	-0.216334	-0.216334	0	-0.299248	-0.18572	-0.0680088

0.8	0.2	1.17215	1.17215	0	1.09331	0.821151	0.640775
	0.5	0.568687	0.568687	0	0.37161	0.0827556	0.0641206
	0.8	-0.281234	-0.281234	5.55112e − 16	-0.389023	-0.241436	-0.0884114

5. Conclusion

In brief, the exact solution of the 3D FHE has been established via FRDTM. In the introduction, the definition of the Helmholtz equation and its most vital applications in science were offered. After that, the fractional derivatives were discussed, and the most essential research and methods used to solve the fractional differential equations are presented. Then, the significance of the research and its features was debated. The method for three variables was submitted in a simplified manner, and then, this method was applied to two homogeneous 3D-FHE subjects to proposed initial conditions.

This method is a very effective approach for resolving diverse categories of fractional partial differential equations in different dimensions and finding exact solutions not only approximate solutions gives this method a significant advantage over other methods of solving fractional differential equations.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors would like to thank the Deanship of Scientific Research, the University of Ha’il for supporting this work. This work has been supported by Scientific Research Deanship at the University of Ha’il-Ha’il, Saudi Arabia, through project number BA-2124.

Open Research

Data Availability

The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.

References

1 Abuasad S., Yildirim A., Hashim I., Abdul Karim S. A., and Gómez-Aguilar J., Fractional multi-step differential transformed method for approximating a fractional stochastic SIS epidemic model with imperfect vaccination, International Journal of Environmental Research and Public Health. (2019) 16, no. 6, 973–988, https://doi.org/10.3390/ijerph16060973, 2-s2.0-85063254434, 30889889.
10.3390/ijerph16060973
PubMed Web of Science® Google Scholar
2 Abuasad S., Moaddy K., and Hashim I., Analytical treatment of two-dimensional fractional Helmholtz equations, Journal of King Saud University - Science. (2019) 31, no. 4, 659–666, https://doi.org/10.1016/j.jksus.2018.02.002, 2-s2.0-85042907238.
10.1016/j.jksus.2018.02.002
Web of Science® Google Scholar
3 Ghaffar F., Badshah N., and Islam S., Multigrid method for solution of 3d helmholtz equation based on hoc schemes, Abstract and Applied Analysis. (2014) 2014, 14, 954658, https://doi.org/10.1155/2014/954658, 2-s2.0-84934954160.
10.1155/2014/954658
Google Scholar
4 Gupta P. K., Yildirim A., and Rai K., Application of he’s homotopy perturbation method for multi-dimensional fractional helmholtz equation, International Journal of Numerical Methods for Heat & Fluid Flow. (2012) 22, no. 4, 424–435, https://doi.org/10.1108/09615531211215738, 2-s2.0-84862079256.
10.1108/09615531211215738
Web of Science® Google Scholar
5 Li W., A fast singular boundary method for 3d helmholtz equation, Computers & Mathematics with Applications. (2019) 77, no. 2, 525–535, https://doi.org/10.1016/j.camwa.2018.09.055, 2-s2.0-85054831892.
10.1016/j.camwa.2018.09.055
Web of Science® Google Scholar
6 Li J., Chen W., Fu Z., and Qin Q.-H., A regularized approach evaluating the near-boundary and boundary solutions for three-dimensional helmholtz equation with wideband wavenumbers, Applied Mathematics Letters. (2019) 91, 55–60, https://doi.org/10.1016/j.aml.2018.11.027, 2-s2.0-85058152739.
10.1016/j.aml.2018.11.027
Web of Science® Google Scholar
7 Bespalov A., Betcke T., Haberl A., and Praetorius D., Adaptive bem with optimal convergence rates for the helmholtz equation, Computer Methods in Applied Mechanics and Engineering. (2019) 346, 260–287, https://doi.org/10.1016/j.cma.2018.12.006, 2-s2.0-85058778319.
10.1016/j.cma.2018.12.006
Web of Science® Google Scholar
8 Wang K., Wong Y. S., and Deng J., Efficient and accurate numerical solutions for helmholtz equation in polar and spherical coordinates, Communications in Computational Physics. (2015) 17, no. 3, 779–807, https://doi.org/10.4208/cicp.110214.101014a, 2-s2.0-84961358316.
10.4208/cicp.110214.101014a
Web of Science® Google Scholar
9 Qu W., Chen W., and Gu Y., Fast multipole accelerated singular boundary method for the 3d helmholtz equation in low frequency regime, Computers & Mathematics with Applications. (2015) 70, no. 4, 679–690, https://doi.org/10.1016/j.camwa.2015.05.017, 2-s2.0-84937725720.
10.1016/j.camwa.2015.05.017
Web of Science® Google Scholar
10 Milici C., Draganescu G., and Machado J. T., Introduction to Fractional Differential Equations vol. 25, 2018, Springer, Switzerland.
Google Scholar
11 Debnath L., Recent applications of fractional calculus to science and engineering, International Journal of Mathematics and Mathematical Sciences. (2003) 54, 3442, https://doi.org/10.1155/S0161171203301486, 2-s2.0-17844372193.
10.1155/S0161171203301486
Google Scholar
12 Atangana A. and Secer A., A note on fractional order derivatives and table of fractional derivatives of some special functions, Abstract and Applied Analysis. (2013) 2013, 8, 279681, https://doi.org/10.1155/2013/279681, 2-s2.0-84877246956.
10.1155/2013/279681
Google Scholar
13 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, Wiley-Interscience, New York.
Google Scholar
14 Oldham K. and Spanier J., The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order, 1974, Academic Press, New York.
Google Scholar
15 Podlubny I., Fractional Differential Equations, 1999, Mathematics in Science and Engineering. Academic Press, San Diego, CA.
Web of Science® Google Scholar
16 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Gordon and Breach Science Publishers, Yverdon.
Google Scholar
17 Bai Z., Zhang S., Sun S., and Yin C., Monotone iterative method for fractional differential equations, Electronic Journal of Differential Equations. (2016) 6, no. 8.
Google Scholar
18 Baleanu D. and Shiri B., Collocation methods for fractional differential equations involving non-singular kernel, Chaos, Solitons & Fractals. (2018) 116, 136–145, https://doi.org/10.1016/j.chaos.2018.09.020, 2-s2.0-85053805425.
10.1016/j.chaos.2018.09.020
Web of Science® Google Scholar
19 Akbulut A. and Kaplan M., Auxiliary equation method for time-fractional differential equations with conformable derivative, Computers & Mathematics with Applications. (2018) 75, no. 3, 876–882, https://doi.org/10.1016/j.camwa.2017.10.016, 2-s2.0-85032929721.
10.1016/j.camwa.2017.10.016
Web of Science® Google Scholar
20 Garrappa R., Trapezoidal methods for fractional differential equations: theoretical and computational aspects, Mathematics and Computers in Simulation. (2015) 110, 96–112, https://doi.org/10.1016/j.matcom.2013.09.012, 2-s2.0-84929320761.
10.1016/j.matcom.2013.09.012
Web of Science® Google Scholar
21 Aksoy E., Kaplan M., and Bekir A., Exponential rational function method for space–time fractional differential equations, Waves in Random and Complex Media. (2016) 26, no. 2, 142–151, https://doi.org/10.1080/17455030.2015.1125037, 2-s2.0-84953775311.
10.1080/17455030.2015.1125037
Web of Science® Google Scholar
22 Bekir A., Güner Ö., and Ünsal Ö., The first integral method for exact solutions of nonlinear fractional differential equations, Journal of Computational and Nonlinear Dynamics. (2015) 10, no. 2, https://doi.org/10.1115/1.4028065, 2-s2.0-84940489366.
10.1115/1.4028065
Web of Science® Google Scholar
23 Demir A., Bayrak M. A., and Ozbilge E., A new approach for the approximate analytical solution of space-time fractional differential equations by the homotopy analysis method, Adv. Math. Phys.(2019) 2019, 1–12, https://doi.org/10.1155/2019/5602565, 2-s2.0-85066029023.
10.1155/2019/5602565
Web of Science® Google Scholar
24 Yang X.-J., Srivastava H., and Cattani C., Local fractional homotopy perturbation method for solving fractal partial differential equations arising in mathematical physics, Romanian Reports in Physics. (2015) 67, no. 3, 752–761.
Web of Science® Google Scholar
25 Prakash A., Goyal M., and Gupta S., Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation, Nonlinear Engineering. (2019) 8, no. 1, 164–171, https://doi.org/10.1515/nleng-2018-0001, 2-s2.0-85049516170.
10.1515/nleng-2018-0001
Google Scholar
26 Hamoud A. A. and Ghadle K. P., Modified Laplace decomposition method for fractional Volterra-Fredholm integro-differential equations, Journal of Mathematical Modeling. (2018) 6, no. 1, 91–104.
Google Scholar
27 Vargas A. M., Finite difference method for solving fractional differential equations at irregular meshes, Mathematics and Computers in Simulation. (2022) 193, 204–216, https://doi.org/10.1016/j.matcom.2021.10.010.
10.1016/j.matcom.2021.10.010
Web of Science® Google Scholar
28 Hashim I., Sharadga M., Syam M., and Al-Refai M., A reliable approach for solving delay fractional differential equations, Fractal and Fractional. (2022) 6, no. 2, https://doi.org/10.3390/fractalfract6020124.
10.3390/fractalfract6020124
Google Scholar
29 Alesemi M., Iqbal N., and Abdo M. S., Novel investigation of fractional-order Cauchy-reaction diffusion equation involving Caputo-Fabrizio operator, Journal of Function Spaces. (2022) 2022, 14, https://doi.org/10.1155/2022/4284060.
10.1155/2022/4284060
Web of Science® Google Scholar
30 Alesemi M., Iqbal N., and Abdo M. S., Novel analysis of the fractional-order system of non-linear partial differential equations with the exponential-decay kernel, Mathematics. (2022) 10, no. 4, https://doi.org/10.3390/math10040615.
10.3390/math10040615
Web of Science® Google Scholar
31 Iqbal N., Yasmin H., Ali A., Bariq A., Al-Sawalha M. M., and Mohammed W. W., Numerical methods for fractional-order Fornberg-Whitham equations in the sense of Atangana-Baleanu derivative, Journal of Function Spaces. (2021) 2021, 10, https://doi.org/10.1155/2021/2197247.
10.1155/2021/2197247
Web of Science® Google Scholar
32 Nonlaopon K., Alsharif A. M., Zidan A. M., Khan A., Hamed Y. S., and Shah R., Numerical investigation of fractional-order Swift–Hohenberg equations via a novel transform, Symmetry. (2021) 13, no. 7, https://doi.org/10.3390/sym13071263.
10.3390/sym13071263
Web of Science® Google Scholar
33 Naeem M., Zidan A. M., Nonlaopon K., Syam M. I., Al-Zhour Z., and Shah R., A new analysis of fractional-order equal-width equations via novel techniques, Symmetry. (2021) 13, no. 5, https://doi.org/10.3390/sym13050886.
10.3390/sym13050886
Web of Science® Google Scholar
34 Alshammari S., Al-Smadi M., Hashim I., and Alias M. A., Residual power series technique for simulating fractional bagley-torvik problems emerging in applied physics, Applied Sciences. (2019) 9, no. 23, https://doi.org/10.3390/app9235029.
10.3390/app9235029
Google Scholar
35 Agarwal R. P., Mofarreh F., Shah R., Luangboon W., and Nonlaopon K., An analytical technique, based on natural transform to solve fractional-order parabolic equations, Entropy. (2021) 23, no. 8, https://doi.org/10.3390/e23081086, 34441226.
10.3390/e23081086
PubMed Web of Science® Google Scholar
36 Nayfeh A. H., Introduction to Perturbation Techniques, 2011, John Wiley & Sons, New York.
Google Scholar
37 Keskin Y. and Oturanc G., The reduced differential transform method: a new approach to fractional partial differential equations, Nonlinear science letters. A. (2010) 1, no. 2, 207–217.
Google Scholar
38 Abuasad S., Hashim I., and Abdul Karim S. A., Modified fractional reduced differential transform method for the solution of multiterm time-fractional diffusion equations, Adv. Math. Phys.(2019) 2019, article 5703916, 14, https://doi.org/10.1155/2019/5703916, 2-s2.0-85066055597.
10.1155/2019/5703916
Web of Science® Google Scholar
39 Saravanan A. and Magesh N., An efficient computational technique for solving the Fokker-Planck equation with space and time fractional derivatives, Journal of King Saud University - Science. (2016) 28, no. 2, 160–166, https://doi.org/10.1016/j.jksus.2015.01.003, 2-s2.0-84925262965.
10.1016/j.jksus.2015.01.003
Web of Science® Google Scholar
40 Arshad M., Lu D., and Wang J., ( N +1)-dimensional fractional reduced differential transform method for fractional order partial differential equations, Communications in nonlinear science and numerical simulation. (2017) 48, 509–519, https://doi.org/10.1016/j.cnsns.2017.01.018, 2-s2.0-85010403524.
10.1016/j.cnsns.2017.01.018
Web of Science® Google Scholar
41 Abuasad S., Alshammari S., Al-rabtah A., and Hashim I., Solving a higher-dimensional time-fractional diffusion equation via the fractional reduced differential transform method, Fractal and Fractional. (2021) 5, no. 4, https://doi.org/10.3390/fractalfract5040168.
10.3390/fractalfract5040168
PubMed Web of Science® Google Scholar
42 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, North Holland Mathematics Studies. Elsevier, Holland.
10.1016/S0304-0208(06)80001-0
Google Scholar
43 Singh B. K. and Srivastava V. K., Approximate series solution of multi-dimensional, time fractional-order (heat-like) diffusion equations using FRDTM, Royal Society Open Science. (2015) 2, no. 4, 140511–140524, https://doi.org/10.1098/rsos.140511, 2-s2.0-84958068891, 26064639.
10.1098/rsos.140511
PubMed Web of Science® Google Scholar
44 Srivastava V. K., Kumar S., Awasthi M. K., and Singh B. K., Two-dimensional time fractional-order biological population model and its analytical solution, Egyptian Journal of Basic and Applied Sciences. (2014) 1, no. 1, 71–76, https://doi.org/10.1016/j.ejbas.2014.03.001.
10.1016/j.ejbas.2014.03.001
Google Scholar
45 Mukhtar S., Abuasad S., Hashim I., and Abdul Karim S. A., Effective method for solving different types of nonlinear fractional burgers’ equations, Mathematics. (2020) 8, no. 5, https://doi.org/10.3390/math8050729.
10.3390/math8050729
Web of Science® Google Scholar
46 Abazari R. and Ganji M., Extended two-dimensional DTM and its application on nonlinear PDEs with proportional delay, International Journal of Computational Methods. (2011) 88, no. 8, 1749–1762.
Google Scholar
47 Lu D., Wang J., Arshad M., and Ali A., Fractional reduced differential transform method for space-time fractional order heat-like and wave-like partial differential equations, Journal of Advances in Physics. (2017) 6, no. 4, 598–607, https://doi.org/10.1166/jap.2017.1383.
10.1166/jap.2017.1383
Google Scholar
48 Yu J., Jing J., Sun Y., and Wu S., (n+1)-Dimensional reduced differential transform method for solving partial differential equations, Applied Mathematics and Computation. (2016) 273, 697–705, https://doi.org/10.1016/j.amc.2015.10.016, 2-s2.0-84946426878.
10.1016/j.amc.2015.10.016
Web of Science® Google Scholar

Citing Literature

All articles

Exact Solutions of the 3D Fractional Helmholtz Equation by Fractional Differential Transform Method

Abstract

1. Introduction